Identifying limits of linear control design validity in nonlinear systems: a continuation-based approach

Abstract

It is well known that a linear-based controller is only valid near the point from which the linearised system is obtained. The question remains as to how far one can move away from that point before the linear and nonlinear responses differ significantly, resulting in the controller failing to achieve the desired performance. In this paper, we propose a method to quantify these differences. By appending a harmonic oscillator to the equations of motion, the frequency responses at different operating points of a nonlinear system can be generated using numerical continuation. In the presence of strong nonlinearities, subtle differences exist between the linear and nonlinear frequency responses, and these variations are also reflected in the step responses. A systematic way of comparing the discrepancies between the linear and the nonlinear frequency responses is presented, which can determine whether the controller performs as predicted by linear-based design. We demonstrate the method on a simple fixed-gain Duffing system and a gain-scheduled reduced-order aircraft model with a manoeuvre-demand controller; the latter presents a case where strong nonlinearities exist in the form of multiple attractors. The analysis is then expanded to include actuator rate saturation, which creates a limit-cycle isola, coexisting multiple solutions (corresponding to the so-called flying qualities cliff), and chaotic motions. The proposed method can infer the influence of these additional attractors even when there is no systematic way to detect them. Finally, when severe rate saturation is present, reducing the controller gains can mitigate—but not eliminate—the risk of limit-cycle oscillation.

1 Introduction

Linear controllers are in widespread use in engineering applications and are well understood. By definition, the controller is designed on a linear plant, which is obtained by linearising the nonlinear system of interest at an operating point. Despite its advantage of providing closed-form solutions, the trade-off is that the nonlinear elements of the plant have to be omitted. Even when gains are scheduled with state variables or parameters, this is typically implemented in a relatively coarse manner. Thus, a linear-based design approach can potentially overlook many important characteristics that only manifest themselves when the controller is tested on the full nonlinear plant using time simulation and displays unsatisfactory performances. On the other hand, true nonlinear controllers have not seen widespread use, one of the reasons being that closed-form solutions do not exist in most cases. Even in cases where the closed-form solutions can be obtained, the process is often too mathematically demanding to justify the approach.

Researchers have proposed bridging this gap by incorporating bifurcation theory into the analysis. The most important benefit of this approach is that the nonlinear elements can be captured, unlike in the linear-based analysis. In weakly nonlinear systems where closed-form solutions exist, the influence of the controller gains on the system’s nonlinearities (represented as bifurcations) can be directly assessed as seen in [1,2,3]. Specifically, in [1, 2], three-dimensional region of controller gains (proportional, integral, and derivative) that guarantees no bifurcation in the closed-loop response were determined. This is especially important in [2], which uses the controller to regulate anaesthesia doses in a patient model and has found that outside the bifurcation-free region, chaotic behaviours can occur. [3] also shows that a PID controller is effective in controlling chaotic behaviour in an epidemiological model by choosing the gains inside the bifurcation-free region. Although the analysis in [3] is mathematically correct, [4] shows that in practice, small variations in the system parameters can lead to large changes in the size of the bifurcation-free region, especially in systems where chaotic behaviour is observed, and it was argued that such an approach is not practical in the presence of model uncertainty.

In more complex examples where closed-form solutions do not exist, such as in flight dynamics applications that utilise both tabular data for the plant and (linear) gain-scheduling method for the controller, bifurcation analysis can be implemented via the numerical continuation technique [5]. This is a powerful method that can identify regions where the controller fails to keep the aircraft stable [6] or track the reference signal [7] as predicted using linear-based design. However, although bifurcation analysis is effective in determining regions of instability (i.e. locating the bifurcations), it cannot assess the performance within the stable regions. This shortcoming can be especially problematic when the underlying nonlinearities are still strong but do not manifest themselves in the form of a bifurcation [8]. In most cases, performance is assessed via either nonlinear time simulation, which can be time consuming if the operating region is wide and is essentially ‘hit or miss’, or via assessing the linear closed-loop poles, which neglects the nonlinear elements. Therefore, the ability to extend bifurcation analysis to quantify the performance variation across different operating points can be valuable, especially in many applications where nonlinearities play a major role in their dynamics.

To develop this capability, this paper investigates the potential of extending bifurcation analysis to the frequency domain to gain further insight into the dynamics of a nonlinear system. This is done by appending a harmonic oscillator to the equations of motion, thereby turning the plant into a periodically forced nonlinear system. In flight dynamics, this approach has been applied in [9, 10] and although the aircraft considered was open loop, it was found that the dynamics was complex and could include period-2 and chaotic motions, none of which could have been captured using linear-based method. This paper will expand the study further by considering a linear gain-scheduled controller in an aircraft model to demonstrate that even in a bifurcation-free environment, the underlying nonlinearities can still manifest themselves in the closed-loop frequency response, and that this information can be utilised to provide an indication of when then linear controller may fail to perform as expected. The goal is to help the control designer decide on the extent to which a linearly designed controller can be trusted, or in other words, to identify regions in which the linear and nonlinear responses differ significantly.

2 Nonlinear frequency response analysis

The process to generate the frequency response of a nonlinear system using numerical continuation is described in this section. All analysis was done in MATLAB with numerical continuation carried out using the Dynamical Systems Toolbox [11], which is a MATLAB version of the software AUTO [12]. To illustrate the process, we will use the Duffing oscillator—a common example used to demonstrate the phenomena in a nonlinear forced system—which has the equation:

$$ \begin{array}{*{20}c} {\ddot{x} + c\dot{x} + kx + \alpha x^{3} = A\cos \left( {\omega t} \right)} \\ \end{array} $$

(1)

This equation describes a mass-spring-damper system with two springs: a linear one described by the term $kx$ and a nonlinear one where the restoring force $\alpha x^{3}$ is proportional to the cubic displacement. Numerical continuation requires the system to be time-invariant. Therefore, we rewrite Eq. (1) into a fourth-order system:

$$ \begin{array}{*{20}c} {\dot{x}_{1} = x_{2} } \\ \end{array} $$

(2)

$$ \begin{array}{*{20}c} {\dot{x}_{2} = - kx_{1} - cx_{2} - \alpha x_{1}^{3} + Ax_{4} } \\ \end{array} $$

(3)

$$ \begin{array}{*{20}c} {\dot{x}_{3} = x_{3} + \omega x_{4} - x_{3} \left( {x_{3}^{2} + x_{4}^{2} } \right)} \\ \end{array} $$

(4)

$$ \begin{array}{*{20}c} {\dot{x}_{4} = - \omega x_{3} + x_{4} - x_{4} \left( {x_{3}^{2} + x_{4}^{2} } \right)} \\ \end{array} $$

(5)

where $x_{1}$ and $x_{2}$ are the first and second derivatives of the displacement $x$, and $\dot{x}_{3}$ and $\dot{x}_{4}$ are used to generate the harmonic forcing term. It can be shown that $x_{3} = \sin \left( {\omega t} \right)$ and $x_{4} = {\text{cos}}\left( {\omega t} \right)$. The forcing term $A\cos \left( {\omega t} \right)$ now becomes $Ax_{4}$, as seen on the right-hand side of Eq. (3). Numerical continuation is then used to calculate the periodic solutions of the system as one of the system parameters (referred to as the continuation parameter) $\left[ {c,k,\alpha ,A,\omega } \right]$ varies. To generate the frequency response, we choose $\omega$ as the continuation parameter. The one-cycle response of every state for each value of $\omega$ is then found. For example, the solutions for Eq. (6) at $\omega$ = 1.2 and 0.27 rad/s are shown in Fig. 1.

$$ \begin{array}{*{20}c} {\ddot{x} + 0.3\dot{x} + 0.5x + x^{3} = 0.5\cos \left( {\omega t} \right) } \\ \end{array} $$

(6)

Fig. 1

Periodic solutions of Eq. (6) for $\omega$ = 1.2 rad/s (a) and 0.27 rad/s (b) generated using numerical continuation

From here, the gain and phase responses can be calculated using the following relationships:

$$ \begin{array}{*{20}c} {{\text{gain}}\;{\text{in}}\;{\text{dB = }}20 \log_{10} \left( {\frac{{Y_{3} - Y_{4} }}{{Y_{1} - Y_{2} }}} \right)} \\ \end{array} $$

(7)

$$ \begin{array}{*{20}c} {{\text{phase}}\;{\text{in}}\;{\text{degree}} = (X_{1} - X_{3} ) \times 360} \\ \end{array} $$

(8)

where $X_{i}$ and $Y_{i}$ refer to the x and y-coordinates of the point $i$ in Fig. 1. Specifically, points 1 and 3 are the peaks and points 2 and 4 are the troughs. It can be seen from Fig. 1b that when the response is nonlinear and contains additional harmonics, this definition of gain and phase can reflect the impact of the nonlinearity on the frequency response, which is shown as a phase jump at low frequencies in Fig. 2. A pair of fold bifurcations is also seen, as has been reported in the literature.

Fig. 2

Frequency response of Eq. (6)

The same approach can be applied to closed-loop systems—the main focus of this paper—which are discussed in the sections to follow.

3 Analysis of the Duffing oscillator with a fixed-gain controller

In this section, the proposed method is illustrated on the Duffing oscillator appended with a fixed-gain PID controller before moving on to a more complex gain-scheduled example in Sect. 4. The proposed analysis method exploits the concept that the more similar the linear and nonlinear frequency responses are, then the more similar their time-domain responses will be. This concept will be explored here and is significant as it has potential to allow us to draw conclusions about time-domain responses based on a frequency-based analysis.

Consider the following open-loop system:

$$ \begin{array}{*{20}c} {\ddot{x} + 0.3\dot{x} - 0.5x + x^{3} = 0.5 \cos \left( {\omega t} \right)} \\ \end{array} $$

(9)

The parameters are chosen so that chaotic motion can be observed (Fig. 3) as well as to somewhat resemble a real-world system that is unstable at the operating point (the origin) but never diverges to infinity due to some physical constraints. In this example, the nonlinear term $x^{3}$ acts as that physical constraint as it provides the restoring force when the displacement is large enough but is mostly negligible when $x$ is small.

Fig. 3

Time simulation of Eq. (9) at $\omega$ = 1.7 rad/s (a) and its phase plot (b), showing chaotic motion

The system is now augmented with a standard position-demand PID controller using the scheme shown in Fig. 4, where the reference signal $r$ is the demanded position. The equation of motion is now:

$$ \begin{array}{*{20}c} {\ddot{x} + 0.3\dot{x} - 0.5x + x^{3} = \left[ {r - x} \right]\left( {K_{P} + K_{I} \smallint {\text{d}}t + K_{D} \frac{{\text{d}}}{{{\text{d}}t}}} \right)} \\ \end{array} $$

(10)

Fig. 4

Block diagram of the closed-loop position-demand Duffing system

The linearised equation of motion about the origin simply omits the nonlinear term:

$$ \begin{array}{*{20}c} {\ddot{x} + 0.3\dot{x} - 0.5x = \left[ {r - x} \right]\left( {K_{P} + K_{I} \smallint {\text{d}}t + K_{D} \frac{{\text{d}}}{{{\text{d}}t}}} \right)} \\ \end{array} $$

(11)

For nonlinear frequency response analysis, we set $r = A \cos \left( {\omega t} \right)$. Equation (10) can now be expanded and rewritten into the following autonomous fifth-order system required for numerical continuation:

$$ \begin{array}{*{20}c} {\dot{x}_{1} = x_{2} } \\ \end{array} $$

(12)

$$ \begin{array}{*{20}c} {\dot{x}_{2} = x_{3} } \\ \end{array} $$

(13)

$$ \begin{aligned} \dot{x}_{3} & = - K_{I} x_{1} - \left( {k + K_{P} + 3\alpha x_{1}^{2} } \right)x_{2} - \left( {c + K_{D} } \right)x_{3} \\ & \quad - K_{P} A\omega x_{4} + (K_{I} - K_{D} \omega^{2} )Ax_{5} \\ \end{aligned} $$

(14)

$$ \begin{array}{*{20}c} {\dot{x}_{4} = x_{4} + \omega x_{5} - x_{4} \left( {x_{4}^{2} + x_{5}^{2} } \right)} \\ \end{array} $$

(15)

$$ \begin{array}{*{20}c} {\dot{x}_{5} = - \omega x_{4} + x_{5} - x_{5} \left( {x_{4}^{2} + x_{5}^{2} } \right)} \\ \end{array} $$

(16)

where $\left[ {c,k,\alpha ,A} \right] = \left[ {0.3, - 0.5, 1, 0.5} \right]$. In this case, $x_{1}$, $x_{2}$, and $x_{3}$ are the first, second, and third derivatives of the displacement $x$, and $x_{4}$ and $x_{5}$ equal $\sin \left( {\omega t} \right)$ and $\cos \left( {\omega t} \right)$.

The effect of the controller gains $\left[ {K_{P} ,K_{I} ,K_{D} } \right]$ on the frequency response and its relationship to the time-domain response are now discussed. It was found that the nonlinear frequency response is bifurcation-free if the $\left[ {K_{P} ,K_{I} ,K_{D} } \right]$ values lie within a bounded surface, which is shown in Fig. 5 in the form of contour plot in the $K_{I} , K_{P}$ plane. The smallest $K_{D}$ calculated in Fig. 5 is 0.145, and the largest value is 0.5. Further analysis shows that the bifurcation-free surface depends on maintaining an appropriate ratio between $K_{P}$, $K_{I}$, $K_{D}$, but this is beyond the scope of the paper.

Fig. 5

Bifurcation-free surface of equation $\left( {10} \right)$ in the $K_{P}$-$K_{I}$-$K_{D}$ space

Although the range of controller gains that guarantees no bifurcation in the frequency response has been determined, this does not guarantee that the time-domain response is similar to that of the linear system. Figure 6 shows the frequency responses and the time-domain step responses for four different combinations of controller gains, all of which lie inside the bifurcation-free surface shown in Fig. 5. In all cases, the nonlinear frequency response has a lower peak and a higher resonant frequency, which is reflected in the step response as lower overshoot and shorter period, although this is much more prominent in Fig. 6c and d.

Fig. 6

Frequency and step responses (amplitude 0.5) of the closed-loop Duffing system at four different combinations of PID gains. Dotted lines show the dynamics of the plant linearised about the origin [$x,\dot{x}$] = [0, 0]. The gains used are also highlighted in Fig. 7c

It can be seen that larger differences between the frequency responses lead to larger discrepancies in the step responses. Particularly, the following information can be inferred from the frequency responses:

• The damping ratio $C$ is related to the ‘width’ of the resonant peak, which can be estimated from the frequency response using the half-power method.

• The overshoot is related to the (absolute) gain at resonance $G_{R}$.

• The damped frequency is related to the resonance frequency $\Omega$.

Using those three parameters, we propose a way to quantify the differences between the linear and nonlinear frequency responses so as to predict the extent of discrepancy to expect in the step responses. This is done using the metric called $E_{3}$ described by Eq. (17), which measures the percentage difference of the three parameters above:

$$ \begin{array}{*{20}c} {E_{3} = \frac{1}{3}\left[ {\frac{{\left| {C_{{{\text{linear}}}} - C_{{{\text{nonlinear}}}} } \right|}}{{C_{{{\text{nonlinear}}}} }} + \frac{{\left| {G_{{R\;{\text{linear}}}} - G_{{R\;{\text{nonlinear}}}} } \right|}}{{G_{{R\;{\text{nonlinear}}}} }} + \frac{{\left| {\Omega_{{{\text{linear}}}} - \Omega_{{{\text{nonlinear}}}} } \right|}}{{\Omega_{{{\text{nonlinear}}}} }}} \right] \times 100} \\ \end{array} $$

(17)

Essentially, $E_{3}$ gives the average percentage error in the estimated damping ratio, overshoot, and resonance frequencies. We choose three terms with equal weighting in this example, but it is entirely up to the designer to decide on the number of terms as well as the appropriate weighting for the system considered. Figure 7 shows the value of $E_{3}$ for a range of [$K_{P}$, $K_{I}$, $K_{D}$] combinations, all of which lie within the bifurcation-free region as shown in Fig. 5.

Fig. 7

Bifurcation-free envelopes of equation $\left( {10} \right)$ at $K_{D}$ = 0.2 (a), 0.3 (b), 0.4 (c), and 0.5 (d). The colours indicate the $E_{3}$ values at the corresponding controller gains

By checking the time-domain responses to a step input of amplitude 0.5, it was found that for this system, $E_{3}$ < 12.5 provides a good match between the linear and nonlinear step responses. Two examples when this condition is satisfied are shown in Fig. 6a and b; the condition is not satisfied in Fig. 6c and d. The gains used in Fig. 6 are also marked as small circles in Fig. 7c. We can see that this system is sensitive to $K_{D}$ as increasing $K_{D}$ slightly will rapidly expand the $K_{I}$-$K_{P}$ envelope and that when $K_{D}$ is not high enough (as seen in Fig. 7a and b), there is no combination of $K_{I}$ and $K_{P}$ that satisfies our criterion of $E_{3}$ < 12.5.

This section has shown that the differences between the linear and nonlinear frequency responses are reflected in the time-domain step responses. Using a weakly nonlinear system with a fixed-gain controller, the combinations of controller gains that ensure the dynamics is similar to what has been predicted using linear-based methods have been identified. The next section will discuss a more complex aircraft model with a gain-scheduled controller designed to give consistent performance across different operating points. We will show how the proposed method can identify cases in which the controller fails to achieve its performance requirements.

4 Analysis of an aircraft model with a gain-scheduled controller

4.1 Description of the model

The method presented is now demonstrated on an aircraft flight dynamics model: the Hypothetical High Angle of Incidence Research Model (HHIRM) created for the Defence Research Agency in the UK (now QinetiQ) [13]. This comprises the standard 6 degree-of-freedom equations of motion for a rigid-body aircraft in atmospheric flight. The six aerodynamic force and moment coefficients are nonlinear functions of the angle-of-attack and sideslip angle, with dynamics representative of a typical fighter aircraft. These force coefficients are in the form of spline functions rather than tabular data in order for the system to be smooth (differentiable), making the model suitable to be used as a testbed for bifurcation-based methods. For this study, a reduced second-order version is used, which contains two states $\alpha$ (angle-of-attack in degree) and $q$ (pitch rate in degree/s) to capture the fast mode in the longitudinal plane (commonly referred to as the short-period mode in flight dynamics). The use of reduced-order models is common in flight control system design, where only the fast mode is important. However, the approach developed in this paper is not limited to such low-order systems. The equations of motions for the two states are:

$$ \begin{array}{*{20}c} {\dot{\alpha } = \frac{{\rho V_{T} S}}{2m}C_{Z} \left( {\alpha ,q,\eta } \right)\cos \left( \alpha \right) + q} \\ \end{array} $$

(18)

$$ \begin{array}{*{20}c} {\dot{q} = \frac{Sc}{{I_{y} }}C_{M} \left( {\alpha ,q,\eta } \right)q} \\ \end{array} $$

(19)

in which $\rho$ (air density in kg/m³), $V_{T}$ (total velocity in m/s), $S$ (wing area in m²), $c$ (reference chord length in m), $m$ (aircraft mass in kg), and $I_{y}$ (moment of inertia about the pitch axis in kg.m²) are constants. $C_{Z}$ and $C_{M}$ are the aerodynamic force and moment coefficients, which are nonlinear functions of $\alpha$ (angle-of-attack in deg), $q$ (pitch rate in deg/s), and $\eta$ (elevator deflection in deg). Further description of the force coefficients can be found in [13, 14]. To illustrate the nonlinear nature of the model, Fig. 8 shows the variation of the aerodynamic coefficients as functions $\alpha$ when $q$ and $\eta$ are fixed at zero.

Fig. 8

Force (a) and moment (b) coefficients of the HHIRM as functions of $\alpha$ while $q$ = 0 and $\eta$ = 0. Negative $C_{M} \left( \alpha \right)$ slope indicates that the aircraft is statically stable and vice versa

Bifurcation analysis of the open-loop second-order longitudinal HHIRM has been studied in [7, 15] and is reproduced here for completeness as well as to provide further understanding of the aircraft’s dynamics. The bifurcation diagrams as functions of the elevator deflection are shown in Fig. 9. These diagrams are the equilibria sets for the two states $\alpha$ and $q$ as functions of $\eta$. It can be seen that due to the fold bifurcations at $\eta$ = − 20° and − 11°, there are three solutions in this region. From a practical perspective, this means that:

• For  − 20° ≤ $\eta$ ≤ − 11°, the aircraft has two stable equilibrium states: one at a lower and one at a higher (‘deep stall’) angle-of-attack. Whichever solution the aircraft converges to will depend on the initial conditions.

• It is not possible to manually fly the aircraft at angles-of-attack between 34° and 45° because the solutions in that range are unstable.

Fig. 9

Open-loop bifurcation diagrams of the HHIRM with elevator deflection as the continuation parameter

4.2 The gain-scheduled controller and performance issues

In order to demonstrate the method’s capability in identifying instances where a linear-based controller fails to achieve the desirable response, the second-order aircraft is now fitted with a gain-scheduled stability-augmentation controller. It utilises both feedforward and feedback paths as described in [7] while also accounting for the dynamics of a first-order actuator. Figure 10a shows the schematic block diagram. In essence, this is a state-feedback controller with a feedforward path that modifies the reference signal (the demanded angle-of-attack $\alpha_{d}$) to create a manoeuvre-demand system. The feedforward signals are shown in Fig. 10b and were calculated by inverting the open-loop bifurcation diagrams in Fig. 9 so that given the demanded angle-of-attack $\alpha_{d}$, the steady-state values of the elevator deflection $\eta_{{{\text{trim}}}}$ and pitch rate $q_{{{\text{trim}}}}$ at that angle-of-attack are obtained. This feedforward scheme eliminates the need for an integral in the forward path, which provides a faster response. The feedback gains are scheduled against the pilot’s input $\alpha_{d}$ as shown in Fig. 10c and were calculated using eigenstructure assignment so that the short-period poles are fixed at $- 2 \pm 2i$ throughout the intended operating range of 0^o ≤ $\alpha_{d}$ ≤ 60°. The use of gain-scheduled feedforward and feedback paths with eigenstructure assignments to ensure consistent handling qualities (i.e. fixed pole positions) can be found in many highly augmented aircraft flight control systems, including the F-22 [16]. Examining the closed-loop poles at each operating point from 0° to 60° in 1° intervals shows that this objective is achieved (Fig. 11), indicating that the linear step responses are similar throughout the entire operating envelope.

Fig. 10

Gain-scheduled controller block diagram (a), feedforward signals (b), and scheduled feedback gains (c). b was constructed from the data in Fig. 9

Fig. 11

Linear poles of the closed-loop aircraft at 61 different operating points from 0° to 60^o

It has been shown in [7] that the local performances in the form of small-amplitude step responses are desirable and similar across the entire operating envelope. However, some large step inputs cause the aircraft to respond in an undesirable manner. This can be explained by examining the closed-loop bifurcation diagram (Fig. 12). The purpose of scaling the input signal using the feedforward path is to ensure that there is a 1:1 mapping between the pilot input $\alpha_{d}$ and the resulting angle-of-attack $\alpha$, which is reflected by the main stable branch in Fig. 12a: a straight line with slope 1 indicating the intended 1:1 mapping between $\alpha_{d}$ and $\alpha$. This scheme, however, does not guarantee the uniqueness of solutions, and an isola with stable solutions around $\alpha_{d}$ = 50° was detected [7]. This isola is a second and undesirable attractor that will influence the aircraft dynamics. For instance, a reference signal of $\alpha_{d}$ = 50° will converge to one of the two angles-of-attack: the demanded α = 50° or the undesirable α = 32° that originated from the isola. The initial conditions will determine which solution the aircraft converges to.

Fig. 12

Closed-loop bifurcation diagrams of the HHIRM with the demanded angle-of-attack as the continuation parameter. The insets show the magnified views of the isola

The rest of this section will further investigate the isola’s influence on the aircraft dynamics before proposing a method to indicate the presence of these nonlinear phenomena. Firstly, three step responses are examined in Fig. 13a along with their phase plots in Fig. 13b. The first case (30° and 35° step input) resembles the ideal response. In the second case ($\alpha_{d}$ steps from 30° to 50°), the trajectory lands on the isola at α = 32° instead of the commanded position at 50°. The final case (30° to 55°) reaches the commanded position, but the response is erratic and does not resemble the usual short-period mode. Examining the phase plot shows that in the third case, the trajectory is attracted to the stable isola before carrying on to its final destination at 55 deg. To reach the commanded angle-of-attack value and avoid the situation seen in the second case, the aircraft must acquire both high angle-of-attack and high pitch rate to keep the trajectory away from the isola’s region of attraction. This can be visualised in Fig. 14a, which was created by running a large number of simulations with different initial conditions in all three states [$\alpha$, $q$, $\eta$]. It can be seen that the aircraft is less susceptible to the isola when both the angle-of-attack and pitch rate are high. In addition, the basins of attraction show little dependency on the elevator position $\eta$. We will see later that this is no longer the case when actuator rate saturation is accounted for.

Fig. 13

Step responses and phase plots of the closed-loop HHIRM

Fig. 14

Basins of attraction at $\alpha_{d}$ = 50° with ideal actuator (a) and rate-limited actuator (b). Simulations with initial conditions outside the black region will converge to the isola

Finally, we have also come across a few cases in which the isola is present in the frequency response. One such case is shown in Fig. 15, where the reference signal is $\alpha_{d} = 41 + 15\sin \left( {2\pi ft} \right)$, i.e. the aircraft is trimmed at 41° angle-of-attack and then forced with a sinusoidal input of amplitude 15° and frequency $f$ Hz. This input corresponds to an $\alpha_{d}$ sweep between 36° and 56°, which passes the isola that exists in the region 49.7° ≤ $\alpha_{d}$ ≤ 51.2° in the unforced bifurcation diagram (Fig. 12) and leads to the formation of a corresponding second attractor in the frequency domain. The isola in Fig. 15 is only present at high frequencies, which further indicates that large and aggressive inputs are more likely to be affected.

Fig. 15

Closed-loop frequency response with $\alpha_{d} = 41 + 15\sin \left( {2\pi ft} \right)$, showing both the main branch and the isola

It has been shown that the presence of an isola can influence the aircraft response if its trajectory approaches the affected region. Although there is no systematic way to detect an isola in practice, we have seen that its existence can be inferred from the deleterious effects on the time-domain response. The next section will show that nonlinear frequency response analysis can also be exploited to reflect these underlying nonlinearities that are observed in the time domain. We can then use this information to identify instances where degraded flying qualities could be expected without relying on excessively large number of time-stepping simulation like in Fig. 14, which comes with considerable computation expense.

4.3 Nonlinear frequency response analysis

Consider the aircraft trimmed at 30° angle-of-attack. Figure 16 shows the $\alpha_{d}$-to-$\alpha$ frequency responses at three different forcing amplitudes $A$, i.e. the reference signal is $\alpha_{d} = 30 + A\sin \left( {2\pi ft} \right)$. Although all three instances look very similar at first glance, it was found that the $A$ = 25° case has a significantly lower roll-off frequency comparing to the other two cases, which have smaller forcing amplitudes. As $A$ = 25° corresponds to an $\alpha_{d}$ sweep from 5° to 55° whereas $A$ = 5° covers only $\alpha_{d}$ between 25° and 35°, the fact that their frequency responses are different suggest that the step response from 30° to 55° will be substantially different from the 30° to 35° one. This fact is verified in Fig. 13a. On the other hand, the frequency responses at $A$ = 5° and $A$ = 1° have similar roll-off frequencies, which indicates that their time-domain responses are similar.

Fig. 16

α-to-α_demand frequency responses of the aircraft trimmed at 30° angle-of-attack. The inset shows magnified view

The next step is to compare the nonlinear frequency responses at different operating points and for a range of forcing amplitudes $A$. Doing this allows us to predict which step responses would differ significantly from the ideal response. It was found that all frequency responses in this example have very similar shapes, so the only viable metric is the bandwidth—defined here as the frequency at which the gain drops to −3 dB. For a more complex system, users can devise a different metric, such as resonance peak or estimated damping of each mode as seen in the Duffing example, depending on the application considered. Figure 17a shows how the bandwidth varies at different operating points $\alpha_{{{\text{trim}}}}$ and different forcing amplitudes $A$ (as a reminder, $\alpha_{d} = \alpha_{{{\text{trim}}}} + A\sin \left( {2\pi ft} \right)$ for the frequency response). The diagram has a triangular shape because the controller was only designed to operate between 0° and 60° angle-of-attack, which leads to the constraint 0° ≤ $\alpha_{d}$ ≤ 60°. Each coloured point represents the bandwidth of the closed-loop frequency response at that combination of $\alpha_{{{\text{trim}}}}$ and $A$. Although no bifurcation was detected as shown in Fig. 17a, it is clear that there is a noticeable bandwidth reduction in the region 30° ≤ $\alpha_{{{\text{trim}}}}$ ≤ 50^o. This is shown as a red area and can be attributed to the presence of the isola. Although the unforced bifurcation diagram in Fig. 12 shows that the isola only exists over a small region of 49.7 ^o ≤ $\alpha_{d}$ ≤ 51.2°, the red region in Fig. 17a indicates that the isola affects the aircraft’s response over a large domain. The proposed method can therefore indicate the existence of the isola or any other underlying nonlinearities, which is potentially very useful when there is no systematic way to detect them.

Fig. 17

Variation in the closed-loop bandwidth (a) and step responses (b). Step responses at points E, F, G are shown in the three panels of Fig. 13a. Frequency response of point H is shown in Fig. 15

It is also inferred from Fig. 17a that regions with similar bandwidths will have similar step responses. Of particular interest is those where the step response is similar to the ideal one, such as point A, which corresponds to a step from 0° to 1°. This is expected as the step amplitude is small, and the operating point is at a low angle-of-attack. Points B and C have similar bandwidths, and their step responses in Fig. 17b are indeed similar to point A’s despite them being far apart in the operating envelope. Additionally, the step responses of points E, F, and G are the three panels shown in Fig. 13a, and the frequency response of point H is shown in Fig. 15.

Apart from the red and brown regions, the envelope in Fig. 17a also shows an additional yellow area that suggests a different dynamics comparing to those found in the other two regions. The step response at point D is shown as the dotted line in Fig. 17b, which has noticeably higher overshoot and does not resemble the other three cases. Examining the frequency response at point D (Fig. 18) shows that the increased bandwidth is caused by the higher resonance peak comparing to the ideal-like response at point A. A higher peak is linked to higher overshoot in the step responses, as seen in Fig. 17b.

Fig. 18

Closed-loop frequency responses at points A and D in Fig. 17a

It has been shown that aerodynamic nonlinearities can have significant influence on the aircraft responses in both the time and the frequency domains. Using nonlinear frequency response analysis, we have presented a method to quantify these effects. The information gained from the triangular envelope can be used to verify whether the controller delivers the intended consistent handling qualities across different operating regions. It is important to point out that the purpose of the triangular envelope is not to compare the closed-loop bandwidth but to indicate that bandwidth could be used as an effective metric to quantify the differences in the frequency response at different operating points.

4.4 Effects of actuator saturation

The analysis presented so far has assumed that the first-order actuator is ideal. In reality, physical limits can cause the actuator to saturate. This can seriously degrade the aircraft handling qualities [17,18,19,20,21,22,23,24,25,26], especially when the demanded manoeuvre rate or the controller gains are too high. Some of the examples presented above already demand unrealistic elevator movements. For example, although the step response at point B from 22° to 44° looks close to ideal in Fig. 17, this manoeuvre requires the elevator to travel 46° within the first 0.07 s – an unrealistic rate of over 550 deg/s (see Fig. 19a) with a high chance of exceeding position limit. It is therefore necessary to expand the analysis to account for actuator saturation. We will now impose a 45 deg/s rate limit on the elevator by replacing the linear first-order actuator with a piecewise function described by Eq. (20). A 45 deg/s rate limit is more representative of actuators found on large airliners as opposed to those on fighter aircraft, which can reach 100 deg/s. We chose this underperforming actuator to exemplify the problem, which makes our method applicable to cases where the gains are too high or when the aircraft is impaired.

$$ \begin{array}{*{20}l} {\dot{\eta } = \left\{ {\begin{array}{*{20}c} { 45 \times {\text{sgn}} \left( { - 30\eta + 30\eta_{d} } \right) \left( {\deg /s} \right)\quad {\text{if}}\;\left| { - 30\eta + 30\eta_{d} } \right| > 45 } \\ { - 30\eta + 30\eta_{d} \left( {\deg /s} \right)\quad {\text{otherwise}} } \\ \end{array} } \right.} \\ \end{array} $$

(20)

Fig. 19

Time simulations of the ideal and rate-limited aircraft to the step inputs at point B (a) and point D (b). Position limit is not modelled

The step responses from 22° to 44° with and without the 45 deg/s rate limiting is shown in Fig. 19a. It is evident that the elevator is heavily rate-saturated, which results in more overshoot and reduced damping—an overall degradation in handling qualities. A less demanding step response from 25° to 37° (point D in Fig. 17) is shown in Fig. 19b. In this case, the rate-limited aircraft enters a limit cycle. This dangerous phenomenon has been reported in analysis and test flights [17,18,19,20] where rate limiting was not accounted for during the controller design process, although no comprehensive analysis using bifurcation theory was done in those studies.

With the limit cycle detected through time simulation, we can now use numerical continuation to trace out the limit-cycle branch. Figure 20 shows the closed-loop unforced bifurcation diagram of the rate-limited aircraft. It was found that the limit cycle is not connected to the main branch via a Hopf bifurcation. Instead, it forms an isola that exists for $\alpha_{d}$ between 34.0° and 46.4°, which covers the range of unstable angles-of-attack in the open-loop aircraft (see Fig. 9). Although it is possible to analytically predict the hidden limit cycle due to rate saturation using the describing function method [20,21,22], the technique can only handle one nonlinear element, meaning that the plant and controller have to be linearised. A numerical approach like continuation, on the other hand, can account for additional nonlinear elements including the aerodynamic terms and gain scheduling as shown.

Fig. 20

Closed-loop unforced bifurcation diagram of the rate-limited aircraft

As before, the basins of attraction are constructed in Fig. 21 using time simulations with different initial conditions to further highlight the nonlinear nature of the dynamics when rate limiting is present. In this instance, the coloured region in Fig. 21 shows large dependency on the actuator state, suggesting that there are many possible ways for the aircraft to enter the limit cycle, thus making it very hard to define a safe flight envelope. This also contrasts with what we have seen in the equilibrium isola with an ideal actuator (Fig. 14a), which is almost unaffected by the actuator state. For completeness, we also show the basins of attraction at $\alpha_{d}$ = 50° (where the equilibrium isola exists) but with rate limiting active in Fig. 14b. The elevator state now also has a major influence on whether the aircraft’s trajectory is attracted to the isola, similar to that shown in Fig. 21 with the limit-cycle isola. To sum up, much of the undesirable and nonlinear behaviours discussed so far are directly caused by actuator rate limiting, which further underlines its deleterious effects on handling qualities.

Fig. 21

Basins of attraction of the equilibrium (normal flight) solutions at $\alpha_{d}$ = 40°. Simulations with initial conditions outside the coloured region will converge to the limit cycle. The equilibrium attractor (not visible) has coordinate [$\alpha$, $q$, $\eta$] = [40, 12.5, -13.3]

The basins of attractions in Figs. 14 and 21 are extremely computationally expensive to generate and do not provide much practical information on whether a pilot command is safe from the secondary attractors. On the other hand, there is no systematic way to detect isolas using numerical continuation. The limit cycle in this example was discovered and subsequently traced from the step response in Fig. 19b. Even without this knowledge, it is still possible to use the nonlinear frequency method to quantify the degradation in handling qualities and infer the existence of additional attractors. We generated the nonlinear frequency responses at every operating point and compare their bandwidth again in Fig. 22. This is equivalent to Fig. 17a above but with rate limiting active. In this case, various bifurcations are detected in the nonlinear frequency responses when the forcing amplitude exceeds around 5°. Points B and D, which encountered serious performance issues as shown in Fig. 19, are very deep in the bifurcation zone. This underlines the nonlinear nature of their dynamics. In practical terms, Fig. 22 suggests that the pilot should fly the aircraft gently and not demanding sudden steps above 5° to avoid encountering undesirable and nonlinear responses.

Fig. 22

Variation in the closed-loop bandwidth of the rate-limited aircraft. Bandwidths of cases in which bifurcations are detected in the nonlinear frequency responses are not shown

A wide range of interesting dynamics can be observed in the nonlinear frequency responses. For simplicity (without loss of generality), we will investigate the dynamics at points I and J, which are close to the no-bifurcation boundary. Firstly, Fig. 23b compares the step responses at point I with and without rate limiting. The rate-limited response is slightly slower, as expected, but the performance reduction is minimal. One might therefore conclude that point I is a safe operating point, especially when it has been reported that aircraft with good handling qualities can still occasionally encounter rate limiting [23, 24]. However, the nonlinear frequency response in Fig. 23a tells a different story. At higher forcing frequencies $f$, there is a reduction in both gain and phase in the rate-limited response as expected. Moreover, as $f$ approaches the roll-off frequency (around 0.55 Hz) where the effect of rate limiting starts to become dominant, a pair of fold bifurcations is detected that covers the region $f$ = [0.56 0.60] Hz. This region contains two stable solutions with a phase difference of roughly 65° for each value of the forcing frequency. Figure 23c verifies the existence of multiple solutions, which was generated by running the simulation with the same inputs but different initial conditions. The high phase lag response suffers from heavy saturation in the elevator (not shown), unlike the low phase lag response. In this instance, if the pilot is operating in the low-lag region, then any increase in input amplitude and/or forcing frequency can abruptly add more lag to the response—unlike the smooth transition as seen in the frequency response of the ideal actuator without rate limiting. This behaviour can explain the flying qualities cliff phenomenon, which is described in [23] as a ‘sudden and dramatic incremental shift in the phase lag, equivalent to the sudden insertion of a significant incremental time delay into the loop, initiated by only a slight change in pilot input command’. Due to its highly nonlinear and elusive nature, the flying qualities cliff has not been systematically investigated. Records of its existence are in the form of anecdotes, mostly after encountering a pilot-induced oscillation [23, 24]. In practice, time delay from the digital flight control computer and sensors can add even more lags to the system. This would further degrade the handling qualities [25], potentially to the point of instabilities [26]. It is worth nothing that the pair of fold bifurcations observed here can be encountered in very simple feedback systems with rate limiting. An example is provided in ‘Appendix’.

Fig. 23

Frequency responses (a), step responses (b), and simulated forced responses (c) at point I (16, 9). The insets in (a) show magnified view near the fold bifurcations. Both $\alpha$ responses in (c) have same inputs but different initial conditions

Point J (30, 6) in Fig. 22 is another example of the complex dynamics induced by rate limiting. Its frequency response in Fig. 24a reveals that apart from the fold bifurcations similar to the case at point I above, there exists a pair of period-doubling bifurcations also near the vicinity of the roll-off frequency. This leads to a period-2 branch with stable solutions, which is verified in time simulation as shown in Fig. 24b. The period-2 branch then undergoes further period-doubling cascades (not shown for clarity), which eventually leads to chaotic responses (Fig. 24c). These complex dynamics can be explained by the limit-cycle isola that exists for $\alpha_{d}$ between 34.0° and 46.4° (see Fig. 20). At point J (30, 6), the forcing parameters involves an $\alpha_{d}$ sweep from 24° to 36°, so its trajectory is likely to have been attracted to the limit-cycle isola at some frequencies.

Fig. 24

Rated-limited frequency response (a) and forced responses (b, c) at point J (30, 6). In the frequency response, only the period-1 and period-2 branches are shown for clarity

We have seen that the inclusion of rate limiting can rapidly deteriorate the aircraft’s handling qualities. Apart from some explosive responses, such as the entry to a limit cycle in Fig. 19b, the degradation in flying qualities can be so subtle that even nonlinear time simulation might suggest no potential issues (Fig. 23b). Using the nonlinear frequency response analysis, it is possible to identify the frequency-domain nonlinearities that negatively influence the aircraft’s dynamics during its transient motion, potentially leading to the dangerous flying qualities cliff phenomena and chaotic responses. We can further utilise nonlinear frequency response analysis to construct the bifurcation-free envelope in the frequency domain, which is useful for determining the maximum permittable step inputs that guarantee a linear-like and bifurcation-free response even in the presence of rate limiting. Furthermore, nonlinear frequency response analysis can also accommodate the effects of both rate and deflection saturations; we only include the former here to isolate the source of the limit cycle and chaotic attractors as shown.

4.5 Continuation in all controller gains: mitigating the effect of rate limiting

Section 4.4 has shown that rate limiting can shrink the safe operating regions significantly and lead to unacceptable flying qualities. In this final study, we will use unforced bifurcation analysis (without the harmonic oscillator) to further reveal the severity of the situation if the bifurcation-free envelope is violated. Although the limit cycle is clearly caused by rate limiting, we notice that this is only an issue for $\alpha_{d}$ between 34° and 46.4°. This can be attributed to the high controller gains required in this region (see Fig. 10c). Therefore, the link between controller gains and the limit cycles should be investigated. We do this by replacing the values of both feedback gains [$K_{\alpha }$, $K_{q}$] with [${\Lambda }K_{\alpha }$, ${\Lambda }K_{q}$], where ${\Lambda }$ is a scalar. ${\Lambda }$ can be interpreted as the ‘global gain parameter’, where ${\Lambda }$ = 1 corresponding to setting the gains at their original values and ${\Lambda }$ = 0 means no feedback gains (i.e. feedforward with no stability augmentation). Setting ${\Lambda }$ as the continuation parameter allows us to directly determine the link between high gains and limit-cycle formation. This method of global gain continuation has been applied in [6, 7].

Figure 25a shows the bifurcation diagram of the limit cycle and equilibrium solutions with ${\Lambda }$ as the continuation parameter when the reference signal is $\alpha_{d}$ = 37°. The limit-cycle branch can be calculated by either starting the continuation run with the aircraft already in a limit cycle or by continuing the periodic solutions at $\alpha_{d}$ = 37° from Fig. 20. We can see from Fig. 25a that the periodic solution branch encounters a fold bifurcation at ${\Lambda }$ just above 0.38, indicating that for $\alpha_{d}$ = 37°, the limit cycle ceases to exist when the feedback gains are reduced to below 38% of its original values. This also verifies that high gain contributes to the formation of the limit cycles. It might be concluded that ${\Lambda }$ should therefore be lowered to 0.37 when the pilot demands an angle-of-attack of 37°. However, such low gains are inadequate to stabilise the aircraft at the current angle-of-attack, which is open-loop unstable. Examining the equilibrium solution branch in Fig. 25a and Fig. 25b shows that below ${\Lambda }$ = 0.48, the 1:1 mapping between $\alpha_{d}$ and $\alpha$ is lost. It has been discussed in [7] that this is caused by the equilibrium isola at ${\Lambda }$ = 1 moving closer and merging with the main branch as ${\Lambda }$ is reduced. This suggests that in the presence of rate limiting, the open-loop unstable operating point $\alpha$ = 37° cannot be globally asymptotically stable. A similar conjecture was made in [27] for a general $n$-th-order system, which explains why the limit-cycle isola only exists in the region of angles-of-attack that is open-loop unstable. Another implication by this conjecture is that an unforced bifurcation diagram like Fig. 25 does not provide useful information on the stability conditions in the presence of rate limiting. Traditionally, this information is obtained using computationally expensive time simulations to construct the basins of attraction as demonstrated in Figs. 14 and 21. The proposed harmonic forcing method, on the other hand, provides a time-efficient alternative to define a safe manoeuvring envelope. For our current example, it is paramount that the pilot uses small stick movements while operating around 37° angle-of-attack to avoid landing on the limit cycle. The amount of maximum permittable stick movement can be inferred from the bifurcation-free envelope in Fig. 22.

Fig. 25

$\alpha$ bifurcation diagram (a) and magnified view (b) with ${\Lambda }$ as the continuation parameter and $\alpha_{d}$ = 37°. Only the maxima of the limit cycle are shown for clarity

Furthermore, we can still use information from Fig. 25 to guide the control law design process and reduce the aircraft’s susceptibility to oscillation. A simple limit-cycle avoidance system is now implemented for demonstration: if $\alpha$ exceeds the commanded value $\alpha_{d}$ by 25%, the controller gains will be immediately reduced to ${\Lambda }$ = 0.49, which is just above the minimum value required to fly at 37° angle-of-attack. Figure 26a compares the step response from 25 ^o to 37° with and without the prevention system active. It is clear that as soon as the aircraft exceeds 46.25° angle-of-attack (equals to 1.25 $\alpha_{d}$), reducing ${\Lambda }$ to 0.49 prevents the transition to a full limit cycle compared to when the gains are kept constant at ${\Lambda }$ = 1. Further inspection of the elevator responses reveals that rate saturation disappears as soon as we reduce the controller gains, which achieves the objective of preventing an oscillation. However, the risk still exists, and the aircraft may be attracted to the limit cycles as a result of aggressive manoeuvring or large perturbations. We note that the purpose here is not redesigning the controller (e.g. by varying the two gains independently to maximise the limit-cycle-free operating region), but simply to illustrate the advantages offered by bifurcation analysis in identifying regions where behaviour degrades and to help guide controller design improvements.

Fig. 26

Step responses from 25° to 37° (a) and from 0° to 37° (b) with and without limit-cycle prevention. The gains are reduced when $\alpha$ exceeds 1.25 $\alpha_{d}$ = 46.25^o

5 Conclusions

Control of nonlinear systems remains a challenge for engineers and researchers. It is therefore important to know how the presence of nonlinearities can alter the effectiveness of a linear-based controller before the performance is reduced to an unacceptable level. We have shown that such information can be inferred by both time- and frequency-domain bifurcation analysis. The latter provides a way to compare the transient response at different operating points even when no bifurcation is detected. Demonstrations of the method on both fixed-gain and gain-scheduled controller examples show that similar performance in the time domain can be expected if the frequency responses are similar. Conversely, the underlying nonlinearities can influence the dynamics in a way that is captured in the nonlinear frequency response but not in equilibrium bifurcation analysis or linear studies, and might be difficult to identify in nonlinear step responses. These effects are magnified in the presence of actuator rate saturation, which can seriously affect the aircraft’s dynamics and lead to the flying qualities cliff, limit cycles, secondary attractors, and chaotic motions. Nonlinear frequency analysis can detect and quantify the extent of these undesirable nonlinearities, as well as identifying a safe manoeuvre envelope to ensure that the response is desirable (linear-like), or at least bifurcation-free. Finally, the insidious link between rate limiting and gain scheduling is further revealed using continuation in all controller gains. It was found that severe rate saturation makes it impossible to fully prevent a limit cycle at high angles-of-attack by simply reducing the controller gains. These results underline the potential of bifurcation analysis and numerical continuation to verify if linear-based controllers achieve the desired performance on nonlinear systems.

Appendix: example of jump resonance in a simple feedback system with rate limiting

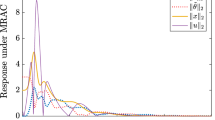
In this section, we provide an example of how jump resonance can be encountered in a very simple system due to rate limiting. This behaviour has been noted in real-world actuators with rate saturation and could be an interesting topic for further research. Consider a second-order feedback system with rate limiting in the forward path as shown in Fig. 

Fig. 27

Block diagram of a simple second-order feedback system with rate limiting in the forward path

27, which resembles a typical of a second-order actuator model. Given a simple harmonic reference signal of the form $r = A {\text{sin}}\left( {\omega t} \right)$, the system can be described by Eqs. (21–24):

$$ \begin{array}{*{20}c} {\dot{x}_{1} = x_{2} } \\ \end{array} $$

(21)

$$ \begin{array}{*{20}l} {\dot{x}_{2} = \left\{ {\begin{array}{*{20}c} { - kx_{1} - cx_{2} + S \times {\text{sgn}} \left( {A\omega x_{4} - x_{1} } \right)\quad {\text{if}}\;\left| {A\omega x_{4} - x_{1} } \right| > S} \\ { - \left( {k + 1} \right)x_{1} - cx_{2} + A\omega x_{4} \quad \quad {\text{otherwise}}} \\ \end{array} } \right.} \\ \end{array} $$

(22)

$$ \begin{array}{*{20}c} {\dot{x}_{3} = x_{3} + \omega x_{4} - x_{3} \left( {x_{3}^{2} + x_{4}^{2} } \right)} \\ \end{array} $$

(23)

$$ \begin{array}{*{20}c} {\dot{x}_{4} = - \omega x_{3} + x_{4} - x_{3} \left( {x_{3}^{2} + x_{4}^{2} } \right)} \\ \end{array} $$

(24)

where $x_{1}$ = $\dot{x}$ (not $x$), $x_{2}$ = $\ddot{x}$, $x_{3}$ = ${\text{sin}}\left( {\omega t} \right)$, and $x_{4}$ = cos $\left( {\omega t} \right)$. ${\text{S}}$ is the maximum rate permitted in the error signal $r - x$, in which $r = A {\text{sin}}\left( {\omega t} \right)$.

For $k$ = 1, $c$ = 0.15, and $A$ = 1, the closed-loop frequency response generated using numerical continuation is shown in Fig. 

Fig. 28

$\dot{x}$-to-$r$ frequency responses for a range of rate limiting level. At $S$ = 7, rate saturation is not encountered, leading to a linear-like frequency response

28. Fold bifurcations are detected in ${\text{S}}$ = 3 and 1, leading to jump resonances as well as regions of two stable solutions that can be verified in time simulation (see Fig. 

Fig. 29

Time simulations at $\left[ {S,\omega } \right] = \left[ {3, 1.316} \right]$ with different initial conditions, leading to two different responses

29). It should be noted that if the exact scheme shown in Fig. 27 is implemented in the Simulink environment using the built-in rate limiter block, the response might be inaccurate at heavy saturation level due to numerical issues involved in approximating the derivative of $r - x$.

A first glance at the nonlinear frequency response may suggest that the rate-limited system exhibits behaviours of a Duffing oscillator. This is not the case, however. In a hardening Duffing oscillator, the resonance curve leans to the right and has lower amplitude compared with the linear response, whereas in the softening case, the peak leans to the left and has higher amplitude. In our current rate-limited example, the resonance curve leans to the left with a reduced amplitude, suggesting that this is not a Duffing-type system. The apparent phase jump behaviour has been noted in engineering examples through measurements and the describing function techniques, although the existence of multiple solutions was not revealed [28]. When a rate-limited actuator is placed inside another feedback loop as part of a control system, potentially with added time delay, jump behaviour can become more severe [29]. Numerical continuation can be employed in these instances to examine the system’s closed-loop frequency response.