1 Introduction

COVID-19 was announced by the World health organization (WHO) as a major health hazard at the end of 2019. This was first seen in Wuhan province, China [1]. After that this infectious disease has been spread out in the whole world. To defeat the epidemic, the different countries of the world were in a lockdown scenario, the also successively unlock process due to socioeconomic and political impacts [2,3,4,5,6]. Moreover, the mortality and morbidity rate has varied across countries of the worlds [7,8,9]. COVID-19 is often present in human being as common symptoms, for example, cold-like illness including fever, muscle pain, fatigue, loss of taste and smell, sore throat, and dry cough [10,11,12,13].

COVID-19 can be transmitted from people to people through respiratory droplets from an infected human being or direct contact with contaminated surfaces or objects [14, 15]. As all vaccinations are in trial positions for the prevention of COVID-19. Various studies have pointed out the stage of comorbidity co-infection (like lung disease, heart disease, diabetes, etc) among the infected people. According to the Centers for Disease Control and Prevention, all people with comorbidity or medical condition have more risk to become infected than healthy or normal human being [16,17,18]. From the survey of clinical reports, this is further suggested that the confirmed COVID-19 patients are most having comorbidity co-infection which includes kidney disease, obesity those having basal metabolic rate (BMR) more than thirty, type-2 diabetes, COPD (chronic obstructive pulmonary disease) [19,20,21]. Moreover, sometimes this confirmed COVID-19 with comorbidity were admitted to the intensive care unit (ICU).

New daily cases of COVID-19 follow a very highly volatile pattern, i.e, deceasing-increasing arbitrarily [22, 23]. To implement fruitful public health measures in a scheduled time within a certain resource according to geographical state [24], it is utmost essential to study the diffusion or force of infection among the wider population. In order to explain this observation, entropy helps us to determine the heterogeneity of a daily number of cases and time of highest diffusion or force of infection [25]. Various methods of measuring entropy, like weighted entropy [26], maximum entropy [27], evolutionary Entropy [28], structural Entropy [29] are employed to forecast and study the transmission dynamics of pandemic like, COVID-19 [30, 31]. Here, the concept of Shannon entropy is indeed used and seemed to be appropriate to determine the spread of an epidemic as there is a significant analogy based on Boltzmann’s classical thermodynamical paradigm [32].

Various mathematical models have been formulated and studied the corresponding dynamics [33, 34]. Lie et al. proposed a data-driven COVID-19 model with distributed delay [35]. Global dynamics of a COVID-19 SEIR epidemic model has been investigated by Khyar et al. [36]. Further, different authors have suggested control strategies for disease transmission of COVID-19 [37,38,39]. The main aim of this paper is to study the qualitative behavior of COVID-19 transmission dynamics by bifurcation theory. Various qualitative dynamics have been studied in different mathematical model [40,41,42]. For this purpose, data-driven modeling is a powerful tool to investigate dynamical behavior in infectious disease [43]. Various mathematical models have been devolved as well as investigated the transmission dynamic of COVID-19 [44,45,46,47,48]. Indeed, considering comorbidity in modelling of COVID-19 is of noteworthy interest in ongoing studies and also has not been yet investigated according to literature.

Fig. 1
figure 1

Schematic illustration of SCEAIHR model. The flow diagram exhibits the interaction of different stages of individuals in the model: susceptible (S), comorbidity (C), exposed (E), asymptomatic (A), infected (I), hospitalized (H) and recovered (R)

Full size image

The subsequent parts of the paper are as follows: In Sect. 2, we propose and explore a mathematical model of COVID-19 with comorbidity. The qualitative dynamics is investigated at feasible equilibrium by performing bifurcation analysis in Sect. 3. In Sect. 4, the model is calibrated and sensitivity analysis is also performed. Moreover, the transmission dynamics of mean fluctuation in force of infection is studied by measuring the corresponding Shannon entropy. Finally, in Sect. 5, we discuss and conclude the results from our proposed study.

2 Mathematical model

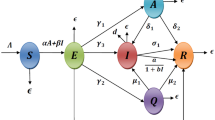
We develop here a SCEAIHR-type model by introducing threatened or comorbidity susceptible and hospitalized individuals in the dynamics of COVID-19 (SARS-Cov-2). The model consists of seven compartments, namely, susceptible individuals (S), comorbidity susceptible individuals (C), exposed individuals (E), asymptomatic individual (A), infected or infectious individuals with clinical symptoms (I), diagnosed and hospitalized individuals (H) and recovered individuals with no more infections (R). The total number of individuals is \(N=S+C+E+A+I+H+R\). Our main aim is to study the dynamics of COVID-19 with comorbidity co-infection. Based on a biological viewpoint, we formulate a nonlinear mathematical model to investigate the COVID-19 or SARS-Cov-2 pandemic in a certain time window:

$$\begin{aligned} {\dot{S}}&= \Pi _{s}-\frac{\beta _{s}(I+\delta _a A+\delta _h H)S}{N} -\phi _s S -\mu S \nonumber \\ {\dot{C}}&= \phi _s S -\frac{\rho \beta _{s}(I+\delta _a A+\delta _h H)C}{N} - \mu C \nonumber \\ {\dot{E}}&= \frac{\beta _{s}(I+\delta _a A+\delta _h H)S}{N} \nonumber \\&\quad + \frac{\rho \beta _{s}(I+\delta _a A+\delta _h H)C}{N} -(\alpha _e +\mu )E \nonumber \\ {\dot{A}}&= (1-\xi )\alpha _e E -(\gamma _a +\mu )A\nonumber \\ {\dot{I}}&= \xi \alpha _e E -(\gamma _i +\theta +\mu )I \nonumber \\ {\dot{H}}&= \theta I -(\gamma _h +\eta +\mu )H\nonumber \\ {\dot{R}}&= \gamma _a A+ \gamma _i I +\gamma _h H -\mu R \end{aligned}$$
(1)
Table 1 The values of the parameters used in the SCEAIHR model (1)
Full size table

The following initial values are considered in model (1) as follows:

$$\begin{aligned}&S(t_0)=S^0 \ge 0, C(t_0)=C^0 \ge 0, \nonumber \\&E(t_0)=E^0 \ge 0, A(t_0)= A^0\ge 0, \nonumber \\&I(t_0)=I^0 \ge 0, H(t_0)=H^0 \ge 0, R(t_0)=R^0 \ge 0 \end{aligned}$$
(2)

Here, it is assumed that \(t\ge t_0\), where \(t_0\) indicates the initial date of the outbreak of COVID-19 for the model (1). Susceptible individuals are generated by the recruitment of persons by birth or immigration to the community at a constant rate of \(\Pi _s\). Population decreases after infection and can be transmitted at a rate \(\frac{\beta _s I}{N}\), \(\frac{\delta _a \beta _s A}{N}\) and \(\frac{\delta _2 \beta _s H}{N}\) by direct interaction between susceptible individuals with symptomatic infected, asymptomatic infected and hospitalized individuals respectively and at a rate \(\frac{\rho \beta _s I}{N}\), \(\frac{\rho \beta _s \delta _a A}{N}\) and \(\frac{\rho \beta _s \delta _h H}{N}\) by direct interaction between co-morbid susceptible individuals with symptomatic infected, asymptomatic individuals and hospitalized individuals respectively. Also, susceptible individuals often develop co-morbidity at a rate of \(\phi _s\). It is assumed that there is a recovery rate for asymptomatic, symptomatic, and hospitalized individuals, such as \(\gamma _a\), \(\gamma _i\), and \(\gamma _h\) respectively. The model incorporates certain demographic impacts by estimating the disease-induced mortality rate \(\eta \) of hospitalized persons and natural death rate \(\mu \) of each of the seven subpopulations. After the disease incubation period, \(\frac{1}{\alpha _e}\), a fraction \(\xi \) of the exposed individuals are symptomatically infected and the remaining fraction \((1-\xi )\) become asymptomatically infected. The exposed population also decreased at a rate of \(\mu \) due to natural death. The pictorial diagram of our model is presented in Fig. 1. The description of model parameters is provided in Table 1.

3 SCEAIHR model analysis

In this section, we study some basic properties of the SCEAIHR model (1) such as positivity and boundedness, basic reproduction number, stability analysis at biologically feasible equilibrium points with non-negative initial conditions \((S^0, C^0, E^0, A^0, I^0, H^0, R^0) \in {\mathbf {R}}^7\).

Lemma 3.1

For initial values (2), the solutions of SCEAIHR model (1) remain positive through out the region in \({\mathbf {R}}^7_+\) for all \(t>0.\)

Proof

To establish the positivity of the system (1), we take any solution emerging from non-negative region \({\mathbf {R}}^7_+\) which remain positive for all \(t>0.\) In order to do this, we prove that the points of vector field on the each hyper plane are bounded by non-negative region \({\mathbf {R}}^7_+\). In the system (1), we see that \(\frac{dS}{dt}|_{S=0}=\Pi _{S} \ge 0,\) \(\frac{dC}{dt}|_{C=0}=\phi _s S\ge 0,\) \(\frac{dE}{dt}|_{E=0}=\frac{\beta _s}{N}(S+\rho T)(I+\delta _a A+\delta _h H) \ge 0,\) \(\frac{dA}{dt}|_{A=0}= (1-\xi )\alpha _e E \ge 0,\) \(\frac{dI}{dt}|_{I=0}=\xi \alpha _e E S\ge 0,\) \(\frac{dH}{dt}|_{H=0}= \theta I \ge 0,\) \(\frac{dR}{dt}|_{R=0}= \gamma _a A+ \gamma _i I +\gamma _h H \ge 0,\) Here, this assures the positivity of solutions in the region \({\mathbf {R}}^7_+\). \({\mathbf {R}}^7_+\) is established as positive invariant set of SCEAIHR model. \(\square \)

Lemma 3.2

For initial values (2), the solutions of SCEAIHR model (1) are uniformly bounded in the region \(\Xi .\)

Proof

In order to prove boundedness, we sum up all equations in the model (1), which provides \(N=S+C+E+A+I+H+R.\) Differentiating both sides, we get

$$\begin{aligned} \frac{dN}{dt}=\Pi _s -\mu N, \end{aligned}$$

which implies \(\lim \limits _{t \rightarrow \infty }\sup N(t) \le \frac{\Pi _s}{\mu }.\) Without of loss of generality, we can express all equations in model (1) as \(\lim \limits _{t \rightarrow \infty } i(t) \le \frac{\Pi _s}{\mu }; i= S, C, E, A, I, H, R\). So, a bounded set can be defined

$$\begin{aligned}&\Xi = \{(S, C, E, A, I, H, R) \\&\quad \in {\mathbf {R}}^7_+ : 0 \le S, C, E, A, I, H, R \le \frac{\Pi _s}{\mu } \}, \end{aligned}$$

which is further a positive invariant set to the SCEAIHR model (1). Therefore, all solution trajectories initiating from interior of \({\mathbf {R}}^7_+\) always remain within the domain \(\Xi \). this assures that the growth of all individuals can’t be unbounded or exponential for time time window. \(\square \)

3.1 Infection free equilibrium and basic reproduction number

The basic reproduction number is a threshold value and characterizes the infectious disease. This is denoted by \(R_0\) and defined by the number of secondarily infected individuals induced by single infected individuals as infectious during its incubation period within susceptible individuals. \(R_0\) is a dimensionless number and quantifies the expectation of decreasing or increasing the disease outbreak. The system (1) has infection free equilibrium \(\epsilon _0\), given by \(\epsilon ^0 (S^0, C^0, E^0, A^0, I^0, H^0, R^0)= (\frac{\Pi _s}{\phi _s +\mu }, \frac{\phi _s \Pi _s}{\mu (\phi _s +\mu )},\) 0, 0, 0, 0, 0, 0). The compartment E, A, I, H in system (1) are explicitly associated with disease outbreak. Thus we get matrix \(\tilde{F}\), \(\tilde{V}\) for new infection and transition part respectively, given by

$$\begin{aligned} \tilde{F}= & {} \begin{bmatrix} \frac{\beta _s}{N}(S+\rho C)(I+\delta _a A+ \delta _h H) \\ 0 \\ 0 \\ 0 \end{bmatrix}, \quad \\ \tilde{V}= & {} \begin{bmatrix} (\alpha _e+\mu )E\\ -(1-\xi )\alpha _e E + (\gamma _a+\mu )A\\ -\xi \alpha _e E + (\gamma _i + \theta + \mu )I\\ -\theta I +(\gamma _a+\eta +\mu )H \end{bmatrix}. \end{aligned}$$

The variational matrix \(F=\frac{d\tilde{F}}{dX}\) and \(V=\frac{d\tilde{V}}{dX}\), where \(X=[E, A, I, H]^{'}\) can be calculated at \(\epsilon ^0(S^0, C^0, E^0, A^0, I^0, H^0, R^0).\) The basic reproduction number is dominant eigenvalue of matrix \(F{V^{-1}}.\) So, we obtain

$$\begin{aligned} R_0&=\frac{\beta _s \alpha _e(\rho \phi _s+\mu )}{(\phi _s+\mu )(\alpha _e+\mu )}\bigg [\frac{\delta _a (1-\xi )}{\gamma _a+\mu }+\frac{\xi }{\gamma _i+\theta +\mu }\\&\qquad +\frac{\theta \xi \delta _h }{(\gamma _i+\theta +\mu )(\gamma _h+\eta +\mu )}\bigg ]. \end{aligned}$$

3.2 Stability of infection free equilibrium

Theorem 1

The infection-free equilibrium \(\epsilon ^0\) is locally asymptotically stable if \(R_0 <1\) and unstable \(R_0 >1.\)

Proof

The variational matrix J of the system (1) is given by

$$\begin{aligned} J=\begin{bmatrix} -(\rho \phi _s +\mu )&{}0&{}0&{}-\frac{\mu \beta _s\delta _a}{\phi _s+\mu }&{}-\frac{\mu \beta _s}{\phi _s+\mu }&{}-\frac{\mu \beta _s\delta _h}{\phi _s+\mu }&{}0\\ \phi _s&{}-\mu &{}0&{}-\frac{\rho \beta _s\delta _a \phi _s}{\phi _s+\mu }&{}-\frac{\rho \beta _s\phi _s}{\phi _s+\mu }&{}-\frac{\rho \beta _s\delta _h \phi _s}{\phi _s+\mu }&{}0\\ 0&{}0&{}-(\alpha _e+\mu )&{}\frac{\beta _s\delta _a(\mu +\rho \phi _s)}{\phi _s+\mu }&{}\frac{\beta _s(\mu +\rho \phi _s)}{\phi _s+\mu }&{}\frac{\beta _s\delta _h(\mu +\rho \phi _s)}{\phi _s+\mu }&{}0\\ 0&{}0&{}(1-\xi )\alpha _a&{}-(\gamma _a+\mu )&{}0&{}0&{}0\\ 0&{}0&{}\xi \alpha _a&{}0&{}-(\gamma _i+\theta +\mu )&{}0&{}0\\ 0&{}0&{}0&{}0&{}\theta &{}-(\gamma _h+\eta +\mu )&{}0\\ 0&{}0&{}0&{}\gamma _a&{}\gamma _i&{}\gamma _h&{}-\mu \end{bmatrix} \end{aligned}$$
(3)

For our convenience, we consider

$$\begin{aligned} \alpha _e+\mu&=k_1, \gamma _2+\mu =k_2, \nonumber \\ \gamma _i+\theta +\mu&=k_3 \quad \text{ and } \quad \gamma _h+\eta +\mu =k_4. \end{aligned}$$
(4)

The matrix \(J_{\epsilon ^0}\) at \(\epsilon ^0\) has unique and repeated eigenvalues as \(-(\rho \phi _s+\mu )\) and \(-\mu \) respectively. The rest of eigenvalues are the roots of following equation as follow:

$$\begin{aligned}&\frac{\beta _s\alpha _e(\mu +\rho \phi _s)}{\phi _s+\mu } \bigg [\delta _a(1-\xi )(k_3+\lambda )(k_4+\lambda )\\&\quad +\xi (k_2+\lambda )(k_4+\lambda ) +\theta \xi \delta _h(k_2+\lambda )\bigg ]\\&\quad -(k_1+\lambda )(k_2+\lambda )(k_3+\lambda )(k_4+\lambda )=0. \end{aligned}$$

which can be expressed as follow:

$$\begin{aligned}&\frac{\beta _s\alpha _e(\mu +\rho \phi _s)}{\phi _s+\mu } \bigg [\frac{\delta _a(1-\xi )}{(k_1+\lambda )(k_2+\lambda )}\\&\qquad +\frac{\xi }{(k_1+\lambda )(k_3+\lambda )}\\&\qquad +\frac{\theta \xi \delta _h}{(k_1+\lambda )(k_3+\lambda )(k_4+\lambda )}\bigg ]=1. \end{aligned}$$

Denote

$$\begin{aligned} n_1(\lambda )&=\frac{\delta _a(1-\xi )}{(k_1+\lambda )(k_2+\lambda )}+\frac{\xi }{(k_1+\lambda )(k_3+\lambda )}\\&\quad +\frac{\theta \xi \delta _h}{(k_1+\lambda )(k_3+\lambda )(k_4+\lambda )}\\&=n_{11}(\lambda )+n_{12}(\lambda )+n_{13}(\lambda ) \quad \text{(say) }. \end{aligned}$$

Now substitute \(\lambda =x+iy\), if \(\mathfrak {R}(\lambda )\ge 0\), where, \(\mathfrak {R}(\lambda )\) represents real part of \(\lambda \), then

$$\begin{aligned} |n_{11}(\lambda )|&\le \frac{\delta _a(1-\xi )}{|(k_1+\lambda )\Vert (k_2+\lambda )|}\le n_{11}(x)\le n_{11}(0)\\ |n_{12}(\lambda )|&\le \frac{\xi }{|(k_1+\lambda )\Vert (k_3+\lambda )|}\le n_{12}(x)\le n_{12}(0)\\ |n_{13}(\lambda )|&\le \frac{\theta \xi \delta _h}{|(k_1+\lambda )\Vert (k_3+\lambda )\Vert (k_4+\lambda )|} \\&\le n_{13}(x)\le n_{13}(0) \end{aligned}$$

Consequently, \(n_{11}(0)+n_{12}(0)+n_{13}(0)=n_1(0)=R_0<1\), which implies \(|n_1(\lambda )|\le 1\). So, eigenvalues corresponding characteristic equation \(n_1(\lambda )=1\) have negative real parts for \(R_0<1.\) Thus, for \(R_0<1\), all eigenvalues are negative. According to Routh–Hurwitz stability criterion, infection free equilibrium \(\epsilon ^0\) is locally asymptotically stable for \(R_0<1.\) Again, if we consider \(R_0>1\), i.e, \(n_1(0)>1,\) then

$$\begin{aligned} \lim \limits _{\lambda \rightarrow \infty }n_1(\lambda )=0; \end{aligned}$$

then, there exits \(\lambda ^*_1>0\) so that \(n_1(\lambda )=1\). This means that there exits non-negative eigenvalue \(\lambda ^*_1>0\) in matrix \(J_{\epsilon ^0}.\) Hence, infection free equilibrium \(\epsilon ^0\) is unstable for \(R_0>1.\) \(\square \)

3.3 Existence of endemic equilibrium

Here, we study the existence of endemic equilibrium. Let \(\epsilon ^* =(S^*, C^*, E^*, A^*, I^*, H^*, R^*)\) be any endemic equilibrium of system (1). Moreover, The force of infection is

$$\begin{aligned} \zeta ^*=\frac{\beta _s(I^*+\delta _a A^*+\delta _h H^*)}{N^*} \end{aligned}$$
(5)

By solving the system (1) at equilibrium state, we get \(S^*=\frac{\Pi _s}{\zeta ^*+\phi _s +\mu },\) \(C^*=\frac{\phi _s S^*}{\rho \zeta ^*+\mu }\), \(E^*={\zeta ^*}{k_1}(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu })S^*,\) \(A^*=\frac{\alpha _e(1-\xi )}{k_1k_2}(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu })S^*\), \(I^*=\frac{\alpha _e\xi }{k_1k_3}(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu })S^*\), \(H^*=\frac{\alpha _e\theta \xi }{k_1k_3k_4}(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu })S^*\), and \(R^*=\frac{1}{\mu }(\frac{\alpha _e(1-\xi )\gamma _a}{k_1k_2})(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu }+\frac{\alpha _e\xi \gamma _i}{k_1k_3}+\frac{\alpha _e\theta \xi \gamma _h}{k_1k_3k_4})(\zeta ^*+\frac{\rho \phi _s}{\rho \zeta ^*+\mu })S^*\).

Substituting the all expressions into (5), we get the non- zero equilibrium of (1) which satisfies quadratic equation in \(\zeta ^*\) as follow:

$$\begin{aligned} P_2\zeta ^{*2}+P_1\zeta ^{*}+P_0=0 \end{aligned}$$
(6)

where,

$$\begin{aligned} P_2&=\rho [\mu k_2k_3k_4+k_2k_4 \xi \alpha _e (\mu +\gamma _i)\nonumber \\&\quad + k_3k_4 \alpha _e(1-\xi )(\mu +\gamma _i)+k_2\theta \xi \alpha _e(\mu +\gamma _h)] \nonumber \\ P_1&=[\mu +k_2k_4\alpha _e \xi \{\gamma _i(\mu +\rho \phi _s)-\mu \beta _s\}\nonumber \\&\quad +k_2\theta \alpha _e \xi \{\gamma _h(\mu +\rho \beta _s)-\mu \beta _s\delta _h\} \nonumber \\&\quad +k_3k_4\alpha _e(1-\xi )\{\gamma _a(\mu +\rho \phi _s)-\mu \beta _s\gamma _a\}]\nonumber \\ P_0&=\mu k_1k_2k_3k_4(\mu +\phi _s)(1-R_0). \end{aligned}$$
(7)

From (6), we can obtain endemic equilibrium of (1). Here, the coefficient A is always positive. The sign of coefficient C depends on lesser or greater value of \(R_0\) than unity. It can be noted that multiple endemic equilibrium can be coexist for \(R_0<1.\) Thus, we can summarize as follows:

Theorem 2

The system (1) has

  1. 1.

    two endemic equilibrium if \(P_0>0\) and \(P_1<0\) and \(P_1^2-4P_2P_1>0.\)

  2. 2.

    at least one endemic equilibrium if \(P_0<0\) iff \(R_0>1.\)

  3. 3.

    a unique endemic equilibrium if (\(P_0=0\) and \(P_1<0\)) or \(P_1^2-4P_2P_1=0.\)

  4. 4.

    no endemic equilibrium if \(P_0>0\) iff \(R_0<1\) and \(P_1>0.\)

From the above theorem, it can be noted that backward bifurcation is possible due to the coexistence of stable infection-free and endemic equilibrium for \(R_0<1.\) For this purpose, we find a critical value \(R^*_0\) of \(R_0\) for unique endemic equilibrium as follow:

$$\begin{aligned} R^*_0=1-\frac{P^2_1}{4\mu k_1k_2k_3k_4(\mu +\phi _s)P_2}. \end{aligned}$$

Hence, backward bifurcation can occur with specific restriction \(R^*_0< R_0<1\). Now, we turn on the analysis for backward bifurcation.

3.4 Backward bifurcation

In order to investigate backward bifurcation at endemic equilibrium \(\epsilon ^*(S^*,C^*, E^*, A^*, I^*, H^*, R^*)\), we apply centre manifold theorem by considering bifurcation parameter \(\beta _s=\beta ^*_s\), corresponded to \(R_0=1.\)

From variational matrix J in (3), we again consider few entries as follows:

$$\begin{aligned} a_{14}&= -\frac{\mu \beta _s\delta _a}{\phi _s+\mu }, a_{15}=-\frac{\mu \beta _s}{\phi _s+\mu },\nonumber \\ a_{16}&=-\frac{\mu \beta _s\delta _h}{\phi _s+\mu }, a_{24}=-\frac{\rho \beta _s\delta _a\phi _s}{\phi _s+\mu },\nonumber \\ a_{25}&=-\frac{\rho \beta _s\phi _s}{\phi _s+\mu }, a_{26}-\frac{\rho \beta _s\delta _h \phi _s}{\phi _s+\mu },\nonumber \\ a_{34}&=\frac{\beta _s\delta _a(\mu +\rho \phi _s)}{\phi _s+\mu }, a_{35}=\frac{\beta _s(\mu +\rho \phi _s)}{\phi _s+\mu },\nonumber \\ a_{36}&=\frac{\beta _s\delta _h(\mu +\rho \phi _s)}{\phi _s+\mu } \end{aligned}$$
(8)

Now, the variational matrix of system (1) at \(\beta _s=\beta ^*_s\) has right eigenvector corresponding to zero eigenvalue, given by \(v= [v_1, v_2, v_3, v_4, v_5, v_6, v_7]^{'}\), where

$$\begin{aligned}&v_1=-\frac{v_3}{a_{11}}\bigg [\frac{a_{14}\alpha _e(1-\xi )}{k_2}+\frac{a_{15}\alpha _e\xi }{k_3}+\frac{a_{16}\alpha _e \theta \xi }{k_3k_4}\bigg ],\\&v_2=\frac{v_3}{\mu }\bigg [-\frac{\phi _s}{a_{11}}\bigg \{\frac{a_{16}\alpha _e(1-\xi )}{k_2}+\frac{a_{15}\alpha _e\xi }{k_3}\\&\qquad +\frac{a_{14}\alpha _e \theta \xi }{k_3k_4}\bigg \}+ \frac{a_{24}\alpha _e(1-\xi )}{k_2}+\frac{a_{25}\alpha _e\xi }{k_3}\\&\qquad +\frac{a_{26}\alpha _e \theta \xi }{k_3k_4}\bigg ]\\&v_3>0, v_4= \frac{v_3(1-\xi )\alpha _e}{k_2}, v_5= \frac{v_3\xi \alpha _e}{k_3}, \\&v_6= \frac{v_3 \theta \xi \alpha _e}{k_3k_4}, \\&v_7= \frac{v_3}{\mu }\bigg [\frac{\gamma _a\alpha _e (1-\xi )}{k_2}+\frac{\gamma _i\alpha _e \xi }{k_3}+\frac{\gamma _h\alpha _e \theta \xi )}{k_3k_4} \bigg ] \end{aligned}$$

Similarly, at at \(\beta _s=\beta ^*_s\), the variational matrix of system (1) has left eigenvector corresponding to zero eigenvalue, given by \(w= [w_1, w_2, w_3, w_4, w_5, w_6, w_7]\), where

$$\begin{aligned} w_1&=0, w_2=0, w_3>0, w_4=\frac{w_3 a_{34}}{k_2},\\ w_5&=\frac{w_3}{k_3}\left( a_{35}+\frac{\theta a_{36}}{k_4}\right) ,\\ w_6&=\frac{w_3a_{36}}{k_4}, w_7=0. \end{aligned}$$

We introduce a few notations for SCEAIHR model system as follows: \(S=x_1; C=x_2; E=x_3; A=x_4; I=x_5; H=x_6; R=x_7;\) and \(\frac{dx_i}{dt}=f_i,\) where \(i=1,2, \ldots , 7.\) Now, we compute second order partial of \(f_i\) at infection-free equilibrium \(\epsilon ^0\) and obtain

$$\begin{aligned}&\frac{\partial ^2 f_3}{\partial x_1 \partial x_4}=\frac{\mu \beta _s \delta _a (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_1 \partial x_5}\\&\quad = \frac{\mu \beta _s (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_1 \partial x_6}= \frac{\mu \beta _s \delta _a (1-\rho )}{\pi _s (\phi _s+\mu )}, \\&\frac{\partial ^2 f_3}{\partial x_2 \partial x_5}= -\frac{\mu ^2 \beta _s (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_2 \partial x_6}\\&\quad = -\frac{\mu ^2 \beta _s (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_4 \partial x_5}\\&\quad = -\frac{\mu \beta _s (1+\delta _a)(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_4 \partial x_6}= -\frac{\mu \beta _s (\delta _a+\delta _h) (\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_4 \partial x_7}\\&\quad = -\frac{\mu \beta _s \delta _a(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_5 \partial x_1}= \frac{\mu \beta _s \phi _s (1-\rho )}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_5 \partial x_2}=- \frac{\mu ^2 \beta _s (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_5 \partial x_6}\\&\quad = -\frac{\mu \beta _s (1+\delta _h)(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_5 \partial x_7}\\&\quad = -\frac{\mu \beta _s (\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_6 \partial x_1}= \frac{\mu \beta _s \phi _s\delta _h(1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_6 \partial x_2}\\&\quad = \frac{\mu ^2 \beta _s \delta _h(1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_6 \partial x_4}\\&\quad = -\frac{\mu \beta _s (\mu +\rho \phi _s)(\delta _a+\delta _h)}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_6 \partial x_5}= -\frac{\mu \beta _s (\mu +\rho \phi _s)(1+\delta _h)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x^2_6 }\\&\quad = -2\frac{\mu \beta _s (\mu +\rho \phi _s)\delta _h}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_6 \partial x_7}\\&\quad = -\frac{\mu \beta _s \delta _h(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_6 \partial x_3}= -\frac{\mu \beta _s \delta _h}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_4 \partial x_1}\\&\quad = -\frac{\mu \beta _s \rho \phi _s\delta _a(1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_4 \partial x_2}= \frac{\mu \beta _s \delta _a(1-\rho )}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x_4 \partial x_3}= -\frac{\mu \beta _s \delta _a(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x^2_4}\\&\quad = 2\frac{\mu \beta _s \delta _a(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )},\frac{\partial ^2 f_3}{\partial x_5 \partial x_3}= -\frac{\mu \beta _s(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )},\\&\frac{\partial ^2 f_3}{\partial x^2_5}= -2\frac{\mu \beta _s(\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_2 \partial x_4}\\&\quad = \frac{\mu \beta _s \delta _a (1-\rho )}{\pi _s (\phi _s+\mu )}, \frac{\partial ^2 f_3}{\partial x_5 \partial x_4}=- \frac{\mu \beta _s (\mu +\rho \phi _s)}{\pi _s (\phi _s+\mu )}. \end{aligned}$$

The remaining partial derivatives at \(\epsilon ^0\) are zero. Now we evaluate the coefficient a and b of well-established Theorem 4.1 in Castillo-Chavez et al. [49] as follows:

$$\begin{aligned} a&=\sum \limits _{i,j,k=1}^{7}w_kv_iv_j\frac{\partial ^2f_k(0, \beta ^*)}{\partial x_i\partial x_j}, \quad \text{ and }\quad \\ b&=\sum \limits _{i,k=1}^{7}w_kv_i\frac{\partial ^2f_k(0, 0)}{\partial x_i \beta _s}. \end{aligned}$$

Now, we substitute all above values to find the coefficient a and b at threshold \(\beta ^*=\beta ^*_s\), we get

$$\begin{aligned} a&=\frac{\mu \beta ^*}{\pi _s(\phi _s+\mu )}[(\rho -1)\{v_1v_5(1-\phi _s)\\&\qquad +v_1v_6(\delta _a+\phi _s \delta _h)+v_1v_4\delta _a(1- \phi _s)\\&\qquad +2\mu v_2v_5\\&\qquad +\mu v_2v_6(1+\delta _h)+2v_4v_2\delta _a\}\\&\qquad -(\mu +\rho \phi _s)\{v_4v_5(2+\delta _a)\\&\qquad +2v_4v_6(\delta _a+\delta _h)+2v_5v_6\\&\qquad +v_7(v_4\delta _a+v_5+v_6\delta _h)+2(v^2_5+v^2_6-v^2_4)\\&\qquad +v_3(v_4\delta _a+v_5)\}] \end{aligned}$$

and

$$\begin{aligned} b=\frac{w_3(\mu +\rho \phi _s)}{\phi _s+\mu }(v_4\delta _a+v_5+v_6\delta _h)>0. \end{aligned}$$

Here, the value of b is always positive, the system (1) undergoes backward bifurcation at \(R_0=1\) if \(a>0\), i.e

$$\begin{aligned}&\rho>\frac{A+\mu B}{A-\phi _s B}, \quad \text{ provided } \quad A-\phi _s B>0, \quad \nonumber \\&\quad \text{ i.e, } \quad \phi _s >A/B \end{aligned}$$
(9)

where,

$$\begin{aligned}&A=v_1v_5(1-\phi _s)+v_1v_6(\delta _a+\phi _s \delta _h)\\&\quad +v_1v_4\delta _a(1- \phi _s)+2\mu v_2v_5+\mu v_2v_6(1+\delta _h)\\&\quad +2v_4v_2\delta _a\\&B=v_4v_5(2+\delta _a)+2v_4v_6(\delta _a+\delta _h)+2v_5v_6\\&\quad +v_7(v_4\delta _a+v_5+v_6\delta _h)+2(v^2_5+v^2_6-v^2_4)\\&\quad +v_3(v_4\delta _a+v_5) \end{aligned}$$

Theorem 3

The SCEAIHR model system (1) exhibits a backward bifurcation at \(R_0=1\), if the parametric restriction in (9) holds.

Moreover, as comorbidity individual becomes always infected, backward bifurcation occurs in SCEAIHR model. Now for a case, it can be noted that comorbidity individuals do not get infection due to maintaining social distancing, wearing mask and proper sanitation, i.e, \(\rho =0.\) The bifurcation coefficient a is as follow :

$$\begin{aligned} a=-(A+\mu B)<0. \end{aligned}$$

As, \(a<0\), \(b>0\), by Theorem 4.1 in Castillo-Chavez et al., a transcritical bifurcation occurs at \(R_0=1\) for \(\rho =0\) and endemic equilibrium and the endemic equilibrium \(\epsilon ^*\) is locally asymptotically stable for \(R_0>1.\) Here, a backward bifurcation do not exist for \(\rho =0\).

Theorem 4

The SCEAIHR model system (1) experiences a transcritical bifurcation at \(R_0=1\) with parametric restriction in (9) holds, i.e, \(\rho =0\).

4 Computer simulation and results

In this section, we perform numerical simulation and its biological interpretation to complement the analytical findings. In the previous section, local stability for infection-free equilibrium and the existence of endemic equilibrium are studied. Moreover, backward bifurcation and transcritical bifurcation are observed. In order to validate the analytical findings, we estimate parameter values of the SCEAIHR model (1).

4.1 Model calibration

For the duration from March, \(25^{th}\) 2020 to October, \(31^{st}\) 2020 is considered for model calibration. For this analysis, we have taken daily COVID-19 cases in India. Daily cases notified by COVID-19 were obtained for India from [53]. The model (1) is fitted for new hospitalized COVID cases in India on a regular basis. Due to the high infectivity, the notified patients become hospitalized quickly and it is also easy to confirm the hospitalized cases from the recorded results. We have enlisted the main model parameters, which are estimated from the data in Table 1. By adopting the model to the new regular cases reported, six parameters of the model have been estimated, such as (a) transmission rate (\(\beta _s\)), (b) modification factor for asymptomatic (\(\delta _a\)) and symptomatic (\(\delta _h\)), (c) rate of co-morbidity development by susceptible individuals (\(\phi _s\)), (d) modification factor for comorbidity development (\(\rho \)) and (e) average hospitalized rate of infected individuals (\(\theta \)). The data will also estimate some of the initial conditions of the model (1). In MATLAB, the nonlinear least-square solver \(fmincon \) has been used during the defined time span to fit the simulated new daily data of COVID-19 recorded by India. The \(95\%\) confidence area is generated by using the Delayed Rejection Adaptive Metropolis (DRAM) algorithm. A description of this model fitting technique is given in [54]. Tables 1 and 2 provide the parameters and initial conditions respectively, which are estimated by the above technique. The fitting of India’s daily new hospitalized COVID-19 cases is seen in Fig. 2. The basic reproduction number is estimated at \(R_0=1.3607\) by using the fixed parameters from Table 1 and parameters that are estimated from the model.

In order to recognize the most significant parameters to infected individual, we next perform sensitivity analysis followed by uncertainty analysis.

Table 2 Estimated initial population sizes for India
Full size table
Fig. 2
figure 2

The SCEAIHR model fitted to daily new confirmed COVID-19 cases in India. Observed data points are shown in black dots and the solid red line depicts the model simulated curve

Full size image
Table 3 Sensitivity indices of the parameters of SCEAIHR model (1) to I and \(R_0\). \(I_i;\) i= 100, 150, 200 th day
Full size table

4.2 Sensitivity analysis

We apply PRCC(Partial rank correlation coefficient) method for sensitivity analysis and LHS (Latin hypercube sampling) method for uncertainty analysis. A detailed technique can obtained in Marino et. al, [55]. We assign uniform distribution the parameters namely, \(\beta _s\), \(\delta _a\), \(\delta _h\), \(\rho \), \(\theta \), \(\phi _s\) \(\eta \) and \(\xi \) with \(95\%\) confidence domain. We consider baseline values as parameter values. The outputs are given in Table 3 with bar diagram in Fig. 3a. From Fig. 3a, it can be seen that \(\beta _s\), \(\rho \) and \(\xi \) are influential parameter to infected individual. Moreover, we study the sensitivity indices of basic reproduction number \(R_0\). Here, only \(\phi _s\) is negatively correlated, and \(\beta _s\), \(\delta _a\), \(\rho \), and \(\xi \) are positively correlated to \(R_0\), given in Fig. 3b.

Fig. 3
figure 3

a and b PRCC indicating sensitivity indices to infected individual (I) and basic reproduction number \((R_0)\). PRCC values of various parameters with the level of significance 0.05. Sample size = 500 for each parameters is taken based on LHS approach with uniform probability distribution

Full size image

As basic reproduction number \((R_0)\) quantifies the expectation of decreasing or increasing the epidemic evolution, we next study the effects of parameter variation on \(R_0\).

4.3 Effects of parametric variation on basic reproduction number

We further study the effects of parameter variations on basic reproduction number \(R_0\) under \( \rho \times \phi _s \in (0,1]\times (0,0.1]\), \(\rho \times \beta _s \in (0,1]\times (0,2]\), \(\phi _s \times \beta _s \in (0,0.1]\times (0,2]\) in Fig. 4. We observe that only the increasing value of \(\rho \) can change \(R_0<1\) to \(R_0>1\) in Fig. 4a. From Fig. 4b, the increasing value simultaneously changes the value of \(R_0\). Further, it can be also seen that the value of \(R_0\) always remains less than one within the parametric plane of \((\phi _s, \beta _s) \in (0,0.1]\times (0,2]\).

Fig. 4
figure 4

Contour plots indicating the nature of change in basic reproduction number(\(R_0\)) of SCEAIHR model under parametric planes. a \(R_0\) versus \( (\rho , \phi _s) \in (0,1]\times (0,0.1]\). b \(R_0\) versus \((\rho , \beta _s) \in (0,1]\times (0,2]\). (c) \(R_0\) versus \((\phi _s, \beta _s) \in (0,0.1]\times (0,2]\)

Full size image

4.4 Bifurcation diagram

On investigation of the existence of endemic equilibrium, we derive the sub-threshold range of bistable equilibrium in the SCEAIHR model (1). Thus backward bifurcation can be seen within the domain \(R_0^*<R_0<1\quad (R_0^*=0.4617)\) with \(\rho \in [0.01,0.8]\), given in Fig. 5a, where two positive endemic equilibrium coexist, i.e, asymptotically stable equilibrium (blue line) and unstable equilibrium (red line). From an epidemiological viewpoint, the scenario of backward bifurcation indicates that the model possesses two endemic equilibrium. However, infection-free equilibrium can exist only for \(R_0< R^*_0\). Indeed, this restriction is sufficient for the eradication of infection from the system. Moreover, it sometimes depends on the initial size of the sub-population of model.

On the other hand, if comorbidity individuals do not acquire infection, i.e, \(\rho =0\), the model (1) experiences transcritical with \(\phi _s \in [10\times 10^{-6},2.7\times 10^{-5}]\) given in Fig. 5b. Here, only one endemic equilibrium (blue line) and infection-free equilibrium (red line) exist for \(R_0>1.\) It indicates that force of infection is not strong enough to spread out as all susceptible individuals take the precaution of disease spreading, like, wearing a mask, social distancing, maintaining sanitation.

Moreover, it can be also noted that increasing the value of \(\phi _s\) becomes a challenging task for the eradication of infection. Numerically, it can be seen that a backward bifurcation regime increases gradually with increases of \(\phi _s\) with \(\rho \in [0.01,0.8]\), given in Fig. 6. Consequently, the value of \(R_0\) is essential to be reduced to ensure the eradication of infection in such a way that \(R_0^*\) and \(R_0\) is close to one.

Fig. 5
figure 5

a \(R_0\) versus \(\zeta ^*\) plot indicating backward bifurcation of SCEAIHR model in \(\rho \in [0.01,0.8]\). b \(R_0\) versus \(\zeta ^*\) plot illustrating transcritical bifurcation of SCEAIHR model in \(\phi _s \in [10\times 10^{-6},2.7\times 10^{-5}]\) with \(\rho =0\). All the remaining parameters values are reported in Table 1

Full size image
Fig. 6
figure 6

Impacts of variation in \(\phi _s\), on backward bifurcation with \(\rho \in [0.01,0.8]\), keeping all parameters value remained same as in Table 1. The diagram exhibits that the extent of backward bifurcation regime increases gradually with the increasing of \(\phi _s\)

Full size image

Now we study the variation of infection intensity. For this purpose, we consider average of force of infection for daily basis cases.

4.5 Effects of parametric variation on force of infection

Now we investigate the fluctuation of force of infection \(\zeta ^*\) by considering \(<\zeta ^*>=\frac{1}{N} \sum \nolimits ^N_{i=1}\zeta ^*(i)\), where N being length of series \(\{\zeta ^*(i)\}\). Figure 7a, b exhibit the fluctuations of average force of infection \(<\zeta ^*>\) under \(\phi _s \in (0, 0.1]\) and \(\beta _s \in (0,2]\) respectively. From Fig. 7a, b, increasing and decreasing trend can be observed in \(<\zeta ^*>\) respectively. It indicates that average force of infection decreases with the increase of \(\phi _s \in (0,0.1]\) and average force of infection increases with the increase of \(\beta _s \in (0,2]\) in the model (1). Moreover, in order to understand the combined effect under \((\phi _s, \beta _s) \in (0,0.1]\times (0,2]\) on \(<\zeta ^*>\), a matrix plot is given in Fig. 7c. In Fig. 7c, it can be mentioned that the average force of infection is dependent on value of \(\phi _s\) for any value of \(\beta _s\), defined in efferent color region of increased value of \(\phi _s \in (0,0.1].\) In order to quantitative measure the degree of disorder in force of infection. Shannon entropy [32] is employed for this purpose. Here, disorder means the non-uniform distribution of infection under distribution of susceptible.

Fig. 7
figure 7

a, b represent \(\phi _s\) versus \(\zeta ^*\) plot (with \(\rho \in (0,0.1])\) and \(\beta _s\) versus \(\zeta ^*\) plot (with \(\beta _s \in (0,2])\). c represent \(\zeta ^*\) over \((\phi _s, \beta _s)\) matrix plot, where \((\phi _s, \beta _s) \in (0.1] \times (0,2]\). The corresponding color bar indicates values of \(\zeta ^*\). The values of the other parameters are taken as same, shown in Table 1

Full size image
Fig. 8
figure 8

a, b represent \(\phi _s\) versus \(En(\zeta ^*)\) plot (with \(\phi _s \in (0,0.1])\) and \(\beta _s\) versus \(En(\zeta ^*)\) plot (with \(\beta _s \in (0,2])\). (c) represent \(En(\zeta ^*)\) over \((\phi _s, \beta _s)\) matrix plot, where \((\phi _s, \beta _s) \in (0,0.1] \times (0,2]\). The corresponding color bar indicates values of \(En(\zeta ^*)\). The values of the other parameters are taken as same, shown in Table 1

Full size image

4.6 Entropy in force of infection

Shannon entropy is generally defined as

$$\begin{aligned} H=-\sum \limits _{i=1}^N p(\zeta ^*_i)\log (p(\zeta ^*_i) \end{aligned}$$

N being length of event \(\zeta ^*_i\) and \(p(\zeta ^*_i)\) is probability of event \(\zeta ^*_i\), i.e, relative frequency of occurrence of non-recurrent event \(\zeta ^*_i\). The trend of \(En(\zeta ^*_i)\) on \(\phi _s \in (0,0.1]\) and \(\beta _s \in (0,2]\) are shown in Fig. 8a, b. Figure 8a shows that deceasing trend of \(En(\zeta ^*_i)\) with increase of \(\phi _s\). On the contrary, \(En(\zeta ^*_i)\) increases with \(\beta _s\) in Fig. 8b. From Figs.7a, b and 8a, b, it can be noted that the trend of \(En(\zeta ^*_i)\) is highly correlated with the fluctuation in force of infection \(\zeta ^*\). Moreover, we also plot in Fig. 8c to study the dependence of \(En(\zeta ^*_i)\) on \((\phi _s, \beta _s)\in (0,0.1]\times (0,2]\). Further comparing Figs. 7c and 8, we observe similar pattern of increasing entropy between \(\zeta ^*\) and \(En(\zeta ^*)\). This result reveals the additional evidence about the measure of dynamical disorder in force of infection in the model (1) for parameter regimes.

5 Discussion and conclusion

In this paper, we have proposed and studied a mathematical model for disease dynamics of COVID-19 accounting of impacts of comorbidities on the complication of COVID-19. The proposed model has been calibrated by using new daily cases of India. The qualitative properties of the model have been studied and the basic reproduction number has been calculated by the method of the next-generation matrix. The model has asymptotically stable infection-free equilibrium for less than a unity of basic reproduction number. Using the center manifold theorem, the phenomena of backward bifurcation have been observed for increasing the modification factor of comorbidity development. This indicates that infection persists for less than a unity of basic reproduction number. The occurrence of backward bifurcation assures the rich dynamics of the model. From an epidemiological viewpoint, comorbidity individuals acquire more re-infection due to lack of surveillance and precautions like wearing masks, social distancing, proper sanitation, etc. Further, endemic equilibrium has become asymptotically stable if the modification factor for comorbidity is zero (\(\rho =0\)), i,e. none of the comorbidity individual gets an infection and keeps maintained themselves with high surveillance. In these circumstances, more susceptible individuals have acquired infection and become exposed individuals as basic reproduction is more than unity, indeed, exposed individuals have a strong immunity to prevent COVID-19 infection in this context. Moreover, the increase of comorbidity development and modification factor simultaneously has increased the backward bifurcation regimes. Consequently, this can lead to a disaster situation.

Sensitivity analysis of the model reveals that transmission rate (\(\beta _s\)), modification factor of comorbidity development (\(\rho \)), comorbidity development (\(\phi _s\)) have a significant influence on infected individuals and basic reproduction number (\(R_0\)). In order to control disease transmission, a policy might be implemented by enhancing surveillance with proper maintaining sanitation and keep safe from infected individuals.

On investigation of the pattern of transmission dynamics, the mean fluctuations of the force of infection have shown decreasing as well as increasing trend with comorbidity development (\(\phi _s\)) and transmission rate (\(\beta _s\)). Consequently, the combined effect has shown an increasing trend to the average force of infection. From the dynamical viewpoint, the measure of disorder in force of infection, i.e, the Shannon entropy has provided evidence towards the higher entropy production indicating the more powerful force of infection, i.e, the infection reaches a significant proportion in susceptible individuals. This might lead to a devastating situation in society regarding disease transmission.

Finally, our study assures that the increase of force of infection builds up with the enhanced entropy production attributed to highly disorder in epidemic evolution. The production of entropy are concepts that can be helpful to guide computational biologists to elucidate the associations between mean fluctuation and changes in parameters to develop policy in disease control and novel vaccination strategies. Thus, it would be useful to include in future publications how vaccination policy can be fruitful.