Modeling and dynamics analysis of Zika transmission with contaminated aquatic environments

Abstract

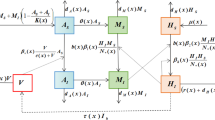
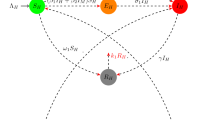
Since the outbreak in Brazil, Zika has received the worldwide attention. Zika virus is mainly transmitted via the bites of Aedes mosquito. Recently, experimental evidence demonstrates that Zika virus in contaminated aquatic environments can be transmitted to aquatic mosquitoes through breeding. To study the effects of contaminated aquatic environments on Zika transmission, we propose a new Zika model by introducing a general incidence function. For a general incidence function, we calculate the basic reproduction number $R_0$, analyze the stability of disease-free equilibria and give general conditions with the occurrence of backward bifurcation. For the two special sublinear incidence functions, $R_0=1$ is a sharp threshold. It means that the disease can be eradicated by reducing $R_{0}$ below 1. For the special nonlinear incidence function, we investigate theoretically backward bifurcation and saddle-node bifurcation and simulate numerically Hopf bifurcation. Analysis results suggest that transmission force from contaminated aquatic environments to aquatic mosquitoes plays an important role in generating complex dynamics. Furthermore, our model is extended to explore the effects of temperature variability on spread of Zika disease.

Appendices

Appendix: A Proof of Lemma 1

Proof

Denote $\varphi (t)=(S_a(t), I_a(t), S_{m}(t), I_{m}(t), S_{h}(t), I_{h}(t), Z(t))$, and $\varphi (t)$ satisfies system (2). It follows from system (2) and $\varphi (0)\ge 0$ that

$$\begin{aligned} \begin{aligned} S_{a}(t)=&S_a(0)\exp \\&\left( - \frac{\rho }{K}\int ^{t}_{0}(S_{m}(s)+I_{m}(s))\mathrm{d}s- \int ^{t}_{0}g(Z(s))\mathrm{d}s-(\omega +\mu _{a})t \right) \\&+\rho \int ^{t}_{0}(S_{m}(s)+I_{m}(s)) \left( 1-\frac{I_{a}(s)}{K}\right) \exp \\&\bigg (- \frac{\rho }{K}\int ^{t}_{s}(S_{m}(\xi )+I_{m}(\xi ))d\xi \\&- \int ^{t}_{s}g(Z(\xi ))d\xi -(\omega +\mu _{a})(t-s) \bigg )\mathrm{d}s\ge 0,\\ S_{m}(t)=&S_m(0)\exp \left( -\frac{b\beta _{1}}{N_{h}}\int ^{t}_{0}I_{h}(s)\mathrm{d}s-\mu _m t\right) \\&+\omega \int ^{t}_{0} S_{a}(s)\exp \left( -\frac{b\beta _{1}}{N_{h}}\int ^{t}_{s}I_{h}(\xi )d\xi -\mu _m (t-s)\right) \mathrm{d}s \ge 0,\\ S_{h}(t)=&S_h(0)\exp \left( -\frac{b\beta _{2}}{N_{h}}\int ^{t}_{0}I_{m}(s)\mathrm{d}s-\mu _h t\right) +\varLambda \int ^{t}_{0} \exp \\&\left( -\frac{b\beta _{2}}{N_{h}}\int ^{t}_{s}I_{m}(\xi )d\xi -\mu _h (t-s)\right) \mathrm{d}s \ge 0,\\ I_{a}(t)=&I_{a}(0)e^{-(\omega +\mu _{a})t} +\int ^{t}_{0}g(Z(s))S_{a}(s)e^{-(\omega +\mu _{a})(t-s)}\mathrm{d}s \ge 0,\\ I_{m}(t)=&I_{m}(0)e^{- \mu _{m}t} +\int ^{t}_{0}\\&\left( \omega I_{a}(s)+\frac{b\beta _{1}}{N_{h}}I_{h}(s)S_{m}(s)\right) e^{-\mu _{m}(t-s)}\mathrm{d}s \ge 0,\\ I_{h}(t)=&I_{h}(0)e^{- (\mu _{h}+r)t} + \frac{b\beta _{2}}{N_{h}}\int ^{t}_{0}I_{m}(s)S_{h}(s)e^{-(\mu _{h}+r)(t-s)}\mathrm{d}s \ge 0,\\ Z(t)=&Z(0)e^{- ct} + \sigma \int ^{t}_{0}I_{h}(s) e^{-c(t-s)}\mathrm{d}s \ge 0. \end{aligned} \end{aligned}$$

If $S_{a}(0)>0,$ $I_{a}(0)>0,$ $S_{m}(0)>0,$ $I_{m}(0)>0,$ $S_{h}(0)>0,$ $I_{h}(0)>0$ and $Z(0)>0,$ then $S_{a}(t)>0,$ $I_{a}(t)>0,$ $S_{m}(t)>0,$ $I_{m}(t)>0,$ $S_{h}(t)>0,$ $I_{h}(t)>0$ and $Z(t)>0,$ $\forall ~t>0.$

From system (2), we can obtain

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}(S_{m}+I_{m})}{\mathrm{d}t}&= \omega (S_a+I_a)- \mu _{m} (S_{m}+I_{m}), \\ \frac{\mathrm{d}(S_{h}+I_{h})}{\mathrm{d}t}&= \varLambda -r I_{h}-\mu _{h} (S_{h}+I_{h}).\\ \end{aligned} \end{aligned}$$

Since $S_a+I_a\le K,$ we have

$$\begin{aligned} \begin{aligned} \frac{\mathrm{d}(S_{m}+I_{m})}{\mathrm{d}t}&\le \omega K -\mu _{m} (S_{m}+I_{m}), \\ \frac{\mathrm{d}(S_{h}+I_{h})}{\mathrm{d}t}&\le \varLambda -\mu _{h} (S_{h}+I_{h}).\\ \end{aligned} \end{aligned}$$

According to the standard comparison theorem (see [49]), we can obtain

$$\begin{aligned} \begin{aligned} S_{m}(t)+I_{m}(t)&\le (S_{m}(0)+I_{m}(0))e^{-\mu _{m} t}+ \frac{ \omega K}{\mu _{m} }(1-e^{-\mu _{m} t}), \\ S_{h}(t)+I_{h}(t)&\le (S_{h}(0)+I_{h}(0))e^{-\mu _{h}t}+\frac{\varLambda }{\mu _{h}}(1-e^{-\mu _{h}t}).\\ \end{aligned} \end{aligned}$$

If $S_{m}(0)+I_{m}(0)\le \frac{ \omega K}{\mu _{m}},~ S_{h}(0)+I_{h}(0)\le \frac{\varLambda }{\mu _{h}}$, then $S_{m}(t)+I_{m}(t)\le \frac{ \omega K}{\mu _{m}},~ S_{h}(t)+I_{h}(t)\le \frac{\varLambda }{\mu _{h}},$ for $\forall ~t\ge 0.$

It follows from the seventh equation of system (2) that

$$\begin{aligned} \frac{\mathrm{d}Z}{\mathrm{d}t}\le \sigma \frac{\varLambda }{\mu _{h}} -c Z. \end{aligned}$$

Similarly, we have $Z\le \frac{\sigma \varLambda }{c\mu _{h}}.$ Therefore, $\varGamma$ is positively invariant of system (2). This completes the proof. $\square$

B The simulation and biological explanation of the next-generation matrix $FV^{-1}$

Based on the idea of P. van den Driessche and James Watmough in [30], the next-generation matrix $FV^{-1}$ is explained below.

Let $x=(x_1,x_2,x_3,x_4,x_5,x_6,x_7)^T,$ where $x_1=I_a,x_2=I_m,x_3=I_h,x_4=Z,x_5=S_a,x_6=S_m,x_7=S_h.$ Let

$$\begin{aligned} \begin{array}{lll} &{}&{}{\mathcal {F}} (x) = \left( \begin{array}{c} g(Z)S_{a} \\ b\beta _{1}\frac{I_{h}S_{m}}{N_{h}} \\ b\beta _{2}\frac{I_{m}S_{h}}{N_{h}}\\ 0\\ 0\\ 0\\ 0\\ \end{array} \right) ,~~~~\\ &{}&{}{\mathcal {V}}^{+}(x)= \left( \begin{array}{c} 0\\ \omega I_{a}\\ 0\\ \sigma I_{h}\\ \rho (S_{m}+I_{m})\left( 1-\frac{S_{a}+I_{a}}{K}\right) \\ \omega S_{a}\\ \varLambda \\ \end{array} \right) , \end{array}\\ \begin{array}{lll} &{}&{}{\mathcal {V}}^{-}(x)= \left( \begin{array}{c} (\omega +\mu _{a})I_{a}\\ \mu _{m}I_{m}\\ (\mu _{h}+r)I_{h}\\ cZ\\ g(Z)S_{a}+(\omega +\mu _{a})S_{a}\\ b\beta _{1}\frac{I_{h}S_{m}}{N_{h}}+\mu _{m}S_{m}\\ b\beta _{2}\frac{I_{m}S_{h}}{N_{h}}+\mu _{h}S_{h}\\ \end{array} \right) . \end{array} \end{aligned}$$

${\mathcal {F}}_i(x)$ represents the input rate of newly infected individuals in the ith compartment, ${\mathcal {V}}_i^{+}(x)$ represents rate of transfer of individuals into the ith compartment by all other means. ${\mathcal {V}}_i^{-}(x)$ represents the rate of transfer of individuals out of the ith compartment. So, the Zika transmission model (1) can be represented as follows

$$\begin{aligned} \frac{\mathrm{d}x_i}{\mathrm{d}t}={\mathcal {F}}_i(x)-{\mathcal {V}}_i(x),i=1,2,...,7, \end{aligned}$$

where ${\mathcal {V}}_i(x)={\mathcal {V}}_i^{-}(x)-{\mathcal {V}}_i^{+}(x).$ Let $F =\left( \frac{\partial {\mathcal {F}}_i}{\partial x_j}(x_0) \right)$ and $V =\left( \frac{\partial {\mathcal {V}}_i}{\partial x_j}(x_0) \right)$ with $x_0=(0,0,0,0,A_0,M_0,S_h^0)$, $1\le i,j\le 4.$ By simple calculation, we can get

$$\begin{aligned} \begin{aligned}&F = \left( \begin{array}{cccc} 0 &{} 0 &{} 0 &{} g'(0)A_0\\ 0 &{} 0 &{} \frac{b\beta _1 M_0}{ N_h} &{}0\\ 0 &{} b\beta _2 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ \end{array} \right) ,~\\&V= \left( \begin{array}{cccc} \omega +\mu _a &{} 0 &{} 0 &{} 0\\ -\omega &{} \mu _m &{} 0 &{} 0\\ 0 &{} 0 &{} \mu _{h}+r &{} 0\\ 0 &{} 0 &{} -\sigma &{} c\\ \end{array} \right) . \end{aligned} \end{aligned}$$

Then, we can obtain

$$\begin{aligned} \begin{aligned} V^-= \left( \begin{array}{cccc} \frac{1}{\omega +\mu _a}&{} 0 &{} 0 &{} 0\\ \frac{\omega }{(\omega +\mu _a) \mu _m }&{} \frac{1}{\mu _m} &{} 0 &{} 0\\ 0 &{} 0 &{} \frac{1}{\mu _{h}+r} &{} 0\\ 0 &{} 0 &{} \frac{\sigma }{(\mu _{h}+r)c} &{} \frac{1}{c}\\ \end{array} \right) . \end{aligned} \end{aligned}$$

$FV^{-1}$ is given by

$$\begin{aligned} \begin{aligned} FV^{-1} = \left( \begin{array}{cccc} 0 &{} 0 &{} \frac{ \sigma A_0}{c( \mu _{h}+r)}g'(0) &{} \frac{A_0}{c }g'(0) \\ 0 &{} 0 &{} \frac{b\beta _1 M_0}{( \mu _{h}+r)N_h} &{} 0 \\ \frac{b\beta _2 \omega }{\mu _m( \omega +\mu _a)} &{} \frac{b\beta _2 }{\mu _m } &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ \end{array} \right) ,\\ \end{aligned} \end{aligned}$$

To explain the meaning of each element of the matrix $FV^{-1}$ and provide a meaningful definition of $R_0$, consider the fate of an infected individual introduced into the kth compartment in a disease free population. The element (j, k) of $V^{-1}$ is the average time that this infected individual spends in the jth compartment during its lifetime, assuming that the population remains near the DFE $x_0$ and barring reinfection. The element (i, j) of F is the rate at which infected individuals in the jth compartment produce new infections in the ith compartment. Therefore, the element (i, k) of the product $FV^{-1}$ is the expected number of new infections in the ith compartment produced by the infected individual originally introduced into the kth compartment. So, following Diekmann et al. [28], P. van den Driessche and James Watmough in [30] call $FV^{-1}$ the next-generation matrix for model (1) and set

$$\begin{aligned} R_{0} =\rho (FV^{-1}). \end{aligned}$$

C Proof of Theorem 2

Proof

Theorem 1 shows the local stability of $E_{01}$. Now, we just prove the global attraction of $E_{01}$.

Denote $f^{ \infty }\doteq \limsup \limits _{t\rightarrow +\infty } f(t)$, $f_{ \infty }\doteq \liminf \limits _{t\rightarrow +\infty }f(t)$, $\varphi (t)=(S_a(t), I_a(t), S_{m}(t),$ $I_{m}(t),$ $S_{h}(t),$ $I_{h}(t),$ Z(t)), $\forall ~ t\ge 0$ and $\varphi (t)$ satisfies system (2). From Lemma 1, we know that $\varphi (t)$ with initial value $\varphi (0)\ge 0$ satisfies $0\le \varphi _{ \infty }\le \varphi ^{ \infty }<+\infty$. From the fluctuation lemma [31], there exists a sequence $\{t_n\}$ such that $t_n\rightarrow +\infty ,~\varphi (t_n)\rightarrow \varphi ^{\infty }$ and $\frac{\mathrm{d}\varphi (t_n)}{\mathrm{d}t}\rightarrow 0$ as $n\rightarrow +\infty$. Substituting $t_n$ into system (2), letting $n\rightarrow +\infty$, and combining $g(Z)\le g'(0)Z$, we can obtain

$$\begin{aligned} \left\{ \begin{aligned}&(\omega +\mu _{a})S_{a}^{\infty }\le \frac{\rho }{K}(S_{a}^{\infty }+I_{a}^{\infty })(S_{m}^{\infty }+I_{m}^{\infty }) \\&\quad +g'(0)Z^{\infty }S_{a}^{\infty }+(\omega +\mu _{a})S_{a}^{\infty }\le \rho (S_{m}^{\infty }+I_{m}^{\infty }),&(12a)\\&(\omega +\mu _{a})I_{a}^{\infty }\le g'(0)Z^{\infty }S_{a}^{\infty },&(12b)\\&\mu _{m}S_{m}^{\infty } \le \mu _{m}S_{m}^{\infty } +\frac{b\beta _{1}}{N_{h}}I_{h}^{\infty }S_{m}^{\infty }\le \omega S_{a}^{\infty },&(12c)\\&\mu _{m}I_{m}^{\infty }\le \omega I_{a}^{\infty }+\frac{b\beta _{1}}{N_{h}}S_{m}^{\infty }I_{h}^{\infty },&(12d)\\&\mu _{h}S_{h}^{\infty }\le \mu _{h}S_{h}^{\infty }+\frac{b\beta _{2}}{N_{h}}I_{m}^{\infty }S_{h}^{\infty } \le \varLambda ,&(12e)\\&(\mu _{h}+r)I_{h}^{\infty }\le \frac{b\beta _{2}}{N_{h}}S_{h}^{\infty }I_{m}^{\infty },&(12f)\\&c Z^{\infty }\le \sigma I_{h}^{\infty }.&(12g)\\ \end{aligned} \right. \nonumber \\ \end{aligned}$$

(12)

Let $A^{\infty }=S_{a}^{\infty }+I_{a}^{\infty },$ $M^{\infty }=S_{m}^{\infty }+I_{m}^{\infty }.$ From (12a) and (12b), we have

$$\begin{aligned} \frac{\rho }{K}M^{\infty }A^{\infty }+ (\omega +\mu _{a})A^{\infty }\le \rho M^{\infty }. \end{aligned}$$

(13)

From (12c) and (12d), we have

$$\begin{aligned} A^{\infty }\ge \frac{\mu _m}{\omega } M^{\infty }. \end{aligned}$$

(14)

Substituting (14) into (13), one has

$$\begin{aligned} M^{\infty }\le \frac{ \omega K}{\mu _{m}}\left( 1-\frac{\mu _{m} (\omega +\mu _{a})}{\rho \omega } \right) =M_0. \end{aligned}$$

(15)

So,

$$\begin{aligned} A^{\infty }\le A_0. \end{aligned}$$

(16)

From (12e), we have

$$\begin{aligned} S_{h}^{\infty }\le \frac{\varLambda }{\mu _h}. \end{aligned}$$

(17)

Substituting (12b), (12f) and (12g) into (12d), we get

$$\begin{aligned} I_{m}^{\infty }\le \frac{b^2 \beta _1\beta _2}{\mu _m (\mu _{h}+r)}\frac{S_{m}^{\infty }}{N_h}I_{m}^{\infty }+ \frac{b \beta _2 \omega \sigma g'(0)}{c \mu _{m}(\omega +\mu _{a}) (\mu _{h}+r)} S_{a}^{\infty }I_{m}^{\infty }.\nonumber \\ \end{aligned}$$

(18)

If $I_{m}^{\infty }>0$, then, from inequality (18) and (12c), we have

$$\begin{aligned} 1\le \frac{b^2 \beta _1\beta _2}{\mu _m (\mu _{h}+r)N_h}\frac{\omega }{\mu _m}S_{a}^{\infty }+ \frac{b \beta _2 \omega \sigma g'(0)}{c \mu _{m}(\omega +\mu _{a}) (\mu _{h}+r)} S_{a}^{\infty }. \end{aligned}$$

Since $R_0<1$, we have $A_{0} < S_{a}^{\infty },$ which is a contradiction since $S_{a}^{\infty }\le A_{0}.$ Thus, $I_{m}^{\infty }=0$. From (12f), (12g) and (12b), we have $I_{h}^{\infty }=0$, $Z^{\infty }=0$ and $I_a^{\infty }=0$. So,

$$\begin{aligned} \lim \limits _{t\rightarrow +\infty }I_a(t)=\lim \limits _{t\rightarrow +\infty }I_m(t) =\lim \limits _{t\rightarrow +\infty }I_h(t)=\lim \limits _{t\rightarrow +\infty }Z(t)=0. \end{aligned}$$

Using the fluctuation lemma again, one can obtain

$$\begin{aligned} S_{a\infty }= A_0,~ S_{m\infty }= M_0,~ S_{h\infty }=\frac{\varLambda }{\mu _h}. \end{aligned}$$

Combining with (15), (16) and (17), we have

$$\begin{aligned}&\lim \limits _{t\rightarrow +\infty }S_a(t)= A_0,~\lim \limits _{t\rightarrow +\infty }S_m(t) =M_0,\\&\lim \limits _{t\rightarrow +\infty }S_h(t)=\frac{\varLambda }{\mu _h}. \end{aligned}$$

This completes the proof. $\square$

D Proof of Theorem 4

Proof

Define

$$\begin{aligned} \begin{aligned} X_{0}&=\{(S_a, I_a, S_{m}, I_{m}, S_{h}, I_{h}, Z )\in \varGamma ~|~I_{a}> 0,\\&\quad I_{m}> 0, I_{h}> 0, Z>0 \},\\ \partial X_{0}&=\varGamma \backslash X_{0}. \end{aligned} \end{aligned}$$

First, it is easy to show that $X_{0}$ is a positively invariant set for system (2), and $\partial X_{0}$ is closed in $\varGamma$. Furthermore, it follows from Lemma 1 that system (2) is point dissipative. Denote $\varphi (0)=(S_a(0), I_a(0), S_{m}(0), I_{m}(0), S_{h}(0), I_{h}(0), Z(0))$. Let $\varphi (t)=(S_a(t), I_a(t), S_{m}(t),I_{m}(t), S_{h}(t), I_{h}(t), Z(t))$ be a solution of system (2) with $\varphi (0)$. Set

$$\begin{aligned} \begin{aligned} G_{\partial }=\{&\varphi (0)~|~\varphi (t)~ \text {satisfies system}~(2) ~\text {and} ~ \varphi (t)\in \partial X_{0}, \forall ~t\ge 0 \}, \\ {\tilde{G}}_{\partial }=\{&(S_a , 0, S_{m}, 0, S_{h}, 0, 0)\in \varGamma ~|~ S_a\ge 0, S_m\ge 0, S_h>0\}. \end{aligned} \end{aligned}$$

Next, we will show that $G_{\partial }={\tilde{G}}_{\partial }.$ It is obvious that ${\tilde{G}} _{\partial } \subseteq G_{\partial },$ then we only need to prove $G_{\partial } \subseteq {\tilde{G}} _{\partial }.$ Assume $\varphi (0)\in G_{\partial }$. Then, $\varphi (t)\in \partial X_{0}, \forall ~t\ge 0$. We will prove that $I_{a}(t)=I_{m}(t)=I_{h}(t)=Z(t)=0, \forall ~t\ge 0.$ Suppose not. Then, there exists $t_0\ge 0$ such that at least one of $I_a(t_0)$, $I_m(t_0)$, $I_h(t_0)$ and $Z(t_0)$ is not zero. Without loss of generality, assume that $I_{a}(t_{0})>0$, $I_{m}(t_{0})=I_{h}(t_{0})=Z(t_{0})=0$. Then, from system (2), we have, for $\forall ~t>t_{0}$,

$$\begin{aligned} \begin{aligned}&I_{a}(t)=I_{a}(t_{0})e^{-(\omega +\mu _{a})(t-t_{0})}\\&\quad +\int ^{t}_{t_{0}}g(Z(s))S_{a}(s)e^{-(\omega +\mu _{a})(t-s)}\mathrm{d}s> 0,\\&\quad I_{m}(t)=I_{m}(t_{0})e^{- \mu _{m}(t-t_{0})}\\&\quad +\int ^{t}_{t_{0}}\left( \omega I_{a}(s)+\frac{b\beta _{1}}{N_{h}}I_{h}(s)S_{m}(s)\right) e^{-\mu _{m}(t-s)}\mathrm{d}s> 0,\\&\quad I_{h}(t)=I_{h}(t_{0})e^{- (\mu _{h}+r)(t-t_{0})}\\&\quad + \frac{b\beta _{2}}{N_{h}}\int ^{t}_{t_{0}}I_{m}(s)S_{h}(s)e^{-(\mu _{h}+r)(t-s)}\mathrm{d}s> 0,\\&Z(t)=Z(t_{0})e^{- c(t-t_{0})}\\&\quad + \sigma \int ^{t}_{t_{0}}I_{h}(s) e^{-c(t-s)}\mathrm{d}s> 0. \end{aligned} \end{aligned}$$

This implies that $\varphi (t)=(S_a(t), I_a(t), S_{m}(t), I_{m}(t), S_{h}(t), I_{h}(t), Z(t))\notin \partial X_{0}$ for $t>t_{0}$. which contradicts $\varphi (t)\in \partial X_{0}, \forall ~t\ge 0$. So, one can obtain $G_{\partial } \subseteq {\tilde{G}}_{\partial }.$ So $G_{\partial }={\tilde{G}}_{\partial }.$ Therefore, it is clear that there are two equilibria $E_{00}$ and $E_{01}$ in $G_{\partial }$.

Next, we will show that $E_{00}$ and $E_{01}$ are isolated invariant sets in $\varGamma$. We need show that $W^{s}(E_{00})\cap X_{0}=\emptyset$ and $W^{s}(E_{01})\cap X_{0}=\emptyset$, where $W^{s}(E_{00})$ and $W^{s}(E_{01})$ are stable manifolds of $E_{00}$ and $E_{01}$, respectively, that is, there exist positive constants $\delta$ and ${\bar{\delta }}$ such that for any solution $\varPhi _{t}(\varphi (0))$ of system (2) with the initial value $\varphi (0)\in X_{0}$, we have

$$\begin{aligned}&\limsup \limits _{t\rightarrow +\infty }d(\varPhi _{t}(\varphi (0)),E_{01})\ge \delta ,\\&\limsup \limits _{t\rightarrow +\infty }d(\varPhi _{t}(\varphi (0)),E_{00})\ge {\bar{\delta }}, \end{aligned}$$

where d is a distant function in $X_{0}$. Here, we only show $\limsup \limits _{t\rightarrow +\infty }d(\varPhi _{t}(\varphi (0)),E_{01})$ $\ge \delta$. If not, then $\limsup \limits _{t\rightarrow +\infty }d(\varPhi _{t}(\varphi (0)),$ $E_{01})< \delta$, that is, there exists $t_1>0$, such that $A_{0}-\delta< S_{a}< A_{0}+\delta$, $M_{0}-\delta< S_{m}< M_{0}+\delta$, $S_h^0-\delta< S_{h}< S_h^0+\delta$, $0< I_{a}<\delta$, $0< I_{m}<\delta$, $0< I_{h}<\delta$ and $0< Z<\delta$ for $\forall ~t>t_1$. Next, we just prove the incidence function $g(Z)=\beta _{3}\frac{Z}{k+Z}.$ For $g(Z)=\beta _3 Z$, its proof is similar. For the incidence function $g(Z)=\beta _{3}\frac{Z}{k+Z},$ one can get, for $\forall$ $t>t_1$,

$$\begin{aligned} \left\{ \begin{aligned}&\frac{\mathrm{d}I_{a}}{\mathrm{d}t}\ge \frac{\beta _{3}(A_{0}-\delta )}{k+\delta }Z-(\omega +\mu _{a})I_{a},\\&\frac{\mathrm{d}I_{m}}{\mathrm{d}t}\ge \omega I_{a}+b\beta _{1}\frac{M_{0}-\delta }{N_{h}}I_{h}-\mu _{m}I_{m},\\&\frac{\mathrm{d}I_{h}}{\mathrm{d}t}\ge b\beta _{2}\frac{S_h^0-\delta }{N_{h}}I_{m}-(\mu _{h}+r)I_{h},\\&\frac{\mathrm{d}Z}{\mathrm{d}t}\ge \sigma I_{h} -c Z.\\ \end{aligned} \right. \end{aligned}$$

Consider an auxiliary system as follows

$$\begin{aligned} \begin{array}{lll} \frac{\mathrm{d}U}{\mathrm{d}t}= B (\delta )U, \end{array} \end{aligned}$$

(19)

where $U=(U_{1},U_{2},U_{3},U_{4})^{T}$ and

$$\begin{aligned} \begin{array}{lll} B(\delta ) = \left( \begin{array}{cccc} -(\omega +\mu _{a}) &{} 0 &{} 0 &{} \frac{\beta _{3}(A_{0}-\delta )}{k+\delta }\\ \omega &{} -\mu _{m} &{} b\beta _{1}\frac{M_{0}-\delta }{N_{h}} &{} 0\\ 0 &{} b\beta _{2}\frac{S_h^0-\delta }{N_{h}} &{} -(\mu _{h}+r) &{}0\\ 0 &{}0&{} \sigma &{} -c\\ \end{array} \right) . \end{array} \end{aligned}$$

We know $B(0)=F-V$. Note that $B(\delta )$ is irreducible and has nonnegative off-diagonal elements. Then, $s(B(\delta ))$ is a simple eigenvalue of $B(\delta )$ with a positive eigenvector (see Theorem A.5 in [50]). Based on Theorem 2 in [30], we have $s(B(0))>0$ when $R_{0}>1.$ We know that $B(\delta )$ is a continuous for small $\delta$. Thus, there exists $\delta$ small enough, such that $s(B(\delta ))>0$. So, there exists a positive eigenvalue of $B(\delta )$ corresponding to a positive eigenvector. Let $U(t)=(U_{1}(t),U_{2}(t),U_{3}(t),U_{4}(t))^{T}$ be positive solution of auxiliary system (19). Then, $U_i(t)$ is strictly increasing with $U_i(t)\rightarrow +\infty$ as $t\rightarrow +\infty$, $i=1,\ldots ,4$. We know that system (19) is quasi-monotonic. Using the comparison principle, we have

$$\begin{aligned}&\lim \limits _{t \rightarrow +\infty }I_{a}(t)=+\infty ,\lim \limits _{t \rightarrow +\infty }I_{m}(t)=+\infty ,\\&\lim \limits _{t \rightarrow +\infty }I_{h}(t)=+\infty ,\lim \limits _{t \rightarrow +\infty }Z(t)=+\infty . \end{aligned}$$

This contradicts with our assumption. Then, $E_{01}$ is an isolated invariant set in $\varGamma$ and $W^{s}(E_{01})\cap X_{0}=\emptyset$. Similarly, we can get that $E_{00}$ is an isolated invariant set in $\varGamma$ and $W^{s}(E_{00})\cap X_{0}=\emptyset .$ Clearly, every orbit in $G_{\partial }$ converges to either $E_{00}$ or $E_{01}$, and $\{E_{00}\}\cup \{E_{01}\}$ is an acyclic covering of $G_{\partial }$. From Theorem 4.1 in [51], system with incidence function $g(Z)=\beta _3\frac{Z}{k+Z}$ or $\beta _3 Z$ is uniformly persistent if $R_{0}>1$. This completes the proof. $\square$

E The expressions of $a_{i}$, $b_{i}$ and $c_{i}$, $i=1, 2, 3$

$$\begin{aligned} \begin{aligned}&a_1=d_1^2-3e_1s_1,~a_2=2d_1 d_2-3(e_1 s_2+e_2 s_1),~a_3=d_2^2-3e_2s_2,~\\&b_1=d_1s_1,~b_2=d_1s_2+d_2s_1-9e_1D_3,~b_3=d_2s_2-9e_2D_3,\\&c_1=s_1^2,~c_2=2s_1s_2-3d_1D_3,~c_3=S_2^2-3d_2 D_3, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} e_1=\,&\mu _m b^3 \beta _2^3\sigma ^2 \varLambda ^2(b\beta _1\mu _h +\mu _m(\mu _h+r)),\\ e_2=\,&\mu _m b^3 \beta _2^3 c^2(\omega +\mu _a)(\mu _{h}+r)^2(b\beta _1\mu _h +\mu _m(\mu _h+r)),\\ d_1=\,&b^2 \beta _2^2\sigma ^2 \varLambda ^2(\mu _m^{2} \varLambda (\mu _{h}+r) -\omega b \beta _2A_0(b\beta _1\mu _h +\mu _m(\mu _h+r))),\\ d_2=\,&2\mu _m \varLambda b^2 \beta _2^2 c^2(\omega +\mu _a)(\mu _{h}+r)^2(b\beta _1\mu _h +\mu _m(\mu _h+r)) \\&+\mu _m^2 \varLambda b^2 \beta _2^2 c^2(\omega +\mu _a)(\mu _{h}+r)^3(1-R_0^2),\\ s_1=\,&-\omega \sigma ^2 \varLambda ^3 b^2 \beta _2^2\mu _m (\mu _{h}+r)A_0,\\ s_2=\,&\mu _m b \beta _2 c^2 \varLambda ^2(\omega +\mu _a)(\mu _{h}+r)^2 (b\beta _1\mu _h +\mu _m(\mu _h+r)) \\&+ 2 \mu _m^2 \varLambda ^2 b \beta _2 c^2(\omega +\mu _a)(\mu _{h}+r)^3(1-R_0^2). \\ \end{aligned} \end{aligned}$$