Dynamics of subthreshold and suprathreshold resonance modulated by hyperpolarization-activated cation current in a bursting neuron

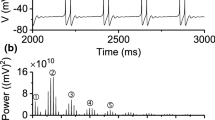
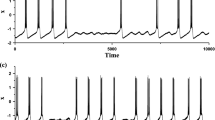
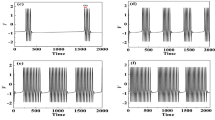
Abstract

Resonance of both subthreshold and suprathreshold membrane potentials has been found in brain or motor neurons involving in the information processing or locomotion control via frequency response, which is mainly related to the hyperpolarization-activated cation current ($I_{{\text {h}}}$). In the present paper, the modulations of $I_{{\text {h}}}$ current on resonance are acquired in a bursting neuron model, which closely match experimental observations. Firstly, the increase of $I_{{\text {h}}}$ current induces stable node changed to stable focus related to Hopf bifurcation, and to bursting via complex bifurcations including the big homoclinic orbit related to type I excitability. Secondly, the subthreshold resonance can be evoked by small stimulation from focus instead of node, resembling the experimental observation that subthreshold resonance appears at strong ($I_{{\text {h}}}$) current. Thirdly, the modulation regularity of $I_{{\text {h}}}$ current on frequency and amplitude of resonance is simulated, closely matching the experimental observations, which can be well explained with the changing trends of imaginary and real part of eigenvalues of the focus. Last, the suprathreshold bursting is induced by strong stimulation from the stable focus near big homoclinic orbit, resembling that observed in the experiment. The bursting exhibits “suprathreshold resonance” similar to those evoked near Hopf bifurcation corresponding to type II excitability. A novel condition for “suprathreshold resonance” and the underlying codimension-2 bifurcations are acquired. The results present the comprehensive viewpoints on the subthreshold resonance and extend the condition for the “suprathreshold resonance”, which are helpful for deep understanding resonance in the brain or motor neurons with $I_{{\text {h}}}$ current.

Appendix

1.1 The Hodgkin-Huxley (HH) model

The HH model, one of the most important models to describe the neural electrical behaviors, is described as follows:

$$\begin{aligned} C\frac{\text {d}V}{\text {d}t}= & {} I-g_{{\text {K}}}n^4(V-E_{{\text {K}}})-g_{{\text {Na}}}m^3h(V-E_{{\text {Na}}})\nonumber \\&-g_{{\text {L}}}(V-E_{{\text {L}}}), \end{aligned}$$

(A.1)

$$\begin{aligned} \frac{\text {d}n}{\text {d}t}= & {} \phi (\alpha _n(V)(1-n)-\beta _n(V)n), \end{aligned}$$

(A.2)

$$\begin{aligned} \frac{\text {d}m}{\text {d}t}= & {} \phi (\alpha _m(V)(1-m)-\beta _m(V)m), \end{aligned}$$

(A.3)

$$\begin{aligned} \frac{dh}{\text {d}t}= & {} \phi (\alpha _h(V)(1-h)-\beta _h(V)h). \end{aligned}$$

(A.4)

where

$$\begin{aligned} \alpha _n(V)= & {} 0.01(V+55)/(1-e^{-(V+55)/10}), \end{aligned}$$

(A.5)

$$\begin{aligned} \beta _n(V)= & {} 0.125e^{-(V+65)/80}, \end{aligned}$$

(A.6)

$$\begin{aligned} \alpha _m(V)= & {} 0.1(V+40)/(1-e^{-(V+40)/10}), \end{aligned}$$

(A.7)

$$\begin{aligned} \beta _m(V)= & {} 4e^{-(V+65)/18}, \end{aligned}$$

(A.8)

$$\begin{aligned} \alpha _h(V)= & {} 0.07e^{-(V+65)/20}, \end{aligned}$$

(A.9)

$$\begin{aligned} \beta _h(V)= & {} 1/(1+e^{-(V+35)/10}). \end{aligned}$$

(A.10)

This model contains three major currents: voltage-gated transient $\mathrm {Na^{+}}$ current, $I_{{\text {Na}}}=-g_{{\text {Na}}}m^3h(V-E_{{\text {Na}}})$; voltage-gated persistent $\mathrm {K^{+}}$ current, $I_{{\text {K}}}=-g_{{\text {K}}}n^4(V-E_{{\text {K}}})$; and ohmic leak current, $I_{{\text {L}}}=-g_{{\text {L}}}(V-E_{{\text {L}}})$. The variable n is the activation variable for $\mathrm {K^{+}}$, m and h are the activation variable and inactivation variable for $\mathrm {Na^{+}}$, respectively. The parameter $g_{{\text {K}}}$, $g_{{\text {Na}}}$, and $g_{{\text {L}}}$ are the maximal conductance of $I_{{\text {K}}}$, $I_{{\text {Na}}}$, and $I_{{\text {L}}}$, respectively, and $E_{{\text {K}}}$, $E_{{\text {Na}}}$, and $E_{{\text {L}}}$ are the reverse potential of the corresponding currents. C is the membrane capacitance, and I is the background current. The parameter values are as follows: C = 1 $\mu$F/cm${}^2$, $\phi$ = 1, $g_{{\text {K}}}$ = 36 mS/cm${}^{2}$, $g_{{\text {Na}}}$ = 120 mS/cm${}^{2}$, $g_{{\text {L}}}$ = 0.3 mS/cm${}^{2}$, $E_{{\text {K}}}$ = −77 mV, $E_{{\text {Na}}}$ = 50 mV, $E_{{\text {L}}}$ = −54.4 mV. The parameters $g_{{\text {Na}}}$ and I are taken as bifurcation parameter.

1.2 The one-parameter bifurcation of HH model and comparison to Leech model

For the HH model with $g_{{\text {Na}}}$ = 120 mS/cm${}^2$, one-parameter bifurcations with respect to I are shown in Fig. 17. With increasing I, there is a subcritical Hopf bifurcation (subH, I $\approx$ 9.779273 $\mu$A/cm${}^2$) through which the stable equilibrium point (focus, red solid curve to the left of the bifurcation point) transforms into unstable equilibrium point (focus, black dashed curve) and a supercritical Hopf bifurcation (supH, I $\approx$ 154.5263 $\mu$A/cm${}^2$) via which the unstable equilibrium point transforms to stable equilibrium point (red solid curve to the right of the bifurcation point), as shown in Fig. 17a. An unstable limit cycle (blue dashed curve) bifurcates from the subH point and a stable limit cycle (green solid curve) bifurcates from the supH point coalesce and annihilate each other to form a fold or saddle-node bifurcation (LPC) of limit cycle at $I \approx 6.264221 \mu$A/cm${}^2$. The insert figure in Fig. 17a is the enlargement near the subH and LPC point.

Fig. 17

Dynamical behaviors of the HH model when $g_{{\text {Na}}}$ = 120 mS/cm${}^2$. a The bifurcations of HH model. The red solid and black dashed curves represent the stable equilibrium and unstable equilibrium respectively. The green solid and blue dashed curves represent the maximum and minimum value of the stable and unstable limit cycle, respectively; The labels subH, supH, and LPC represent the subcritical Hopf, supercritical Hopf, and saddle node of limit cycle bifurcation points respectively. b The subthreshold oscillations evoked from the resting state for I = 2 $\mu$A/cm${}^2$; c Changes of firing frequency with respect to I; d Spike trains of spiking when I = 6.28 $\mu$A/cm${}^2$

The left stable focus corresponds to the resting state. After a small perturbation to the resting state for I = 2 $\mu$A/cm${}^2$, damping subthreshold oscillations with an intrinsic frequency about 71.84 Hz (the period of subthreshold oscillations is about 13.92 ms) appears, as demonstrated in Fig. 17b.

The stable limit cycle corresponds to spiking behavior. The change of firing frequency with respect to I is shown in Fig. 17c (Insert is the enlargement near LPC point). Near the LPC point, the firing exhibits a non-zero but nearly fixed frequency ($\sim$50.26 Hz), implying that HH model is type II excitable system, which is different from the Leech model which shows type I excitability (Fig. 4b of the main text). The firing frequency manifests a slow changing trend with increasing I. For example, the firing frequency is from $\sim$50.26 Hz for I = 6.26422 $\mu$A/cm${}^2$ to 70 Hz for I = 10.7196 $\mu$A/cm${}^2$. When I = 6.28 $\mu$A/cm${}^2$, the period of firing is about 19.37 ms and the frequency is about 51.63 Hz. The spike trains for I = 6.28 $\mu$A/cm${}^2$ is shown in Fig. 17d.

Fig. 18

a Two-parameter bifurcation and codimension-2 bifurcation of HH model in (I, $g_{{\text {Na}}}$) plane. The red dashed, red solid, and blue solid curves represent the subcritical Hopf bifurcation (subH) curve, supercritical Hopf bifurcation (supH) curve, and fold bifurcation (LPC) of limit cycle, respectively. The black triangle represents the codimension-2 bifurcation point, a generalized Hopf (GH) bifurcation point; b Enlargement of a near the codimension-2 bifurcation point

Compared with the one-parameter bifurcation of Leech model shown in Fig. 5 of the main text, two important distinctions can be found. One is that the firing terminates via a big homoclinic orbit bifurcation (BHom) for the Leech model while via a fold bifurcation of limit cycle (LPC) for the HH model, which results in zero frequency for the firing near BHom point of the Leech model and non-zero frequency but a near fixed frequency near LPC point of the HH model. The other is that the LPC and subH is connected by the unstable limit cycle in the HH model, which is different from that no connections appear between the BHom and SubH2 of the Leech model (Fig. 5 in the main text).

1.3 The codimension-2 bifurcation of HH model and comparison to Leech model

No connections between BHom and subH2 further is identified in the two-parameter space in the Leech model (Fig. 8 in the main text), In the present subsection, the relationship between LPC and subH in HH model is identified in a two-parameter space, as demonstrated in Fig. 18. Figure 18b is the enlargement near a codimension-2 bifurcation point labeled with a black triangle in Fig. 18a. In (I, $g_{{\text {Na}}}$) plane, the red solid, red dashed, and blue solid curves represent the supercritical Hopf bifurcation (supH), subcritical Hopf (subH) bifurcation, and saddle-node bifurcation of limit cycle (LPC), respectively. The three codimension-1 bifurcation curves intersect to form the codimension-2 bifurcation point labeled with the triangle, which is a generalized Hopf (GH) bifurcation point. Therefore, the LPC and subH in the HH model have relationship, which is that both of them are bifurcated from the GH point. Such a result is different from the Leech model wherein BHom and subH2 have no connections.

1.4 Subthreshold resonance

When I = 2 $\mu$A/cm${}^2$ and $g_{{\text {Na}}}$ = 120 mS/cm${}^2$, the HH model neuron is in a resting state corresponding to a stable focus. A Chirp current ($I_{{\text {Chirp}}}$ = $0.01sin(2\pi f(t)t)$, where the time-dependent frequency f(t) increases from 0 Hz to 200 Hz in a total duration T of 1000 ms) can evoke subthreshold resonance from the stable focus. The impedance profile exhibits an inverse U shape, which shows that subthreshold resonance appears, as shown in Fig. 19a. The maximal value appears at $\sim$ 74.0 Hz, which nearly equals the intrinsic frequency of the subthreshold oscillations corresponding to the focus. Such a result shows that focus of both HH model and Leech model exhibits subthreshold resonance, which implies that the subthreshold resonance is mainly determined by the dynamics of focus itself.

Fig. 19

Resonance of stable focus of HH model when I = 2 $\mu$A/cm${}^2$ and $g_{{\text {Na}}}$ = 120 mS/cm${}^2$. a The impedance profile; b the critical amplitude curve

1.5 “Suprathreshold resonance”

For the stable focus with I = 2 $\mu$A/cm${}^2$ and $g_{{\text {Na}}}$ = 120 mS/cm${}^2$, when a stimulation signal A$sin(2\pi f_{{\text {sti}}}t$) is applied, the critical amplitude A to evoke firing exhibits an U-shaped curve with respect to stimulation frequency $f_{{\text {sti}}}$, which shows that the stimulation signal to induce firing has a preferred frequency and “suprathreshold resonance” appears, as shown in Fig. 19b. Such a result has been reported in Ref [28]. The minimal value appears at $f_{{\text {sti}}}$ $\approx$ 64.8 Hz, which is the “suprathreshold resonance” frequency. The $f_{{\text {sti}}}$ $\approx$ 64.8 Hz is a value between the firing frequency near LPC point and the subthreshold resonance frequency. The result implies that the “suprathreshold resonance” maybe influenced by the dynamics of the both firing pattern near the focus and the stable focus.