Eigenvalue analysis for predicting the onset of multiple subcritical limit cycles of an airfoil with a control surface

Abstract

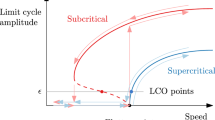
The aeroelastic system of an airfoil with a control surface usually encounters non-smooth nonlinearities such as freeplay. Freeplay can have a significant influence on aeroelastic behavior, such as reducing the flow velocity at which a limit cycle (LC) could abruptly arise. This means that a subcritical LC might occur much below the linear flutter velocity. It has been a difficult task for years to predict the lowest velocity for the onset of LC. Here, a simple yet efficient approach to this problem is proposed. This approach is based on eigenvalue analysis of a generalized Jacobian matrix (GJM), which is deduced according to the Filippov convex theory. With this method, the lowest velocity for the GJM having positive real parts can be calculated easily. More importantly, this method can be used to determine the lowest velocity above which a subcritical LC can occur, and it also appears that it can detect multiple subcritical LCs. In addition, the distribution of the positive real parts provides us with a convenient way to judge whether the arising LCs will be subcritical or supercritical. The point transform method and the Floquet theory are employed to validate the presented approach numerically, showing that good precision can be achieved for the estimated lowest velocity and the frequency of the arising LC. It leaves an open question for this method, as at the present stage a complete and rigorous proof is urgently needed.

Appendices

Appendix A

See Table 1.

Appendix B

Theodorsen constants

$$ T_{1} = - \frac{1}{3}\sqrt {1 - c^{2} } \left( {2 + c^{2} } \right) + c\arccos c $$

$$ T_{2} = T_{6} = c\left( {1 - c^{2} } \right) - \sqrt {1 - c^{2} } \left( {1 + c^{2} } \right)\arccos c + c(\arccos c)^{2} $$

$$ T_{3} = \frac{1}{4}c\sqrt {1 - c^{2} } \arccos c\left( {7 + 2c^{2} } \right) - \left( {\frac{1}{8} + c^{2} } \right)(\arccos c)^{2} - \frac{1}{8}\left( {1 - c^{2} } \right)\left( {5c^{2} + 4} \right) $$

$$ T_{4} = c\sqrt {1 - c^{2} } - \arccos c $$

$$ T_{5} = - \left( {1 - c^{2} } \right) + 2c\sqrt {1 - c^{2} } \arccos c - \left( {\arccos c} \right)^{2} $$

$$ T_{7} = \frac{1}{8}c\sqrt {1 - c^{2} } \left( {7 + 2c^{2} } \right) - \left( {\frac{1}{8} + c^{2} } \right)\arccos c $$

$$ T_{8} = - \frac{1}{3}\left( {1 + 2c^{2} } \right)\sqrt {1 - c^{2} } + c\arccos c $$

$$ T_{9} = \frac{1}{2}\left[ {\frac{1}{3}\left( {\sqrt {1 - c^{2} } } \right)^{3} + aT_{4} } \right] $$

$$ T_{10} = \sqrt {1 - c^{2} } + \arccos c $$

$$ T_{11} = \left( {1 - 2c} \right)\arccos c + \sqrt {1 - c^{2} } \left( {2 - c} \right) $$

$$ T_{12} = \sqrt {1 - c^{2} } \left( {2 + c} \right) - \left( {2c + 1} \right)\arccos c $$

$$ T_{13} = \frac{1}{2}\left[ { - T_{7} - \left( {c - a} \right)T_{1} } \right] $$

$$ T_{14} = \frac{1}{16} + \frac{1}{2}ac $$

Appendix C

Some parameters used in the computation of the coefficient matrixes in Eq. (1)

$$ \begin{aligned} \kappa & = \rho \pi b^{2} /m,\,r_{\alpha } = \sqrt {I_{\alpha } /mb^{2} } ,\,r_{\beta } = \sqrt {I_{\beta } /mb^{2} } ,\,x_{\alpha } = S_{\alpha } /mb,\,x_{\beta } = S_{\beta } /mb, \\ \omega_{\alpha } & = \sqrt {C_{\alpha } /I_{\alpha } } ,\,\omega_{\beta } = \sqrt {C_{\beta } /I_{\beta } } ,\,\omega_{h} = \sqrt {C_{h} /m} . \\ \end{aligned} $$

Appendix D

Modal parameters used in the computation of the coefficient matrixes in Eq. (1)

$$ M_{s} = \left[ {\begin{array}{*{20}c} {r_{\alpha }^{2} } & {r_{\beta }^{2} + \left( {c - a} \right)x_{\beta } } & {x_{\alpha } } \\ {r_{\beta }^{2} + \left( {c - a} \right)x_{\beta } } & {r_{\beta }^{2} } & {x_{\beta } } \\ {x_{\alpha } } & {x_{\beta } } & {M_{total} /m} \\ \end{array} } \right],\,K_{s} = \left[ {\begin{array}{*{20}c} {r_{\alpha }^{2} \omega_{\alpha }^{2} } & 0 & 0 \\ 0 & {r_{\beta }^{2} \omega_{\beta }^{2} } & 0 \\ 0 & 0 & {\omega_{h}^{2} } \\ \end{array} } \right]. $$

The model mass $m_{i}$ and the coupled natural frequency $\omega_{i}$ are computed according to $M_{s}$ and $K_{s}$ by the following procedures [12]

• (1) Calculate eigenvalues $\lambda_{i}$ and eigenvectors $\Lambda$ from free vibration system $M_{s} q^{\prime\prime} + K_{s} q = 0$

• (2) Let $\omega_{i} = \sqrt {\lambda_{i} }$

• (3) Define $M_{mod} =\Lambda ^{\text{T}} M_{s}\Lambda$, and $m_{i}$ is extracted from the diagonal entries of $M_{mod}$.

In addition, the model damping matrix is defined as

$$ B_{mod} = \left[ {\begin{array}{*{20}c} {2m_{1} \omega_{1} \varsigma_{1} } & 0 & 0 \\ 0 & {2m_{2} \omega_{2} \varsigma_{2} } & 0 \\ 0 & 0 & {2m_{3} \omega_{3} \varsigma_{3} } \\ \end{array} } \right] $$

and the structural damping matrix is given by $B_{s} = (\Lambda ^{\text{T}} )^{ - 1} B_{mod}\Lambda ^{ - 1}$, which presents some parameters that will be used to get the coefficients matrixes in Eq. (1), such as

$$ B_{s} = (s_{ij} )_{1 \le i,j \le 3} . $$

The modal damping coefficients, $\varsigma_{1}$, $\varsigma_{2}$ and $\varsigma_{3}$, are adopted according to the experimental test of an airfoil-aileron structure made by Corner et al. [12]. Note that in the equations of motions, i.e., Equation (1), the damping matrix is not only dependent on the entries of $B_{mod}$ but also on the aerodynamics modeled by the Theodorsen theory. More details can be referred to “Appendix E.”

Appendix E

The entries of the coefficient matrixes in Eq. (1)

$$ A_{1} = r_{\alpha }^{2} + \kappa \left( {\frac{1}{8} + a^{2} } \right),\,A_{2} = r_{\beta }^{2} + \left( {c - a} \right)x_{\beta } - \frac{{\kappa \left( {c - a} \right)T_{1} }}{\pi } - \frac{{\kappa T_{7} }}{\pi },\,A_{3} = x_{\alpha } - a\kappa , $$

$$ A_{4} = \kappa \left( {\frac{1}{2} - a} \right) - 2\kappa \left( {\frac{1}{2} - a} \right)\left( {\frac{1}{2} + a} \right)\left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{s_{11} b}}{V}, $$

$$ A_{5} = \frac{\kappa }{\pi }[\frac{2}{3}\left( {1 - c^{2} )^{{\frac{3}{2}}} - \left( {0.5 - a} \right)T_{4} - \left( {\frac{1}{2} + a} \right)\left( {1 - \psi_{1} - \psi_{2} } \right)} \right] + \frac{{s_{12} b}}{V}, $$

$$ A_{6} = - 2\kappa \left( {\frac{1}{2} + a} \right)\left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{s_{13} b}}{V}, $$

$$ A_{7} = \frac{{r_{\alpha }^{2} \omega_{\alpha }^{2} }}{{V^{2} }} - 2\kappa \left( {\frac{1}{2} + a} \right)\left[ {1 - \psi_{1} - \psi_{2} + \left( {\frac{1}{2} - a} \right)\left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right], $$

$$ A_{8} = \frac{\kappa }{{\pi (T_{4} + T_{10} )}} - \frac{2\kappa }{\pi }\left( {\frac{1}{2} + a} \right)\left[ {T_{10} \left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{T_{11} }}{2}\left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right], $$

$$ A_{9} = - 2\kappa \left( {\frac{1}{2} + a} \right)\left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right),\,A_{10} = r_{\alpha }^{2} \omega_{\alpha }^{2} \frac{{b^{2} }}{{V^{2} }}, $$

$$ A_{11} = - 2\kappa \left( {\frac{1}{2} + a} \right)\left[ {\psi_{1} \varepsilon_{1} - \left( {\frac{1}{2} - a} \right)\psi_{1} \varepsilon_{1}^{2} } \right], $$

$$ A_{12} = - 2\kappa \left( {\frac{1}{2} + a} \right)\left[ {\psi_{2} \varepsilon_{2} - \left( {\frac{1}{2} - a} \right)\psi_{2} \varepsilon_{2}^{2} } \right], $$

$$ A_{13} = - \frac{2\kappa }{\pi }\left( {\frac{1}{2} + a} \right)\left[ {T_{10} \psi_{1} \varepsilon_{1} - \frac{1}{2}T_{11} \psi_{1} \varepsilon_{1}^{2} } \right], $$

$$ A_{14} = - \frac{2\kappa }{\pi }\left( {\frac{1}{2} + a} \right)\left[ {T_{10} \psi_{2} \varepsilon_{2} - \frac{1}{2}T_{11} \psi_{2} \varepsilon_{2}^{2} } \right], $$

$$ A_{15} = 2\kappa \left( {\frac{1}{2} + a} \right)\psi_{1} \varepsilon_{1}^{2} ,A_{16} = 2\kappa \left( {\frac{1}{2} + a} \right)\psi_{2} \varepsilon_{2}^{2} , $$

$$ B_{1} = r_{\beta }^{2} + \left( {c - a} \right)x_{\beta } + \frac{2\kappa }{\pi }T_{13} ,\,B_{2} = r_{\beta }^{2} - \frac{\kappa }{{\pi^{2} }}T_{3} ,\,B_{3} = x_{\beta } - \frac{\kappa }{\pi }T_{1} , $$

$$ B_{4} = \frac{\kappa }{\pi }[ - \frac{1}{3}\left( {1 - c^{2} )^{{\frac{3}{2}}} - T_{1} - \frac{1}{2}T_{4} + T_{11} \left( {\frac{1}{2} - a} \right)\left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{s_{21} b}}{V}} \right], $$

$$ B_{5} = \frac{\kappa }{{2\pi^{2} }}\left[ { - T_{4} T_{11} + T_{12} T_{11} \left( {1 - \psi_{1} - \psi_{2} } \right)} \right] + \frac{{s_{22} b}}{V}, $$

$$ B_{6} = \frac{\kappa }{\pi }T_{12} \left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{s_{23} b}}{V},\,B_{7} = \frac{\kappa }{\pi }T_{12} \left[ {\left( {1 - \psi_{1} - \psi_{2} } \right) + \left( {\frac{1}{2} - a} \right)\left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right], $$

$$ B_{8} = \frac{{r_{\beta }^{2} \omega_{\beta }^{2} }}{{V^{2} }} + \frac{\kappa }{{\pi^{2} }}\left( {T_{5} - T_{4} T_{10} } \right) + \frac{\kappa }{{\pi^{2} }}T_{12} \left[ {T_{10} \left( {1 - \psi_{1} - \psi_{2} } \right) + T_{11} \left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right], $$

$$ B_{9} = \frac{\kappa }{\pi }T_{12} \left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right),\,B_{11} = \frac{\kappa }{\pi }T_{12} \left( {\psi_{1} \varepsilon_{1} - \left( {\frac{1}{2} - a} \right)\psi_{1} \varepsilon_{1}^{2} } \right),\,B_{10} = \frac{{r_{\beta }^{2} \omega_{\beta }^{2} b^{2} }}{{V^{2} }}, $$

$$ B_{12} = \frac{\kappa }{\pi }T_{12} \left( {\psi_{2} \varepsilon_{2} - \left( {\frac{1}{2} - a} \right)\psi_{2} \varepsilon_{2}^{2} } \right),\,B_{13} = \frac{\kappa }{{\pi^{2} }}T_{12} \left( {T_{10} \psi_{1} \varepsilon_{1} - T_{11} \psi_{1} \varepsilon_{1}^{2} } \right), $$

$$ B_{14} = \frac{\kappa }{{\pi^{2} }}T_{12} \left( {T_{10} \psi_{2} \varepsilon_{2} - T_{11} \psi_{2} \varepsilon_{2}^{2} } \right),\,B_{15} = - \frac{\kappa }{\pi }T_{12} \psi_{1} \varepsilon_{1}^{2} ,\,B_{16} = - \frac{\kappa }{\pi }T_{12} \psi_{2} \varepsilon_{2}^{2} , $$

$$ C_{1} = x_{\alpha } - a\kappa ,\,C_{2} = x_{\beta } - \frac{\kappa }{\pi }T_{1} ,\,C_{2} = \frac{{m_{total} }}{m} + \kappa , $$

$$ C_{4} = \kappa \left[ {1 + 2\left( {\frac{1}{2} - a} \right)\left( {1 - \psi_{1} - \psi_{2} } \right)} \right] + \frac{{s_{31} b}}{V}, $$

$$ C_{5} = \frac{\kappa }{\pi }\left[ { - T_{4} + T_{11} \left( {1 - \psi_{1} - \psi_{2} } \right)} \right] + \frac{{s_{32} b}}{V},\,C_{6} = 2\kappa \left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{{s_{33} b}}{V}, $$

$$ C_{7} = 2\kappa \left[ {1 - \psi_{1} - \psi_{2} + \left( {\frac{1}{2} - a} \right)\left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right], $$

$$ C_{8} = \frac{2\kappa }{\pi }\left[ {T_{10} \left( {1 - \psi_{1} - \psi_{2} } \right) + \frac{1}{2}T_{11} \left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right)} \right],C_{9} = \frac{{\omega_{\xi }^{2} }}{{V^{2} }} + 2\kappa \left( {\psi_{1} \varepsilon_{1} + \psi_{2} \varepsilon_{2} } \right), $$

$$ C_{10} = \omega_{h}^{2} \frac{{b^{2} }}{{V^{2} }},\,C_{11} = 2\kappa \left( {\psi_{1} \varepsilon_{1} - \left( {\frac{1}{2} - a} \right)\psi_{1} \varepsilon_{1}^{2} } \right),\,C_{12} = 2\kappa \left( {\psi_{2} \varepsilon_{2} - \left( {\frac{1}{2} - a} \right)\psi_{2} \varepsilon_{2}^{2} } \right), $$

$$ C_{13} = \frac{2\kappa }{\pi }\left( {T_{10} \psi_{1} \varepsilon_{1} - \frac{1}{2}T_{11} \psi_{1} \varepsilon_{1}^{2} } \right),\,C_{14} = \frac{2\kappa }{\pi }\left( {T_{10} \psi_{2} \varepsilon_{2} - \frac{1}{2}T_{11} \psi_{2} \varepsilon_{2}^{2} } \right), $$

$$ C_{15} = - 2\kappa \psi_{1} \varepsilon_{1}^{2} ,\,C_{16} = - 2\kappa \psi_{2} \varepsilon_{2}^{2} . $$

Herein $\psi_{1} = 0.165, \psi_{2} = 0.335$, and $\varepsilon_{1} = 0.0455, \varepsilon_{2} = 0.3$.

Appendix F

The construction of the coefficient matrices and vectors in Eqs. (10–11)

First of all, both ${\varvec{\Psi}}_{1}$ and ${\varvec{\Psi}}_{2}$ are square matrix of dimension 12. The nonzero entries of ${\varvec{\Psi}}_{1}$ are listed as follows: ${\varvec{\Psi}}_{1} \left( {1,2} \right) = {\varvec{\Psi}}_{1} \left( {3,4} \right) = {\varvec{\Psi}}_{1} \left( {5,6} \right) = 1$,

$$ {\varvec{\Psi}}_{1} \left( {7,1} \right) = {\varvec{\Psi}}_{1} \left( {8,1} \right) = {\varvec{\Psi}}_{1} \left( {9,3} \right) = {\varvec{\Psi}}_{1} \left( {10,3} \right) = {\varvec{\Psi}}_{1} \left( {11,5} \right) = {\varvec{\Psi}}_{1} \left( {12,5} \right) = 1, $$

$$ {\varvec{\Psi}}_{1} \left( {7,7} \right) = {\varvec{\Psi}}_{1} \left( {9,9} \right) = {\varvec{\Psi}}_{1} \left( {11,11} \right) = - \varepsilon_{1} ,{\varvec{\Psi}}_{1} \left( {8,8} \right) = {\varvec{\Psi}}_{1} \left( {10,10} \right) = {\varvec{\Psi}}_{1} \left( {12,12} \right) = - \varepsilon_{2} , $$

$$ {\mathbf{J}} = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } & {A_{3} } \\ {B_{1} } & {B_{2} } & {B_{3} } \\ {C_{1} } & {C_{2} } & {C_{3} } \\ \end{array} } \right],{\varvec{\Psi}}_{{1,{\text{J}}1}} = \left[ {\begin{array}{*{20}c} {A_{7} + A_{10} } & {A_{4} } & {A_{8} } \\ {B_{7} } & {B_{4} } & {B_{8} + M_{f} B_{10} } \\ {C_{7} } & {C_{4} } & {C_{8} } \\ \end{array} } \right], $$

$$ {\varvec{\Psi}}_{{1,{\text{J}}2}} = \left[ {\begin{array}{*{20}c} {A_{5} } & {A_{9} } & {A_{6} } \\ {B_{5} } & {B_{9} } & {B_{6} } \\ {C_{5} } & {C_{6} + C_{10} } & {C_{86} } \\ \end{array} } \right],\,{\varvec{\Psi}}_{{1,{\text{J}}3}} = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {A_{11} } & {A_{12} } \\ \end{array} } & {\begin{array}{*{20}c} {A_{13} } & {A_{14} } \\ \end{array} } & {\begin{array}{*{20}c} {A_{15} } & {A_{16} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {B_{11} } & {B_{12} } \\ \end{array} } & {\begin{array}{*{20}c} {B_{13} } & {B_{14} } \\ \end{array} } & {\begin{array}{*{20}c} {B_{15} } & {B_{16} } \\ \end{array} } \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {C_{11} } & {C_{12} } \\ \end{array} } & {\begin{array}{*{20}c} {C_{13} } & {C_{14} } \\ \end{array} } & {\begin{array}{*{20}c} {C_{15} } & {C_{16} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right], $$

$$ {\varvec{\Psi}}_{{1,{\text{J}}}} = - {\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}c} {{\varvec{\Psi}}_{{1,{\text{J}}1}} } & {{\varvec{\Psi}}_{{1,{\text{J}}2}} } & {{\varvec{\Psi}}_{{1,{\text{J}}3}} } \\ \end{array} } \right], $$

$$ {\varvec{\Psi}}_{1} \left( {2, :} \right) = {\varvec{\Psi}}_{{1,{\text{J}}}} \left( {1, :} \right),{\varvec{\Psi}}_{1} \left( {4, :} \right) = {\varvec{\Psi}}_{{1,{\text{J}}}} \left( {2, :} \right),{\varvec{\Psi}}_{1} \left( {6, :} \right) = {\varvec{\Psi}}_{{1,{\text{J}}}} \left( {3, :} \right). $$

Importantly, ${\varvec{\Psi}}_{2}$ is a special case of ${\varvec{\Psi}}_{1}$ as $M_{f} = 1$. And both $\varvec{\varphi }_{1}$ and $\varvec{\varphi }_{2}$ are column vectors of dimension 12.

$$ \varvec{\varphi }_{1,J} = - {\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}c} 0 \\ {(1 - M_{f} )\delta_{1} } \\ 0 \\ \end{array} } \right],\varvec{\varphi }_{2,J} = {\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}c} 0 \\ {(1 - M_{f} )\delta_{2} } \\ 0 \\ \end{array} } \right], $$

$$ {\text{and}}\,\varvec{\varphi }_{1} \left( 2 \right) = \varvec{\varphi }_{{1,{\text{J}}}} \left( 1 \right),\,\varvec{\varphi }_{1} \left( 4 \right) = \varvec{\varphi }_{{1,{\text{J}}}} \left( 2 \right),\,\varvec{\varphi }_{1} \left( 6 \right) = \varvec{\varphi }_{{1,{\text{J}}}} \left( 3 \right); $$

$$ \varvec{\varphi }_{2} \left( 2 \right) = \varvec{\varphi }_{{2,{\text{J}}}} \left( 1 \right),\,\varvec{\varphi }_{2} \left( 4 \right) = \varvec{\varphi }_{{2,{\text{J}}}} \left( 2 \right),\,\varvec{\varphi }_{2} \left( 6 \right) = \varvec{\varphi }_{{2,{\text{J}}}} \left( 3 \right). $$

The matrices for ${\mathbf{T}}_{1}$ and ${\mathbf{T}}_{2}$ in Eq. (16).

First of all, ${\mathbf{T}}_{1}$ and ${\mathbf{T}}_{2}$ are square matrices of dimension 12. And, ${\mathbf{T}}_{1}$ is a special case of ${\varvec{\Psi}}_{1}$ when $M_{f} = 0$.

$$ {\varvec{\Psi}}_{{2,{\text{J}}1}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & {B_{10} } \\ 0 & 0 & 0 \\ \end{array} } \right], $$

$$ {\varvec{\Psi}}_{{2,{\text{J}}}} = - {\mathbf{J}}^{ - 1} \left[ {\begin{array}{*{20}c} {{\varvec{\Psi}}_{{2,{\text{J}}1}} } & {0_{3 \times 9} } \\ \end{array} } \right],\,{\mathbf{T}}_{2} \left( {2, :} \right) = {\varvec{\Psi}}_{{2,{\text{J}}}} \left( {1, :} \right),\,{\mathbf{T}}_{2} \left( {4, :} \right) = {\varvec{\Psi}}_{{2,{\text{J}}}} \left( {2, :} \right),\,{\mathbf{T}}_{2} \left( {6, :} \right) = {\varvec{\Psi}}_{{2,{\text{J}}}} \left( {3, :} \right). $$