On the effect of model uncertainty on the Hopf bifurcation of aeroelastic systems

Abstract

This paper investigates the effect of model uncertainty on the nonlinear dynamics of a generic aeroelastic system. Among the most dangerous phenomena to which these systems are prone, Limit Cycle Oscillations are periodic isolated responses triggered by the nonlinear interactions among elastic deformations, inertial forces, and aerodynamic actions. In a dynamical systems setting, these responses typically emanate from Hopf bifurcation points, and thus a recently proposed framework, which address the problem of robustness from a nonlinear dynamics viewpoint, is employed. Briefly, the notion of robust bifurcation margin extends the concept of $\mu$ analysis technique from the robust control theory. The main contribution of this article is a systematic investigation of the numerous scenarios arising in the study of nonlinear flutter when uncertainties in the model are accounted for in the analyses. The advantages of adopting this framework include the possibility to: quantify relevant information for the determination of the nonlinear stability envelope; gain a more in-depth understanding of the physical mechanisms triggering subcritical and supercritical Hopf bifurcations; and reveal properties of the nominal system by identifying isolated branches not straightforward to detect with conventional numerical approaches.

1 Introduction

Aeroelasticity studies fluid-structure interaction problems governed by the coupling among inertial, elastic, and aerodynamic forces. These problems are particularly relevant for flexible aerodynamic bodies, where these interactions result in different stress levels and aerodynamic performance compared to those computed considering a purely structural dynamics and aerodynamic problem, respectively. Another possible effect of this coupling is the onset of a dynamic instability characterized by self-sustained oscillations of the structure, known as flutter [6]. Due to potentially critical failures associated with this phenomenon, its study is of well acknowledged interest for aircraft design, thus motivating a large body of research on flutter prediction methods [36]. The standard approach in the case of nominal (i.e., when an accurate model describing the physical problem is available) and linear dynamics is to look for the smallest flight speed V such that the system’s spectrum has a pair of complex eigenvalues on the imaginary axis. The distance of these eigenvalues from the origin provides information on the frequency of the oscillations, and the predicted speed, termed flutter speed $V_{f}$, is such that for $V<V_{f}$ the (unique) equilibrium is globally asymptotically stable.

State-of-the art computational techniques for flutter predictions are considered, however, only partially reliable. For this reason, on the one hand conservative safety margins on the flutter occurrence are required by design, and on the other expensive flights test campaigns must be carried out before certifying the aircraft. One of the main sources of inaccuracy is the sensitivity to uncertainty of the conditions at which flutter occurs. Uncertainty is caused for example by variations in system parameters or incorrect modeling hypotheses [35]. To address this problem, robust flutter analysis algorithms were proposed originally in [7, 28], aimed at quantifying the mismatch between nominal (i.e., based on a fixed model assumed as exact) and worst-case (i.e., considering a family of models associated with a given uncertainty set) stability analysis tests. They build on the robust control concepts of Linear Fractional Transformation (LFT) and $\mu$ (or structured singular value) analysis [43] and are applicable to linear time-invariant systems only.

Another critical aspect is that the currently observed increase in flexibility of aircraft structures (primarily driven by the need to reduce fuel consumption) and the concurrent demand for a more realistic description of the system compel the consideration of cases where the linear hypothesis no longer holds [14]. The presence of nonlinearities not only can invalidate the results obtained with a linear approach (e.g., the value of the flutter speed), but can also trigger inherently nonlinear phenomena which are not captured by linear analysis [9]. For example, nonlinear aeroelastic systems typically exhibit loss of stability of the equilibrium in the form of Limit Cycle Oscillations (LCO), which are isolated periodic orbits occurring in unforced systems [12, 25]. Investigations of these phenomena are of well-ascertained interest as they are necessary in order to accomplish a satisfactory aircraft design [3]. Specifically, studying the dependence on V of the features of the LCO (e.g., amplitude) is paramount, and in this regard bifurcation theory [25] offers an effective tool. In fact, the onset of LCOs corresponds to an Hopf bifurcation point in the system, where the stable branch of equilibria (corresponding to the stable configuration of the system at low speeds) loses stability and meets a branch of periodic solutions. By applying numerical continuation [10] to the emanating branch of periodic orbits, information is obtained about period, amplitude and stability of the LCO as the speed is varied.

The simultaneous effect of uncertainties and nonlinearities on flutter has not received much attention. Most of the related prior work has built on the uncertainty quantification (UQ) framework, see the recent survey [5]. In UQ, a stochastic approach for modeling uncertainty is taken, and the analysis tools generally consist of Monte Carlo methods and spectral methods, such as polynomial chaos expansions. The aims in UQ works devoted to aeroelastic problems are typically to investigate the effect of uncertainty on: the change of linear (or linearized) flutter speed [37]; features of the post-critical behavior (e.g., amplitude or frequencies of the LCO) [4, 16]. Aimed at the latter goal, but building on different tools, namely robust control techniques, in [22] a method was developed to allow the degradation of the LCO properties in the worst-case scenario to be analyzed. Specifically, integral quadratic constraints were used to compute the worst-case LCO curve, which quantifies the increase in the amplitude of oscillations in the face of uncertainties.

In contrast with the previously discussed works, the goal of this paper is to study the effect of the uncertainty from a bifurcation viewpoint, i.e., the problem of robustness to qualitative changes in the steady-state solutions is considered. To this aim, we make use of the concept of robust bifurcation margin $k_m$ [19], recently introduced as a framework to compute the distance, in the uncertainty parameter space, from a given nominally stable equilibrium to the closest Hopf bifurcation. The approach in [19], applicable to generic polynomial vector fields, builds on robust control concepts, the key idea being to describe the uncertain nonlinear system in a Linear Fractional Transformation fashion. The singularity of the LFT is then associated with the occurrence of a Hopf bifurcation, and in that regard the bifurcation margin $k_m$ (technically, its reciprocal) can be regarded as an extension of the structured singular value $\mu$ for studying robust stability of nonlinear dynamics.

The determination of the margins is posed as an optimization problem (aided by a continuation-based multi-start strategy), which also allows the type of Hopf bifurcation (subcritical or supercritical) to be specified by constraining the sign of the first Lyapunov coefficient [25].

While in [19], the theoretical and computational aspects were addressed, this article presents as a case study a thorough investigation of the rich nonlinear dynamics arising in the robust flutter problem by means of the robust bifurcation margin approach.

This effort represents a new contribution in the study of nonlinear aeroelastic systems subject to parametric uncertainty for two main reasons: uncertainties are analyzed from a deterministic worst-case viewpoint as classically done, but for linear systems only, in robust control [43]; the objective is to shed light and provide insights on the effect of uncertainties on the Hopf bifurcation landscapes of these complex coupled systems. It is noted that unique features of the robust bifurcation margin method, such as the possibility to focus the analyses on bifurcations with specified criticality (sub- or supercritical) and associated with frequencies only in pre-defined ranges, allow non-intuitive findings to be revealed. Examples include the onset of supercritical Neimark–Sacker bifurcations and, even for the system without uncertainty, the existence of multiple stable and unstable steady-states solutions for speeds much smaller than the Hopf bifurcation speed.

The analyzed aeroelastic system is an airfoil model (also known as typical section) equipped with a control surface and capturing unsteady aerodynamics effects. The typical section model has been widely used in the literature for studying the complex dynamic responses of nonlinear aeroelastic systems, both numerically [29, 31, 38] and experimentally [13]. Indeed, while its modeling complexity is low compared to high-fidelity fluid-structure interaction solvers, it captures essential physical aspects of the problem (e.g., unsteady aerodynamics, frequency separation among structural modes), which will be leveraged in the work. This has the important benefit of enhancing interpretability of the results and allowing full understanding of the analysis framework’s capabilities. Moreover, we consider a benchmark model from the literature [24] for which results of nominal robust analyses are available [21]. After having introduced the essential background in Section 2, Section 3 will discuss the application of two advanced flutter analysis methods, namely the $\mu$-based (linear) robust analysis [28] and the continuation-based (nominal) bifurcation analysis [12]. This is preparatory for the analysis methodology applied in Sect. 4, which represents a reconciliation of the previous ones and, as supported by the results, combines some of their advantages. A thorough discussion of the findings, together with a broad overview of the insights that can be gained and their critical interpretation, is also provided in order to clearly present the potential benefits of this novel analysis approach. Preliminary results of this work were presented in [18].

2 Background

A brief overview of the mathematical tools employed in the paper is given in this section. Section 2.1 outlines the basic features of LFT and $\mu$ from robust control [43], whereas Sect. 2.2 gives a cursory summary of bifurcation theory [25]. Finally, Sect. 2.3 reviews the recently proposed concept of robust bifurcation margins [19]. As for the notation, standard convention is used. Note also that bold is used for vectors and matrices.

2.1 Linear fractional transformation and $\mu$

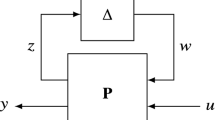
The LFT paradigm [30, 43] is an established modeling framework in robust control for analysis and design of uncertain systems, building on the idea of representing them as a feedback interconnection between a known part ${\mathbf {M}}$ and an unknown part ${\varvec{\Delta }}$, see Fig. 1.

Fig. 1

Uncertain feedback representation of an LFT

The former is typically partitioned as

${\mathbf {M}}=[{{\mathbf {M}}_{\mathbf {11}}} ~ {{\mathbf {M}}_{\mathbf {12}}}; ~ {{\mathbf {M}}_{\mathbf {21}}} ~ {{\mathbf {M}}_{\mathbf {22}}}]$. A common example of the unknown part is the structured uncertainty set ${{\varvec{\Delta }}_{\mathbf {u}}}$:

$$\begin{aligned} \begin{aligned} {{\varvec{\Delta }}_{\mathbf {u}}}&= \text {diag}(\delta _{i}{{\mathbf {I}}_{{\mathbf {d}}_{\mathbf {i}}}}, \delta _{j} {{\mathbf {I}}}_{{\mathbf {d}}_{\mathbf {j}}}, {{\varvec{\Delta }}}_{{\mathbf {D}}_{\mathbf {k}}}), \\&\quad i=1,\ldots ,n_{R}, \;\; j=1,\ldots ,n_{C}, \;\; k=1,\ldots ,n_{D}, \end{aligned} \end{aligned}$$

(1)

which gathers the uncertainties associated with $n_{R}$ real parameters $\delta _{i}$, $n_{C}$ complex scalars $\delta _{j}$, and $n_{D}$ full complex blocks (or dynamic uncertainties) ${{\varvec{\Delta }}}_{{\mathbf {D}}_{\mathbf {k}}}$, and $\mathbf {I_d}$ denotes the identity matrix of size equal to the number of repetitions d.

The upper LFT with respect to the uncertainty ${\varvec{\Delta }}$ is:

$$\begin{aligned} {\mathcal {F}}_{u}({\mathbf {M}},{\varvec{\Delta }}) = {{\mathbf {M}}_{\mathbf {22}}} +{{\mathbf {M}}_{\mathbf {21}}} {\varvec{\Delta }}({\mathbf {I}}-{{\mathbf {M}}_{\mathbf {11}}} {\varvec{\Delta }})^{-1}{{\mathbf {M}}_{\mathbf {12}}}. \end{aligned}$$

(2)

and can be interpreted as a generalized transfer function from the input to the output of a linear time-invariant system ${{\mathbf {M}}_{\mathbf {22}}}$ when this is subject to uncertainties. It is worth observing that this mapping is well posed if and only if the inverse of $({\mathbf {I}}-{{\mathbf {M}}_{\mathbf {11}}} {\varvec{\Delta }})$ exists. Otherwise, ${\mathcal {F}}_{u}({\mathbf {M}},{\varvec{\Delta }})$ is said to be singular.

The structured singular value, or $\mu$, analysis technique investigates robustness of uncertain linear time-invariant systems to structured uncertainties (1) by leveraging the aforementioned observation on the singularity of the LFT. The definition of $\mu$ is:

$$\begin{aligned} \mu = \bigg (\min _{{\varvec{\Delta }}} (\kappa :\det ( I - \kappa {{\mathbf {M}}_{\mathbf {11}}} {\varvec{\Delta }}) = 0; \quad {\bar{\sigma }}({\varvec{\Delta }})\le 1)\bigg )^{-1}, \end{aligned}$$

(3)

where $\kappa$ is a real positive scalar. Note that, without loss of generality, the maximum singular value ${\bar{\sigma }}(\cdot )$ of the matrices in the set ${\varvec{\Delta }}$ is bounded in the optimization problem. By virtue of this, the robust stability test in (3) can be interpreted as follows: if $\mu \le 1$, then there is no perturbation matrix inside the allowed set ${\varvec{\Delta }}$ that makes ${\mathcal {F}}_{u}({\mathbf {M}},{\varvec{\Delta }})$ ill posed and thus the associated plant is robustly stable within the range of uncertainty affecting the system. Conversely, if $\mu > 1$, there exists a perturbation matrix that violates the well-posedness of the LFT and thus for an adverse combination of the uncertainty the system can lose stability.

Problem (3) is for generic uncertainty sets an NP-hard problem; therefore, $\mu$ is approximated by its upper $\mu _{UB}$ and lower $\mu _{LB}$ bounds [8, 33]. The lower bound algorithms also provide a matrix $\frac{1}{\mu _{LB}}\mathbf {\Delta ^{cr}}$ which verifies the singularity of the LFT, i.e., such that $\det ( I - \frac{1}{\mu _{LB}}{{\mathbf {M}}_{\mathbf {11}}} \mathbf {\Delta ^{cr}})=0$.

2.2 Bifurcation theory and numerical continuation

The objective of bifurcation analysis is to predict qualitative changes in the steady-states of a nonlinear system as a result of the variation of parameters which influence the dynamics. A general expression for an autonomous nonlinear system is:

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}&={\mathbf {f}}({\mathbf {x}},p),\\ {\mathbf {J}}&\equiv \nabla _x {\mathbf {f}}({\mathbf {x}},p),\\ \end{aligned} \end{aligned}$$

(4)

where: ${\mathbf {x}} \in {\mathbb {R}}^{n_x}$ and $p \in {\mathbb {R}}$ are, respectively, the vector of states and the bifurcation parameter; ${\mathbf {f}}: {\mathbb {R}}^{n_x} \times {\mathbb {R}} \rightarrow {\mathbb {R}}^{n_x}$ is the vector field; and ${\mathbf {J}}: {\mathbb {R}}^{n_x} \times {\mathbb {R}} \rightarrow {\mathbb {R}}^{n_x \times n_x}$ is the Jacobian matrix. The vector ${{\mathbf {x}}_{\mathbf {0}}}$ is called an equilibrium of (4) corresponding to $p_0$ if ${\mathbf {f}}({{\mathbf {x}}_{\mathbf {0}}},p_0)=0$.

Bifurcations of fixed points are concerned with the change of stability or number of solutions as p is varied. Hopf bifurcations are characterized by the coalescence of branches of fixed points and periodic solutions. The Hopf bifurcation theorem [25] prescribes for its occurrence that (4) has an equilibrium $({{\mathbf {x}}_{\mathbf {H}}},p_{H})$ at which the following two conditions must hold: ${\mathbf {J}}({{\mathbf {x}}_{\mathbf {H}}},p_{H})$ has a simple pair of purely imaginary eigenvalues $\nu (p_H)=\pm i \omega _0$; and the transversality condition $\frac{d}{d p} \left. ({\text {Re}} \nu (p))\right| _{p=p_H} \ne 0$ is fulfilled, that is the eigenvalues are not stationary with respect to p at the bifurcation. These conditions ensure the existence of a surface tangent to the eigenspace of $\nu (p_H)$ where periodic solutions exist. If the Lyapunov coefficient $l_1$ (associated with the central manifold reduction at $p=p_H$) is negative, then the periodic orbits are stable, whereas if $l_1$ is positive, the periodic solutions are repelling. The sign of $l_1$ thus determines whether the Hopf bifurcation is supercritical ($l_1<0$) or subcritical ($l_1>0$).

The computational tool of bifurcation analysis is numerical continuation [15], which provides path-following algorithms to efficiently compute families of steady-state solutions and assess their stability, as p is varied. Examples of numerical techniques are Newton–Raphson, arclength, and pseudo-arclength continuation, all of which are efficiently implemented in freely available software. An example is COCO [10], which will be used for the continuation analyses performed in this work.

2.3 Robust bifurcation margins

A framework was recently proposed [19] which allows the robustness of stable equilibria to the onset of Hopf bifurcations in the presence of real parametric uncertainties to be studied. This is briefly reviewed in this section.

To model the presence of uncertainties, the uncertainty vector ${\varvec{\delta }}$ of $n_{\delta }$ real scalar parameters is first introduced:

$$\begin{aligned} {\varvec{\delta }} = [\delta _1; \ldots ; \delta _i; \ldots \delta _{n_{\delta }}], \quad {\varvec{\delta }} \in {\mathbb {R}}^{n_{\delta }}. \end{aligned}$$

(5)

Then, the uncertain vector field $\tilde{{\mathbf {f}}}$ and the associated Jacobian $\tilde{{\mathbf {J}}}$, both depending on ${\varvec{\delta }}$, ${\mathbf {x}}$, and p, are defined:

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}&= \tilde{{\mathbf {f}}}({\mathbf {x}},p,{\varvec{\delta }}),\\ \tilde{{\mathbf {J}}}&\equiv \nabla _x \tilde{{\mathbf {f}}}({\mathbf {x}},p,{\varvec{\delta }}).\\ \end{aligned} \end{aligned}$$

(6)

Consider the case where the nominal system ${\mathbf {f}}$ undergoes a Hopf bifurcation at $({{\mathbf {x}}_{\mathbf {H}}},p_{H})$, while for another value of the bifurcation parameter, denoted by ${\bar{p}}_{0}$, the system has a stable fixed point $\bar{{\mathbf {x}}}_{0}$. The objective of the robust bifurcation margin is to determine the worst-case perturbation $\hat{{\varvec{\delta }}} \in {\varvec{\delta }}$ such that $\tilde{{\mathbf {f}}}$ undergoes a Hopf bifurcation at ${\bar{p}}_{0}$. By doing so, it characterizes robustness of the system at that value of the bifurcation parameter.

Following a robust control theory approach, the meaning of worst-case perturbation shall be interpreted here as smallest among the critical ones. That is, $\hat{{\varvec{\delta }}}$ is the smallest perturbation among those determining a Hopf bifurcation at ${\bar{p}}_{0}$. The scalar metric used to express the magnitude of the perturbation is the largest of the absolute values of the elements in ${\varvec{\delta }}$, i.e., ${\bar{\sigma }}(\text {diag}({\varvec{\delta }}))$.

To achieve this, an LFT model of the Jacobian ${\tilde{\mathbf {J}}}$ is considered, and an optimization problem that computes the worst-case perturbation matrix for which the LFT becomes singular is formulated. A value for the continuation parameter ${\bar{p}}_0$ for which ${\mathbf {f}}$ has a stable equilibrium ${\bar{\mathbf {x}}}_{0}$ is selected by the analyst, and the uncertainty in the system is described by means of the vector ${\varvec{\delta }}$ (5). This allows the LFT ${\mathcal {F}}_{u}({\mathbf {M}}_{\tilde{\mathbf {J}}},{{\varvec{\Delta }})}$ to be constructed, where ${\varvec{\Delta }}=\text {diag}(\text {diag}({\varvec{\delta }}); {{\varvec{\Delta }}_{\mathbf {x}}}; \omega {{\mathbf {I}}_{{\mathbf {n}}_{\mathbf {x}}}})$.

It is noted that ${{\varvec{\Delta }}_{\mathbf {x}}}= \text {diag}(x_{1}{{\mathbf {I}}_{{\mathbf {x}}_{\mathbf {1}}}},\ldots ,x_{j} {{\mathbf {I}}_{{\mathbf {x}}_{\mathbf {j}}}},\ldots ,x_{n_{x}}$${{\mathbf {I}}_{{\mathbf {x}}_{{\mathbf {n}}_{\mathbf {x}}}}})$ reflects the dependence of the Jacobian on the equilibrium (unknown due to the uncertainties), and it does not feature in the LFTs employed for $\mu$ analysis (1). It is also worth remarking that the (unknown) frequency $\omega$ at which the closest Hopf bifurcation occurs features explicitly in the LFT representation.

The robust bifurcation margin $k_m$ is defined as the solution of the following optimization problem with linear objective function (7a), linear inequality constraints (7d), and nonlinear equality constraints (7b)–(7c).

$$\begin{aligned}&\min _{{\mathbf {X}}=[{\mathbf {x}};{\varvec{\delta }};\omega ]} k_m, \end{aligned}$$

(7a)

$$\begin{aligned}&{\tilde{\mathbf {f}}}({\mathbf {x}},{\bar{p}}_0,{\varvec{\delta }})=0, \end{aligned}$$

(7b)

$$\begin{aligned}&\det ({\mathbf {I}} - {{\mathbf {M}}_{{\tilde{\mathbf {J}}}}\;{\mathbf {11}}}{\varvec{\Delta }})=0, \end{aligned}$$

(7c)

$$\begin{aligned}&-k_m \le \delta _{i} \le k_m, \quad i=1,\ldots ,n_{\delta }. \end{aligned}$$

(7d)

where ${\mathbf {X}}$ is the vector of optimization variables including: the state equilibrium ${\mathbf {x}}$; the uncertainty vector ${\varvec{\delta }}$; and the frequency $\omega$. The symbol hat will be used to denote a solution of the optimization (e.g., ${\hat{\varvec{\delta }}}$ is the worst-case perturbation). Observing more closely the problem, it is noted that Eq. (7b) guarantees that the solution $({\hat{\mathbf {x}}},{\bar{p}}_0,{\hat{\varvec{\delta }}})$ corresponds to an equilibrium point for the system. Eq. (7c) ensures that ${\tilde{\mathbf {J}}}$ has a pair of complex eigenvalues $\nu =\pm {\hat{\omega }}$ by enforcing the determinant condition. The latter is indeed a necessary and sufficient condition for well posedness of the associated LFT, and it is also used in the $\mu$ test (3). Finally, Eq. (7d) bounds the size of the perturbation. Notably, $\omega$ is a variable of the optimization problem and thus the margin $k_m$ is sought over all possible Hopf bifurcations having different frequencies. This results in the advantage of not having to fix a priori a grid for the frequency (as in standard $\mu$ analysis [8]) and in more flexibility when performing the analyses [19].

Note that this approach is qualitatively similar to the problem solved in $\mu$ analysis (3). In fact, by thinking of the Jacobian ${\tilde{\mathbf {J}}}$ as the uncertain state-matrix of the linear case, the robust bifurcation margin $k_{m}$ can be seen as an extension of the structured singular value $\mu$ to the case of polynomial vector field. More precisely, it follows from (7) that $k_{m}={\bar{\sigma }}(\text {diag}({\varvec{\delta }}))$, and thus it is equivalent to the reciprocal of $\mu$ (in the linear case, where $\mu$ is defined).

An important feature of this nonlinear robustness formulation is that it allows one to specify whether the analyzed closest bifurcation is supercritical or subcritical by adding a constraint on the sign of $l_1$. The Lyapunov coefficient $l_1$ depends on the eigenvectors of ${\tilde{\mathbf {J}}}$ associated with $\nu$ and the second- and third-order tensors of ${\tilde{\mathbf {J}}}$ [25], thus, it can be written as a function of the optimization variables ${\mathbf {X}}$, and a constraint $s_l l_1 >0$ ($s_l=1$ for subcritical and $s_l=-1$ for supercritical) can be appended to (7).

Finally, it is important to stress that, since the calculation of $k_m$ is based on a non-convex program, global minima might be missed and thus, there could be an uncertainty vector featuring a smaller norm than ${\hat{\varvec{\delta }}}$ causing a Hopf bifurcation. In other words, the solution of (7) gives upper bounds on $k_m$ (analogous to the lower bounds for $\mu$). Various strategies were discussed in [19] and are employed in this work, to mitigate this issue, including the possibility to: solve the optimization in Eq. (7) at fixed frequency; perform a multi-start strategy based on the concept of extended continuation [10] (and consisting of constructing a manifold of Hopf points connected to a given solution ${\hat{\mathbf {X}}}$). The interested reader is referred to [19] for more details on the theoretical and algorithmic formulation of $k_{m}$.

3 Advanced methods for flutter analysis

In this section, the application of two well-known advanced flutter analysis methods to a benchmark case study, presented in Sect. 3.1, is discussed. The first method is the $\mu$-based linear robust analysis (Sect. 3.2), while the second (Sect. 3.3) is the continuation-based nonlinear bifurcation analysis.

3.1 Typical section model and preliminary analyses

The system sketched in Fig. 2 is commonly referred to as the typical section. It has been introduced in the early stages of aeroelasticity to investigate dynamic instabilities such as flutter [6], and it has been since then widely used for analysis of linear and nonlinear aeroelastic systems [12, 29, 31, 38]. It consists of a rigid airfoil with lumped springs simulating the 3 structural degrees of freedom (DOFs): plunge h, pitch $\alpha$, and control surface (or flap) rotation $\beta$ (Fig. 2).

The parameters in the model are: $K_h$, $K_{\alpha }$, and $K_{\beta }$—respectively, the plunge, pitch, and control surface stiffness; half chord distance b; dimensionless distances a, c (from the mid-chord to, respectively, the elastic axis and the hinge location), and $x_{\alpha }$ and $x_{\beta }$ (from elastic axis to airfoil center of gravity and from hinge location to control surface center of gravity); wing mass per unit span $m_s$; moment of inertia of the section about the elastic axis $I_{\alpha }$; and the moment of inertia of the control surface about the hinge $I_{\beta }$. Based on these parameters, the structural mass ${{\mathbf {M}}_{\mathbf {s}}}$ and stiffness ${{\mathbf {K}}_{\mathbf {s}}}$ matrices are defined as:

$$\begin{aligned} \begin{aligned} {{\mathbf {M}}_{\mathbf {s}}}&= m_s b^2 \left[ \begin{array}{ccc} 1 &{} x_{\alpha } &{} x_{\beta }\\ x_{\alpha } &{} r^2_{\alpha } &{} r^2_{\beta }+x_{\beta }(c-a)\\ x_{\beta } &{} r^2_{\beta }+x_{\beta }(c-a) &{} r^2_{\beta }\\ \end{array} \right] ,\\ {{\mathbf {K}}_{\mathbf {s}}}&= \left[ \begin{array}{ccc} K_h &{} 0 &{} 0\\ 0 &{} K_{\alpha } &{} 0\\ 0 &{} 0 &{} K_{\beta } \\ \end{array} \right] ,\\ \end{aligned} \end{aligned}$$

(8)

where $r_{\alpha }=\sqrt{\frac{I_{\alpha }}{m_s b^2}}$ and $r_{\beta }=\sqrt{\frac{I_{\beta }}{m_s b^2}}$ are, respectively, the dimensionless radius of gyration of the section and of the control surface. Theodorsen’s unsteady formulation is employed to model the aerodynamics [24]. This provides the aerodynamic operator as a transfer matrix ${\mathbf {Q}}$ giving the relationship between the elastic degrees of freedom and the aerodynamic load components. The matrix ${\mathbf {Q}}$ has a non-rational dependence on the Laplace variable s; thus, a rational approximation is computed here via the Minimum State method [24]:

Fig. 2

Typical section sketch

$$\begin{aligned} {\mathbf {Q}} \approx {{\mathbf {A}}_{\mathbf {2}}} {\bar{s}}^2 + {{\mathbf {A}}_{\mathbf {1}}}{\bar{s}}+{{\mathbf {A}}_{\mathbf {0}}} + {\bar{\mathbf {D}}} \begin{bmatrix} \frac{1}{{\bar{s}}+\gamma _{1}} &{} \ldots &{} 0 \\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \ldots &{} \frac{1}{{\bar{s}}+\gamma _{n_{a}}} \\ \end{bmatrix} {\bar{\mathbf {E}}} {\bar{s}}, \end{aligned}$$

(9)

where ${\bar{s}}=\frac{s b}{V}$ and: ${{\mathbf {A}}_{\mathbf {2}}}$, ${{\mathbf {A}}_{\mathbf {1}}}$, and ${{\mathbf {A}}_{\mathbf {0}}}$ are real coefficient matrices modeling the quasi-steady contribution to the aerodynamic loads; while ${\bar{\mathbf {D}}}$ and ${\bar{\mathbf {E}}}$ are real coefficient matrices capturing, together with the lag roots $\gamma _{i}$, the memory effect of the wake. The rational approximation entails the addition of the aerodynamic states ${{\mathbf {x}}_{\mathbf {a}}}$, equal in number to the number of lag roots $n_a$. By defining the vector of structural states ${{\mathbf {x}}_{\mathbf {s}}}=[\frac{h}{b}; \alpha ; \beta ]$, the system can be finally described in matrix form as:

$$\begin{aligned} \begin{aligned}&\dot{{\mathbf {x}}}={\mathbf {A}} {\mathbf {x}},\\&\begin{bmatrix} \dot{{\mathbf {x}}}_{\mathbf {s}} \\ \ddot{{\mathbf {x}}}_{\mathbf {s}} \\ \ddot{{\mathbf {x}}}_{\mathbf {a}} \\ \end{bmatrix} = \begin{bmatrix} {\mathbf {0}} &{} {\mathbf {I}} &{} {\mathbf {0}} \\ -{\mathbf {M}}^{-1}{\mathbf {K}} &{} -{\mathbf {M}}^{-1}{\mathbf {B}} &{} q_{\infty } {\mathbf {M}}^{-1} {\bar{\mathbf {D}}} \\ {\mathbf {0}} &{} {\bar{\mathbf {E}}} &{} -\frac{V}{b}{\mathbf {R}} \\ \end{bmatrix}, \\ \end{aligned} \end{aligned}$$

(10)

where $q_{\infty }=\frac{1}{2}\rho _{\infty } V^2$, $\rho _{\infty }$ is the air density, ${\mathbf {R}}$ is a diagonal matrix with the lag roots $\gamma _{i}$ in the nonzero terms, and:

$$\begin{aligned} \begin{aligned}&{{\mathbf {M}}_{\mathbf {a}}} = {{\mathbf {M}}_{\mathbf {s}}}-\frac{1}{2}\rho _{\infty }b^2 {{\mathbf {A}}_{\mathbf {2}}},\\&{{\mathbf {B}}_{\mathbf {a}}} = -\frac{1}{2}\rho _{\infty }b V {{\mathbf {A}}_{\mathbf {1}}},\\&{{\mathbf {K}}_{\mathbf {a}}} = {{\mathbf {K}}_{\mathbf {s}}}-\frac{1}{2}\rho _{\infty } V^2 {{\mathbf {A}}_{\mathbf {0}}}. \end{aligned} \end{aligned}$$

(11)

The matrices ${{\mathbf {M}}_{\mathbf {a}}}$, ${{\mathbf {B}}_{\mathbf {a}}}$ and ${{\mathbf {K}}_{\mathbf {a}}}$ are, respectively, the aeroelastic inertial, damping, and stiffness matrices. They include the structural terms (note that structural damping is null for this case study) plus the aerodynamic quasi-steady matrices. The parameters defining the model are taken from [24] and are reported in Appendix. The total size $n_x$ is 9 (6 structural and 3 aerodynamic states).

Nonlinearities in the stiffness will be considered in this work. Specifically, hardening cubic terms for the plunge and pitch DOFs are assumed, and thus, the matrix ${{\mathbf {K}}_{\mathbf {s}}}$ is rewritten as:

$$\begin{aligned} \begin{aligned} {{\mathbf {K}}_{\mathbf {s}}}&= {{\mathbf {K}}_{\mathbf {s}}}^L+{{\mathbf {K}}_{\mathbf {s}}}^{NL},\\&=\left[ \begin{array}{ccc} K_h^L &{} 0 &{} 0\\ 0 &{} K_{\alpha }^L &{} 0\\ 0 &{} 0 &{} K_{\beta } \\ \end{array} \right] +\left[ \begin{array}{ccc} K_h^{NL} K_h^L \big (\frac{h}{b}\big )^2 &{} 0 &{} 0\\ 0 &{} K_{\alpha }^{NL} K_{\alpha }^L \alpha ^2 &{} 0\\ 0 &{} 0 &{} 0\\ \end{array} \right] ,\\ \end{aligned} \end{aligned}$$

(12)

where the linear ${{\mathbf {K}}_{\mathbf {s}}}^L$ and nonlinear ${{\mathbf {K}}_{\mathbf {s}}}^{NL}$ structural stiffness matrices have been introduced. As common practice [12], the coefficients of the nonlinear terms are assumed proportional to the corresponding linear ones through the coefficients $K_{h}^{NL}$ and $K_{\alpha }^{NL}$.

Given the dependence of the state-matrix ${\mathbf {A}}$ (10) on the parametric uncertainties, standard LFT modeling steps provide an uncertainty description in the form of Eq. (2) and Fig. 1. One possible way to achieve this consists of writing the uncertain parameters in symbolic form and then using the LFR toolbox [30] to directly obtain the partitioned matrix ${\mathbf {M}}$. This matrix will comprise the transfer matrix of the known (nominal) part of the aeroelastic system ($M_{22}$) and matrices $M_{11}$, $M_{12}$ and $M_{21}$, which depend on the considered uncertain parameters and describe how the uncertainty in ${\varvec{\Delta }}$ affects the nominal system. In [19], a detailed derivation of LFT models for state-space representations was carried out. Details on the construction of LFT models specifically tailored to aeroelastic systems of increasing complexity have been addressed in previous works (see [21] for the typical section and [20] for high-fidelity systems generated by finite element methods). It is important to emphasize that, in the nonlinear case, the matrix ${\mathbf {A}}$ (or system’s Jacobian) will also depend in general on the states, which will also appear in the definition of the LFT. That is, as also discussed in Sect. 2.3, ${\varvec{\Delta }}$ will now include the block ${{\varvec{\Delta }}_{\mathbf {x}}}$ gathering the states featuring in the Jacobian. Once the matrix ${\mathbf {M}}_{\tilde{\mathbf {J}}}$ is obtained, and bounds for the parametric uncertainties are established, the optimization problem in Eq. (7) can be solved.

3.1.1 Comments on the modeling rationale

The typical section model (Fig. 2) is a popular case study in aeroelasticity and, despite its modeling simplicity, is a valid schematization for studying the dynamics of an unswept and untapered wing when the geometrical and structural properties are taken at a station 70–75% from the centerline [6]. The inertial and stiffness matrices (8) can indeed be determined from the Lagrange’s equations for a rectangular cantilevered continuous wing model with linear and quadratic mode shapes [42, Chapters 10]. In this context, the degrees of freedom h, $\alpha$, and $\beta$ can be interpreted as the generalized coordinates associated with the bending, torsion, and control surface rotation modes of the wing. Note that, in the case of unswept and untapered geometry, the coupling among the degrees of freedom of the wing’s equation of motions is only due to inertial and aerodynamic forces, while the elastic forces are uncoupled. This is reflected in the matrices defining the typical section model, where the stiffness matrix ${{\mathbf {K}}_{\mathbf {s}}}$ is diagonal and ${{\mathbf {M}}_{\mathbf {s}}}$ and ${\mathbf {Q}}$ are full. This fact motivates the selection of a diagonal nonlinear stiffness matrix ${{\mathbf {K}}_{\mathbf {s}}}^{NL}$, a choice also made in other works that investigated nonlinear aeroelastic phenomena within the typical section framework [12, 29].

The hardening effect modeled in (12) takes into account the fact that the stiffness properties change when the system undergoes large deformations (as is the case for very flexible aircraft), and typically an increase in the stiffness is observed. Softening effects can also be exhibited in systems subject, for example, to compressive loads or heating at high Mach numbers [41], but since these instances are less relevant to the study of flutter they will not be considered here.

Another important aspect is the choice made here to neglect aerodynamic nonlinearities. This is primarily motivated by the fact that in the literature it has often been reported that structural nonlinearities are the main drivers for the onset of bifurcations and LCOs [9, 27, 40]. In fact, prior works that used the typical section to explore nonlinear aeroelastic behaviors generally considered structural nonlinearities only [29, 31, 38]. Nonetheless, capturing aerodynamic effects might also have an important impact on the results depending on the considered system and could therefore also be investigated. For low-speed conditions, nonlinearities typically arise in the case of boundary layer separation, for example in the case of bluff bodies or high angle of attack configurations. In high-speed regimes, compressibility and shock waves can also determine important nonlinear effects. While the use of high-fidelity solvers is often required to accurately capture these phenomena, in [12, Chapters 8,9] modeling approaches to incorporate some of these effects in the typical section model are considered. The systematic investigation carried out in this paper could be seamlessly applied if this type of nonlinear aerodynamics effects was incorporated in the model.

3.1.2 Classic flutter analysis

Linear (i.e., $K_{h}^{NL}=K_{\alpha }^{NL}=0$) flutter of this case study, originally studied in [24], is shown in Fig. 3. The variation with speed of the eigenvalues of the three elastic modes is displayed in Fig. 3a. The system exhibits a binary flutter, featured by a merging of the plunge and pitch frequencies just before the instability occurs at the flutter speed $V_{f}=302.7~\frac{\mathrm{m}}{\mathrm{s}}$ with a flutter frequency $\omega _f=70.7~\frac{\mathrm{rad}}{\mathrm{s}}$. The coalescence is clearly visible in Fig. 3b, where the natural frequencies of the plunge ($\omega _h$) and pitch ($\omega _{\alpha }$) modes are plotted. The poles at the stable speed $V= 270~\frac{\mathrm{m}}{\mathrm{s}}$ are highlighted with an asterisk.

Fig. 3

Linear nominal flutter analysis

3.2 Robust linear analysis with $\mu$

Table 1 Hopf bifurcations of the nominal system for different combinations of nonlinearities and trim states

The $\mu$-based robust linear flutter analysis of this case study was performed in [21], where the effect of different combinations of uncertainties was investigated at the nominally stable speed $V=270~\frac{\mathrm{m}}{\mathrm{s}}<V_{f}$. The part of the analyses which took into account perturbations in the coefficients of the structural matrices is briefly discussed here. The uncertainty definition consists of a range of variation of 10% from the nominal value for the coefficients $M_{s,11}$, $M_{s,22}$, $K_{h}^L$ and of 5% for $M_{s,12}$ and $K_{\alpha }^L$, where the subscripts of the mass parameters denote the coefficients of the relative matrix ( , $M_{s,11}$ is the coefficient 11 of ${{\mathbf {M}}_{\mathbf {s}}}$). By recalling the definition of the mass matrix ${{\mathbf {M}}_{\mathbf {s}}}$ in (8), it can be noted that the described uncertainty on the mass takes into account possible inaccuracies in the knowledge of: the total section mass ($M_{{s}_{11}}$), the moment of inertia of the section about the elastic axis ($M_{{s}_{22}}$); the offset of elastic axis and the center of gravity ($M_{{s}_{12}}$). The corresponding structured uncertainty set, with dimension 5, is:

$$\begin{aligned} {{\varvec{\Delta }}_{\mathbf {u}}} = \text {diag}(\delta _{M_{s,11}}; \delta _{M_{s,12}}; \delta _{M_{s,22}}; \delta _{K^L_{h}}; \delta _{K^L_{\alpha }}). \end{aligned}$$

(13)

In Fig. 4 (taken from [21] and reproduced here for comparison with the other methods), the upper $\mu _{UB}$ (UB) and lower $\mu _{LB}$ (LB) bounds of the structured singular value $\mu$ computed with the default algorithms from the Robust Control Toolbox in MATLAB R2015b [2] are shown. Note that the bounds are very close, thus the actual value of $\mu$ is well predicted. In particular, it can be concluded from this plot that the system is not robustly stable within the allowed uncertainty range because the peak value is $\mu \cong 1.38$. Therefore, the system is flutter free only for structural uncertainties up to approximately 73% ($\approx \frac{1}{1.38}$) of the assumed size.

Fig. 4

Robust linear analysis with $\mu$ for uncertainties in ${{\mathbf {M}}_{\mathbf {s}}}$ and ${{\mathbf {K}}_{\mathbf {s}}}$

Due to the accurate estimation of the lower bound, it is also possible to extract the smallest perturbation matrix $\mathbf {\Delta _{u}^{cr}}$ capable of causing instability, which corresponds to the peak in Fig. 4

$$\begin{aligned} {{\varvec{\Delta }}_{\mathbf {u}}^{\mathbf {cr}}} = \text {diag}(-0.7245; 0.7245 I_2; 0.711; 0.6460;-0.7213). \end{aligned}$$

(14)

It is also interesting to observe that the peak of the curves take place at about $72.2~\frac{\mathrm{rad}}{\mathrm{s}}$, which is close to the nominal flutter frequency $\omega _f=70.7~\frac{\mathrm{rad}}{\mathrm{s}}$ shown in Fig. 3a.

3.3 Bifurcation analysis of the nominal nonlinear system

When the nonlinear stiffness effects are non-negligible, the matrix ${{\mathbf {K}}_{\mathbf {s}}}$ is given by Eq. (12) and, if it is assumed a nominal vector field, the problem can be studied in the setting of bifurcation analysis. Consider the dynamics:

$$\begin{aligned} \begin{aligned} \dot{{\mathbf {x}}}={\mathbf {f}}({\mathbf {x}},V)&={\mathbf {A}}^{L}(V){\mathbf {x}}+{\mathbf {f}}^{NL}({\mathbf {x}},V),\\ {\mathbf {J}}({\mathbf {x}},V)&= {\mathbf {A}}^{L}(V) + \nabla _x {\mathbf {f}}^{NL}(x,V),\\ \end{aligned} \end{aligned}$$

(15)

where ${\mathbf {A}}^{L}:{\mathbb {R}} \rightarrow {\mathbb {R}}^{n_x \times n_x}$ is obtained from the definition of ${\mathbf {A}}$ in Eq. (10) by setting the nonlinear terms to zero, and ${\mathbf {f}}^{NL}:{\mathbb {R}}^{n_x} \times {\mathbb {R}} \rightarrow {\mathbb {R}}^{n_x}$ is the nonlinear part of the vector field. The bifurcation parameter p is typically the speed V in the context of flutter analysis, but other options could be considered. Note that, for the particular nonlinearities assumed here, $f^{NL}$ (and thus also $\nabla _x f^{NL}$) does not depend on the speed.

Numerical continuation can be applied to Eq. (15). First, the value of the trim state ${{\mathbf {x}}_{\mathbf {t}}}$ has to be specified since this has an influence on nonlinear flutter analysis [34]. Two trim conditions will be considered to exemplify its effect. The first corresponds to a zero trim state, i.e., ${{\mathbf {x}}_{\mathbf {t}}}=0$, whereas the second has a nonzero value for some of the entries of ${{\mathbf {x}}_{\mathbf {t}}}$. This could be physically motivated by the need to generate positive lift to counterbalance gravitational forces (i.e., $\alpha _t \ne 0$) or to provide static equilibrium about the aircraft’s center of gravity (i.e., $\beta _t \ne 0$). More refined descriptions for ${{\mathbf {x}}_{\mathbf {t}}}$ could consider a dependence on speed or the presence of a pre-deformed shape (with nonzero values for $h_t$ and $\beta _t$). In here, the case $\alpha _t=1^{\circ }$, which is sufficient to illustrate the role played by a nonzero ${{\mathbf {x}}_{\mathbf {t}}}$, is considered.

In order to present an overview of the possible nonlinear responses of the system, 6 scenarios are defined. These arise from considering, for each trim state, the cases of: plunge nonlinear stiffness only ($K_{\alpha }^{NL}=0$), pitch nonlinear stiffness only ($K_{h}^{NL}=0$), and both nonlinear stiffnesses present (with $K_{\alpha }^{NL}=K_{h}^{NL}=100$). The results are presented in Table 1, where, for each scenario (s#, with $\#=1,\ldots ,6$), the speed $V_{H}$ at which the Hopf bifurcation occurs, the frequency of the associated imaginary eigenvalues $\omega _{H}$, and the type of bifurcation (sub for subcritical and super for supercritical) are reported.

Figure 5 shows the corresponding bifurcation diagrams with V on the x-axis and the pitch DOF on the y-axis (in case of branches of LCO, this indicates the maximum value over a period). Specifically, Fig. 5a shows the cases featuring ${{\mathbf {x}}_{\mathbf {t}}}=0$, while Fig. 5b shows the cases with $\alpha _t=1^{\circ }$. The convention of representing stable steady-states (equilibria and LCOs) with solid lines and unstable ones with dashed lines is adopted, and different line colors are used for the 6 different scenarios (s#).

Fig. 5

Bifurcation diagram of the nominal system for different combinations of nonlinearities and trim states (solid and dashed lines denote, respectively, stable and unstable steady-states) obtained with COCO

The first important observation from Fig. 5a is that when ${{\mathbf {x}}_{\mathbf {t}}}=0$ the branch of equilibria is ${{\mathbf {x}}_{\mathbf {0}}}=0$ regardless of V. This implies that ${\mathbf {J}}={\mathbf {A}}^{L}$, thus the occurrence of the Hopf bifurcation is independent of the nonlinear terms. This is seen in Table 1, where for s1, s2, and s3 the results of the linear case (Fig. 3a) are retrieved (i.e., $V_{H}=V_f$ and $\omega _{H}=\omega _f$). Nonlinear terms, however, do have an effect on the type of bifurcation (subcritical for s1 and supercritical for s2 and s3).

When $\alpha _t=1^{\circ }$, it can be seen from Fig. 5b that the branch of equilibria has a nonzero (speed dependent) value—it is noted that the cases s4 and s6 overlap in the figure. Moreover, different values of $V_{H}$ (this is the speed, different for each case, at which a branch of LCO emanates from the branch of equilibria) are obtained depending on the nonlinearities affecting the system. This is due to the fact that the linearization of the Jacobian, since ${{\mathbf {x}}_{\mathbf {0}}}\ne 0$, is now affected by the nonlinear term of the vector field ${\mathbf {f}}^{NL}$.

Another important trend observed in the figures, irrespective of the value of ${{\mathbf {x}}_{\mathbf {t}}}$, is that a subcritical bifurcation only occurs for the cases of nonlinearity in plunge (i.e., s1 and s4, for which the folding point of the limit cycle branch takes place at high amplitudes and is thus out of the plot). Conversely, when there are nonlinearities in the pitch degree of freedom (s2, s3, s5, and s6), the bifurcation is always supercritical. This scenario was confirmed by performing extensive time marching simulations with random initial conditions.

The influence of the type of nonlinearity on the nature of the Hopf bifurcation is in agreement with the interpretation given in [12], where the concept of intermittent flutter, based on the instantaneous natural frequencies of the underlying linear system, is used to qualitatively explain the mechanisms activating different LCOs. This is briefly discussed here with regard to s1 and s2 (similar arguments could be used for s4 and s5). As a preamble, recall the trend of the plunge and pitch natural frequencies emphasized in Fig. 3b (where $V_{f}=V_{H}$ for these cases as stressed above). Consider a speed $V_{H}^{\epsilon }$ slightly larger than $V_{H}$. Since the equilibrium is unstable, the system will start oscillating and the nonlinear terms will become important. In s2, the pitch frequency $\omega _{\alpha }$ will increase and, as the oscillations become larger, the plunge frequency $\omega _{h}$ (which remains constant) will be far from $\omega _{\alpha }$ and thus, the binary flutter mechanism triggering the instability will cease to exist. As a result, the oscillations will decay and reach a level which is compatible with the existence of a flutter mechanism. Since $\omega _{\alpha }>\omega _{h}$ at $V_{H}^{\epsilon }$, the growth in amplitude must be gradual and thus a supercritical LCO emanates from the Hopf point. The situation is different for s1. Indeed, the hardening plunge stiffness now promotes an instantaneous higher value of $\omega _h$ as the system starts oscillating, and this, in addition to the fact that $\omega _{\alpha }>\omega _{h}$, will make possible the existence at $V_{H}^{\epsilon }$ of a flutter mechanism featuring large amplitudes. Moreover, if V is decreased below $V_{H}$, an LCO can still exist because oscillations in the system are compatible with coalescence of the natural frequencies.

In the case of s3, where both nonlinear terms are present, a supercritical bifurcation occurs here. This is ascribed to the particular choice of $K_{h}^{NL}$ and $K_{\alpha }^{NL}$ in Table 1, which makes a mechanism qualitatively similar to that of s2 prevail on the other. By increasing the coefficient $K_{h}^{NL}$, it is noted that a subcritical bifurcation would occur.

4 Robustness of the Hopf bifurcation in the face of modeling uncertainty

The advanced methods applied in the previous section are able to cope with the two acknowledged issues in flutter analysis: uncertainties (through $\mu$ analysis) and nonlinearities (through bifurcation). However, these approaches fail individually to give an answer to the question of robustness if both uncertainties and nonlinearities must be taken into account. For this reason, the concept of robust bifurcation margins (reviewed in Sect. 2.3) is applied here to study the effect of modeling uncertainties on nonlinear aeroelastic instabilities.

Including uncertainties in the nominal vector field (15) yields the following expression:

$$\begin{aligned} \dot{{\mathbf {x}}}={\tilde{\mathbf {f}}}({\mathbf {x}},V,{\varvec{\delta }})&={\tilde{\mathbf {A}}}^{L}(V,{\varvec{\delta }}){\mathbf {x}}+{\tilde{\mathbf {f}}}^{NL}({\mathbf {x}},V,{\varvec{\delta }}) \end{aligned}$$

(16a)

$$\begin{aligned} {\tilde{\mathbf {J}}}({\mathbf {x}},V,{\varvec{\delta }})&= {\tilde{{\mathbf {A}}}}^{L}(V,{\varvec{\delta }}) + \nabla _x {\tilde{\mathbf {f}}}^{NL}({\mathbf {x}},V,{\varvec{\delta }}) \end{aligned}$$

(16b)

Given a speed ${\bar{V}}_0$ for which there exists a stable equilibrium and the definition of a vector ${\varvec{\delta }}$ of uncertain parameters, the distance in the parameter space from the closest Hopf bifurcation is computed by means of the robust bifurcation margin $k_m$.

Table 2 Robust bifurcation margins at ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$

In the analyses presented in this section, the uncertainty set ${\varvec{\delta }}$ is incrementally augmented in order to investigate in depth the rich nonlinear dynamics triggered by modeling uncertainties. In order to emphasize the benefits of the newly proposed framework and the relationship with the standard robust analysis approach, Sect. 4.1 will investigate the case where the same uncertainty description considered in the $\mu$ analyses of Sect. 3.2 holds, i.e., only structural uncertainties. Then, Sect. 4.2 will consider the case including also aerodynamic parameters, while Sect. 4.3 will augment the analysis to include the effect of perturbation in the nonlinear coefficients. The influence of uncertain control surface stiffness is investigated in Sect. 4.4, where interesting connections with findings from the literature concerned with freeplay-induced subcritical LCOs are addressed. Finally, Sect. 4.5 shows that the robust bifurcation analyses can also aid in better understanding the properties of the nominal system by detecting isolated branches in the landscape of steady-state solutions of the system, typically difficult to do by only relying on numerical continuation.

The speed ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$, smaller than all the speeds $V_H$ found by the nominal bifurcation analyses (Table 1), will be considered throughout the section.

4.1 Structural uncertainties

The parameters in ${\varvec{\delta }}$ are the same as those in the set (13), i.e., ${\varvec{\delta }} = [\delta _{M_{s,11}}; \delta _{M_{s,12}}; \delta _{M_{s,22}}; \delta _{K^L_{h}}; \delta _{K^L_{\alpha }}]$. Note that, consistently with the analyses in Sect. 3.2, only the linear coefficients of the stiffness matrix are assumed uncertain here. All the six (nominal) cases considered in Table 1 are analyzed, and the results are reported in Table 2 in terms of robust bifurcation margin $k_m$, frequency ${\hat{\omega }}$ of the imaginary eigenvalues at ${\bar{V}}_0$, and type of Hopf bifurcation (this was inferred a posteriori by performing continuation analysis of the perturbed system). Indeed, in these analyses the criticality of the predicted Hopf bifurcation is not specified in the optimization (i.e., no constraint on the sign of $l_1$ is enforced).

The results relative to s1–s2–s3 (corresponding to the trim state ${{\mathbf {x}}_{\mathbf {t}}}=0$) present the same robust margins and frequencies. Recall from the nominal analyses (Fig. 5) that the branch of equilibria ${{\mathbf {x}}_{\mathbf {0}}}=0$ was found for all these cases and observe that ${\tilde{\mathbf {f}}}^{NL}(0,\cdot ,\cdot )=0$, i.e., ${{\mathbf {x}}_{\mathbf {0}}}=0$ are also equilibria of the uncertain vector field. Therefore, $\nabla _x {\tilde{\mathbf {f}}}^{NL}= 0$ and thus the determination of $k_m$, since it does not depend on the nonlinear terms, is equivalent to the problem solved by $\mu$ in the linear case. That is, both aim at finding the smallest perturbation matrix such that $\tilde{{\mathbf {A}}}^{L}$ is neutrally stable. This result complements the discussion in Sect. 3.3 concerning the effect of ${{\mathbf {x}}_{\mathbf {t}}}$ on nonlinear flutter. While the role played by the trim state ${{\mathbf {x}}_{\mathbf {t}}}$ on (nominal) nonlinear flutter is better understood [34], that on robustness to uncertain parameters is relatively unexplored and should be considered when making the simplifying assumption of zero trim states [39].

Table 3 Worst-case perturbations and margins to the onset of supercritical and subcritical Hopf bifurcations for structural and aerodynamic uncertainties

For the reason above, one would also expect that nonlinear and linear robust analyses should provide the same outcome for the tests s1–s2–s3. Indeed, the margin $k_m$ computed for the first three cases is within less than 1% from the maximum singular value of the perturbation matrix (14) found by $\mu$ in Sect. 3.2. Because $\mu _{LB}$ and $\mu _{UB}$ are close around the peak of Fig. 4, this also indicates that results in Table 2 are actual worst-case predictions (i.e., the global maximum of problem 7 has been found). Both these observations are important confirmation of the soundness of the analyses.

The uncertainty vector found by the optimizer is:

$$\begin{aligned} \begin{aligned} {\hat{\varvec{\delta }}} =&\left[ \delta _{M_{s,11}}; \delta _{M_{s,12}}; \delta _{M_{s,22}}; \delta _{K^L_{h}}; \delta _{K^L_{\alpha }}\right] ,\\ =&\left[ -0.7328;0.5027;0.7328;0.7328;-0.7328\right] .\\ \end{aligned} \end{aligned}$$

(17)

Examining the signs and values of the above worst-combination, it is noted that these are very close to those predicted by $\mu$ in Eq. (14). Moreover, it is interesting to observe that the structural parameters have opposite perturbations if grouped according to the affected degrees of freedom (i.e., plunge and pitch). Specifically, the plunge equilibrium sees a reduction in $M_{s,11}$ and an increase in $K^L_{h}$, while the pitch equilibrium sees an increase in $M_{s,22}$ and a reduction in $K^L_{\alpha }$. This corresponds to getting the plunge and pitch natural frequencies closer, which is known to be detrimental in systems prone to binary flutter.

Attention is turned now to the instance when ${{\mathbf {x}}_{\mathbf {t}}} \ne 0$ (cases s1–s2–s3). Since $k_m$ is smaller than 1, then it is again concluded from Table 2 that the Hopf bifurcation can be shifted to $V=270~\frac{\mathrm{m}}{\mathrm{s}}$ for perturbations within the allowed uncertainty range. Moreover, the values of $k_m$ are consistent with the nominal analyses, for which s4 and s6 presented a smaller $V_{H}$ than s5. Thus, it is expected that they will present smaller margins since their corresponding nominal bifurcation speeds (see Table 1) are closer to the analyzed speed ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$.

Another insight available from Table 2 is that the closest Hopf bifurcations are of the same nature as the corresponding ones in nominal conditions. Based on the greater attention devoted to subcritical LCOs in view of the associated risks [12, 38], the rest of the analyses will try to understand whether perturbations in the parameters can drive the Hopf bifurcation from supercritical to subcritical. Prompted by this, and because of the greater interest in the case when ${{\mathbf {x}}_{\mathbf {t}}} \ne 0$ owing to the previously described effect, only the two cases s5 and s6 are studied thereafter.

4.2 Structural and aerodynamic uncertainties

Uncertainties in two aerodynamic parameters are added to the set of structural parameters studied in the previous section in order to assess potential effects when their knowledge is only approximate. Specifically, the terms $A_{0,12}$ and $A_{0,22}$ of the steady aerodynamic matrix ${{\mathbf {A}}_{\mathbf {0}}}$ (9) are allowed to vary within $20\%$ from their nominal values. These coefficients correspond, respectively, to the static lift and moment coefficients of the airfoil.

An additional reason to account for these perturbations is that the case of static stall, a type of aerodynamic nonlinearity arising due to boundary layer separation, can be approximately modeled as the variation of these aerodynamic coefficients with respect to the linear conditions. Therefore, this type of analysis can be used as a first exploratory study into the effect of some aerodynamic nonlinearities on the typical section system.

Table 3 shows the results when the type of the closest Hopf bifurcation is specified by now adding a constraint on the sign of $l_1$. In the first and second columns, the normalized perturbations leading to supercritical bifurcations are listed (in the brackets the percent variation from the nominal value), whereas the third and fourth columns report the subcritical cases. The margin $k_m$ and the frequency are also indicated.

The supercritical cases ($l_1<0$) are coherent with the results from Sect. 4.1. The margins approximatively halve in both cases in comparison with those of Table 2 as a result of additional uncertainty in the system, with the frequencies keeping similar values. By looking at the predicted variations in the parameters, it is noted that the structural ones have the same pattern with regard to the predictions evaluated earlier (17). Indeed, $M_{s,12}$ is the only one to change sign, and this can be explained with the small sensitivity of $k_m$ to this parameter. The predicted worst-case perturbations for $A_{0,22}$ and $A_{0,12}$ have also a physical interpretation. Due to the sign conventions (Fig. 2), a simultaneous increase in $A_{0,22}$ and decrease in $A_{0,12}$ means that a positive pitch rotation determines a larger clockwise pitching moment and upwards vertical force, respectively, thus making the system less stiff. This reconciles with the fact that an increased flexibility under the action of the aerodynamic forces will amplify the coupling between elastic and aerodynamic terms, leading to earlier onset of instability.

Consider now the subcritical cases ($l_1>0$), which occur for higher perturbations in the system ($k_m>3$). While all parameters show the same trend as in the supercritical cases, this does not hold for $A_{0,12}$, which has an opposite perturbation and, in absolute value, it is smaller than the others. This is an interesting aspect, because according to the previous discussion a negative perturbation for $A_{0,12}$ would have been expected. The interpretation for this is that, in order for the subcritical Hopf bifurcation to take place, the natural frequencies of the system must substantially change (this aspect will be further investigated next) and for this to happen, it is necessary to have the large perturbations observed in Table 3 for the structural parameters. These have the same sign as for the supercritical cases, but are about one order of magnitude larger, thus they would cause the system instability at much smaller speeds than the pre-fixed one, i.e., ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$. Therefore, sign and norm of the perturbation of $A_{0,12}$ are such that this perturbation has a stabilizing effect and thus, the bifurcation point occurs at ${\bar{V}}_0$. This result is distinctive of the nonlinear uncertain problem, where different (possibly conflicting) constraints define the worst-case conditions. While robustness in the linear context focuses on the loss of stability, from a dynamical systems perspective this becomes a multi-faceted concept characterized by concurrent conditions (for example here criticality and onset of the bifurcation).

With the aim to further understand the role of the uncertainties, additional investigations are carried out by focusing on the worst-case perturbations predicted for s5. Fig. 6a shows bifurcation diagrams obtained from numerical continuation considering the perturbed parameters in the first and third column of Table 3. As expected, they give rise to, respectively, a supercritical and subcritical Hopf bifurcation at $V={\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$.

Figure 6b reports plunge ($\omega _{h}$) and pitch ($\omega _{\alpha }$) natural frequencies linearized around the branch of equilibria as the speed is increased. Two apparent differences between the supercritical and subcritical cases can be appreciated. The first concerns the coalescence between the natural frequencies. This takes place after the bifurcation for the supercritical case, and before for the subcritical one. This is in agreement with the intermittent flutter interpretation of the LCO described for the nominal case in Sect. 3.3. Indeed, the pattern for Column 3 is such that $\omega _{\alpha }<\omega _{h}$ at the bifurcation speed, unlike in the nominal (Fig. 3b) and Column 1 cases where the opposite holds. As a result, even with a hardening pitch stiffness, large oscillations are compatible with the establishment of a flutter mechanism and thus a subcritical Hopf takes place. Secondly, Fig. 6b shows that the gap between the natural frequencies across all the speeds is markedly narrower in the subcritical case. This is a result of the large perturbations associated with the margin $k_m=3.4$, which have the effect of amplifying the coupling between the modes, and hence bringing the frequencies closer across all speeds. This aspect is connected with the interpretation of the perturbation of the parameter $A_{0,12}$ discussed above.

Fig. 6

System s5 perturbed with structural and aerodynamic uncertainties

Table 4 Robustness to uncertainty also in the proportional coefficients of the nonlinear stiffness terms

4.3 Effect of uncertainties in the nonlinear terms

Up until now, only uncertainties in the linear plunge and pitch stiffness coefficients $K_{h}^{L}$ and $K_{\alpha }^{L}$ have been considered. Recalling that the plunge and pitch nonlinear stiffness coefficients are given, respectively, by the products $K_{h}^{NL}K_{h}^{L}$ and $K_{\alpha }^{NL} K_{\alpha }^{L}$ (12), it is clear that this uncertainty had also an effect on the nonlinear structural stiffness matrix ${{\mathbf {K}}_{\mathbf {s}}}^{NL}$. However, the proportional coefficients $K_{h}^{NL}$ and $K_{\alpha }^{NL}$ have been assumed fixed and equal to 100 (see Table 1). Since their accurate determination is far from being a consolidated practice, it is reasonable to account for a dispersion in their values. Specifically, $K_{h}^{NL}$ and $K_{\alpha }^{NL}$ will be allowed to vary within $20\%$ from their nominal values and, as a result, each entry of ${{\mathbf {K}}_{\mathbf {s}}}^{NL}$ is given by the multiplication of two independent uncertain parameters.

Table 4 gathers the worst-case perturbations and bifurcation margins obtained for the new augmented set of uncertainties. The supercritical cases barely change with respect to the analyses in Table 3, and this is due to the fact that the predicted perturbations for $K_h^{NL}$ and $K_{\alpha }^{NL}$ are identical to the ones for the linear coefficients $K_h^{L}$ and $K_{\alpha }^{L}$. Thus, the extra degree of freedom of perturbing individually the two terms defining the nonlinear stiffness coefficients worsens the margins only slightly. This reasoning also applies to the subcritical case but only for the pitch nonlinearity case (s5 $l_1>0$), which also features a slightly smaller $k_m$ than the corresponding case analyzed in Table 3. The only detectable change concerns the last column (s6 $l_1>0$), where interestingly a positive perturbation for $K_{\alpha }^{NL}$ is predicted by the optimization, opposite to the one for the linear term $K_{\alpha }^{L}$. The perturbation to $K_{\alpha }$ is thus now decoupled in the linear $K_{\alpha }^{L}$ and nonlinear $K_{\alpha }^{NL}$ part, resulting in a lower bifurcation margin $k_m$. Another way to think of it is that the uncertainty has here more degrees of freedom than when uncertainty in $K_{\alpha }$ is only given by one parameter.

Figure 7 shows, for the two s6 cases, the reciprocal of the robust bifurcation margin as a function of the frequency. This representation is adopted in view of the close connection, discussed in Sect. 2.3, between the reciprocal of $k_m$ and the structured singular value $\mu$. In fact, Fig. 7 resembles Fig. 4, and in general the plots employed in linear robust analysis [7, 28, 43], which feature peaks for frequencies associated with potential instabilities. The plots are obtained by computing $k_m$ on a grid of frequencies $\omega$ and presents the supercritical and subcritical Hopf in Fig. 7a and b, respectively.

Fig. 7

Frequency representation of the reciprocal of the robust bifurcation margin

According to the definition of the margin (Eq. 7), when $\frac{1}{k_m} \ge 1$ a perturbation in the allowed range of uncertainties exist such that a Hopf bifurcation is experienced by the system when perturbed. Figure 7a features indeed a pronounced peak of approximately 4, corresponding to a margin of 0.25. This margin equals the result in the second column of Table 4 which was obtained without frequency gridding. The analyses thus confirm that the closest supercritical and subcritical Hopf bifurcations take place in the range of frequencies where the pitch and plunge modes coalesce, which is the binary flutter mechanism already ascertained in nominal conditions.

Based on all the analyses so far, it can be established that the presence of the uncertainties is able to trigger the onset of the Hopf bifurcation at lower speeds as well as to change its nature (from supercritical to subcritical), but the underlying physical mechanism is unaltered. The next section shows that the proposed analysis framework can also anticipate new mechanisms not observed in nominal conditions which, depending on the perturbations of the parameters, could become critical.

4.4 Effect of control surface stiffness uncertainty

The destabilizing mechanism analyzed so far is the result of a coupling between the two elastic states plunge (h) and pitch ($\alpha$), which is not affected by the third state representing the control surface rotation ($\beta$). This observation, supported by a wide frequency separation between the dynamics of $\beta$ and the other two states, is sometimes leveraged to reduce the size of the problem by neglecting the flap motion [17]. However, this hypothesis might be invalidated by a decrease in the stiffness of the control surface $K_{\beta }$. A possible cause for this, in addition to the lack of confidence on its exact value, could be the presence of nonlinear behaviors which typically affect control surfaces. For example, freeplay is known to significantly influence the flutter results and to be an important driving force behind the onset of subcritical LCOs [26]. The computation of $k_m$ is currently only possible for polynomial vector fields, thus freeplay cannot be exactly modeled, but its effect can be approximated as a reduction in the value of $K_{\beta }$. This is the rationale, for example, behind the application of the Describing Function method, which provides a relationship between the reduction in stiffness and the amplitude of the LCO [11]. Specifically, a standard procedure consists in discretizing the control surface stiffness in the interval $[0, K_{\beta }]$ and performing for each value a linear flutter analysis, which then allows a diagram $V_f$-LCO amplitude to be derived. An alternative formulation whereby gridding is avoided by making use of integral quadratic constraints lead in [22] to the proposal of the worst-case LCO curve for the cases where the system is also subject to parametric uncertainties. Previous studies thus confirm that freeplay has an uncertain softening effect on the associated stiffness, and thus, the addition of $K_{\beta }$ to the set of uncertainties is physically justified. This will be investigated in this section by augmenting the previous section’s uncertainty set with an uncertainty ranging 40% from nominal for $K_{\beta }$.

Figure 8 presents a comparison between the cases with (curve B1) and without (curve B2, i.e., the same curve from Fig. 7b) uncertainty in $K_{\beta }$ by showing the reciprocal of $k_m$ as a function of the frequency for system s6 (case of subcritical Hopf bifurcation).

Fig. 8

Comparison of the reciprocal of $k_m$ for the cases with and without uncertainty in $K_{\beta }$ (subcritical Hopf bifurcation)

The analyses reveal that including uncertainty in $K_{\beta }$ has a strong impact on the potential onset of a subcritical LCO in the system. Note indeed that, even though $k_m > 1$ (equivalently, $\frac{1}{k_m} < 1$ from the plot) and thus, the predicted perturbation provoking the bifurcation lies outside the allowed set, the value of $k_m$ has drastically decreased compared to the previous analyses. Moreover, the peak of the plot is in a different frequency interval, specifically around $100 \frac{\mathrm{rad}}{\mathrm{s}}$, which suggests a different physical mechanism prompting the Hopf bifurcation. The worst-case perturbations associated with the peak of curve B1 are then inspected in Table 5.

Table 5 Worst-case perturbations for the onset of a subcritical Hopf bifurcation when including uncertainty in $K_{\beta }$

The predicted variations for the structural parameters are markedly different from those encountered in all the previous analyses. The linear stiffness and mass parameters, for example, have opposite signs when compared to the results in Tables 3 and 4, and $M_{s,11}$ is almost unperturbed. In fact, the perturbations do not bring the plunge and pitch modes closer in this case, but determine an increase in $\omega _{\alpha }$ and a decrease in the flap frequency $\omega _{\beta }$ (while not affecting the plunge properties).

Figure 9 attempts to interpret this result by looking at indicators commonly used in flutter analyses. Specifically, the Modal Assurance Criterion (MAC) [1] enables the mode tracking problem to be addressed by quantifying the linearity between two mode shapes. Given two vectors (typically a reference and a tested eigenmode), MAC is a scalar number between 0 and 1, with the former corresponding to two orthogonal modal vectors and the latter to two identical ones (for values in between there is a certain degree of similarity between the reference and the tested modes).

Fig. 9

Linearized frequencies and MAC around the branch of equilibria for nominal (red) and perturbed (black) case s6. (Color figure online)

In Fig. 9a, the natural frequencies of the three structural modes (obtained linearizing the Jacobian

around the branch of equilibria) are reported, whereas Fig. 9b shows the MAC among the three structural modes in order to monitor how their coupling vary with speed. The labels $MAC(\alpha ,\beta )$ and $MAC(\alpha ,h)$ in Fig. 9b indicate the MAC between the pitch and flap modes, and the pitch and plunge modes, respectively. In both figures, the system Pert with perturbations from Table 5 is compared with Nom (i.e., the nominal s6 from Table 1).

The perturbed system presents in Fig. 9a a significant reduction in $\omega _{\beta }$ together with an increase in $\omega _{\alpha }$ compared to the nominal system, as expected from Table 5. However, there is still a considerable frequency gap between the pitch and flap modes, thus based on this plot there seems to be no strong coupling between them. A different perspective is given by Fig. 9b, where a marked increase in the coupling between the $\alpha$ and $\beta$ modes is apparent for the perturbed system (i.e., a higher MAC value throughout speed for the solid black line with respect to the nominal solid red line), and a decrease in that between $\alpha$ and h (dashed black and red lines). In particular, $MAC(\alpha ,\beta )$ and $MAC(\alpha ,h)$ are comparable in magnitude for the perturbed system around ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$, but the slope of the curve is opposite. This might suggest that at subcritical speeds there is opportunity for stable oscillations in the system as indicated by the coupling between $\alpha$ and $\beta$ becoming stronger (and amplified as the speed decreases). In order to further support these claims, the Jacobian is linearized around the stable LCO occurring at ${\bar{V}}_0$ (this is provided by the solver COCO as an outcome of the continuation analysis and is depicted in Fig. 10a). This allows MAC to be computed at each time and its variation over a period to be plotted (Fig. 10b). The horizontal lines correspond to the MAC associated with the equilibrium point at the Hopf bifurcation speed ${\bar{V}}_0$.

Fig. 10

Periodic behavior of the perturbed system s6 at ${\bar{V}}_0=270~\frac{\mathrm{m}}{\mathrm{s}}$

Figure 10b shows that oscillations in the system allow for a strong coupling between the $\beta$ and $\alpha$ modes to take place. Their MAC indeed has a value just below 0.9 for large parts of the period, which is much larger than the one corresponding to the equilibrium (the horizontal solid line). It is thus confirmed that the system has a stable (high amplitude) LCO at ${\bar{V}}_0$ due to the detrimental interaction between these two modes.

The analyses are concluded by showing in Fig. 11 the bifurcation diagram of the perturbed system s6 relative to the pitch state $\alpha$ (equilibria are plotted in red and LCOs in black). Analogous trends are observed for h and $\beta$.

Fig. 11

Bifurcation diagram of the perturbed system s6 (stable and unstable steady-states in solid and dashed line, respectively)

The plot features a branch of equilibria which loses stability at ${\bar{V}}_0$ where the subcritical Hopf bifurcation occurs (circle marker), and an unstable LCO branch emanating from it. Note that this branch does not fold into a stable LCO as typically happens (recall for example the curves in Fig. 6a). The stable LCO branch is constructed by initializing the continuation solver with the periodic response obtained with time-marching simulations at ${\bar{V}}_0$. As the speed is decreased, this branch undergoes a supercritical Neimark–Sacker (NS), or torus, bifurcation [25] (square marker at $V \cong 40~\frac{\mathrm{m}}{\mathrm{s}}$), with quasi-periodic solutions present in the system at smaller speeds. The occurrence of this type of bifurcation in aeroelastic systems has already been ascertained in the literature [29], and here, its possible appearance as a result of uncertainty in the system has been revealed.

These results show that the perturbations in Table 5 are able to drive the system into a global complex scenario featuring bi-stability for very low values of V. This implies, for example, that the equilibrium branch is only locally stable for $0<V<{\bar{V}}_0$ and thus region of attraction analyses [23, 32] are required to guarantee a safe operation of the system. Moreover, for speeds greater than ${\bar{V}}_0$ the system will jump onto a stable LCO featuring very high amplitudes. The amplitude is indeed much higher than the one seen for $\alpha$ on the branch emanating from the subcritical Hopf in Fig. 6a (in that case only uncertainty on linear stiffness and aerodynamics were considered). This feature is even more critical considering that the margin $k_m$ associated with the scenario in Fig. 11 is the smallest among all the subcritical cases detected in the analyses.

4.5 Insights into the bifurcation diagram of the nominal system

The robust bifurcation margin addresses robustness of local bifurcation [25] (i.e., the Hopf one), and thus in principle only provides a local information. It is then of interest to investigate whether the global scenario commented with respect to Fig. 11 (involving, for example, bi-stability at lows speeds) is determined by the particular worst-case combination of the uncertainties or if it reflects features already existing in the nominal system.

To this end, a series of ad hoc continuation analyses are performed. Let us introduce first a scalar k and consider the uncertain vector field:

$$\begin{aligned} \dot{{\mathbf {x}}}={\tilde{\mathbf {f}}}({\mathbf {x}},V,k{\hat{\varvec{\delta }}}), \end{aligned}$$

(18)

where ${\hat{\varvec{\delta }}}$ is fixed to the perturbation in Table 5 (leading to the results in Fig. 11). Therefore, k can be used as a bifurcation parameter contracting and expanding the perturbations along the direction given by ${\hat{\varvec{\delta }}}$ (where $k=0$ corresponds to the nominal condition and $k=1$ to the perturbation in Table 5).

In Fig. 12a, the continuation of the Neimark–Sacker point is shown. Since this bifurcation has codimension 2, it is computed by allowing k and V to vary simultaneously (starting from the square marker). Figure 12b instead continues the stable and unstable LCO branches at $V=100~\frac{\mathrm{m}}{\mathrm{s}}$ (visible in Fig. 11) in the interval $k \in [0, 1]$, starting from $k=1$.

Fig. 12

Tests on the branches of the LCO detected in the perturbed system

While from Fig. 12a, it can be inferred that the Neimark–Sacker bifurcation does not exist when the perturbations are contracted below a factor of 0.85, Fig. 12b reveals that the stable and unstable branches of the LCOs observed in Fig. 11 exist at $V=100~\frac{\mathrm{m}}{\mathrm{s}}$ for every value of k in the interval [0, 1]. In fact, these LCOs exist also in the nominal system ($k=0$) and the dependence of this family of periodic orbits on the speed can be tracked with numerical continuation by starting from the LCO point of the nominal system at $V=100~\frac{\mathrm{m}}{\mathrm{s}}$. This solution is available from the continuation analysis performed in Fig. 12b, specifically it is the point with $k=0$. The results of this analysis are reported in Fig. 15a, where a bifurcation diagram for the nominal system with all the detected branches of steady-states (equilibria in red and LCOs in black) are shown.

Fig. 13

Bifurcation diagram of the nominal system s6 (stable and unstable steady-states in solid and dashed line, respectively)

The stable and unstable branches of LCO addressed above are indeed shown to exist within the considered speed range, featuring a markedly higher amplitude when compared to the supercritical LCO emanating from the Hopf bifurcation. Recall that the latter was the only LCO detected in the initial analyses of Fig. 5b (curve s6). Time-marching simulations are hence carried out to verify the predicted scenario and further assess the dependence of the response of the system on the initial conditions (IC). The two speeds marked by a vertical line in Fig. 15a, namely $V=54~\frac{\mathrm{m}}{\mathrm{s}}$ and $V=300~\frac{\mathrm{m}}{\mathrm{s}}$, are considered since they clearly belong to distinct regions of the bifurcation diagram. Then, an extensive simulation campaign is carried out consisting of: randomly sampling hundreds of initial conditions; simulating the nonlinear vector field; grouping the IC according to the observed steady state. For both speeds, two different steady states are detected, and the associated initial conditions is denoted by IC1 and IC2. The analyses are reported in Fig. 14 ($V=54~\frac{\mathrm{m}}{\mathrm{s}}$) and Fig. 15 ($V=300~\frac{\mathrm{m}}{\mathrm{s}}$).

Fig. 14

Time-marching simulation of the nominal system s6 at $V=54~\frac{\mathrm{m}}{\mathrm{s}}$

Figure 14a shows that, in agreement with the previously described bifurcation analysis, the nominal system at $V=54~\frac{\mathrm{m}}{\mathrm{s}}$ can experience self-sustained periodic oscillations (IC1) or converge to the equilibrium (IC2) depending on the initial conditions. Frequency and amplitude of the LCO can be better inspected in Fig. 14b, where a match with the amplitude of the stable branch of (high amplitude) LCO in Fig. 15a can also be observed.

From Fig. 15a, it is confirmed that, for speeds greater than $V_H=270~\frac{\mathrm{m}}{\mathrm{s}}$, all the responses converge to an LCO, either the one emanating from the Hopf bifurcation (IC1) or the high amplitude LCO (IC2). The different properties of the periodic orbits in terms of frequency and amplitude are apparent in Fig. 15b.

Fig. 15

Time-marching simulation of the nominal system s6 at $V=300~\frac{\mathrm{m}}{\mathrm{s}}$

The scenario emerging from Figs. 13, 14, 15 could have not been predicted based on the standard bifurcation analyses performed in Sect. 3.3, where a supercritical Hopf bifurcation at $V_H= 289~\frac{\mathrm{m}}{\mathrm{s}}$ was detected, and the only predicted steady-state solutions for speeds $V<V_H$ were stable equilibria (curve s6 in Fig. 5b). In fact, other solutions can exist since the results obtained with numerical continuation depend on the initial guesses. Even though by continuing along a parameter hidden solutions might be identified, it is rather difficult to detect isolated branches of periodic orbits not emanating from a Hopf bifurcation. The analyses here point out that the robust bifurcation margins framework can thus represent also an auxiliary tool to tackle these known problematic issues.

Table 6 Parameters for the typical section case study

5 Conclusion

The paper applies a novel framework for robust analysis of nonlinear systems to study the effect of modeling uncertainties on the onset of Hopf bifurcations in aeroelastic systems. The case study is a typical section featuring hardening stiffness coefficients and unsteady aerodynamics. A first important outcome is that, for an analysis case where a comparison with $\mu$ is possible, the results match with those obtained from the structured singular value technique, of which the robust bifurcation margin concept is a nonlinear extension. The uncertainty set is then augmented in order to assess the effect of different types of perturbations on the nonlinear behavior. The capability offered by the framework to specify the type of the closest Hopf bifurcation (subcritical or supercritical) is exploited to ascertain whether the uncertainties are able to change the criticality with respect to what is observed in the nominal system. One of the main findings is that uncertainty in the control surface stiffness can drastically lower the margin to the onset of subcritical Hopf bifurcation even when the control surface dynamics do not participate in nominal conditions in the destabilizing mechanism. Complex dynamics such as quasi-periodicity and bi-stability at low speeds are also revealed suggesting the need to carefully consider the effect of uncertainties in bifurcation analysis. Moreover, it is shown how this analysis approach can aid in investigating the behavior of the nominal system by detecting isolated branches difficult to identify with conventional (initial condition-dependent) strategies.

Appendix: Case study parameters

The nominal values of the parameters defining the typical section are reported in Table 6. They are taken from [24] where this case study was originally studied.

As for the aerodynamic model, the matrices providing a rational approximation of the Theodorsen operator ${\mathbf {Q}}$ with the Minimum State method (9) are tabulated next.

$$\begin{aligned} {{\mathbf {A}}_{\mathbf {0}}}&=\left[ \begin{array}{ccc} 0 &{} -12.5664 &{} -6.9092\\ 0 &{} 1.2566 &{} -1.8691\\ 0 &{} -0.0799 &{} -0.1477\\ \end{array} \right] \\ {{\mathbf {A}}_{\mathbf {1}}}&=\left[ \begin{array}{ccc} -6.3575 &{} -12.5431 &{} -2.0987\\ 0.5992 &{} -4.9772 &{} -1.3092\\ -0.0419 &{} -0.5428 &{} -0.1375\\ \end{array} \right] \\ {{\mathbf {A}}_{\mathbf {2}}}&=\left[ \begin{array}{ccc} -6.2462 &{} -2.4150 &{} -0.1238\\ -2.5148 &{} -1.8662 &{} -0.1583 \\ -0.1456 &{} -0.1225 &{} -0.0157\\ \end{array} \right] \\ {\bar{\mathbf {D}}}&= \left[ \begin{array}{ccc} 3.3222 &{} 3.3842 &{} 3.4547 \\ -0.3441 &{} -0.4108 &{} -0.4886 \\ 0.0211 &{} 0.0189 &{} 0.0152 \\ \end{array} \right] \\ {\bar{\mathbf {E}}}&= \left[ \begin{array}{ccc} -0.2062 &{} 2.8065 &{} 1.5861 \\ -0.0901 &{} -3.8931 &{} -1.9994 \\ -0.1171 &{} 2.7814 &{} 1.4709 \end{array} \right] \\ {\mathbf {R}}&= \left[ \begin{array}{ccc} 0.2 &{} 0 &{} 0\\ 0 &{} 0.4 &{} 0\\ 0 &{} 0 &{} 0.6\\ \end{array} \right] \end{aligned}$$