Skip to main content
SpringerLink
Log in

Precise motion control of tractor-trailer wheeled mobile structures via a newly observed key motion law

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

We present a curvature tracking approach for a tractor-trailer wheeled mobile structure (TTWMS), such that the trailer can track a desired trajectory curve accurately. A key motion law related to the curvature functions of trajectory curves is discovered for the first time, in terms of the tractor and the trailer with nonholonomic constraints. Then, based on this key motion law, the target trajectory curve of the trailer is converted to a dynamical tracking target matching the dynamics equation of the TTWMS, so as to transform the original motion task into a common tracking control problem. Finally, LQR optimal control and integral sliding mode control are introduced to design a robust tracking controller for the TTWMS. Simulation results show that the proposed method can make the TTWMS follow a given target trajectory curve accurately, even if the forward and yaw rotational speed errors are divergent.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Latif, A.R., Chalhoub, N., Pilipchuk, V.: Control of the nonlinear dynamics of a truck and trailer combination. Nonlinear Dyn. 99(4), 2505–2526 (2020)

    Article  Google Scholar 

  2. Kayacan, E., Kayacan, E., Ramon, H., Saeys, W.: Nonlinear modeling and identification of an autonomous tractor-trailer system. Comput. Electron. Agric. 106, 1–10 (2014)

    Article  Google Scholar 

  3. Khanpoor, A., Khalaji, A.K., Moosavian, S.A.A.: Modeling and control of an underactuated tractor-trailer wheeled mobile robot. Robotica 35(12), 2297–2318 (2017)

    Article  Google Scholar 

  4. Binh, N.T., Tung, N.A., Nam, D.P., Quang, N.H.: An adaptive backstepping trajectory tracking control of a tractor trailer wheeled mobile robot. Int. J. Control Autom. Syst. 17(2), 465–473 (2019)

    Article  Google Scholar 

  5. David, J., Manivannan, P.V.: Control of truck-trailer mobile robots: a survey. Intell. Serv. Robot. 7(4), 245–258 (2014)

    Article  Google Scholar 

  6. Jujnovich, B.A., Cebon, D.: Path-following steering control for articulated vehicles. J. Dyn. Syst. Meas. Control. 135(3), 031006 (2013)

    Article  Google Scholar 

  7. Yue, M., Hou, X.Q., Zhao, X.D., Wu, X.M.: Robust tube-based model predictive control for lane change maneuver of tractor-trailer vehicles based on a polynomial trajectory. IEEE Trans. Syst. Man Cybern. Syst. (2018). https://doi.org/10.1109/TSMC.2018.2867807

    Article  Google Scholar 

  8. Yue, M., Wu, X.M., Guo, L., Gao, J.J.: Quintic polynomial-based obstacle avoidance trajectory planning and tracking control framework for tractor-trailer system. Int. J. Control Autom. Syst. 17(10), 2634–2646 (2019)

    Article  Google Scholar 

  9. Shojaei, K.: Neural network formation control of a team of tractor-trailer systems. Robotica 36(1), 39–56 (2018)

    Article  Google Scholar 

  10. Zhou, S.B., Zhao, H.C., Chen, W., Miao, Z.Q., Liu, Z., Wang, H.S., Liu, Y.H.: Robust path following of the tractor-trailers system in GPS-denied environments. IEEE Robot. Autom. Lett. 5(2), 500–507 (2020)

    Article  Google Scholar 

  11. Kassaeiyan, P., Tarvirdizadeh, B., Alipour, K.: Control of tractor-trailer wheeled robots considering self-collision effect and actuator saturation limitations. Mech. Syst. Signal Process. 127, 388–411 (2019)

    Article  Google Scholar 

  12. Yue, M., Hou, X.Q., Gao, R.J.: Trajectory tracking control for tractor-trailer vehicles: a coordinated control approach. Nonlinear Dyn. 91(2), 1061–1074 (2018)

    Article  Google Scholar 

  13. Khalaji, A.K., Moosavian, S.A.A.: Robust adaptive controller for a tractor-trailer mobile robot. IEEE/ASME Trans. Mechatron. 19(3), 943–953 (2014)

    Article  Google Scholar 

  14. Khalaji, A.K., Jalalnezhad, M.: Control of a tractor-trailer robot subjected to wheel slip. Proc. Inst. Mech. Eng. Part K J. Multi-body Dyn. 233(4), 956–967 (2019)

    Google Scholar 

  15. Alipour, K., Robat, A.B., Tarvirdizadeh, B.: Dynamics modeling and sliding mode control of tractor-trailer wheeled mobile robots subject to wheels slip. Mech. Mach. Theory 138, 16–37 (2019)

    Article  Google Scholar 

  16. Leng, Z., Minor, M.A.: Curvature-based ground vehicle control of trailer path following considering sideslip and limited steering actuation. IEEE Trans. Intell. Transp. Syst. 18(2), 332–348 (2017)

    Article  Google Scholar 

  17. Zhou, Y.S., Wen, X.R., Wang, Z.H.: On the nonholonomic constraints and motion control of wheeled mobile structures. Chin. J. Theor. Appl. Mech. 52(4), 1143–1156 (2020)

    Google Scholar 

  18. Prasad, A., Sharma, B., Vanualailai, J., Kumar, S.A.: A geometric approach to target convergence and obstacle avoidance of a nonstandard tractor-trailer robot. Int. J. Robust Nonlinear Control 30, 4924–4943 (2020)

    Article  MathSciNet  Google Scholar 

  19. He, Y., Islam, M.: An automated design method for active trailer steering systems of articulated heavy vehicles. J. Mech. Des. 134(4), 041002 (2012)

    Article  Google Scholar 

  20. Odhams, A., Roebuck, R., Jujnovich, B., Cebon, D.: Active steering of a tractor-semi-trailer. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 225(7), 847–869 (2011)

    Article  Google Scholar 

  21. Yuan, J., Sun, F.C., Huang, Y.L.: Hierarchical motion planning for multisteering tractor-trailer mobile robots with on-axle hitching. IEEE ASME Trans. Mechatron. 22(4), 1652–1662 (2017)

    Article  Google Scholar 

  22. Yuan, J., Sun, F.C., Huang, Y.L.: Robust path following of the tractor-trailers system in GPS-denied environments. IEEE Robot. Autom. Lett. 5(2), 500–507 (2020)

    Article  Google Scholar 

  23. Liu, Z.Y., Yue, M., Guo, L., Zhang, Y.S.: Trajectory planning and robust tracking control for a class of active articulated tractor-trailer vehicle with on-axle structure. Eur. J. Control. 54, 87–98 (2020)

    Article  MathSciNet  Google Scholar 

  24. Kassaeiyan, P., Alipour, K., Tarvirdizadeh, B.: A full-state trajectory tracking controller for tractor-trailer wheeled mobile robots. Mech. Mach. Theory 150, 103872 (2020)

    Article  Google Scholar 

  25. Shojaei, K., Abdolmaleki, M.: Output feedback control of a tractor with N-trailer with a guaranteed performance. Mech. Syst. Signal Process. 142, 106746 (2020)

    Article  Google Scholar 

  26. Galicki, M.: The planning of optimal motions of non-holonomic systems. Nonlinear Dyn. 90(3), 2163–2184 (2017)

    Article  MathSciNet  Google Scholar 

  27. Zhou, Y.S., Wang, Z.H., Chung, K.K.: Turning motion control design of a two-wheeled inverted pendulum using curvature tracking and optimal control. J. Optim. Theory Appl. 181(2), 634–652 (2019)

  28. Zhou, Y.S., Wang, Z.H.: Robust motion control of a two-wheeled inverted pendulum with an input delay based on optimal integral sliding mode manifold. Nonlinear Dyn. 85(3), 2065–2074 (2016)

    Article  MathSciNet  Google Scholar 

  29. Defoort, M., Floquet, T., Kokosy, A., Perruquetti, W.: Integral sliding mode control for trajectory tracking of a unicycle type mobile robot. Integr. Comput. Aided Eng. 13(3), 277–288 (2006)

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank the Associate Editor and all anonymous reviewers for their valuable comments and suggestions which have improved the quality of this paper. This work has received the financial support of NSF of China under Grant (11802065, 11702227), the Science and Technology Program of Guizhou Province ([2018]1047), the fund Project of Key Laboratory of Advanced Manufacturing Technology, Ministry of Education, Guizhou University (KY[2018]478).

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, Guizhou University, Guiyang, 550025, China

    Yusheng Zhou & Xiangrong Wen

  2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Qi Xu

Authors
  1. Yusheng Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xiangrong Wen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Qi Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yusheng Zhou.

Ethics declarations

Conflict of interest

The authors declare that they have no potential conflict of interest with respect to the research, authorship, and/or publication of this article.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

1.1 Appendix A: Coefficient matrixes of Eq.  (13)

$$\begin{aligned}&{\mathbf {A}}(\mathbf{q })=\left[ \begin{array}{cccccc} a_{11} &{} 0 &{} a_{13} &{} a_{14} &{} 0 &{} 0 \\ 0 &{} a_{22} &{} a_{23} &{} a_{24} &{} 0 &{} 0 \\ a_{31} &{} a_{32} &{} a_{33} &{} a_{34} &{} 0 &{} 0 \\ a_{41} &{} a_{42} &{} a_{43} &{} a_{44} &{} 0&{} 0\\ 0 &{} 0 &{} 0 &{} 0&{} a_{55} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0&{} 0 &{} a_{66} \\ \end{array} \right] ,\\&\quad {\mathbf {U}}(\text {q},\dot{\text {q}})=\left[ \begin{array}{c} u_{11}\\ u_{21}\\ 0\\ u_{41}\\ 0\\ 0\\ \end{array} \right] , \end{aligned}$$

where

$$\begin{aligned} a_{11}&=a_{22}=M_f+M_B+(2M_\mathrm{w}+\frac{2I_\mathrm{w}}{r^2}+M_r)\mathrm{cos}^2\varphi ,\\ a_{13}&=a_{31}=-a_{14}=a_{41}=\frac{1}{2}M_B a\mathrm{sin}(\theta -\varphi ),\\ a_{23}&=a_{32}=-a_{24}=a_{42}=-\frac{1}{2}M_B a\mathrm{cos}(\theta -\varphi ),\\ a_{33}&=4I_{wd}+I_{fd}+I_{rd}+I_B+\frac{a^2}{4}M_B+\frac{d^2}{2}(M_\mathrm{w}+\frac{I_\mathrm{w}}{r^2}),\\ a_{34}&=-a_{43}=a_{44}=-I_{rd}-I_B-2I_{wd}\\&\quad -\, \frac{a^2}{4} M_B-\frac{d^2}{2}(M_\mathrm{w}+\frac{I_\mathrm{w}}{r^2}),\\ a_{55}&=a_{66}=M_\mathrm{w} r^2+I_\mathrm{w},\\ u_{11}&=-\frac{4 av{\dot{\varphi }}\mathrm{cos}^2\varphi \mathrm{sin}\varphi (M_r r^2+ 2 M_\mathrm{w} r^2 + 2 I_\mathrm{w})}{2 a r^2}\\&\quad -\, \frac{ M_B v^2 r^2 \mathrm{cos}(\theta - \varphi )\mathrm{sin}^{2}\varphi }{2 a r^2},\\ u_{21}&=-\frac{4av{\dot{\varphi }}\mathrm{sin}^2\varphi \mathrm{cos}\varphi ( M_r r^2+ 2 M_\mathrm{w} r^2+ 2 I_\mathrm{w})}{2 a r^2}\\&\quad -\, \frac{ M_B v^2 r^2 \mathrm{sin}^2\varphi \mathrm{sin}(\theta - \varphi )}{2 a r^2},\\ u_{41}&=-(2M_\mathrm{w}+\frac{2I_\mathrm{w}}{r^2}+M_r)v^2\mathrm{sin}\varphi \mathrm{cos}\varphi . \end{aligned}$$

1.2 Appendix B: Related expressions of Eq. (15)

$$\begin{aligned} \varDelta _1&=\alpha _4\mathrm{cos}^{2} \varphi +\alpha _5,\\ \varDelta _2&=\alpha _1 v \dot{\theta } \mathrm{sin}\varphi \mathrm{cos}\varphi \\&\quad +\, \alpha _2 \dot{\varphi } v \mathrm{sin}\varphi \mathrm{cos}\varphi +\alpha _3 v^2 \mathrm{sin}^2\varphi \mathrm{cos}\varphi ,\\ \varDelta _3&= \beta _{10}\mathrm{cos}^2\varphi +\beta _{11},\\ \varDelta _4&=\beta _1v \dot{\theta }\mathrm{cos}^3\varphi +\beta _2v\dot{\theta }\mathrm{cos}\varphi \\&\quad +\, \beta _3\dot{\varphi } v\mathrm{cos}^3\varphi +\beta _4\dot{\varphi }v\mathrm{cos}\varphi \\&\quad +\, \beta _5v^2\mathrm{sin}\varphi \mathrm{cos}^3\varphi +\beta _6v^2\mathrm{sin}\varphi \mathrm{cos}\varphi +\beta _9\mathrm{sin}\varphi u_2, \\ \varDelta _5&= \beta _7\mathrm{cos}^2\varphi +\beta _8.\\ \end{aligned}$$

where

$$\begin{aligned} \alpha _1&= 2a^2(-M_Br^2+4M_r r^2+8M_\mathrm{w} r^2+8 I_\mathrm{w}),\\ \alpha _2&= (3M_B a^2\!+\!2 M_\mathrm{w} d^2\!+\!4 I_B\!+\!4 I_{rd}\!+\!8 I_{wd})r^2\!+\!2 I_\mathrm{w} d^2,\\ \alpha _3&= -2a(M_Br^2+6 M_r r^2+12 M_\mathrm{w} r^2+12 I_\mathrm{w}),\\ \alpha _4&= M_Ba^2 r^2\!+\!4 M_r a^2 r^2\!+\!8 M_\mathrm{w} a^2 r^2\!\\&\quad +\, \!2 M_\mathrm{w} d^2 r^2\!+\!4 I_B r^2 +4 I_{rd} r^2+8 I_\mathrm{w} a^2+2 I_\mathrm{w} d^2+8 I_{wd}r^2, \\ \alpha _5&= 3M_Ba^2r^2+4M_fa^2r^2+8M_\mathrm{w} a^2 r^2-2 M_\mathrm{w} d^2 r^2\\&\quad -\, 4 I_B r^2-4 I_{rd} r^2+8 I_\mathrm{w} a^2-2 I_\mathrm{w} d^2-8 I_{wd} r^2,\\ \beta _1&= a^2 ((4 M_B^2 a^2+16 M_r M_\mathrm{w} d^2+32 M_\mathrm{w}^2 d^2\\&\quad +\, 32 I_B M_r +32 I_{rd} M_r+64 I_B M_\mathrm{w}+64 I_{rd} M_\mathrm{w}+64 I_{wd} M_r \\&\quad +\, 128 I_{wd} M_\mathrm{w}) r^4+(16 I_\mathrm{w} M_r d^2+64 I_\mathrm{w} M_\mathrm{w} d^2+64 I_B I_\mathrm{w}\\&\quad +\, 64 I_{rd} I_\mathrm{w}+128 I_\mathrm{w} I_{wd})r^2+32 I_\mathrm{w}^2 d^2),\\ \beta _2&= (4M_B^2+8M_B M_f+8 M_B M_r+32 M_B M_\mathrm{w}) r^4 a^4 \\&\quad -\, (16 M_r M_\mathrm{w} d^2+32 M_\mathrm{w}^2 d^2+32 I_B M_r+64 I_B M_\mathrm{w} \\&\quad +\, 32 I_{rd} M_r+64 I_{rd} M_\mathrm{w}+64 I_{wd} M_r+128 I_{wd} M_\mathrm{w}) r^4 a^2\\&\quad -\, (I_\mathrm{w} M_r d^2 -32 I_\mathrm{w} M_B a^216+64 I_\mathrm{w} M_\mathrm{w} d^2\\&\quad +\, 64 I_B I_\mathrm{w} +64 I_{rd} I_\mathrm{w}+128 I_\mathrm{w} I_{wd}) a^2 r^2-32 I_\mathrm{w}^2 a^2 d^2,\\ \beta _3&= -(4 M_B^2+4 M_B M_r+8 M_B M_\mathrm{w}) r^4 a^4-8 a^4 I_\mathrm{w} r^2 M_B \\&\quad -\, (8 M_r M_\mathrm{w} d^2+16 M_\mathrm{w}^2 d^2+16 I_B M_r+32 I_B M_\mathrm{w}\\&\quad +\, 16 I_{rd} M_r+32 I_{rd} M_\mathrm{w}+32 I_{wd} M_r+64 I_{wd} M_\mathrm{w}) r^4 a^2\\&\quad -\, (8 I_\mathrm{w} M_r d^2+32 I_\mathrm{w} M_\mathrm{w} d^2+32 I_B I_\mathrm{w}+32 I_{rd} I_\mathrm{w}\\&\quad +\, 64 I_\mathrm{w} I_{wd}) r^2 a^2-16 I_\mathrm{w}^2 a^2 d^2,\\ \beta _4&= -\!(4 M_B M_f\!+\!8 M_B M_\mathrm{w}) r^4 a^4\!\\&\quad -\, \!8 a^4 I_\mathrm{w} r^2 M_B\!-\!(8 M_B M_\mathrm{w} d^2 +\!8 M_f M_\mathrm{w} d^2\!\\&\quad +\, \!16 M_\mathrm{w}^2 d^2\!+\!16 I_B M_B\!+\!16 I_B M_f\!+\!32 I_B M_\mathrm{w} +\!16 I_{rd} M_B\!\\&\quad +\, \!16 I_{rd} M_f\!+\!32 I_{rd} M_\mathrm{w}\!+\!32 I_{wd} M_B\!+\!32 I_{wd} M_f \\&\quad +\, \!64 I_{wd} M_\mathrm{w}) r^4 a^2\!-\!(8 I_\mathrm{w} M_B d^2\!+\!8 I_\mathrm{w} M_f d^2\!\\&\quad +\, \!32 I_\mathrm{w} M_\mathrm{w} d^2 +32 I_B I_\mathrm{w}+32 I_{rd} I_\mathrm{w}\\&\quad + 64 I_\mathrm{w} I_{wd}) r^2 a^2-16 I_\mathrm{w}^2 a^2 d^2,\\ \beta _5&= (2M_B^2+14M_B M_r+28 M_B M_\mathrm{w}+8 M_r^2+32 M_r M_\mathrm{w} \\&\quad +\, 32 M_\mathrm{w}^2) r^4 a^3+(28 I_\mathrm{w} M_B+32 I_\mathrm{w} M_r+64 I_\mathrm{w} M_\mathrm{w}) r^2 a^3 \\&\quad +\, \!32 I_\mathrm{w}^2 a^3\!-\!(4 M_B M_\mathrm{w} d^2\!+\!20 M_r M_\mathrm{w} d^2\!\\&\quad +\, \!40 M_\mathrm{w}^2 d^2\!+\!8 I_B M_B \\&\quad +\, 40 I_B M_r+80 I_B M_\mathrm{w}+8 I_{rd} M_B+40 I_{rd} M_r+80 I_{rd} M_\mathrm{w} \\&\quad +\, 16 I_{wd} M_B+80 I_{wd} M_r+160 I_{wd} M_\mathrm{w}) r^4 a-(4 I_\mathrm{w} M_B d^2 \\&\quad +\, 20 I_\mathrm{w} M_r d^2+80 I_\mathrm{w} M_\mathrm{w} d^2+80 I_B I_\mathrm{w}+80 I_{rd} I_\mathrm{w}\\&\quad +\, 160 I_\mathrm{w} I_{wd}) r^2 a-40 I_\mathrm{w}^2 a d^2,\\ \beta _6&=-(2M_B^2+6 M_B M_r+12 M_B M_\mathrm{w}\\&\quad -\,8 M_f M_r-16 M_f M_\mathrm{w} -16 M_r M_\mathrm{w}\! -\, \!32 M_\mathrm{w}^2) r^4 a^3\\&\quad -(12 I_\mathrm{w} M_B-16 I_\mathrm{w} M_f-16 I_\mathrm{w} M_r \\&\quad -\, 64 I_\mathrm{w} M_\mathrm{w}) r^2 a^3+32 I_\mathrm{w}^2 a^3+40 I_\mathrm{w}^2 a d^2+(4 M_B M_\mathrm{w} d^2\\&\quad -\, 20 M_r M_\mathrm{w} d^2\!+\!40 M_\mathrm{w}^2 d^2\!\\&\quad +\, \!8 I_B M_B\!-\!40 I_B M_r\!+\!80 I_B M_\mathrm{w} +8 I_{rd} M_B\!\\&\quad +\, \!40 I_{rd} M_r\!+\!80 I_{rd} M_\mathrm{w}\!+\!16 I_{wd} M_B\!+\!80I_{wd} M_r \\&\quad +\, 160 I_{wd} M_\mathrm{w}) r^4 a+(4 I_\mathrm{w} M_B d^2-20 I_\mathrm{w} M_r d^2\\&\quad +\, 80 I_\mathrm{w} M_\mathrm{w} d^2-80 I_B I_\mathrm{w}+80 I_{rd} I_\mathrm{w}+160 I_\mathrm{w} I_{wd}) r^2 a,\\ \beta _7&= (M_B a^3 d+4 M_r a^3 d+8 M_\mathrm{w} a^3 d+2 M_\mathrm{w} a d^3+4 I_B a d\\&\quad +4 I_{rd} a d+8 I_{wd} a d) r^3 +\, (8 I_\mathrm{w} a^3 d+2 I_\mathrm{w} a d^3)r,\\ \beta _8&= (3M_B a^3 d+4 M_f a^3 d+8 M_\mathrm{w} a^3 d-2 M_\mathrm{w} a d^3-4 I_B a d\\&\quad -\, 4 I_{rd} a d-8 I_{wd} a d) r^3+(8 I_\mathrm{w} a^3 d-2 I_\mathrm{w} a d^3) r,\\ \beta _9&= (4M_B a^4\!-\!8 M_\mathrm{w} a^2 d^2\!-\!16 I_B a^2\!-\!16 I_{rd} a^2\!-\!32 I_{wd} a^2) r^3\\&\quad -\, 8 I_\mathrm{w} a^2 d^2 r,\\ \beta _{10}&= (M_\mathrm{w} a d^2 r^2+2 I_{fd} a r^2+I_\mathrm{w} a d^2+4 I_{wd} a r^2) (M_B a^2 r^2\\&\quad +\, 4 M_r a^2 r^2+8 M_\mathrm{w} a^2 r^2+2 M_\mathrm{w} d^2 r^2+4 I_B r^2+4 I_{rd} r^2\\&\quad +\, 8 I_\mathrm{w} a^2+2 I_\mathrm{w} d^2+8 I_{wd} r^2),\\ \beta _{11}&= (M_\mathrm{w} a d^2 r^2+2 I_{fd} a r^2+I_\mathrm{w} a d^2+4 I_{wd} a r^2) (3 M_B a^2 r^2\\&\quad +\, 4 M_f a^2 r^2+8 M_\mathrm{w} a^2 r^2-2 M_\mathrm{w} d^2 r^2-4 I_B r^2-4 I_{rd} r^2\\&\quad +\, 8 I_\mathrm{w} a^2-2 I_\mathrm{w} d^2-8 I_{wd} r^2). \end{aligned}$$

1.3 Appendix C: Another proof of Eq. (24)

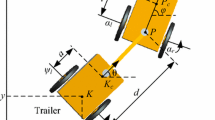
As can be seen in Fig. 1, the positional relationship of point Q and P can be expressed as

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} x=x_0+a \mathrm{cos}\theta _0, \\ y=y_0+a \mathrm{sin}\theta _0. \end{array}\right. } \end{aligned} \end{aligned}$$
(45)

Taking the first and second derivatives of Eq. (45) with respect to t, respectively, one has

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}}={\dot{x}}_0-a{\dot{\theta }}_0\mathrm{sin}\theta _0, \\ {\dot{y}}={\dot{y}}_0+a{\dot{\theta }}_0 \mathrm{cos}\theta _0, \end{array}\right. } \end{aligned} \end{aligned}$$
(46)

and

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}=\ddot{x}_0-a\ddot{\theta }_0 \mathrm{sin}\theta _0-a{\dot{\theta }}_0^2 \mathrm{cos}\theta _0, \\ \ddot{y}=\ddot{y}_0+a\ddot{\theta }_0 \mathrm{cos}\theta _0-a {\dot{\theta }}_0^2 \mathrm{sin}\theta _0. \end{array}\right. } \end{aligned} \end{aligned}$$
(47)

By substituting Eqs. (46) and (47) into Eq. (18), the forward speed and yaw rotation speed of point P can be given by

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} {\dot{v}}=\sqrt{{\dot{x}}_0^2+{\dot{y}}_0^2+a^2 {\dot{\theta }}_0^2},\\ {\dot{\theta }}= \frac{a \ddot{\theta }_0({\dot{x}}_0 \mathrm{cos}\theta _0+{\dot{y}}_0 \mathrm{sin}\theta _0)-a {\dot{\theta }}_0 (\ddot{x}_0 \mathrm{cos}\theta _0+\ddot{y}_0 \mathrm{sin} \theta _0)}{{\dot{x}}_0^2+{\dot{y}}_0^2+a^2 {\dot{\theta }}_0^2}\\ \qquad +\, \frac{a^2 {\dot{\theta }}_0^3+{\dot{x}}_0 \ddot{y}_0-\ddot{x}_0 {\dot{y}}_0}{{\dot{x}}_0^2+{\dot{y}}_0^2+a^2 {\dot{\theta }}_0^2} \end{array}\right. } \end{aligned} \end{aligned}$$
(48)

Similar to Eq. (4) of the tractor, and together with (18), the trailer also satisfies the following equations, described by

$$\begin{aligned} {\left\{ \begin{array}{ll} -{\dot{x}}_0\mathrm{sin}\theta _0+ {\dot{y}}_0\mathrm{cos}\theta _0 = 0, \\ v_0=\sqrt{{\dot{x}}_{0}^2+{\dot{y}}_{0}^2}={\dot{x}}_0\mathrm{cos}\theta _0+{\dot{y}}_0\mathrm{sin}\theta _0, \\ {\dot{\theta }}_0=\frac{{\dot{x}}_0\ddot{y}_0-\ddot{x}_0{\dot{y}}_0}{{\dot{x}}_{0}^2+{\dot{y}}_{0}^2}. \end{array}\right. } \end{aligned}$$
(49)

By substituting Eq. (49) into Eq. (48) results

$$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} v = \sqrt{v_0^2+a^2{\dot{\theta }}_0^2}, \\ {\dot{\theta }}=\frac{a \ddot{\theta }_0 v_0-a {\dot{\theta }}_0 {\dot{v}}_0+a^2 {\dot{\theta }}_0^3+{\dot{\theta }}_0 v_0^2}{v_0^2+a^2{\dot{\theta }}_0^2}, \end{array}\right. } \end{aligned} \end{aligned}$$

which is exactly the same as Eq. (24).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, Y., Wen, X. & Xu, Q. Precise motion control of tractor-trailer wheeled mobile structures via a newly observed key motion law. Nonlinear Dyn 103, 833–848 (2021). https://doi.org/10.1007/s11071-020-06162-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-06162-9

Keywords

Search

Navigation