An elastic rotative nonlinear vibration absorber (ERNVA) as a passive suppressor for vortex-induced vibrations

Abstract

Vortex-induced vibration (VIV) is a self-excited and self-limited flow-induced vibration phenomenon of importance for both the academic and the technological communities. Particularly for the offshore engineering scenario, VIV plays an important role in the structural fatigue analysis. Hence, VIV suppression is a relevant topic. Among different solutions for VIV mitigation, this paper focuses on the numerical analysis of an elastic rotative nonlinear vibration absorber (ERNVA) as a device for passive suppression. The ERNVA consists of a mass placed at the tip of an axially elastic beam hinged to the cylinder by means of a linear dashpot. In this paper, the hydrodynamic loads are calculated using a wake-oscillator model, allowing comprehensive parametric studies for assessing the influence of the ERNVA parameters on its efficiency for the whole range of reduced velocities associated with the lock-in. Among other novel results, it is found that ERNVA can lead to a $25\%$ decrease in the maximum oscillation amplitude, being significantly more efficient than its counterpart characterized by a rigid rotating arm. Passive suppression is obtained not only for the peak, but within a certain range of reduced velocities. Curves showing the influence of the ERNVA parameters on the force coefficients for different values of reduced velocity are also innovative.

Appendices

Derivation of the equations of motion

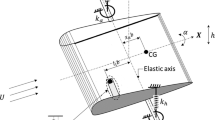
This Appendix details the derivation of the dimensional equations of motion. For this, consider the inertial reference frame O${\mathbf {i}}{\mathbf {j}}$ illustrated in Fig. 1b. The position vectors of the center of the cylinder and of the NVA mass are, respectively, ${\mathbf {r}}_c=Y{\mathbf {j}}$ and ${\mathbf {r}}_m=(r_0+r)\sin \theta {\mathbf {i}}+(Y+(r_0+r)\cos \theta ){\mathbf {j}}$.

The kinetic and the potential energies (${\mathcal {T}}$ and ${\mathcal {U}}$, respectively) are written as:

$$\begin{aligned} {\mathcal {T}}=&\frac{1}{2}M\dot{{\mathbf {r}}}_c.\dot{{\mathbf {r}}}_c +\frac{1}{2}m_N\dot{{\mathbf {r}}}_m.\dot{{\mathbf {r}}}_m=\frac{1}{2}(M+m_N) \left( \frac{dY}{dt}\right) ^2+\nonumber \\&+\frac{1}{2}m_N(r_0+r)^2\left( \frac{d\theta }{dt} \right) ^2+ \frac{1}{2}m_N\left( \frac{dr}{dt}\right) ^2+\nonumber \\&+m_N\cos \theta \frac{dr}{dt}\frac{dY}{dt}-m_N(r_0+r)\sin \theta \frac{d\theta }{dt}\frac{dY}{dt} \end{aligned}$$

(8)

$$\begin{aligned} {\mathcal {U}}=&\frac{1}{2}k_yY^2+\frac{1}{2}k_rr^2 \end{aligned}$$

(9)

The non-conservative forces include the hydrodynamic load on cylinder $F_y$ and the dissipative ones on the cylinder and on the NVA. According to the adopted hypotheses, the virtual work of the non-conservative forces is given by Eq. 10.

$$\begin{aligned} \delta W_{nc}=\left( F_y-c_y\frac{dY}{dt}\right) \delta Y-c_\theta \frac{d\theta }{dt}\delta \theta -c_r\frac{dr}{dt}\delta r \nonumber \\ \end{aligned}$$

(10)

Now, the main aspects of the wake-oscillator model proposed in [32] are presented, provided the present contribution does not intend to further discuss the hypothesis and the empirical parameters of this model. According to [32], the force exerted by the fluid on cylinder $F_y$ can be decomposed into a potential term proportional to the cylinder acceleration (term associated with the potential added mass) and another one associated with the vortex shedding. The latter term is related to wake-variable $q_y$. For the problem of the flow around a fixed cylinder, $q_y$ is the solution of the homogeneous van der Pol equation.

$$\begin{aligned} \frac{d^2q_y}{dt^2}+\epsilon _y\omega _f(q_y^2-1)\frac{dq_y}{dt}+\omega _f^2q_y=0 \end{aligned}$$

(11)

$\epsilon _y$ being an empirically obtained constant. One can easily obtain that the solution of Eq. 11 oscillates with vortex-shedding frequency $\omega _f$ and has amplitude ${\hat{q}}_y=2$. Hence, the time history of the lift coefficient in the flow around a fixed cylinder can be written in terms of $q_y$ as $C_L=q_y{\hat{C}}_L/{\hat{q}}_y$, where ${\hat{C}}_L$ is the amplitude of the lift coefficient for the considered case.

On the other hand, the van der Pol equation is forced by the cylinder motion when VIV is considered. Following [15, 32] includes the term $\frac{A_y}{D}\frac{d^2Y}{dt^2}$ on the right-hand side of Eq. 11 for modeling the influence of the cylinder motion on the hydrodynamic force. Within this framework, the cross-wise force exerted by the fluid on the cylinder reads:

$$\begin{aligned} F_y=\frac{1}{2}\rho U_\infty ^2 LD C_y=-m_a^{pot}\frac{d^2Y}{dt^2}+\frac{1}{2}\rho U_\infty ^2 DL C_{y,v} \nonumber \\ \end{aligned}$$

(12)

In Eq. 12, the first term is associated with the potential added mass $m_a^{pot}$ and the second one is associated with the viscous effects. According to [32], the cross-wise coefficient arisen from the viscous effects $C_{y,v}$ results from the decomposition of the drag and the lift coefficients obtained from fixed cylinders ($C_D$ and $C_L$, respectively), both oriented with respect to the relative velocity between the fluid and the cylinder as follows:

$$\begin{aligned} C_{y,v}=&\left( C_L-C_D\frac{1}{U_\infty }\frac{dY}{dt} \right) \sqrt{1+\left( \frac{1}{U_\infty }\frac{dY}{dt} \right) ^2}\nonumber \\ =&\left( \frac{{\hat{C}}_L}{{\hat{q}}_y}q_y-C_D\frac{1}{U_\infty }\frac{dY}{dt} \right) \sqrt{1+\left( \frac{1}{U_\infty }\frac{dY}{dt} \right) ^2} \end{aligned}$$

(13)

The equations of motion are obtained by means of the joint use of the Euler–Lagrange equations and the wake-oscillator model. For this, one needs to develop some intermediate steps. In these steps, partial derivatives of both kinetic and potential energy are computed, as listed below.

• Intermediate steps for the equation in Y:

  $$\begin{aligned}&\frac{\partial {\mathcal {T}}}{\partial \left( \frac{dY}{dt} \right) }=(M+m_N)\frac{dY}{dt}\nonumber \\&\quad +m_N\frac{dr}{dt}\cos \theta -m_N(r_0+r) \sin \theta \frac{d\theta }{dt}\nonumber \\&\frac{d}{dt}\left( \frac{\partial {\mathcal {T}}}{\partial \left( \frac{dY}{dt} \right) } \right) =(M+m_N)\frac{d^2Y}{dt^2}\nonumber \\&\quad +m_N\frac{d^2r}{dt^2}\cos \theta -2m_N\sin \theta \frac{dr}{dt}\frac{d\theta }{dt}-\nonumber \\&-m_N(r_0+r)\frac{d}{dt}\left( \sin \theta \frac{d\theta }{dt}\right) \nonumber \\&\frac{\partial \mathcal {{\mathcal {T}}}}{\partial Y}=0\nonumber \\&\frac{\partial {\mathcal {U}}}{\partial Y}=k_yY \end{aligned}$$

  (14)

• Intermediate steps for the equation in $\theta$:

  $$\begin{aligned}&\frac{\partial {\mathcal {T}}}{\partial \left( \frac{d\theta }{dt} \right) } =m_N(r_0+r)^2\frac{d\theta }{dt}\nonumber \\&\quad -m_N(r_0+r)\sin \theta \frac{dY}{dt}\nonumber \\&\frac{d}{dt}\left( \frac{\partial {\mathcal {T}}}{\partial \left( \frac{d\theta }{dt} \right) } \right) =m_N(r_0+r)^2\frac{d^2 \theta }{dt^2}\nonumber \\&\quad +2m_N(r_0+r)\frac{dr}{dt} \frac{d\theta }{dt}-\nonumber \\&\quad -m_N(r_0+r)\frac{d^2 Y}{dt^2}\sin \theta -m_N(r_0+r)\frac{dY}{dt}\nonumber \\&\quad \frac{d\theta }{dt}\cos \theta \nonumber \\&\quad -m_N\frac{dr}{dt}\frac{dY}{dt}\sin \theta \nonumber \\&\quad \frac{\partial \mathcal {{\mathcal {T}}}}{\partial \theta }=-m_N\sin \theta \frac{dY}{dt}\frac{dr}{dt}-m_N(r_0+r)\nonumber \\&\quad \frac{d\theta }{dt}\frac{dY}{dt}\cos \theta \nonumber \\&\frac{\partial {\mathcal {U}}}{\partial \theta }=0 \end{aligned}$$

  (15)

• Intermediate steps for the equation in r:

  $$\begin{aligned}&\frac{\partial {\mathcal {T}}}{\partial \left( \frac{dr}{dt} \right) } =m_N\frac{dr}{dt}+m_N\cos \theta \frac{dY}{dt}\nonumber \\&\quad \frac{d}{dt}\left( \frac{\partial {\mathcal {T}}}{\partial \left( \frac{dr}{dt} \right) } \right) =m_N\frac{d^2r}{dt^2}-m_N\sin \theta \frac{d\theta }{dt}\frac{dY}{dt}\nonumber \\&\quad +m_N\cos \theta \frac{d^2Y}{dt^2}\nonumber \\&\quad \frac{\partial \mathcal {{\mathcal {T}}}}{\partial r}=m_N(r_0+r) \left( \frac{d\theta }{dt}\right) ^2-m_N\frac{dY}{dt}\frac{d\theta }{dt}\sin \theta \nonumber \\&\quad \frac{\partial {\mathcal {U}}}{\partial r}=k_rr \end{aligned}$$

  (16)

The joint use of the Euler–Lagrange equations and the wake-oscillator model leads to the dimensional mathematical model given by Eqs. 17 - 20.

$$\begin{aligned}&(M+m_N+m_a^{pot})\frac{d^2Y}{dt^2}+c_y\frac{dY}{dt}+k_yY\nonumber \\&\quad =\frac{1}{2}\rho U_\infty ^2DLC_{y,v}+\nonumber \\&\quad +m_N\left( -\frac{d^2r}{dt^2}\cos \theta + 2\sin \theta \frac{dr}{dt}\frac{d\theta }{dt}+(r_0+r) \nonumber \right. \\&\left. \quad \left( \cos \theta \left( \frac{d\theta }{dt} \right) ^2+\sin \theta \frac{d\theta ^2}{dt^2} \right) \right) \end{aligned}$$

(17)

$$\begin{aligned}&m_N(r_0+r)^2\frac{d^2\theta }{dt^2}+\left( c_\theta +2m_N(r_0+r)\frac{dr}{dt} \right) \nonumber \\&\quad \frac{d\theta }{dt}-m_N(r_0+r)\frac{d^2Y}{dt^2}\sin \theta =0 \end{aligned}$$

(18)

$$\begin{aligned}&m_N\frac{d^2r}{dt^2}+c_r\frac{dr}{dt}+\left( k_r-m_N\left( \frac{d\theta }{dt} \right) ^2\right) r\nonumber \\&\quad +m_N\left( \frac{d^2Y}{dt^2} \cos \theta - r_0\left( \frac{d\theta }{dt}\right) ^2\right) =0 \end{aligned}$$

(19)

$$\begin{aligned}&\frac{d^2q_y}{dt^2}+\epsilon _y\omega _f(q_y^2-1)\frac{dq_y}{dt}\nonumber \\&\quad +\omega _f^2q_y=\frac{A_y}{D}\frac{d^2Y}{dt^2} \end{aligned}$$

(20)

“Pure VIV” results

This Appendix brings the numerical-experimental correlation for the “Pure VIV” condition. Even though this comparison has already been discussed in [44], it is herein readdressed for the sake of completeness of the present paper.

Figure 14 brings the numerical-experimental correlation, showing characteristic oscillation amplitude ${\hat{A}}_y$, mean in-line force coefficient ${\bar{C}}_x$ and r.m.s cross-wise force coefficient $C_y^\prime$ plotted as functions of reduced velocity. The numerical results are obtained with the wake-oscillator model proposed in [32], and the experimental data are those presented in [18].

Fig. 14

Numerical-experimental correlation

As clearly shown in Fig. 14, the results numerically obtained very well agree with the experimental ones. The characteristic oscillation amplitude plot (Fig. 14a) indicates that the maximum amplitude is ${\hat{A}}_y=0.94$ for both the numerical simulation and the experiments. The amplitude of the lower branch is also close to ${\hat{A}}_y=0.60$ in both approaches. Still considering Fig. 14a, notice that the transitions from the upper branch to the lower branch and from the lower branch to the desynchronization are slightly anticipated in the numerical results.

Figure 14b shows that curve $C_y^\prime (U_r)$ numerically obtained practically matches the experimental one. Finally, Fig. 14c reveals that the ${\bar{C}}_x(U_r)$ plot numerically obtained follows the experimental results, despite a decrease in the maximum value of ${\bar{C}}_x$. As expected, the mean in-line force coefficient ${\bar{C}}_x$ is close to 1.2 if the oscillation amplitudes are small.

Aiming at illustrating the cylinder response due to VIV, Fig. 15 presents the displacement time history and the corresponding amplitude spectrum obtained for $U_r=5.5$. Notice that $y(\tau )$ is characterized by a narrow-banded amplitude spectrum centered at ${\hat{f}}=f/f_{n,y}=1$ and has no amplitude modulation.

Fig. 15

Displacement time history $y(\tau )$ and corresponding amplitude spectrum. Only the interval $1500 \le \tau \le 2000$ is shown. “Pure VIV” case

Despite being a reduced-order model for evaluating the hydrodynamic loads due to VIV, the wake-oscillator model is able to reproduce not only the ${\hat{A}}_y(U_r)$ curve but also capture intrinsic aspects of the phenomenon, such as the amplification of the force coefficients within the lock-in range of reduced velocities.