Damping and gyroscopic effects on the stability of parametrically excited continuous rotor systems

Abstract

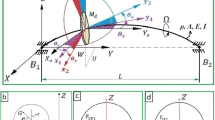
This study is aimed at analysing damping and gyroscopic effects on the stability of parametrically excited continuous rotor systems, taking into account both external (non-rotating) and internal (rotating) damping distributions. As case-study giving rise to a set of coupled differential Mathieu–Hill equations with both damping and gyroscopic terms, a balanced shaft is considered, modelled as a spinning Timoshenko beam loaded by oscillating axial end thrust and twisting moment, with the possibility of carrying additional inertial elements like discs or flywheels. After discretization of the equations of motion into a set of coupled ordinary differential Mathieu–Hill equations, stability is studied via eigenproblem formulation, obtained by applying the harmonic balance method. The occurrence of simple and combination parametric resonances is analysed introducing the notion of characteristic circle on the complex plane and deriving analytical expressions for critical solutions, including combination parametric resonances, valid for a large class of rotors. A numerical algorithm is then developed for computing global stability thresholds in the presence of both damping and gyroscopic terms, also valid when closed-form expressions of critical solutions do not exist. The influence on stability of damping distributions and gyroscopic actions is then analysed with respect to frequency and amplitude of the external loads on stability charts in the form of Ince–Strutt diagrams.

Appendix

The numerical algorithm developed for computing global stability thresholds is able to trace in a single run the entire unknown locus, on a fixed δ-ε domain, in the presence of a nonzero damping distribution, and under the assumption of having a single, continuous global stability threshold.

After the initialization, discussed below, the algorithm evaluates the eigenvalues λ of the quadratic problem in Eq. (28) only in few points (δ, ε) in a neighbourhood of the predicted critical point. The output of each step is a point of the stability threshold. The input of the generic step consists of two points of the stability threshold (the outputs of the previous two steps) and the operator H, in which only δ, ε and λ are unknown. Thus, each step is developed in the following phases:

Phase 1. The code takes the last two points of the discretized stability threshold (output of the previous steps, say P_j−1 and P_j) and computes the vector v₁^(A) (first attempt), as follows:

$$ {\mathbf{v}}_{1}^{\left( A \right)} = V\frac{{\left( {{\mathbf{P}}_{j} - {\mathbf{P}}_{j - 1} } \right)}}{{\left\| {{\mathbf{P}}_{j} - {\mathbf{P}}_{j - 1} } \right\|}} $$

(A1)

in which V is the norm of a chosen real function F = F(P_j − P_j−1), dependent on the slope of the stability threshold. A first-attempt critical point is then computed as follows:

$$ {\mathbf{P}}_{1}^{\left( A \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}_{1}^{\left( A \right)} $$

(A2)

P₁^(A) is a critical point if, in a neighbourhood of P_j, the stability threshold does not change its slope, or, in other words, if P₁^(A) represents a first-order approximation in a neighbourhood of P_j. A first check can be performed on P₁^(A) introducing the following operator:

$$ M( \cdot ) = \max \left\{ {{\text{Re}} \left[ {S\left( {\mathbf{H}} \right)} \right]} \right\}_{{{\mathbf{H}} = {\mathbf{H}}\left[ {( \cdot )} \right]}} $$

(A3)

where S(H) is the spectrum of a generalized eigenproblem resulting from Eq. (28). Thus, the operator $M( \cdot )$ returns the maximum real part of the characteristic exponents λ, when Eq. (28) is evaluated for (δ, ε) = (⋅). Explicitly, the check on P₁^(A) reads:

$$ \left| {M(\,{\mathbf{P}}_{1}^{\left( A \right)} )} \right| = \left| {M(\,\updelta _{1}^{\left( A \right)} ,\,\upvarepsilon _{1}^{\left( A \right)} )} \right|\, \le \,u $$

(A4)

where u is some adjustable positive real number. The choice of u depends on the precision adopted for the whole computation. If Eq. (A4) is respected, then P₁^(A) = P_j+1 is appended to the list of critical points that make up the discretized stability threshold and the algorithm restart from phase 1 with an updated list of critical points. If Eq. (A4) is not respected, then there are only two possibilities:

$$ \left| {M(\,{\mathbf{P}}_{1}^{\left( A \right)} )} \right| > \,u\quad \Rightarrow \quad M(\,{\mathbf{P}}_{1}^{\left( A \right)} ) < \, - u < 0\,\,\,\, \vee \,\,\,\,M(\,{\mathbf{P}}_{1}^{\left( A \right)} ) > \,u > 0 $$

(A5)

Suppose that $M(\,{\mathbf{P}}_{1}^{\left( A \right)} ) < \, - u < 0$, then P₁^(A) lies in the stability region, the maximum real part of λ is negative and all the multipliers lie within the unit circle. At this stage, the code generates a rotation matrix ${\mathbf{R}}\left( {\hat{\gamma }} \right)$ such that:

$$ \left\{ \begin{aligned} & {\mathbf{v}}_{2}^{\left( A \right)} = {\mathbf{R}}\left( {\hat{\gamma }} \right){\mathbf{v}}_{1}^{\left( A \right)} \quad \Rightarrow \quad {\mathbf{P}}_{2}^{\left( A \right)} = {\mathbf{P}}_{j} + {\mathbf{R}}\left( {\hat{\gamma }} \right){\mathbf{v}}_{1}^{\left( A \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}_{2}^{\left( A \right)} \\ & \hat{\gamma } = \pi /k_{1} \\ \end{aligned} \right. $$

(A6)

where k₁ is a positive integer, and the angle $\hat{\gamma }$ is a scalar step which can be tuned through k_1. Matrix ${\mathbf{R}}\left( {\hat{\gamma }} \right)$ is such that the resulting vector v₂^(A) forms a positive angle $\hat{\gamma }$ with respect to v₁^(A) (counterclockwise rotation). The new point P₂^(A) is checked through the operator $M( \cdot )$ as in Eq. (A4) and Eq. (A5). If P₂^(A) lies again in the global stability region, the procedure is repeated. This sub-routine produces a sequence of points P_i^(A) (each vector v_i^(A) forms an angle equal to $\hat{\gamma }$ with respect to v_i−1^(A)), that lie on a circumference centred in P_j, of radius equal to the norm of P_i^(A) − P_j. The latter sub-routine stops when $\left| {M({\mathbf{P}}_{i}^{\left( A \right)} )} \right|\, \le u$, or when a point P^(S) is found such that $M\,({\mathbf{P}}^{\left( S \right)} )\, > u > 0$.

The above described procedure is methodologically the same, but with $\hat{\gamma } < 0$ (clockwise rotations) if, instead of a stable starting point P₁^(A), $M(\,{\mathbf{P}}_{1}^{\left( A \right)} ) < \, - u < 0,$ an unstable starting point occurs, $M\,(\,{\mathbf{P}}_{1}^{\left( A \right)} ) > \,u > 0$. This is due the fact that the global stability region is supposed to be simply connected, hence, moving on the stability threshold, starting from a neighbourhood of the origin of the axes, with initial tangent vector that has positive component along the increasing δ direction, means having the global stability region always facing right. Phase 1 of a generic step is schematized in Fig. 

Fig. 13

a Phase 1 for stable P₁^(A) (continuous curve: exact stability threshold); b Phase 2 for unstable P^(S) and k₂ = 4 (continuous black curve: exact stability threshold)

13a, in the case of stable initial point P₁^(A).

In Fig. 13a, U and S stay for unstable and stable (regions), respectively, the continuous curve is the exact stability threshold, while circles represent the approximated critical points (discretized stability threshold, output of the previous steps). Grey dots represent stable points, and the black dot is the unstable point found by the sub-routine contained in phase 1. In Fig. 13, the norm V of the vectors v is exaggerated on purpose for the sake of clarity. Notice that, by the definition of $\hat{\gamma }$, the searching sub-routine of phase 1 can span a maximum angle equal to π for a maximum of k₁ sub-steps, thus, it is able to handle even cusp points.

Phase 2. This phase takes as inputs two points: P^(S) and the last point of the sequence P_i^(A) say P^(R). These two points lie on different regions, i.e. if P^(S) is unstable then P^(R) is stable and vice versa. Since the global stability region is simply connected, there exist a continuous path, passing through the two points, which intersects the stability threshold and, for sufficiently small $\hat{\gamma },$ this intersection is unique. An arc of the circle centred in P_j is now considered as selected path, having P^(R) and P^(S) as extremal points. This arc is discretized taking a sequence of evenly spaced points (say P_z^(M), other than P^(R) and P^(S)):

$$ {\mathbf{P}}^{\left( R \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}^{\left( R \right)} ,\quad {\mathbf{P}}_{1}^{\left( M \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}_{1}^{\left( M \right)} ,\quad {\mathbf{P}}_{2}^{\left( M \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}_{2}^{\left( M \right)} ,\quad ...\,,\quad {\mathbf{P}}^{\left( S \right)} = {\mathbf{P}}_{j} + {\mathbf{v}}^{\left( S \right)} $$

(A7)

As a consequence of phase 1, the module of the angle spanned by P^(R) and P^(S) is $\left| {\hat{\gamma }} \right|$. Considering once again the case in which P^(S) is unstable (hence P^(R) is stable), it follows that the vectors v_z^(M) can be computed starting from vector v^(R), which is known from phase 1, with a sequence of counterclockwise rotations. Hence:

$$ \left\{ \begin{aligned} & {\mathbf{v}}_{z}^{\left( M \right)} = {\mathbf{R}}\left( {z\,\hat{\beta }} \right){\mathbf{v}}^{\left( R \right)} \quad \Rightarrow \quad {\mathbf{P}}_{z}^{\left( M \right)} = {\mathbf{P}}_{j} + {\mathbf{R}}\left( {z\,\hat{\beta }} \right){\mathbf{v}}^{\left( R \right)} ,\quad z = 1\,,2\,,...\,,\,k_{2} - 1 \\ & \hat{\beta } = \hat{\gamma }/k_{2} \\ \end{aligned} \right. $$

(A8)

where k₂ is a positive integer. It is now possible to build a function, say $\sum \left( {\hat{\alpha }} \right)$, through interpolation of the values returned by the operator $M( \cdot ),$ evaluated in the k₂ + 1 points of the sequence P^(R), P₁^(M),…, ${\mathbf{P}}_{{k}_{2}-1}^{(M)}$, P^(S):

$$ \left\{ {0\,,M({\mathbf{P}}^{\left( R \right)} )} \right\}\,,\,\left\{ {\hat{\beta }\,,M({\mathbf{P}}_{1}^{\left( M \right)} )} \right\}\,,\,...\,,\,\left\{ {\left( {k_{2} - 1} \right)\,\hat{\beta }\,,M({\mathbf{P}}_{{k_{2} - 1}}^{\left( M \right)} )} \right\}\,,\,\left\{ {\hat{\gamma }\,,M({\mathbf{P}}^{\left( S \right)} )} \right\}\quad \Rightarrow \quad \sum \left( {\hat{\alpha }} \right) $$

(A9)

Function $\sum \left( {\hat{\alpha }} \right)$ has exactly one root on the interval $\left( {0\,,\,\hat{\gamma }} \right)$, say $\hat{\alpha }_{R}$. The latter procedure allows to compute a point for which the maximum real part of the characteristic exponents, returned by Eq. (23), is zero:

$$ {\mathbf{P}}_{j + 1} = {\mathbf{P}}_{j} + {\mathbf{R}}\left( {\hat{\alpha }_{R} } \right){\mathbf{v}}^{\left( R \right)} $$

(A10)

In Fig. 13b, phase 2 is schematized for k₂ = 4, in the case of unstable P^(S). The continuous black curve represents the exact stability threshold and, in this example, P^(R) and P₁^(M) are stable (grey dots), while P₂^(M), P₃^(M) and P^(S) are unstable (black dots). The cross represents the approximated critical point P_j+1, which is the output of phase 2 (and of the whole generic step of the algorithm).

The root $\hat{\alpha }_{R}$ can be easily found through Newton–Raphson method. Once the algorithm has computed P_j+1, it restarts from phase 1 with an updated list of approximated critical points. Notice that, if P^(S) is stable, the procedure related to phase 2 is still valid, but exchanging the roles played by P^(S) and P^(R).

Initialization. It yields two points, from which phase 1 and 2 can return a third point as output. These two points can be computed as in the second part of phase 2, choosing two simple paths, i.e. two vertical lines, two horizontal lines or two operation lines. Alternatively, the two points can be arbitrarily chosen (close to each other) near to the origin of the axes. The algorithm automatically changes V in Eq. (A1) until an intersection with the stability threshold is found.

The proposed algorithm was tested in comparison with the monodromy matrix method [4], adopting a reduced number of shape functions in the Galerkin expansion (N = 2, yielding dimension 16 in a state space representation), and reducing the number of terms in the Fourier series to 12 (for computing the operator H).

The two methods lead to the same global stability threshold, as it is shown for example in Fig. 2d (damping distribution 1, $\zeta_{0} = 0.01$), adopting a 200 × 200 grid (40,000 points) for representing the results obtained by the monodromy matrix method.