Reconstruction of pitchfork bifurcation with exogenous disturbances based on equivalent-input-disturbance approach

Abstract

Reconstructing a pitchfork bifurcation that is destroyed by an exogenous disturbance is important to control it. This paper extends the equivalent-input-disturbance (EID) approach to solve the problem of reconstructing a pitchfork bifurcation when there is an exogenous disturbance for the first time. A nonlinear term and a bifurcation parameter are designed in the system to reconstruct the pitchfork bifurcation. The bifurcation characteristics of the equilibriums of the system are analyzed by exploring the features of the EID-based system. This provides us analytic solutions for a system with a degree higher than four for the first time. Unlike other pitchfork-bifurcation control systems, the EID-based control system only rejects the disturbance and retains the nonlinearity. Numerical examples demonstrate the effectiveness of the presented method and show its superiority over others. The robustness of the reconstruction with respect to measurement noise and control of a pitchfork bifurcation are also shown by the examples.

Appendix

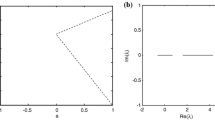
Convergence of the stable equilibrium in Fig. 1 for $\lambda =\pm 1.5$ is analyzed below.

We first analyze the convergence of the stable equilibrium for

$$\begin{aligned} \lambda =1.5. \end{aligned}$$

(A.1)

Substituting (A.1) in (1) yields

$$\begin{aligned} \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t}=f_1(x,\lambda )=1.5x(t)-x^3(t). \end{aligned}$$

(A.2)

Solving

$$\begin{aligned} 1.5x(t)-x^3(t)=0 \end{aligned}$$

(A.3)

obtains the equilibriums

$$\begin{aligned} x_o=0,~\pm \sqrt{1.5}. \end{aligned}$$

(A.4)

For

$$\begin{aligned} x_o=0, \end{aligned}$$

(A.5)

the Jacobian matrix is

$$\begin{aligned} \alpha _1=\frac{\partial f_1(x,\lambda )}{\partial x}\bigg |_{x=0}=1.5>0.\nonumber \\ \end{aligned}$$

(A.6)

Thus, $x_o=0$ is an unstable equilibrium. For

$$\begin{aligned} x_o=~\pm \sqrt{1.5}, \end{aligned}$$

(A.7)

the Jacobian matrix is

$$\begin{aligned} \alpha _1=\frac{\partial f_1(x,\lambda )}{\partial x}\bigg |_{x=\pm \sqrt{1.5}}=1.5-4.5=-3<0. \end{aligned}$$

(A.8)

Thus, $x_o=~\pm \sqrt{1.5}$ are stable equilibriums. To analyze the convergence of the stable equilibrium, we have to make a coordinate transformation. Let

$$\begin{aligned} z(t)=x(t)-\sqrt{1.5}. \end{aligned}$$

(A.9)

Substituting (A.9) in (A.2) yields

$$\begin{aligned} \begin{aligned} \displaystyle \frac{\mathrm{{d}}z(t)}{\mathrm{{d}}t}&= h(z)= 1.5 (z(t)+\sqrt{1.5})\\ \displaystyle&\quad -(z(t)+\sqrt{1.5})^3= A_Nz(t)+f_z(z),\\ \end{aligned} \end{aligned}$$

(A.10)

where

$$\begin{aligned} A_N=-3,~f_z(z)=-3\sqrt{1.5}z^2(t)-z^3(t). \end{aligned}$$

(A.11)

The stable equilibrium $x_o=\sqrt{1.5}$ for (A.2) is transformed to the stable equilibrium $z_o=0$ for (A.10).

Since

$$\begin{aligned} A_N<0 \end{aligned}$$

is Hurwitz, for any positive definite symmetric matrix $Q_N$, the solution, $P_N$, of

$$\begin{aligned} P_NA_N+A_N^\mathrm{{T}}P_N=-Q_N \end{aligned}$$

is positive definite. Let

$$\begin{aligned} V_N(z)=z^{\mathrm{T}}(t)P_Nz(t) \end{aligned}$$

be a Lyapunov function candidate of (A.10). The derivative of $V_N(z)$ along the trajectories of (A.10) is given by

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}{V_N(z)}}{\mathrm{{d}}t}=-z^\mathrm{{T}}(t)Q_Nz(t)+2z^\mathrm{{T}}(t)P_Nf_z(z). \end{aligned} \end{aligned}$$

(A.12)

The first term on the right side of (A.12) is negative definite, while the second term is indefinite. Since the function $f_z(z)$ satisfies

$$\begin{aligned} \frac{\Vert f_z\Vert _2}{\Vert z\Vert _2}\rightarrow 0 ~\mathrm{{as}} ~\Vert z\Vert _2\rightarrow 0. \end{aligned}$$

(A.13)

Therefore, for any $\gamma >0$, there exists $\nu >0$ such that

$$\begin{aligned} \Vert f_z\Vert _2<\gamma \Vert z\Vert _2,~\forall \Vert z\Vert _2<\nu . \end{aligned}$$

Hence,

$$\begin{aligned} \begin{aligned} \frac{\mathrm{{d}}{V_N(z)}}{\mathrm{{d}}t}<-z^\mathrm{{T}}(t)Q_Nz(t)+2{\gamma }\Vert P_N\Vert _2\Vert z\Vert _2^2,~\forall \Vert z\Vert _2<\nu . \end{aligned} \end{aligned}$$

However,

$$\begin{aligned} z^\mathrm{{T}}(t)Q_Nz(t)\ge {\delta _{\min }(Q_N)}\Vert z\Vert _2^2. \end{aligned}$$

Note that $\delta _{\min }(Q_N)$ is real and positive because $Q_N$ is symmetric and positive definite. Thus,

$$\begin{aligned} \frac{\mathrm{{d}}{V_N(z)}}{\mathrm{{d}}t}<-\left[ \delta _\mathrm{{min}}(Q_N)-2\gamma \Vert P_N\Vert _2 \right] \Vert z\Vert _2^2,~\forall \Vert z\Vert _2<\nu . \end{aligned}$$

Choosing

$$\begin{aligned} \displaystyle \gamma <\frac{\delta _\mathrm{{min}}(Q_N)}{2\Vert P_N\Vert _2} \end{aligned}$$

ensures that $\mathrm{d}{V}_N(z)/\mathrm{d}t$ is negative definite. Thus, $z_o=0$ is asymptotically stable, which means that for $z(0)<\nu$, z(t) converges to 0 as $t\rightarrow \infty$.

The proof for $x_o=-\sqrt{1.5}$ is the same as that for $x_o=\sqrt{1.5}$. Thus, it is omitted.

Next, we analyze the convergence of the stable equilibrium for

$$\begin{aligned} \lambda =-1.5. \end{aligned}$$

(A.14)

Substituting (A.14) in (1) yields

$$\begin{aligned} \frac{\mathrm{{d}}x(t)}{\mathrm{{d}}t}=f_1(x,\lambda )=A_Mx(t)-f_x(x), \end{aligned}$$

(A.15)

where

$$\begin{aligned} A_M=-1.5,~f_x(x)=-x^3(t). \end{aligned}$$

Solving

$$\begin{aligned} -1.5x(t)-x^3(t)=0 \end{aligned}$$

(A.16)

obtains the equilibrium

$$\begin{aligned} x_o=0. \end{aligned}$$

(A.17)

For (A.17),

$$\begin{aligned} \alpha _1=\frac{\partial f_1(x,\lambda )}{\partial x}\bigg |_{x=0}=-1.5<0. \end{aligned}$$

(A.18)

Thus, $x_o=0$ is a stable equilibrium.

Since

$$\begin{aligned} A_M<0 \end{aligned}$$

is Hurwitz, for any positive definite symmetric matrix $Q_M$, the solution, $P_M$, of

$$\begin{aligned} P_MA_M+A_M^\mathrm{{T}}P_M=-Q_M \end{aligned}$$

is positive definite. Let

$$\begin{aligned} V_M(x)=x^{\mathrm{T}}(t)P_Mx(t) \end{aligned}$$

be a Lyapunov function candidate of (A.15). The derivative of $V_M(x)$ along the trajectories of (A.15) is given by

$$\begin{aligned} \frac{\mathrm{{d}}{V_M(x)}}{\mathrm{{d}}t}=-x^\mathrm{{T}}(t)Q_Mx(t)+2x^\mathrm{{T}}(t)P_Mf_x(x).\nonumber \\ \end{aligned}$$

(A.19)

The first term on the right side of (A.19) is negative definite, while the second term is indefinite. Since the function $f_x(x)$ satisfies

$$\begin{aligned} \frac{\Vert f_x\Vert _2}{\Vert x\Vert _2}\rightarrow 0 ~\mathrm{{as}} ~\Vert x\Vert _2\rightarrow 0, \end{aligned}$$

which is the same as (A.13), the convergence analysis of $x_o=0$ for $\lambda =-1.5$ is the same as that of $x_o=\sqrt{1.5}$ for $\lambda =1.5$, thus is omitted.