On the optimization of n-sub-step composite time integration methods

Abstract

A family of n-sub-step composite time integration methods, which employs the trapezoidal rule in the first $n-1$ sub-steps and a general formula in the last one, is discussed in this paper. A universal approach to optimize the parameters is provided for any cases of $n\ge 2$, and two optimal sub-families of the method are given for different purposes. From linear analysis, the first sub-family can achieve nth-order accuracy and unconditional stability with controllable algorithmic dissipation, so it is recommended for high-accuracy purposes. The second sub-family has second-order accuracy, unconditional stability with controllable algorithmic dissipation, and it is designed for heuristic energy-conserving purposes, by preserving as much low-frequency content as possible. Finally, some illustrative examples are solved to check the performance in linear and nonlinear systems.

1 Introduction

Direct time integration methods are frequently used to predict accurate numerical responses for general dynamic problems after spatial discretization. Driven by the pursuit of desirable properties, including higher accuracy and efficiency, robust stability, and many others, a number of excellent methods were proposed in the past decades.

In terms of the formulations, existing methods are generally classified into explicit and implicit schemes. Explicit methods are mostly used in wave propagation problems, as their conditional stability limits the allowable time step size to the highest system frequency. Implicit methods have fewer restrictions on the problems to be solved due to the unconditional stability, but they require more computational efforts per step.

In another way, the integration methods can also be divided into single-step, multi-sub-step and multi-step techniques. The single-step methods only adopt the states of the last step to predict the current one, while the multi-sub-step methods also need the states at the intermediate collocation points, and the multi-step methods require the states of more than one previous step. Each of them has specific advantages and disadvantages.

From the literature, representative single-step methods include the Newmark method [25], the HHT-$\alpha$ method (by Hilbert, Hughes, and Taylor) [17], the WBZ-$\alpha$ method (by Wood, Bossak, and Zienkiewicz) [29], the generalized-$\alpha$ method [9], the GSSSS (generalized single-step single-solve) method [34], and many others [28]. These single-step methods were proved to be spectrally identical to the linear multi-step methods [34], so they suffer from the Dahlquist’s barrier [10], which states that the methods of higher than second-order accuracy cannot be unconditionally stable. Therefore, the methods mentioned above are all second-order accurate and unconditionally stable; some of them can also provide controllable algorithmic dissipation.

In the multi-step class, the Dahlquist’s barrier certainly works, but in terms of accuracy, the linear two-step method [24, 33] is superior to most existing single-step methods under the same degree of algorithmic dissipation. In this class, BDFs (backward differentiation formulas) [11, 16] also represent a widely-used branch, particularly useful for stiff problems owing to the strong algorithmic dissipation. These popular multi-step methods are also second-order accurate and unconditionally stable. However, the multi-step methods are not self-starting, so another method has to be also used to solve the initial steps, which makes the multi-step methods not as convenient to use as the single-step ones.

The multi-sub-step methods, also known as multi-stage methods, allow more possibilities in terms of properties. The most representative method is the famous Runge–Kutta family [6, 7, 19], which can be designed to be arbitrarily higher-order accurate and unconditionally stable by choosing proper parameters and enough stages. Besides, Fung [12,13,14,15] provided some methods to reproduce the generalized Padé approximation. These methods can reach up to 2nth-order accuracy by employing n sampling grid points per step, but the dimension of the implicit equation to be solved is n times that of the original, resulting in huge computational costs. In the multi-sub-step class, the composite methods [3], which divide each step into several sub-steps and employ different methods in each sub-step, have received a lot of attention in recent years.

Based on Bank et al.’s work [1], Bathe et al. [3] introduced the concept of the n-sub-step composite method by utilizing the trapezoidal rule in the first $n-1$ sub-steps and the $(n+1)$-point backward difference scheme at the end of the step. The two-sub-step scheme is known as the Bathe method, which is asymptotically stable with second-order accuracy. Thanks to its strong dissipation and preferable accuracy, the Bathe method has been found to perform well in many fields [2, 4, 27]. The three-, and four-sub-step composite methods [8, 32], which are asymptotically stable with higher accuracy, were also developed adopting the similar idea. Furthermore, to acquire controllable algorithmic dissipation, the two-sub-step methods [20, 21, 26], and the controllable three-sub-step methods [18, 23], were proposed by replacing the backward difference scheme with a more general formula. However, with the increase in the number of sub-steps, the number of scalar parameters required to be designed also increases, so the basic requirements, including second-order accuracy, unconditional stability, controllable algorithmic dissipation, are not enough to determine these parameters uniquely. Two optimal sub-families of the controllable three-sub-step method were proposed in [23], since different conditions are considered as a supplement.

On this basis, this paper purposes to provide a universal approach to optimize the parameters of generalized n-sub-step composite method, where n can be any integer greater than 2, and the trapezoidal rule is employed in the first $n-1$ sub-steps. Two kinds of optimization goals are considered, producing two optimal sub-families for different purposes. The first one intends to achieve higher-order accuracy, under the premises of unconditional stability and controllable algorithmic dissipation. The second one is dedicated to conserving low-frequency behavior, while still providing controllable high-frequency dissipation. From linear analysis, the resulting schemes in the first sub-family can reach up to nth-order accuracy by using n sub-steps, and the schemes in the second sub-family exhibit very small algorithmic dissipation in the low-frequency domain. Most of these schemes are developed for the first time, and in each sub-family, the accuracy can be improved by using more sub-steps. Finally, the proposed methods are applied to solve several numerical examples to check the performance.

This paper is organized as follows. The formulations of the n-sub-step composite method are shown in Sect. 2. The optimization of the parameters is implemented in Sect. 3. The detailed properties of the two sub-families are discussed in Sect. 4. Numerical examples are provided in Sect. 5, and conclusions are drawn in Sect. 6.

2 Formulation

In the literature, the composite methods were mostly developed to solve the problems in structural dynamics, as

$$\begin{aligned} {\varvec{M}}\ddot{{\varvec{x}}}+{\varvec{F}}\left( {\varvec{x}},\dot{{\varvec{x}}},t\right) ={\varvec{0}}, \, {\varvec{x}}\left( t_0\right) ={\varvec{x}}_0, \, \dot{{\varvec{x}}}\left( t_0\right) ={\varvec{v}}_0 \end{aligned}$$

(1)

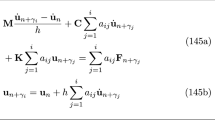
where ${\varvec{M}}$ is the mass matrix, ${\varvec{F}}$ collects the damping force, internal force and external load, ${\varvec{x}}$, $\dot{{\varvec{x}}}$ and $\ddot{{\varvec{x}}}$ are the displacement, velocity and acceleration vectors, respectively, t is the time, and $t_0$, ${\varvec{x}}_0$ and ${\varvec{v}}_0$ are the given initial time, displacement and velocity, respectively. When this method is applied using n sub-steps, it can be formulated as

$$\begin{aligned}&{\varvec{M}}\ddot{{\varvec{x}}}_{k+2j\gamma }+{\varvec{F}}\left( {\varvec{x}}_{k+2j\gamma }, \dot{{\varvec{x}}}_{k+2j\gamma },t_{k}+2j\gamma h\right) ={\varvec{0}} \end{aligned}$$

(2a)

$$\begin{aligned}&{\varvec{x}}_{k+2j\gamma }={\varvec{x}}_{k+2(j-1)\gamma }+\gamma h\left( \dot{{\varvec{x}}}_{k+2(j-1)\gamma }+\dot{{\varvec{x}}}_{k+2j\gamma }\right) \end{aligned}$$

(2b)

$$\begin{aligned}&\dot{{\varvec{x}}}_{k+2j\gamma }=\dot{{\varvec{x}}}_{k+2(j-1)\gamma }+\gamma h\left( \ddot{{\varvec{x}}}_{k+2(j-1)\gamma }+\ddot{{\varvec{x}}}_{k+2j\gamma }\right) \end{aligned}$$

(2c)

$$\begin{aligned}&j=1,2,3,\cdots ,n-1 \end{aligned}$$

(2d)

and

$$\begin{aligned}&{\varvec{M}}\ddot{{\varvec{x}}}_{k+1}+{\varvec{F}}\left( {\varvec{x}}_{k+1},\dot{{\varvec{x}}}_{k+1}, t_{k}+h\right) ={\varvec{0}}\end{aligned}$$

(3a)

$$\begin{aligned}&{\varvec{x}}_{k+1}={\varvec{x}}_{k}+ h\left( \sum _{j=0}^{n-1}q_j\dot{{\varvec{x}}}_{k+2j\gamma } +q_n\dot{{\varvec{x}}}_{k+1}\right) \end{aligned}$$

(3b)

$$\begin{aligned}&\dot{{\varvec{x}}}_{k+1}=\dot{{\varvec{x}}}_k+ h\left( \sum _{j=0}^{n-1}q_j \ddot{{\varvec{x}}}_{k+2j\gamma }+q_n\ddot{{\varvec{x}}}_{k+1}\right) \end{aligned}$$

(3c)

where ${\varvec{x}}_k\approx {\varvec{x}}\left( t_k\right)$ is the numerical solution at step k, ${\varvec{x}}_{k+2j\gamma }\approx {\varvec{x}}\left( t_k+2j\gamma h\right) \left( j=1,2,\cdots ,n-1\right)$ denotes the numerical solution at collocation points, h is the step size, and $\gamma$, $q_0$, $q_1$, $\cdots$, $q_n$ are the control parameters. The current step $\left[ t_k,t_k+h\right]$ is divided into n sub-steps: $\left[ t_k,t_k+2\gamma h\right]$, $\left[ t_k+2\gamma h,t_k+4\gamma h\right]$,$\cdots$, $\left[ t_k+2(n-2)\gamma h,t_k+2(n-1)\gamma h\right]$, and $\left[ t_k+2(n-1)\gamma h,t_k+h\right]$. In the first $n-1$ sub-steps, the trapezoidal rule is adopted. In the last one, a general formula containing information about all collocation points is utilized. The present formulation can reduce to the $\rho _{\infty }$-Bathe method [26] when $n=2$ and to the three-sub-step method [18, 23] when $n=3$.

In this method, because the same form of assumptions is used to solve ${\varvec{x}}_{k+1}$ and $\dot{{\varvec{x}}}_{k+1}$, Eqs. (2) and (3) can be reformulated based on the general first-order differential equation ${\varvec{f}}({\varvec{y}},\dot{{\varvec{y}}},t)={\varvec{0}}$, as

$$\begin{aligned}&{\varvec{f}}\left( {\varvec{y}}_{k+2j\gamma },\dot{{\varvec{y}}}_{k+2j\gamma },t_k+2j\gamma h\right) ={\varvec{0}}\end{aligned}$$

(4a)

$$\begin{aligned}&{\varvec{y}}_{k+2j\gamma }={\varvec{y}}_{k+2(j-1)\gamma }+\gamma h\left( \dot{{\varvec{y}}}_{k+2(j-1)\gamma }+\dot{{\varvec{y}}}_{k+2j\gamma }\right) \end{aligned}$$

(4b)

$$\begin{aligned}&j=1,2,3,\cdots ,n-1 \end{aligned}$$

(4c)

and

$$\begin{aligned}&{\varvec{f}}\left( {\varvec{y}}_{k+1},\dot{{\varvec{y}}}_{k+1},t_k+h\right) ={\varvec{0}}\end{aligned}$$

(5a)

$$\begin{aligned}&{\varvec{y}}_{k+1}={\varvec{y}}_{k}+ h\left( \sum _{j=0}^{n-1}q_j\dot{{\varvec{y}}}_{k+2j\gamma }+q_n\dot{{\varvec{y}}}_{k+1}\right) \end{aligned}$$

(5b)

where $\left\{ {\varvec{x}};\dot{{\varvec{x}}}\right\}$ is replaced by ${\varvec{y}}$, and the dynamics equations can be equivalently formulated as first-order differential equations by adding the trivial equation $\dot{{\varvec{x}}}=\dot{{\varvec{x}}}$. Equations (4) and (5) present more general formulations for solving first-order and arbitrarily higher-order differential equations. However, for solving the second-order dynamic problems, Eqs. (2) and (3) are still more recommended, since in the equivalent first-order expressions, the number of implicit equations to be solved doubles.

From the formulation, the first $n-1$ sub-steps can share the same procedure in a loop, whereas the last sub-step needs to be implemented separately. The assumption $q_n=\gamma$ is introduced here, which imposes that the last sub-step shares the same form of Jacobi matrix as the first $n-1$ sub-steps. This assumption is particularly useful when applied to linear problems, since it allows the constant Jacobi matrix to be factorized only once, like in the single-step methods. For applications, Table 1 shows the computational procedures of the n-sub-step composite method for the general first-order differential equation ${\varvec{f}}({\varvec{y}},\dot{{\varvec{y}}},t)={\varvec{0}}$, where the Newton-Raphson iteration is utilized to solve the nonlinear equation per sub-step.

Table 1 Computational procedure of the n-sub-step composite method for solving ${\varvec{f}}({\varvec{y}},\dot{{\varvec{y}}},t)={\varvec{0}},{\varvec{y}}(t_0)={\varvec{y}}_0$

Besides, by reorganizing the formulations, the composite method can be regarded as a special case of the diagonally-implicit Runge–Kutta methods (DIRKs) with the explicit first-stage. The corresponding Butcher’s tableau [6] has the form as

$$\begin{aligned} \begin{array}{c|c c c c c c} 0 &{} 0 &{} 0 &{} 0 &{} \cdots &{} 0 &{} 0\\ 2\gamma &{} \gamma &{} \gamma &{} 0 &{} \cdots &{} 0 &{} 0\\ 4\gamma &{} \gamma &{} 2\gamma &{} \gamma &{} \ddots &{} 0 &{} 0\\ \vdots &{} \vdots &{} \vdots &{} \ddots &{} \ddots &{} \vdots &{} \vdots \\ 2(n-1)\gamma &{} \gamma &{} 2\gamma &{} 2\gamma &{} \cdots &{} \gamma &{} 0\\ 1 &{} q_0 &{} q_1 &{} q_2 &{} \cdots &{} q_{n-1} &{} \gamma \\ \hline \ &{} q_0 &{} q_1 &{} q_2 &{} \cdots &{} q_{n-1} &{} \gamma \end{array} \end{aligned}$$

3 Optimization

In linear spectral analysis, owing to the mode superposition principle, it is common and enough to consider the single degree-of-freedom equation

$$\begin{aligned} \ddot{x}+2\xi \omega {\dot{x}}+\omega ^2x=0 \end{aligned}$$

(6)

where $\xi$ is the damping ratio, and $\omega$ is the natural frequency. To simplify the analysis, the equivalent first-order differential equation is discussed, as

$$\begin{aligned} \dot{{\varvec{y}}}=\left[ \begin{array}{cc} 0 &{} 1 \\ -\omega ^2 &{} -2\xi \omega \end{array}\right] {\varvec{y}}, \, {\varvec{y}}=\left[ \begin{array}{cc} x \\ {\dot{x}} \end{array}\right] \end{aligned}$$

(7)

Decomposing the coefficient matrix in Eq. (7) yields the simplified first-order equation

$$\begin{aligned} {\dot{y}}=\lambda y, \, \lambda =(-\xi \pm \text {i}\sqrt{1-\xi ^2})\omega \end{aligned}$$

(8)

where ${i}=\sqrt{-1}$. When the composite method is applied, the recursive scheme becomes

$$\begin{aligned} y_{k+1}=A\left( \lambda h\right) y_k \end{aligned}$$

(9)

where the amplification factor A is

$$\begin{aligned} A\left( z\right)&=\left( 1-q_n z\right) ^{-1}\left( 1+z\sum _{j=0}^{n-1}q_{j} \left( \frac{1+\gamma z}{1-\gamma z}\right) ^j\right) ,\nonumber \\ z&=\lambda h \end{aligned}$$

(10)

Since $q_n=\gamma$ is assumed in Sect. 2, Eq. (10) is updated as

$$\begin{aligned} A\left( z\right)&=\frac{\left( 1-\gamma z\right) ^{n-1}+z\sum \nolimits _{j=0}^{n-1}\left( q_{j} \left( 1+\gamma z\right) ^j\left( 1-\gamma z\right) ^{n-j-1}\right) }{\left( 1-\gamma z\right) ^n}\\\nonumber&=\frac{1+a_1z+a_2z^2+\cdots +a_n z^n}{\left( 1-\gamma z\right) ^n} \end{aligned}$$

(11)

where the coefficient of $z^p \left( p=1,2,\cdots ,n\right)$ is represented by $a_p \left( p=1,2,\cdots ,n\right)$, expressed as

$$\begin{aligned}&a_p=\genfrac(){0.0pt}0{p}{n-1}(-\gamma )^p\nonumber \\&\quad +\,\gamma ^{p-1}\sum _{j=0}^{n-1}\left( q_j\sum _{m=\text {max}\{0,p+j-n\}}^{\text {min} \{j,p-1\}}P(m,j,p,n)\right) ,\nonumber \\&P(m,j,p,n)=(-1)^{p-m-1} \genfrac(){0.0pt}0{m}{j}\genfrac(){0.0pt}0{p-m-1}{n-j-1},\nonumber \\&p=1,2,\cdots ,n-1 \end{aligned}$$

(12)

and

$$\begin{aligned} a_n=\gamma ^{n-1}\sum _{j=0}^{n-1}\left( (-1)^{n-j-1}q_j\right) \end{aligned}$$

(13)

For example, $n=5$ follows

$$\begin{aligned} a_1&=-4\gamma +q_0+q_1+q_2+q_3+q_4 \end{aligned}$$

(14a)

$$\begin{aligned} a_2&=6\gamma ^2+\gamma \left( -4q_0-2q_1+2q_3+4q_4\right) \end{aligned}$$

(14b)

$$\begin{aligned} a_3&=-4\gamma ^3+\gamma ^2\left( 6q_0-2q_2+6q_4\right) \end{aligned}$$

(14c)

$$\begin{aligned} a_4&=\gamma ^4+\gamma ^3\left( -4q_0+2q_1-2q_3+4q_4\right) \end{aligned}$$

(14d)

$$\begin{aligned} a_5&=\gamma ^4\left( q_0-q_1+q_2-q_3+q_4\right) \end{aligned}$$

(14e)

Consequently, the parameters under analysis change from $q_j\left( j=0,1,\cdots ,n-1\right)$ and $\gamma$, to $a_p\left( p=1,2,\cdots ,n\right)$ and $\gamma$ in the following. When $a_p$ and $\gamma$ are given, the parameters $q_j$ can be obtained uniquely by solving Eqs. (12) and (13). For applications, Table 2 shows the formulas of $q_j$ expressed by $a_p$ and $\gamma$ for the cases $n=2,3,4,5$.

Table 2 Formulas of $q_j\left( j=0,1,\cdots ,n-1\right)$

3.1 Higher-order schemes

A numerical method is naturally expected to be as accurate as possible, so the higher-order schemes are considered first. From the scheme of Eq. (9), the composite method uses the amplification factor A, rewritten as

$$\begin{aligned} A\left( z\right) =\frac{1+a_1z+a_2z^2+\cdots +a_n z^n}{\left( 1-\gamma z\right) ^n} \end{aligned}$$

(15)

to approximate the exact amplification factor ${\hat{A}}$

$$\begin{aligned} {\hat{A}}\left( z\right) =\text {e}^{z}=1+z+\frac{1}{2}z^2+\frac{1}{6}z^3+\cdots \end{aligned}$$

(16)

Hence the local truncation error $\sigma$ can be defined as

$$\begin{aligned} \sigma =y_{k+1}-y\left( t_{k+1}\right) =\left( A(z)-{\hat{A}}(z)\right) y(t_k) \end{aligned}$$

(17)

If $\sigma =\text {O}\left( z^{s+1}\right)$, the method is said to be sth-order accurate, which requires that up to sth derivatives of A at $z=0$ are all equal to 1, that is

$$\begin{aligned} A(0)=A^{(1)}(0)=A^{(2)}(0)=\cdots =A^{(s)}(0)=1 \end{aligned}$$

(18)

To satisfy Eq. (18), $a_p\left( p=1,2,\cdots ,n\right)$ can be solved as

$$\begin{aligned}&A^{(1)}(0)=1\Rightarrow {a_1=1-n\gamma } \end{aligned}$$

(19a)

$$\begin{aligned}&A^{(2)}(0)=1\Rightarrow {a_2=\frac{1}{2}-n\gamma +\frac{n(n-1)}{2}\gamma ^2}\end{aligned}$$

(19b)

$$\begin{aligned}&A^{(3)}(0)=1\Rightarrow \end{aligned}$$

(19c)

$$\begin{aligned}&{a_3=\frac{1}{6}-\frac{n}{2}\gamma +\frac{n(n-1)}{2}\gamma ^2-\frac{n(n-1)(n-2)}{6}\gamma ^3}\nonumber \\&\cdots \end{aligned}$$

(19d)

$$\begin{aligned}&A^{(s)}(0)=1\Rightarrow {a_s=\sum _{j=0}^{s}\left( \frac{(-1)^j}{(s-j)!}\genfrac(){0.0pt}0{j}{n}\gamma ^j\right) } \end{aligned}$$

(19e)

Therefore, if all $a_p\left( p=1,2,\cdots ,n\right)$ follow the relationships in Eq. (19), this method can achieve nth-order accuracy, and then $\gamma$ becomes the only free parameter to control the stability.

A time integration method is said to be unconditionally stable if $\left| A(z)\right| \le 1$ for all ${\mathbb {R}}(z)\le 0$ where $z=\lambda h=(-\xi \pm \text {i}\sqrt{1-\xi ^2})\omega h$. According to Ref. [19], the bounds on $\gamma$ can be given by considering the stability on the imaginary axis ($\xi =0$), which can result in the unconditional stability when the accuracy order $s=n$ in the DIRKs. Therefore, let $z=\pm \text {i}\tau$ where $\tau =\omega h$ is a real number, and

$$\begin{aligned}&N(z)=1+a_1z+a_2z^2+\cdots +a_n z^n \end{aligned}$$

(20a)

$$\begin{aligned}&D(z)=\left( 1-\gamma z\right) ^n \end{aligned}$$

(20b)

which are the numerator and denominator of A(z) in Eq. (15), respectively, $\left| A(z)\right| \le 1$ is equivalent to

$$\begin{aligned} \left| A(z)\right| ^2=A(\text {i}\tau )A(-\text {i}\tau )=\frac{N(\text {i}\tau )N(-\text {i}\tau )}{D(\text {i}\tau )D(-\text {i}\tau )}\le 1 \end{aligned}$$

(21)

Then the condition for unconditional stability can be transformed into

$$\begin{aligned} S(\tau )&=D(\text {i}\tau )D(-\text {i}\tau )-N(\text {i}\tau )N(-\text {i}\tau )\nonumber \\&=\sum _{j=0}^{n}\left( c_{2j}\tau ^{2j}\right) \ge 0\ \text {for}\ \tau \ge 0 \end{aligned}$$

(22)

where the function $S(\tau )$ is introduced, and the coefficients $c_{2j}(j=0,1,2,\cdots ,n)$ are expressed as

$$\begin{aligned} c_{2j}&=\genfrac(){0.0pt}0{j}{n}\gamma ^{2j}\nonumber \\&\quad +\,\left( -1\right) ^{j+1}\sum _{m=\text {max}\{0,2j-n\}}^{\text {min}\{n,2j\}} \left( \left( -1\right) ^ma_{m}a_{2j-m}\right) \end{aligned}$$

(23)

in which $a_0$ is set to 1. By Eq. (22), the bounds on $\gamma$ of the cases $n=2,3,4,5$ are provided in Table 3 . It follows that, with $s=n$, the allowable range of $\gamma$ narrows as n increases and, in some cases, the n-sub-step method can achieve $(n+1)$th-order accuracy with a fixed $\gamma$.

Table 3 Bounds on $\gamma$ for unconditional stability (s is the accuracy order) in the higher-order schemes

Besides, algorithmic dissipation is also a desirable property for a time integration method, to filter out the inaccurate high-frequency content. Generally, it is measured by the spectral radius $\rho _{\infty }$ at high-frequency limit, that is

$$\begin{aligned} \left| A(z)\right| \rightarrow {\rho _{\infty }}\ \text {as}\ \left| z\right| =\omega h\rightarrow {+\infty },\ \rho _{\infty }\in \left[ 0,1\right] \end{aligned}$$

(24)

and it gets stronger with a smaller $\rho _{\infty }$. With A(z) from Eq. (15), Eq. (24) can be satisfied if

$$\begin{aligned} a_n^2=\left( \sum _{j=0}^{n}\left( \frac{(-1)^j}{(n-j)!}\genfrac(){0.0pt}0{j}{n} \gamma ^j\right) \right) ^2=\rho _{\infty }^2\gamma ^{2n} \end{aligned}$$

(25)

which can be used to solve $\gamma$ for a given $\rho _{\infty }$. Table 4 shows the solutions of $\gamma$ for several specific $\rho _{\infty }$ in the cases $n=2,3,4,5$. Note that Eq. (25) has multiple solutions; the smallest one that meets the requirement of unconditional stability, as shown in Table 3, is selected.

Table 4 $\gamma$ for controllable algorithmic dissipation in the higher-order schemes

So far, the unconditionally stable higher-order accurate schemes with controllable algorithmic dissipation have been developed, whose parameter $\gamma$ can be solved for a given $\rho _{\infty }$ by Eq. (25), $a_p(p=1,2,\cdots ,n)$ are determined by $\gamma$ as shown in Eq. (19), and then $q_j(j=0,1,2,\cdots ,n-1)$ can be obtained by solving Eqs. (12) and (13). These information for the cases $n=2,3,4,5$ are shown in Tables 2,  3 and 4. The special case $n=2$ is identical to the $\rho _{\infty }$-Bathe method [26], whereas the other cases are presented here for the first time. In addition, the accuracy and algorithmic dissipation are discussed in more detail in Sect. 4.

3.2 Conserving schemes

An original intention of the composite methods was to conserve the energy of the system [2], which explains why the trapezoidal rule is utilized in most sub-steps. Existing two- and three-sub-step methods [18, 22, 26] really show preferable energy-conserving characteristic over other single- and multi-step methods. In this work, a simple and general approach to determine the parameters, which enable the n-sub-step composite method to conserve as much low-frequency content as possible, is proposed.

First of all, to be competitive, the method needs to have some basically useful properties, including at least second-order accuracy, which requires

$$\begin{aligned}&a_1=1-n\gamma \end{aligned}$$

(26a)

$$\begin{aligned}&a_2=\frac{1}{2}-n\gamma +\frac{n(n-1)}{2}\gamma ^2 \end{aligned}$$

(26b)

and controllable algorithmic dissipation, achieved by

$$\begin{aligned} a_n^2=\rho _{\infty }^2\gamma ^{2n} \end{aligned}$$

(27)

In addition, unconditional stability also needs to be satisfied, which will be checked last.

To conserve the energy as much as possible, the spectral radius $\rho =\left| A(z)\right|$ should be as close to 1 as possible over the low-frequency range. For the special case $\rho _{\infty }=1$, $\rho$ should remain 1 in the whole frequency domain. For other cases $0\le \rho _{\infty }<1$, the departure of $\rho$ from unit value should be as slow as possible from $\rho (0)=1$. Considering the conservative system ($\xi =0$), this purpose can be realized by making the function $S(\tau )$, defined in Eq. (22), as smooth as possible. It follows that $S(0)=S^{(1)}(0)=S^{(2)}(0)=\cdots =S^{(m)}(0)=0$, where $S^{(m)}(0)$ is the mth-order derivative of $S(\tau )$ at $\tau =0$, and m should be as large as possible. As $S(\tau )$ is a linear polynomial, the condition transforms into its coefficients $c_{2j}(j=0,1,2,\cdots ,m)=0$. To clarify, $c_{2j}(j=0,1,2,\cdots ,n)$ are enumerated as

$$\begin{aligned}&c_0=0 \end{aligned}$$

(28a)

$$\begin{aligned}&c_2=n\gamma ^2-a_1^2+2a_0a_2 \end{aligned}$$

(28b)

$$\begin{aligned}&c_4=\frac{n(n-1)}{2}\gamma ^4-a_2^2+2a_1a_3-2a_0a_4 \end{aligned}$$

(28c)

$$\begin{aligned}&c_6=\frac{n(n-1)(n-2)}{6}\gamma ^6-a_3^2+2a_2a_4-2a_1a_5\nonumber \\&~~~~~~~+2a_0a_6 \end{aligned}$$

(28d)

$$\begin{aligned}&\cdots \end{aligned}$$

(28e)

$$\begin{aligned}&c_{2n-2}=n\gamma ^{2n-2}-a_{n-1}^2+2a_{n-2}a_n \end{aligned}$$

(28f)

$$\begin{aligned}&c_{2n}=\gamma ^{2n}-a_n^2 \end{aligned}$$

(28g)

From Eqs. (26) and (27), we can obtain $c_2=0$ and $c_{2n}=(1-\rho _{\infty }^2)\gamma ^{2n}\ge 0$, respectively. For the case $n=2$, the conditions on accuracy and algorithmic dissipation are enough to determine all parameters, resulting again in the $\rho _\infty$-Bathe method [26]. For other cases with $n>2$, the $n-2$ remaining parameters, $a_3$, $a_4$, $\cdots$, $a_{n-1}$ and $\gamma$, are obtained by solving the equations $c_4=c_6=\cdots =c_{2n-2}=0$. The values of these parameters for the cases $n=3,4,5$ are shown in Table 5, where the set with $\gamma$ close to $\frac{1}{2n}$ is selected, which requires $a_n=\rho _{\infty }\gamma ^n$.

Then all parameters of the conserving schemes have been given by combining Eqs. (12), (13), (26), (27) and $c_4=c_6=\cdots =c_{2n-2}=0$. The resulting scheme of $n=3$ is equivalent to the first sub-family of the three-sub-step method proposed in [23]; the other cases are presented here for the first time.

In particular, when $\rho _{\infty }=1$, the resulting scheme is a n-sub-step method with the trapezoidal rule in all sub-steps, which is supposed to be unconditionally stable in the linear analysis. Empirically, the algorithmic dissipation is acquired by reducing the spectral radius $\rho$, so the dissipative schemes are likely to be also unconditionally stable, and even present more robust stability. For the undamped case ($\xi =0$), the stability can be guaranteed since $S(\tau )=(1-\rho _{\infty }^2)\gamma ^{2n}\tau ^{2n}\ge 0$; for other cases, the stability conditions of the schemes listed in Table 5 are checked one by one by considering $\xi \in (0,1]$ and $\tau \in [0,10000]$ numerically. As expected, $\rho \le 1$ is satisfied at every point in all schemes, so these methods can be said to possess unconditional stability for linear problems. Other properties are discussed in Sect. 4.

Table 5 $a_p(p=3,4,\cdots ,n-1)$ and $\gamma$ for controllable algorithmic dissipation in the conserving schemes

4 Properties

Fig. 1

Percentage amplitude decay for MSSTH(2,3,4,5), G-$\alpha$ and LTS

Fig. 2

Percentage period elongation for MSSTH(2,3,4,5), G-$\alpha$ and LTS

Fig. 3

Percentage amplitude decay for MSSTC(2,3,4,5), G-$\alpha$ and LTS

Fig. 4

Percentage period elongation for MSSTC(2,3,4,5), G-$\alpha$ and LTS

Two sub-families of the n-sub-step composite method have been presented for different purposes. To identify them, the higher-order schemes are referred to as MSSTH(n), and the conserving schemes are MSSTC(n), where MSST means the multi-sub-step composite method which employs the trapezoidal rule in all sub-steps except the last one, H and C are utilized to distinguish the two sub-families, and n is the number of sub-steps.

In this section, the representative methods in the literature, including the single-step generalized-$\alpha$ method [9] (G-$\alpha$) and the linear two-step method [33] (LTS) are also considered for comparison. As the employed methods are all implicit, their computational cost is mainly spent on the iterative calculation when used for nonlinear problems, or the matrix factorization for linear problems. The vector operations brought by the recursive scheme of the method itself is generally considered to have little effect on overall efficiency. Therefore, G-$\alpha$ and LTS are recognized as having equivalent efficiency if the same step size is used. As the composite methods implement a single-step or multi-step scheme in each sub-step, they have the equivalent efficiency to G-$\alpha$ and LTS, if their required number of sub-steps is equal to the number of steps required by G-$\alpha$ and LTS. For this reason, to compare the properties under the close computational costs, the same h/n, where n is the number of sub-steps in the composite methods, and $n=1$ for the G-$\alpha$ and LTS, is used in these methods.

As discussed in Sect. 3, MSSTH(n) has nth-order accuracy under the premises of unconditional stability and controllable algorithmic dissipation. Figures 1 and 2 display the percentage amplitude decay (AD($\%$)) and period elongation (PE($\%$)) respectively, of which the definition can refer to [34], of MSSTH(2,3,4,5), G-$\alpha$ and LTS, considering the undamped case ($\xi =0$). The abscissa is set as $\tau /n$ to compare these methods under the close computational costs.

The results illustrate that the amplitude and period accuracy cannot be improved simultaneously as the order of accuracy increases in MSSTH(n). In terms of amplitude, with a small $\rho _\infty$, the $\rho _\infty$-Bathe method (the same as MSSTH(2)) is the most accurate, and when $0.4<\rho _\infty \le 1$, LTS shows smaller dissipation error, followed by the G-$\alpha$ and the $\rho _\infty$-Bathe method. From Fig. 2, MSSTH(3,4,5) have smaller period error than the second-order methods, and MSSTH(5) is the best among them.

In the same way, the percentage amplitude decay and period elongation of MSSTC(2,3,4,5), G-$\alpha$ and LTS for the undamped case are shown in Figs. 3 and 4, respectively. It can be observed that under the similar efficiency, MSSTC(n) presents higher amplitude and period accuracy with a larger n. The gap is more obvious as $\rho _\infty$ decreases, and when $\rho _\infty =1$, all the schemes have the same properties as the trapezoidal rule. Both G-$\alpha$ and LTS are less accurate than MSSTC(3,4,5) in the low-frequency range.

Fig. 5

Spectral radius for $n=3$

Fig. 6

Spectral radius for $n=4$

Fig. 7

Spectral radius for $n=5$

Fig. 8

Percentage amplitude decay for $n=3$

Fig. 9

Percentage amplitude decay for $n=4$

Fig. 10

Percentage amplitude decay for $n=5$

Fig. 11

Percentage period elongation for $n=3$

Fig. 12

Percentage period elongation for $n=4$

Fig. 13

Percentage period elongation for $n=5$

Besides, with the same n, MSSTH(n) and MSSTC(n) are compared in Figs. 5, 6, 7, 8, 9, 10, 11, 12 and 13, where Figs. 5, 6 and 7 show the spectral radius (SR) of the cases $n=3,4,5$, respectively, Figs. 8, 9 and 10 show the percentage amplitude decay, Figs. 11, 12 and 13 show the percentage period elongation, all considering the undamped case. The generalized Padé approximation [14, 15], referred to as Padé(n), is also employed for comparison. It is known as the most accurate rational approximation of $\text {e}^z$ by using

$$\begin{aligned} A(z)=\frac{(1-\rho _\infty )P_{n-1,n}(z)+2\rho _\infty P_{n,n}(z)}{(1-\rho _\infty )Q_{n-1,n}(z)+2\rho _\infty Q_{n,n}(z)} \end{aligned}$$

(29)

where

$$\begin{aligned}&P_{i,j}(z)=\sum _{p=0}^{i}\frac{i!(j+i-p)!}{(i-p)!(j+i)!}\frac{z^p}{p!} \end{aligned}$$

(30a)

$$\begin{aligned}&Q_{i,j}(z)=\sum _{p=0}^{i}(-1)^p\frac{j!(j+i-p)!}{(j-p)!(j+i)!}\frac{z^p}{p!} \end{aligned}$$

(30b)

Padé(n) has $(2n-1)$th-order accuracy if $0\le \rho _\infty <1$ and (2n)th-order accuracy if $\rho _\infty =1$.

As expected, Figs. 5, 6 and 7 demonstrate that MSSTC(n) preserves wider low-frequency range, followed by Padé(n), and MSSTH(n). Note that MSSTH(n) with $\rho _\infty =1$ exhibits mild algorithmic dissipation in the medium frequency range, so these schemes are not recommended if all frequencies are requested. Figures 8, 9 and 10 also show that MSSTC(n) has the smallest amplitude dissipation in the low-frequency content. The amplitude decay ratio of MSSTC(5) is very close to 0 over $\tau \in \left[ 0,2\right]$. In terms of period accuracy, Figs. 11, 12 and 13 show that Padé(n) is the most accurate, followed by MSSTH(n), and MSSTC(n), consistent with the sequence of the accuracy order.

From the comparison, MSSTC(n) performs really good at conserving the low-frequency content, and its overall accuracy can be improved by using more sub-steps. MSSTH(n) shows higher period accuracy than the second-order methods, whereas its dissipation error is larger in the low-frequency content.

5 Numerical examples

To validate the performance, several numerical examples are solved in this section. As the spectral analysis has revealed the properties based on the linear model, this section focuses more on the application and discussion for nonlinear systems.

5.1 Single degree-of-freedom examples

Firstly, two single degree-of-freedom examples, including a simple linear example and the nonlinear van der Pol’s equation, are solved to check the convergence rate. The $\rho _\infty$-Bathe method, MSSTC(3,4,5) and MSSTH(3,4,5) with $\rho _\infty =0.6$ is employed.

Linear example The linear equation of motion

$$\begin{aligned} \ddot{x}+4x=0, \, x(0)=1, \, {\dot{x}}(0)=1 \end{aligned}$$

(31)

is considered, and the absolute errors of the displacement $x_k$, velocity ${\dot{x}}_k$, and acceleration $\ddot{x}_k$ versus h at $t=10$ are plotted in Fig. 14.

The results are consistent with the accuracy order. That is, MSSTC(n) and MSSTH(n) respectively present second-order and nth-order convergence rate. As a result, the higher-order MSSTH(n) enjoys significant accuracy advantage over the second-order methods. However, when h decreases from $10^{-2}$, it seems that MSSTH(5) cannot maintain fifth-order accuracy. This is because when h is small enough, all effective numbers stored in the computer are exactly precise, so if h continues to decrease, the accumulated rounding error can greatly spoil the numerical precision [31].

Van der Pol’s equation The van der Pol’s equation [19]

$$\begin{aligned}&{\dot{x}}_1=x_2,{\dot{x}}_2=\epsilon ^{-1}((1-x_1^2)x_2-x_1)\nonumber \\&x_1(0)=2,x_2(0)=-\frac{2}{3}+\frac{10}{81}\epsilon -\frac{292}{2187}\epsilon ^2 +\frac{15266}{59049}\epsilon ^3 \end{aligned}$$

(32)

is solved, where $\epsilon$ is an adjustable parameter. For the cases $\epsilon =0.01, 0.001, 0.0001$, the absolute errors of $x_{1,k}$ and $x_{2,k}$ at $t=1$ versus h are plotted in Fig. 15, where the reference solution is obtained by the $\rho _\infty$-Bathe method with $h=10^{-7}$.

From Fig. 15, in most cases, the second- and nth-order convergence rate can be observed from errors of MSSTC(n) and MSSTH(n), respectively, but for the stiffer case of $\epsilon =0.0001$, MSSTH(3) and MSSTH(5) show obvious order reduction in both $x_1$ and $x_2$. It indicates that the accuracy order also depends on the problem to be solved when applied to nonlinear systems. The order reduction also occurs in other higher-order DIRKs when used for nonlinear problems, see Ref. [19]. Nevertheless, MSSTH(n) still shows significant accuracy advantage over the second-order MSSTC(n) with a small step size.

Fig. 14

Convergence rates for the single degree-of-freedom linear example

Fig. 15

Convergence rates for the van der Pol’s equation

Fig. 16

Spring-pendulum model

Fig. 17

Numerical results of the spring-pendulum model ($f(r)=kr$, $k=98.1~\text {N/m}$)

Fig. 18

Numerical results of the spring-pendulum model ($f(r)=kr^3$, $k=98.1~\text {N/m}$)

Fig. 19

Numerical results of the spring-pendulum model ($f(r)=k\tanh {r}$, $k=98.1~\text {N/m}$)

5.2 Multiple degrees-of-freedom examples

In this subsection, some illustrative examples are solved by using the $\rho _\infty$-Bathe method, MSSTC(3,4,5), MSSTH(3,4,5), G-$\alpha$ and LTS. In these methods, the parameter $\rho _\infty$ is set as 0 uniformly, and the same h/n is used for comparison under close computational costs. The reference solutions are obtained by the $\rho _\infty$-Bathe method with an extremely small time step.

Spring-pendulum model As shown in Fig. 16, the spring-pendulum model, where the spring is fixed at one end and with a mass at the free end, is simulated. Its motion equation can be written as

$$\begin{aligned}&m\ddot{r}+f(r)-m(L_0+r){\dot{\theta }}^2-mg\cos {\theta }=0 \end{aligned}$$

(33a)

$$\begin{aligned}&m\ddot{\theta }+\frac{m(2{\dot{r}}{\dot{\theta }}+g\sin {\theta })}{L_0+r}=0 \end{aligned}$$

(33b)

where f(r) denotes the elastic force of the spring and other system parameters are assumed as $m=1~\text {kg}$, $L_0=0.5~\text {m}$, $g=9.81~\text {m/s}^2$. Three kinds of constitutive relations, as

$$\begin{aligned}&f(r)=kr \end{aligned}$$

(34a)

$$\begin{aligned}&f(r)=kr^3 \end{aligned}$$

(34b)

$$\begin{aligned}&f(r)=k\tanh {r} \end{aligned}$$

(34c)

where $k=98.1~\text {N/m}$, are considered. The initial conditions are set as

$$\begin{aligned} r_0=0~\text {m},{\dot{r}}_0=1~\text {m/s},\theta _0=\frac{\pi }{4}~ \text {rad},{\dot{\theta }}_0~\text {rad/s} \end{aligned}$$

(35)

Let $h/n=0.01\ \text {s}$; the numerical solutions of $E-E_0$ (E denotes the system energy and $E_0$ is the initial value), r and $\theta$ for the three cases are summarized in Figs. 17, 18 and 19. From the curves of $E-E_0$, it can be observed that MSSTC(3,4,5) can almost preserve the numerical energy from decaying in all cases, despite the oscillations. MSSTH(5) can preserve more energy than the Bathe method, while G-$\alpha$, LTS, and MSSTH(3,4) show obvious energy-decaying. From the numerical results of r and $\theta$, one can see that with the step size, the numerical solutions of these methods have clearly deviated from the reference solution after a period of simulation. Among these methods, MSSTH(5) predicts the closest solutions to the reference ones, and G-$\alpha$ shows the largest errors. In addition, MSSTC(3,4,5) exhibit good amplitude accuracy thanks to their energy-preserving characteristic. These conclusions are all consistent with the results from linear analysis.

Moreover, to check the algorithmic dissipation, the stiff case, where $f(r)=kr$ ($k=98.1\times 10^{10}~\text {N/m}$), is also simulated with $h/n=0.01~\text {s}$. The numerical results of $E-E_0$, r and $\theta$ are plotted in Fig. 20. The results of r indicate that all employed schemes with $\rho _\infty =0$ can effectively filter out the stiff component in the first few steps. After the initial decaying, MSSTC(3,4,5) can still preserve the remaining energy in the following simulation.

Fig. 20

Numerical results of the spring-pendulum model ($f(r)=kr$, $k=98.1\times 10^{10}~\text {N/m}$)

Slider-pendulum model The slider-pendulum model, shown in Fig. 21, is considered in this case. The slider is constrained by the spring, and one end of the pendulum is hinged to the center of mass of the slider. The motion is described by the differential-algebraic equations

$$\begin{aligned}&m_1\ddot{x}_1+k x_1=-\lambda _1 \end{aligned}$$

(36a)

$$\begin{aligned}&m_2\ddot{x}_2=\lambda _1\end{aligned}$$

(36b)

$$\begin{aligned}&m_2\ddot{y}_2=\lambda _2-m_2g\end{aligned}$$

(36c)

$$\begin{aligned}&J_2\ddot{\theta }=-\frac{L}{2}\lambda _1\cos {\theta }-\frac{L}{2}\lambda _2\sin {\theta }\end{aligned}$$

(36d)

$$\begin{aligned}&x_2-x_1=\frac{L}{2}\sin {\theta }\end{aligned}$$

(36e)

$$\begin{aligned}&y_2=-\frac{L}{2}\cos {\theta } \end{aligned}$$

(36f)

The system parameters are $m_1=m_2=1~\text {kg}$, $L=1~\text {m}$, $J_2=\frac{1}{12}~\text {kg}\cdot \text {m}^2$, $g=9.81~\text {m/s}^2$, $k=1~\text {N/m}$ and $10^{10}~\text {N/m}$ respectively for the compliant and stiff systems. The slider is excited by the initial horizontal velocity $1\ \text {m/s}$.

By using $h/n=0.01\ \text {s}$, the numerical solutions of $E-E_0$, $x_1$ and $\theta$ for the compliant and stiff cases are shown in Figs. 22 and 23, respectively. From the results of $x_1$ and $\theta$, these methods all perform well in terms of accuracy and algorithmic dissipation. However, the numerical energies of MSSTH(4) show a slightly upward trend in the stiff case, so this method cannot give stable results for the problem.

As already discussed in several papers [5, 30], the unconditional stability of a time integration method derived from linear analysis cannot be guaranteed when they are applied to nonlinear problems. For nonlinear problems, the stability of a method depends not only on its recursive scheme, but also on the problem itself. Therefore, it is hard to give a definite conclusion about the stability of a method for general problems. From the numerical results, all employed methods, except MSSTH(4), provide stable results when solving stiff problems and differential-algebraic equations, so they can be said to have relatively strong stability. MSSTH(4) is not recommended for these problems due to its poorer stability.

Fig. 21

Slider-pendulum model

Fig. 22

Numerical results of the slider-pendulum model ($k=1~\text {N/m}$)

Fig. 23

Numerical results of the slider-pendulum model ($k=10^{10}~\text {N/m}$)

N-degree-of-freedom mass-spring system The N-degree-of-freedom mass-spring system [23], shown in Fig. 24, is considered to check the computational efficiency. The system parameters are set as

$$\begin{aligned}&m_i=1~\text {kg},f_i=\sin {t}~\text {N},i=1,2,\cdots ,N \end{aligned}$$

(37a)

$$\begin{aligned}&k_i=\left\{ \begin{aligned}&10^5~\text {N/m},i=1\\&10^5\left[ 1-2(x_i-x_{i-1})^2\right] ~\text {N/m},2\le i\le N \end{aligned} \right. \end{aligned}$$

(37b)

Fig. 24

Mass-spring model

Fig. 25

Computed $x_N$ of the mass-spring model

With zero initial conditions, three cases, $N=500, 1000$ and 1500, are simulated by these methods using $h/n=0.01~\text {s}$. Figure 25 shows the numerical solutions of $x_N$. It follows that with the step size, all methods can provide reliable results. The CPU time and total number of iterations required by these methods in the simulation of $[0,30~\text {s}]$ are summarized in Table 6. With $h/n=0.01~\text {s}$, these methods need to proceed 3000 steps (sub-steps for the composite methods) in the whole simulation. Table 6 shows that in addition to MSSTH(4,5), other methods only require one iteration per step/sub-step, so their computational costs are almost equal to each other. One can also see that the required CPU time is approximately proportional to the number of iterations. MSSTH(4,5), especially MSSTH(4), take slightly longer time than other methods.

To check the generality of this conclusion, the required total number of iterations in the above spring-pendulum and slider-pendulum examples are also listed in Table 7. In the two examples, $h/n=0.01~\text {s}$ is adopted, and the simulation of $[0, 30~\text {s}]$ is also performed. The results indicate that the total numbers of iterations required by the second-order methods are very close in all cases. Although the higher-order methods need more iterations sometimes, the increased numbers, especially in MSSTH(3,5), are not very large in most cases. Therefore, it is reasonable to say that these methods with the same h/n have similar efficiency for nonlinear problems, and the above comparisons in terms of properties are conducted under the close computational costs.

Table 6 CPU time and total number of iterations required by these methods in the mass-spring example

Table 7 Total number of iterations required by these methods in the spring-pendulum and slider-pendulum example

Overall, the numerical examples in this section demonstrate that when applied to nonlinear problems, the proposed methods can still take advantage of their properties, including the energy-conserving characteristic of MSSTC(n), the high-accuracy of MSSTH(n), and the strong dissipation ability of both sub-families. However, MSSTH(n) shows reduced order and energy instability in some examples. From the presented solutions, MSSTH(5) is more recommended in the higher-order sub-family because of its high accuracy and robust stability, whereas MSSTH(4) is not so preferable, since it shows energy-instability and needs more iterations in some examples.

6 Conclusions

In this work, the n-sub-step composite method ($n\ge 2$), which employs the trapezoidal rule in the first $n-1$ sub-steps and a general formula in the last one, is discussed. By optimizing the parameters, the two sub-families, named MSSTC(n) and MSSTH(n), are developed, respectively for the energy-conserving and high-accuracy purposes. From linear analysis, MSSTC(n) and MSSTH(n) are second-order and nth-order accurate, respectively, and they can both achieve unconditional stability with controllable algorithmic dissipation. In MSSTC(n), the purpose of energy-conserving is realized by maximizing the spectral radius in the low-frequency range.

A general approach of parameter optimization, suitable for all schemes with $n\ge 2$, is proposed; in this work, the cases $n=2,3,4,5$ are discussed in detail. When $n=2$, both sub-families reduce to the $\rho _\infty$-Bathe method. As n increases, MSSTC(n) shows higher amplitude and period accuracy; its amplitude accuracy is even higher than that of the $(2n-1)$th-order Padé(n) approximation. MSSTH(3,4,5) exhibits lower period errors than the second-order methods, but their dissipation errors are larger.

The proposed methods are checked on several illustrative examples. The numerical results are mostly consistent with the conclusions from linear analysis. That is, MSSTC(n) can conserve the energy corresponding to the low-frequency content, and MSSTH(n) shows higher-order convergence rate for linear and nonlinear equations. However, in the nonlinear examples, some unexpected situations, such as order reduction and energy instability, emerged in MSSTH(n). In this sub-family, MSSTH(5) is more recommended thanks to its high-accuracy and robust stability, and MSSTH(4) is not so preferable, since it shows energy instability and lower efficiency in these examples. However, these conclusions about nonlinear problems are obtained from the existing numerical results. The theoretical analysis is still desired in the future.