1 Introduction

Nonlinear aeroelastic phenomena affect several types of aeroelastic systems such as flexible wings, helicopter rotor blades and wind turbines. Nonlinear aeroelasticity studies the interactions between inertial, elastic and aerodynamic forces on flexible structures that are exposed to airflow and feature non-negligible nonlinearity [1]. The theory of aeroelasticity is extensively covered in the literature [2,3,4].

The sources of nonlinearity in aeroelastic systems include geometric nonlinearity, structural nonlinearity, flow separation, friction, free-play in actuators, backlash in gears, nonlinear control laws, oscillating shock waves and other nonlinear phenomena [5, 6]. A comprehensive study for such nonlinearities was presented by Lee et al. in [7] together with the derivation of the equations of motion of a 2D airfoil oscillating in pitch and plunge. Dowell et al. [8] summarized the physical basis and the effect of nonlinear aeroelasticity on the flight and its association with limit cycle oscillations (LCO). The effect of structural nonlinearities on the dynamical behavior of the system was investigated in [9, 10]. Aerodynamic nonlinearities were studied by Dowell et al. in [11] using the describing function method. A combination of structural nonlinearity and the nonlinear ONERA stall aerodynamic model was investigated in the aeroelastic response of a nonrotating helicopter blade in the work of Tang et al. [12]. The airfoil model consisted of a NACA 0012 profile (the same used in this paper) with three types of nonlinearities: nonlinear structure linear aerodynamics, linear structure nonlinear aerodynamics and nonlinear structure with nonlinear aerodynamics. CFD-based aeroelastic investigations are described in [13,14,15].

Gilliatt et al. [16] studied structural and aerodynamic nonlinearities arising from stall conditions. Experimental investigation of a NACA0012 airfoil undergoing stall flutter oscillations in a low-speed wind tunnel was presented by Dimitriadis et al. in [17]. Santos et al. [18] carried out an experimental and numerical study of a NACA 0012 airfoil under the influence of structural and aerodynamic nonlinearities due to dynamic stall effects at high angles of attack. Jian et al. [19] developed a first-order, state-space model by combining a geometrically exact, nonlinear beam model with nonlinear ONERA-EDLIN dynamic stall model to investigate high-aspect-ratio flexible wings.

Nonlinear aeroelastic forces can produce complex bifurcation scenarios leading to chaotic oscillations. Sarkar et al. [20] observed a period-doubling route to chaos in the case of a 2-DOF aeroelastic model using the ONERA nonlinear aerodynamic dynamic stall model. In a recent study, Bose et al. [21] confirmed the Ruelle–Takens–Newhouse quasi-periodic route to chaos in a nonlinear aeroelastic system.

Flexible aeroelastic systems can lose stability by flutter or divergence depending on the system parameters. When flexible airfoils experience wind excitation, dynamic stability loss (called flutter instability), triggered by a Hopf bifurcation, may occur. The flow velocity for which the instability starts is called flutter velocity.

The starting point of the paper by Kalmár-Nagy et al. [22] was the observation that the coefficient of lift function can be well approximated by a piecewise linear function. Piecewise linear functions are often used to model free-play, nonlinear stiffness, nonlinear aerodynamic forces, and hysteresis nonlinearity in aeroelastic systems [10, 23,24,25]. Free-play nonlinearity is often studied in aeroelasticity, as it is a common occurrence within the actuated control surface [26]. Sales et al. [27] studied an aeroviscoelastic system with a nonsmooth, free-play-type nonlinearities in their control surface. The dynamic aeroelastic response of multi-segmented hinged wings with bilinear stiffness characteristics was studied theoretically and experimentally in [28]. Dimitriadis et al. [29] investigated a complex mathematical wing model in unsteady flow with a piecewise linear nonlinearity.

Piecewise nonlinear functions are also used to analyze aeroelastic systems with complex piecewise nonlinear structural stiffness [30, 31]. Sun et al. [32] approximated the static lift coefficient by a fourth-order piecewise polynomial function. A piecewise aerodynamic flutter equation was established by Goodman in [33], which uses a piecewise aerodynamic interpolation function. Replacing the nonlinearities of a dynamical system with piecewise linear makes the problem more analytically tractable. The phase space of piecewise linear systems consists of regions, each of which has linear dynamic equations of motion [34]. Magri et al. [35] proved that a typical airfoil section applying nonsmooth definition of the dynamic stall model can generate a nonsmooth Hopf bifurcation, similar to a rapid bifurcation.

Once the dynamics of the system is understood (at least on a rudimentary level), engineering questions can be addressed. Important questions are how to reduce the oscillation amplitude for a given range of parameters or how to control the flutter instability in an aeroelastic system. The linear tuned vibration absorber (LTVA), developed by Frahm [36], is a classical passive device for controlling flutter instabilities. This device consists of a small lumped mass attached to the primary structure through a linear spring and a damper. The first detailed study of properties and optimization of LTVAs was presented by Den Hartog [37]. If its parameters are correctly tuned, the LTVA can significantly shift the flutter speed [38]. The parameter optimization of nonlinear tuned vibration absorber for flutter control was carried out by Mahler et al. in [39]. Kassem et al. [40] presented an analytical and experimental study of an active dynamic vibration absorber for flutter control.

This work investigates the dynamics of a 2-DOF piecewise linear aeroelastic system for a broad range of the angle of attack. In Sect. 2, dimensional governing equations of the 2-DOF aeroelastic system are presented. The piecewise linear modeling of quasi-steady aerodynamic forces is summarized in Sect. 3. The piecewise linear models of lift coefficient as the function of the effective angle of attack were determined for NACA \(0009,\,0012,\,23012\) profiles. Section 4 is devoted to the nondimensionalization of the governing equations. In Sect. 5, the equilibrium points of the aeroelastic system are determined. The stability of the equilibria is investigated in Sect. 6. In Sect. 7, the classical and discontinuity-induced equilibrium bifurcations are studied. In the case of NACA 0012 and 23012 stall flutter oscillations occurred. A linear tuned vibration absorber was attached to the primary aeroelastic system to eliminate these oscillations. The effect of the absorber parameters is studied in Sect. 8. The parameter optimization of the vibration absorber is investigated, showing in particular how the stall flutter can be eliminated using a well-tuned absorber. The summary and conclusions are presented in Sect. 9.

2 The aeroelastic model

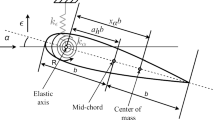
We analyze the two-degrees-of-freedom (2-DOF) aeroelastic system shown in Fig. 1. Coordinates y and \(\alpha \) describe the vertical (plunge) displacement (positive downward) and angular (pitch) displacement (positive in the clockwise direction), respectively. The semichord of the airfoil is denoted by b. In this model, we assume that the center of gravity (denoted by \(\varvec{\mathrm {G}}\)) is located at three quarters of the chord length. The elastic axis passes through the center of gravity. The mass of the wing is m, and \(I_\mathrm{cg}\) is the moment of inertia about the center of gravity. The linear spring constant is \(k_{y}\), and the damping is \(c_{y}\) for the plunge DOF. The linear spring constant is \(k_{\alpha }\), and the damping is \(c_{\alpha }\) for the pitch DOF. The aerodynamic lift force (positive upward) and moment (positive in the clockwise direction) applied at the airfoils aerodynamic center (denoted by \(\varvec{\mathrm {A}}\)) are L and M.

Fig. 1
figure 1

The 2-DOF pitch–plunge aeroelastic model

Full size image

The system equations are given by

$$\begin{aligned} \begin{array} [c]{l} m\ddot{y}+c_{y}{\dot{y}}+k_{y}y=-{L}\left( C_{l}\left( \alpha _\mathrm{eff}\right) \right) ,\\ I_\mathrm{cg}\ddot{\alpha }+c_{\alpha }{\dot{\alpha }}+k_{\alpha }\alpha ={M}\left( C_{l}\left( \alpha _\mathrm{eff}\right) \right) . \end{array} \end{aligned}$$
(1)

The aerodynamic lift force L and moment M are functions of the lift coefficient \(C_{l}\). The lift coefficient is a function of the effective angle of attack \(\alpha _\mathrm{eff}\), which takes into account the instantaneous motion of the system and the freestream velocity \(U>0\) as

$$\begin{aligned} \alpha _\mathrm{eff}=\alpha +\frac{{\dot{y}}}{U}. \end{aligned}$$
(2)

The system parameters used in this study were taken from the paper by Gilliatt et al. [41] and are summarized in Table 1.

Table 1 System parameters [41]
Full size table

3 Aerodynamic forces

The aerodynamic lift force and moment on the right-hand side of Eq. (1) are assumed to be proportional to the lift coefficient, i.e.,

$$\begin{aligned} \begin{array} [c]{l} L\left( C_{l}\left( \alpha _\mathrm{eff}\right) \right) =\rho U^{2}Sb\,C_{l} \left( \alpha _\mathrm{eff}\right) ,\\ M\left( C_{l}\left( \alpha _\mathrm{eff}\right) \right) =\rho U^{2}Sb^{2} \,C_{l}\left( \alpha _\mathrm{eff}\right) , \end{array} \end{aligned}$$
(3)

where \(\rho \) is the air density, S is the wing span, and b is the semichord. The measured static lift coefficient versus effective angle of attack for different airfoil sections [42, 43] is illustrated in Fig. 2.

Fig. 2
figure 2

Data points and piecewise fitted models

Full size image

Kalmár-Nagy et al. [22] introduced a piecewise linear continuous model for the aerodynamic lift coefficient. Here we extend this model for a larger range of \(\alpha _\mathrm{eff}\). The piecewise linear continuous model consists of five regions \(( -\infty ,\alpha _\mathrm{switch}^{-}] \), \([ \alpha _\mathrm{switch}^{-},\alpha _\mathrm{stall}^{-}] \), \([ \alpha _\mathrm{stall}^{-} ,\alpha _\mathrm{stall}^{+}] \), \([ \alpha _\mathrm{stall}^{+},\alpha _\mathrm{switch}^{+}] \), \([ \alpha _\mathrm{switch}^{+},\infty ) \) as shown in Fig. 3.

Fig. 3
figure 3

Piecewise linear model of the aerodynamic lift coefficient

Full size image

The lift coefficient is given as the piecewise linear function

$$\begin{aligned} C_{l}({\alpha _\mathrm{eff}})=\left\{ \begin{array} [c]{ll} c_{2}^{-}\alpha _\mathrm{eff}+d_{2}^{-}\quad &{} \alpha _\mathrm{eff}\in \left( -\infty ,\alpha _\mathrm{switch}^{-}\right] ,\\ c_{1}^{-}\alpha _\mathrm{eff}+d_{1}^{-}\quad &{} \alpha _\mathrm{eff}\in \left[ \alpha _\mathrm{switch}^{-},\alpha _\mathrm{stall}^{-}\right] ,\\ c_{0}\alpha _\mathrm{eff}+d_{0}\quad &{} \alpha _\mathrm{eff}\in \left[ \alpha _\mathrm{stall} ^{-},\alpha _\mathrm{stall}^{+}\right] ,\\ c_{1}^{+}\alpha _\mathrm{eff}+d_{1}^{+}\quad &{} \alpha _\mathrm{eff}\in \left[ \alpha _\mathrm{stall}^{+},\alpha _\mathrm{switch}^{+}\right] ,\\ c_{2}^{+}\alpha _\mathrm{eff}+d_{2}^{+}\quad &{} \alpha _\mathrm{eff}\in \left[ \alpha _\mathrm{switch}^{+},\infty \right) . \end{array} \right. \end{aligned}$$
(4)

Parameter \(\alpha _\mathrm{stall}^{+}\) characterizes the stall condition for positive \(\alpha _\mathrm{eff}\) at which lift starts to decrease as \(\alpha _\mathrm{eff}\) is increased. Parameter \(\alpha _\mathrm{switch}^{+}\) corresponds to the switching point at which the slope of \(C_{l}\) starts to increase again. The negative angles of attack \(\alpha _\mathrm{stall}^{-}\) and \(\alpha _\mathrm{switch}^{-}\) are defined analogously. We also impose the following continuity constraints to hold

$$\begin{aligned}{}\begin{array}[c]{l} c_{2}^{-}\alpha _\mathrm{switch}^{-}+d_{2}^{-}=c_{1}^{-}\alpha _\mathrm{switch}^{-}+d_{1} ^{-},\\ c_{1}^{-}\alpha _\mathrm{stall}^{-}+d_{1}^{-}=c_{0}\alpha _\mathrm{stall}^{-}+d_{0},\\ c_{0}\alpha _\mathrm{stall}^{+}+d_{0}\,\,\,=c_{1}^{+}\alpha _\mathrm{stall}^{+}+d_{1} ^{+},\\ c_{1}^{+}\alpha _\mathrm{switch}^{+}+d_{1}^{+}=c_{2}^{+}\alpha _\mathrm{switch}^{+}+d_{2} ^{+}. \end{array} \end{aligned}$$
(5)

Symmetric profiles give rise to an odd coefficient of lift function with parameters

$$\begin{aligned}{}\begin{array}[c]{c} \alpha _\mathrm{stall}^{+}=-\alpha _\mathrm{stall}^{-}=\alpha _\mathrm{stall},\\ \alpha _\mathrm{switch}^{+}=-\alpha _\mathrm{switch}^{-}=\alpha _\mathrm{switch},\\ d_{0}=0,\\ c_{1}^{+}=c_{1}^{-}=c_{1},\quad d_{1}^{+}=-d_{1}^{-}=d_{1},\\ c_{2}^{+}=c_{2}^{-}=c_{2},\quad d_{2}^{+}=-d_{2}^{-}=d_{2}. \end{array} \end{aligned}$$
(6)

The piecewise linear models of the lift coefficient for the NACA 0012, 0009 and 23012 profiles are shown in Fig. 2. The parameters \(c_{0},d_{0},c_{1}^{\pm },d_{1}^{\pm },c_{2}^{\pm },d_{2}^{\pm }\) were determined by least square method using piecewise linear model (4) and continuity constraints (5). The parameters are given in Table 2. We point out that the NACA 0012, 0009 profiles are symmetric, while NACA 23012 is asymmetric.

Table 2 Piecewise linear fit parameters
Full size table

In the next section, the governing nondimensional equations are derived for symmetric airfoil profiles (for the nonsymmetric case the derivation can be done similarly).

4 Nondimensional equations for symmetric profiles

Nondimensionalization results in a better understanding of the physical phenomenon (via the nondimensional groups obtained) and in a reduction of system parameters [44]. Following [22] we choose the length scale \({\mathcal {L}}\), the timescale \({\mathcal {T}}\), and the nondimensional freestream velocity \(\mu >0\) as

$$\begin{aligned} {\mathcal {L}}= & {} \sqrt{\frac{I_\mathrm{cg}}{\rho b^{2}S}},\quad {\mathcal {T}}=\sqrt{\frac{m}{k_{y}}},\nonumber \\ \mu= & {} \frac{U}{{\mathcal {L}}/{\mathcal {T}}}=\sqrt{\frac{m\rho b^{2}S}{k_{y}I_\mathrm{cg}}}U. \end{aligned}$$
(7)

These scales yield the nondimensional plunge \({\hat{y}}=y/{\mathcal {L}}\), the nondimensional time \(\tau =t/{\mathcal {T}}\). The derivative with respect to the nondimensional time is denoted by \(()^{\prime }=\mathrm {d()}/\mathrm {d}\tau \). The nondimensional effective angle of attack can now be expressed as

$$\begin{aligned} \alpha _\mathrm{eff}=\alpha +\frac{1}{\mu }{\hat{y}}^{\prime }. \end{aligned}$$
(8)

The nondimensional form of Eq. (1) is

$$\begin{aligned}{}\begin{array}[c]{l} {\hat{y}}^{\prime \prime }+p_{1}{\hat{y}}^{\prime }+{\hat{y}}=-p_{2}\mu ^{2}C_{l} \left( \alpha +\frac{1}{\mu }{\hat{y}}^{\prime }\right) ,\\ {\alpha }^{\prime \prime }+p_{3}{\alpha }^{\prime }+p_{4}\alpha =\mu ^{2}C_{l} \left( \alpha +\frac{1}{\mu }{\hat{y}}^{\prime }\right) , \end{array} \end{aligned}$$
(9)

where the nondimensional parameters \(p_{1},\) \(p_{2},\) \(p_{3}\) and \(p_{4}\) are

$$\begin{aligned} p_{1}= & {} \frac{c_{y}}{\sqrt{mk_{y}}},\quad p_{2}=\frac{\sqrt{\rho I_\mathrm{cg}S}}{m},\nonumber \\ p_{3}= & {} \frac{c_{\alpha }}{I_\mathrm{cg}}\sqrt{\frac{m}{k_{y}}},\quad p_{4}=\frac{k_{\alpha }m}{I_\mathrm{cg}k_{y}}. \end{aligned}$$
(10)

Using trilinear approximation (4) of the lift coefficient for symmetric profiles (see Eq. (6)), we obtain the following equations:for \(|\alpha _\mathrm{eff}|\le \alpha _\mathrm{stall}\)

$$\begin{aligned}{}\begin{array}[c]{l} {\hat{y}}^{\prime \prime }+(p_{1}+p_{2}\mu c_{0}){\hat{y}}^{\prime }+{\hat{y}}+p_{2} \mu ^{2}c_{0}\alpha =0,\\ {\alpha }^{\prime \prime }+p_{3}{\alpha }^{\prime }+(p_{4}-\mu ^{2}c_{0})\alpha -\mu c_{0}{\hat{y}}^{\prime }=0, \end{array} \end{aligned}$$
(11)

for \(\alpha _\mathrm{stall}\le |\alpha _\mathrm{eff}|\le \alpha _\mathrm{switch}\)

$$\begin{aligned}&{\hat{y}}^{\prime \prime }+(p_{1}+p_{2}\mu c_{1}){\hat{y}}^{\prime }+{\hat{y}}+p_{2} \mu ^{2}c_{1}\alpha \nonumber \\&\quad +\mathrm {sgn}(\alpha _\mathrm{eff})p_{2}\mu ^{2}d_{1}=0,\nonumber \\&{\alpha }^{\prime \prime }+p_{3}{\alpha }^{\prime } +(p_{4}-\mu ^{2}c_{1})\alpha -\mu c_{1}{\hat{y}}^{\prime }\nonumber \\&\quad -\mathrm {sgn}(\alpha _\mathrm{eff})\mu ^{2}d_{1}=0, \end{aligned}$$
(12)

and for \(\alpha _\mathrm{switch}\le |\alpha _\mathrm{eff}|\)

$$\begin{aligned}&{\hat{y}}^{\prime \prime }+(p_{1}+p_{2}\mu c_{2}){\hat{y}}^{\prime }+{\hat{y}}+p_{2} \mu ^{2}c_{2}\alpha \nonumber \\&\quad +\mathrm {sgn}(\alpha _\mathrm{eff})p_{2}\mu ^{2}d_{2}=0,\nonumber \\&{\alpha }^{\prime \prime }+p_{3}{\alpha }^{\prime }+(p_{4}-\mu ^{2}c_{2})\alpha -\mu c_{2}{\hat{y}}^{\prime }\nonumber \\&\quad -\mathrm {sgn}(\alpha _\mathrm{eff})\mu ^{2}d_{2}=0. \end{aligned}$$
(13)

We introduce the state vector

$$\begin{aligned} {\varvec{x}}= \begin{bmatrix} {\hat{y}}\\ {\hat{y}}^{\prime }\\ \alpha \\ \alpha ^{\prime } \end{bmatrix} , \end{aligned}$$
(14)

the system matrices

$$\begin{aligned} {\varvec{A}}_{k}= \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0\\ -1 &{} -(p_{1}+p_{2}\mu c_{k}) &{} -p_{2}\mu ^{2}c_{k} &{} 0\\ 0 &{} 0 &{} 0 &{} 1\\ 0 &{} \mu c_{k} &{} -(p_{4}-\mu ^{2}c_{k}) &{} -p_{3} \end{bmatrix} ,\,\,\,k=0,1,2, \end{aligned}$$
(15)

and translation vectors

$$\begin{aligned} {\varvec{b}}_{k}= \begin{bmatrix} 0\\ -p_{2}\mu ^{2}d_{k}\\ 0\\ \mu ^{2}d_{k} \end{bmatrix} ,\,\,\,k=1,2. \end{aligned}$$
(16)

Equations (11)–(13) can now be concisely written as a collection of affine systems, together with their domains of validity

$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{A}}_{2}{\varvec{x}}-{\varvec{b}} _{2},\qquad {\varvec{x}}\in \Omega _{2}^{-}\,\cup \,\Sigma _{2}^{-}, \end{aligned}$$
(17)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{A}}_{1}{\varvec{x}}-{\varvec{b}} _{1},\qquad {\varvec{x}}\in \Sigma _{2}^{-}\,\cup \,\Omega _{1}^{-}\,\cup \,\Sigma _{1}^{-}, \end{aligned}$$
(18)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{A}}_{0}{\varvec{x}},\qquad {\varvec{x}} \in \Sigma _{1}^{-}\,\cup \,\Omega _{0}\,\cup \,\Sigma _{1}^{+}, \end{aligned}$$
(19)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{A}}_{1}{\varvec{x}}+{\varvec{b}} _{1},\qquad {\varvec{x}}\in \Sigma _{1}^{+}\,\cup \,\Omega _{1}^{+}\,\cup \,\Sigma _{2}^{+}, \end{aligned}$$
(20)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{A}}_{2}{\varvec{x}}+{\varvec{b}} _{2},\qquad {\varvec{x}}\in \Sigma _{2}^{+}\,\cup \,\Omega _{2}^{+}, \end{aligned}$$
(21)

where the domains of subsystems (17)–(21) are given by

$$\begin{aligned} \Omega _{2}^{-}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu }\in \left( -\infty ,-\alpha _\mathrm{switch}\right) \right\} , \end{aligned}$$
(22)
$$\begin{aligned} \Omega _{1}^{-}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu }\in \left( -\alpha _\mathrm{switch},-\alpha _\mathrm{stall}\right) \right\} , \end{aligned}$$
(23)
$$\begin{aligned} \Omega _{0}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\alpha +\frac{\hat{y}^{\prime }}{\mu }\in \left( -\alpha _\mathrm{stall},\alpha _\mathrm{stall}\right) \right\} , \end{aligned}$$
(24)
$$\begin{aligned} \Omega _{1}^{+}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\alpha +\frac{\hat{y}^{\prime }}{\mu }\in \left( \alpha _\mathrm{stall},\alpha _\mathrm{switch}\right) \right\} , \end{aligned}$$
(25)
$$\begin{aligned} \Omega _{2}^{+}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\alpha +\frac{\hat{y}^{\prime }}{\mu }\in \left( \alpha _\mathrm{switch},\infty \right) \right\} . \end{aligned}$$
(26)

These domains are separated by the switching planes defined by

$$\begin{aligned} \Sigma _{1}^{\pm }:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu }=\pm \alpha _\mathrm{stall}\right\} , \end{aligned}$$
(27)
$$\begin{aligned} \Sigma _{2}^{\pm }:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{4}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu }=\pm \alpha _\mathrm{switch}\right\} . \end{aligned}$$
(28)

With these pairwise disjoint sets, the full state space \({\mathbb {R}}^{4}\) can be decomposed as

$$\begin{aligned} {\mathbb {R}}^{4}= & {} \Omega _{2}^{-}\cup \Sigma _{2}^{-}\cup \Omega _{1}^{-}\cup \Sigma _{1}^{-}\nonumber \\&\cup \,\Omega _{0}\cup \Sigma _{1}^{+}\cup \Omega _{1}^{+}\cup \Sigma _{2}^{+}\cup \Omega _{2}^{+}. \end{aligned}$$
(29)
Fig. 4
figure 4

The admissible equilibria of the symmetric aeroelastic models

Full size image

5 Equilibrium points

The equilibrium points of system (17)–(21) are formally given by \(\varvec{{\dot{x}}}={\varvec{0}}\). Clearly, an equilibrium point only exists if it is inside the corresponding domain of validity. Following Di Bernardo et al. [45] we refer to such an equilibrium point as admissible. We call an equilibrium point virtual if it is not admissible (i.e., it satisfies \(\varvec{{\dot{x}}}={\varvec{0}}\) but falls outside the domain of validity). Virtual equilibria play an important role in organizing the dynamics of the corresponding region [46].

The admissible equilibrium points of system (17)–(21) are

$$\begin{aligned} {\varvec{E}}_{0}= & {} {\varvec{0}},\qquad {\varvec{E}}_{0}\in \Sigma _{1} ^{-}\,\cup \,\Omega _{0}\,\cup \,\Sigma _{1}^{+}, \end{aligned}$$
(30)
$$\begin{aligned} {\varvec{E}}_{1}^{\pm }= & {} \mp {\varvec{A}}_{1}^{-1}{\varvec{b}}_{1}=\mp \frac{d_{1}\mu ^{2}}{c_{1}\mu ^{2}-p_{4}} \begin{bmatrix} -p_{2}p_{4}\\ 0\\ 1\\ 0 \end{bmatrix},\nonumber \\&{\varvec{E}}_{1}^{\pm }\in \Sigma _{1}^{\pm }\,\cup \,\Omega _{1}^{\pm }\,\cup \,\Sigma _{2}^{\pm }, \end{aligned}$$
(31)
$$\begin{aligned} {\varvec{E}}_{2}^{\pm }= & {} \mp {\varvec{A}}_{2}^{-1}{\varvec{b}}_{2}=\mp \frac{d_{2}\mu ^{2}}{c_{2}\mu ^{2}-p_{4}} \begin{bmatrix} -p_{2}p_{4}\\ 0\\ 1\\ 0 \end{bmatrix},\nonumber \\&{\varvec{E}}_{2}^{\pm }\in \Sigma _{2}^{\pm }\,\cup \,\Omega _{2}^{\pm } . \end{aligned}$$
(32)

We express the admissibility conditions embedded in Eqs. (30 )–(32) in terms of the system parameters.

$$\begin{aligned}&\varvec{E_{0}}\,\text {is always admissible for symmetric airfoil profiles,}\nonumber \\ \end{aligned}$$
(33)
$$\begin{aligned}&{\varvec{E}}_{1}^{+}\,\text {is admissible if}\,\quad \alpha _\mathrm{stall}\nonumber \\&\quad \le -\dfrac{d_{1}\mu ^{2}}{c_{1}\mu ^{2}-p_{4}}\le \alpha _\mathrm{switch}, \end{aligned}$$
(34)
$$\begin{aligned}&{\varvec{E}}_{2}^{+}\,\text {is admissible if}\quad \alpha _\mathrm{switch}\nonumber \\&\quad \le -\dfrac{d_{2}\mu ^{2}}{c_{2}\mu ^{2}-p_{4}}. \end{aligned}$$
(35)

From admissibility condition (34) we obtain that equilibrium \({\varvec{E}}_{1}^{+}\) is admissible if \(\mu \in [\mu _{1},\mu _{2}]\), where

$$\begin{aligned} \begin{array} [c]{l} \mu _{1}=\sqrt{\dfrac{p_{4}\alpha _\mathrm{stall}}{d_{1}+c_{1}\alpha _\mathrm{stall}}},\\ \mu _{2}=\sqrt{\dfrac{p_{4}\alpha _\mathrm{switch}}{d_{1}+c_{1}\alpha _\mathrm{switch}}}. \end{array} \end{aligned}$$
(36)

One can utilize continuity condition (5) and symmetry condition (6) to express \(\mu _{1}\) as

$$\begin{aligned} \mu _{1}=\sqrt{\dfrac{p_{4}}{c_{0}}}. \end{aligned}$$
(37)

Let us define (provided \(c_{2}>0\))

$$\begin{aligned} \mu _{A}=\sqrt{\dfrac{p_{4}}{c_{2}}}. \end{aligned}$$
(38)

From condition (35) we find that equilibrium \({\varvec{E}}_{2}^{+}\) is admissible in \(\mu \,\in \,(\mu _{A},\mu _{2}]\) (\(\mu \,\in \,[\mu _{2},\mu _{A})\)) if \(\mu _{A}<\mu _{2}\) (\(\mu _{A}>\mu _{2}\)).

Systems (17)–(21) is symmetric; therefore, \({\varvec{E}}_{1} ^{-}\) and \({\varvec{E}}_{2}^{-}\) have the same admissibility range of \(\mu \) as \({\varvec{E}}_{1}^{+}\) and \({\varvec{E}}_{2}^{+}\).

The admissible equilibria of system (17)–(21) in the \((\mu ,\alpha )\) plane are illustrated in Fig. 4 for the parameters of the NACA 0012 and NACA 0009 profiles (listed in Tables 1 and 2). Even though the derivation here does not include formulae for asymmetric profiles, we nevertheless show admissible equilibria for the aerodynamic parameters of the asymmetric NACA 23012 profile in Fig. 5. In Figs. 4 and 5 the solid lines correspond to the admissible equilibrium points, and the dotted lines are the switching lines defined in Eqs. (27) and (28).

Fig. 5
figure 5

The admissible equilibria of the asymmetric aeroelastic model NACA 23012

Full size image

6 Classical stability of equilibria

In this section the asymptotic stability of equilibrium points (30)–(32) is investigated (these correspond to symmetric profiles). We apply the Liénard–Chipart criterion [47] to the characteristic polynomials \(R_{k} (\lambda ,\mu )\) of the coefficient matrices \({\varvec{A}}_{k}\) given in Eq. (15) to determine the necessary and sufficient conditions for asymptotic stability. The stability criterion of Liénard and Chipart expresses the necessary and sufficient conditions for the stability of polynomials in terms of the coefficients and the so-called Hurwitz determinants.

Theorem (Stability Criterion of Liénard and Chipart [47]): Necessary and sufficient conditions for all the roots of the real nth-degree polynomial \(R(\lambda )=\) \(\lambda ^{n} +a_{1}\lambda ^{n-1}+\cdots +a_{n-1}\lambda +a_{n},\) to have negative real parts, can be given in any one of the following forms:

$$\begin{aligned} \begin{array}{ll} 1)\quad a_{n} &{}>0,\,a_{n-2}>0,\ldots ;\Delta _{1}>0,\,\Delta _{3}>0,\ldots \\ 2)\quad a_{n} &{}>0,\,a_{n-2}>0,\ldots ;\Delta _{2}>0,\,\Delta _{4}>0,\ldots \\ 3)\quad a_{n} &{}>0;\,a_{n-1}>0,\,a_{n-3}>0,\ldots ;\Delta _{1}>0,\,\Delta _{3}>0,\ldots \\ 4)\quad a_{n} &{}>0;\,a_{n-1}>0,\,a_{n-3}>0,\ldots ;\Delta _{2}>0,\,\Delta _{4}>0,\ldots \end{array}\nonumber \\ \end{aligned}$$
(39)

Here

$$\begin{aligned} \Delta _{i}=\left| \begin{array} [c]{cccccc} a_{1} &{}\quad a_{3} &{}\quad a_{5} &{}\quad \dots &{}\quad \, &{}\quad \,\\ 1 &{}\quad a_{2} &{}\quad a_{4} &{}\quad \dots &{}\quad \, &{}\quad \,\\ 0 &{}\quad a_{1} &{}\quad a_{3} &{}\quad \dots &{}\quad \, &{}\quad \,\\ 0 &{}\quad 1 &{}\quad a_{2} &{}\quad a_{4} &{}\quad \, &{}\quad \,\\ \, &{}\quad \, &{}\quad \, &{}\quad \, &{}\quad \ddots &{}\quad \,\\ \, &{}\quad \, &{}\quad \, &{}\quad \, &{}\quad \, &{}\quad a_{i} \end{array} \right| ,\quad (a_{k}=0\,\mathrm {for}\,k>n) \nonumber \\ \end{aligned}$$
(40)
Fig. 6
figure 6

The expressions \(a_{2}(k,\mu ),\,a_{4}(k,\mu ),\Delta _{1}(k,\mu )\) and \(\Delta _{3}(k,\mu )\) as the function of \(\mu \)

Full size image
Fig. 7
figure 7

Typical trajectories a before and b after the first-border collision

Full size image

are the Hurwitz determinant of order \(i,\,\)e.g.,

$$\begin{aligned} \Delta _{1}= & {} a_{1}, \end{aligned}$$
(41)
$$\begin{aligned} \Delta _{3}= & {} \begin{vmatrix} a_{1}&\quad a_{3}&\quad a_{5}\\ 1&\quad a_{2}&\quad a_{4}\\ 0&\quad a_{1}&\quad a_{3} \end{vmatrix} , \end{aligned}$$
(42)
$$\begin{aligned} \Delta _{5}= & {} \begin{vmatrix} a_{1}&\quad a_{3}&\quad a_{5}&\quad a_{7}&\quad a_{9}\\ 1&\quad a_{2}&\quad a_{4}&\quad a_{6}&\quad a_{8}\\ 0&\quad a_{1}&\quad a_{3}&\quad a_{5}&\quad a_{7}\\ 0&\quad 1&\quad a_{2}&\quad a_{4}&\quad a_{6}\\ 0&\quad 0&\quad a_{1}&\quad a_{3}&\quad a_{5} \end{vmatrix}. \end{aligned}$$
(43)

In this paper we use the Liénard–Chipart criterion for 4th- and 6th-degree polynomials. The easiest-to-apply Liénard–Chipart criterion for our 4th-degree polynomials \(R(\lambda )=\) \(\lambda ^{4}+a_{1}\lambda ^{3} +a_{2}\lambda ^{2}+a_{3}\lambda + a_{4}\) is

$$\begin{aligned}&a_{2}>0,\,a_{4}>0;\,\,\Delta _{1}=a_{1}>0,\nonumber \\&\Delta _{3}=a_{1}a_{2}a_{3} -a_{1}^{2}a_{4}-a_{3}^{2}>0, \end{aligned}$$
(44)

while for the 6th-degree polynomials \(R(\lambda )=\) \(\lambda ^{6}+a_{1} \lambda ^{5}+a_{2}\lambda ^{4}+a_{3}\lambda ^{3}+a_{4}\lambda ^{2}+a_{5} \lambda +a_{6}\) of Sect. 8 is

$$\begin{aligned} a_{2}> & {} 0,\,a_{4}>0,a_{6}>0;\,\,\nonumber \\ \Delta _{1}= & {} a_{1}>0,\,\Delta _{3}=a_{1}a_{2}a_{3}+a_{1}a_{5}\nonumber \\&-\,a_{1}^{2} a_{4}-a_{3}^{2}>0,\nonumber \\ \Delta _{5}= & {} a_{1}a_{2}a_{3}a_{4}a_{5}-a_{6}^{2}a_{1}^{3}-a_{4}^{2}a_{5} a_{1}^{2}\nonumber \\&+\,a_{3}a_{4}a_{6}a_{1}^{2}+2a_{2}a_{5}a_{6}a_{1}^{2}-a_{2}^{2} a_{5}^{2}a_{1}\nonumber \\&+\,2a_{4}a_{5}^{2}a_{1}-a_{2}a_{3}^{2}a_{6}a_{1}-3a_{3}a_{5}a_{6} a_{1}\nonumber \\&-\,a_{5}^{3}+a_{2}a_{3}a_{5}^{2}-a_{3}^{2}a_{4}a_{5}+a_{3}^{3}a_{6}>0. \end{aligned}$$
(45)

The characteristic polynomials \(R_{k}(\lambda ,\mu )\) of the coefficient matrices \({\varvec{A}}_{k}\) given in Eq. (15) are

$$\begin{aligned} R_{k}(\lambda ,\mu )= & {} \mathrm {det}\left( {\varvec{A}}_{k}-\lambda {\varvec{I}}\right) =\lambda ^{4}+a_{1}(k,\mu )\lambda ^{3}\nonumber \\&+\,a_{2} (k,\mu )\lambda ^{2}+a_{3}(k,\mu )\lambda +a_{4}(k,\mu ),\nonumber \\ \end{aligned}$$
(46)

where

$$\begin{aligned} a_{1}(k,\mu )= & {} p_{3}+p_{1}+p_{2}c_{k}\mu , \end{aligned}$$
(47)
$$\begin{aligned} a_{2}(k,\mu )= & {} 1+p_{4}+p_{1}p_{3}+p_{2}p_{3}c_{k}\mu -c_{k}\mu ^{2}, \end{aligned}$$
(48)
$$\begin{aligned} a_{3}(k,\mu )= & {} p_{3}+p_{1}p_{4}+p_{2}p_{4}c_{k}\mu -p_{1}c_{k}\mu ^{2}, \end{aligned}$$
(49)
$$\begin{aligned} a_{4}(k,\mu )= & {} p_{4}-c_{k}\mu ^{2}. \end{aligned}$$
(50)

Expression \(a_{1}(k,\mu )\) is a linear function of \(\mu \), and \(a_{2}(k,\mu )\), \(a_{3}(k,\mu )\) \(a_{4}(k,\mu )\) are quadratic polynomials of \(\mu \). The Hurwitz determinants expressed by the system parameters are

$$\begin{aligned} \Delta _{1}(k,\mu )= & {} p_{3}+p_{1}+p_{2}c_{k}\mu , \end{aligned}$$
(51)
$$\begin{aligned} \Delta _{3}(k,\mu )= & {} p_{1}p_{3}\Big ( p_{3}^{2}+\left( p_{4}-1\right) ^{2}+p_{1}^{2}p_{4}\nonumber \\&+p_{1}p_{3}\left( p_{4}+1\right) \Big ) \nonumber \\&+p_{2}p_{3}c_{k}\left( 3p_{4}p_{1}^{2}+2p_{3}\left( p_{4}+1\right) p_{1}\right. \nonumber \\&\left. +p_{3}^{2}+\left( p_{4}-1\right) ^{2}\right) \mu \nonumber \\&+p_{3}c_{k}\left( p_{1}\left( p_{4}\left( 3p_{2}^{2}c_{k}-2\right) +2\right) \right. \nonumber \\&\left. +p_{2}^{2}p_{3}\left( p_{4}+1\right) c_{k}-p_{1}^{2}\left( p_{1}+p_{3}\right) \right) \mu ^{2}\nonumber \\&+p_{2}c_{k}^{2}\left( p_{3}\left( p_{4}\left( p_{2}^{2}c_{k}-1\right) +1\right) \right. \nonumber \\&\left. -2p_{3}p_{1}^{2}-\left( p_{3}^{2}+p_{4}-1\right) p_{1}\right) \mu ^{3}\nonumber \\&+c_{k}^{2}\left( p_{1}p_{3}-p_{2}^{2}\big ( p_{1}p_{3}+p_{4}-1\big ) c_{k}\right) \mu ^{4}\nonumber \\&+c_{k}^{3}p_{1}p_{2}\mu ^{5}. \end{aligned}$$
(52)
Fig. 8
figure 8

Typical trajectories a before and b after the rapid bifurcation

Full size image
Fig. 9
figure 9

Typical trajectories a before and b after the second-border collision

Full size image

To determine the point of stability loss (bifurcation) of equilibria (30)–(32), we need to find the smallest positive \(\mu \) for which any of inequalities (44) is violated.

In other words, we are looking for the smallest positive root \(\mu \) of any of

$$\begin{aligned} a_{2}(k,\mu )= & {} 0,\,a_{4}(k,\mu )=0,\,\Delta _{1}(k,\mu )=0,\nonumber \\ \Delta _{3} (k,\mu )= & {} 0,\quad k=0,1,2. \end{aligned}$$
(53)
Fig. 10
figure 10

Bifurcation diagram of the model with symmetric NACA 0012 profile parameters

Full size image
Fig. 11
figure 11

Bifurcation diagrams of admissible equilibria of the model with symmetric NACA 0009 and asymmetric NACA 23012 profile parameters

Full size image

Now we show the results of stability analysis for structural and aerodynamic parameters of the model with a NACA 0012 profile (Tables 1 and 2). For the equilibrium points \({\varvec{E}}_{0} ,\,{\varvec{E}}_{1}^{\pm },\,{\varvec{E}}_{2}^{\pm }\) defined in Eqs. (30)–(32) condition (44) is fulfilled at \(\mu =0\) (see Fig. 6). For \({\varvec{E}}_{0}\) the Hurwitz determinants \(\Delta _{1}(0,\mu ),\,\Delta _{3}(0,\mu )\) are positive for \(\mu \ge 0\), since

$$\begin{aligned} \Delta _{1}(0,\mu )= & {} 0.2025+0.0873\mu>0,\nonumber \\ \Delta _{3}(0,\mu )= & {} 0.0044+0.0027\mu +0.0675\mu ^{2}\nonumber \\&+0.0746\mu ^{3}+0.3145\mu ^{4}+0.4560\mu ^{5}>0.\nonumber \\ \end{aligned}$$
(54)

We observe that

$$\begin{aligned}&a_{4}(0,\mu )<a_{2}(0,\mu )\nonumber \\&\quad =a_{4}(0,\mu )+p_{2}p_{3}c_{0}\mu +p_{1}p_{2}+1, \end{aligned}$$
(55)

and \(a_{2}(0,\mu )\), \(a_{4}(0,\mu )\) are quadratic in \(\mu \) with negative leading coefficients. Hence \(a_{4}(0,\mu )=0\) has the smallest positive root (where equilibrium \({\varvec{E}}_{0}\) loses its stability) and is given by (see Eq. (37))

$$\begin{aligned} \mu _{1}=\sqrt{\frac{p_{4}}{c_{0}}}=0.215. \end{aligned}$$
(56)

For equilibria \({\varvec{E}}_{1}^{\pm }\), it can easily be seen that expressions \(a_{2}(1,\mu ),\,a_{4}(1,\mu )\) are positive for \(\mu \ge 0\). Therefore we need to find the smallest positive root of

$$\begin{aligned} \Delta _{1}(1,\mu )= & {} 0.2025 - 0.1007\mu =0, \nonumber \\ \Delta _{3}(1,\mu )= & {} 0.0044 - 0.0031 \mu - 0.0779 \mu ^{2} + 0.0993 \mu ^{3} \nonumber \\&+ 0.3259\mu ^{4} + 0.7009 \mu ^{5}=0. \end{aligned}$$
(57)

The smallest positive root of Eq. (57) is

$$\begin{aligned} \mu _\mathrm{RB}=0.304. \end{aligned}$$
(58)

At \(\mu =\mu _\mathrm{RB}\) equilibria \({\varvec{E}}_{1}^{\pm }\) undergo a rapid bifurcation (see Sect. 7).

Fig. 12
figure 12

Numerical bifurcation diagrams of the model with symmetric NACA 0012, NACA 0009 and asymmetric NACA 23012 profile parameters

Full size image

For equilibria \({\varvec{E}}_{2}^{\pm }\) the Hurwitz determinants \(\Delta _{1}(2,\mu ), \Delta _{3}(2,\mu )\) are positive for \(\mu \ge 0\) (similarly as in the case of \({\varvec{E}}_{0}\)). From equations \(a_{2}(2,\mu )=0,\,a_{4} (2,\mu )=0\) the smallest positive root is

$$\begin{aligned} \mu _{A}=0.321. \end{aligned}$$
(59)

To summarize, equilibrium \({\varvec{E}}_{0}\) is admissible and asymptotically stable for \(\mu \in [0,\mu _{1})\), stable at \(\mu =\mu _{1}\) and unstable for \(\mu >\mu _{1}\). Equilibria \({\varvec{E}}_{1}^{\pm }\) are admissible and asymptotically stable for \(\mu \in [\mu _{1},\mu _\mathrm{RB})\), stable at \(\mu =\mu _\mathrm{RB}\) and unstable for \(\in (\mu _\mathrm{RB},\mu _{2}]\). Equilibria \({\varvec{E}}_{2}^{\pm }\) are admissible and unstable for \(\mu \in (\mu _{A} ,\mu _{2}]\).

7 Classical and discontinuity-induced bifurcations

The results in this section pertain to structural and aerodynamic parameters of the model with a NACA 0012 profile (Tables 1 and 2). This profile is symmetric; therefore, we only state the results for equilibria with the \(+\) superscript. In piecewise linear aeroelastic system (17)–(21) discontinuity-induced bifurcations [45, 46, 48, 49] are also observed in addition to their classical counterparts: border collision and rapid bifurcation.

Border collision is a boundary equilibrium bifurcation where virtual equilibrium points become admissible. The rapid bifurcation is the abrupt appearance of stable periodic oscillations [50, 51]. The rapid bifurcation of a piecewise linear system is also called a focus-center-limit cycle bifurcation, describing its bifurcation scenario [52]. As shown in Sect. 6, loss of stability of equilibria corresponds to the values of dimensionless freestream velocity

$$\begin{aligned} 0<\mu _{1}<\mu _\mathrm{RB}<\mu _{A}, \end{aligned}$$
(60)

where \(\mu _{1}=0.215,\,\mu _\mathrm{RB}=0.304\) and \(\mu _{A}=0.321\).

The first classical bifurcation occurs when equilibrium \({\varvec{E}}_{0}\) loses stability at \(\mu _{1}=0.215\). At this bifurcation point the roots of the characteristic equation \(R_{0}(\lambda ,\mu _{1})=0\) (Eq. (46)) are

$$\begin{aligned} \lambda _{1}= & {} 0,\,\lambda _{2}=-0.059,\,\lambda _{3}=-0.081- 0.996i,\nonumber \\ \lambda _{4}= & {} -0.081+ 0.996i. \end{aligned}$$
(61)

From these eigenvalues we conclude that equilibrium \({\varvec{E}}_{0}\) loses its stability by undergoing a saddle-node bifurcation.

The second bifurcation of system (17)–(21) is a border collision (BC) of equilibrium \({\varvec{E}}_{1}^{+}\) at \(\mu _{1}=0.215\). This border collision occurs simultaneously with the saddle node bifurcation of equilibrium \({\varvec{E}}_{0}\). At \(\mu =\mu _{1}\) the virtual equilibrium \({\varvec{E}}_{1}^{+}\) becomes admissible in the \(\Omega _{1}^{+}\) region by crossing the switching plane \(\Sigma _{1}^{+}\). The typical trajectories of system (17)–(21) before and after the first-border collision bifurcation (\(\mu _{1}=0.215\)) are illustrated in Fig. 7.

Fig. 13
figure 13

The 2-DOF pitch–plunge model with LTVA

Full size image
Fig. 14
figure 14

Stable and unstable regions of equilibria \({\varvec{F}}_{1}^{\pm }\) in the parameter space \((\eta ,\mu )\), for aerodynamic parameters of the NACA 0012 profile

Full size image
Fig. 15
figure 15

Regions of stable of equilibria \({\varvec{F}}_{1}^{\pm }\) in the parameter space \((\xi ,\eta ,\mu )\) for aerodynamic parameters of the NACA 0012 profile (Table 2)

Full size image
Fig. 16
figure 16

Stable and unstable regions of equilibrium \({\varvec{F}}_{1}^{+}\) in the parameter space \((\eta ,\mu )\), for aerodynamic parameters of the NACA 23012 profile (\(\zeta =0.05\))

Full size image

The third bifurcation is a rapid bifurcation [53] of equilibrium \({\varvec{E}}_{1}^{+}\) at \(\mu _\mathrm{RB}=0.304\). At the rapid bifurcation point the roots of the characteristic equation \(R_{1}(\lambda ,\mu _\mathrm{RB})=0\) (Eq. (46)) are:

$$\begin{aligned} \lambda _{1}= & {} 1.023i,\,\lambda _{2}=-1.023i,\nonumber \\ \lambda _{3}= & {} -0.086- 0.926i,\,\lambda _{4}=-0.086+ 0.926i. \end{aligned}$$
(62)

At this point the pair of complex conjugate roots \(\lambda _{1},\lambda _{2}\) of the characteristic equation \(R_{1}(\lambda ,\mu )=0\) crosses the imaginary axis with positive speed, similarly to the Hopf bifurcation for smooth systems. Figure 8 demonstrates that at the rapid bifurcation the stable spiral equilibrium \({\varvec{E}}_{1}^{+}\) becomes unstable, and a finite-amplitude limit cycle is born. We note that the limit cycle amplitude decreases by increasing the bifurcation parameter \(\mu \).

The limit cycle oscillations are the consequence of the piecewise linear nature of the system as follows. For \(\mu \in [\mu _\mathrm{RB},\mu _{A}]=[0.304,0.321]\) aeroelastic systems (17)–(21) have only unstable admissible equilibria. The stable virtual equilibria \({\varvec{E}}_{2}^{\pm }\) influence the global dynamics by “creating” a limit cycle oscillation after the rapid bifurcation. For \(\mu \in (\mu _{A},\mu _{2}]=(0.321,0.391]\) aeroelastic system (17)–(21) has only unstable admissible equilibrium points; therefore, the limit cycle is created by unstable equilibria. The limit cycle oscillations exist for \(\mu \in [\mu _\mathrm{RB},\mu _{2})=[0.304,0.391)\). At \(\mu _{2}=0.391\) two branches of unstable equilibria intersect. At this point, the amplitude of the limit cycle becomes 0.

The fourth bifurcation of system (17)–(21) is a border collision (BC) of equilibria \({\varvec{E}}_{1}^{+}\) and \({\varvec{E}}_{2}^{+}\) at \(\mu _{2}=0.391\). At this border collision the admissible equilibria \({\varvec{E}}_{1}^{+}\) and \({\varvec{E}}_{2}^{+}\) become virtual by simultaneously crossing the switching plane \(\Sigma _{2}^{+} \). This type of border collision (when two admissible equilibria simultaneously cross the same switching plane and become virtual) is also called as a nonsmooth fold bifurcation of piecewise systems [45].Typical trajectories of system (17 )–(21) before and after the second-border collision bifurcation (\(\mu _{2}=0.391\)) are illustrated in Fig. 9.

The bifurcation diagram of system (17)–(21) is shown in Fig. 10, where the solid line indicates the stable, and the dashed line the unstable equilibrium points. The bifurcation points are denoted by dots.

Even though the derivation here does not include formulae for the NACA 0009 and NACA 23012 profiles, we nevertheless show their bifurcation diagrams in Fig. 11.

The above results were confirmed numerically using Mathematica. The built-in event location method with a maximum step size of 0.001 was used to solve the piecewise linear system. For a given \(\mu \), a one-dimensional Poincaré section (the set of points for which \(\alpha ^{\prime }=0\)) was computed, and these sections were spliced together to obtain the diagrams as a function of \(\mu \) (see Fig. 12). The numerical results were overlaid on top of the bifurcation diagrams of Figs. 10 and 11.

8 Stall flutter reduction with a linear tuned vibration absorber

Stall flutter is a dynamic aeroelastic instability resulting in unwanted oscillatory loads on the structure [54]. Stall flutter of aircraft wings is caused by nonlinear aerodynamic characteristics at very high angles of attack, when a partial or complete separation of the fluid flow from the airfoil occurs periodically during the oscillation [3, 55]. Static divergence can cause asymmetric stall flutter oscillations around nonzero pitch angles [17, 56]. Piecewise linear model (17)–(21) captures the stall flutter aeroelastic phenomenon influenced by the static divergence.

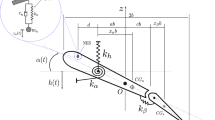
Increasing the nondimensional freestream velocity above the rapid bifurcation point (for NACA 0012 profile aerodynamic parameters) the system starts to oscillate. To eliminate these stall flutter oscillations we applied a linear tuned vibration absorber (LTVA) to the primary system, see Fig. 13. The absorber is attached along the mid-chord of the airfoil at distance z from the center of gravity (G). It is composed of a mass \(m_{ltva}\), a spring of linear stiffness \(k_{ltva}\) and a linear damper \(c_{ltva}\).

Fig. 17
figure 17

Regions of stable of equilibrium \({\varvec{F}}_{1}^{+}\) in the parameter space \((\xi ,\eta ,\mu )\), for aerodynamic parameters of the NACA 23012 profile (\(\zeta =0.05\))

Full size image
Fig. 18
figure 18

Effect of the absorber on the bifurcation points with parameters listed in Eq. (101)

Full size image
Fig. 19
figure 19

Suppression of limit cycle oscillation at \(\mu =0.31>\mu _\mathrm{RB}\) (aerodynamic parameters: NACA 0012 profile, absorber parameters: \(\varepsilon =0.1,\,\xi =0.2,\,\eta =0.05,\,\zeta =0.05\))

Full size image

The equations of motion of the aeroelastic system with the absorber are

$$\begin{aligned}&m\ddot{y}+c_{y} {\dot{y}}+k_{y}y-f(y, {\dot{y}},\alpha ,{\dot{\alpha }},h,{\dot{h}})=-L\left( C_{l}(\alpha _\mathrm {eff})\right) ,\nonumber \\&I_\mathrm {cg}\ddot{\alpha }+c_{\alpha }{\dot{\alpha }}+k_{\alpha }\alpha +zf(y,\dot{y},\alpha , {\dot{\alpha }},h, {\dot{h}})\nonumber \\&\quad =M\left( C_{l} (\alpha _\mathrm {eff})\right) ,\nonumber \\&m_{ltva} \ddot{h}+f(y,{\dot{y}},\alpha , {\dot{\alpha }},h, {\dot{h}})=0, \end{aligned}$$
(63)

where

$$\begin{aligned} f(y,{\dot{y}},\alpha ,{\dot{\alpha }},h,{\dot{h}})= & {} {} c_{ltva}({\dot{h}}-({\dot{y}}-z{\dot{\alpha }}))\nonumber \\&+k_{ltva}\left( h-(y-z{\alpha })\right) . \end{aligned}$$
(64)

Equations (63) and (64) are nondimensionalized by a length scale \({\mathcal {L}}\), a timescale \({\mathcal {T}}\) and a nondimensional freestream velocity \(\mu > 0\), given in Eq. (7). We define the damping ratio \(\xi ={c_{ltva}}/{c_{y}}\), the stiffness ratio \(\eta ={k_{ltva} }/{k_{y}}\) and the mass ratio \(\varepsilon ={m_{ltva}}/{m}\). The nondimensional distance of the absorber from the center of gravity is defined as \(\zeta =z/{\mathcal {L}}\). The nondimensional displacement of the absorber is denoted by \({\hat{h}}={h}/{{\mathcal {L}}}\). The nondimensional equation will be the following

$$\begin{aligned}&{\hat{y}}^{\prime \prime }+p_{1}{\hat{y}}^{\prime }+{\hat{y}}- {\hat{f}}({\hat{y}},\hat{y}^{\prime },\alpha ,{\alpha }^{\prime },{\hat{h}},{\hat{h}}^{\prime }) \nonumber \\&\quad =-p_{2}\mu ^{2}C_{l}(\alpha +\frac{1}{\mu }{\hat{y}^{\prime }}),\nonumber \\&{\alpha }^{\prime \prime }+p_{3}{\alpha }^{\prime }+p_{4}\alpha + w \zeta p_{4} {\hat{f}}({\hat{y}},{\hat{y}}^{\prime },\alpha ,{\alpha }^{\prime },{\hat{h}},{\hat{h}}^{\prime })\nonumber \\&\quad =\mu ^{2} C_{l}(\alpha +\frac{1}{\mu }{\hat{y}}^{\prime }),\nonumber \\&\varepsilon {\hat{h}}^{\prime \prime }+{\hat{f}}({\hat{y}},{\hat{y}}^{\prime },\alpha ,{\alpha }^{\prime },\hat{h},{\hat{h}}^{\prime })=0, \end{aligned}$$
(65)

where

$$\begin{aligned} {\hat{f}}({\hat{y}},{\hat{y}}^{\prime },\alpha ,{\alpha }^{\prime },{\hat{h}},{\hat{h}}^{\prime })&= \xi p_{1}\left( {\hat{h}}^{\prime }-({\hat{y}}^{\prime }-\zeta {\alpha }^{\prime })\right) \nonumber \\&\quad +\eta \left( {\hat{h}}-({\hat{y}}-\zeta \alpha )\right) , \end{aligned}$$
(66)

and the nondimensional coupling ratio is

$$\begin{aligned} w=\frac{k_{y}}{k_{\alpha }}{\mathcal {L}}^{2}=\frac{k_{y}}{k_{\alpha }}\frac{I_\mathrm{cg}}{\rho b^{2} S}. \end{aligned}$$
(67)

We extend the state vector as

$$\begin{aligned} {\varvec{x}}= \begin{bmatrix} {\hat{y}}\\ {\hat{y}}^{\prime }\\ \alpha \\ \alpha ^{\prime }\\ {\hat{h}}\\ {\hat{h}}^{\prime }\\ \end{bmatrix}. \end{aligned}$$
(68)

We define the new system matrices

$$\begin{aligned} {{{\varvec{Q}}}_{k}= \begin{bmatrix} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0\\ -1-\eta &{} -(p_{1}+p_{2}\mu c_{k)}-\xi p_{1} &{} -p_{2}\mu ^{2}c_{k}+{\zeta \eta } &{} {\zeta \xi p_{1}} &{} \eta &{} \xi p_{1}\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0\\ {w\zeta \eta p_{4}} &{} \mu c_{k}+{w \zeta \xi p_{1}p_{4}} &{} -(p_{4}-\mu ^{2} c_{k})-{w\zeta ^{2}\eta p_{4}} &{} -p_{3}-{w \zeta ^{2}\xi p_{1}p_{4}} &{} -{w\zeta \eta p_{4}} &{} -{w\zeta \xi p_{1}p_{4}}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\\ \frac{\eta }{\varepsilon } &{} \frac{\xi p_{1}}{\varepsilon } &{} -{\frac{\zeta \eta }{\varepsilon }} &{} -{\frac{\zeta \xi p_{1}}{\varepsilon }} &{} -\frac{\eta }{\varepsilon } &{} -\frac{\xi p_{1}}{\varepsilon } \end{bmatrix} , k=0,1,2,} \end{aligned}$$
(69)

and translation vectors

$$\begin{aligned} {{\varvec{r}}}_{k}= \begin{bmatrix} 0\\ -p_{2}\mu ^{2}d_{k}\\ 0\\ \mu ^{2}d_{k}\\ 0\\ 0 \end{bmatrix} ,\,\,\,k=1,2. \end{aligned}$$
(70)

The equations of the extended system are

$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{Q}}_{2}{\varvec{x}}-{\varvec{r}} _{2},\qquad {\varvec{x}}\in \Omega _{2}^{-}\,\cup \,\Sigma _{2}^{-}, \end{aligned}$$
(71)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{Q}}_{1}{\varvec{x}}-{\varvec{r}} _{1},\qquad {\varvec{x}}\in \Sigma _{2}^{-}\,\cup \,\Omega _{1}^{-}\,\cup \,\Sigma _{1}^{-}, \end{aligned}$$
(72)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{Q}}_{0}{\varvec{x}},\qquad {\varvec{x}} \in \Sigma _{1}^{-}\,\cup \,\Omega _{0}\,\cup \,\Sigma _{1}^{+}, \end{aligned}$$
(73)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{Q}}_{1}{\varvec{x}}+{\varvec{r}} _{1},\qquad {\varvec{x}}\in \Sigma _{1}^{+}\,\cup \,\Omega _{1}^{+}\,\cup \,\Sigma _{2}^{+}, \end{aligned}$$
(74)
$$\begin{aligned} \varvec{{\dot{x}}}= & {} {\varvec{Q}}_{2}{\varvec{x}}+{\varvec{r}} _{2},\qquad {\varvec{x}}\in \Sigma _{2}^{+}\,\cup \,\Omega _{2}^{+}, \end{aligned}$$
(75)

where the domains of subsystems (71)–(75) are given by

$$\begin{aligned} \Omega _{2}^{-}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{6}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu } \in \left( -\infty ,-\alpha _\mathrm{switch}\right) \right\} , \end{aligned}$$
(76)
$$\begin{aligned} \Omega _{1}^{-}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{6}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu } \in \left( -\alpha _\mathrm{switch},-\alpha _\mathrm{stall}\right) \right\} , \end{aligned}$$
(77)
$$\begin{aligned} \Omega _{0}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{6}:\alpha +\frac{\hat{y}^{\prime }}{\mu }\in \left( - \alpha _\mathrm{stall},\alpha _\mathrm{stall}\right) \right\} , \end{aligned}$$
(78)
$$\begin{aligned} \Omega _{1}^{+}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{6}:\alpha +\frac{\hat{y}^{\prime }}{\mu } \in \left( \alpha _\mathrm{stall},\alpha _\mathrm{switch}\right) \right\} , \end{aligned}$$
(79)
$$\begin{aligned} \Omega _{2}^{+}:= & {} \left\{ {\varvec{x}}\in {\mathbb {R}}^{6}:\alpha +\frac{\hat{y}^{\prime }}{\mu } \in \left( \alpha _\mathrm{switch},\infty \right) \right\} . \end{aligned}$$
(80)

These domains are separated by the switching planes defined by

$$\begin{aligned} \Sigma _{1}^{\pm }:= & {} \{{\varvec{x}}\in {\mathbb {R}}^{6}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu } =\pm \alpha _\mathrm{stall}\}, \end{aligned}$$
(81)
$$\begin{aligned} \Sigma _{2}^{\pm }:= & {} \{{\varvec{x}}\in {\mathbb {R}}^{6}:\,\alpha +\frac{{\hat{y}}^{\prime }}{\mu } =\pm \alpha _\mathrm{switch}\}. \end{aligned}$$
(82)

With these pairwise disjoint sets, the full state space \({\mathbb {R}}^{6}\) can be decomposed as

$$\begin{aligned} {\mathbb {R}}^{6}= & {} \Omega _{2}^{-}\cup \Sigma _{2}^{-}\cup \Omega _{1}^{-}\cup \Sigma _{1}^{-}\cup \Omega _{0}\nonumber \\&\cup \Sigma _{1}^{+}\cup \Omega _{1}^{+}\cup \Sigma _{2}^{+}\cup \Omega _{2}^{+}. \end{aligned}$$
(83)

8.1 Equilibrium points

The admissible equilibrium points of subsystems (71)–(75) are

$$\begin{aligned} {\varvec{F}}_{0}= & {} {\varvec{0}},\qquad {\varvec{F}}_{0}\in \Sigma _{1} ^{-}\,\cup \,\Omega _{0}\,\cup \,\Sigma _{1}^{+}, \end{aligned}$$
(84)
$$\begin{aligned} {\varvec{F}}_{1}^{\pm }= & {} \mp {\varvec{Q}}_{1}^{-1}{\varvec{r}}_{1}= \begin{bmatrix} \varvec{E_{1}^{\pm }}\\ \pm \dfrac{d_{1}(p_{2}p_{4}+\zeta ) \mu ^{2}}{c_{1}\mu ^{2}-p_{4}}\\ 0 \end{bmatrix},\nonumber \\&{\varvec{F}}_{1}^{\pm }\in \Sigma _{1}^{\pm }\,\cup \,\Omega _{1}^{\pm } \,\cup \,\Sigma _{2}^{\pm }, \end{aligned}$$
(85)
$$\begin{aligned} {\varvec{F}}_{2}^{\pm }= & {} \mp {\varvec{Q}}_{2}^{-1}{\varvec{r}}_{2}= \begin{bmatrix} \varvec{E_{2}^{\pm }}\\ \pm \dfrac{d_{2}(p_{2}p_{4}+\zeta ) \mu ^{2}}{c_{2}\mu ^{2}-p_{4}}\\ 0 \end{bmatrix},\nonumber \\&{\varvec{F}}_{2}^{\pm }\in \Sigma _{2}^{\pm }\,\cup \,\Omega _{2}^{\pm } . \end{aligned}$$
(86)

The expression of equilibria \({\varvec{F}}_{0},{\varvec{F}}_{1}^{\pm },\,{\varvec{F}}_{2}^{\pm }\) and their range of validity (Eqs. (84)–(86)) determine the admissible ranges depending on the bifurcation parameter \(\mu \) as

$$\begin{aligned}&\varvec{F_{0}}\,\text {is always admissible for symmetric airfoil profiles,} \end{aligned}$$
(87)
$$\begin{aligned}&{\varvec{F}}_{1}^{\pm }\,\text {is admissible if}\,\quad \mu \in [\mu _{1},\mu _{2}], \end{aligned}$$
(88)
$$\begin{aligned}&{\varvec{F}}_{2}^{\pm }\,\text {is admissible if}\quad \mu \in (\mu _{A},\mu _{2}]. \end{aligned}$$
(89)

8.2 Effects of the absorber parameters

In this section we investigate the effects of the absorber parameters on the stability of equilibria \({\varvec{F}}_{0},\,{\varvec{F}}_{1}^{\pm },\,{\varvec{F}}_{2}^{\pm }\). To reduce the number of parameters we fixed the mass ratio \(\varepsilon =0.1\). The other absorber parameters were varied in the following intervals: \(\zeta \in \left[ -0.01,0.05\right] \), \(\eta \in \left[ 0,0.3\right] \), \(\xi \in \left[ 0,1\right] \).

First, we investigate the asymptotic stability of these equilibria of the aeroelastic system with the LTVA. To determine the asymptotic stability of the equilibrium points, we study the characteristic polynomial of the coefficient matrices \({\varvec{Q}}_{k}\) defined in Eq. (69)

$$\begin{aligned} P_{k}(\lambda ,\mu )= & {} \lambda ^{6}+q_{1}(k,\mu )\lambda ^{5}\nonumber \\&+q_{2}(k,\mu )\lambda ^{4}+q_{3}(k,\mu )\lambda ^{3}+q_{4}(k,\mu )\lambda ^{2}\nonumber \\&+q_{5}(k,\mu )\lambda +q_{6}(k,\mu ), \end{aligned}$$
(90)

where

$$\begin{aligned}&q_{1}(k,\mu ) =p_{3}+p_{1}+p_{2}c_{k}\mu +\xi p_{1}\left( \zeta ^{2}wp_{4} +\frac{1}{\varepsilon }+1\right) , \end{aligned}$$
(91)
$$\begin{aligned}&q_{2}(k,\mu ) = \dfrac{{p_{4}}\left( \xi {p_{1}}({c_{k}}\mu {p_{2}}+{p_{1} })+\varepsilon \left( \zeta \eta w\left( {c_{k}}\mu ^{2}{p_{2}}+\zeta \right) +\eta +1\right) +\eta \right) }{\varepsilon }\nonumber \\&\qquad \qquad \qquad +\dfrac{\xi {p_{1}}\left( {p_{3}}-{c_{k}}\mu ^{2}{p_{1}}\right) +{c_{k}} \mu (\eta {p_{2}}{p_{3}}-\mu (\eta +\eta \varepsilon +\varepsilon ))+\eta +\eta {p_{1} }{p_{3}}}{\varepsilon }, \end{aligned}$$
(92)
$$\begin{aligned}&q_{3}(k,\mu ) = \dfrac{{p_{1}}\left( {p_{4}}\left( \varepsilon \left( \zeta w\left( {c_{k}}\mu ^{2}\xi {p_{2}}+\zeta (\eta +\xi )\right) +\xi +1\right) +\xi \right) -{c_{k}}\mu ^{2}(\xi +\xi \varepsilon +\varepsilon )+\eta +\xi \right) }{\varepsilon }\nonumber \\&\qquad \qquad \qquad +\dfrac{{c_{k}}\mu \left( {p_{2}}\left( \eta +\zeta ^{2}\eta {p_{4} }w\varepsilon +{p_{4}}\varepsilon \right) -\zeta \eta \varepsilon \right) +{p_{3}}(\xi {p_{1}}({c_{k}}\mu {p_{2}}+{p_{1}})+\eta +\eta \varepsilon +\varepsilon )}{\varepsilon }, \end{aligned}$$
(93)
$$\begin{aligned}&q_{4}(k,\mu ) = \dfrac{{p_{4}}\left( \xi {p_{1}}({c_{k}}\mu {p_{2}}+{p_{1} })+\varepsilon \left( \zeta \eta w\left( {c_{k}}\mu ^{2}{p_{2}}+\zeta \right) +\eta +1\right) +\eta \right) }{\varepsilon }\nonumber \\&\qquad \qquad \qquad +\dfrac{\xi {p_{1}}\left( {p_{3}}-{c_{k}}\mu ^{2}{p_{1}}\right) +{c_{k}} \mu (\eta {p_{2}}{p_{3}}-\mu (\eta +\eta \varepsilon +\varepsilon ))+\eta +\eta {p_{1} }{p_{3}}}{\varepsilon }, \end{aligned}$$
(94)
$$\begin{aligned}&q_{5}(k,\mu ) =\frac{\eta p_{3}+\eta p_{2}p_{4}c_{k}\mu +(\eta +\xi )p_{1} (p_{4}-c_{k}\mu ^{2})}{\varepsilon }, \end{aligned}$$
(95)
$$\begin{aligned}&q_{6}(k,\mu )=\frac{\eta (p_{4}-\mu ^{2}c_{k})}{\varepsilon }. \end{aligned}$$
(96)

the parameters \(\varepsilon ,\,\zeta ,\,\eta ,\,\xi \), but this dependence is not explicitly shown to keep the notation short. Applying the Liénard–Chipart stability criterion (see Eq. (45)), the aeroelastic system with the linear tuned vibration absorber is asymptotically stable if the following conditions are fulfilled

$$\begin{aligned} q_{2}(k,\mu )> & {} 0,\quad q_{4}(k,\mu )>0,\quad q_{6}(k,\mu )>0, \end{aligned}$$
(97)
$$\begin{aligned} q_{1}(k,\mu )> & {} 0,\quad \Delta _{3}(k,\mu )>0,\quad \Delta _{5}(k,\mu )>0, \end{aligned}$$
(98)

where the Hurwitz determinants \(\Delta _{3} (k,\mu )\) and \(\Delta _{5}(k,\mu )\) are calculated according to Eq. (45).

In Sect. 6 we determined that equilibrium \({\varvec{E}}_{0}\) is admissible and asymptotically stable for \(\mu \in [0,\mu _{1})\), stable at \(\mu =\mu _{1}\) and unstable for \(\mu >\mu _{1}\). The range of asymptotic stability \(\mu \in [0,\mu _{1})\) of equilibrium \({\varvec{F}}_{0}\) is the same as that of \({\varvec{E}}_{0}\). This is the consequence of

$$\begin{aligned} q_{6}(0,\mu )=\frac{\eta }{\varepsilon }a_{4}(0,\mu ), \end{aligned}$$
(99)

which means that the zero of \(q_{6}(0,\mu )\) (\(\mu =\mu _{1}\)) coincides with that of \(a_{4}(0,\mu )\) at \(\mu =\mu _{1}\).

Equilibria \({\varvec{E}}_{1}^{\pm }\) are admissible and asymptotically stable for \(\mu \in [\mu _{1},\mu _\mathrm{RB})\), stable at \(\mu =\mu _\mathrm{RB}\) and unstable for \(\in (\mu _\mathrm{RB},\mu _{2}]\).

The range of asymptotic stability \(\mu \in [\mu _{1},\mu _\mathrm{RB})\) of equilibria \({\varvec{F}}_{1}^{\pm }\) can, however, be extended by tuning the parameters of the absorber. In other words, we can shift \(\mu _\mathrm{RB}\) to larger \(\mu \) values by appropriate absorber parameters.

The stable regions of equilibria \({\varvec{F}} _{1}^{\pm }\) in the 2-dimensional parameter space \((\eta ,\mu )\) for different \(\xi \) and \(\zeta \) values, determined by conditions (97)–(98), are illustrated in Fig. 14. The stable regions of equilibria \({\varvec{F}}_{1}^{\pm }\) can also be visualized in the 3-dimensional parameter space \((\xi ,\eta ,\mu )\) for \(\zeta \in \{0,0.01,0.05,-0.01\}\), see Fig. 15. The range of admissibility and instability \(\mu \in (\mu _{A},\mu _{2}]\) of equilibrium \({\varvec{F}}_{2}^{\pm }\) is the same as that of \({\varvec{E}} _{2}^{\pm }\). This is the consequence of

$$\begin{aligned} q_{6}(2,\mu )=\frac{\eta }{\varepsilon }a_{4}(2,\mu ), \end{aligned}$$
(100)

which means that the zero of \(q_{6}(2,\mu )\) coincides with that of \(a_{4}(2,\mu )\) at \(\mu =\mu _{A}\).

Even though the derivation here does not include formulae for NACA 23012 profile, we nevertheless show the stable regions of equilibria \({\varvec{F}} _{1}^{+}\) in Figs. 16 and 17.

8.3 Quenching oscillations with the absorber

In this section we demonstrate that oscillations can be eliminated in certain regions of the parameter space of the absorber. Once again we use the structural and aerodynamic parameters of the model with NACA 0012 profile (Tables 1 and 2). Using absorber parameters

$$\begin{aligned} \varepsilon =0.1,\,\xi =0.2,\,\zeta =0.05, \end{aligned}$$
(101)

we draw the bifurcation values \(\mu _{1},\,\mu _\mathrm{RB},\,\mu _{2}\) as the functions of \(\eta \) see Fig. 18a. For parameter values (101) and \(\eta =0.05\) the rapid bifurcation is eliminated and the limit cycle oscillations (see Fig. 18b). For parameter values (101) and \(\eta =0.12\) the value of \(\mu _\mathrm{RB}\) is increased and the limit cycle oscillations still exist if \(\mu \in [\mu _\mathrm{RB},\mu _{2})\) (see Fig. 18c). Typical trajectories with and without absorber are shown in Fig. 19.

9 Conclusions

A piecewise linear aeroelastic system with and without a tuned vibration absorber was studied. A piecewise linear model was utilized using experimental data for the lift coefficient versus the angle of attack for NACA 0012, NACA 0009 and NACA 23012 airfoil profiles. The equations of motion for the system were nondimensionalized for symmetric airfoil profiles. The nondimensional freestream velocity was introduced as the system bifurcation parameter. The equilibria of the piecewise linear aeroelastic system were determined analytically as a function of the bifurcation parameter. The admissibility conditions of the equilibria were analyzed. The stability of those equilibrium points was studied by applying the Liénard–Chipart criterion.

The bifurcation analysis found classical and discontinuity-induced bifurcations as saddle-node, border collision and rapid bifurcation. The saddle-node bifurcation corresponds to the static divergence of the aeroelastic system. The rapid bifurcation is the abrupt appearance of stable periodic stall flutter oscillations of the aeroelastic system. The bifurcation analysis showed that the pitch–plunge model with a simple piecewise linear approximation of the aerodynamic force can reproduce the complex aeroelastic phenomenon of stall flutter. Finally, the effect of absorber parameters was investigated. The stall flutter oscillations were eliminated using a well-tuned absorber. This parametric study of the linear tuned vibration absorber predicts that not only active [32, 54] but also passive vibration reduction methods can be applied to suppress stall flutter.