Is it really chaos? The complexity of transient dynamics of double pendula

Abstract

In this paper, we re-examine the dynamics of double pendulum in numerical simulations and experimental observations. Typical types of behaviors of the parametrically excited double pendula are presented, including chaos, rotations and periodic oscillations, and the bifurcation analysis is performed, exhibiting complex transitions from one type of motion into another. The character of the observed dynamics is analyzed using Lyapunov exponents, which confirms the hyperchaotic nature of the system. Particular attention is paid to the transient behaviors, showing that the length of the irregular motion can be extremely sensitive to both parameters and initial conditions. Apart from the single double pendulum, we consider also the case of two coupled double pendula, connected by a typical linear scheme. Our results show that depending on the network’s parameters, one can observe the phenomenon of a transient chaotic synchronization, during which the units spontaneously synchronize and desynchronize. The loss of coherence is strictly related to the motion of the pendula around the unstable equilibrium of the system, which has been confirmed in the scenario of pure chaotic oscillations. We determine the regions of the occurrence of transient synchronization in the coupling parameters’ plane, as well as study the statistical properties of the observed patterns. We show that the problem of determining the final dynamical attractor of the system is not straightforward.

1 Introduction

Chaotic dynamics [1,2,3,4] is one of the most intriguing phenomena in the dynamical systems’ discipline. The unpredictable character of behavior, caused by the presence of nonlinearities in the evolutionary equations of a particular model, can been found in almost any area of modern science, including physics, biology or chemistry [4]. Although known for decades, the chaos theory still evolves, leading to the birth of such new concepts as chimera states [5, 6] or hidden, chaotic oscillations [7, 8].

Double pendulum is one of a few physical chaotic systems which have been deeply investigated using numerical, rigorous mathematical and experimental approaches, and in which the results predicted by the computer simulations coincided almost exactly with experimental measurements [9,10,11,12,13,14,15,16,17,18,19,20]. Chua’s circuit [21,22,23], an electronic device which can be equally easily built like double pendulum, is an another example of such a physical chaotic system. Contrary to Chua’s circuit, where one has to monitor chaotic behavior on the oscilloscope, double pendulum allows direct observation of the unpredictable oscillatory or rotational motion of pendulum’s bobs. In the 1980s and 1990s, some speakers (e.g., Yorke [9] or Ott [10]) started their seminar or conference talks with the presentation of the transient chaotic motion of double pendulum which they took out of the pocket. Among many other studies on the pendulum systems (see, e.g. John W. Miles works [11,12,13]), in [16] one can find the thorough bifurcation analysis of the system, while in [17, 18] the problem of its control. The scenarios of distributed mass and parametric excitation have been discussed in [19, 20], respectively. The simplicity of the double pendulum allows to investigate the chaotic concept from the very basis, making it possible to obtain the results both numerically and experimentally, which has a big advantage over typical, more complex systems.

In this paper, we study the properties of the double pendulum, focusing on the possible transient behaviors occurring in the system. The problem of transient dynamics is well known for researchers [24, 25] and has been found in variety of models, e.g. memristor oscillators [26], systems with random uncertainties [27] or neural networks [28,29,30]. In [31], the authors show that transient chaos may generate small chimera states, while in [32, 33] the problem has been related to the concept of hidden attractors, appearing unexpectedly in the system’s phase space. Transient dynamics plays a major role in all biologically based systems [34,35,36], where the determination of potential behaviors becomes essential for predicting future states and control of the undesired ones. An overview on recent results on the transient phenomenon and its possible applications can be found in [37].

Additionally, we have investigated a small network of two double pendula, which allowed to observe and describe the phenomenon of chaotic synchronization [38,39,40]. This type of behavior is common for coupled complex systems and has been reported in Chua’s circuits [41, 42], models with coexisting attractors [43] or linearly connected units [44]. In [45], Park discusses the possibility of the occurrence of such pattern between two different chaotic oscillators, while in [46, 47] the concept is examined using nonlinear control methods. A general approach to the phenomenon and its possible applications to communication can be found in [48]. It should be noted that in this study, we present the patterns of chaotic synchronization in two variants, i.e. the permanent and transient ones, showing that the concept may become not straightforward even for the very fundamental systems.

This paper is organized as follows. In Sect. 2, we introduce the model of the double pendulum (both numerical and experimental), describing its typical dynamics and transient behaviors. Then, in Sect. 3, we investigate the network of two coupled oscillators, discussing possible synchronization scenarios and their statistical properties. The conclusions of this paper are included in Sect. 4, and the supplementary material is described in Sect. 5.

2 Dynamics of the double pendulum

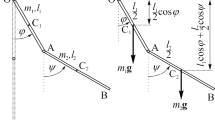
In this section, we investigate the dynamics of the double pendulum, which is presented in Fig. 1.

Fig. 1

(colour online). A single experimental double pendulum (a) and the experimental rig of an oscillating platform with suspended unit (b). In c, the scheme of the considered model used to perform numerical research is presented

The oscillator shown in Fig. 1a consists of two elements, i.e. the larger pendulum (upper bob) which holds the smaller one (lower bob) at its end. Both pendulum bobs are manufactured in the form of aluminum beams with additional masses made from the brass. All bearings are made from low-friction plastic materials, which along with the aluminum and brass allow to avoid any influence from the electromagnetic field created inside the exciter body.

The double pendulum is mounted at the steel shaft, which is connected through the support with the exciter, as shown in Fig. 1b. In our research, we have used the LDS Air Cooled Vibrator v780 (the shaker), which is the source of the external excitation. The parameters of the latter one are controlled by HAMEG Arbitrary Function Generator HMF2525, which allows to produce the sine function with varying frequency and amplitude.

The physical model of the experimental setup shown in Fig. 1a, b is presented in Fig. 1c. The upper pendulum bob of mass $m_1 \, [\text {kg}]$ and moment of inertia $I_{C_1} \, [\text {kg m}^2]$ (in regard to the bob’s mass center $C_1$) can oscillate or rotate around the axis, which is perpendicular to the figure’s plane in point $B_1$ (the location of the upper bearing). On the other hand, the lower pendulum bob of mass $m_2 \, [\text {kg}]$ and moment of inertia $I_{C_2} \, [\text {kg m}^2]$ (in regard to mass center $C_2$) can move around the axis perpendicular to the figure’s plane in point $B_2$ (where the lower bearing is mounted). The shaft (connected with the base support and the shaker) crosses point $B_1$ and can oscillate, which allows to parametrically excite the upper pendulum bob. The external oscillations are described by the harmonic function $A \sin (2 \pi f t)$, where $A \, [\text {m}]$ and $f \, [\text {Hz}]$ denote, respectively, the amplitude and the frequency.

The Lagrange equations of motion of the considered model are given as follows:

$$\begin{aligned} \left\{ \begin{array}{l} (m_1 l_{B_1 C_1}^2 + m_2 l_{B_1 B_2}^2 + I_{C_1}) \ddot{\varphi }_1 \\ + m_2 l_{B_1 B_2} l_{B_2 C_2} \cos (\varphi _1 - \varphi _2) \ddot{\varphi }_2 \\ - (m_1 l_{B_1 C_1} + m_2 l_{B_1 B_2}) (4 A \pi ^2 f^2 \sin (2 \pi f t) - g) \sin \varphi _1 \\ + d_1 \dot{\varphi }_1 + m_2 l_{B_1 B_2} l_{B_2 C_2} {\dot{\varphi }_2}^2 \sin (\varphi _1 - \varphi _2) = 0,\\ (m_2 l_{B_2 C_2}^2 + I_{C_2}) \ddot{\varphi }_2 \\ + m_2 l_{B_1 B_2} l_{B_2 C_2} \cos (\varphi _1 - \varphi _2) \ddot{\varphi }_1 \\ - m_2 l_{B_2 C_2} (4 A \pi ^2 f^2 \sin (2 \pi f t) - g) \sin \varphi _2 +d_2 \dot{\varphi }_2 \\ - m_2 l_{B_1 B_2} l_{B_2 C_2} {\dot{\varphi }_1}^2 \sin (\varphi _1 - \varphi _2) = 0, \end{array}\right. \nonumber \\ \end{aligned}$$

(1)

where the angular displacements of the upper and lower pendulum bobs are denoted by the variables $\varphi _1, \varphi _2 \in (- \pi , \pi ]$, respectively (see Fig. 1c for details). System (1) is nonautonomous and has been numerically integrated using initial dynamical time $t_0 = 0 \, [\text {s}]$.

The physical properties of the investigated system have been measured and equal: $m_1 = 0.4 \, [\text {kg}]$, $m_2 = 0.023766 \, [\text {kg}]$, $I_{C_1} = 0.0001244 \, [\text {kg m}^2]$, $I_{C_2} = 0.000010327 \, [\text {kg m}^2]$, $l_{B_1 B_2} = 0.06 \, [\text {m}]$ (the length between the bearings), $l_{B_1 C_1} =0.0303 \, [\text {m}]$ (the length between the upper bearing $B_1$ and the center of mass $C_1$) and $l_{B_2 C_2} = 0.0218 \, [\text {m}]$ (the length between the lower bearing $B_2$ and the center of mass $C_2$). The damping coefficients of free vibrations of the upper ($d_1$) and lower ($d_2$) bobs (not shown in Fig. 1c) have been measured separately (the dismantled model) and equal $d_1 = 0.0000921695$: [N m s], $d_2 = 0.00000551932$: [N m s]. The standard gravity has been fixed at $g = 9.81 \, [\text {m/s}^2]$. It should be noted that the ratio between the masses of the lower and the upper pendulum bobs equals $m_2 / m_1 =0.059415 \ll 1$. The small value of this ratio is typically required to produce chaotic behaviors.

The excitation parameters, i.e. the amplitude $A \, [\text {m}]$ and the frequency $f \, [\text {Hz}]$, have been varied during the experiments. The natural frequencies of the linearization of model (1) equal $f_1 = 2.147 \, [\text {Hz}]$, $f_2 =2.858 \, [\text {Hz}]$ and are separated from the excitation frequency considered in this study ($f > 4 \, [\text {Hz}]$).

Fig. 2

(colour online). Typical types of dynamics of model (1) in the form of time plots (left panel) and Poincare sections (right panel). Red and blue colors correspond to the upper and lower pendulum bobs, respectively. From the top to the bottom: a chaotic behavior for $A = 4.61 \, [\text {mm}], f = 4.5 \, [\text {Hz}]$; b periodic rotations for $A = 5.66 \, [\text {mm}], f = 4.5 \, [\text {Hz}]$; c periodic oscillations for $A = 2.23 \, [\text {mm}], f = 4.5 \, [\text {Hz}]$

Typical dynamical patterns found for system (1) are discussed in Fig. 2 and movies M1–M3 (see Supplementary Material in Sect. 5 for details). In the left panel in Fig. 2, the time plots of the upper ($\varphi _1$—red) and the lower ($\varphi _2$—blue) pendulum bobs have been presented, while in the right one, the Poincare sections are shown. The points for the latter maps have been collected after each excitation’s period (the basic period of the exciter is denoted by parameter $T = 1/f$). As one can see, the system can behave both chaotically and periodically, which depends on the external parameters. The example of chaotic motion is shown in Fig. 2a and movie M1 for $A = 4.61 \, [\text {mm}], f =4.5 \, [\text {Hz}]$. In this case, both pendulum bobs oscillate and rotate and the behavior is highly irregular (as shown in the Poincare map). It should be noted that due to the difference between the masses, the rotations of the smaller bob are observed more often than the rotations of the bigger one. Apart from chaotic behavior, the double pendulum can also exhibit periodic dynamics. The regular rotations of both pendulum bobs are presented in Fig. 2b and movie M2, where the system moves with the same frequency as the source of the external excitation (parameters: $A = 5.66 \, [\text {mm}], f = 4.5 \, [\text {Hz}]$). In this case, the bobs can rotate in the phase or in the antiphase to the shaker, depending on the initial conditions. Another example of regular motion is shown in Fig. 2c and movie M3 for $A = 2.23 \, [\text {m}], f = 4.5 \, [\text {Hz}]$, where the periodic oscillations of the double pendulum are possible. The amplitude of the lighter bob (blue) is greater than the amplitude of the heavier one (red), and both units move with the half of the exciter’s frequency. In this scenario, the bobs can oscillate in the phase to each other (as shown in Fig. 2c), or in the antiphase, which has been also observed during the experiments.

To investigate the transitions from one type of behavior into another, we have performed the bifurcation analysis and calculated the Lyapunov exponents [49, 50] of system (1). Our results are discussed in Fig. 3.

Fig. 3

(colour online). In a and b, the bifurcation diagrams for the upper (red) and lower (blue) pendulum bobs are presented, respectively. The corresponding two largest Lyapunov exponents ($\lambda _1$—violet, $\lambda _2$—green) are shown in c. Results obtained for fixed frequency $f = 4.3 \, [\text {Hz}]$ and varied amplitude $A \in (0, 10) \, [\text {mm}]$

In Fig. 3a, b, the bifurcation diagrams of the upper (red) and lower (blue) pendulum bobs have been presented, respectively. The values of two largest Lyapunov exponents of model (1) (denoted by $\lambda _1$—violet and $\lambda _2$—green) are shown in Fig. 3c. It should be noted that the remaining two exponents ($\lambda _3$ and $\lambda _4$) have been below zero during the whole experiment ($\lambda _i = 0$ threshold is marked as the dashed line in Fig. 3c). In this scenario, we have set the frequency at $f = 4.3 \, [\text {Hz}]$ and varied the amplitude $A \in (0, 10) \, [\text {mm}]$. Each iteration of the diagrams has been calculated for $t = 50{,}000 \, T \, [\text {s}]$, using fixed initial conditions (this allowed to observe possible multistability of the system; see the details discussed below).

As one can see, when the amplitude is below $A < 0.4 \, [\text {mm}]$, the double pendulum stops, converging to the stationary zero equilibrium. With the increase in parameter A, the period 2 solution arises and both pendulum bobs oscillate. This behavior is continued until the series of bifurcations around $A \approx 2 \, [\text {mm}]$, which finally lead to the appearance of chaotic attractors. Indeed, for $A \in (2.05, 2.45) \, [\text {mm}]$, one can observe the irregular motion of both units. It should be noted that in this case, the double pendulum only oscillates (rotations are excluded), as the points in the diagrams in Fig. 3a, b do not reach $\pm \pi$ border. Moreover, the dynamics is correlated with two positive Lyapunov exponents ($\lambda _1, \lambda _2 > 0$), exhibiting the hyperchaotic nature of the observed patterns. With further increase in the amplitude A, one can observe a narrow region of periodic states, leading to the occurrence of wide area of chaos for $A \in (2.9, 5.1) \, [\text {mm}]$. In this scenario, both upper and lower pendulum bobs oscillate and rotate. The magnitude of positive Lyapunov exponents is greater when compared to the previous case, exhibiting the increase in the complexity of the observed hyperchaos. The region described above is filled with spontaneously appearing gaps, corresponding to periodic windows. As one can see in the bifurcation diagrams, with further increase in parameter A, the number of such periodic solutions suddenly expands, filling almost the whole interval $A \in (5.1, 7.8) \, [\text {mm}]$. Finally, for $A > 7.8 \, [\text {mm}]$, the double pendulum jumps from one type of dynamics into another, which may happen even for a slight change in the excitation’s amplitude.

The results presented in Fig. 3 exhibit the complex nature of system (1). The double pendulum can behave in various ways, strictly depending on the shaker’s parameters. Since the latter ones are always vulnerable to unpredictable perturbations, it is possible to observe spontaneous transitions from chaos to regularity. Moreover, the structure of the bifurcation diagrams shown in Fig. 3a, b suggests that the system can be multistable for particular values of parameters, possibly possessing many coexisting attractors [51,52,53]. Depending on the basins of attraction of the system around the equilibrium point (the unmoving double pendulum), the states can be self-excited or hidden (see, e.g. [54], where similar problems have been considered).

It should be noted that the Lyapunov exponents presented in Fig. 3c have been calculated numerically, using the methods described in [49, 50]. The initial conditions used to obtain the results have been chosen through the bifurcation procedure (as the conditions from the previous integration step), with the finite-time interval [32] equal $1000 \, T \, [\text {s}]$. Some of the problems related to the numerical calculations of LEs can be found in [32, 55].

Fig. 4

(colour online). In a the histogram of the length of transient chaos (parameter $\tau$) for fixed $A = 5 \, [\text {mm}]\ \hbox {and}\ f =4.3 \, [\text {Hz}]$ is shown, while in b the average duration of the phenomenon (parameter $\left\langle \tau \right\rangle$) versus amplitude $A \in (4, 10) \, [\text {mm}]$ is presented. The lengths of the transient behaviors for varied displacements of the double pendulum bobs ($\varphi _{1,2} \in (- \pi , \pi ]$) and their velocities ($\dot{\varphi }_{1,2} \in [- 2 \pi f, 2 \pi f]$) are marked in maps c and d, respectively (parameters: $A = 5 \, [\text {mm}], f = 4.3 \, [\text {Hz}]$)

To investigate the transitions between different solutions and the transient character of chaotic dynamics in the double pendulum, we have studied the statistical properties of the considered system, which are described in Fig. 4.

At first, we have performed a series of 1000 numerical simulations for fixed parameters $A = 5 \, [\text {mm}], f = 4.3 \, [\text {Hz}]$ (in this case the double pendulum converges to periodic attractor, i.e. rotation with the excitation’s frequency). The initial conditions for each trial have been chosen randomly from the following intervals: $\varphi _{1,2} \in (- \pi , \pi ]$, $\dot{\varphi }_{1,2} \in [- 2 \pi f, 2 \pi f]$. In Fig. 4a, one can see the histogram of measure $\tau \, [\text {s}]$, which denotes the duration of the transient chaotic behavior observed before the double pendulum has periodized. The timescale in the horizontal axis in Fig. 4a is expressed in thousands of excitation’s periods ($T = 1/f \, [\text {s}]$), while parameter n in the vertical axis describes the number of samples belonging to histogram’s intervals (the whole range $\tau \in [0, 184{,}000 \, T]$ has been split into 40 equal intervals). As one can see, the majority of results lie close to the left border of $\tau$ range ($\tau < 40{,}000 \, T \, [\text {s}]$), showing that the system typically reaches the periodic solution in a reasonable time. However, for some of the trials, we have observed an enormous length of the transient chaos, which corresponds to the bars above $\tau > 60{,}000 \, T - 80{,}000 \, T \, [\text {s}]$. In particular cases, it took the system more than $\tau > 100{,}000 \, T - 120{,}000 \, T \, [\text {s}]$ to finally converge to the regular attractor (the largest result exceeded $\tau = 180{,}000 \, T \, [\text {s}]$). The existence of such long chaotic transients may be related to the concept of extreme events [56,57,58,59], which can appear spontaneously in nonlinear complex systems.

To analyze the influence of the excitation on the duration of the observed transients, we have varied the amplitude $A \in (4, 10) \, [\text {mm}]$ (setting $f = 4.3 \, [\text {Hz}]$) and for each value of parameter’s iteration (A), performed a series of trials, similar to the ones described above. In this case, we have calculated the mean length of the transient chaos, which is marked by parameter $\left\langle \tau \right\rangle \, [\text {s}]$ in the vertical axis in Fig. 4b (the scale in thousands of excitation’s period). As can be observed, with the increase in the shaker’s amplitude A, the mean duration of chaotic transients decreases, falling from $\left\langle \tau \right\rangle \approx 100{,}000 \, T \, [\text {s}]$ for $A \approx 4 \, [\text {mm}]$ to around $\left\langle \tau \right\rangle \approx 13{,}000 \, T \, [\text {s}]$ for $A \approx 5.5 - 7.5 \, [\text {mm}]$. The results from the latter interval seem very similar and correspond well to the wide region of periodic windows shown in the bifurcation diagrams in Fig. 3a, b. With further increase in coefficient A, the mean duration of transient chaos increases, reaching the peak $\left\langle \tau \right\rangle \approx 70{,}000 \, T \, [\text {s}]$ around $A \approx 8.3 \, [\text {mm}]$, above which the measure decreases again.

The results discussed in Fig. 4a, b have been obtained using random initial conditions. In order to study the influence of the latter ones on the transient character of chaotic states, we have again fixed both excitation’s parameters ($A = 5 \, [\text {mm}], f = 4.3 \, [\text {Hz}]$) and calculated the length of transients (measure $\tau \, [\text {s}]$) varying displacements and velocities of the double pendulum bobs. Our results are discussed in Fig. 4c, d. In Fig. 4c, the map of the chaotic transient time $\tau$ for $\varphi _{1,2} \in (- \pi , \pi ]$ and fixed $\dot{\varphi }_{1,2} = 0$ is shown, while in Fig. 4d the map for $\dot{\varphi }_{1,2} \in [- 2 \pi f, 2 \pi f]$ and $\varphi _{1,2} = 0$ is presented. As one can see, both maps are very intermingled and there are no particular regions, where the values of the $\tau$ measure seem similar. The majority of area is filled with red and black colors (corresponding to $\tau < 100{,}000 \, T \, [\text {s}]$), but there are also points marked by the light ones (yellow and white), for which the transient scenario is more complex and can be observed for enormous amount of time. The structure of the regions in Fig. 4c, d (the lack of density) makes it impossible to precisely determine the length of potential transient behavior, since even a slight perturbation in the initial conditions can dramatically change the final result. In this sense, the chaotic transients are extremely sensitive on the system’s conditions, which agrees with the hyperchaotic nature of the double pendulum.

It should be noted that the phenomena discussed in Fig. 4 have also been observed experimentally on our rig. During our practical research, we have noticed transient chaotic behaviors reaching many hours of real time, before the system finally stabilized on the periodic state.

3 Dynamics of two coupled double pendula

In this section, we investigate the system of two double pendula, coupled through typical linear scheme. The dynamics of such coupled pendula is given by:

$$\begin{aligned} \left\{ \begin{array}{l} (m_1 l_{B_1 C_1}^2 + m_2 l_{B_1 B_2}^2 + I_{C_1}) \ddot{\varphi }_1^i \\ + m_2 l_{B_1 B_2} l_{B_2 C_2} \cos (\varphi _1^i - \varphi _2^i) \ddot{\varphi }_2^i \\ - (m_1 l_{B_1 C_1} + m_2 l_{B_1 B_2}) (4 A \pi ^2 f^2 \sin (2 \pi f t) - g) \sin \varphi _1^i \\ + d_1 \dot{\varphi }_1^i + m_2 l_{B_1 B_2} l_{B_2 C_2} {(\dot{\varphi }_2^i)}^2 \sin (\varphi _1^i - \varphi _2^i) \\ + 2 k_1 (\varphi _1^i - \varphi _1^{i \, \text {mod} \, 2 + 1}) = 0,\\ (m_2 l_{B_2 C_2}^2 + I_{C_2}) \ddot{\varphi }_2^i \\ + m_2 l_{B_1 B_2} l_{B_2 C_2} \cos (\varphi _1^i - \varphi _2^i) \ddot{\varphi }_1^i \\ - m_2 l_{B_2 C_2} (4 A \pi ^2 f^2 \sin (2 \pi f t) - g) \sin \varphi _2^i + d_2 \dot{\varphi }_2^i \\ - m_2 l_{B_1 B_2} l_{B_2 C_2} {(\dot{\varphi }_1^i)}^2 \sin (\varphi _1^i - \varphi _2^i) \\ + 2 k_2 (\varphi _2^i - \varphi _2^{i \, \text {mod} \, 2 + 1}) = 0, \end{array}\right. \nonumber \\ \end{aligned}$$

(2)

where $i = 1, 2$. Variables $\varphi _1^i, \varphi _2^i$ denote the displacement of the upper and lower ith pendulum bobs, respectively. Both oscillators are identical, and their parameters are the same as for the model considered in Sect. 2. It should be noted that the double pendula of system (2) are connected through both upper and lower parts, where the coefficients $k_1, k_2 \, [\text {N m}]$ describe the strength of coupling.

Practical implementation of model (2) is not straightforward (since all of the pendula bobs can rotate) and the study in this section is based on the numerical approach.

During our investigations on network (2), we have found that when the coupling strength is properly chosen, both units can synchronize on a chaotic attractor. However, depending on the system’s parameters, the phenomenon can have transient or persistent character. An example of the former behavior is discussed in Fig. 5.

Fig. 5

(colour online). The phenomenon of transient chaotic synchronization of two coupled double pendula (2). An example of synchronization rise is shown in a for difference $(\varphi _2^1-\varphi _2^2)$ between the lower pendula bobs. A zoom on the desynchronization point is presented in the time plot in b ($\varphi _2^1$—blue, $\varphi _2^2$—cyan). In c, one can observe the process of synchronization birth and disappearance for a large timescale (equals 20,000 periods of external excitation). Parameters: $A = 3.5 \, [\text {mm}], f = 4.4 \, [\text {Hz}], k_1 = 0.033 \, [\text {N m}], k_2 = 0.053 \, [\text {N m}]$

In Fig. 5a, one can observe a sample of the time plot, which has been calculated for the system with coefficients $A = 3.5 \, [\text {mm}], f = 4.4 \, [\text {Hz}], k_1 = 0.033 \, [\text {N m}], k_2 = 0.053 \, [\text {N m}]$. The excitation parameters correspond to the case of both oscillations and rotations of the upper and lower pendula bobs. The evolution of the difference between the displacements of the lower bobs $(\varphi _2^1-\varphi _2^2)$ marked in the vertical axis in Fig. 5a exhibits that after some transient, random movements, the oscillators begin to synchronize. The coherent state is reached around $t \approx 250 \, T \, [\text {s}]$ and has been observed also for the upper pendula bobs (not shown in the figure). However, at some critical point ($t \approx 440 \, T \, [\text {s}]$), the oscillators desynchronize and the common chaotic behavior is lost. To investigate the mechanism of the synchronization disappearance, we have zoomed the time plots around the critical point ($t \approx 440 \, T \, [\text {s}]$), which is shown in Fig. 5b. The displacements of the first and the second lower pendula bobs are marked in blue and cyan, respectively. As can be seen from the very beginning in Fig. 5b, the rotations of both pendula induce small differences in their movements, which is caused by the hyperchaotic character of the systems. Typically, such irregularities disappear due to the coupling components, but in this case, their presence has a significant influence on the whole pattern. Indeed, when the almost synchronized bobs reach the unstable equilibrium of the system, i.e. point $\varphi _1^1 = \varphi _2^1 = \varphi _1^2 =\varphi _2^2 = -\pi$ (marked by the orange arrow), the first bob crosses the point, while the second turns back (blue and cyan trajectories, respectively). At this point, the synchronization is broken and the double pendula begin to move independently.

The transient chaotic synchronization discussed in Fig. 5a, b is repeatable, which is shown in Fig. 5c for a large timescale equal to $t = 20{,}000 \, T \, [\text {s}]$. As one can see, the difference $(\varphi _2^1-\varphi _2^2)$ plot is filled with synchronization windows, which seem to appear spontaneously and vanish after transient time. We have studied many examples of the synchronization loss for system (2), and in the majority of cases, the pattern has been destroyed in the same way as described above.

Fig. 6

(colour online). Permanent chaotic synchronization of two coupled double pendula (2). The time plots of the displacements ($\varphi _2^1$—blue, $\varphi _2^2$—cyan) of the lower pendula bobs are presented in a, while the time plot of the difference $(\varphi _2^1-\varphi _2^2)$ for a large time scale is shown in b. Parameters: $A = 2.15 \, [\text {mm}], f = 4.3 \, [\text {Hz}], k_1 = 0.033 \, [\text {N m}], k_2 = 0.053 \, [\text {N m}]$

To confirm that the motion of pendula around the unstable equilibrium is the main reason for the transient character of the discussed phenomenon, we have changed the excitation’s parameters to $A = 2.15 \, [\text {mm}], f = 4.3 \, [\text {Hz}]$, leaving the coupling coefficients $k_1, k_2$ unchanged. In this case, both upper and lower bobs of the double pendulum can only chaotically oscillate and the rotations are excluded. This type of behavior has been observed and discussed in the bifurcation diagrams in Fig. 3 (see Sect. 2 for details).

The results of the considered scenario are described in Fig. 6, where the time plots of displacements ($\varphi _2^1$—blue, $\varphi _2^2$—cyan) and the difference plot $(\varphi _2^1-\varphi _2^2)$ are presented in Fig. 6a, b, respectively. As one can see in Fig. 6a, both double pendula are synchronized, exhibiting chaotic oscillations (a similar behavior can be observed for the upper pendula bobs). Moreover, the pattern seems permanent, which is marked by the $(\varphi _2^1-\varphi _2^2) = 0$ horizontal line in Fig. 6b. In this case, the dynamics of system (2) has been examined for the timescale $t = 1{,}000{,}000 \, T \, [\text {s}]$ (not shown in the figure) and the chaotic synchronization between both upper and lower bobs of the double pendula persisted till the end of the numerical experiment.

The obtained results suggest that the chaotic synchronization between double pendula is possible but its character (and stability) highly depends on the excitation parameters, which determine the ability of the pendula to rotate.

To investigate the properties of the observed transient behaviors, we have performed the statistical analysis, similar to the one discussed in Fig. 4 (see Sect. 2 for details). Our results are presented in Fig. 7.

Fig. 7

(colour online). In a, the duration of consecutive transient chaotic synchronizations (parameter $\tau _{\mathrm{sync}}$) observed during one numerical experiment is shown (index $i_{\mathrm{sync}}$ denotes the number of synchronization windows—see Fig. 5c for details). The maximum transient synchronization length (parameter $\tau _{\mathrm{sync}}^{\mathrm{max}}$) for fixed $k_1 = 0.033 \, [\text {N m}]$ and varied $k_2 \in (0, 0.1) \, [\text {N m}]$ is presented in (b). The regions of different types of final behavior of network (2) and maximum chaotic synchronization duration ($\tau _{\mathrm{sync}}^{\mathrm{max}}$) in the coupling parameters plane $k_1, k_2 \in (0, 0.1) \, [\text {N m}]$ are marked in (c) and (d), respectively. Excitation parameters: $A = 3.5 \, [\text {mm}], f = 4.4 \, [\text {Hz}]$

At first, we have studied the lengths of synchronization windows in Fig. 5c, evolving the system till $t = 1{,}000{,}000 \, T \, [\text {s}]$ (parameters as previously, i.e. $A = 3.5 \, [\text {mm}], f = 4.4 \, [\text {Hz}], k_1 = 0.033 \, [\text {N m}], k_2 = 0.053 \, [\text {N m}]$). For each of such windows (labeled by parameter $i_{\mathrm{sync}}$), the duration of synchronization has been calculated (measure $\tau _{\mathrm{sync}} \, [\text {s}]$). The results obtained in this case are shown in Fig. 7a. It should be noted that $\tau _{\mathrm{sync}}$ parameter is expressed in the excitation period and the scale in the vertical axis is logarithmic. During our research, we have characterized the synchronization by the following criteria: $\left| \varphi _1^1-\varphi _1^2 \right| < 2^{\circ }$ $\wedge$ $\left| \varphi _2^1-\varphi _2^2 \right| < 2^{\circ }$ and considered only the states lasting at least $t > 100 \, T \, [\text {s}]$ (the latter choice is arbitrary and has been applied to exclude accidental coherence, which seems irrelevant). As one can see in Fig. 7a, we have observed 25 windows of the transient chaotic synchronization and the majority of them survived for less than $t < 1000 \, T \, [\text {s}]$. However, some of the states have lasted for more than $t > 10^4 \, T \, [\text {s}]$, or even $t > 10^5 \, T \, [\text {s}]$. In these particular cases, the dynamics of the network may be easily mistaken with the final synchronized attractor, which in fact is only a transient state.

The study discussed in Fig. 7a is extended in Fig. 7b, where the maximum duration of the transient chaotic synchronization (parameter $\tau _{\mathrm{sync}}^{\mathrm{max}}$; expressed in thousands of excitation period in the vertical axis) is shown. In this case, the upper coupling strength is fixed: $k_1 = 0.033 \, [\text {N m}]$, while the lower one is varied: $k_2 \in (0, 0.1) \, [\text {N m}]$. For each diagram iteration, system (2) has been run from the same initial conditions and evolved for $t = 500{,}000 \, T \, [\text {s}]$. As one can see, for $k_2 < 0.01 \, [\text {N m}]$, the transient synchronization is almost unnoticeable (due to the small coupling), but with the increase in the parameter, it bursts. The majority of the results are below $t < 250{,}000 \, T \, [\text {s}]$, but some of them reach the upper levels of $t = 300{,}000 \, T - 400{,}000 \, T \, [\text {s}]$. The diagram can be split into two regions, i.e. (i) $k_2 \in (0.01, 0.06) \, [\text {N m}]$ and (ii) $k_2 \in (0.06, 0.1) \, [\text {N m}]$. In the former interval, the mean duration of the maximum chaotic transients is higher than in the latter one, which can be noticed by the increased density of the plotted bars.

During our study, we have observed that for the particular values of the coupling in system (2), the transient behavior can finally converge to complete synchronization on a periodic attractor. In such a case, both double pendula rotate or oscillate, depending on the excitation parameters and initial conditions. To determine the regions of different final dynamics, we have varied both coefficients $k_1, k_2 \in (0, 0.1) \, [\text {N m}]$, evolving the model in each iteration for $t = 500{,}000 \, T \, [\text {s}]$ (from the same initial conditions). The parameters’ plane $(k_1, k_2)$ shown in Fig. 7c allows to distinguish the location of three types of behaviors that have been found: (i) the periodic synchronization (PER—green), (ii) the absence of synchronization (NO SYNC—violet; this includes also coherent movements lasting for less than $t = 100 \, T \, [\text {s}]$—see the description of Fig. 7a for details) and (iii) the transient chaotic synchronization (CH SYNC—blue). The map in Fig. 7c exhibits that in a wide region of parameters, the transient synchronization is the only possible type of behavior (blue region without any gaps). On the other hand, for $(k_1, k_2) \in (0.025, 0.1) \times (0.01, 0.1)$ one can observe the existence of all three types of phenomena (i)–(iii), accompanied by a complex structure of their basins.

The map shown in Fig. 7c has been reproduced in Fig. 7d, with an additional calculation of the transients’ lengths. Indeed, the regions of periodic synchronization (i) and the absence of synchronization (ii) have been marked in grey. For the points corresponding to the transient chaotic synchronization (iii) (blue palette in Fig. 7c), we have calculated the maximum length of the phenomenon (parameter $\tau _{\mathrm{sync}}^{\mathrm{max}}$) and marked the results in the color scale in Fig. 7d (values expressed in thousands of excitation’s period). As can be observed, the region where only the transient synchronization is possible (wide blue area in Fig. 7c) is correlated with the lowest duration of the state appearance (wide dark region in Fig. 7d). On the other hand, one can distinguish the regime in Fig. 7d, i.e. $(k_1, k_2) \in (0.025, 0.05) \times (0.01, 0.1)$, where the transients reach the highest peaks (the points shown in yellow and white in the map). The data obtained in the latter region correspond well to the diagram presented in Fig. 7b, which has been calculated for $k_1 = 0.033 \, [\text {N m}]$.

The results discussed in Fig. 7 confirm the complex nature of network (2). Enormous durations of the transient chaotic synchronization phenomenon along with the intermingled nature of maps suggest that even though the model is fundamental, it can behave in various, surprising ways and the final dynamics of the coupled double pendula is hard to predict.

4 Conclusions

In this paper, we have studied the dynamics of mechanical double pendula with parametric excitation (induced by the external shaker). The motion of the single oscillator has been investigated, showing that the system can behave chaotically, as well as periodically. Different types of patterns have been confirmed both numerically and experimentally. The bifurcation analysis of the double pendulum allowed to observe that the character of dynamical response strictly depends on the excitation parameters, leading to the regions where the transitions from one type of pattern into another take place (periodic windows). The potential multistability of the system and its hyperchaotic character (two positive Lyapunov exponents) confirm the complex nature of the considered pendulum. Moreover, the study on transient behaviors exhibits that the duration of the irregular motion (before the unit converges to regular attractor) can vary in an unpredictable way, leading to the scenarios where chaotic response is observed for a very long time. We have shown that the average length of transients strictly depends on the system parameters and can drastically change even for a slight perturbation of the initial conditions. In our research, we have also examined a small network of two coupled double pendula, connected through a linear components (both upper and lower bobs of each unit). In this case, we have observed two variants of chaotic synchronization: (i) the transient one, when the oscillators spontaneously synchronize and desynchronize and (ii) the permanent one, which persists for significant amount of time (the behavior seems asymptotic). The occurrence of the former scenario is induced by chaotic rotations of the pendula around the unstable equilibrium of the system. Indeed, when the lower bobs get close to the fixed point, it might happen that one of them turns back, while the second crosses the point, which leads to the desynchronization between the oscillators. This phenomenon is probably caused by the presence of natural perturbations in the system (the global behavior is still chaotic) and occurs randomly. It should be noted that the permanent character of chaotic synchronization in scenario (ii) is accompanied by the absence of such irregular rotations (the pendula only oscillate). We have shown that the duration of transient synchronization varies and similarly to the case of the single oscillator, it can persist for significantly long time. The analysis of the coupling parameters’ plane allowed to determine the regions, where the phenomenon occurs and to estimate its magnitude (measured by the maximum length of the coherent state). The results discussed in this paper exhibit that the problem of transient dynamics may become very complex even for the simplest nonlinear systems, like the ones considered. The dynamics of the double pendula which prototypes the most fundamental chaotic oscillators in mechanics is not straightforward, suggesting that similar phenomena can be also found in more complex models from different areas of modern dynamical science.