Nonlinear structural dynamics of a new sliding-mode triboelectric energy harvester with multistability

Abstract

A new sliding-mode triboelectric energy harvester in the form of a cantilever beam with a tip mass that is acted upon by both magnetic and friction forces is modelled and simulated. A numerical scheme based on the trapezoidal rule with the second-order backward difference formula (TR-BDF2) method is introduced to solve the combined non-smooth mechanical and stiff electrical system. This is the first study of the structural dynamics of the sliding-mode triboelectric energy harvesting; additionally, a magnetic field that induces multistability is present. A comparison between the coupled and uncoupled electromechanical models suggests that the electrostatic force between the electrodes can be ignored, which makes the uncoupled model preferable in the dynamical analysis. The influence of the non-conservative force (the friction force) on the multistability of the system is investigated. It is found that the distribution of the multistability on the parametric plane changes even when a small amount of friction is involved, and the areas of bistability and tristability shrink while that of the monostability expands. A comparison among these three types of stability reveals the superiority of invoking bistability as it facilitates broadband energy harvesting. The excitation level plays an important role in inducing the snap-through motion (the interwell oscillation) by enabling the crossing of the energy barriers between wells. The increase in the friction shrinks the frequency band of interwell oscillations from high frequencies down to low frequencies on the discrete frequency sweep. An analysis of the basins of attraction finds that at low frequencies the bistable system can undergo only interwell oscillations, while the tristable system can merely experience intrawell oscillations. The basins can intermingle with each other in both bistable and tristable systems. Finally, an increase in the excitation level can break the basins into discrete pieces and/or points.

1 Introduction

1.1 Triboelectric energy harvesting

Harvesting vibrational energy from ambient vibration and converting it into useful electric energy is a topic that has received substantial attention. Piezoelectric [1] and electromagnetic [2] energy harvesters are the two most common types and have been studied extensively. The triboelectric nanogenerator (TENG), which was first introduced in 2012 [3], offers a new fashion of energy transduction. It works through a combination of contact electrification and electrostatic induction [4], both of which happen between two triboelectric materials of opposite tribo-polarities. (e.g., PTFE and aluminium) [4]. During interaction, materials of positive tribo-polarities tend to lose electrons while materials of negative tribo-polarities tend to gain electrons, and thus an electrical current.

Compared with piezoelectric and electromagnetic energy harvesters, triboelectric energy harvesters (TEHs) have several advantages: They can be constructed from a wide range of common materials that are much cheaper than piezoelectric crystals and ceramics and neodymium magnets, TEHs have a high conversion efficiency, are easy to fabricate, have widespread applications, and are cost-effective [5]. Moreover, the outputs of TEHs are usually high in voltage but low in current, while piezoelectric and electromagnetic energy harvesters are the opposite, which makes TEHs a better choice when the targeted sensors in application need high-voltage inputs. In addition, TEHs have four different working modes which offer more freedom when designing TEHs for a specific application, and they are the vertical contact-separation mode [6], the in-plane sliding mode [7], the single-electrode mode [8], and the freestanding triboelectric-layer mode [9]. Although the four modes differ from each other, the electrical outputs of TEHs based on them can all be described using the V–Q–x relationship [4], where V, Q, and x are the voltage, the transferred charge, and the separation distance between electrodes, respectively.

A variety of TENG-based prototypes have been developed for practical applications such as, triboelectric motion sensing [10], human health monitoring [11], wind speed sensing [12], plasmonic ultraviolet detection [13], and virtual reality 3D-control sensing [14]. In these devices, the triboelectric materials are usually etched to have micro- or nanoscale surface patterns including nanowire arrays [7], nanopores [15], or pyramid and cubic patterns [16]. Patterned triboelectric materials have been demonstrated to be much more efficient than non-patterned ones [5]. In addition to surface modification, an electron blocking layer-based interfacial design has been found to dramatically increase the output of TENGs [17]. Moreover, instead of modifying a material’s surface to improve its performance, some new triboelectric materials have been developed, such as a friction material [18] and a flexible fibre material [19].

Despite the development of diverse TENGs, research into their structural dynamics is rare, and a study investigating sliding-mode TEHs is still missing. Structural vibration is closely related to harvesting performance and thus should be considered. Piecewise stiffness may be introduced to widen the effective frequency bandwidth of TEHs that use the vertical contact-separation mode [20]. Investigations of vibro-impact dynamics benefit the design of harvesters involving repeated impact (or contact) and separation, such as in a contact freestanding mode TEHs [21]. Further, a velocity-dependent coefficient of restitution can be identified experimentally and used in the modelling of impact to better approximate a physical device [22]. The electrostatic force between two charged electrodes may be too weak to affect the structural dynamics and thus may be ignored in modelling, which then leads to decoupling of the mechanical system from the electrical system [22]. The frequency-shifting phenomenon, which often appears in piezoelectric energy harvesting due to the resistive shunt damping effect [1], may disappear in TEHs [22]. It has also been found that a TR-BDF2 numerical integration scheme can be effectively used when the electrical system is stiff [22].

In microelectromechanical systems (MEMS), electrostatic transducers (or generators) have been studied extensively [23]. However, the necessity of using a charge source along with switching losses reflects the limitations of the standard (electret-free) electrostatic generators [24]. Electret-based electrostatic generators can eliminate the need for an initial charge source and, therefore, are now prevalent [24, 25]. Their working mechanisms are similar to the TEHs in the vertical contact-separation mode or the in-plane sliding mode, but usually without any contact between the electret and the counter-electrode [25]. The main difference is that a variable open-circuit electric potential difference ($V_{\text{oc}}$) is used in TEHs [4] while a fixed surface voltage (V) is used in electret-based electrostatic energy harvesters [26]. In terms of the topology of the harvesters themselves, most of the electrostatic converters are miniaturized and comb-shaped with designs that are usually derived from accelerometers [23,24,25,26], whereas TEHs can adopt various shapes and dimensions [4].

1.2 Bistable energy harvesting

Bistability is often exploited in piezoelectric energy harvesters, though it can also be found in electromagnetic energy harvesters [27,28,29]. However, the application and study of bistability in triboelectric energy harvesting was only very recently reported in the context of a tuneable shock sensor [30]. Bistable energy harvesters can be categorized into three different mechanisms according to their manifestations of bistability [31]: magnetic attraction bistability [32,33,34], magnetic repulsion bistability [28, 35], and mechanical bistability [30, 36, 37]. The former two mechanisms rely on a magnetic force while the latter depends on either a mechanical pre-load [30, 36] or material anisotropy [37].

Bistable systems are well known for having a double-well potential energy curve which results in two distinct types of oscillation: low-energy intrawell and high-energy interwell oscillations, the latter of which has been found to be more efficient in energy harvesting applications [31]. Bistability, as a particular case of multistability, has been extensively studied in the context of symmetries, phase transitions, and hysteresis [38]. Numerous attractors can coexist for a fixed set of parameters of a bistable system. For instance, a small change in initial conditions can turn a steady-state intrawell oscillation into an interwell oscillation owing to their coexistence [39]. For such systems, basins of attraction are often investigated, such as in Refs. [40, 41]. In addition, bistability has been shown to broaden the frequency range from which energy can be extracted, and to provide a high-energy orbit over a wide range of frequencies [42]—two features that are highly desirable in energy harvesting applications. In addition to numerical and experimental studies, some approximate analytical methods have been used to investigate bistable harvesters, such as harmonic balance method [43], the method of multiple scales [44], and Melnikov’s method [45]. By analysing the bifurcation and stability characteristics of the system, design and operation guidance can be provided. For example, the frequency span between a saddle-node and a period-doubling bifurcation might be used to approximate the bandwidth within which the harvester can achieve high-energy orbits and thus produce high-energy outputs [46]. In addition, multistability rather than bistability has also been utilized in energy harvesting, such as in Refs. [47, 48]. Although various nonlinearities have been exploited in vibration energy harvesters, it should be noted that there still exists a notable knowledge gap in integrating nonlinear energy harvesters with effective nonlinear rectifying and power management circuits for practical applications [49], because using energy harvesters as the sources is quite different from using batteries [50]. However, this paper will not target on bridging this knowledge gap.

1.3 Aim and objectives of this study

A new triboelectric energy harvester that works in a sliding mode and includes bistability is presented. This study aims to investigate as well as optimize it from a structural dynamics perspective. The following contributions concerning TEHs are made:

• 1. A sliding-mode triboelectric energy harvester is modelled and studied from a structural dynamics perspective.

• 2. Both the coupled and uncoupled electromechanical models are established and compared to investigate the effect of electrostatic force between the electrodes.

• 3. The different types of stability resulting from a magnetic field are identified and compared for a TEH device.

• 4. The effect of friction in triboelectric energy harvesting is studied in the context of structural dynamics.

The outline for the rest of this paper is as follows: Section 2 introduces the design of the harvester and describes its working mechanism. Section 3 presents the mechanical modelling of the vibration of a cantilever beam when its tip is subject to both magnetic and frictional forces. The electrical modelling of the harvester’s output is given in Sect. 4. The method used to solve the non-smooth mechanical dynamical system and the stiff electrical system is described in Sect. 5.1. Section 5.2 analyses the effect of the electrostatic force. Coupled and uncoupled electromechanical models are compared. The influence of the non-conservative force (the friction force) on the multistability of the system is investigated in Sect. 5.3. Section 5.4 makes the comparison among three types of stability of the system via discrete numerical frequency sweeps. Section 5.5 presents a study investigating the effect of the excitation level on the system response. The influence of the friction is discussed in Sect. 5.6. Afterwards, the basins of attraction are analysed in Sect. 5.7. The conclusions of this study are drawn in Sect. 6.

2 Design

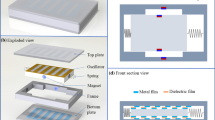
The configuration of the proposed sliding-mode triboelectric energy harvester is shown in Fig. 1a. All the components are integrated onto a base which receives a sinusoidal excitation. A cantilever beam is clamped onto the base and its free end is attached with a slider in which a cylindrical magnet is embedded. Additionally, two identical magnets are fixed to the base and symmetrically located to attract the oscillating magnet. As shown in Fig. 1b, the slider has a circular contact area and slides over two specially made patches. The slider is attached with an electrode (known as the top electrode) and a dielectric (such as PTFE). The base is composed by an electrically active patch (EAP, aluminium) and an electrically inert patch (EIP, PTEG). The circular electrically active area works as the bottom electrode and has the same circular area as the top electrode. Both the top and bottom electrodes are wired into an outside circuit to form a loop (not shown in Fig. 1). Under the base excitation, the slider can oscillate, and its motion will be affected by the magnetic field.

Fig. 1

Configurations of a the sliding-mode triboelectric energy harvester and b the slider on patches

During sliding, triboelectrification only happens in the contact area between the slider and the electrically active patch (EAP). The charge transfer process [51] of the TEH is depicted in Fig. 2, where a resistor denoted by R is wired with the harvester and the current in the circuit is represented by I (note that the electrically inert patch (EIP) is not shown in Fig. 2). When the top dielectric fully overlaps the bottom electrode (the EAP), charge transfer occurs at the contact area owing to the triboelectric effect, and the aluminium loses electrons, while the PTFE gains electrons. The charge transfer process at this stage will result in net positive charges on the EAP and equivalent net negative charges on the dielectric, as shown in Fig. 2a. As the slider slides out of the EAP, an electric potential difference between the two electrodes is established simultaneously, which drives the electrons in the top electrode to flow to the bottom electrode. The electron flow induces an instantaneous current that flows in an opposite direction as shown in Fig. 2b. When the slider fully slides outside the EAP, the electrons will be balanced between the top dielectric and top electrode, as shown in Fig. 2c. Once the slider starts sliding back, as illustrated in Fig. 2d, the balance gets broken and the current will flow from the top electrode to the bottom electrode until the slider fully overlaps the EAP again. Thereafter, the process is repeated as slider oscillates. Here, a relatively simple or a purely resistive circuit rather than a more complicated circuit is used, because this study is mainly focused on the structural dynamics rather than the electrical dynamics of the proposed vibration energy harvester. This is commonly seen in the study of vibration energy harvesters from the perspective of structural dynamics. Nevertheless, the use of more complicated circuits can also be found in the literature. In the study of a piezoelectric energy harvester, a resistor-inductor resonant circuit, which is in serial connection with the harvester, has been demonstrated to be able to enhance the energy harvesting efficiency [52]. Thus, it would be interesting to investigate the influence of such circuits on the performance of triboelectric energy harvesters, and this might be carried out in a future study.

Fig. 2

The charge transfer process of the presented sliding-mode triboelectric energy harvester

Note that although the configuration is similar to some bistable piezoelectric energy harvesters [39], the energy harvesting mechanism is completely new and the system is no longer smooth due to the involvement of friction between the slider and the patches. Nevertheless, the presented triboelectric energy harvester can be combined with a bistable piezoelectric energy harvester to form a hybrid energy harvester, in which case the harvesting performance may be enhanced. As for the practical applications, the proposed vibration energy harvester can be used to power sensors for structural health monitoring, such as those installed on bridges, wind turbines, and oil pipelines. The integrated network of the harvesters and sensors can be wireless as well as self-powered, which no longer needs the use of conventional batteries and thus avoids the associated motoring, replacement and recycling costs.

3 Modelling of the mechanical system

The equations modelling the mechanical system can be derived using the Lagrange-d^’Alembert principle which is an extended Hamilton’s principle in the presence of external forces, such as friction force. The corresponding variational equation is

$$ \mathop \int \limits_{{t_{1} }}^{{t_{2} }} \left[ {\delta \left( {T - U} \right) + \delta W} \right]{\text{d}}t = 0 $$

(1)

where T and U are the kinetic and the potential energies, W is the work done by the external force, i.e., the friction force (kinetic) $F_{\text{f}}$, and $W = \mathop \int \nolimits_{0}^{{L_{\text{b}} }} F_{\text{f}} \delta \left( {x - L_{\text{b}} } \right)w_{\text{rel}} \left( {x,t} \right){\text{d}}x$ where $L_{\text{b}}$ is the length of the cantilever beam, $\delta \left( {x - L_{\text{b}} } \right)$ is the Dirac’s delta function and $w_{\text{rel}} \left( {x,t} \right)$ is the transverse displacement relative to the base, $\delta$ represents an infinitesimal variation, and $t_{1}$ and $t_{2}$ are the start and the end times.

The kinetic energy of the cantilever beam can be given as

$$ T_{\text{b}} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} \rho_{\text{b}} A_{\text{b}} \left[ {\frac{{\partial w_{\text{rel}} \left( {x,t} \right)}}{\partial t} + \frac{{{\text{d}}g(t)}}{{{\text{d}}t}}} \right]^{2} {\text{d}}x $$

(2)

where $\rho_{\text{b}}$ and $A_{\text{b}}$ are the cantilever beam’s density and cross-sectional area, and $g(t)$ is the base displacement.

The kinetic energy of the slider is

$$ T_{\text{s}} = \frac{1}{2}m_{\text{s}} \left[ {\frac{{\partial w_{\text{rel}} \left( {x,t} \right)}}{\partial t} + \frac{{{\text{d}}g(t)}}{{{\text{d}}t}}} \right]_{{x = L_{\text{b}} }}^{2} + \frac{1}{2}J_{\text{s}} \left[ {\frac{{\partial^{2} w_{\text{rel}} \left( {x,t} \right)}}{\partial x\partial t}} \right]_{{x = L_{\text{b}} }}^{2} $$

(3)

where $m_{\text{s}}$ and $J_{\text{s}}$ are the mass and the second moment of inertia of the slider, where the latter is considered negligible for the small tip mass used in this harvester.

The elastic potential energy of the cantilever beam is

$$ U_{\text{b}} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} EI\left[ {\frac{{\partial^{2} w_{\text{rel}} \left( {x,t} \right)}}{{\partial x^{2} }}} \right]^{2} {\text{d}}x $$

(4)

where $E$ is the Young’s modulus of the beam and $I$ is the second moment of area of the beam’s cross section.

The relative locations of the magnets are shown in Fig. 3. Magnetic dipoles are used to represent them and the modelling work below follows Refs [42, 53].

Fig. 3

Relative locations of the magnets

The elastic potential energy provided by the magnetic field is given as

$$ U_{\text{m}} = - \mathop \sum \limits_{i = 1}^{n} {\mathbf{B}}_{i} \cdot {\varvec{\upmu}}_{\text{s}} $$

(5)

where $n$ is the number of fixed magnets (two in this case), ${\mathbf{B}}_{i}$ is the magnetic field generated by the $i$th fixed magnet at the location of the tip magnet (in the slider), ${\varvec{\upmu}}_{\text{s}}$ is the magnetic moment vector of the tip magnet and is expressed as

$$ {\varvec{\upmu}}_{\text{s}} = M_{\text{s}} V_{\text{s}} { \cos }\theta {\hat{\mathbf{e}}}_{x} + M_{\text{s}} V_{\text{s}} { \sin }\theta {\hat{\mathbf{e}}}_{y} $$

(6)

where $M_{\text{s}}$ is the magnitude of the magnetization of the magnet at the cantilever tip and can be estimated using the residual flux density $B_{\text{r}}$ as $M_{\text{s}} = B_{\text{r}} /\mu_{0}$, where $\mu_{0}$ is the vacuum permeability; $V_{\text{s}}$ is the magnet’s volume, $\theta$ is the slope of the beam at the tip, ${\hat{\mathbf{e}}}_{x}$ and ${\hat{\mathbf{e}}}_{y}$ are the unit vectors along the $x$- and the $y$-axis, respectively.

Similarly, the magnetic moment vectors for the fixed magnets are given as

$$ {\varvec{\upmu}}_{i} = M_{i} V_{i} {\hat{\mathbf{e}}}_{x} $$

(7)

where $M_{i}$ and $V_{i}$ are the magnitude of the magnetization and the volume of the ith fixed magnet, respectively.

The separation vectors from the positions of the fixed magnets to that of the tip magnet are expressed as

$$ \begin{aligned} & {\mathbf{r}}_{1} = - \left( {d_{x} + \delta_{x} } \right) {\hat{\mathbf{e}}}_{x} + \left[ {w_{\text{rel}} \left( {L_{\text{b}} ,t} \right) - d_{y} } \right] {\hat{\mathbf{e}}}_{y} \\ & {\mathbf{r}}_{2} = - \left( {d_{x} + \delta_{x} } \right){\hat{\mathbf{e}}}_{x} + \left[ {w_{\text{rel}} \left( {L_{\text{b}} ,t} \right) + d_{y} } \right] {\hat{\mathbf{e}}}_{y} \\ \end{aligned} $$

(8)

where $\delta_{x}$ is the longitudinal displacement of the tip and it can be derived as

$$ \delta_{x} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} \left[ {\frac{{\partial w_{\text{rel}} (x,t)}}{\partial x}} \right]^{2} {\text{d}}x $$

(9)

Then, the magnetic field generated by the $i$th fixed magnet upon the tip magnet is of the form

$$ {\mathbf{B}}_{i} = - \frac{{\mu_{0} }}{4\pi }\nabla \frac{{{\varvec{\upmu}}_{i} \cdot {\mathbf{r}}_{i} }}{{\left\| {{\mathbf{r}}_{i} } \right\|_{2}^{3} }} $$

(10)

where $\left\| \cdot \right\|_{2}$ denotes the Euclidean norm and $\nabla$ represents the gradient operator.

Assuming the cantilever beam is a uniform Euler–Bernoulli beam and supposing the first mode is dominant, the transverse displacement of the beam can be written in the form

$$ w_{\text{rel}} \left( {x,t} \right) = \phi (x)q\left( t \right) $$

(11)

where $q\left( t \right)$ is the temporal modal coordinate, $\phi (x)$ is the mode shape function

$$ \phi \left( x \right) = C\left\{ {\left[ {\cos \left( {\frac{\beta }{{L_{\text{b}} }}x} \right) - \cosh \left( {\frac{\beta }{{L_{\text{b}} }}x} \right)} \right] + \sigma \left[ {\sin \left( {\frac{\beta }{{L_{\text{b}} }}x} \right) - { \sinh }\left( {\frac{\beta }{{L_{\text{b}} }}x} \right)} \right]} \right\} $$

(12)

where $\sigma$ and $\beta$ are determined from the associated eigensystem, $C$ can be derived from the corresponding orthonormality conditions (the corresponding formulas are not given here).

Substituting Eq. (11) into Eqs. (2) to (5), one can get the expressions of kinetic energies of the beam and the slider and potential energies of the beam and the magnetic field in the form of the modal coordinate and mode shape function as

$$ \begin{aligned} & T_{\text{b}} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} \rho_{\text{b}} A_{\text{b}} \left( {\dot{q}^{2} \phi^{2} + \dot{g}^{2} + 2\dot{q}\phi \dot{g}} \right){\text{d}}x \\ & T_{\text{s}} = \frac{1}{2}m_{\text{s}} \left[ {\dot{q}^{2} \phi^{2} (L_{\text{b}} ) + \dot{g}^{2} + 2\dot{q}\phi (L_{\text{b}} )\dot{g}} \right] + \frac{1}{2}J_{\text{s}} \dot{q}^{2} \left[ {\phi^{'} } \right]_{{x = L_{\text{b}} }}^{2} \\ & U_{\text{b}} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} EIq^{2} \left( {\phi^{''} } \right)^{2} {\text{d}}x \\ & U_{\text{m}} = \mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{0} M_{i} V_{i} M_{\text{s}} V_{\text{s}} }}{4\pi }\left\{ {\frac{{{ \cos }\theta }}{{r_{i}^{3} }} - \frac{3}{{r_{i}^{5} }}\left[ {\left( {d_{x} + q^{2} \delta_{\text{c}} } \right)^{2} { \cos }\theta - \left( {d_{x} + q^{2} \delta_{\text{c}} } \right)\left[ {q\phi \left( {L_{\text{b}} } \right) + ( - 1)^{i} d_{y} } \right]{ \sin }\theta } \right]} \right\} \\ \end{aligned} $$

(13)

where the over-dot and the prime denote a derivative with respect to time, $t$, and location, $x$, respectively, $r_{i}$ are the Euclidean norms of vectors ${\mathbf{r}}_{i}$, and ${ \cos }\theta$ and ${ \sin }\theta$ can be obtained through geometrical approximation. These terms are given by

$$ r_{i} = \left[ {\left( {d_{x} + q^{2} \delta_{\text{c}} } \right)^{2} + \left[ {q\phi \left( {L_{\text{b}} } \right) + ( - 1)^{i} d_{y} } \right]^{2} } \right]^{1/2} $$

$$ \delta_{\text{c}} = \frac{1}{2}\mathop \int \limits_{0}^{{L_{\text{b}} }} \left( {\phi^{{\prime }} } \right)^{2} {\text{d}}x $$

$$ { \cos }\theta = 1 - \frac{1}{2}q^{2} \left[ {\phi^{{\prime }} } \right]_{{x = L_{\text{b}} }}^{2} $$

$$ { \sin }\theta = q\left[ {\phi^{{\prime }} } \right]_{{x = L_{\text{b}} }} $$

The Lagrangian of the mechanical system is expressed as

$$ L = T_{\text{b}} + T_{\text{s}} - U_{\text{b}} - U_{\text{m}} $$

(14)

Based on the Lagrange–d^’Alembert principle, which is equivalent to the Euler–Lagrange equations with external forces, the governing equation of the mechanical system can be obtained as

$$ \frac{\text{d}}{{{\text{d}}t}}\left( {\frac{\partial L}{{\partial \dot{q}}}} \right) - \frac{\partial L}{\partial q} = F_{\text{f}} \phi (L_{\text{b}} ) $$

(15)

where $F_{\text{f}}$ is the kinetic friction force exerting on the slider and will be detailed in the following section.

Incorporating Eqs. (11), (13) and (14) into Eq. (15) and applying the orthonormality conditions and including damping yield

$$ \ddot{q} + 2\zeta \omega \dot{q} + \omega^{2} q + F_{\text{m}} = \alpha \ddot{g} + F_{\text{f}} \phi (L_{\text{b}} ) $$

(16)

where $\zeta$ is the damping ratio, $\omega$ is the undamped natural frequency of the first mode of the beam without the tip mass, $\ddot{g} = \hat{A}{ \sin }\varphi \left( t \right)$ is the base excitation, where $\hat{A}$ is the acceleration amplitude and $\dot{\varphi }\left( t \right)/2\pi = f$ is the excitation frequency in Hz, and $F_{\text{m}}$ is the magnetic force exerted by the magnetic field at the tip. The expression for $F_{\text{m}}$ and those of $\alpha$ and $\omega$ are given as

$$ F_{\text{m}} = \frac{{\partial U_{\text{m}} }}{\partial q} $$

$$ \alpha = - \rho_{\text{b}} A_{\text{b}} \mathop \int \limits_{0}^{{L_{\text{b}} }} \phi {\text{d}}x - m_{\text{s}} \phi (L_{\text{b}} ) $$

$$ \omega = \beta^{2} \sqrt {\frac{EI}{{\rho_{\text{b}} A_{\text{b}} L_{\text{b}}^{4} }}} $$

Owing to the rotation of the cantilever tip mass, a circular contact area between the slider and the patches is more convenient for modelling the charge transfer process and calculating the friction force in between. As shown in Fig. 1b, $w_{\text{rel}}$ is the displacement of the slider, $A_{1}$ and $A_{2}$ are the contact areas between the slider and the EAP, and between the slider and the EIP, respectively. The slider has the same circular area as the EAP, and its radius is $r$ and hence $A_{1} + A_{2} = \pi r^{2}$.

According to Coulomb’s law of friction, the kinetic friction force on the slider can be given as

$$ F_{\text{f}} = - (\mu_{{{\text{k}}1}} A_{1} + \mu_{{{\text{k}}2}} A_{2} )\frac{N}{A}{\text{sgn}}\left( {\dot{q}\phi (L_{\text{b}} )} \right) $$

(17)

where $\mu_{{{\text{k}}1}}$ and $\mu_{{{\text{k}}2}}$ are the kinetic coefficients of friction between the slider and the EAP and between the slider and the EIP, respectively; ${\text{sgn}}\left( \cdot \right)$ is the signum function, $A$ is the total contact area, and $N$ is the normal force are expressed as

$$ N = C_{\text{r}} m_{\text{s}} {\text{g}} $$

$$ A = \pi r^{2} $$

$$ A_{1} = \left\{ {\begin{array}{*{20}l} {2r^{2} { \cos }^{ - 1} \left( {\frac{{\left| {q\phi (L_{\text{b}} )} \right|}}{2r}} \right) - \frac{1}{2}\left| {q\phi (L_{\text{b}} )} \right|\sqrt {4r^{2} - \left[ {q\phi (L_{\text{b}} )} \right]^{2} } , } \hfill & { \left| {q\phi (L_{\text{b}} )} \right| < 2r } \hfill \\ {0,} \hfill & {\left| {q\phi (L_{\text{b}} )} \right| \ge 2r} \hfill \\ \end{array} } \right. $$

$$ A_{2} = \left\{ {\begin{array}{*{20}l} {A - A_{1} ,} \hfill & {\left| {q\phi (L_{\text{b}} )} \right| < 2r} \hfill \\ {A,} \hfill & { \left| {q\phi (L_{\text{b}} )} \right| \ge 2r} \hfill \\ \end{array} } \right. $$

where $C_{\text{r}} \in \left[ {\begin{array}{*{20}c} 0 & 1 \\ \end{array} } \right]$ is the contact force ratio describing the contact situation between the slider and patches and ${\text{g}}$ is the gravitational acceleration.

Without loss of generality, stick–slip may happen between the slider and the patches during oscillation. During sticking, the beam slider system is in a dynamically balanced state and the slider has no motion relative to the moving base. The static friction force between the slider and the patches is given by

$$ f_{\text{s}} = - \left[ {EIq\left[ {\phi^{'''} } \right]_{{x = L_{\text{b}} }} - \frac{{F_{\text{m}} }}{{\phi (L_{\text{b}} )}} - \left( {m_{\text{s}} + m_{\text{e}} } \right)\ddot{g}} \right] $$

(18)

where $m_{\text{e}}$ is the equivalent mass of the cantilever beam and can be expressed as $m_{\text{e}} = \frac{33}{140}\rho_{\text{b}} A_{\text{b}} L_{\text{b}}$.

The maximal static friction force is as follows

$$ f_{ \hbox{max} } = \left\{ {\begin{array}{*{20}l} {\left( {\mu_{{{\text{s}}1}} A_{1} + \mu_{{{\text{s}}2}} A_{2} } \right)\frac{N}{A},} \hfill & {\left| {q\phi (L_{\text{b}} )} \right| < 2r} \hfill \\ {\mu_{{{\text{s}}2}} N,} \hfill & {\left| {q\phi (L_{\text{b}} )} \right| \ge 2r} \hfill \\ \end{array} } \right. $$

(19)

where $\mu_{{{\text{s}}1}}$ and $\mu_{{{\text{s}}2}}$ are the static coefficients of friction between the slider and the EAP and between the slider and the EIP, respectively.

The conditions for sticking are then

$$ \begin{aligned} & \dot{q}\phi (L_{\text{b}} ) = 0 \\ & \left| {f_{\text{s}} } \right| \le f_{ \hbox{max} } . \\ \end{aligned} $$

(20)

4 Modelling of the electrical system

According to Ref. [51], during slipping and when $\left| {w_{\text{rel}} \left( {L_{\text{b}} ,t} \right)} \right| < 2r$, the equivalent capacitance, i.e., $C_{\text{e}}$, and the open-circuit voltage, i.e., $V_{\text{oc}}$, for the presented triboelectric energy harvester can be derived as

$$ C_{\text{e}} = \frac{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} }}{{t_{\text{d}} }} $$

(21)

$$ V_{\text{oc}} = \frac{{\sigma A_{2} t_{\text{d}} }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} }} $$

(22)

where $\varepsilon_{0}$ and $\varepsilon_{\text{r}}$ are the vacuum permittivity and the relative permittivity of the top dielectric (PTFE), respectively, $t_{\text{d}}$ is the thickness of the top dielectric, and $\sigma$ is the tribo-charge surface density.

The relationship between the voltage across a resistor $R$ in an outer circuit, i.e., $V$, and the amount of transferred charges between electrodes, i.e., $Q$, of the harvester can be given by [4, 51]

$$ V = - \frac{1}{{C_{\text{e}} }}Q + V_{\text{oc}} $$

(23)

Applying Ohm’s law, i.e., $V = RI = R\frac{{{\text{d}}Q}}{{{\text{d}}t}}$, and substituting Eqs. (21) and (22) into Eq. (23) yield the differential equation

$$ R\frac{{{\text{d}}Q}}{{{\text{d}}t}} + \frac{{t_{\text{d}} }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} }}Q - \frac{{\sigma A_{2} t_{\text{d}} }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} }} = 0 $$

(24)

However, a singularity will occur in Eq. (24) when the top electrode (attached to the slider) fully slides out of the bottom one (the EAP), i.e., the denominators of the coefficients of the second and the third terms become zero when $w_{\text{rel}} \left( {L_{\text{b}} ,t} \right) \ge 2r$, and it will result in a zero equivalent capacitance and an infinitely large open-circuit voltage. Nevertheless, the transferred charges between the electrodes will saturate when the top electrode fully slides out of the bottom one [7, 51], and the open-circuit voltage $V_{\text{oc}}$ has been measured to be finite in experiment when the two electrodes fully slide out of each other [7]. To avoid this singularity, it is assumed that the top electrode will not fully slide out of the bottom electrode during oscillation. This will be monitored during the numerical simulations.

When sticking, the transferred charges between electrodes can be given by

$$ \begin{aligned} & Q = Q\left( {q = q_{\text{s}} } \right) = {\text{const}}. \\ & \frac{{{\text{d}}Q}}{{{\text{d}}t_{\text{s}} }} = 0 \\ \end{aligned} $$

(25)

where $q_{\text{s}}$ is the temporal modal coordinate when sticking motion starts to take place and $t_{\text{s}}$ is the corresponding time instant.

5 Numerical simulation

5.1 Numerical scheme

Since the order of magnitude of the vacuum permittivity $\varepsilon_{0}$ is − 12 and the load resistance $R$ can vary in a wide range, the ODE of the electrical output, i.e., Equation (24), is likely to be stiff. The TR-BDF2 (trapezoidal-backward differentiation formula of order two) method, which is an implicit single-step method of second-order accuracy, is prevalent in circuit and semiconductor simulations and has demonstrated good performance among various one-step methods [54,55,56,57] and, therefore, is used to solve Eq. (24).

The method is composed of two substeps: a trapezoidal step from $t_{n}$ to $t_{n + \gamma }$ and a second-order backward difference step from $t_{n + \gamma }$ to $t_{n + 1}$, where $t_{n + \gamma } = t_{n} + \gamma \Delta t_{n}$, $\gamma \in (0, 1)$ and $t_{n + 1} = t_{n} + \Delta t_{n}$, and $\Delta t_{n}$ is the time step. For the integration of a smooth system described by $\frac{{{\text{d}}q}}{{{\text{d}}t}} = h(q)$, the solution is firstly advanced from $t_{n}$ to $t_{n + \gamma }$ using the trapezoidal rule as

$$ q_{n + \gamma } - \gamma \frac{{\Delta t_{n} }}{2}h_{n + \gamma } = q_{n} + \gamma \frac{{\Delta t_{n} }}{2}h_{n} $$

(26)

In the second sub-step, the solution is then advanced from $t_{n + \gamma }$ to $t_{n + 1}$ using the second-order backwards difference rule as

$$ q_{n + 1} - \frac{1 - \gamma }{2 - \gamma }\Delta t_{n} h_{n + 1} = \frac{1}{\gamma (2 - \gamma )}q_{n + \gamma } - \frac{{(1 - \gamma )^{2} }}{\gamma (2 - \gamma )}q_{n} $$

(27)

The choice of $\gamma$ can affect the solution in many ways [54, 58], and it is suggested to take $\gamma = 2 - \sqrt 2$ because it results in the least truncation error [54], the same Jacobian matrix for both sub-steps (the Newton–Raphson method is used to solve the implicit difference equations), and the largest linearized stability region [58].

However, owing to the non-smoothness of the mechanical system, i.e., the sign change of the friction force and the stick–slip motion, the TR-BDF2 method can only be directly applied to steps without any non-smooth events. For a time step containing non-smooth events, only the trapezoidal rule or the TR method is used for the whole step. The derivation of the corresponding difference equations is given in “Appendix A”.

The values of the main parameters used in simulation are given in Table 1.

Table 1 The values of the main parameters used in simulation

5.2 The effect of the electrostatic force

Theoretically, there exists an attractive electrostatic force between the slider and the EAP because the dielectric on the slider, i.e., the PTFE film, and the EAP (Al) are oppositely charged. The electrostatic force can be expressed as

$$ F_{\text{e}} = \frac{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} V_{\text{c}}^{2} }}{{2t_{\text{d}}^{2} }} $$

(28)

And the voltage across a capacitor, i.e., $V_{\text{c}}$, can be given by

$$ V_{\text{c}} = \frac{Q}{{C_{\text{e}} }} $$

(29)

Substituting Eqs. (21) and (29) into Eq. (28), the electrostatic force can be rewritten as

$$ F_{\text{e}} = \frac{{Q^{2} }}{{2\varepsilon_{0} \varepsilon_{\text{r}} A_{1} }} $$

(30)

Since the harvester is of the sliding mode, the electrostatic force will act as part of the normal force exerted on the slider, and the new normal force is then

$$ N = C_{\text{r}} \left( {m_{\text{s}} {\text{g}} + F_{\text{e}} } \right) $$

(31)

The electrostatic force, therefore, may affect the system’s behaviour through friction, which is thus worth investigating. It is noted that the mechanical system described by Eq. (16) and the electrical system modelled by Eq. (24) are coupled when the electrostatic force is considered, in which case, the Jacobian matrix should be updated accordingly, and the new matrix elements are given in the appendix.

To simplify the comparison, the two fixed magnets are removed and the slider no longer experiences the magnetic force. The comparison of the tip displacements and the RMS voltage outputs under discrete numerical frequency sweeps (from 5 to 15 Hz with a step of 0.05 Hz) with and without the consideration of the electrostatic force (EF), is shown in Fig. 4. If the EF is adequately big, the model that includes the EF should produce a smaller amplitude response relative to the model without the EF because of the increase in the friction force caused by the EF. However, it can be seen in Fig. 4 that both the mechanical and electrical responses are almost identical in the two cases. Therefore, it can be concluded that the electrostatic force between the two electrodes (or between the slider and the EAP) for this TEH can be neglected and the EF will be not be modelled in the subsequent results. Nevertheless, the feedback of the EF into the electromechanical system may be taken into consideration in some miniaturized/MEMS-based electrostatic transducers, such as in Ref. [23].

Fig. 4

Comparisons of a the tip displacements and b the RMS voltage outputs of the cases with and without the electrostatic force (EF) under discrete numerical frequency sweeps when $\hat{A} = 0.10\,{\text{g}}$ and $C_{\text{r}} = 0.1$

5.3 Analysis of multistability

At first, friction is not considered. The total potential energy of the system, $U$, consists of two parts: the strain energy of the cantilever beam, $U_{\text{b}}$, and the magnetic potential energy, $U_{\text{m}}$. The variation of the strain energy of the cantilever beam only depends on the deflection of the beam. The magnetic potential energy, however, not only is related to the distance between the magnets but also the alignment of the magnets within the field. Therefore, the horizontal and vertical distances between magnets, i.e., $d_{x}$ and $d_{y}$, can notably affect the total potential energy, and thus the behaviour of the system.

When the horizontal distance is fixed at $d_{x} = 17$ mm, the variation of the total potential energy with the vertical distance and the tip displacement is shown in Fig. 5a, and the corresponding projections on the $U$-$w_{\text{rel}}$ plane are given in Fig. 5b. It can be seen that the system is monostable when the two fixed magnets are close (i.e., $d_{y}$ is small). In this case, the two fixed magnets act as one stronger magnet. As the two fixed magnets are placed farther away from each other, the system exhibits monostability, bistability, and weak tristability.

Fig. 5

The variation of the total potential energy ($U$) with the vertical distance ($d_{y}$) and the tip displacement ($w_{\text{rel}}$); a 3D surface plot and b its projections on the U-$w_{\text{rel}}$ plane

The system has different stabilities at different combinations of $d_{x}$ and $d_{y}$, and the possible scenarios are shown in Fig. 6 on the parametric plane of $d_{x}$-$d_{y}$ which is divided into three areas according to their stabilities. Therefore, the multistability of the friction-free (conservative) system can be determined analytically through the potential energy function, i.e., the sum of $U_{\text{b}}$ and $U_{\text{m}}$ in Eq. (13). Apparently, there is no potential energy function for a non-conservative force or system. Thus, the multistability of the system with the presence of friction can no longer be revealed by Eq. (13). However, it is interesting to see how those three areas will evolve on the parametric plane with the involvement of friction, and such a study of the effect of non-conservative forces on the multistability of a system is rare in the open literature.

Fig. 6

The system stability shown on the $d_{x}$-$d_{y}$ plane; black parametric area indicates monostability, blue indicates bistability, and red indicates tristability (For interpretation of the references to colours in this figure, readers are referred to the web version of this article)

Using numerical simulations, the system involving friction at each combination of $d_{x}$ and $d_{y}$ (a grid of $101 \times 101$ is used) is integrated at different excitation frequencies with different initial conditions. The algorithm used for the categorization of different types of stability is shown in a flowchart in Fig. 14 in “Appendix B”. Even though the multistability of the system is not dependent on the level of the external excitation, a proper selection of the excitation frequency and amplitude can improve the efficiency of the categorization. This is because in multistable systems, large excitations can easily result in interwell oscillations and small excitations will mostly lead to intrawell oscillations. In practice, this means that more tip displacement time history samples (or more sets of initial conditions) are needed to confidently determine the type of the multistability at a given combination of $d_{x}$ and $d_{y}$.

In simulation, the excitation amplitude $\hat{A}$ is fixed at 0.15 g, and two excitation frequencies, 3 Hz and 13 Hz, are used. Generally, it is easier for an oscillator to settle down into a well if the initial displacement is within the potential well (assuming the initial velocity is zero). Therefore, 15 samples of the initial tip displacement linearly spaced between − 0.025 m and − 0.001 m are used with each of the two excitation frequencies (initial velocities and transferred charge are zero). The categorized results with three different contact force ratios are shown in Fig. 7. It can be seen that the categorization scheme performs quite well, and the performance at boundaries can be enhanced by using more sets of initial conditions and/or excitation frequencies. In comparison with Fig. 6, the bistable and tristable areas have shrunk while the monostable area has enlarged. These differences between Figs. 6 and 7 seem to require only a small amount of friction to materialize. With the increase in the contact force ratio or the friction force, there is no obvious change of the areas of various stabilities.

Fig. 7

Numerically categorized different types of stability on the parametric plane of $d_{x}$ and $d_{y}$; a for $C_{r} = 0.001$, b for C_r = 0.1, and c for C_r = 0.5 (For interpretation of the references to colours in this figure, readers are referred to the web version of this article)

5.4 Comparisons between various types of stability

The dynamics of the system can be highly dependent on the magnetic field. The magnetic field is mostly influenced by the relative locations between the magnets, i.e., $d_{x}$ and $d_{y}$. As shown in the last section, the relative locations of magnets result in different types of stability. Besides, the system is non-smooth owing to the presence of friction. Thus, the steady state of the system can be dependent on the initial conditions [41], and various dynamic regimes can theoretically coexist, though only one of them can practically appear under certain conditions. Moreover, broad harvesting frequency span and large vibration amplitude are often beneficial to vibration energy harvesting. Therefore, discrete numerical frequency sweeps can be used to study the coexisting regimes (mainly the coexistence of intrawell and interwell oscillations) and compare between various types of stability.

To generate the discrete numerical frequency sweeps, 50 pairs of initial conditions ${\mathbf{w}}_{0} = \left( {w_{\text{rel}} \left( {L,0} \right), \dot{w}_{\text{rel}} \left( {L,0} \right),0} \right)$ are randomly selected from the set

$$ \left\{ {\left( {w_{\text{rel}} \left( {L,0} \right), \dot{w}_{\text{rel}} \left( {L,0} \right)} \right): w_{\text{rel}} \left( {L,0} \right) \in \left[ {\begin{array}{*{20}c} { - 0.025} & {0.025} \\ \end{array} } \right], \dot{w}_{\text{rel}} \left( {L,0} \right) \in \left[ {\begin{array}{*{20}c} { - 1.5} & {1.5} \\ \end{array} } \right]} \right\} $$

where both $w_{\text{rel}} \left( {L,0} \right)$ and $\dot{w}_{\text{rel}} \left( {L,0} \right)$ follow uniform distributions. The tip displacement $w_{\text{rel}} \left( {L,t} \right)$ with these initial conditions under the discrete numerical frequency sweeps are shown in Fig. 8. The maximal and minimal vibration amplitudes in steady states at each excitation frequency are marked and connected through vertical line in this figure (blue circles for interwell oscillations and red asterisk for intrawell oscillations except the results of the monostable system shown in Fig. 8a), and the response of the latest instant at one frequency is used as the initial conditions for the integration of the system under the next frequency. Obviously, there are no coexisting behaviours in the monostable system. However, intrawell and interwell oscillations can coexist in the bistable system. The situation is similar in the tristable system. The bistable system has the broadest frequency span over which the oscillation is at high amplitude. Therefore, bistability is superior to both monostability and tristability in terms of broadband energy harvesting.

Fig. 8

Tip vibration amplitudes under discrete numerical frequency sweeps of a monostable system with $d_{x} = 0.019\,{\text{m}}$ and $d_{y} = 0.020 \,{\text{m}}$, b bistable system with $d_{x} = 0.017 {\text{m}}$ and $d_{y} = 0.018 \,{\text{m}}$ and c tristable system with $d_{x} = 0.013\,{\text{m}}$ and $d_{y} = 0.025\,{\text{m}}$; $\hat{A} = 0.50\,{\text{g}}$ and $C_{\text{r}} = 0.1$

It is clear that there exist sudden jumps of the tip displacement in Fig. 8 in all the three kinds of systems. For a better explanation, the tip vibration amplitudes under the single forward (blue circles) and backward (red asterisks) frequency sweeps of the monostable system are shown in Fig. 9. It can be seen that there exist hysteresis and stiffness hardening, which are believed to be caused by the magnetic force.

Fig. 9

Tip vibration amplitudes under forward (blue circles) and backward (red asterisks) discrete numerical frequency sweeps; $d_{x} = 0.019\,{\text{m}}$$d_{y} = 0.020\,{\text{m}}$, $\hat{A} = 0.30\,{\text{g}}$, $C_{\text{r}} = 0.1$ and $w_{0} = \left( {0.001,0,0} \right)$ for both sweeps

5.5 The effect of the excitation level

In multistable systems, the excitation level often plays an important role in exciting high-energy orbit oscillations, especially when it comes to high and wide potential barriers between wells. The tip vibration amplitudes under discrete numerical frequency sweeps of the bistable system at different excitation levels are shown in Fig. 10. In combination with Fig. 9b, it can be observed that the frequency bandwidths at which interwell oscillations occur, shrinks considerably with the decrease in the excitation level. For reduction of excitation level from 0.5 to 0.3 g, there still exists a considerable frequency span over which the system performs interwell oscillations, though intrawell oscillations completely become dominant at high frequencies. A further decrease to 0.1 g results in a significant reduction of the frequency span for interwell oscillations, and a much smaller excitation level ceases to excite any interwell oscillations, see Fig. 10c.

Fig. 10

Tip vibration amplitudes under discrete numerical frequency sweeps of the bistable system at a$\hat{A} = 0.30\,{\text{g}}$, b$\hat{A} = 0.10\,{\text{g}}$, and c$\hat{A} = 0.01\,{\text{g}}$; $d_{x} = 0.017\,{\text{m}}$, $d_{y} = 0.018\,{\text{m}}$, $C_{\text{r}} = 0.1$

5.6 The effect of the friction

Triboelectrification is largely influenced by friction and can be enhanced through repeated rubbing [58]. Thus friction is essential in sliding-mode TEHs. On the other hand, friction is well known for dissipating energy by means of generating waves, atomic motions, and heat [59], and hence friction is also a limitation with regards to maximal energy harvesting. Therefore, the relationship between friction and energy harvesting (or electrical output) becomes even more complicated in TEHs and a study investigating this relationship is still missing. The mechanism by which friction affects triboelectrification is beyond the scope of this paper. Nevertheless, it is intended to study the effect of friction on the performance of the current TEH by investigating its influence on the system dynamics.

There are various combinations of triboelectric materials and each combination has its own values of coefficients of friction (both static and kinetic). Besides, the contact between the slider and the patches (and thus the friction) can be affected by the tilt of the tip slider and the assembly of the harvester. The tip vibration amplitudes under discrete numerical frequency sweeps of the bistable system with different values of contact force ratio are shown in Fig. 11. By combining with Fig. 10a, it can be seen that the distribution of the intrawell oscillation spreads from high frequencies down to relatively low frequencies with the increase in the contact force ratio. In addition, the jump frequency (due to the hardening effect) shifts towards lower frequencies. In comparison, low frequencies are unlikely to result in intrawell oscillations. Since the base excitation amplitude is fixed in terms of the applied acceleration, the resultant base displacement is inversely proportional to the forcing frequency square. Thus, the displacement response tends to be small at high frequencies.

Fig. 11

Tip vibration amplitudes under discrete numerical frequency sweeps of the bistable system under different contact force ratios b$C_{r} = 0.3$ and b$C_{r} = 0.5$; $\hat{A} = 0.30\,{\text{g}}$; $d_{x} = 0.017\,{\text{m}}$, $d_{y} = 0.018\,{\text{m}}$

5.7 Basins of attraction

Since the dynamics of the system can be sensitively dependent on the initial conditions, basins of attraction are computed to investigate the eventual dynamic behaviour of the system given a set of initial conditions.

The initial conditions ${\mathbf{w}}_{0} = \left( {w_{\text{rel}} \left( {L,0} \right), \dot{w}_{\text{rel}} \left( {L,0} \right),0} \right)$ are taken from the phase plane below using a grid of $250 \times 250$.

$$ \left\{ {\left( {w_{\text{rel}} \left( {L,0} \right), \dot{w}_{\text{rel}} \left( {L,0} \right)} \right): w_{\text{rel}} \left( {L,0} \right) \in \left[ {\begin{array}{*{20}c} { - 0.025} & {0.025} \\ \end{array} } \right], \dot{w}_{\text{rel}} \left( {L,0} \right) \in \left[ {\begin{array}{*{20}c} { - 1.5} & {1.5} \\ \end{array} } \right]} \right\} $$

The steady-state of the system at each sampling point is categorized according to the attractor onto which the system eventually settles down. The attractors are categorized into period-1 intrawell oscillations (shown in red), non-periodic or high-periodicity intrawell oscillations (in black), period-1 interwell oscillations (in blue), and non-periodic or high-periodicity interwell oscillations (in green).

The generated basins of attraction of the bistable system under the excitation of $\hat{A} = 0.3\,{\text{g}}$ and $\hat{A} = 0.5\,{\text{g}}$ at two different excitation frequencies are shown in Fig. 12. It can be seen that the increase in the excitation level has profound effects on the evolution of the basins of attraction. At $f = 8 {\text{Hz}}$, the spiral basins both for the period-1 interwell oscillations and the non-periodic or high-periodicity interwell oscillations become scattered with the increase in the excitation level, and the basin of the former becomes dominant, see Fig. 12a. At $f = 13 {\text{Hz}}$, the weak spiral structure at $\hat{A} = 0.3\,{\text{g}}$ disappears due to the rise of the excitation level to $\hat{A} = 0.5\,{\text{g}}$, and the basins of the non-periodic or high-periodicity intrawell oscillations and the period-1 interwell oscillations seem to intermingle in the off-centre area at $\hat{A} = 0.5\,{\text{g}}$. Additionally, it has been found that the system undergoes purely interwell oscillations at lower frequencies (such as at $f = 2\,{\text{Hz}}$) even for smaller excitation levels. The corresponding basins of attraction are purely green and are not presented here.

Fig. 12

Basins of attraction of the bistable system under the excitation of $\hat{A} = 0.30\,{\text{g}}$ (left column) and $\hat{A} = 0.50\,{\text{g}}$ (right column) at a$f = 8 {\text{Hz}}$ and b$f = 13\,{\text{Hz}}$; $d_{x} = 0.017\,{\text{m}}$, $d_{y} = 0.018\,{\text{m}}$, $C_{\text{r}} = 0.1$ (For interpretation of the references to colours in this figure, readers are referred to the web version of this article)

Similarly, the basins of attraction of the tristable system under the excitation of $\hat{A} = 0.3\,{\text{g}}$ and $\hat{A} = 0.5\,{\text{g}}$ at these two excitation frequencies are obtained and shown in Fig. 13. Interesting structures appear at $f = 8\,{\text{Hz}}$, see Fig. 13a. Basins of non-periodic or high-periodicity intrawell oscillations arise around the two side stable equilibria while the basin of period-1 intrawell oscillations emerges in the middle and has a fractal boundary. In addition, the tail of the spiral basin of the period-1 interwell oscillation is separated by an intermingled spiral basin of the period-1 and non-periodic or high-periodicity intrawell oscillations, and the increase in the excitation level thickens the tail of the basin of the period-1 interwell oscillation. At the relatively higher frequency of $f = 13\,{\text{Hz}}$, the system merely performs intrawell oscillations at a relatively low excitation level, and basins of interwell oscillations start to emerge in a fractal structure with the increase in the excitation level; see Fig. 13b. The tristable system only performs intrawell oscillations at low frequencies (such as at $f = 2\,{\text{Hz}}$) even when the excitation level is increased (the corresponding basins of attraction are not given here), and relative to the bistable system, the tristable system always settles down onto attractors of intrawell oscillations at low frequencies, which is not beneficial for energy harvesting.

Fig. 13

Basins of attraction of the tristable system under the excitation of $\hat{A} = 0.30\,{\text{g}}$ (left column) and $\hat{A} = 0.50\,{\text{g}}$ (right column) at a$f = 8\,{\text{Hz}}$ and b$f = 13\,{\text{Hz}}$; $d_{x} = 0.013 {\text{m}}$, $d_{y} = 0.025 {\text{m}}$, $C_{\text{r}} = 0.1$ (For interpretation of the references to colours in this figure, readers are referred to the web version of this article)

6 Conclusions

This paper presents the investigation of a new TEH which works in a sliding mode and involves three kinds of stabilities. The design concept is first introduced. The modelling of the mechanical vibration of a cantilever beam with a tip mass subjected to both magnetic and frictional forces under base excitation is then presented. The modelling of the electrical dynamics of the sliding-mode TEH based on the established mechanical system is presented accordingly. A numerical scheme, which is based on the TR-BDF2 method, for solving the system comprised of the non-smooth mechanical and the stiff electrical systems is discussed. Detailed numerical simulations are then carried out. This paper includes the first studies of both the sliding-mode TEH and magnetic multistability in TEHs from the perspectives of structural dynamics. The main conclusions are drawn as follows:

• 1. The comparison between the coupled and uncoupled electro-mechanical models (with and without the consideration of the electrostatic force between the electrodes, respectively) suggests that the electrostatic force can be ignored, which makes the uncoupled model preferable in the dynamical analysis.

• 2. The effect of the non-conservative force (the friction force) on the multistability of the system is investigated. It is found that the distribution of the multistability on the $d_{x}$–$d_{y}$ (two distances describing the relative locations of two magnets fixed to the base in relation to one magnet embedded in the slider) parametric plane changes when friction is involved, and the proportions of occurrence of the bistability and tristability decrease while that of the monostability increases.

• 3. Among the three types of stability, bistability is found to provide the broadest frequency band over which the system oscillates on high-energy orbits or in interwell oscillations. Additionally, the stiffness-hardening effect caused by the magnetic force appears in systems of all three kinds of stabilities.

• 4. The base excitation level plays an important role in bistable or multistable system for broadband energy harvesting. Low excitation levels will not enable the systems to cross the energy barriers between the potential wells and achieve interwell motions. In addition, the increase in friction will transfer intrawell oscillations from high frequencies down to low frequencies and shrink the frequency band over which energy harvesting is effective.

• 5. The study of the basins of attraction reveals that at low frequencies the bistable system can undergo purely interwell oscillations while the tristable system will undergo intrawell oscillations. Intermingled basins can appear in both bistable and tristable systems. An increase in the excitation level can break the basins into discrete pieces and/or points.

Appendices

Appendix A

To use the TR-BDF2 method, the second-order ODE of the equation of motion, i.e., Equation (16), is turned into the first-order ODE. Let $z_{1} = q$, $z_{2} = \dot{q}$, and $z_{3} = Q$. If there is no sticking motion, the governing equations of the whole system can be given as

$$ \begin{aligned} & \dot{z}_{1} = z_{2} \\ & \dot{z}_{2} = \alpha \ddot{g} + s_{1} \left[ {\left( {\mu_{k1} - \mu_{k2} } \right)A_{1} \left( {z_{1} } \right) + \mu_{k2} A} \right]\frac{N}{A}\phi (L_{\text{b}} ) - 2\zeta \omega z_{2} - \omega^{2} z_{1} \\ & \quad - \mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{0} M_{i} V_{i} M_{\text{s}} V_{\text{s}} }}{4\pi }\left[ {\frac{{G_{1} \left( {z_{1} } \right)}}{{r_{i}^{6} \left( {z_{1} } \right)}} - \frac{{3G_{2} \left( {z_{1} } \right)}}{{r_{i}^{10} \left( {z_{1} } \right)}}} \right] \\ & \dot{z}_{3} = \frac{{\sigma t_{\text{d}} \left[ {A - A_{1} \left( {z_{1} } \right)} \right] - t_{\text{d}} z_{3} }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} \left( {z_{1} } \right)R}} \\ \end{aligned} $$

(A.1)

where

$$ A_{1} \left( {z_{1} } \right) = 2r^{2} { \cos }^{ - 1} \left( {\frac{{s_{2} z_{1} \phi (L_{\text{b}} )}}{2r}} \right) - \frac{1}{2}s_{2} z_{1} \phi (L_{\text{b}} )\sqrt {4r^{2} - \left[ {z_{1} \phi (L_{\text{b}} )} \right]^{2} } $$

$$ G_{1} \left( {z_{1} } \right) = - r_{i}^{3} \left( {z_{1} } \right)z_{1} \left[ {\phi^{'} } \right]_{{x = L_{\text{b}} }}^{2} - 3r_{i}^{2} \left( {z_{1} } \right)\frac{{{\text{d}}r_{i} \left( {z_{1} } \right)}}{{{\text{d}}z_{1} }}{ \cos }\theta $$

$$ \begin{aligned} & G_{2} \left( {z_{1} } \right) = r_{i}^{5} \left( {z_{1} } \right)\left\{ { - z_{1} \left[ {\phi^{'} } \right]_{{x = L_{\text{b}} }}^{2} \left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right)^{2} + 4\delta_{\text{c}} z_{1} \left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right){ \cos }\theta - \left[ {d_{x} \phi \left( {L_{\text{b}} } \right) + 3\delta_{\text{c}} z_{1}^{2} \phi \left( {L_{\text{b}} } \right) + 2\left( { - 1} \right)^{i} d_{y} \delta_{\text{c}} z_{1} } \right]{ \sin }\theta - \left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right)\left[ {z_{1} \phi \left( {L_{\text{b}} } \right) + \left( { - 1} \right)^{i} d_{y} } \right]\left[ {\phi^{'} } \right]_{{x = L_{\text{b}} }} } \right\} \\ & \quad - 5r_{i}^{4} \left( {z_{1} } \right)\left\{ {\left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right)^{2} { \cos }\theta - \left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right)\left[ {z_{1} \phi \left( {L_{\text{b}} } \right) + \left( { - 1} \right)^{i} d_{y} } \right]{ \sin }\theta } \right\}\frac{{{\text{d}}r_{i} \left( {z_{1} } \right)}}{{{\text{d}}z_{1} }} \\ \end{aligned} $$

$$ \frac{{{\text{d}}r_{i} \left( {z_{1} } \right)}}{{{\text{d}}z_{1} }} = r_{i}^{ - 1} \left( {z_{1} } \right)\left[ {2\delta_{\text{c}} z_{1} \left( {d_{x} + z_{1}^{2} \delta_{\text{c}} } \right) + \left[ {z_{1} \phi \left( {L_{\text{b}} } \right) + \left( { - 1} \right)^{i} d_{y} } \right]\phi \left( {L_{\text{b}} } \right)} \right] $$

in which the expressions of $r_{i} \left( {z_{1} } \right)$, ${ \sin }\theta$ and ${ \cos }\theta$ can be obtained by replacing the $q$ s in the equations given in the context with $z_{1}$, and the values of $s_{1}$ and $s_{2}$ are given as

$$ s_{1} = \left\{ {\begin{array}{*{20}l} { - 1,} \hfill & {\dot{z}_{1} \phi \left( {L_{\text{b}} } \right) > 0} \hfill \\ {1,} \hfill & {\dot{z}_{1} \phi \left( {L_{\text{b}} } \right) < 0} \hfill \\ \end{array} } \right. $$

$$ s_{2} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {z_{1} \phi \left( {L_{\text{b}} } \right) > 0} \hfill \\ { - 1,} \hfill & {z_{1} \phi \left( {L_{\text{b}} } \right) < 0} \hfill \\ \end{array} } \right. $$

By applying the TR rule to the first sub-step, one can get the implicit difference equations as follows

$$ \begin{aligned} & z_{1,n + \gamma } - \gamma \frac{{\Delta t_{n} }}{2}z_{2,n + \gamma } = z_{1,n} + \gamma \frac{{\Delta \Delta t_{n} }}{2}z_{2,n} \\ & z_{2,n + \gamma } - \gamma \frac{{\Delta t_{n} }}{2}\left\{ {\alpha \ddot{g}_{n + \gamma } + s_{1} \left[ {\left( {\mu_{k1} - \mu_{k2} } \right)A_{1} \left( {z_{1,n + \gamma } } \right) + \mu_{k2} A} \right]\frac{N}{A}\phi (L_{\text{b}} ) - 2\zeta \omega z_{2,n + \gamma } - \omega^{2} z_{1,n + \gamma } - \mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{0} M_{i} V_{i} M_{\text{s}} V_{\text{s}} }}{4\pi }\left[ {\frac{{G_{1} \left( {z_{1,n + \gamma } } \right)}}{{r_{i}^{6} \left( {z_{1,n + \gamma } } \right)}} - \frac{{3G_{2} \left( {z_{1,n + \gamma } } \right)}}{{r_{i}^{10} \left( {z_{1,n + \gamma } } \right)}}} \right]} \right\} \\ & \quad = z_{2,n} + \gamma \frac{{\Delta t_{n} }}{2}\left\{ {\alpha \ddot{g}_{n} + s_{1} \left[ {\left( {\mu_{k1} - \mu_{k2} } \right)A_{1} \left( {z_{1,n} } \right) + \mu_{k2} A} \right]\frac{N}{A}\phi (L_{\text{b}} ) - 2\zeta \omega z_{2,n} - \omega^{2} z_{1,n} - \mathop \sum \limits_{i = 1}^{n} \frac{{\mu_{0} M_{i} V_{i} M_{\text{s}} V_{\text{s}} }}{4\pi }\left[ {\frac{{G_{1} \left( {z_{1,n} } \right)}}{{r_{i}^{6} \left( {z_{1,n} } \right)}} - \frac{{3G_{2} \left( {z_{1,n} } \right)}}{{r_{i}^{10} \left( {z_{1,n} } \right)}}} \right]} \right\} \\ & z_{3,n + \gamma } - \gamma \frac{{\Delta t_{n} }}{2}\frac{{\sigma t_{\text{d}} \left[ {A - A_{1} \left( {z_{1,n + \gamma } } \right)} \right] - t_{\text{d}} z_{3,n + \gamma } }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} \left( {z_{1,n + \gamma } } \right)R}} = z_{3,n} + \gamma \frac{{\Delta t_{n} }}{2}\frac{{\sigma t_{\text{d}} \left[ {A - A_{1} \left( {z_{1,n} } \right)} \right] - t_{\text{d}} z_{3,n} }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} \left( {z_{1,n} } \right)R}} \\ \end{aligned} $$

(A.2)

To use the Newton–Raphson method to solve these implicit difference equations for the state variables at the intermediate time instant, i.e., $z_{i,n + \gamma } (i = 1, 2, 3)$, the Jacobian matrix is first obtained as

$$ {\mathbf{J}} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{1} } \\ {{\mathbf{H}}_{2} } \\ {{\mathbf{H}}_{3} } \\ \end{array} } \right] $$

(A.3)

where the component matrices are

$$ {\mathbf{H}}_{1} = \left[ {\begin{array}{*{20}c} 1 & { - \gamma \frac{{\Delta t_{n} }}{2}} & 0 \\ \end{array} } \right] $$

$$ {\mathbf{H}}_{2} = \left[ {\begin{array}{*{20}c} {{\text{H}}_{21} } & {1 + \gamma \Delta t_{n} \zeta \omega } & 0 \\ \end{array} } \right] $$

$$ {\mathbf{H}}_{3} = \left[ {\begin{array}{*{20}c} {{\text{H}}_{31} } & 0 & {1 + } \\ \end{array} \frac{{\gamma \Delta t_{n} t_{\text{d}} }}{{2\varepsilon_{0} \varepsilon_{\text{r}} A_{1} \left( {z_{1,n + \gamma } } \right)R}}} \right] $$

in which

$$ {\text{H}}_{21} = - \frac{{\gamma \Delta t_{n} s_{1} \left( {\mu_{k1} - \mu_{k2} } \right)N\phi (L_{\text{b}} )}}{2A}\frac{{\partial A_{1} \left( {z_{1,n + \gamma } } \right)}}{{\partial z_{1,n + \gamma } }} + \gamma \omega^{2} \frac{{\Delta t_{n} }}{2} + \mathop \sum \limits_{i = 1}^{n} \frac{{\gamma \Delta t_{n} \mu_{0} M_{i} V_{i} M_{\text{s}} V_{\text{s}} }}{8\pi }\frac{\partial }{{\partial z_{1,n + \gamma } }}\left( {\frac{{G_{1} \left( {z_{1,n + \gamma } } \right)}}{{r_{i}^{6} \left( {z_{1,n + \gamma } } \right)}} - \frac{{3G_{2} \left( {z_{1,n + \gamma } } \right)}}{{r_{i}^{10} \left( {z_{1,n + \gamma } } \right)}}} \right) $$

$$ {\text{H}}_{31} = - \gamma \frac{{\Delta t_{n} }}{2}\frac{\partial }{{\partial z_{1,n + \gamma } }}\left( {\frac{{\sigma t_{\text{d}} \left[ {A - A_{1} \left( {z_{1,n + \gamma } } \right)} \right] - t_{\text{d}} z_{3,n + \gamma } }}{{\varepsilon_{0} \varepsilon_{\text{r}} A_{1} \left( {z_{1,n + \gamma } } \right)R}}} \right) $$

By using Eq. (27), one can obtain the difference equations for the BDF2 sub-step (the derived equations are not detailed here). The Jacobian matrix of the difference equations of the BDF2 sub-step is same with that of the TR sub-step if $\gamma = 2 - \sqrt 2$.

When the electrostatic force is involved, matrix ${\mathbf{H}}_{2}$ (${\mathbf{H}}_{2} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}_{2} \left( 1 \right)} & {{\mathbf{H}}_{2} \left( 2 \right)} & {{\mathbf{H}}_{2} \left( 3 \right)} \\ \end{array} } \right]$) should be updated, and the updated elements are

$$ \begin{aligned} & {\mathbf{H}}_{2} \left( 1 \right) = {\text{H}}_{21} + \frac{{\gamma \Delta t_{n} s_{1} \mu_{k2} z_{3,n + \gamma }^{2} C_{\text{r}} \phi (L_{\text{b}} )}}{{4\varepsilon_{0} \varepsilon_{\text{r}} A_{1}^{2} }}\frac{{\partial A_{1} \left( {z_{1,n + \gamma } } \right)}}{{\partial z_{1,n + \gamma } }} \\ & {\mathbf{H}}_{2} \left( 3 \right) = - \frac{{\gamma \Delta t_{n} s_{1} z_{3,n + \gamma } C_{\text{r}} \phi (L_{\text{b}} )}}{{2\varepsilon_{0} \varepsilon_{\text{r}} }}\left( {\frac{{\mu_{k1} - \mu_{k2} }}{A} + \frac{{\mu_{k2} }}{{A_{1} }}} \right) \\ \end{aligned} $$

(A.4)

Appendix B

The algorithm used for the categorization of different types of stability is shown in a flowchart in Fig. 14, where ${\mathbf{f}}$ is the excitation frequency array, ${\mathbf{w}}_{{{\mathbf{rel}}}} \left( {L,0} \right)$ the initial tip displacement array, $t_{\text{s}}$ the time within steady state, and $\varvec{w}_{{{\mathbf{mean}}}} \left( h \right)$ the mean of $\varvec{w}_{{{\mathbf{max}}2}} \left( h \right)$ and $\varvec{w}_{{{\mathbf{min}}2}} \left( h \right)$.

Fig. 14

Flowchart of the algorithm used for the categorization of different types of stability