1 Introduction

The impacting systems represent a field of research that is fundamentally important and it has a wide range of applications. The recent fundamental studies on impact oscillators include those with a focus on grazing bifurcations [2,3,4,5,6,7], control [8, 9], uncertainty [10], energy flow and harvesting [11, 12] and nonlinear resonances [13,14,15]. Machining [16], drilling [17] and rotor dynamics [18] can be given as illustrative examples of application fields. The understanding of impact mechanics is essential for getting a deeper insight into the intricacies of dynamical systems with impacts, which have been studied by various authors, e.g., [19,20,21]. In some cases, impacts are an essential part of system’s operation, for example, in drill-string jarring operations [22], Resonance Enhanced Drilling (RED) [23,24,25] and seismic mitigation [26]. In other instances, the impact phenomena can be a side effect due to ageing of the mechanical parts, thermal deformation or design tolerances. In any case, impacts introduce nonlinearities to those systems, which in turn may induce various behaviours ranging from periodic responses of high period to chaotic motions [27, 28]. On one hand, these new types of vibration can be highly undesired, for example in machining where imperfections are directly related to nonlinear phenomena [16, 29]. On the other hand, in some applications such as energy harvesters, one can take advantage of chaotic phenomena to improve the frequency bandwidth of energy generation [30].

The cantilever beam impact dynamics has been a target of various studies reviewed in [31], including experimental and numerical investigations that can be traced back to the decade of 1980 [32,33,34]. Most of them consider hard impact behaviour, where a simple Newton law with a restitution coefficient is used to describe the impact. The works done by Wagg et al. [35,36,37] try to characterize the coefficient of restitution and predict the dynamics of the cantilever system. Other studies look directly into the first grazing incidence and the dynamics of the system near this frequency [13, 38]. Taking into account soft impacts, newer numerical studies focus on adding other nonlinearities to the system, like nonlinear damping [39] or structural nonlinearities [40], while experimental studies manage to identify the stiffness of the impact beam through the system dynamics and indirect measurements [41].

From the experimental point of view, early studies often had focus on hard impacts [42, 43] while more recent ones look more into symmetrical [44] and asymmetrical soft impacts [45]. A series of publications from the Centre of Applied Dynamics at Aberdeen presents the dynamics of a base excited experimental impact oscillator rig, with a free one-sided impact [46,47,48,49] and a pre-loaded impact [50]. In these studies, various nonlinear phenomena were observed experimentally including chaos and periodic motions of high period, but a much wider range of responses were found numerically including co-existing of multiple attractors. The base excited experimental apparatus could only provide indirect excitation through the structure, which means that amplitude was coupled with the excitation frequency.

One of the most interesting phenomena observed in impact systems is the multi-stability including co-existing of impacting and non-impacting responses. It can be observed when depending on the initial conditions, the system’s response gravitates towards one of two (or more) co-existing attractors. This phenomenon occurs in many systems including rattling gears systems [51], impact oscillators [52] and in rotor systems [53, 54]. Depending on the specific system requirements, switching between co-existing attractors should either be avoided to increase operational lifetime or desired to rapidly bring the system from one stable state to another while minimizing the control effort and the transition time. The latter case can have useful applications in smart structures (see, e.g. [55, 56]) or energy harvesters, e.g. [57]. Several control strategies can be implemented to perform or suppress switching between co-existing attractors, such as intermittent (see e.g. [52]) or extended time delayed feedback control [58, 59]. Bifurcation control can also be studied following the works by De Paula et al. [60, 61]. Having a versatile experimental rig, which exhibits multi-stability, would be ideal for implementing, testing and developing new control strategies.

Recently, a new experimental impact oscillator rig with easily tunable parameters has been developed by the Centre for Applied Dynamics Research at the University of Aberdeen, and the detailed description of the rig, its design and capabilities, together with preliminary experimental results, are given in [1]. The current work is a comprehensive study on the oscillator described in [1], and it focuses on parameters characterisation and comparison with the results obtained using previous base excited impact oscillator rig.

Fig. 1
figure 1

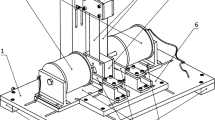
Schematic diagram (left) and the corresponding photograph (right) of the experimental rig. The main components of the system are highlighted as: sensors (eddy current probe, piezoelectric load cell and accelerometers mounted on the mass, frame and impact beam) in blue, coil in orange, main mass in grey, impact beams in pink, leaf springs in red and permanent magnet in white

Full size image

This paper is structured as follows. In Sect. 2 the experimental rig schematics, its main components and data acquisition system are described. This section also discusses calibration of the sensors, the influence of higher-order modes of the impact beam, the precision of measurements and filtering. In addition, a new way to process the experimental data based on the periodicity of the response is proposed here. Subsequently, a full characterization of the excitation system is performed and the numerical model of the rig is introduced, together with its experimentally calibrated parameters. In Sect. 3, we compare the results obtained using the base excited impact oscillator rig [49] with the ones recorded using the new design, where the compared scenarios are constructed so that both rigs exhibit the same grazing frequency. In Sect. 4, bifurcation analysis using frequency and forcing amplitude as branching parameters are presented to explore the rich dynamics of the experimental rig. A particular attention is paid to the observed chaotic experimental response, and the 0-1 test is performed on the experimental results, whereas Lyapunov exponents are calculated numerically to verify the chaotic behaviour. Finally, a sensitivity analysis is performed studying how frequency bifurcation diagrams change with different gaps and forcing amplitudes. In Sect. 5, concluding remarks are drawn.

2 Experimental apparatus

In this work, dynamics of the impact oscillator rig shown in Fig. 1 is studied. A detailed description of the experimental apparatus and its design is presented in [1], while the current configuration is depicted in Fig. 1. The oscillator is fixed upon a base plate that provides alignment of components and flexibility of their placement. The rig includes a stabilizing rigid structure mounted on the base to suppress any spurious external vibrations that may affect the main mass (highlighted in grey in Fig. 1). The main mass is attached to the leaf springs (coloured in red), which themselves are clamped between two beams and a grooved base, ensuring their proper alignment. A strong permanent cylindrical neodymium magnet, with a \(15~\hbox {kg}\) pull, is attached to one side of the main mass by a stainless steel rod and fixed by two stainless steel nuts. The magnet itself is placed approximately in the middle of an in-house built coil (coloured in orange), capable of generating a variable magnetic field that provides direct excitation to the system. The inner diameter of the coil is close to the diameter of the cylindrical magnet to improve the coupling between the varying field of the coil and the fixed field of the magnet, thereby limiting the nonlinear effects in the excitation system.

The current I running through the coil is supplied by a signal generator composed of a current amplifier, two power suppliers and an National Instruments board. There are secondary supports on either side of the main mass (coloured in pink) made of the beams which can be inserted to produce impact. The distance g between an impact beam and the main mass can be adjusted by a treated bolt fixed to the tip of the beam. The beams themselves can be replaced by others made of different material and/or cross sections. The design accommodates a range of leaf springs lengths ranging from 50 to \(120~\hbox {mm}\).

Fig. 2
figure 2

Fast Fourier transforms of a acceleration of the mass, b acceleration of the impact beam, c acceleration of the base and d time histories of the beam displacement (in black) and acceleration (in blue) used to measure impact events and vibration of the impact beam. Vertical red dashed lines indicate where the impacts start and green vertical lines indicate when they finish. The impact boundary is shown by dashed grey horizontal line

Full size image

The experimental data are collected by a LabView data acquisition system. The coil input current is measured by a multimeter, while the displacement of the main mass is measured by an eddy current probe attached to the structure close to the base of the leaf springs. Accelerometers are placed on the structure, the main mass and the impact beam, as shown in Fig. 1. Finally, a piezoelectric load cell is also placed between the coil and the rigid structure to measure the reaction force due to the mass excitation.

The eddy current probe signal is calibrated using the voltage measured for specified displacements of the mass, which are generated by inserting metric gauges between the main mass and a fixed support. A linear correlation between eddy current signal and displacements is obtained for interval from \(-8\) up to \(8~\hbox {mm}\), with a proportional coefficient of \(-1.76~\hbox {mm/V}\). Note that the reference signal is always considered to be the one where the mass is at the rest position. The force sensor is also calibrated and compensates for the static force due to the weight of the coil acting on the sensor, which is measured when there is no input current. All other calibrations are as specified by the sensors’ manufacturers. It is important to highlight a need for the eddy current probe to be re-calibrated after any change to the leaf springs (length, position or type).

2.1 Filtering of structural support and higher-mode vibrations

An analysis of the structural vibration (especially the higher modes) is carried out in order to eliminate the spurious vibration that can interfere with the experiment and to verify whether any higher modes of the impact beam or leaf spring are activated and to determine their influence on the main behaviour of the oscillator. Hence, the fast Fourier transforms (FFT) of the main mass, structure’s and impact beam accelerations are calculated for the worst-case scenario with the maximum excitation amplitude of \(3.2~\hbox {N}\) and forcing frequency of \(11~\hbox {Hz}\).

The acceleration of the main mass is obtained by differentiating the displacement signal, and its FFT shown in Fig. 2a presents three families of peaks, one below \(100~\hbox {Hz}\), one between \(100~\hbox {Hz}\) and \(200~\hbox {Hz}\) and another around \(250~\hbox {Hz}\). Analysing the FFT of the acceleration for the impact beam (Fig. 2b), it becomes clear that the peaks around \(250~\hbox {Hz}\) are in fact related to the first mode of vibration of the impact beam, which frequency is calculated as \(252~\hbox {Hz}\). Therefore, it appears that only the first mode of vibration should be considered, as no other peaks are distinguishable from the background noise. The FFT of the base acceleration (Fig. 2c) reveals that the peaks from \(100~\hbox {Hz}\) to \(200~\hbox {Hz}\) are related to the vibrations of the rig’s structure. Finally, the peaks below \(100~\hbox {Hz}\) can be identified as higher modes of vibration of the leaf springs. The influence of these modes is much smaller than the first mode when the position signal is considered, roughly one order of magnitude less than the first mode, and have no direct influence on the main behaviour of the system for the analysed cases. Finally, in Fig. 2d one can verify that a sudden peak of the impact beam acceleration signal can be identified when an impact event occurs, which in turn allow us to precisely measure the time of impact and the gap between the impact beam and the main mass. As shown, the vibration of the beam does not interfere with the position of impact events or produce any secondary impacts, since there is only one peak on the base acceleration for each impact and no interference in the displacement of the mass from previous impacts have been observed. Hence, the gap between the impact beam and the mass can be considered as constant throughout the analysis presented in this work.

2.2 New technique for data processing of periodic responses

The main idea behind the method is to use the periodicity of the system response itself to filter noise and obtain a clearer trajectory.

Let us consider an experimental observation of a system which has a periodic behaviour of period \(T_\mathrm{{res}}\). These observations are generated for one variable of the system with a sampling frequency of \(f_s\), producing an experimental data set \(\mathbf {P}\). In this case for each period of the response, a number of points \(N_\mathrm{{per}}=T_\mathrm{{res}} f_s\) are recorded. The data set \(\mathbf {P}\) is recorded with N data points that is a multiple of \(N_\mathrm{{per}}\). We assume that each measurement will have a noise component \(\mathbf {E}\). Hence, \(\mathbf {P}\) follows the equation:

$$\begin{aligned} \mathbf {P}[n]=\mathbf {S}[n]+\mathbf {E}[n] , \end{aligned}$$
(1)

where \(\mathbf {S}\) is noise-free system response. The idea of this processing is to create another set, \(\mathbf {P}^{*}\), containing \(N_\mathrm{{per}}\) points, which are obtained by the averages of all points in \(\mathbf {P}\) separated by \(N_\mathrm{{per}}\). This is expressed by the following equation:

$$\begin{aligned}&\mathbf {P}^{*}[n]=\dfrac{1}{N_\mathrm{{aver}}}\sum _{j=1}^{N_\mathrm{{aver}}} \mathbf {P}[n+(j-1)N_\mathrm{{per}}],\nonumber \\&\quad \text {with }n=1,2,...,N_\mathrm{{per}}, \end{aligned}$$
(2)

where \(N_\mathrm{{aver}}=N/N_\mathrm{{per}}\). Substituting Eq. (1) into Eq. (2), one obtains:

$$\begin{aligned} \mathbf {P}^{*}[n]= & {} \dfrac{1}{N_\mathrm{{aver}}}\sum _{j=1}^{N_\mathrm{{aver}}} \mathbf {S}[n+(j-1)N_\mathrm{{per}}] \nonumber \\&+ \dfrac{1}{N_\mathrm{{aver}}}\sum _{j=1}^{N_\mathrm{{aver}}} \mathbf {E}[n+(j-1)N_\mathrm{{per}}]. \end{aligned}$$
(3)

The first term of Eq. (3) represents the average of a constant value as \(\mathbf {S}[n]=\mathbf {S}[n+N_\mathrm{{per}}]\), while the second term is the expected value of a noise process sampled with a period \(T_\mathrm{{res}}\), divided by \(N_\mathrm{{aver}}\). Given \(N_\mathrm{{aver}}\) is large enough the second term of Eq. 3 vanishes leading to:

$$\begin{aligned} \mathbf {P}^{*}[n]=\mathbf {S}[n]. \end{aligned}$$
(4)

Hence, this averaging technique can eliminate noise and improve clarity of the periodic signal.

Figure 3a shows an example of experimental data (\(\mathbf {P}\)) extracted from a dynamical system exhibiting a period-3 behaviour. Figure 3b depicts the system phase diagram with noise in grey for 100 periods of excitation while the nominal behaviour (\(\mathbf {S}\)) is shown in blue. Figure 3c demonstrates 10 periods of the raw data superimposed in grey and the processed data \(\mathbf {P}^{*}\) in red, while Fig. 3d compares the phase diagram of the processed signals with the nominal response. It is clear that the proposed technique can remove noise from the raw data available and depicts a behaviour much closer to the nominal one.

Fig. 3
figure 3

Example of the experimental data set \(\mathbf {P}\) and processed set \(\mathbf {P}^{*}\) compared with the nominal data \(\mathbf {S}\). a Raw data set \(\mathbf {P}\) time series; b phase diagram of the experimental data in grey and nominal response in blue; c 10 superimposed periods of the raw data set in grey and processed data, \(\mathbf {P}^{*}\), in red; d phase diagram comparing the nominal behaviour in blue and processed data set in red

Full size image

When the technique is applied to identify period M responses of a dynamical system, or if the period of the signal is unknown, extra considerations are necessary. Consider that the method is applied to verify a period \(T_\mathrm{{res}}\) response when a system is exhibiting a period \(2T_\mathrm{{res}}\) response. In this case, Eq. (3), becomes:

$$\begin{aligned} \mathbf {P}^{*}[n]= & {} \dfrac{1}{N_\mathrm{{aver}}}\bigg (\sum _{j=1}^{N_\mathrm{{aver}}/2} \mathbf {S}[n+(2j-2)N_\mathrm{{per}}]\nonumber \\&+\sum _{j=1}^{N_\mathrm{{aver}}/2}\mathbf {S}[n+(2j-1)N_\mathrm{{per}}]\nonumber \\&+\sum _{j=1}^{N_\mathrm{{aver}}} \mathbf {E}[n+(j-1)N_\mathrm{{per}}\bigg ) . \end{aligned}$$
(5)

And using the periodicity of the signal and the white noise properties, Eq. (5) becomes:

$$\begin{aligned} \mathbf {P}^{*}[n]=\frac{\mathbf {S}[n]+\mathbf {S}[n+N_\mathrm{{per}}]}{2}. \end{aligned}$$
(6)

Equation (6) generates a closed orbit on a phase diagram that traces the average of the period 2 orbit points separated by \(T_\mathrm{{res}}\) in time. This orbit can be misread as a \(T_\mathrm{{res}}\) periodic one. In fact, it can be proven following the same procedure that any response or sum of responses with a period \(M T_\mathrm{{res}}\) will generate a closed orbit and can be mistaken to a period \(T_\mathrm{{res}}\) response. Therefore, it is proposed to use \(2N_\mathrm{{per}}\) points and a period of \(2T_\mathrm{{res}}\) to calculate \(\mathbf {P}^{*}\) for the identification of a period \(T_\mathrm{{res}}\) behaviour, modifying Eq. (2) to:

$$\begin{aligned}&\mathbf {P}^{*}[n]=\dfrac{2}{N_\mathrm{{aver}}}\sum _{j=1}^{N_\mathrm{{aver}}/2} \mathbf {P}[n+(j-1)2N_\mathrm{{per}}],\nonumber \\&\quad \text {with }n=1,2,...,2 N_\mathrm{{per}}. \end{aligned}$$
(7)

This ensures that any higher periodic signal will produce at least a set \(\mathbf {P}^{*}\) with a period of \(2T_\mathrm{{res}}\), which can be distinguished from a \(T_\mathrm{{res}}\) response.

Finally, if there is no periodic behaviour with period \(M T_\mathrm{{res}}\) or \(T_\mathrm{{res}}/M\), the proposed method will produce a very small or open orbit on the phase diagram. It is also important to highlight that this method is very sensitive to the period \(T_\mathrm{{res}}\) and small variations may result in phase diagrams with only destructive interference.

Fig. 4
figure 4

Example of processed data using the proposed method. a Raw Signal; b processed data for a period-8 response; c processed data for a period-2 response. In this case a numerical period-4 response is observed; however, this solution is discarded as it represents a numerical artefact produced by the method; d processed data with a slightly different period than the original one, which leads only to destructive interference

Full size image

Figure 4 presents an example of the cases discussed above. The raw data (\(\mathbf {P}\)) containing a period-8 orbit are shown in Fig. 4a, while Fig. 4b depicts the processed data (\(\mathbf {P}^{*}\)) obtained by targeting this period-8 orbit. Figure 4c depicts a test using the same set of data when the processed data are obtained targeting a non-existent period-2 response. In this case, the data should be discarded as the orbit displays a period-4 behaviour instead of the tested period-2 response; thereby, the closed orbit is just a numerical artefact. Figure 4d depicts the case where the number of recorded points in processed set \(2 N_\mathrm{{per}}\) is slightly changed from the periodic solution giving only destructive interference, as there is no dynamic response of the considered period in the data, which should be discarded.

2.3 Excitation system calibration

A calibration of the electromagnetic exciter to determine a constant describing a relationship between the applied current and the generated force on the mass was carried out. Four different tests were carried out to establish the limits of a linear relation between the applied current and the reaction force: \(F_\mathrm{{coil}}(t)=aI(t)\). In the first case we fix the main mass in its resting position and vary the coil current, while measuring the reaction force. Initially, the current changes quasi-statically. As shown in Fig. 5a, a linear response is observed for the currents up to \(4.0~\hbox {A}\), with a constant \(a=-0.799~\hbox {N}\)/A and variance of \(0.005~\hbox {N}/\hbox {A}\). This indicates that the maximum force amplitude generated through the excitation system can be up to \(3.2~\hbox {N}\).

Fig. 5
figure 5

Tests for characterization of force versus current dependency. Experimental data are shown by black points and calibrated linear fit as red line. a Static current I versus measured force at the rest position. b Correlation of voltage versus displacement for the main mass on the static current free vibration test. c Force versus applied current for a sinusoidal signal, \(f=10~\hbox {Hz}\). d Linear parameter a versus forcing frequency of a sinusoidal signal. The linear relations hold for all values of current and force achieved, and no apparent hysteresis is presented in the obtained curves either

Full size image

The second test is focused on analysing the correlation between current and mass displacement to verify whether the moving magnet has any effect on the coils current I. The main mass was displaced up to \(\pm \,6~\hbox {mm}\) from its rest position and, afterwards, released to perform free vibration motion. These tests were performed with various static currents in the coil ranging from \(-3.5\) to \(3.5~\hbox {A}\). No meaningful correlation has been observed between position and current, as the maximum correlation achieved \(cor(I;x) = 0.008\), shown in Fig. 5b, was not significant.

The effect of hysteresis was explored in the third test. Two experiments were performed for each frequency in the range varying from 6 to \(10~\hbox {Hz}\). One test was carried out by applying a sinusoidal signal to the coil current and fixing the mass into its rest position, and the other is conducted by applying a sinusoidal current to the coil and letting the mass to vibrate freely. In Fig. 5c we depict the force signal against position for a frequency of \(10~\hbox {Hz}\) in a dynamical test, which is the most likely scenario to exhibit hysteretic behaviour. However, no hysteresis was found for this excitation frequency or for any other frequencies up to \(10~\hbox {Hz}\).

The fourth test was performed with a sinusoidal current \(I(t) = I_0\hbox {sin}(2\pi t/f)\) for various frequencies f, with an amplitude \(I_0=2.5~\hbox {A}\). The proportionality coefficient between measured reaction force and current in relation \(F_\mathrm{{coil}}(t)=aI(t)\) was obtained to verify the influence of frequency variations, as shown in Fig. 5d. The proportional coefficient a varies less than 0.5 % and almost all values are within precision tolerance, hence, the coefficient a can be considered constant for the frequency range from 6 to \(10~\hbox {Hz}\), for which experiments were performed. Also, the linear dependency between the current and the force holds for all frequencies analysed. Hence, the linear relation between the current and the reaction force appears to be valid for signals with frequencies from 6 to \(10~\hbox {Hz}\), current amplitudes up to \(2.5~\hbox {A}\) and displacements from \(-6\) to \(6~\hbox {mm}\) resulting in:

$$\begin{aligned} F_\mathrm{{coil}}(t)=-0.799I(t). \end{aligned}$$
(8)

As shown in Fig. 6, for a non-impacting and impacting cases of gap \(g=0.94~\hbox {mm}\) for a sinusoidal excitation signal of \(f=9.1~\hbox {Hz}\) and \(I_0=0.298~\hbox {A}\), a good agreement between the measured reaction force (in black) and the force predicted (in red) using Eq. (8) has been obtained.

Fig. 6
figure 6

Tests for characterization of force versus current dependency. Input current time histories for a non-impacting and c impacting cases. Predicted and measured force time histories in red and black respectively for b non-impacting case d impacting case

Full size image

2.4 Numerical model and parameter identification

The schematic of the mathematical model representing the experimental rig, depicted in Fig. 1, can be seen in Fig. 7. Here a piecewise linear impact oscillator model is used to describe the displacement X of the main mass m. The excitation force, \(F_\mathrm{{coil}}\), is applied directly onto the main mass, while the leaf springs are characterised by a linear stiffness \(k_1\). The impact beam can be described by another linear spring of stiffness \(k_2\), separated from the main mass by gap g. A linear viscous damping coefficient c is used to represent an equivalent damping in the system, leading to the equation of motion:

$$\begin{aligned} m \ddot{X}=-k_1 X- c \dot{X} - k_2 (X-g) H(X-g) + F_\mathrm{{coil}}(t),\nonumber \\ \end{aligned}$$
(9)

where H is a Heaviside step function and dot represents derivative with respect to time t.

Fig. 7
figure 7

Schematics of physical model representing the experimental rig (Fig. 1), with its main components: main mass m, leaf springs of stiffness \(k_1\), impact beam of stiffness \(k_2\), coil generating force \(F_\mathrm{{coil}}\) and the gap g between the main mass and the impact beam

Full size image

If non-dimensional variables are considered, the equation of motion takes the form:

$$\begin{aligned} x''=- x - 2 \zeta x'-\kappa (x-1)H(x-1)+\dfrac{F_\mathrm{{coil}}(\tau /\omega _0)}{k_1g}, \end{aligned}$$
(10)

where \(x=X/g\), \(\tau =\omega _0 t\), \(\omega _0=\sqrt{k_1/m}\), \(\zeta =c/\left( 2\sqrt{k_1m}\right) \), \(\kappa =k_2/k_1\) and prime represents derivatives with respect to non-dimensional time \(\tau \).

Two types of excitation are studied in this work. The first one is the excitation provided by the previous design [47] that has the frequency and amplitude of vibration coupled

$$\begin{aligned} F_\mathrm{{coil}}=\dfrac{A_d \omega ^2}{\omega _0^2}\sin \left( \dfrac{\omega }{\omega _0}\tau \right) , \end{aligned}$$
(11)

where \(A_d\) is amplitude of the base displacement. The second one is the uncoupled excitation given by:

$$\begin{aligned} F_\mathrm{{coil}}=A \sin \left( \dfrac{\omega }{\omega _0}\tau \right) , \end{aligned}$$
(12)

where A is the forcing amplitude.

There are three main parameters that dictate the dynamics of Eq. (10) for both types of excitation, which are the stiffness ratio \(\kappa =k_2/k_1\), the damping ratio \(\zeta =c/\left( 2\sqrt{k_1m}\right) \) and the relation between dynamic force amplitude and static force necessary to reach the gap \(F^*=A/k_1g\). When using the uncoupled excitation, these parameters can be easily independently modified on the rig by exchanging the impact beam (\(k_2\)), the main mass (m) and the forcing amplitude (A) or gap (g), respectively, which enables us to explore a range of possible phenomena and ensures the rig versatility. However, if the coupled excitation is used, the coefficient \(F^*\) becomes \(F^*=A_d \omega ^2/\left( \omega _0^2g\right) \) and the non-dimensional parameters cannot be easily independently changed.

Fig. 8
figure 8

Non-impacting responses at \(I_0=0.125~\hbox {A}\): a Amplitude diagram with frequency as a branching parameter. Numerical results are shown by black line, experimental data points obtained for increasing frequency (forward diagram) are given by blue triangles and experimental data points obtained for decreasing frequency (backward diagram) are shown by red circles. b Trajectories on the phase plane (velocity [mm/s] versus displacement [mm]) at the excitation frequency of \(8.20~\hbox {Hz}\). (Linear model response is shown in black and experimental orbit is in red.) c Co-existing orbits recorded experimentally at \(9.15~\hbox {Hz}\) compared with the numerical responses obtained using nonlinear cubic restoring force at \(9.21~\hbox {Hz}\). d An FFT of the displacement at the frequency of \(9.15~\hbox {Hz}\) for high-amplitude orbit. Dashed vertical black lines represent frequencies where the phase portraits are taken. (Color figure online)

Full size image

All experimental results are recorded for a leaf spring of \(125~\hbox {mm}\) length, a lumped mass which include the main mass, steel rod, and a magnet, in total \(1.325~\hbox {kg}\) and a mild steel impact beam with dimensions of \(6\times 15\times 105~\hbox {mm}\). Bifurcation diagrams are constructed by discarding the first \(40~\hbox {s}\) of data for each quasi static variation of frequency and afterwards recording 100 periods of the excitation force. This ensures that at least 240 periods are discarded as transient responses of the system. Finally, the resolution of bifurcation diagrams goes to \(0.01~\hbox {Hz}\) to capture grazing.

Initially, the impact beam is removed, so that the spring stiffness \(k_1\) and the viscous linear damping coefficient c can be identified. Six free vibration tests were performed with different initial conditions to extract the linear parameters, while keeping the displacements within \(-4\) to \(4~\hbox {mm}\) to ensure a linear behaviour of the leaf spring. A damped sine function is fitted into each set of experimental data to extract the linear coefficients leading to \(k=4331~\hbox {N}/\hbox {m}\) with variance of \(150~\hbox {N}/\hbox {m}\) and \(c=0.27~\hbox {kg}/\hbox {s}^2\) with variance of \(0.01~\hbox {kg}/\hbox {s}^2\).

To determine the range of the linear oscillator model applicability, a series of tests has been carried out with the secondary constraints removed. The current amplitude was fixed at \(I_0=0.125~\hbox {A}\), and amplitude bifurcation diagram was constructed by varying the excitation frequency. Figure 8a presents amplitude of the calculated linear system response shown by black line and the amplitude of the experimental responses shown by red circles for increasing frequency and by blue triangles for decreasing frequency. As can be seen from this figure, the experimental data follow the linear model prediction up to displacement amplitude of \(6~\hbox {mm}\), and an example of the trajectory comparison is given in Fig. 8b for frequency of \(8.2~\hbox {Hz}\). However, near the resonance peak at approximately \(9.15~\hbox {Hz}\) two co-existing attractors are recorded experimentally, which are demonstrated in Fig. 8c. An FFT of displacement recorded for the high-amplitude orbit is shown in Fig. 8d where the peaks related to higher-order frequencies have an amplitude two orders of magnitude lower than the peak associated with the period-1 behaviour, demonstrating that nonlinearities are present in the response. Our analysis indicates that this co-existence of attractors and associated hardening behaviour is related to the large deformation of the leaf springs [62] which at these amplitudes can no longer be described by a linear stiffness. Modelling the restoring force of the leaf spring with a cubic nonlinearity as \(F_\mathrm{{leaf}}=-k_1 x-k_bx^3\) where \(k_b=3,368,400~\hbox {N}/\hbox {m}^3\), one can trace the numerical orbits depicted in Fig. 8c achieving a good correspondence with the recorded experimental orbits. However, as can be seen from Fig. 8c there is still a symmetry break which is not currently explained by the cubic restoring force. Hence, to lower the influence of the cubic term and the asymmetric nonlinearity a restriction of displacements of \(6~\hbox {mm}\) should be placed.

As the main objective of this study is to explore the grazing incidence and the nonlinearities arising from the impacts, we restrict the displacements of the main mass to the interval from \(-6\) to \(6~\hbox {mm}\). This ensures that any other nonlinear effects are mitigated, enabling us to focus on the impact nonlinearities only.

Initially, the gap between the main mass and the impact beam is set and measured precisely by analysing the peaks on the beam acceleration signal resulting in a value of \(g=0.94~\hbox {mm}\). It was also verified using amplitude diagrams shown in Fig. 9a (increasing frequency) and Fig. 9b (decreasing frequency) which are constructed using experimental data by taking the maximum positive value of displacement of the steady state response. The data were recorded at the input current amplitude of \(I_0=0.215~\hbox {A}\) (non-dimensional forcing amplitude of \(F^*=0.042\)). In Fig. 9a, b the amplitude of the linear non-impacting response is shown by pink line, experimental responses are depicted by blue and red circles, and numerical non-impacting and impacting responses are given by black and green triangles. As can be seen from this figure at the frequency of 8.87 Hz, the non-impacting response becomes an impacting one resulting in impact oscillator response amplitude deviating from pink line of linear oscillator amplitude. Thus, the value of the amplitude at this frequency allows to establish the gap value of \(g=0.95\) which is in agreement with the method using the beam acceleration peaks. The beam’s stiffness \(k_2\) in Eq. (9) can be determined by fitting the model forward amplitude diagram to the experimental data in the region after grazing incidence. Using this method, we obtain \(k_2=87125~\hbox {N}/\hbox {m}\) with variance of \(1500~\hbox {N}/\hbox {m}\), which is in agreement with the stiffness estimated by a quasi static test.

Fig. 9
figure 9

Amplitude bifurcation diagram with frequency as a branching parameter for a gap of \(g=0.94~\hbox {mm}\) and input current amplitude \(I_0=0.215~\hbox {A}\). The dashed grey horizontal line represents the impact boundary, whereas the black dashed vertical lines represent the frequencies where the trajectories on the phase planes are shown. a Forward (increasing frequency) numerical and experimental bifurcation diagrams. b Backward (decreasing frequency) experimental and numerical bifurcation diagrams. c Trajectories on the phase planes [velocity (mm/s) versus displacement (mm)] at 8.7, 8.87, 9.15 and \(9.5~\hbox {Hz}\), respectively. Dashed grey vertical lines represent the impact boundary on the phase plane. Colours of the trajectories are the same as for the system responses shown in the bifurcation diagrams

Full size image

The forward amplitude diagram shown in Fig. 9a follows the non-impacting model solution up to the first grazing incidence. Afterwards, it presents an impacting response that extends for frequencies where the linear non-impacting system amplitude is smaller than the gap. On the other hand, the backward diagram from Fig. 9b follows the linear non-impacting system for all amplitudes lower than the gap. This highlights the coexistence of impacting and non-impacting responses after the second grazing frequency around 9.30 Hz (Fig. 9c). At the first grazing incidence at \(8.87~\hbox {Hz}\) results also suggest a continuous transition instead of an abrupt change of the system periodicity or amplitude. All results were tested to verify that the system presented a period-1 behaviour. Finally, the impacting model has good agreement with the experimental results, as shown in the diagrams and trajectories in Fig. 9c.

Fig. 10
figure 10

Bifurcation diagram with frequency as control parameter, an impact gap \(g=0.66~\hbox {mm}\) and input current amplitude \(I_0=1.00~\hbox {A}\). Black dashed vertical lines represent the frequencies where the trajectories on the phase planes are shown. a Forward numerical and experimental bifurcation diagrams. b Backward numerical and experimental bifurcation diagrams. c Period-3, d period-7 and e period-2 responses recorded at frequencies of \(8.00~\hbox {Hz}\), \(7.65~\hbox {Hz}\) and \(8.26~\hbox {Hz}\), respectively. The numerical period-2 orbit is computed for \(f=8.18~\hbox {Hz}\). Dashed grey vertical lines represent the impact boundary on the phase plane. Colours of the trajectories are the same as for the system responses shown in the bifurcation diagrams

Full size image

Some additional experimental studies were carried and are presented here to further validate the mathematical model demonstrating more complicated dynamic behaviour. Bifurcation diagrams are constructed for a gap of \(g=0.66~\hbox {mm}\) and excitation current \(I_0=1.000~\hbox {A}\) (non-dimensional forcing amplitude of \(F^*=0.28\)) and depicted in Figs. 10a, b for increasing and decreasing frequency respectively, while trajectories on the phase planes are shown in Figs. 10c-e for selected values of frequencies. In the forward diagram shown in Fig. 10a, a non-impacting response is observed until grazing incidence occurring at \(7.66~\hbox {Hz}\), where the system response jumps to a period-7 orbit which is demonstrated in Fig. 10d. As the frequency increases, the period-7 orbit disappears at \(7.7~\hbox {Hz}\) and the system responds with a period-3 orbit shown in Fig 10c. Further increases in frequency make the system jump to an impacting period-1 orbit at \(8.22~\hbox {Hz}\), which is maintained up to the end of the diagram. In the backward diagram shown in Fig 10b, at around \(8.2~\hbox {Hz}\) the system undergoes a transition from the impacting period-1 to a period-2 orbit which has only one impact per period. As the frequency decreases, the grazing incidence of period-2 orbit’s inner loop, depicted in Fig. 10e, causes it to become unstable and disappear at around \(8.14~\hbox {Hz}\) where a jump to period-3 orbit is observed which lasts up to \(7.68\hbox {Hz}\). Further decreases in frequency leads to the same behaviour as was observed and discussed in the forward diagram. The results presented demonstrate a good agreement between the numerical and experimental data as seen on the selected trajectories and bifurcation diagrams for almost all frequencies. The only discrepancy is recorded for the transition of the period-1 to the period-2 orbit on the backward diagram at the range from 8.14 to \(8.25~\hbox {Hz}\). Finally, because of this discrepancy the numerical data present the coexistence of attractors between 8.14 and \(8.2~\hbox {Hz}\) while the experimental results do not present this co-existence.

3 Comparison with the base excited system

In this section, the new rig experimental responses are compared with the previously recorded results for the base excited impact oscillator rig presented by Ing et al. [45,46,47, 49, 50], with particular attention to the behaviour shown in [45] and [49]. Note that all experiments presented in this section are performed for the gap of \(g=0.84~\hbox {mm}\). The other parameters of the new rig were chosen so that the non-dimensional coefficients are closely related to the ones reported in the literature and the rig is able to reproduce the same scenarios. To fine tune the non-dimensional grazing frequency \(\omega _g/\omega _0\) to the ones presented in the literature, the excitation frequency was set to the desired value and then the forcing amplitude was raised until grazing incidence occurs. As the experimental results in [45, 49] are obtained using a value \(y_0=1~\hbox {mm}\) as its non-dimensionalisation reference, we perform a re-scaling of the new results by the quotient of old, \(g_\mathrm{{old}}\), and new, \(g_{new}\), gaps, leading to a coefficient \(g_\mathrm{{old}}/(y_0g_{new})\), which compensates for the non-dimensional units in previous works.

Fig. 11
figure 11

Comparison between the experimental bifurcation diagrams for the base and directly excited impact oscillator rigs. The non-dimensional parameters are close to the ones presented in [45] for the base excited system, while the forcing amplitude is adjusted so that grazing occurs for the same frequency. a Experimental results for the base excited impact oscillator rig for the base excitation amplitude of 0.38 mm, [45]. b New experimental results with the same phase as in (a). c Phase portraits of new experimental results for the non-dimensional frequency of 0.847,  0.885,  0.915 and 0.930, respectively. d Numerical bifurcation diagram for the base excited impact oscillator, [45]. e New experimental bifurcation diagram with the same phase as in (d). f Numerical phase portraits for the non-dimensional frequency of 0.853, 0.885, 0.9151 and 0.930, respectively. The black dashed lines indicate the frequencies where the trajectories on the phase plane are presented, and dashed grey lines represent the impact boundary on the phase planes

Full size image
Fig. 12
figure 12

Comparison between the experimental bifurcation diagrams for the base and directly excited impact oscillator rigs. The non-dimensional parameters are close to the ones presented in [49] for the base excited system, while the forcing amplitude is adjusted so that grazing occurs for the same frequency. a Experimental results for the base excited impact oscillator rig for the base excitation amplitude of 0.44 mm, [49]. b New experimental results with the same phase as in (a). c Phase portraits and Poincaré maps of new experimental results for the non-dimensional frequency of 0.802,  0.840,  0.91 and 0.912 respectively. d Numerical bifurcation diagram for the base excited impact oscillator rig, [49]. e New experimental diagram with the same phase as in (a). f Numerical phase portraits and Poincaré maps for the non-dimensional frequency of 0.802,  0.840,  0.910 and 0.915, respectively. The black dashed lines indicate the frequencies where the trajectories on the phase plane are presented, and dashed grey lines represent the impact boundary on the phase planes

Full size image

In Fig. 11 we compare the diagrams obtained using the new impact oscillator rig with the bifurcation diagram presented in [45] and produced using the based driven system. In order to generate the new experimental results for this comparison, for each value of the applied excitation frequency, \(\omega \), the value of the excitation amplitude was adjusted to simulate the base excitation, i.e. \(A(\omega )=A_d \omega ^2\). Figures 11a and b present the results obtained by two different rigs for the same phase shift. Comparing these two figures, one can clearly see a better frequency resolution as well as a better spatial resolution which enables one to distinguish the period three branches at the non-dimensional frequency of 0.88, while the old results only depict two clearly distinguishable branches. The bifurcation diagrams shown in Fig. 11d, e depict the comparison between the previously published numerical results and new experimental ones generated for the phase shift used to compute the numerical diagram. The diagrams show a great similarity to each other, which is also confirmed using the phase portraits as can be seen in Fig. 11c and Fig. 11f demonstrating experimental and numerical results, respectively.

Figure 12 shows the second scenario used for the comparison. The published experimental results [49] are shown in Fig. 12a and new experimental results in Fig. 12b. Again, one can see a better resolution in displacement and frequency for the new results, which provides better insight into the system’s behaviour. If the experimental results, shown in Fig. 12d, are compared (for the same phase shift) to the published numerical data [49] (Fig. 12c), one can verify that the new results have a greater similarity to the predicted responses, specially around the chaotic response at the non-dimensional frequency of 0.9, where previously published experimental results present only the chaotic region at different frequencies.

Moreover, in the second case a great number of coexistent attractors are identified at the non-dimensional frequency of 0.8044 [49], which are shown in the numerical bifurcation diagram in Fig. 13a. However, previous studies failed to capture these co-existing orbits experimentally as the basins of attraction have a fractal structure and the co-existence only happened in a small frequency interval, as shown in Fig. 13b [49]. Using the new rig, we perform a series of tests aimed at locating experimentally the co-existing attractors by two different approaches. The first one is based on stabilising the system response on a more favourable frequency, which has a less fractal basin of attraction and afterwards slowly bringing the system to the desired frequency. In the second approach, we apply small perturbations to one of the responses, which basically means that the system is restarted from different initial conditions. Both of those two approaches can be successfully applied, as there is a much better control on the excitation of the system and a higher frequency resolution. This allows us to obtain the co-existing attractors, which have an excellent agreement with the predicted orbits, as shown in Fig.13c, d. The experimental results were enhanced using the new processing technique proposed in Sect. 3, allowing us to observe the period-3 and period-8 orbits, which were not distinguishable otherwise due to noise.

Fig. 13
figure 13

Numerical and experimental analysis of co-existing orbits. a Numerical bifurcation diagram displaying various co-existent attractors (the dashed black line represents the frequency where the trajectories on the phase plane are plotted) [49]. b Basins of attraction for co-existent orbits at non-dimensional frequency of 0.8043 [49]. c Numerical phase portraits of co-existent orbits at non-dimensional frequency of 0.8044. d Experimental phase portraits of co-existent orbits at non-dimensional frequency of 0.804. The period-8 response is extracted by applying the average method to 100 recorded periods of excitation. Vertical dashed grey lines represent the impact boundary, and Poincaré sections of the orbits are marked by red dots. (Color figure online)

Full size image

4 Mass excited impact oscillator

In this section, we investigate the dynamics of the impact oscillator with uncoupled excitation numerically and experimentally by constructing bifurcation diagrams near grazing using frequency and forcing amplitude as the branching parameters. Two cases are considered: in the first one, frequency bifurcation diagrams are obtained for different values of the excitation amplitudes and gaps, while in the second one the excitation amplitude is used as branching parameter. It should be noted that the latter case was not previously analysed in the base excited impact oscillator.

4.1 System dynamics

In Fig. 14 the system dynamics is explored for the current amplitude \(I_0=1.10~\hbox {A}\) and the same gap of \(g=0.66~\hbox {mm}\) as in Fig 10 (\(F^*=0.305\)). This slight change in the system parameters results in numerical and experimental bifurcation diagrams displaying a very different scenario, shown in Fig. 14a, b, than the one presented earlier in Fig. 10a, b for the model validation. For lower frequencies, both numerical and experimental diagrams present a non-impacting response until approximately \(f=7.30~\hbox {Hz}\), where a region with co-existence of solutions begin. At this frequency, a long-lasting chaotic transient behaviour is observed shown in Fig. 14c together with the stable non-impacting solution. The co-existence of a non-impacting period-1 orbit and period-3 orbit with two impacts per period presented in Fig. 14d lasts up to \(7.5~\hbox {Hz}\). In the interval from 7.61 to \(7.72~\hbox {Hz}\) period-3 orbit with two impacts per period and period-3 orbit with one impact per period co-exist and they are shown in Fig. 14e. Between \(7.72~\hbox {Hz}\) and \(8.20~\hbox {Hz}\) only the period-3 orbit with one impact per period is present, and around \(8.20~\hbox {Hz}\) this period-3 orbit co-exists with a period-2 orbit with two impacts per period as shown in Fig. 14f.

Finally, above \(8.24~\hbox {Hz}\), an impacting period-1 orbit persists up to the end of the frequency range analysed. Experimental and numerical results are in a very good agreement. The only discrepancy visible is on the backward diagram near the jump from a period-2 orbit to the period-3 behaviour due to small variations in excitation amplitude.

Fig. 14
figure 14

Bifurcation diagram obtained with the frequency as branching parameter with the gap \(g=0.66~\hbox {mm}\) and input current amplitude \(I_0=1.100~\hbox {A}\). Black dashed vertical lines represent the frequencies where the trajectories on the phase planes are shown. Forward and backward a numerical and b experimental bifurcation diagrams. c Non-impacting period-1 orbit and Poincaré section of the chaotic transient response, d co-existing period-1 and period-3 orbits, e co-existing period-3 orbits and f co-existing period-3 and period-2 orbits. Phase portraits are presented at 7.31, \(7.40~\hbox {Hz}\), \(7.65~\hbox {Hz}\) and \(8.26~\hbox {Hz}\), respectively. The numerical period-2 orbit in panel f is calculated at \(8.20~\hbox {Hz}\). Dashed grey vertical lines represent the impact boundary on the phase plane. Colours of the trajectories are the same as for the system responses shown in the bifurcation diagrams

Full size image
Fig. 15
figure 15

Bifurcation diagram obtained with the frequency as branching parameter with the gap \(g=0.61~\hbox {mm}\) and input current amplitude \(I_0=1.250~\hbox {A}\). Black dashed vertical lines represent the frequencies where the trajectories on the phase planes are shown. The dashed magenta lines represent the chaotic behaviour analysed in Fig. 16. Forward and backward a numerical and b experimental bifurcation diagrams. c Co-existing Period-1 and period-7 orbits at \(7.16~\hbox {Hz}\). d Co-existing period-5 and period-2 orbits at \(7.25~\hbox {Hz}\). e Second pair of co-existing period-5 and period-2 orbits at \(7.40~\hbox {Hz}\). f Poincaré section of chaotic behaviour and co-existing period-3 response at \(8.00~\hbox {Hz}\). Dashed grey vertical lines represent the impact boundary on the phase plane. Colours of the trajectories and Poincaré section are the same as for the system responses shown in the bifurcation diagrams

Full size image
Fig. 16
figure 16

Analysis of the experimentally observed chaotic behaviour. a Numerical and experimental phase portraits in grey [velocity (mm/s) versus displacement (mm)] with the corresponding Poincaré sections in red. b Detailed Poincaré section for numerical and experimental results, respectively. c 0-1 test convergence with number of points analysed. d Maximum Lyapunov exponent convergence for the numerical data

Full size image

Numerical and experimental bifurcation diagrams recorded for the gap of \(g=0.61~\hbox {mm}\) and the current amplitude \(I_0=1.250~\hbox {A}\) (\(F^*=0.38\)) are shown in Fig. 15a, b respectively. These diagrams present a period-1 non-impacting orbit up to the grazing frequency of 7.18 Hz. At \(7.1~\hbox {Hz}\) this non-impacting orbit co-exists with a period-7 orbit with four impacts per period shown in Fig. 15c that lasts up to \(7.15~\hbox {Hz}\), where a narrow band of chaos [48] is recorded for a frequency range of \(0.03~\hbox {Hz}\). Shortly after grazing the system presents the co-existence of a period-2 orbit with one impact per period and a period-5 orbit with three impacts per period which are shown in Fig. 15d. At \(7.38~\hbox {Hz}\) other period-5 orbit with two impacts per period is observed which still co-exists with the period-2 orbit as shown in Fig. 15e until the frequency of \(7.52~\hbox {Hz}\). At \(7.80~\hbox {Hz}\) a chaotic response appears on both diagrams and the structure of the calculated chaotic attractor is demonstrated in Figure 15f. It is observed until \(8.24~\hbox {Hz}\) where it is suddenly replaced by a period-1 impacting response which lasts until the end of the diagram. The main dynamics of the impact oscillator rig is captured by the model; however, in the chaotic region observed in the experimental rig, the model indicates windows of a period-3 orbit seen in the lower panel of Fig. 15f, hinting on the co-existence of chaotic and periodic behaviours. Hence, another forward and backward experimental diagrams, starting at 7.99 and \(8.04~\hbox {Hz}\) respectively, were recorded to capture this attractor and the results, shown by purple squares in Fig. 15b, show the predicted orbit in almost the same frequency range as the calibrated numerical model. Finally, as results presented above suggest a possible large chaotic region in the window between 7.80 and \(8.25~\hbox {Hz}\), further analysis is carried out for the frequency of \(8.20~\hbox {Hz}\).

Experimental and numerical Poincaré maps were obtained to verify the chaotic behaviour at \(f=8.20~\hbox {Hz}\), and the results are shown in Fig. 16a, b. The stroboscopic Poincaré maps were constructed by taking 4000 points once per period of the external force. Also, the sampling frequency of the experimental data was set to be a multiple integer of the forcing frequency. This was to minimize the frequency differences when constructing the experimental Poincaré maps. As can be seen from Fig. 16b, the simulated and experimental Poincaré maps have similar structures; however, the experimental data are more defused due to signal noise. Lyapunov exponents were calculated resulting in a maximum exponent of \(\lambda _{max}=4.14~\hbox {bit/s}\), which indicates that the motion obtained numerically is chaotic, and the convergence of the maximum Lyapunov exponent can be seen in Fig. 16d. To analyse the experimental response, a 0-1 test described in [63] was performed on the experimental data, using the correlation method on the modified mean square displacement, which mitigates the influence of noise on the data. If the result K(N) tends to 0 as the number of points N increases, the response is regular while if K(N) tends to 1, the test indicates a chaotic response. The convergence of K(N) to 1 is shown in Fig. 16c, clearly pointing towards a chaotic motion.

Fig. 17
figure 17

Bifurcation diagram obtained with input current amplitude as branching parameter with a gap of \(g=0.84~\hbox {mm}\) and forcing frequency \(f=7.3~\hbox {Hz}\). Forward and backward a numerical and b experimental bifurcation diagrams. Here black dashed lines indicate the amplitude values where the trajectories on the phase planes are shown in c numerical and d experimental Poincaré section of chaotic response at current amplitudes of \(1.605~\hbox {A}\). e Period-2 orbit near internal grazing at \(1.635~\hbox {A}\). f Period-2 solution recorded at \(1.755~\hbox {A}\). The dashed grey lines represent impact boundaries. Colours of the trajectories and Poincaré sections are the same as for the system responses shown in the bifurcation diagrams. (Color figure online)

Full size image

Bifurcations diagrams with the current amplitude as the branching parameter were constructed next. The diagrams shown in Fig. 17a, b are obtained for a forcing frequency of \(7.3~\hbox {Hz}\) around the first grazing incidence. As can be seen from these figures, at lower amplitudes, the linear non-impacting response is observed up to the first grazing incidence where a narrow band region of chaotic behaviour [48] appears. As the current amplitude increases, it is followed by a period-2 response with one impact per period which is observed until the end of the diagrams. Both backward and forward diagrams present the same behaviour. The numerical Poincaré map of the chaotic response at 1.605 A is shown in Fig. 17c. This observed behaviour of the system is the same as the one reported in the earlier studies [49], where period-1 impacting orbit loses stability shortly after grazing where the region of chaotic attractor begins. The unstable period-1 orbit then undergoes period doubling bifurcation which results in period-2 orbit with two impacts per period. Shortly after, the grazing incidence of one of the loops of the period-2 orbit creates a period-2 orbit with one impact per period which becomes stable. This grazing incidence ends the region of the chaotic behaviour. The recorded period-2 response with one impact per period is shown in Fig. 17d, and as the current amplitude increases, the non-impacting loop of this period-2 response moves away from the impact boundary as shown in Fig. 17e. Finally, it should be noted that the experimental bifurcation diagrams and phase portraits have a good agreement with the calibrated numerical model.

Fig. 18
figure 18

Bifurcation diagram obtained with input current amplitude as branching parameter with a gap of \(g=0.84~\hbox {mm}\) and forcing frequency \(f=7.60~\hbox {Hz}\). Forward and backward a numerical and b experimental bifurcation diagrams. Here black dashed lines indicate the amplitude values where the trajectories on the phase planes are shown. c Co-existing impacting period-3 orbit with two impacts and non-impacting orbits recorded at current amplitude of \(1.325~\hbox {A}\). d Co-existing period-3 orbits at \(1.370~\hbox {A}\). e Numerical (upper panel) and experimental (lower panel) Poincaré maps of chaotic attractor at \(1.580~\hbox {A}\). f Period-2 orbit with one impact at \(1.610~\hbox {A}\). The dashed grey lines represent impact boundaries. Colours of the trajectories and Poincaré sections are the same as for the system responses shown in the bifurcation diagrams. (Color figure online)

Full size image

Another case obtained for an excitation frequency of \(7.60~\hbox {Hz}\) is shown in Figure 18. Initially, the diagrams presented in Fig. 18a, b demonstrate a linear non-impacting response and, between 1.24 and \(1.31~\hbox {A}\), a period-3 with two impacts per period and a period-1 non-impacting orbit depicted in Fig. 18c co-exist. After the first grazing, the period-1 orbit disappears and a period-3 orbit with one impact per period is recorded which co-exists up to \(1.4~\hbox {A}\) with the previously observed period-3 orbit with two impacts as shown in Fig. 18d. As the excitation amplitude increases, the system exhibits a chaotic response shown in Fig. 18e between \(1.505~\hbox {A}\) and \(1.6~\hbox {A}\). Afterwards, the chaotic region gives way by a reversed period doubling cascade to a period-2 orbit with one impact per period in Fig. 18f that lasts for the rest of the diagram. The period doubling behaviour is verified by numerical simulations. Again the calibrated model presents a very good estimate of the system behaviour as can be seen from the presented phase portraits and bifurcation diagrams.

Fig. 19
figure 19

Bifurcation diagrams with excitation frequency as branching parameter for increasing values of \(F^*\). a, c, e, g Numerical and b, d, f, h experimental bifurcation diagrams for \(F^*\): 0.31,  0.33,  0.35 and 0.37, respectively

Full size image
Fig. 20
figure 20

Evolution of the chaotic attractors presented by Poincaré maps near first grazing frequencies at a \(F^*=0.35\) and \(f=7.288~\hbox {Hz}\); b \(F^*=0.36\) and \(f=7.288~\hbox {Hz}\); c \(F^*=0.37\) and \(f=7.16~\hbox {Hz}\); d \(F^*=0.38\) and \(f=7.17~\hbox {Hz}\); and above the first grazing at the frequency \(f=7.78~\hbox {Hz}\) and e \(F^*=0.35\); f \(F^*=0.36\); g \(F^*=0.37\) and h \(F^*=0.38\)

Full size image

4.2 Parameter sensitivity

The very different behaviour of the system demonstrated in the bifurcation diagrams shown in Figs. 10 and 14 occurs for only a slight change in the excitation amplitude reflected in the parameter \(F^*=aI_0/k_1g\) values. Therefore, this ratio between the dynamic force amplitude (\(aI_0\)) and the static force needed to reach the gap (\(k_1g\)) dictates the system dynamics and is the parameter most prone to variations in many applications. In fact, due to ageing, the size of the gap may vary drastically over time, leading to significant changes in the system dynamics. Hence, a sensitivity analysis to the variations of this parameter is of extreme importance on establishing tolerances and safe regions of operation.

Figure 9 shows the bifurcation diagrams for a low value \(F^*=0.042\). Increases in \(F^*\) result in observing the first grazing incidence at a lower frequency while maintaining the same non-impacting period-1 orbit before it. This goes up to the point where further increases in \(F^*\) generate a period-3 orbit right after grazing incidence. At this point, a high-period orbit also appears on the backward diagram, which co-exists with a linears non-impacting period-1 orbit. Figure 10 shows these phenomena and the related orbits for \(F^*=0.28\), while Fig. 19 presents numerical and experimental bifurcation diagrams for higher values of \(F^*\). As can be seen in Fig. 19a, b and 19c, d, further increases in \(F^*\) up to \(F^*=0.33\) do not change the bifurcation structure presented in Fig. 10. The only difference is the narrowing of the region where non-impacting period-1 and the period-3 orbit with two impacts per period co-exist and emergence of this period-3 orbit closer to the grazing frequency for the higher values of \(F^*\). For \(F^*=0.35\) a sudden change in the system behaviour happens at grazing incidence, when two chaotic regions separated by a window of period-3 orbit with two impacts pers period appear, whereas one of the previously observed period-3 orbits vanishes. The first chaotic region appears only in a small range of frequencies between \(f=[7.26,7.3]~\hbox {Hz}\), and the second one is recorded for \(f=[7.46,7.8]~\hbox {Hz}\) and co-exists with the previously observed period-3 orbit with one impact per period from \(f=7.7~\hbox {Hz}\) up to \(7.8~\hbox {Hz}\). At \(F^*=0.37\) the system has a behaviour very similar to Fig. 15 obtained for \(F^*=0.38\). Here a period-2 orbit with one impact per period observed in the range \(f=[7.26,7.74]~\hbox {Hz}\) separates two chaotic regions. Two period-5 orbits are similar to the ones presented in Fig. 15d,e (upper panels) and exist in the same frequency range, while the chaotic region to the right of the diagram co-exists with the period-3 orbit as described before. On the last diagram, the co-existence of the period-3 and the chaotic response is not captured on the experimental data. However, if the system is brought to the proximity of the period-3 orbit, the rig is able to capture the co-existent behaviour in the same way as was done to obtained the results shown in Fig. 15. Also, all model results have a good agreement with experimental data.

An analysis of the evolution of the two chaotic attractors presented in Fig. 19 was carried out numerically. Figure 20 depicts the results for the chaotic attractors recorded around first grazing frequencies in Fig. 20a–d and in the second chaotic interval at \(7.78~\hbox {Hz}\) in Fig. 20e–h for increasing values of \(F^*\). At lower values of \(F^*\) the attractor near first grazing frequency presents a small void in the centre due to the basin of attraction of the period-1 non-impacting co-existing orbit. As \(F^*\) increases, the grazing frequency decreases restricting the co-existence of chaotic and period-1 non-impacting orbits to a small range of frequencies, which reflects on the chaotic attractor that slowly grows and engulfs the period-1 basin as the co-existence is eliminated. The attractor in the second chaotic interval presents at the lower values of \(F^*\) three regions where branches seem to swirl around. As \(F^*\) increases, these swirls become smaller and more clustered as the arms that connect each swirling region get smaller and the attractor itself becomes smaller until the three points merge into one.

5 Conclusions

In this work, the dynamics of a newly constructed mass excited impact oscillator [1] was investigated both experimentally and numerically. The parameters of the rig were characterised and are presented in the paper. The detailed study of the excitation provided by the magnetic coil revealed a linear relationship between the applied current and the force acting on the mass in the considered parameters range. It was shown that in this case a precise control of the excitation through the coil current becomes possible resulting in improvements in obtained resolution of the excitation amplitude and frequency for the construction of bifurcation diagrams. It was identified that experimentally recorded nonlinear effects observed in the oscillator rig without impacts are associated with large deflections of the leaf springs which provide the elastic support of the mass. To improve the quality of the recorded phase portraits, a new method for processing the experimental data was proposed allowing to reduce the influence of noise and to generate clear high-period orbits.

The comparison with previous base excited impact oscillator confirms that the rig has better spatial and frequency resolution as well as the ability to provide much more flexible excitation. Also, the rig is able to capture co-existent attractors and multi-stability experimentally by reproducing various predicted numerical responses, which was not possible before. The characterisation of the rig and its parameters suggests a linear behaviour of the leaf spring in low peak to peak amplitude forces (\(<3.5~\hbox {N}\)) and low amplitudes of displacement (\(<6~\hbox {mm}\)). The results obtained using simple impact oscillator model are in a good agreement with the experimental results, which indicates that the rig can be used for further fundamental studies of impact phenomena. The rig is also sensitive enough to study grazing incidence and to characterize chaotic attractors through the 0–1 test.

The conducted experimental and numerical sensitivity analysis of the frequency bifurcation diagrams show that there is a window of excitation amplitude \(F^* \in [0.28,0.33]\), where there is no significant change in the system dynamics, while for small changes of \(F^*\in [0.33,0.35]\), chaotic and high-period orbits emerge abruptly and quickly change the behaviour near grazing.

The rig described in this paper can be a useful tool to study nonlinear control, including bifurcation control and control of co-existing orbits, which will be considered in future works. In addition, the rig has potential to be adopted to study energy harvesting by the attachment of piezoelectric materials to the impact beam or to the leaf spring.

Finally, reflecting on the chaotic dynamics and the lessons learned from studying impacts systems, it is clearly seen that this field have brought many fundamental and practical benefits. We have discovered and classified new type of bifurcations occurring in impacting systems. We have shed more lights on grazing and grazing induced bifurcations. Most of all we have demonstrated that a new technology can be developed from the new findings rooted in chaotic behaviour of impacting systems [23,24,25].