Dynamic output feedback control for nonlinear networked control systems with a two-terminal event-triggered mechanism

Abstract

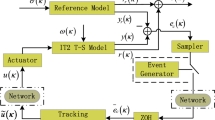
This paper is mainly concerned with the stabilization problem for nonlinear networked control systems (NCSs) with a two-terminal event-triggered mechanism. Firstly, Takagi–Sugeno (T–S) fuzzy models are introduced as the presentation of the nonlinear object. A two-terminal event-triggered mechanism, which adopts the relative event-triggered conditions as the communication mode of data transmission, is distributed in the controller-to-actuator link besides sensor-to-controller link in order to reduce congestion on network servers. By taking different membership function information from the T–S fuzzy model into account, the dynamic output feedback controller is designed under imperfect premise matching to construct closed-loop model. Secondly, to ensure the asymptotic stability of NCSs, valuable theorems are derived by defining Lyapunov functions which involve time-delay information. Thirdly, using boundary information of membership functions, LMI-based membership-function-dependent stability conditions are developed to reduce the conservativeness of the imperfect premise matching, from which the explicit form of controller gain matrices is obtained. Finally, one practical example illustrates the reliability of derived results.

Appendices

Appendix A

Choose the following Lyapunov functional candidate as

$$\begin{aligned} V\left( t \right) = {V_1}\left( t \right) + {V_2}\left( t \right) + {V_3}\left( t \right) \end{aligned}$$

(23)

where

$$\begin{aligned} {V_1}\left( t \right)&= {\xi ^T}\left( t \right) P\xi \left( t \right) \\ {V_2}\left( t \right)&= \int \limits _{t - {\tau _M}}^t {{\xi ^T}\left( s \right) {Q_1}\xi \left( s \right) ds }\\&\quad + \int \limits _{t - {d_M}}^t {{\xi ^T}\left( s \right) {Q_2}\xi \left( s \right) ds}\\ {V_3}\left( t \right)&= \int \limits _{t - {\tau _M}}^t {\int \limits _s^t {{{\dot{\xi } }^T}\left( v \right) {R_1}\dot{\xi } \left( v \right) dvds} } \\&\quad +\int \limits _{t - {d_M}}^t {\int \limits _s^t {{{\dot{\xi } }^T}\left( v \right) {R_2}\dot{\xi } \left( v \right) dvds} } \end{aligned}$$

and $P > 0$, ${Q_m} > 0$, ${R_m} > 0\left( {m = 1,2} \right)$.

We obtain (24) as follow by taking the derivative of equations above

$$\begin{aligned} \dot{V}\left( t \right) \mathrm{{ }} = {\dot{V}_1}\left( t \right) + {\dot{V}_2}\left( t \right) + {\dot{V}_3}\left( t \right) \end{aligned}$$

(24)

$$\begin{aligned} {\dot{V}_1}\left( t \right)&= 2{\xi ^T}\left( t \right) P\dot{\xi } \left( t \right) \\&= \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } 2{\xi ^T}\left( t \right) P\Lambda \\ {\dot{V}_2}\left( t \right)&= {\xi ^T}\left( t \right) \left( {{Q_1} + {Q_2}} \right) \xi \left( t \right) \\&\quad - {\xi ^T}\left( {t - {\tau _M}} \right) {Q_1}\xi \left( {t - {\tau _M}} \right) \\&\quad - {\xi ^T}\left( {t - {d_M}} \right) {Q_2}\xi \left( {t - {d_M}} \right) \\ {{\dot{V}}_3}\left( t \right)&= \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {{\dot{\xi } }^T}\left( t \right) \left( {{\tau _M}{R_1}} \right. \\&\quad \left. { + {d_M}{R_2}} \right) \dot{\xi } \left( t \right) - \int \limits _{t - {\tau _M}}^t {{{\dot{\xi } }^T}\left( s \right) {R_1}\dot{\xi } \left( s \right) } ds\\&\quad -\int \limits _{t - {d_M}}^t {{{\dot{\xi } }^T}\left( s \right) {R_2}\dot{\xi } \left( s \right) } ds \end{aligned}$$

where

$$\begin{aligned} \Lambda&= {\bar{A}_{ij}}\xi \left( t \right) + {\bar{A}_{{d_{ijm}}}}\xi \left( {t - d\left( t \right) } \right) + {\bar{A}_{{\tau _{ijn}}}}\xi \left( {t - \tau \left( t \right) } \right) \\&\quad + {\bar{B}_{{u_i}}}{e_u}\left( t \right) + {\bar{B}_{{y_j}}}{e_y}\left( t \right) . \end{aligned}$$

Notice that from ${{\dot{V}}_3}\left( t \right)$

$$\begin{aligned}&{\dot{\xi } ^T}\left( t \right) \left( {{\tau _M}{R_1} + {d_M}{R_2}} \right) \dot{\xi } \left( t \right) \\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\Lambda ^T}\left( {{\tau _M}{R_1} + {d_M}{R_2}} \right) \Lambda . \end{aligned}$$

To unify the communication mechanism and the network mechanism under the same frame, $\dot{V}\left( t \right) \mathrm{{ }}$ can be managed as follows.

Considering the conditions in event-triggered schemes (5) and (9) distributed in sensor-to-controller and controller-to-actuator respectively, we can obtain

$$\begin{aligned} \dot{V}\left( t \right)&\le {{\dot{V}}_1}\left( t \right) + {{\dot{V}}_2}\left( t \right) + {{\dot{V}}_3}\left( t \right) \nonumber \\&\quad + \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } \left\{ {} \right. \nonumber \\&\qquad {\sigma _y}{\xi ^T}\left( {t - \tau \left( t \right) } \right) H_2^TC_n^T{\Omega _y}{C_n}{H_2}\xi \left( {t - \tau \left( t \right) } \right) \nonumber \\&\quad - e_y^T\left( t \right) {\Omega _y}{e_y}\left( t \right) \nonumber \\&\quad + {\sigma _u}{\xi ^T}\left( {t {-} d\left( t \right) } \right) H_1^TC_{{c_m}}^T{\Omega _u}{C_{{c_m}}}{H_1}\xi \left( {t {-} d\left( t \right) } \right) \nonumber \\&\quad - e_u^T\left( t \right) {\Omega _u}{e_u}\left( t \right) \left. {} \right\} . \end{aligned}$$

(25)

For the purpose of eliminating the nonlinear integral terms in ${\dot{V}_3}\left( t \right)$, we apply the free-weighting matrix method [51] to obtain

$$\begin{aligned}&2\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\bar{\xi } ^T}\left( t \right) {M_{ijmn}}\nonumber \\&\quad \left[ {\xi \left( t \right) - \xi \left( {t - \tau \left( t \right) } \right) - \int \limits _{t - \tau \left( t \right) }^t {\dot{\xi } \left( s \right) ds} } \right] = 0 \end{aligned}$$

(26)

$$\begin{aligned}&\quad 2\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\bar{\xi } ^T}\left( t \right) {N_{ijmn}}\nonumber \\&\quad \left[ {\xi \left( {t - \tau \left( t \right) } \right) - \xi \left( {t - {\tau _M}} \right) - \int \limits _{t - {\tau _M}}^{t - \tau \left( t \right) } {\dot{\xi } \left( s \right) ds} } \right] = 0 \end{aligned}$$

(27)

$$\begin{aligned}&\quad 2\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\bar{\xi } ^T}\left( t \right) {T_{ijmn}}\nonumber \\&\quad \left[ {\xi \left( t \right) - \xi \left( {t - d\left( t \right) } \right) - \int \limits _{t - d\left( t \right) }^t {\dot{\xi } \left( s \right) ds} } \right] = 0 \end{aligned}$$

(28)

$$\begin{aligned}&\quad 2\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\bar{\xi } ^T}\left( t \right) {S_{ijmn}}\nonumber \\&\quad \left[ {\xi \left( {t - d\left( t \right) } \right) - \xi \left( {t - {d_M}} \right) - \int \limits _{t - {d_M}}^{t - d\left( t \right) } {\dot{\xi } \left( s \right) ds} } \right] = 0 \end{aligned}$$

(29)

where ${M_{ijmn}}$, ${N_{ijmn}}$, ${T_{ijmn}}$, ${S_{ijmn}}$ are matrices with appropriate dimensions, and

$$\begin{aligned}&{\bar{\xi } ^T}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{{\bar{\xi } }_1}^T\left( t \right) }&{{{\bar{\xi } }_2}^T\left( t \right) } \end{array}} \right] \\&{\bar{\xi } _1}^T\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{\xi ^T}\left( t \right) }&{{\xi ^T}\left( {t - d\left( t \right) } \right) }&{{\xi ^T}\left( {t - {d_M}} \right) } \end{array}} \right] \\&{\bar{\xi } _2}^T\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{\xi ^T}\left( {t - \tau \left( t \right) } \right) }&{{\xi ^T}\left( {t - {\tau _M}} \right) }&{e_u^T\left( t \right) }&{e_y^T\left( t \right) } \end{array}} \right] .\\ \end{aligned}$$

By Lemma 1, we can get

$$\begin{aligned}&\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau \left\{ {} \right. } } } } - 2{{\bar{\xi } }^T}\left( t \right) {M_{ijmn}} \ldots \nonumber \\&\qquad \int \limits _{t - \tau \left( t \right) }^t {\dot{\xi } \left( s \right) ds} \nonumber \\&\quad \le \tau \left( t \right) {{\bar{\xi } }^T}\left( t \right) {M_{ijmn}}R_1^{ - 1}M_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + \int \limits _{t - \tau \left( t \right) }^t {{{\dot{\xi } }^T}\left( s \right) {R_1}\dot{\xi } \left( s \right) } ds\left. {} \right\} \end{aligned}$$

(30)

$$\begin{aligned}&\qquad \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau \left\{ {} \right. } } } } - 2{{\bar{\xi } }^T}\left( t \right) {N_{ijmn}}\ldots \nonumber \\&\qquad \int \limits _{t - {\tau _M}}^{t - \tau \left( t \right) } {\dot{\xi } \left( s \right) ds} \nonumber \\&\quad \le \left( {{\tau _M} - \tau \left( t \right) } \right) {{\bar{\xi } }^T}\left( t \right) {N_{ijmn}}R_1^{ - 1}N_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + \int \limits _{t - {\tau _M}}^{t - \tau \left( t \right) } {{{\dot{\xi } }^T}\left( s \right) {R_1}\dot{\xi } \left( s \right) } ds\left. {} \right\} \end{aligned}$$

(31)

$$\begin{aligned}&\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau \left\{ {} \right. } } } } - 2{{\bar{\xi } }^T}\left( t \right) {T_{ijmn}}\ldots \nonumber \\&\qquad \int \limits _{t - d\left( t \right) }^t {\dot{\xi } \left( s \right) ds} \nonumber \\&\quad \le d\left( t \right) {{\bar{\xi } }^T}\left( t \right) {T_{ijmn}}R_2^{ - 1}T_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + \int \limits _{t - d\left( t \right) }^t {{{\dot{\xi } }^T}\left( s \right) {R_2}\dot{\xi } \left( s \right) } ds\left. {} \right\} \end{aligned}$$

(32)

$$\begin{aligned}&\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau \left\{ {} \right. } } } } - 2{{\bar{\xi } }^T}\left( t \right) {S_{ijmn}}\ldots \nonumber \\ \nonumber&\qquad \int \limits _{t - {d_M}}^{t - d\left( t \right) } {\dot{\xi } \left( s \right) ds} \nonumber \\&\quad \le \left( {{d_M} - d\left( t \right) } \right) {{\bar{\xi } }^T}\left( t \right) {S_{ijmn}}R_2^{ - 1}S_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + \int \limits _{t - {d_M}}^{t - d\left( t \right) } {{{\dot{\xi } }^T}\left( s \right) {R_2}\dot{\xi } \left( s \right) } ds\left. {} \right\} . \end{aligned}$$

(33)

By combining (25)–(33), one obtains that

$$\begin{aligned}&\dot{V}\left( t \right) \nonumber \\&\quad \le \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau \left\{ {} \right. } } } } 2{\xi ^T}\left( t \right) P\Lambda \nonumber \\&\qquad + {\xi ^T}\left( t \right) \left[ {{Q_1} {+} {Q_2}} \right] \xi \left( t \right) {-} {\xi ^T}\left( {t {-} {\tau _M}} \right) {Q_1}\xi \left( {t {-} {\tau _M}} \right) \nonumber \\&\qquad - {\xi ^T}\left( {t - {d_M}} \right) {Q_2}\xi \left( {t - {d_M}} \right) \nonumber \\&\qquad + \tau \left( t \right) {{\bar{\xi } }^T}\left( t \right) {M_{ijmn}}R_1^{ - 1}M_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + 2{{\bar{\xi } }^T}\left( t \right) {M_{ijmn}}\left[ {\xi \left( t \right) - \xi \left( {t - \tau \left( t \right) } \right) } \right] \nonumber \\&\qquad + \left( {{\tau _M} - \tau \left( t \right) } \right) {{\bar{\xi } }^T}\left( t \right) {N_{ijmn}}R_1^{ - 1}{N_{ijmn}}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + 2{{\bar{\xi } }^T}\left( t \right) {N_{ijmn}}\left[ {\xi \left( {t - \tau \left( t \right) } \right) - \xi \left( {t - {\tau _M}} \right) } \right] \nonumber \\&\qquad + d\left( t \right) {{\bar{\xi } }^T}\left( t \right) {T_{ijmn}}R_2^{ - 1}T_{ijmn}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + 2{{\bar{\xi } }^T}\left( t \right) {T_{ijmn}}\left[ {\xi \left( t \right) - \xi \left( {t - d\left( t \right) } \right) } \right] \nonumber \\ \nonumber&\qquad + \left( {{d_M} - d\left( t \right) } \right) {{\bar{\xi } }^T}\left( t \right) {S_{ijmn}}R_2^{ - 1}{S_{ijmn}}^T\bar{\xi } \left( t \right) \nonumber \\&\qquad + 2{{\bar{\xi } }^T}\left( t \right) {S_{ijmn}}\left[ {\xi \left( {t - d\left( t \right) } \right) - \xi \left( {t - {d_M}} \right) } \right] \nonumber \\&\qquad + {\Lambda ^T}\left( {{\tau _M}{R_1} + {d_M}{R_2}} \right) \Lambda \nonumber \\&\qquad +{\sigma _y}{\xi ^T}\left( {t - \tau \left( t \right) } \right) H_2^TC_n^T{\Omega _y}{C_n}{H_2}\xi \left( {t - \tau \left( t \right) } \right) \nonumber \\&\qquad - e_y^T\left( t \right) {\Omega _y}{e_y}\left( t \right) \nonumber \\&\qquad + {\sigma _u}{\xi ^T}\left( {t - d\left( t \right) } \right) H_1^TC_{{c_m}}^T{\Omega _u}{C_{{c_m}}}{H_1}\xi \left( {t - d\left( t \right) } \right) \nonumber \\&\qquad - e_u^T\left( t \right) {\Omega _u}{e_u}\left( t \right) \left. {} \right\} \end{aligned}$$

(34)

then, from (34), we have

$$\begin{aligned}&\dot{V}\left( t \right) \nonumber \\&\quad \le \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) \left\{ {} \right. } } } } {\Omega _{11}} {+} \Gamma {+} {\Gamma ^T} \nonumber \\&\qquad + \Omega _{31}^T{\Omega _{33}}{\Omega _{31}} + \Omega _{\mathrm{{4}}1}^T{\Omega _{\mathrm{{44}}}}{\Omega _{\mathrm{{4}}1}} + \Omega _{\mathrm{{5}}1}^T{\Omega _{\mathrm{{55}}}}{\Omega _{\mathrm{{5}}1}}\nonumber \\&\qquad + \tau \left( t \right) {M_{ijmn}}R_1^{ - 1}M_{ijmn}^T \nonumber \\&\qquad + \left( {{\tau _M} - \tau \left( t \right) } \right) {N_{ijmn}}R_1^{ - 1}N_{ijmn}^T\nonumber \\&\qquad + d\left( t \right) {T_{ijmn}}R_2^{ - 1}T_{ijmn}^T \nonumber \\&\qquad + \left( {{d_M} - d\left( t \right) } \right) {S_{ijmn}}R_2^{ - 1}S_{ijmn}^T\left. {} \right\} \bar{\xi } \left( t \right) . \end{aligned}$$

(35)

Applying Lemma 2 and Schur complement, we can finally obtain the following inequalities to guarantee $\dot{V}\left( t \right) < 0$.

$$\begin{aligned} \left\{ \begin{array}{l} \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) {\Omega _{ijmn}}\left( 1 \right) \bar{\xi } \left( t \right)< 0} } } } \\ \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) {\Omega _{ijmn}}\left( 2 \right) \bar{\xi } \left( t \right)< 0} } } } \\ \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) {\Omega _{ijmn}}\left( 3 \right) \bar{\xi } \left( t \right)< 0} } } } \\ \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) {\Omega _{ijmn}}\left( 4 \right) \bar{\xi } \left( t \right) < 0} } } } \end{array} \right. \end{aligned}$$

In conclusion, there exists ${\Omega _{ijmn}}\left( s \right) < 0$, $s = 1,2,3,4$, then the system (14) is asymptotically stable. The proof is completed.

Appendix B

The positive definite symmetric matrix P is decomposed as follows:

$$\begin{aligned} P = \left[ {\begin{array}{*{20}{c}} {{P_1}}&{} * \\ {P_2^T}&{}{P_2^T{{\left( {{P_1} - P_3^{ - 1}} \right) }^{ - 1}}{P_2}} \end{array}} \right] \end{aligned}$$

(36)

where ${P_1}$, ${P_2}$, ${P_3} \in {\mathbb {R}^{n \times n}}$.

Through Schur complement, $P > 0$ is equivalent to ${P_3} > 0$ and ${P_1} - P_3^{ - 1} > 0$. Therefore, we use $\hat{P} = \left[ {\begin{array}{*{20}{c}} {{P_3}}&{} * \\ I&{}{{P_1}} \end{array}} \right] > 0$ to guarantee $P > 0$.

Define the matrix J

$$\begin{aligned} {J^T} = \left[ {\begin{array}{*{20}{c}} {{P_3}}&{}I\\ {P_2^{ - 1}\left( {I - {P_1}{P_3}} \right) }&{}0 \end{array}} \right] . \end{aligned}$$

(37)

Define the matrix $\Upsilon$

$$\begin{aligned} \Upsilon = \mathrm{diag}\left\{ {\underbrace{J,J,J,J,J}_5,I,I,\underbrace{J,J,J,J}_4,I,I} \right\} \end{aligned}$$

(38)

Multiplying (18) by $\Upsilon$ from the left side and its transpose from the right side.

Define

$$\begin{aligned} \hat{P}&= JP{J^T} = \left[ {\begin{array}{*{20}{c}} {{P_3}}&{} * \\ I&{}{{P_1}} \end{array}} \right] \end{aligned}$$

$$\begin{aligned} {\hat{Q}_m}&= J{Q_m}{J^T}, {\hat{R}_m} = J{R_m}{J^T}\left( {m = 1,2} \right) \\ {{\hat{M}}_{ijmn1}}&= J{M_{ijmn1}}{J^T},{{\hat{M}}_{ijmn2}} = J{M_{ijmn2}}{J^T}\\ {{\hat{N}}_{ijmn2}}&= J{N_{ijmn2}}{J^T},{{\hat{N}}_{ijmn3}} = J{N_{ijmn3}}{J^T}\\ {{\hat{T}}_{ijmn1}}&= J{T_{ijmn1}}{J^T},{{\hat{T}}_{ijmn4}} = J{T_{ijmn4}}{J^T}\\ {{\hat{S}}_{ijmn4}}&= J{S_{ijmn4}}{J^T},{{\hat{S}}_{ijmn5}} = J{S_{ijmn5}}{J^T}. \end{aligned}$$

Then, we can derive that

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{{\hat{\Omega } }_{11}} + \hat{\Gamma } + {{\hat{\Gamma } }^T}}&{}*&{}*&{}*&{}*\\ {{{\hat{\Omega } }_{\mathrm{{2}}1}}\left( s \right) }&{}{{{\hat{\Omega } }_{22}}}&{}*&{}*&{}*\\ {{{\hat{\Omega } }_{31}}}&{}0&{}{{\Omega _{33}}}&{}*&{}*\\ {{{\hat{\Omega } }_{41}}}&{}0&{}0&{}{{\Omega _{44}}}&{}*\\ {{{\hat{\Omega } }_{51}}}&{}0&{}0&{}0&{}{{\Omega _{55}}} \end{array}} \right] < 0 \end{aligned}$$

(39)

where

$$\begin{aligned} {\Omega _{33}}&= \mathrm{diag}\left\{ { - PR_2^{ - 1}P, - PR_1^{ - 1}P} \right\} \\ {\Omega _{44}}&= - \Omega _u^{ - 1},\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\Omega _{55}} = - \Omega _y^{ - 1}. \end{aligned}$$

Due to

$$\begin{aligned} \left( {{R_m} - P} \right) R_m^{ - 1}\left( {{R_m} - P} \right) \ge 0,\left( {m = 1,2} \right) \end{aligned}$$

$$\begin{aligned}&\left( {{\Omega _u} - I} \right) \Omega _u^{ - 1}\left( {{\Omega _u} - I} \right) \ge 0\\&\left( {{\Omega _y} - I} \right) \Omega _y^{ - 1}\left( {{\Omega _y} - I} \right) \ge 0 \end{aligned}$$

we have

$$\begin{aligned} - PR_m^{ - 1}P \le - 2P + {R_m} \end{aligned}$$

and

$$\begin{aligned}&- \Omega _u^{ - 1} \le - 2I + {\Omega _u}\\&- \Omega _y^{ - 1} \le - 2I + {\Omega _y} \end{aligned}$$

. Substitute $- PR_m^{ - 1}P$, $- \Omega _u^{ - 1}$ and $- \Omega _y^{ - 1}$ with $- 2P + {R_m}$, $- 2I + {\Omega _u}$ and $- 2I + {\Omega _y}$ into (39) respectively. we can obtain (40)

$$\begin{aligned} {\hat{\Omega } _{ijmn}} = \left[ {\begin{array}{*{20}{c}} {{{\hat{\Omega } }_{11}} + \hat{\Gamma } + {{\hat{\Gamma } }^T}}&{}*&{}*&{}*&{}*\\ {{{\hat{\Omega } }_{\mathrm{{2}}1}}\left( s \right) }&{}{{{\hat{\Omega } }_{22}}}&{}*&{}*&{}*\\ {{{\hat{\Omega } }_{31}}}&{}0&{}{{{\hat{\Omega } }_{33}}}&{}*&{}*\\ {{{\hat{\Omega } }_{41}}}&{}0&{}0&{}{{{\hat{\Omega } }_{44}}}&{}*\\ {{{\hat{\Omega } }_{51}}}&{}0&{}0&{}0&{}{{{\hat{\Omega } }_{55}}} \end{array}} \right] < 0 \end{aligned}$$

(40)

where

$$\begin{aligned} {\hat{\Omega } _{33}}&= \mathrm{diag}\left\{ { - 2P + {R_2}, - 2P + {R_1}} \right\} \\ {\hat{\Omega } _{44}}&= - 2I + {\Omega _u}, {\hat{\Omega } _{55}} = - 2I + {\Omega _y}. \end{aligned}$$

The following expression can be obtained:

$$\begin{aligned} \dot{V}\left( {x\left( t \right) } \right) \le \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {\hat{\Omega } _{ijmn}} < 0. \end{aligned}$$

(41)

Similar to [52], we have the slack matrix ${\widehat{\mathrm{{H}}}_i} = \widehat{\mathrm{{H}}}_i^T > 0\left( {i = 1,2,\ldots ,r} \right)$ with appropriate dimensions as follows

$$\begin{aligned}&\sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\left( {\omega _j^0 - m_j^0} \right) m_m^d\omega _n^\tau } } } } {{\hat{\mathrm{H}}}_i}\\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0} } } m_m^d\omega _n^\tau \left( {\sum \limits _{j = 1}^r {\omega _j^0} - \sum \limits _{j = 1}^r {m_j^0} } \right) {{\hat{\mathrm{H}}}_i}\\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0} } } m_m^d\omega _n^\tau \left( {1 - 1} \right) {{\hat{\mathrm{H}}}_i} = 0 \end{aligned}$$

where ${{\hat{\mathrm{H}}}_i}$ are arbitrary matrices. Then, we have that

$$\begin{aligned}&\dot{V}\left( {x\left( t \right) } \right) \\&\quad \le \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {{\bar{\xi } }^T}\left( t \right) {{\hat{\Omega } }_{ijmn}}\bar{\xi } \left( t \right) \\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {{\bar{\xi } }^T}\left( t \right) {{\hat{\Omega } }_{ijmn}}\bar{\xi } \left( t \right) \\&\qquad + \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\left( {\omega _j^0 - m_j^0} \right. } } } }\\&\qquad \left. { + \,{\kappa _j}\omega _j^0 - {\kappa _j}\omega _j^0} \right) m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) {{\hat{\mathrm{H}}}_i}\bar{\xi } \left( t \right) \\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\omega _j^0m_m^d\omega _n^\tau } } } } {{\bar{\xi } }^T}\left( t \right) \left( {{\kappa _j}{{\hat{\Omega } }_{ijmn}}} \right. \\&\qquad \left. { -\, {\kappa _j}{{\hat{\mathrm{H}}}_i} + {{\hat{\mathrm{H}}}_i}} \right) \bar{\xi } \left( t \right) \\&\qquad + \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\left( {m_j^0} \right. } } } } \\&\qquad \left. { - \,{\kappa _j}\omega _j^0} \right) m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) \left( {{{\hat{\Omega } }_{ijmn}} - {{\hat{\mathrm{H}}}_i}} \right) \bar{\xi } \left( t \right) \\&\quad = \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\left( {m_j^0} \right. } } } } \\&\qquad \left. { - \,{\kappa _j}\omega _j^0} \right) m_m^d\omega _n^\tau {{\bar{\xi } }^T}\left( t \right) \left( {{{\hat{\Omega } }_{ijmn}} - {{\hat{\mathrm{H}}}_i}} \right) \bar{\xi } \left( t \right) \\&\qquad + \sum \limits _{i = 1}^r {\sum \limits _{j = i}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0\omega _i^0m_m^d\omega _n^\tau } } } } {{\bar{\xi } }^T}\left( t \right) \left( {{\kappa _i}{{\hat{\Omega } }_{iimn}}} \right. \\&\qquad \left. { - \,{\kappa _i}{{\hat{\mathrm{H}}}_i} + {{\hat{\mathrm{H}}}_i}} \right) \bar{\xi } \left( t \right) \\&\qquad + \sum \limits _{i = 1}^{r - 1} {\sum \limits _{j = i + 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {\omega _i^0m_j^0m_m^d\omega _n^\tau } } } } {{\bar{\xi } }^T}\left( t \right) \left( {{\kappa _j}{{\hat{\Omega } }_{ijmn}}} \right. \\&\qquad \left. { -\, {\kappa _j}{{\hat{\mathrm{H}}}_i} + {{\hat{\mathrm{H}}}_i} + {\kappa _i}{{\hat{\Omega } }_{jimn}} - {\kappa _i}{{\hat{\mathrm{H}}}_j} + {{\hat{\mathrm{H}}}_j}} \right) \bar{\xi } \left( t \right) . \end{aligned}$$

With $m_j^0 - {\kappa _j}\omega _j^0 > 0$ for all $j = 1,2,\ldots ,r$, equations (32)–(35) stand for that (41) is satisfied.

In order to deal with the unknown matrix ${P_2}$, we define the following parameters firstly:

$$\begin{aligned} {{\hat{A}}_{{c_{ij}}}}&= {P_2}{A_{{c_{ij}}}}P_2^{ - 1}\quad {{\hat{B}}_{{c_j}}} = {P_2}{B_{{c_j}}}\\ {{\hat{C}}_{{c_m}}}&= {C_{{c_m}}}P_2^{ - 1}\quad {{\hat{A}}_{c{p_{ijm}}}} = {P_2}{A_{c{p_{ijm}}}}P_2^{ - 1}\\ {{\hat{A}}_{c{d_{ijn}}}}&= {P_2}{A_{c{d_{ijn}}}}P_2^{ - 1}. \end{aligned}$$

Then we consider about linear transformations ${x_c}\left( t \right) = P_2^{ - 1}{\hat{x}_c}\left( t \right)$, and the dynamic output feedback controller model (12) is equivalent as

$$\begin{aligned} \left\{ {\begin{array}{*{20}{l}} {{{\mathop {\hat{x}}\limits ^. }_c}\left( t \right) = \sum \limits _{i = 1}^r {\sum \limits _{j = 1}^r {\sum \limits _{m = 1}^r {\sum \limits _{n = 1}^r {{\omega _i}\left( {x\left( t \right) } \right) {m_j}\left( {\theta \left( t \right) } \right) } } } } }\\ {\begin{array}{*{20}{l}} {{m_m}\left( {\theta \left( {t - d\left( t \right) } \right) } \right) {\omega _n}\left( {x\left( {t - \tau \left( t \right) } \right) } \right) }\\ {\left\{ {{{\hat{A}}_{{c_{ij}}}}{{\hat{x}}_c}\left( t \right) + {{\hat{A}}_{c{d_{ijn}}}}{{\hat{x}}_c}\left( {t - \tau \left( t \right) } \right) } \right. } \end{array}}\\ {\left. { + {{\hat{A}}_{c{p_{ijm}}}}{{\hat{x}}_c}\left( {t - d\left( t \right) } \right) + {{\hat{B}}_{{c_j}}}{\hat{y}}\left( t \right) } \right\} }\\ {u\left( t \right) = \sum \limits _{j = 1}^r {{m_j}\left( {\theta \left( t \right) } \right) {{\hat{C}}_{{c_j}}}{{\hat{x}}_c}\left( t \right) } } \end{array}} \right. \end{aligned}$$

(42)

where the controller parameters can be obtained in an explicit form.

$$\begin{aligned} {\hat{A}_{{c_{ij}}}}&= \left( {\hat{\gamma } _{11}^{ij} - {P_1}{A_i}{P_3}} \right) {\left( {I - {P_1}{P_3}} \right) ^{ - 1}}\\ {\hat{B}_{{c_j}}}&= \hat{\gamma } _{32}^j,\;\;\;\;\;\;\;\;\;{\hat{C}_{{c_m}}} = \hat{\gamma } _{21}^m{\left( {I - {P_1}{P_3}} \right) ^{ - 1}}\\ {{\hat{A}}_{c{p_{ijm}}}}&= \left( {\hat{\gamma } _{22}^{ijm} - {P_1}{B_i}\hat{\gamma } _{21}^m} \right) {\left( {I - {P_1}{P_3}} \right) ^{ - 1}}\\ {\hat{A}_{c{d_{ijn}}}}&= \left( {\hat{\gamma } _{31}^{ijn} - {{\hat{B}}_{{c_j}}}{C_n}{P_3}} \right) {\left( {I - {P_1}{P_3}} \right) ^{ - 1}} \end{aligned}$$

The proof is completed. $\square$