Skip to main content
SpringerLink
Log in

Various exact analytical solutions of a variable-coefficient Kadomtsev–Petviashvili equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

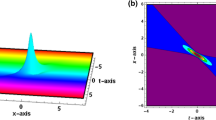
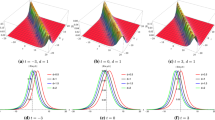
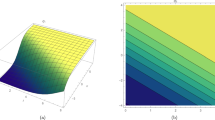
Under investigation is a generalized (3 + 1)-dimensional variable- coefficient Kadomtsev– Petviashvili equation in fluid mechanics. Various exact analytical solutions are obtained by Hirota’s bilinear method, such as lump-type, breather wave and kink-solitary wave solutions. We discuss the interaction between lump wave and solitary waves, and the interaction between lump wave and periodic wave. The physical structure and propagation characteristics of obtained solutions are shown by some 3D graphics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Gao, W., Rezazadeh, H., Pinar, Z., Baskonus, H.M., Sarwar, S., Yel, G.: Novel explicit solutions for the nonlinear Zoomeron equation by using newly extended direct algebraic technique. Opt. Quantum Electron. 52(1), 52 (2020)

    Google Scholar 

  2. Rezazadeh, H., Korkmaz, A., Eslami, M., Alizamini, S.M.M.: A large family of optical solutions to Kundu–Eckhaus model by a new auxiliary equation method. Opt. Quantum Electron. 51, 84 (2019)

    Google Scholar 

  3. Kaup, D.J.: The lump solutions and the Bäcklund transformation for the three-dimensional three-wave resonant interaction. J. Math. Phys. 22(6), 1176–1181 (1981)

    MathSciNet  MATH  Google Scholar 

  4. Gilson, C.R., Nimmo, J.J.C.: Lump solutions of the BKP equation. Phys. Lett. A 147(8–9), 472–476 (1990)

    MathSciNet  Google Scholar 

  5. Minzoni, A.A., Smyth, N.F.: Evolution of lump solutions for the KP equation. Wave Motion 24(3), 291–305 (1996)

    MathSciNet  MATH  Google Scholar 

  6. Imai, K., Nozaki, K.: Lump solutions of the Ishimori-II equation. Prog. Theor. Phys. 96(3), 521–526 (1996)

    MathSciNet  Google Scholar 

  7. Estevez, P.G., Prada, J., Villarroel, J.: On an algorithmic construction of lump solutions in a 2+1 integrable equation. J. Phys. A Math. Theor. 40(26), 7213–7231 (2007)

    MathSciNet  MATH  Google Scholar 

  8. Zhu, X.M., Zhang, D.J., Chen, D.Y.: Lump solutions of Kadomtsev–Petviashvili I equation in non-uniform media. Commun. Theor. Phys. 55(1), 13–19 (2011)

    MathSciNet  MATH  Google Scholar 

  9. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A 379(36), 1975–1978 (2015)

    MathSciNet  MATH  Google Scholar 

  10. Lü, X., Chen, S.T., Ma, W.X.: Constructing lump solutions to a generalized Kadomtsev–Petviashvili–Boussinesq equation. Nonlinear Dyn. 86(1), 523–534 (2016)

    MathSciNet  MATH  Google Scholar 

  11. Ma, H.C., Deng, A.P.: Lump solution of (2+1)-dimensional Boussinesq equation. Commun. Theor. Phys. 65(5), 546–552 (2016)

    MathSciNet  MATH  Google Scholar 

  12. Sun, H.Q., Chen, A.H.: Lump and lump–kink solutions of the (3+1)-dimensional Jimbo–Miwa and two extended Jimbo–Miwa equations. Appl. Math. Lett. 68, 55–61 (2017)

    MathSciNet  MATH  Google Scholar 

  13. Huang, L.L., Chen, Y.: Lump solutions and interaction phenomenon for (2+1)-dimensional Sawada–Kotera equation. Commun. Theor. Phys. 67(5), 473–478 (2017)

    MathSciNet  MATH  Google Scholar 

  14. Wang, C.J., Fang, H.: Bilinear Bäcklund transformations, kink periodic solitary wave and lump wave solutions of the Bogoyavlenskii-Kadomtsev–Petviashvili equation. Comput. Math. Appl. 76(1), 1–10 (2018)

    MathSciNet  MATH  Google Scholar 

  15. Chen, S.T., Ma, W.X.: Lump solutions to a generalized Bogoyavlensky–Konopelchenko equation. Front. Math. China 13(3), 525–534 (2018)

    MathSciNet  MATH  Google Scholar 

  16. Wang, J., An, H.L., Li, B.: Non-traveling lump solutions and mixed lump–kink solutions to (2+1)-dimensional variable-coefficient Caudrey–Dodd–Gibbon–Kotera–Sawada equation. Mod. Phys. Lett. B 33(22), 1950262 (2019)

    MathSciNet  Google Scholar 

  17. Lan, Z.Z., Su, J.J.: Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system. Nonlinear Dyn. 96, 2535–2546 (2019)

    Google Scholar 

  18. Wang, X.B., Han, B.: Novel rogue waves and dynamics in the integrable pair-transition-coupled nonlinear Schrödinger equation. Appl. Math. Lett. 99, 105987 (2020)

    MathSciNet  MATH  Google Scholar 

  19. He, J.S., Charalampidis, E.G., Kevrekidis, P.G., Frantzeskakis, D.J.: Rogue waves in nonlinear Schrodinger models with variable coefficients: application to Bose–Einstein condensates. Phys. Lett. A 378, 577–583 (2014)

    MATH  Google Scholar 

  20. Kaur, L., Wazwaz, A.M.: Lump, breather and solitary wave solutions to new reduced form of the generalized BKP equation. Int. J. Numer. Method Heat Fluid Flow 29(2), 569–579 (2019)

    Google Scholar 

  21. Kaur, L., Wazwaz, A.M.: Dynamical analysis of lump solutions for (3 + 1) dimensional generalized KP-Boussinesq equation and its dimensionally reduced equations. Phys. Scr. 93(7), 075203 (2018)

    Google Scholar 

  22. Kadomtsev, B.B., Petviashvili, V.I.: On the stability of solitary waves in weakly dispersive media. Sov. Phys. Dokl. 15, 539–541 (1970)

    MATH  Google Scholar 

  23. Liu, J.G., Eslami, M., Rezazadeh, H., Mirzazadeh, M.: Rational solutions and lump solutions to a non-isospectral and generalized variable-coefficient Kadomtsev–Petviashvili equation. Nonlinear Dyn. 95(2), 1027–1033 (2019)

    Google Scholar 

  24. Yong, X.L., Ma, W.X., Huang, Y.H., Liu, Y.: Lump solutions to the Kadomtsev–Petviashvili I equation with a self-consistent source. Comput. Math. Appl. 75(9), 3414–3419 (2018)

    MathSciNet  MATH  Google Scholar 

  25. Horowitza, S., Zarmib, Y.: Kadomtsev–Petviashvili II equation: structure of asymptotic soliton webs. Phys. D 300, 1–14 (2015)

    MathSciNet  Google Scholar 

  26. Seadawy, A.R., El-Rashidy, K.: Dispersive solitary wave solutions of Kadomtsev–Petviashvili and modified Kadomtsev–Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 8, 1216–1222 (2018)

    Google Scholar 

  27. Sun, Y.L., Ma, W.X., Yu, J.P., Khalique, C.M.: Dynamics of lump solitary wave of Kadomtsev–Petviashvili–Boussinesq-like equation. Comput. Math. Appl. 78(3), 840–847 (2019)

    MathSciNet  Google Scholar 

  28. Ding, C.C., Gao, Y.T., Deng, G.F.: Breather and hybrid solutions for a generalized (3 + 1)-dimensional B-type Kadomtsev–Petviashvili equation for the water waves. Nonlinear Dyn. 97(4), 2023–2040 (2019)

    MATH  Google Scholar 

  29. Hamid, M., Usman, M., Zubair, T., Haq, R.U., Shafee, A.: An efficient analysis for N-soliton, Lump and lump–kink solutions of time-fractional (2+1)-Kadomtsev–Petviashvili equation. Phys. A 528, 121320 (2019)

    MathSciNet  Google Scholar 

  30. Wazwaz, A.M., El-Tantawy, S.A.: A new (3+1)-dimensional generalized Kadomtsev–Petviashvili equation. Nonlinear Dyn. 84, 1107–1112 (2016)

    MathSciNet  Google Scholar 

  31. Wazwaz, A.M.: Negative-order KdV and negative-order KP equations: multiple soliton solutions. Proc. Natl. Acad. Sci. India A 87(2), 291–296 (2017)

    MathSciNet  MATH  Google Scholar 

  32. Wazwaz, A.M., El-Tantawy, S.A.: Solving the (3+1)-dimensional KP-Boussinesq and BKP-Boussinesq equations by the simplified Hirota’s method. Nonlinear Dyn. 88(4), 3017–3021 (2017)

    MathSciNet  Google Scholar 

  33. Wu, X.Y., Tian, B., Liu, L., Sun, Y.: Rogue waves for a variable-coefficient Kadomtsev–Petviashvili equation in fluid mechanics. Comput. Math. Appl. 76(2), 215–223 (2018)

    MathSciNet  MATH  Google Scholar 

  34. Gao, X.Y.: Bäcklund transformation and shock-wave-type solutions for a generalized (3+1)-dimensional variable-coefficient B-type Kadomtsev–Petviashvili equation in fluid mechanics. Ocean Eng. 96, 245–247 (2015)

    Google Scholar 

  35. Yan, Z.Y., Zhang, H.Q.: Similarity reductions for 2+1-dimensional variable coefficient generalized Kadomtsev–Petviashvili equation. Appl. Math. Mech. 21(6), 645–650 (2000)

    MathSciNet  MATH  Google Scholar 

  36. Liu, J.G., Zhu, W.H., Zhou, L.: Interaction solutions for Kadomtsev–Petviashvili equation with variable coefficients. Commun. Theor. Phys. 71(7), 793–797 (2019)

    MathSciNet  Google Scholar 

  37. Luo, X.Y., Chen, Y.: Darboux transformation and N-soliton solution for extended form of modified Kadomtsev–Petviashvili equation with variable-coefficient. Commun. Theor. Phys. 66(8), 179–188 (2016)

    MathSciNet  MATH  Google Scholar 

  38. Osman, M.S.: Nonlinear interaction of solitary waves described by multi-rational wave solutions of the (2 + 1)-dimensional Kadomtsev–Petviashvili equation with variable coefficients. Nonlinear Dyn. 87(2), 1209–1216 (2017)

    MathSciNet  MATH  Google Scholar 

  39. Wang, X., Wang, L.: Darboux transformation and nonautonomous solitons for a modified Kadomtsev–Petviashvili equation with variable coefficients. Comput. Math. Appl. 75(12), 4201–4213 (2018)

    MathSciNet  MATH  Google Scholar 

  40. Xu, H., Ma, Z., Fei, J., Zhu, Q.: Novel characteristics of lump and lump–soliton interaction solutions to the generalized variable-coefficient Kadomtsev–Petviashvili equation. Nonlinear Dyn. 98(1), 551–560 (2019)

    MATH  Google Scholar 

  41. Jaradat, H.M., Shara, S.A., Awawdeh, F., Alquran, M.: Variable coefficient equations of the Kadomtsev–Petviashvili hierarchy: multiple soliton solutions and singular multiple soliton solutions. Phys. Scr. 85(3), 035001 (2012)

    MATH  Google Scholar 

  42. Xie, X.Y., Tian, B., Jiang, Y., Zhong, H., Sun, Y., Wang, Y.P.: Painlevé analysis, soliton collision and Bäcklund transformation for the (3+1)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in fluids or plasmas. Commun. Theor. Phys. 62, 26–32 (2014)

    MathSciNet  MATH  Google Scholar 

  43. Chai, J., Tian, B., Sun, W.R., Xie, X.Y.: Solitons and rouge waves for a generalized (3 + 1)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in fluid mechanics. Comput. Math. Appl. 71, 2060–2068 (2016)

    MathSciNet  Google Scholar 

  44. Yin, Y., Tian, B., Chai, H.P., Yuan, Y.Q., Du, Z.: Lumps and rouge waves for a (3 + 1)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in fluid mechanics. Pramana J. Phys. 91, 43 (2018)

    Google Scholar 

  45. Chai, J., Tian, B., Wu, X.Y., Liu, L.: Fusion and fission phenomena for the soliton interactions in a plasma. Eur. Phys. J. Plus 132, 60 (2017)

    Google Scholar 

  46. Chen, S.S., Tian, B.: Gramian solutions and soliton interactions for a generalized (3 + 1)-dimensional variable-coefficient Kadomtsev–Petviashvili equation in a plasma or fluid. Proc. R. Soc. A 475, 20190122 (2019)

    MathSciNet  Google Scholar 

  47. Liu, J.G., Zhu, W.H., Zhou, L.: Breather wave solutions for the Kadomtsev–Petviashvili equation with variable coefficients in a fluid based on the variable-coefficient three-wave approach. Math. Method Appl. Sci. 43(1), 458–465 (2020)

    MathSciNet  Google Scholar 

  48. Tian, S.F., Zhang, H.Q.: On the integrability of a generalized variable-coefficient Kadomtsev–Petviashvili equation. J. Phys. A 45, 055203 (2012)

    MathSciNet  MATH  Google Scholar 

  49. Huang, W.H.: A polynomial expansion method and its application in the coupled Zakharov–Kuznetsov equations. Chaos Solitons Fract. 29(2), 365–371 (2006)

    MathSciNet  MATH  Google Scholar 

  50. Liu, J.G., Zhu, W.H., He, Y., Lei, Z.Q.: Characteristics of lump solutions to a (3 + 1)-dimensional variable-coefficient generalized shallow water wave equation in oceanography and atmospheric science. Eur. Phys. J. Plus 134, 385 (2019)

  51. Liu, J.G., Ye, Q.: Stripe solitons and lump solutions for a generalized Kadomtsev–Petviashvili equation with variable coefficients in fluid mechanics. Nonlinear Dyn. 96, 23–29 (2019)

    Google Scholar 

  52. Liu, J.G., Zhu, W.H., Zhou, L., Xiong, Y.K.: Multi-waves, breather wave and lump–stripe interaction solutions in a (2+1)-dimensional variable-coefficient Korteweg–de Vries equation. Nonlinear Dyn. 97, 2127–2134 (2019)

    MATH  Google Scholar 

  53. Korkmaz, A., Hepson, O.E., Hosseini, K., Rezazadeh, H., Eslami, M.: Sine-Gordon expansion method for exact solutions to conformable time fractional equations in RLW-class. J. King Saud Univ. Sci. 32(1), 567–574 (2020)

    Google Scholar 

  54. Raza, N., Afzal, U., Butt, A.R., Rezazadeh, H.: Optical solitons in nematic liquid crystals with Kerr and parabolic law nonlinearities. Opt. Quantum Electron. 51, 107 (2019)

    Google Scholar 

  55. Rezazadeh, H., Korkmaz, A., Khater, M.M.A., Eslami, M., Lu, D., Attia, R.A.M.: New exact traveling wave solutions of biological population model via the extended rational sinh–cosh method and the modified Khater method. Mod. Phys. Lett. B 33(28), 1950338 (2019)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Computer, Jiangxi University of Traditional Chinese Medicine, Jiangxi, 330004, China

    Jian-Guo Liu

  2. Institute of Artificial Intelligence, Nanchang Institute of Science and Technology, Jiangxi, 330108, China

    Wen-Hui Zhu

Authors
  1. Jian-Guo Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Wen-Hui Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jian-Guo Liu.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this article.

Ethical standard

The authors state that this research complies with ethical standards. This research does not involve either human participants or animals.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$\begin{aligned} (1)\,\,\, \alpha _4(t)= & {} -\left[ \left( \alpha _1^2+\alpha _6^2\right) \alpha _1 h(t)+\alpha _3 \alpha _1^2 l(t)\right. \nonumber \\&+\,\alpha _3 \alpha _6^2 l(t)+\alpha _2^2 \alpha _1 m(t)\nonumber \\&-\,\alpha _7^2 \alpha _1 m(t)+2 \alpha _2 \alpha _6 \alpha _7 m(t)\nonumber \\&+\,\alpha _3^2 \alpha _1 n(t)-\alpha _8^2 \alpha _1 n(t)\nonumber \\&+\,2 \alpha _3 \alpha _6 \alpha _8 n(t)+\alpha _2 \nonumber \\&\left. \left( \alpha _1^2+\alpha _6^2\right) q(t)\right] /[\alpha _1^2+\alpha _6^2],\nonumber \\ \alpha _9(t)= & {} -\left[ \alpha _6 \left( \alpha _1^2+\alpha _6^2\right) h(t)\right. \nonumber \\&+\,\alpha _8 \left( \left( \alpha _1^2+\alpha _6^2\right) l(t)+2 \alpha _1 \alpha _3 n(t)\right) \nonumber \\&+\,\left( -\alpha _6 \alpha _2^2+2 \alpha _1 \alpha _7 \alpha _2+\alpha _6 \alpha _7^2\right) m(t)\nonumber \\&+\,\alpha _6 \left( \alpha _6 \alpha _7 q(t)-\alpha _3^2 n(t)\right) \nonumber \\&\left. +\,\alpha _6 \alpha _8^2 n(t)+\alpha _7 \alpha _1^2 q(t)\right] \bigg /\left[ \alpha _1^2+\alpha _6^2\right] ,\nonumber \\ \end{aligned}$$
(23)

with the constraints

$$\begin{aligned} \alpha _6\ne & {} 0, \alpha _1^2+\alpha _6^2\ne 0, 3 \left( \alpha _1^2+\alpha _6^2\right) {}^3 g(t)\nonumber \\&+\,\alpha _{11} \left[ \left( \alpha _2 \alpha _6-\alpha _1 \alpha _7\right) {}^2 m(t)\right. \nonumber \\&\left. +\left( \alpha _3 \alpha _6-\alpha _1 \alpha _8\right) {}^2 n(t)\right] =0.\nonumber \\ (2)\,\,\,\alpha _7= & {} -\frac{\alpha _1 \alpha _2}{\alpha _6},\nonumber \\ \alpha _8= & {} \frac{\alpha _3 \alpha _6}{\alpha _1},\nonumber \\ \alpha _4(t)= & {} -\alpha _1 h(t)-\alpha _3 l(t)+\frac{\alpha _1 \alpha _2^2 m(t)}{\alpha _6^2}\nonumber \\&-\,\frac{\alpha _3^2 n(t)}{\alpha _1}-\alpha _2 q(t),\nonumber \\ \alpha _9(t)= & {} \frac{\alpha _2 [\alpha _2 m(t)+\alpha _1 q(t)]}{\alpha _6}\nonumber \\&-\,\frac{\alpha _6 \left[ \alpha _1^2 h(t)+\alpha _3 \left( \alpha _1 l(t)+\alpha _3 n(t)\right) \right] }{\alpha _1^2}, \end{aligned}$$
(24)

with the constraints

$$\begin{aligned} \alpha _6\ne & {} 0, \alpha _1\ne 0,\nonumber \\&3 \left( \alpha _1^2+\alpha _6^2\right) g(t)\nonumber \\&+\,\frac{\alpha _{11} \alpha _2^2 m(t)}{\alpha _6^2}=0.\nonumber \\ (3)\,\,\,\alpha _7= & {} \frac{\alpha _2 \alpha _6}{\alpha _1}, \alpha _8{=} {-}\frac{\alpha _1 \alpha _3}{\alpha _6}{,}\nonumber \\ \alpha _4(t)= & {} {-}\alpha _1 h(t){-}\alpha _3 l(t){-}\frac{\alpha _2^2 m(t)}{\alpha _1}\nonumber \\&{+}\,\frac{\alpha _1 \alpha _3^2 n(t)}{\alpha _6^2}{-}\alpha _2 q(t){,}\nonumber \\ \alpha _9(t)= & {} \frac{\alpha _3 [\alpha _1 l(t){+}\alpha _3 n(t)]}{\alpha _6} \nonumber \\&{-}\,\frac{\alpha _6 \left[ \alpha _1^2 h(t)+\alpha _2 \left( \alpha _2 m(t)+\alpha _1 q(t)\right) \right] }{\alpha _1^2}, \end{aligned}$$
(25)

with the constraints

$$\begin{aligned} \alpha _6\ne & {} 0, \alpha _1\ne 0,\nonumber \\&3 \left( \alpha _1^2+\alpha _6^2\right) g(t)+\frac{\alpha _{11} \alpha _3^2 n(t)}{\alpha _6^2}=0.\nonumber \\ (4)\,\,\,\alpha _6= & {} 0{,} \alpha _9(t){=}{-}\frac{\alpha _8 \left( \alpha _1 l(t){+}2 \alpha _3 n(t)\right) {+}\alpha _7 \left( 2 \alpha _2 m(t){+}\alpha _1 q(t)\right) }{\alpha _1}{,}\nonumber \\ \alpha _4(t)= & {} {-}[\alpha _1^2 h(t){+}\alpha _3 \alpha _1 l(t){+}\left( \alpha _2^2{-}\alpha _7^2\right) m(t)\nonumber \\&{+}\,\alpha _3^2 n(t){-}\alpha _8^2 n(t){+}\alpha _2 \alpha _1 q(t)]/\alpha _1{,} \end{aligned}$$
(26)

with the constraints

$$\begin{aligned} \alpha _1\ne 0, 3 \alpha _1^4 g(t)+\alpha _{11} [\alpha _7^2 m(t)+\alpha _8^2 n(t)]=0. \end{aligned}$$

Substituting Eqs. (19), (20), (21) and (22) into Eqs. (3) and (4), respectively, the corresponding lump solution can be obtained. All solutions have been verified as correct by Mathematica.

Appendix B

$$\begin{aligned} (1)\,\,\, \theta _3(t)= & {} \pm \varphi _1 \sqrt{\varphi _2^2+\varphi _6^2} \sqrt{\frac{\lambda _3^2}{\varphi _2^2 \left( \varphi _1^2+\varphi _{10}^2\right) }+\frac{4}{\varphi _1^2 \varphi _6^2-\varphi _2^2 \varphi _{10}^2}} \nonumber \\&\sqrt{\theta _1(t)}, \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _6 \left( \varphi _1^2+2 \varphi _5^2-\varphi _{10}^2\right) +\varphi _2 \varphi _5 \left( \varphi _{10}^2-\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2+\varphi _5^2\right) },\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _5= & {} \frac{\varphi _1 \varphi _6}{\varphi _2}. \end{aligned}$$
(27)
$$\begin{aligned} (2)\,\,\, \theta _3(t)= & {} \pm \sqrt{\varphi _5^2+\varphi _{10}^2} \sqrt{\frac{\lambda _3^2 \varphi _5^2-\lambda _3^2 \varphi _{10}^2+8 \varphi _{10}^2}{2 \varphi _5^2 \varphi _{10}^2-2 \varphi _{10}^4}} \nonumber \\&\sqrt{\theta _1(t)}, \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _6 \left( \varphi _1^2+2 \varphi _5^2-\varphi _{10}^2\right) +\varphi _2 \varphi _5 \left( \varphi _{10}^2-\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2+\varphi _5^2\right) },\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}, \nonumber \\ \varphi _1= & {} \pm \varphi _{10}. \end{aligned}$$
(28)
$$\begin{aligned} (3)\,\,\, \theta _3(t)= & {} \pm \sqrt{\varphi _5^2+\varphi _{10}^2} \sqrt{\frac{\lambda _3^2 \varphi _5^2-\lambda _3^2 \varphi _{10}^2+8 \varphi _{10}^2}{2 \varphi _5^2 \varphi _{10}^2-2 \varphi _{10}^4}} \nonumber \\&\sqrt{\theta _1(t)}, \varphi _1=\pm \varphi _{10}, \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _6 \left( \varphi _1^2+2 \varphi _5^2-\varphi _{10}^2\right) +\varphi _2 \varphi _5 \left( \varphi _{10}^2-\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2+\varphi _5^2\right) },\nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _7 \left( \varphi _1^2+2 \varphi _5^2-\varphi _{10}^2\right) +\varphi _3 \varphi _5 \left( \varphi _{10}^2-\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2+\varphi _5^2\right) }.\nonumber \\ \end{aligned}$$
(29)
$$\begin{aligned} (4)\,\,\, \theta _3(t)= & {} \pm \sqrt{\varphi _5^2+\varphi _{10}^2} \sqrt{\frac{\lambda _3^2 \varphi _5^2-\lambda _3^2 \varphi _{10}^2+8 \varphi _{10}^2}{2 \varphi _5^2 \varphi _{10}^2-2 \varphi _{10}^4}} \nonumber \\&\sqrt{\theta _1(t)}, \varphi _1=\pm \varphi _{10}, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _7 \left( \varphi _1^2+2 \varphi _5^2-\varphi _{10}^2\right) +\varphi _3 \varphi _5 \left( \varphi _{10}^2-\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2+\varphi _5^2\right) }.\nonumber \\ \end{aligned}$$
(30)
$$\begin{aligned} (5)\,\,\, \theta _3(t)= & {} \pm \varphi _5 \sqrt{\varphi _3^2+\varphi _7^2} \nonumber \\&\sqrt{\frac{\lambda _3^2}{\varphi _3^2 \varphi _5^2 +\varphi _7^2 \varphi _{10}^2}+\frac{4}{\varphi _7^2 \left( \varphi _5^2-\varphi _{10}^2\right) }}\nonumber \\&\sqrt{\theta _1(t)}, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _1= & {} \frac{\varphi _3 \varphi _5}{\varphi _7}, \nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \varphi _1 \varphi _7 \left( \varphi _1^2{+}2 \varphi _5^2{-}\varphi _{10}^2\right) {+}\varphi _3 \varphi _5 \left( \varphi _{10}^2{-}\varphi _5^2\right) \right) }{\varphi _1 \varphi _5 \left( \varphi _1^2{+}\varphi _5^2\right) }{.}\nonumber \\ \end{aligned}$$
(31)
$$\begin{aligned} (6)\,\,\, \theta _3(t)= & {} \pm \sqrt{\varphi _1^2+\varphi _5^2} \nonumber \\&\sqrt{\frac{\lambda _3^2}{\varphi _1^2{+}\varphi _{10}^2}+\frac{2}{\varphi _5 \left( \varphi _5{+}\varphi _{10}\right) }{+}\frac{2}{\varphi _5^2{-}\varphi _5 \varphi _{10}}} \sqrt{\theta _1(t)}{,} \nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3{+}\varphi _5 \varphi _7\right) \varphi _{10}^2{+}\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7{-}\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}{,} m(t){=}0{.}\nonumber \\ \end{aligned}$$
(32)

In the above solutions, \(\varphi _4(t)\), g(t), \(\theta _2(t)\), \(\varphi _8(t)\) and \(\varphi _{13}(t)\) are the same as those of Eq. (18).

$$\begin{aligned} (7)\,\,\theta _2(t)= & {} 0, \theta _3(t)=\lambda _4 \sqrt{\theta _1(t)}, \nonumber \\ g(t)= & {} \frac{\left( \lambda _4^2{-}4\right) [\left( \varphi _2 \varphi _{10}{-}\varphi _1 \varphi _{11}\right) {}^2 m(t){+}\left( \varphi _3 \varphi _{10}{-}\varphi _1 \varphi _{12}\right) {}^2 n(t)]}{3 \left( \varphi _1^2{+}\varphi _{10}^2\right) {}^2 \left( \lambda _4^2 \varphi _{10}^2{+}4 \varphi _1^2\right) }{,}\nonumber \\ \varphi _4(t)= & {} \left[ \theta _1(t) \left[ -4 g(t) \left( \lambda _4^2 \varphi _{10}^4+4 \varphi _1^4\right) \right. \right. \nonumber \\&+\,h(t) \left( \lambda _4^2 \varphi _{10}^2-4 \varphi _1^2\right) +\lambda _4^2 \varphi _{10} \varphi _{12} l(t)\nonumber \\&-\,4 \varphi _1 \varphi _3 l(t)+\lambda _4^2 \varphi _{11}^2 m(t)-4 \varphi _2^2 m(t)\nonumber \\&+\,\lambda _4^2 \varphi _{12}^2 n(t)-4 \varphi _3^2 n(t)\nonumber \\&\left. +\lambda _4^2 \varphi _{10} \varphi _{11} q(t)-4 \varphi _1 \varphi _2 q(t)+\lambda _4^2 \varphi _{10} \varphi _{13}(t)\right] \nonumber \\&\left. -2 \varphi _1 \theta _1'(t)\right] /[4 \varphi _1 \theta _1(t)],\nonumber \\ \varphi _{13}(t)= & {} -\left[ -4 \lambda _4^2 \varphi _{10}^5 g(t)-16 \varphi _1^2 \varphi _{10}^3 g(t)\right. \nonumber \\&+\,h(t) \left( \lambda _4^2 \varphi _{10}^3+4 \varphi _1^2 \varphi _{10}\right) \nonumber \\&+\,\varphi _{12} \left( \lambda _4^2 \varphi _{10}^2 l(t)+4 \varphi _1^2 l(t)+8 \varphi _3 \varphi _1 n(t)\right) \nonumber \\&+\,(\lambda _4^2 \varphi _{10} \varphi _{11}^2-4 \varphi _{10} \varphi _2^2\nonumber \\&+\,8 \varphi _1 \varphi _{11} \varphi _2) m(t)+\lambda _4^2 \varphi _{12}^2 \varphi _{10} n(t)\nonumber \\&-\,4 \varphi _3^2 \varphi _{10} n(t)+\,\lambda _4^2 \varphi _{11} \varphi _{10}^2 q(t)\nonumber \\&\left. +4 \varphi _1^2 \varphi _{11} q(t)\right] /(\lambda _4^2 \varphi _{10}^2+4 \varphi _1^2), \end{aligned}$$
(33)

where \(\lambda _4\) is integral constant.

$$\begin{aligned} (8)\,\,\, \theta _2(t)= & {} \lambda _3 \sqrt{\theta _1(t)}, \theta _3(t)=0, \nonumber \\ g(t)= & {} \frac{\left( \lambda _3^2{-}4\right) [\left( \varphi _2 \varphi _5{-}\varphi _1 \varphi _6\right) {}^2 m(t){+}\left( \varphi _3 \varphi _5{-}\varphi _1 \varphi _7\right) {}^2 n(t)]}{3 \left( \varphi _1^2{+}\varphi _5^2\right) {}^2 \left( \lambda _3^2 \varphi _5^2{+}4 \varphi _1^2\right) }{,}\nonumber \\ \varphi _4(t)= & {} -\left[ 2 \theta _1(t) \left[ g(t) \left[ \left( \lambda _3^2-16\right) \varphi _1^4\right. \right. \right. \nonumber \\&\left. -6 \lambda _3^2 \varphi _5^2 \varphi _1^2-3 \lambda _3^2 \varphi _5^4\right] \nonumber \\&+\,\left( \lambda _3^2-4\right) \varphi _1^2 h(t)+\left( \lambda _3^2-4\right) \nonumber \\&\left[ \varphi _1 \varphi _3 l(t)+\varphi _2^2 m(t)+\varphi _3^2 n(t)\right. \nonumber \\&\left. \left. +\varphi _1 \varphi _2 q(t)\right] \right] +\left( \lambda _3^2-4\right) \nonumber \\&\left. \varphi _1 \theta _1'(t)\right] /\left[ 2 \left( \lambda _3^2-4\right) \varphi _1 \theta _1(t)\right] ,\nonumber \\ \varphi _8(t)= & {} \left[ 4 g(t) \left[ \left( \lambda _3^2-1\right) \varphi _5^4+3 \varphi _1^4+6 \varphi _5^2 \varphi _1^2\right] \right. \nonumber \\&-\,\left( \lambda _3^2-4\right) \left[ \varphi _5^2 h(t)+\varphi _7 \varphi _5 l(t)+\varphi _6^2 m(t)\right. \nonumber \\&\left. \left. +\varphi _7^2 n(t)+\varphi _6 \varphi _5 q(t)\right] \right] /\left[ \left( \lambda _3^2-4\right) \varphi _5\right] . \end{aligned}$$
(34)
$$\begin{aligned} (9)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)=\lambda _6, \varphi _5=\pm \varphi _{10} \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _6-\varphi _1 \varphi _2\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _2 \varphi _5+\varphi _1 \varphi _6\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2},\nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _7-\varphi _1 \varphi _3\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _3 \varphi _5+\varphi _1 \varphi _7\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2},\nonumber \\ g(t)= & {} \frac{\left( \varphi _2 \varphi _{10}-\varphi _1 \varphi _{11}\right) {}^2 m(t)+\left( \varphi _3 \varphi _{10}-\varphi _1 \varphi _{12}\right) {}^2 n(t)}{3 \varphi _5^2 \left( \varphi _1^2+\varphi _{10}^2\right) {}^2},\nonumber \\ \varphi _8(t)= & {} -\left[ -\left( \varphi _1^2+\varphi _{10}^2\right) \left( \varphi _5^4+3 \right. \right. \nonumber \\&\left. \left( \varphi _1^2+2 \varphi _5^2\right) \varphi _{10}^2\right) g(t)+\varphi _5^2 (\varphi _1^2\nonumber \\&+\,\varphi _{10}^2) h(t)+\varphi _5 \varphi _7 \varphi _1^2 l(t)+\varphi _5 \varphi _7 \varphi _{10}^2 l(t)\nonumber \\&+\,\varphi _6^2 \varphi _1^2 m(t)+\varphi _{11}^2 \varphi _1^2 m(t)\nonumber \\&-\,2 \varphi _2 \varphi _{10} \varphi _{11} \varphi _1 m(t)+\varphi _2^2 \varphi _{10}^2 m(t)\nonumber \\&+\,\varphi _6^2 \varphi _{10}^2 m(t)+\varphi _7^2 \varphi _1^2 n(t)\nonumber \\&+\,\varphi _{12}^2 \varphi _1^2 n(t)-2 \varphi _3 \varphi _{10} \varphi _{12} \varphi _1 n(t)+\varphi _3^2 \varphi _{10}^2 n(t)\nonumber \\&+\,\varphi _7^2 \varphi _{10}^2 n(t)\nonumber \\&\left. +\varphi _5 \varphi _6 \varphi _1^2 q(t)+\varphi _5 \varphi _6 \varphi _{10}^2 q(t)\right] \bigg /\left[ \varphi _5 \left( \varphi _1^2+\varphi _{10}^2\right) \right] ,\nonumber \\ \varphi _4(t)= & {} -\left[ \left( \varphi _1^2+\varphi _5^2\right) \left( \varphi _1^2-\varphi _5^2-6 \varphi _{10}^2\right) g(t)\right. \nonumber \\&+\,\left( \varphi _1^2+\varphi _5^2\right) h(t)\nonumber \\&+\varphi _1 \varphi _3 l(t)+\varphi _5 \varphi _7 l(t)+\varphi _2^2 m(t)\nonumber \\&+\,\varphi _6^2 m(t)+\varphi _3^2 n(t)\nonumber \\&+\,\varphi _7^2 n(t)+\varphi _1 \varphi _2 q(t)+\varphi _5 \varphi _6 q(t)\nonumber \\&\left. +\varphi _5 \varphi _8(t)\right] /\varphi _1,\nonumber \\ \varphi _{13}(t)= & {} -\left[ -\left( \varphi _5^4+6 \varphi _{10}^2 \varphi _5^2+\varphi _{10}^4\right) g(t)\right. \nonumber \\&+\,\left( \varphi _5^2+\varphi _{10}^2\right) h(t)+\varphi _5 \varphi _7 l(t)\nonumber \\&+\,\varphi _{10} \varphi _{12} l(t)+\varphi _6^2 m(t)+\varphi _{11}^2 m(t)\nonumber \\&+\,\varphi _7^2 n(t)+\varphi _{12}^2 n(t)\nonumber \\&+\,\varphi _5 \varphi _6 q(t)+\varphi _{10} \varphi _{11} q(t)\nonumber \\&\left. +\varphi _5 \varphi _8(t)\right] /\varphi _{10}. \end{aligned}$$
(35)

where \(\lambda _5\) and \(\lambda _6\) are integral constants.

$$\begin{aligned} (10)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)=\lambda _6, \varphi _5=\pm \varphi _{10}, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _7-\varphi _1 \varphi _3\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _3 \varphi _5+\varphi _1 \varphi _7\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2}. \end{aligned}$$
(36)
$$\begin{aligned} (11)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)\nonumber \\= & {} \pm \varphi _1 \sqrt{\frac{\varphi _3^2+\varphi _7^2}{\varphi _1^2 \varphi _3^2+\varphi _{10}^2 \varphi _3^2}} \lambda _5, \varphi _5=\frac{\varphi _1 \varphi _7}{\varphi _3}, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _{12}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _7-\varphi _1 \varphi _3\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _3 \varphi _5+\varphi _1 \varphi _7\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2}. \end{aligned}$$
(37)
$$\begin{aligned} (12)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)=\sqrt{\frac{\varphi _1^2+\varphi _5^2}{\varphi _1^2+\varphi _{10}^2}} \lambda _5, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}. \end{aligned}$$
(38)
$$\begin{aligned} (13)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)\nonumber \\= & {} \sqrt{\frac{\varphi _1^2+\varphi _5^2}{\varphi _1^2+\varphi _{10}^2}} \lambda _5, \varphi _5=\pm \varphi _{10}, \nonumber \\ \varphi _{11}= & {} \frac{\left( \varphi _1 \varphi _2+\varphi _5 \varphi _6\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _6-\varphi _2 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}},\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}. \end{aligned}$$
(39)
$$\begin{aligned} (14)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)\nonumber \\= & {} \varphi _1 \sqrt{\frac{\varphi _2^2+\varphi _6^2}{\varphi _2^2 \left( \varphi _1^2+\varphi _{10}^2\right) }} \lambda _5, \varphi _5=\frac{\varphi _1 \varphi _6}{\varphi _2}, \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _6-\varphi _1 \varphi _2\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _2 \varphi _5+\varphi _1 \varphi _6\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2},\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}. \end{aligned}$$
(40)
$$\begin{aligned} (15)\,\,\, \theta _1(t)= & {} 0, \theta _2(t)=\lambda _5, \theta _3(t)\nonumber \\= & {} \varphi _1 \sqrt{\frac{\varphi _2^2+\varphi _6^2}{\varphi _2^2 \left( \varphi _1^2+\varphi _{10}^2\right) }} \lambda _5, \varphi _5=\pm \varphi _{10}, \nonumber \\ \varphi _{11}= & {} \frac{\varphi _{10} \left( \left( \varphi _5 \varphi _6-\varphi _1 \varphi _2\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _2 \varphi _5+\varphi _1 \varphi _6\right) \right) }{2 \varphi _1^2 \varphi _5^2+\left( \varphi _5^2-\varphi _1^2\right) \varphi _{10}^2},\nonumber \\ \varphi _{12}= & {} \frac{\left( \varphi _1 \varphi _3+\varphi _5 \varphi _7\right) \varphi _{10}^2+\varphi _1 \varphi _5 \left( \varphi _1 \varphi _7-\varphi _3 \varphi _5\right) }{\left( \varphi _1^2+\varphi _5^2\right) \varphi _{10}}. \end{aligned}$$
(41)

In Eqs. (36)–(41), \(\varphi _4(t)\), g(t), \(\theta _2(t)\), \(\varphi _8(t)\) and \(\varphi _{13}(t)\) are the same as those of Eq. (35). All solutions have been verified as correct by Mathematica.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, JG., Zhu, WH. Various exact analytical solutions of a variable-coefficient Kadomtsev–Petviashvili equation. Nonlinear Dyn 100, 2739–2751 (2020). https://doi.org/10.1007/s11071-020-05629-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05629-z

Keywords

Search

Navigation