Skip to main content
SpringerLink
Log in

Twistor-based pose control for asteroid landing with path constraints

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

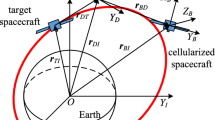
In this paper, a six-degree-of-freedom (6-DOF) control scheme for asteroid landing subject to collision avoidance and line-of-sight (LOS) constraints is developed within the newly established twistor framework. The controller guarantees a spacecraft touches down at a specified landing site in a desired attitude, meanwhile satisfies the constraints with the coupling effect between the translational and rotational motions involved. First, 6-DOF dynamics of a spacecraft relative to an asteroid is described by the twistor representation to model the translational and rotational motions in a unified way. Then, the collision avoidance and LOS constraints are formulated and expressed as functions of the twistor. Following that, the constraints are encoded into an artificial potential function (APF) and a control scheme that enforces the constraints is proposed by virtue of the APF technique with the stability of the controlled closed-loop system proved via Lyapunov analysis. Finally, numerical simulations are conducted, and the results demonstrate the effectiveness of the proposed controller.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19

Similar content being viewed by others

References

  1. Furfaro, R., Cersosimo, D., Wibben, D.R.: Asteroid precision landing via multiple sliding surfaces guidance techniques. J. Guid. Control Dyn. 36(4), 1075–1092 (2013)

    Article  Google Scholar 

  2. Zhang, B., Cai, Y., Li, F.: Adaptive double-saturated control for hovering over an asteroid. Adv. Space Res. 63(7), 2035–2051 (2019)

    Article  Google Scholar 

  3. Zhang, Z., Wang, W., Li, L., Huang, X., Cui, H., Li, S., Cui, P.: Robust sliding mode guidance and control for soft landing on small bodies. J. Frankl. Inst. 349(2012), 493–509 (2012)

    MathSciNet  MATH  Google Scholar 

  4. Lan, Q., Li, S., Yang, J., Guo, L.: Finite-time soft landing on asteroids using nonsingular terminal sliding mode control. Trans. Inst. Meas. Control 36(2), 216–223 (2014)

    Article  Google Scholar 

  5. Liu, K., Liu, F., Wang, S., Li, Y.: Finite-time spacecraft’s soft landing on asteroids using PD and nonsingular terminal sliding mode control. Math. Probl. Eng. 1–10, 2015 (2015)

    Google Scholar 

  6. Lunghi, P., Lavagna, M., Armellin, R.: A semi-analytical guidance algorithm for autonomous landing. Adv. Space Res. 55(11), 2719–2738 (2015)

    Article  Google Scholar 

  7. Liao-McPherson, D., Dunham, W.D., Kolmanovsky, I.: Model predictive control strategies for constrained soft landing on an asteroid. In: AIAA/AAS Astrodynamics Specialist Conference, Long Beach, California. AIAA (2016)

  8. AlandiHallaj, M.A., Assadian, N.: Soft landing on an irregular shape asteroid using multiple-horizon multiple-model predictive control. Acta Astronaut. 140, 225–234 (2017)

    Article  Google Scholar 

  9. Yang, H., Bai, X., Baoyin, H.: Finite-time control for asteroid hovering and landing via terminal sliding-mode guidance. Acta Astronaut. 132, 78–89 (2017)

    Article  Google Scholar 

  10. Kang, S., Wang, J., Li, C., Shan, J.: Nonlinear optimal control with disturbance rejection for asteroid landing. J. Frankl. Inst. 355, 8027–8048 (2018)

    Article  MathSciNet  Google Scholar 

  11. Filipe, N., Tsiotras, P.: Adaptive position and attitude-tracking controller for satellite proximity operations using dual quaternions. J. Guid. Control Dyn. 38(4), 566–577 (2015)

    Article  Google Scholar 

  12. Gui, H., Vukovich, G.: Dual-quaternion-based adaptive motion tracking of spacecraft with reduced control effort. Nonlinear Dyn. 83, 597–614 (2015)

    Article  MathSciNet  Google Scholar 

  13. Wang, J., Liang, H., Sun, Z., Zhang, S., Liu, M.: Finite-time control for spacecraft formation with dual-number-based description. J. Guid. Control Dyn. 35(3), 950–962 (2012)

    Article  Google Scholar 

  14. Dong, H., Hu, Q., Akella, M.R.: Dual-quaternion-based spacecraft autonomous rendezvous and docking under six-degree-of-freedom motion constraints. J. Guid. Control Dyn. 41(5), 1150–1162 (2018)

    Article  Google Scholar 

  15. Deng, Y., Wang, Z.: Modeling and control for spacecraft relative pose motion by using twistor representation. J. Guid. Control Dyn. 39(5), 1144–1151 (2016)

    Article  Google Scholar 

  16. Deng, Y., Wang, Z., Liu, L.: Unscented Kalman filter for spacecraft pose estimation using twistors. J. Guid. Control Dyn. 39(8), 1844–1856 (2016)

    Article  Google Scholar 

  17. Li, Q., Liu, L., Deng, Y., Tang, S., Zhao, Y.: Twistor-based synchronous sliding mode control of spacecraft attitude and position. Chin. J. Aeronaut. 31(5), 1153–1164 (2018)

    Article  Google Scholar 

  18. Lee, D., Vukovich, G.: Adaptive sliding mode control for spacecraft body-fixed hovering in the proximity of an asteroid. Aerosp. Sci. Technol. 46(2015), 471–483 (2015)

    Article  Google Scholar 

  19. Lee, D., Vukovich, G.: Adaptive finite-time control for spacecraft hovering over an asteroid. IEEE Trans. Aerosp. Electron. Syst. 52(3), 1183–1196 (2016)

    Article  Google Scholar 

  20. Dang, Q., Gui, H., Xu, M., Wen, H.: Dual-quaternion immersion and invariance velocity observer for controlling asteroid-hovering spacecraft. Acta Astronaut. 161, 304–312 (2019)

    Article  Google Scholar 

  21. Dang, Q., Gui, H., Wen, H.: Dual-quaternion-based spacecraft pose tracking with a global exponential velocity observer. J. Guid. Control Dyn. 42(9), 2106–2115 (2019)

    Article  Google Scholar 

  22. Hestenes, D., Fasse, E.D.: Applications of Geometric Algebra in Computer Science and Engineering, pp. 197–212. Birkhäuser, Boston (2002)

    Book  Google Scholar 

  23. Wu, Y., Hu, X., Hu, D., Li, T., Lian, J.: Strapdown inertial navigation system algorithms based on dual quaternions. IEEE Trans. Aerosp. Electron. Syst. 41(1), 110–132 (2005)

    Article  Google Scholar 

  24. Filipe, N., Valverde, A., Tsiotras, P.: Pose tracking without linearand angular-velocity feedback using dual quaternions. IEEE Trans. Aerosp. Electron. Syst. 52(1), 411–422 (2016)

    Article  Google Scholar 

  25. Açıkmeşe, B., Ploen, S.R.: Convex programming approach to powered descent guidance for Mars landing. J. Guid. Control Dyn. 30(5), 1353–1366 (2007)

    Article  Google Scholar 

  26. Zhang, B., Tang, S., Pan, B.: Multi-constrained suboptimal powered descent guidance for lunar pinpoint soft landing. Aerosp. Sci. Technol. 48, 203–213 (2016)

    Article  Google Scholar 

  27. Zhang, Y., Guo, Y., Ma, G., Zeng, T.: Collision avoidance ZEM/ZEV optimal feedback guidance for powered descent phase of landing on Mars. Adv. Space Res. 59, 1514–1525 (2017)

    Article  Google Scholar 

  28. Izzo, D., Pettazzi, L.: Autonomous and distributed motion planning for satellite swarm. J. Guid. Control Dyn. 30(2), 449–459 (2007)

    Article  Google Scholar 

  29. Wang, Z., Xu, Y., Jiang, C., Zhang, Y.: Self-organizing control for satellite clusters using artificial potential function in terms of relative orbital elements. Aerosp. Sci. Technol. 84, 799–811 (2019)

    Article  Google Scholar 

  30. Rimon, E., Koditschek, D.E.: Exact robot navigation using artificial potential functions. IEEE Trans. Robot. Autom. 8(5), 501–518 (1992)

    Article  Google Scholar 

  31. Tsuji, T., Tanaka, Y., Morasso, P.G., Sanguineti, V., Kaneko, M.: Bio-mimetic trajectory generation of robots via artificial potential field with time base generator. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 32(4), 426–439 (2002)

    Article  Google Scholar 

  32. Sabattini, L., Secchi, C., Fantuzzi, C.: Arbitrarily shaped formations of mobile robots: artificial potential fields and coordinate transformation. Auton. Robot. 30(4), 385–397 (2011)

    Article  Google Scholar 

  33. Zhang, J., Yan, J., Zhang, P.: Fixed-wing UAV formation control design with collision avoidance based on an improved artificial potential field. IEEE Access 6, 78342–78351 (2018)

    Article  Google Scholar 

  34. Slotine, J.E., Li, W.: Applied Nonlinear Control. Prentice Hall, Englewood Cliffs (1991)

    MATH  Google Scholar 

  35. Li, X., Warier, R.R., Sanyal, A.K., Qiao, D.: Trajectory tracking near small bodies using only attitude control. J. Guid. Control Dyn. 42(1), 109–122 (2019)

    Article  Google Scholar 

  36. Hofmann-Wellenhof, B., Moritz, H.: Physical Geodesy, 2nd edn. Springer, New York (2005)

    Google Scholar 

  37. Winkler, T.M.: Fuel-efficient feedback control of orbital motion around irregular-shaped asteroids. Master’s thesis, Iowa State University (2013)

  38. Werner, R.A., Scheeres, D.J.: Exterior gravitation of a polyhedron derived and compared with harmonic and mascon gravitation representations of asteroid 4769 Castalia. Celest. Mech. Dyn. Astron. 65, 313–344 (1997)

    Article  Google Scholar 

Download references

Funding

This study was funded by the China Postdoctoral Science Foundation (Grant No. 2018M640995).

Author information

Authors and Affiliations

  1. Unmanned System Research Institute, Northwestern Polytechnical University, Xi’an, 710072, China

    Bo Zhang

  2. Department of Automation Science and Technology, Xi’an Jiaotong University, Xi’an, 710049, China

    Yuanli Cai

Authors
  1. Bo Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yuanli Cai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Zhang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A: Expressions of \(\nabla f_1\), \(\nabla f_2\), \(\varPi ^{-\mathrm {T}}\), and \(\varGamma \)

  1. (1)

    The expansion of \(\nabla f_1\) is

    $$\begin{aligned} \nabla f_1 = \left( \frac{\partial f_1}{\partial {\varvec{r}} _{\mathrm {BD}}^{\mathrm {D}}} \right) ^\mathrm {T}\frac{\partial {\varvec{r}} _{\mathrm {BD}}^{\mathrm {D}}}{\partial {\varvec{B}}_{\mathrm {BD}}^\mathrm {T}} \end{aligned}$$
    (52)

where

$$\begin{aligned} \frac{\partial f_1}{\partial {\varvec{r}}_{\mathrm {BD}}^{\mathrm {D}}}=\left[ \begin{array}{c} 2 k_{f_1} \alpha \gamma x_{\mathrm {BD}}^{\mathrm {D}} \left[ \alpha \left( (x_{\mathrm {BD}}^{\mathrm {D}})^2 + \beta (y_{\mathrm {BD}}^{\mathrm {D}})^2 \right) \right] ^{\gamma - 1}\\ 2 k_{f_1} \alpha \beta \gamma y_{\mathrm {D}} \left[ \alpha \left( x_{\mathrm {D}}^2 + \beta y_{\mathrm {D}}^2 \right) \right] ^{\gamma - 1}\\ -k_{f_1} \end{array} \right] \end{aligned}$$
(53)
$$\begin{aligned}&\left( \frac{\partial {\varvec{r}}_{\mathrm {BD}}^{\mathrm {D}}}{\partial {\varvec{B}}_{\mathrm {BD}}^\mathrm {T}} \right) ^\mathrm {T}= \\&\left[ \begin{array}{ccc} \frac{A_{11}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{12}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{13}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} \\ \frac{A_{21}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{22}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{23}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} \\ \frac{A_{31}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{32}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} &{}\quad \frac{A_{33}}{\left( b_1^2+b_2^2+b_3^2+1\right) ^3} \\ 0 &{}\quad 0 &{}\quad 0 \\ \frac{4 \left( b_1^2-b_2^2-b_3^2+1\right) }{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} &{}\quad \frac{8 (b_1 b_2+b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} &{}\quad -\frac{8 (b_2-b_1 b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} \\ \frac{8 (b_1 b_2-b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} &{} -\frac{4 \left( b_1^2-b_2^2+b_3^2-1\right) }{\left( b_1^2+b_2^2+b_3^2 +1\right) ^2} &{}\quad \frac{8 (b_1+b_2 b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} \\ \frac{8 (b_2+b_1 b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} &{}\quad -\frac{8 (b_1-b_2 b_3)}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} &{}\quad -\frac{4 \left( b_1^2+b_2^2-b_3^2-1\right) }{\left( b_1^2+b_2^2+b_3^2 +1\right) ^2} \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{array} \right] \\ A_{11}&= -8 \left[ b_5 b_1^3+3 (b_2 b_6+b_3 b_7) b_1^2\right. \\&\quad \left. +\,\left( -3 b_5 b_2^2 +4 b_7 b_2-3 b_3^2 b_5+b_5-4 b_3 b_6\right) b_1 \right. \\&\quad \left. -\,\left( b_2^2+b_3^2+1\right) (b_2 b_6+b_3 b_7)\right] \\ A_{12}&= 4 \left[ -4 b_1 \left( -b_6 b_1^2+2 b_2 b_5 b_1-2 b_7 b_1+2 b_3 b_5\right. \right. \\&\quad \left. \left. +\, b_2^2 b_6-b_3^2 b_6+b_6+2 b_2 b_3 b_7\right) \right. \\&\quad \left. -\,2 \left( b_1^2+b_2^2+b_3^2+1\right) (-b_2 b_5+b_1 b_6+b_7) \right] \\ A_{13}&= 8 \left[ b_7 b_1^3-3 (b_3 b_5+b_6) b_1^2\right. \\&\quad \left. +\,\left( b_7 b_2^2 +4 (b_5-b_3 b_6) b_2-3 \left( b_3^2+1\right) b_7\right) b_1 \right. \\&\quad \left. +\,\left( b_2^2+b_3^2+1\right) (b_3 b_5+b_6)\right] \\ A_{21}&= 8 \left[ b_5 b_2^3-3 (b_1 b_6+b_7) b_2^2\right. \\&\quad \left. +\,\left( \left( -3 b_1^2 +b_3^2-3\right) b_5+4 b_3 (b_6-b_1 b_7)\right) b_2 \right. \\&\quad \left. +\,\left( b_1^2+b_3^2+1\right) (b_1 b_6+b_7)\right] \\ A_{22}&= 4 \left[ -4 b_2 \left( -b_6 b_1^2+2 b_2 b_5 b_1-2 b_7 b_1\right. \right. \\&\quad \left. \left. +\,2 b_3 b_5 +b_2^2 b_6-b_3^2 b_6+b_6+2 b_2 b_3 b_7\right) \right. \\&\quad +\, \left. 2 \left( b_1^2+b_2^2+b_3^2+1\right) (b_1 b_5+b_2 b_6+b_3 b_7)\right] \\ A_{23}&= 4 \left[ -4 b_2 \left( -b_7 b_1^2+2 b_3 b_5 b_1+2 b_6 b_1\right. \right. \\&\quad \left. \left. -\,\,2 b_2 b_5 +2 b_2 b_3 b_6-b_2^2 b_7+b_3^2 b_7+b_7\right) \right. \\&\quad \left. -\,2 \left( b_1^2+b_2^2+b_3^2+1\right) (b_5-b_3 b_6+b_2 b_7)\right] \\ A_{31}&= 8 \left[ b_5 b_3^3+3 (b_6-b_1 b_7) b_3^2-\left( \left( 3 b_1^2 -b_2^2+3\right) b_5\right. \right. \\&\quad \left. \left. +\,4 b_2 (b_1 b_6+b_7)\right) b_3 \right. \\&\quad \left. +\,\left( b_1^2+b_2^2+1\right) (b_1 b_7-b_6)\right] \\ A_{32}&= 8 \left[ b_6 b_3^3-3 b_2 b_7 b_3^2\right. \\&\quad \left. +\,\left( \left( b_1^2-3 b_2^2 -3\right) b_6+4 b_1 b_7\right) b_3 + \left( b_1^2+b_2^2+1\right) b_2 b_7\right. \\&\quad \left. +\left( b_1^2-4 b_2 b_3 b_1+b_2^2-3 b_3^2+1\right) b_5 \right] \\ A_{33}&= 4 \left[ -4 b_3 \left( -b_7 b_1^2+2 b_3 b_5 b_1+2 b_6 b_1\right. \right. \\&\quad \left. \left. -\,2 b_2 b_5 +2 b_2 b_3 b_6-b_2^2 b_7+b_3^2 b_7+b_7\right) \right. \\&\quad \left. +\, 2 \left( b_1^2+b_2^2+b_3^2+1\right) (b_1 b_5+b_2 b_6+b_3 b_7)\right] \end{aligned}$$
  1. (2)

    The expression of \(\nabla f_2\) is

    $$\begin{aligned} \nabla f_2 = \left[ \begin{array}{c} -\frac{2 \left( (b_3 b_5-b_6) b_1^2+2 \left( b_7 b_3^2+b_2 b_6 b_3+b_2 b_5+b_7\right) b_1-\left( b_2^2+b_3^2+1\right) (b_3 b_5-b_6)\right) }{\left( b_1^2+b_2^2+b_3^2+1\right) ^3 \sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}}} \\ -\frac{2 \left( (b_5+b_3 b_6) b_2^2+2 \left( b_7 b_3^2+b_1 b_5 b_3-b_1 b_6+b_7\right) b_2-\left( b_1^2+b_3^2+1\right) (b_5+b_3 b_6)\right) }{\left( b_1^2+b_2^2+b_3^2+1\right) ^3 \sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}}} \\ -\frac{2 \left( (b_1 b_5+b_2 b_6) b_3^2-2 \left( b_7 b_2^2-b_2 b_5+b_1 (b_6+b_1 b_7)\right) b_3-\left( b_1^2+b_2^2+1\right) (b_1 b_5+b_2 b_6)\right) }{\left( b_1^2+b_2^2+b_3^2+1\right) ^3 \sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}}}\\ 0 \\ \frac{\sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}} \left( b_5 b_7 b_1^2+2 \left( b_5 b_6+b_3 \left( b_6^2+b_7^2\right) \right) b_1+b_2^2 b_5 b_7-\left( b_3^2+1\right) b_5 b_7+2 b_2 \left( b_6^2-b_3 b_5 b_6+b_7^2\right) \right) }{\left( b_5^2+b_6^2+b_7^2\right) ^2}\\ \frac{\sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}} \left( b_6 b_7 b_1^2-2 \left( b_5^2+b_3 b_6 b_5+b_7^2\right) b_1+b_2^2 b_6 b_7-\left( b_3^2+1\right) b_6 b_7+2 b_2 \left( b_3 \left( b_5^2+b_7^2\right) -b_5 b_6\right) \right) }{\left( b_5^2+b_6^2+b_7^2\right) ^2}\\ -\frac{\sqrt{\frac{b_5^2+b_6^2+b_7^2}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2}} \left( \left( b_1^2+b_2^2-b_3^2-1\right) b_5^2+2 (b_2+b_1 b_3) b_7 b_5+b_6 \left( \left( b_1^2+b_2^2-b_3^2-1\right) b_6-2 (b_1-b_2 b_3) b_7\right) \right) }{\left( b_5^2+b_6^2+b_7^2\right) ^2} \\ 0 \end{array} \right] \end{aligned}$$
  2. (3)

    \({\varvec{\varPi }}_{\mathrm {BD}}^{-\mathrm {T}}\) is expanded as

    $$\begin{aligned} {\varvec{\varPi }}_{\mathrm {BD}}^{-\mathrm {T}}&= \frac{1}{\left( b_1^2+b_2^2+b_3^2+1\right) ^2} \left[ \begin{array}{ccc} 4 \left( b_1^2-b_2^2-b_3^2+1\right) &{} 8 (b_1 b_2 + b_3) &{} -8 (b_2 - b_1 b_3) \\ 8 (b_1 b_2 - b_3) &{} -4 \left( b_1^2-b_2^2+b_3^2-1\right) &{} 8 (b_1 + b_2 b_3) \\ 8 (b_2 + b_1 b_3) &{} -8 (b_1 - b_2 b_3) &{} -4 \left( b_1^2+b_2^2-b_3^2-1\right) \\ \end{array} \right] \end{aligned}$$
  3. (4)

    The expansion of \({\varvec{\varGamma }}\) is

    $$\begin{aligned} {\varvec{\varGamma }} = \left[ \begin{array}{cc} {\varvec{\varGamma }}_1 &{} {\varvec{\varGamma }}_2\\ {\varvec{0}}_{4\times 4} &{} {\varvec{\varGamma }}_3 \end{array} \right] \end{aligned}$$

    where

    $$\begin{aligned} {\varvec{\varGamma _{1}}}&= \left[ \begin{array}{cccc} b_1^2-b_2^2-b_3^2+1 &{} 2 b_1 b_2+2 b_3 &{} 2 b_1 b_3-2 b_2 &{} 0\\ 2 b_1 b_2-2 b_3 &{} -b_1^2+b_2^2-b_3^2+1 &{} 2 b_1+2 b_2 b_3 &{} 0\\ 2 b_2+2 b_1 b_3 &{} 2 b_2 b_3-2 b_1 &{} -b_1^2-b_2^2+b_3^2+1 &{} 0\\ 0 &{} 0 &{} 0 &{} b_1^2+b_2^2+b_3^2+1 \end{array} \right] \\ {\varvec{\varGamma _{2}}}&= \left[ \begin{array}{cccc} 2 b_1 b_5-2 b_2 b_6-2 b_3 b_7 &{} 2 b_2 b_5+2 b_1 b_6+2 b_7 &{} 2 b_3 b_5-2 b_6+2 b_1 b_7 &{} 0\\ 2 b_2 b_5+2 b_1 b_6-2 b_7 &{} -2 b_1 b_5+2 b_2 b_6-2 b_3 b_7 &{} 2 b_5+2 b_3 b_6+2 b_2 b_7 &{} 0\\ 2 b_3 b_5+2 b_6+2 b_1 b_7 &{} -2 b_5+2 b_3 b_6+2 b_2 b_7 &{} -2 b_1 b_5-2 b_2 b_6+2 b_3 b_7 &{} 0\\ 0 &{} 0 &{} 0 &{} 2 b_1 b_5+2 b_2 b_6+2 b_3 b_7 \end{array} \right] \\ {\varvec{\varGamma _{3}}}&= \left[ \begin{array}{cccc} b_1^2-b_2^2-b_3^2+1 &{} 2 b_1 b_2+2 b_3 &{} 2 b_1 b_3-2 b_2 &{} 0\\ 2 b_1 b_2-2 b_3 &{} -b_1^2+b_2^2-b_3^2+1 &{} 2 b_1+2 b_2 b_3 &{} 0\\ 2 b_2+2 b_1 b_3 &{} 2 b_2 b_3-2 b_1 &{} -b_1^2-b_2^2+b_3^2+1 &{} 0\\ 0 &{} 0 &{} 0 &{} b_1^2+b_2^2+b_3^2+1 \end{array} \right] \end{aligned}$$

Appendix B: Reduction of \({\dot{V}}_1^\prime \) and \({\dot{V}}_2^\prime \)

Substituting the definitions of \({\varvec{P}}\) and the velocity motor into (31) and (32), one can write \({\dot{V}}_1^\prime \) and \({\dot{V}}_2^\prime \) as:

$$\begin{aligned} {\dot{V}}_1^\prime&=\, {\varvec{Q}}^\mathrm {T}\left[ p {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}+ \varepsilon p_{\varepsilon } \left( \dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\right) \right] ^s \\&\quad \circ \left\{ \left[ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}+ \varepsilon \left( \dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\right) \right] \right. \\&\quad \, \left. \times {\varvec{M}} \left[ {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} + \varepsilon \left( \dot{{\varvec{r}}}_{\mathrm {BI}}^{\mathrm {B}} + {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} \times {\varvec{r}}_{\mathrm {BI}}^{\mathrm {B}} \right) \right] \right\} \\ {\dot{V}}_2^\prime&=\, {\varvec{Q}}^\mathrm {T}\left[ p {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}+ \varepsilon p_{\varepsilon } \left( \dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\right) \right] ^s \\&\quad \circ \left\{ {\varvec{V}}_{\mathrm {DI}}^{\mathrm {B}} \times \left[ m \left( \dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\right) \right. \right. \\&\quad \,\, \left. \left. + \varepsilon J {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right] \right. \\&\quad \, \left. - {\varvec{M}} \left\{ \left[ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}+ \varepsilon \left( \dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\right) \right] \times {\varvec{V}}_{\mathrm {DI}}^{\mathrm {B}} \right\} \right\} \end{aligned}$$

Let \({\varvec{\alpha }}=\dot{{\varvec{r}}}_\mathrm {BD}^\mathrm {B}+ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{r}}_\mathrm {BD}^\mathrm {B}\), \({\varvec{\beta }} = \dot{{\varvec{r}}}_{\mathrm {BI}}^{\mathrm {B}} + {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} \times {\varvec{r}}_{\mathrm {BI}}^{\mathrm {B}}\), \({\varvec{V}}_{\mathrm {DI}}^{\mathrm {B}} = {\varvec{\zeta }} + \varepsilon {\varvec{\eta }}\), and then \({\dot{V}}_1^\prime \) and \({\dot{V}}_2^\prime \) can be reduced to

$$\begin{aligned} {\dot{V}}_1^\prime&=\, \left( p_{\varepsilon } q {\varvec{\alpha }} + \varepsilon p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) \\&\quad \circ \left[ \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}+ \varepsilon {\varvec{\alpha }} \right) \times \left( m {\varvec{\beta }} + \varepsilon J {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} \right) \right] \\&=\, \left( p_{\varepsilon } q {\varvec{\alpha }} + \varepsilon p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) \\&\quad \circ \left\{ m {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\beta }} + \varepsilon \left[ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times \left( J {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} \right) + m {\varvec{\alpha }} \times {\varvec{\beta }} \right] \right\} \\&=\, m p_{\varepsilon } q {\varvec{\alpha }} \cdot \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\beta }} \right) + p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\\&\quad \cdot \left[ {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times \left( J {\varvec{\omega }}_{\mathrm {BI}}^{\mathrm {B}} \right) + m {\varvec{\alpha }} \times {\varvec{\beta }} \right] \\&=\, m p_{\varepsilon } q {\varvec{\alpha }} \cdot \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\beta }} \right) \\&\quad \,+ m p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\cdot \left( {\varvec{\alpha }} \times {\varvec{\beta }} \right) \\ {\dot{V}}_2^\prime&=\, \left( p_{\varepsilon } q {\varvec{\alpha }} + \varepsilon p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) \\&\quad \circ \left\{ m {\varvec{\zeta }} \times {\varvec{\alpha }} + \varepsilon \left[ {\varvec{\zeta }} \times \left( {\varvec{J}} {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) + m {\varvec{\eta }} \times {\varvec{\alpha }} \right] \right. \\&\quad \left. - \left[ m \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\eta }} + {\varvec{\alpha }} \times {\varvec{\zeta }} \right) + \varepsilon {\varvec{J}}\left( {\varvec{\omega }} _\mathrm {BD}^\mathrm {B}\times {\varvec{\zeta }} \right) \right] \right\} \\&=\, m p_{\varepsilon } q {\varvec{\alpha }} \cdot \left( {\varvec{\zeta }} \times {\varvec{\alpha }} \right) + p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\\&\quad \cdot \left[ {\varvec{\zeta }} \times \left( {\varvec{J}} {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) + m {\varvec{\eta }} \times {\varvec{\alpha }} \right] \\&\quad - m p_{\varepsilon } q {\varvec{\alpha }} \cdot \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\eta }} + {\varvec{\alpha }} \times {\varvec{\zeta }} \right) \\&\quad - p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\cdot {\varvec{J}}\left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\zeta }} \right) \\&=\, p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\cdot \left[ {\varvec{\zeta }} \times \left( {\varvec{J}} {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\right) \right] - m p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\cdot \left( {\varvec{\alpha }} \times {\varvec{\eta }} \right) \\&\quad - m p_{\varepsilon } q {\varvec{\alpha }} \cdot \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\eta }} \right) - p q_{\varepsilon } {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\cdot {\varvec{J}} \left( {\varvec{\omega }}_\mathrm {BD}^\mathrm {B}\times {\varvec{\zeta }} \right) \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, B., Cai, Y. Twistor-based pose control for asteroid landing with path constraints. Nonlinear Dyn 100, 2427–2448 (2020). https://doi.org/10.1007/s11071-020-05610-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05610-w

Keywords

Search

Navigation