1 Introduction

The impulsive Goodwin’s oscillator is a mathematical model comprised of a linear third-order time-invariant continuous plant controlled by a pulse-modulated feedback, [1, 2]. The closed-loop dynamics are hybrid and lack equilibria due to the form of the amplitude modulation function. On the one hand, the model generalizes the classical continuous Goodwin’s oscillator [3,4,5,6,7,8,9] and provides a modeling framework to describe numerous oscillatory biological control systems exploiting neurally implemented impulsive feedback. Exactly as its predecessor, the impulsive Goodwin’s oscillator possesses positivity of the state variables. On the other hand, it presents an analytically tractable example of a hybrid oscillator with rich nonlinear dynamics including, e.g., high-periodic solutions and deterministic chaos. At the same time, and in contrast with the continuous counterpart, the considered impulsive oscillator is validated through system identification on human endocrine data with respect to testosterone regulation in the male, [10]. The latter fact secures the utility of the model. A structurally similar to the impulsive Goodwin’s oscillator model has been more recently proposed to describe the pharmacokinetics of levodopa, the mainstay drug in Parkinson’s disease, subject to intermittently interrupted gastric emptying.

The impulsive feedback signal of the Goodwin’s oscillator is intrinsic to the closed loop and essentially cannot be measured in biomedical applications, which property poses an interesting and practically meaningful problem for estimating the full hybrid state of a system from only continuous measurements. In endocrinology, the problem of reconstructing the episodic firings of a pulsatile feedback is standard and usually handled by applying deconvolution algorithms under assumptions on the signal shape of the pulse; see, e.g., [11, 12]. While deconvolution algorithms are widely used in practice due to readily available software, being applied to pulsatile endocrine regulation, they basically ignore the pulse-modulated feedback nature of the underlying system and are not suitable for online implementation. The deconvolution per se (i.e., blind deconvolution) is not a well-posed problem and needs regularization. Further, all the deconvolution methods used in practice enforce, in some way, solution sparsity and merge the pulses near to each other to one. Faced with a signal shape that deviates much from linear dynamics, the deconvolution methods allow for multiple pulses within a short time interval. This results in a deceptively insignificant output modeling error but yet does not properly capture the impulsive feedback characteristics. Therefore, it is motivated to consider output error feedback observer algorithms for the reconstruction of the impulsive feedback action along with the continuous states from a continuous output since they project measured data onto an analytically defined mathematical model.

Notice that in most of the studies covering state reconstruction in hybrid system, the discrete states (or switching events) are assumed to be known, as they typically belong to the engineered part of the system, as, e.g., in automotive applications [13]. Because control and observation over computer network become ubiquitous, the opposite problem of estimating the states of a continuous system from irregular discrete measurements is considered much more broadly and actively, e.g., [14].

Observers for hybrid systems that utilize only continuous measurements are rarely considered in the literature and limited to specific plant types. Since the impulsive Goodwin’s oscillator only exhibits periodic and non-periodic (i.e., quasiperiodic and chaotic) oscillations, the observer design problem can be formulated as synchronization of the plant states with those of the observer. This approach has been proposed in [15] and does not formally demand observability of the hybrid plant solution. In a certain way, the idea is similar to that of the observers for unobservable but detectable linear time-invariant systems, where the state estimates that cannot be corrected by output error feedback converge due to the stable intrinsic dynamics. Similarly, the dynamics governing the observed periodical solution to the impulsive Goodwin’s oscillator have to be orbitally stable for the observer to be functional. Further, since the oscillator dynamics are highly nonlinear, the state estimation problem is considered with respect to particular solutions of the observed system, whose characteristics are assumed to be known, but not the initial conditions. This can be compared to the situation with the Luenberger observer, where the model of the plant is available and the state estimation error due to the mismatch in the initial conditions on the plant and the observer asymptotically vanishes.

The observer design problem for the impulsive Goodwin’s oscillator consists of assigning desired properties to a discrete map that captures the observer state transitions from one impulse firing to another through manipulating the degrees of freedom provided by the observer structure. A simplest observer structure includes just one output error feedback matrix for the continuous state estimates, as proposed in [15]. Then, it is proven that there is a sufficiently high observer gain that guarantees asymptotic convergence of all the components of the hybrid state estimate.

Since the simplest observer structure suffers from slow convergence in the discrete state estimate (i.e., the impulsive feedback firing time), an additional observer gain from the output error to the discrete state estimate is introduced in [16]. In fact, even with a slightly unstable (physiologically infeasible) linear part of the model, the hybrid state estimation error can be asymptotically stabilized solely by the gain to the discrete state estimate; see [17]. With two nonzero gains, the observer design becomes an intricate highly nonlinear problem of balancing the gain to the continuous state variable estimates against that to the discrete state estimate in order to achieve a desirable overall performance. With high continuous gain, the estimation error in the continuous states converges fast which implies that the (continuous) output estimation error is virtually zero and does not provide correction to the discrete state. When the discrete observer gain is set too high, the hybrid state estimate convergence is disrupted by so-called overjumps that result in postponing the synchronization of the plant and observer by one or, more often, several periods of the observed plant solution.

Control and observer design for nonlinear and hybrid systems is heavily focused on analytical techniques and global stability properties of the designed structure. This is in a sharp contrast with the engineering practices that are based on simulation of complex plants and tuning of control and estimation algorithms through more or less formal optimization algorithms. Bifurcation analysis is an established tool for discerning and studying in depth the mechanisms of complex dynamics of a given system. Applying bifurcation analysis to design of nonlinear control is not a novel idea but more accepted and utilized in certain specific areas of engineering that are challenged with nonlinear dynamical phenomena. Flight control [18], chemical reactor control [19], and closed-loop control of drug delivery [20] are just few examples of nonlinear control applications, where bifurcation analysis and continuation techniques serve design purposes well. However, analysis of nonlinear dynamics becomes computationally heavy in higher dimensions which fact limits the number of controller/observer design degrees of freedom. Further, the structure of a control or estimation algorithm to be analyzed has to be specified beforehand.

The problem considered in this paper is how to select the design parameters of a hybrid state observer that render appropriate state estimation performance. Since the observer is based on a model describing the plant, the achievable state reconstruction performance is restricted by the complex nonlinear plant dynamics. Bifurcation analysis is used to discover and observe these limitations in the proposed observer design algorithm.

Novelty of the proposed approach is ensured by the fact that bifurcation analysis for hybrid observer design has not been covered before in the literature. The main contributions of this study are three and stand as follows:

  • Firstly, to enable a bifurcation analysis, an approach to determine the periodic motions and investigating their local stability is proposed. The problem of periodic motion evaluation is reduced to solving a system of transcendental equations with respect to the fixed points of the periodic orbit of the discrete mapping. This allows for the evaluation of stable as well as unstable cycles.

  • Secondly, a complete bifurcation analysis of a hybrid observer for the impulsive Goodwin’s oscillator is performed elucidating the complex dynamics phenomena that arise in it.

  • Finally, a systematic design procedure that guaranties the observer function for all feasible initial conditions of the hybrid state estimate is proposed.

The rest of the paper is structured as follows. First, the equations of the impulsive Goodwin’s oscillator are recapitulated and the main dynamical properties of it are summarized. To reconstruct the hybrid state vector from the continuous output, an observer structure equipped with two output error feedback gains, one correcting the continuous state variables and another adjusting the discrete one, is introduced. Further, a discrete map describing the hybrid dynamics of the observer is derived and studied by bifurcation analysis highlighting the distinctive nonlinear phenomena. Based on those findings, a systematic observer design algorithm is proposed and illustrated by numerical examples.

2 The impulsive Goodwin’s oscillator

The impulsive version of Goodwin’s oscillator has been introduced in [1] to portray the hybrid dynamics of testosterone (Te) regulation arising due to the pulse-modulated feedback implemented by the hypothalamus. Pulses of gonadotropin releasing hormone (GnRH) are secreted from the hypothalamus to stimulate the release of luteinizing hormone (LH) from the pituitary gland that, in its turn, stimulates the release of testosterone (Te) from the testes. Then, Te inhibits the secretion of GnRH through a negative feedback by lowering the amplitude and frequency of the pulses.

The continuous part of the impulsive Goodwin’s oscillator is given by

$$\begin{aligned} \begin{aligned} \dot{x}_1(t)&=-b_1x_1(t),\quad \dot{x}_2(t)=g_1x_1(t)-b_2x_2(t),\\ \dot{x}_3(t)&=g_2x_2(t)-b_3x_3(t), \end{aligned} \end{aligned}$$
(1)

where \(x_1(t)\) undergoes jumps at the time instants \(t_n\), \(n>0\):

$$\begin{aligned} x_1(t^+_n)= & {} x_1(t^-_n) + \lambda _n,\quad t_{n+1} =t_n + T_n,\\ \lambda _n= & {} F(x_3(t_n)),\quad T_n=\varPhi (x_3(t_n)). \end{aligned}$$

In terms of Te regulation in the male, \(x_1\) is interpreted as the concentration of GnRH, \(x_2\) as the concentration of LH, and \(x_3\) as the concentration of Te. The positive parameters \(b_1\), \(b_2\) and \(b_3\) denote the reciprocal half-life times of the hormones, and \(g_1\) and \(g_2\) are the secretion rate factors of LH and Te, respectively. The nonlinear functions \(F(\cdot )\) and \(\varPhi (\cdot )\) are positive and bounded; \(F(\cdot )\) is decreasing and \(\varPhi (\cdot )\) is increasing. In particular, the positivity of \(F(\cdot )\) explains why there are no equilibria in the impulsive Goodwin’s oscillator. The superscripts \(``-''\) and \(``+''\) denote the left- and right-side limits, respectively. The concentration of GnRH is subject to jumps due to the pulse-modulated frequency and amplitude feedback from Te implemented via the hypothalamic neurons. The positivity of \(\varPhi (\cdot )\) corresponds to the necessity for the neuron to have a refractory period between firings.

The impulsive hormonal feedback modulation functions \(F(\cdot )\) and \(\varPhi (\cdot )\) are assumed to be Hill functions of the form:

$$\begin{aligned} \varPhi (x_3)= & {} \varPhi _1 + \varPhi _2\dfrac{(x_3/h)^\beta }{1+(x_3/h)^\beta }, \quad \\ F(x_3)= & {} F_1 + \dfrac{F_2}{1+(x_3/h)^\beta }, \end{aligned}$$

where \(\varPhi _1\), \(\varPhi _2\), \(F_1\), \(F_2\), h are positive constants and \(\beta \) is the order of the Hill functions. For biological feasibility of the model, the following bounds apply:

$$\begin{aligned} 0< & {} \varPhi _1\leqslant \varPhi (\cdot )<\varPhi _1+\varPhi _2, \quad \nonumber \\ 0< & {} F_1< F(\cdot )\leqslant F_1+F_2. \end{aligned}$$
(2)

With the state vector \(\mathrm {x}=[x_1\quad x_2\quad x_3]^{\top }\), model Eq. (1) can be rewritten as

$$\begin{aligned} \begin{aligned} \dot{\mathrm {x}}(t)&= A\mathrm {x}(t), \quad \mathrm {y}(t)=L\mathrm {x}(t),\quad z(t)=C\mathrm {x}(t), \\ \mathrm {x}(t^+_n)&= \mathrm {x}(t^-_n) + \lambda _n B,\quad t_{n+1} =t_n + \varPhi (z(t_n)),\\ \lambda _n&=F(z(t_n)), \quad n=0,1,2,\ldots , \end{aligned} \end{aligned}$$
(3)

where

$$\begin{aligned} A= & {} \begin{bmatrix} -b_1 &{}\quad 0 &{}\quad 0\\ g_1 &{}\quad -b_2 &{}\quad 0\\ 0 &{}\quad g_2 &{}\quad -b_3 \end{bmatrix}, B = \begin{bmatrix} 1 \\ 0\\ 0 \end{bmatrix},\\ L= & {} \begin{bmatrix} 0&{}\quad 1&{}\quad 0 \\ 0&{}\quad 0&{}\quad 1 \end{bmatrix}, C = \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}^\top . \end{aligned}$$

Thus, \(\mathrm {y}(t)\) comprises the measurable serum concentrations of LH and Te, and z(t) is the concentration of Te that drives the impulsive feedback. Since the equalities \(CB=0\), \(LB=0\) hold, the outputs \(\mathrm {y}(t)\) and z(t) are continuous. Notice that all eigenvalues of the matrix A are real and negative. This property corresponds to the fact that all organic molecules eventually decay. In addition, the matrix A is also Metzler. This implies that the positive octant \(\mathbb {R}^3_+\) is invariant with respect to Eq. (3) and the continuous part of Eq. (3) is a positive system. System positivity is an important property in mathematical modeling of biological systems, in particular those whose state variables stand for concentrations of chemicals. It can be checked that the pair (A, L) is observable and the fact immediately follows from the cascaded structure of Eq. (1).

As shown in [1], any solution of model Eq. (1) is bounded and the considered impulsive feedback system does not possess an equilibrium point. For biologically motivated parameter values, dynamical system Eq. (3) exhibits a stable periodic solution with one or two pulses in the period, i.e., a stable 1-cycle, or a stable 2-cycle. However, as demonstrated in [21], more complicated phenomena are also possible, including period-doubling transition to chaos, period-adding phenomena and quasiperiodicity. Importantly, the impulsive Goodwin’s oscillator is currently the only endocrine feedback regulation model that is validated on human Te and LH data [10].

The pulses of amplitude \(\lambda _n\) produced by the impulsive feedback at the firing times \(t_n\) are immeasurable thus motivating their model-based reconstruction. Therefore, the state observation problem at hand consists of producing the estimates \(({\hat{t}}_n,\,{\hat{\lambda }}_n)\) of the firing times \(t_n\) and the amplitudes \(\lambda _n\) of the pulses. In the endocrine closed-loop system, the GnRH pulses cannot be measured for ethical reasons as they are secreted deep in the brain and the hormone has a short half-life time. Note that, with a completely known impulse sequence, estimates of the continuous state vector \(\mathrm {x}(t)\) can be obtained by conventional state estimation techniques.

3 Observer structure

In order to estimate the state vector of system Eq. (3), a hybrid observer is introduced in [16] as

$$\begin{aligned} \dot{\hat{\mathrm {x}}}(t)= & {} A\hat{\mathrm {x}}(t)+K({\mathrm {y}}(t)-\hat{\mathrm {y}}(t)), \quad \hat{\mathrm {y}}(t) = L \hat{\mathrm {x}}(t), \nonumber \\ {\hat{z}}(t)= & {} C\hat{\mathrm {x}}(t),\quad {\hat{t}}_n<t<{\hat{t}}_{n+1}, \end{aligned}$$
(4)
$$\begin{aligned} \hat{\mathrm {x}}(t_n^+)= & {} \hat{\mathrm {x}}(t_n^-) +{\hat{\lambda }}_n B, \quad {\hat{t}}_{n+1} ={\hat{t}}_n+{\hat{T}}_n, \end{aligned}$$
(5)

with

$$\begin{aligned} {\hat{\lambda }}_n =F({\hat{z}}(t_n)),\quad {\hat{T}}_n=\varPhi \left( \hat{z}({\hat{t}}_n)+k_d(z({\hat{t}}_n)-{\hat{z}}({\hat{t}}_n))\right) ,\nonumber \\ \end{aligned}$$
(6)

where \(K\in {\mathbb {R}}^{3\times 2}\) is the continuous feedback matrix and \(k_d\) is the gain in the discrete part of the observer. The gains \(K,k_d\) represent the design degrees of freedom. The discrete dynamics of Eq. (4) are directly impacted by the scalar gain \(k_d\), while K controls the convergence of the continuous estimate \(\hat{\mathrm {x}}(t)\) in between the firings of the pulse-modulated feedback.

Notably, even with zero value of either gain, the observer is still able to converge to the hybrid state vector of the plant. With \(k_d=0\), the observer is known to suffer from slow convergence; see [15]. Since the pair (A, L) is observable, the gain K assigns the convergence rate of the continuous state estimation error. As the matrix A is Hurwitz stable, the continuous gain is not necessary. In fact, even the gain matrices K that result in (slightly) non-Hurwitz matrices

$$\begin{aligned} D=A-KL \end{aligned}$$

can still produce stable hybrid dynamics through the stabilizing action of \(k_d\), as the continuous and discrete observer dynamics interact.

4 Synchronous mode

To completely characterize the hybrid system dynamics of Eq. (3), not only the continuous state vector x(t), but also the sequence of time instants \(t_n\) should be taken into account.

Let \((\mathrm {x}(t),\,t_n)\) be a solution of Eq. (3) that undergoes jumps at time instants \(t_n\), \(n\geqslant 0\):

$$\begin{aligned} \mathrm {x}(t^+_n)= & {} \mathrm {x}(t^-_n) + \lambda _n B,\\ t_{n+1}= & {} t_n + \varPhi (z(t_n)),\quad \lambda _n=F(z(t_n)), \end{aligned}$$

and denote \(\mathrm {x}_n=\mathrm {x}(t_n^-)\).

Suppose that the hybrid state \((\mathrm {x}(t),\,t_n)\) is reconstructed by means of observer Eqs. (4)–(6). Without loss of generality, assume that \(t_0 \leqslant {\hat{t}}_0 < t_1\). Obviously, the solution \((\hat{\mathrm {x}}(t),\,{\hat{t}}_n)\) of observer equations (4)–(6) subject to the initial conditions \({\hat{t}}_0=t_0\), \(\hat{\mathrm {x}}(\hat{t}_0^-)={\mathrm {x}}(t_0^-)\), yields \(\hat{\mathrm {x}}(t)={\mathrm {x}}(t)\) for all \(t\geqslant t_0\). Then, \((\hat{\mathrm {x}}(t),\,{\hat{t}}_n)\) is called a synchronous mode of observer Eqs. (4)–(6) with respect to the solution \(({\mathrm {x}}(t),\,t_n)\) of plant Eq. (3); see [15]. Thus, a synchronous mode corresponds to the zero dynamics of the hybrid observer.

Since the continuous plant output \({\mathrm {y}}(t)\) is the only source of information about the hybrid plant state, the result below is instrumental.

Proposition 1

([17]) The following conditions are equivalent

  1. 1.

    \((\hat{\mathrm {x}}(t),\,{\hat{t}}_n)\) is a synchronous mode of observer Eqs. (4)–(6) with respect to \(({\mathrm {x}}(t),\,t_n)\) ;

  2. 2.

    \(\hat{\mathrm {y}}(t)\equiv {\mathrm {y}}(t)\,\,\text{ for } \text{ all }\,\,\, t\geqslant t_0\).

Conditions in Proposition 1 ensure that reducing the plant output estimation error to zero brings the observer into a synchronous mode and, therefore, solves the hybrid state estimation problem.

To ensure practical usefulness of the observer, stability properties of the synchronous mode have to be investigated. Indeed, once perturbed, the observer in a synchronous mode has to rapidly return into it. A synchronous mode with respect to \(({\mathrm {x}}(t),\,t_n)\) is called locally asymptotically stable (see [15]) if, for any solution \((\hat{\mathrm {x}}(t),\,{\hat{t}}_n)\) of Eqs. (4)–(6) such that the initial estimation errors \(|{\hat{t}}_0-t_0|\) and \(\Vert \hat{\mathrm {x}}({\hat{t}}_0^-)-{\mathrm {x}}(t_0^-)\Vert \) are sufficiently small, it follows that \({\hat{t}}_n-t_n\rightarrow 0\) and \(\Vert \hat{\mathrm {x}}({\hat{t}}_n^-)-{\mathrm {x}}(t_n^-)\Vert \rightarrow 0\) as \(n\rightarrow \infty \). This also implies \({\hat{\lambda }}_n-\lambda _n\rightarrow 0\) as \(n\rightarrow \infty \).

Observing a periodic solution \(({\mathrm {x}}(t),\,t_n)\) of system Eq. (3) with exactly \(m\geqslant 1\) pulses within the least period of the solution is of special interest. Such a solution is called m-cycle. Then, \({\mathrm {x}}_{n+m}\equiv {\mathrm {x}}_n\), \(\lambda _{n+m}\equiv \lambda _n\), \(T_{n+m}\equiv T_n\). Logically, the synchronous mode \((\hat{\mathrm {x}}(t),\,{\hat{t}}_n)\) is also an m-cycle with \(\hat{\mathrm {x}}_{n+m}\equiv \hat{\mathrm {x}}_n\equiv {\mathrm {x}}_n\), \({\hat{\lambda }}_{n+m}\equiv {\hat{\lambda }}_n \equiv \lambda _n\), \({\hat{T}}_{n+m}\equiv {\hat{T}}_k \equiv T_n\). Denote the m-cycles of the plant and the observer by \({{\mathscr {C}}}^m ({\mathrm {x}}(t), t_n)\) and \({{\mathscr {C}}}^m (\hat{\mathrm {x}}(t), {\hat{t}}_n)\) , respectively.

Consider the set

$$\begin{aligned}&\mathscr {Z}=\left\{ \zeta \in {\mathbb {R}}^{3}:\,\,\,\, V_1\leqslant \zeta _1\leqslant H_1,\right. \\&\quad \left. V_2\leqslant \zeta _2\leqslant H_2,\,\,\, V_3\leqslant \zeta _3\leqslant H_3\right\} , \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lcl} V_1 = \dfrac{F_1}{{\mathrm {e}}^{b_1(\varPhi _1+\varPhi _2)}-1}, &{} V_2 = \dfrac{g_1V_1}{b_2}, &{} V_3 = \dfrac{g_1g_2V_1}{b_2b_3},\nonumber \\ H_1 = \dfrac{F_1+F_2}{1-{\mathrm {e}}^{-b_1\varPhi _1}}, &{} H_2 = \dfrac{g_1H_1}{b_2}, &{} H_3 = \dfrac{g_1g_2H_1}{b_2b_3}. \end{array}\nonumber \\ \end{aligned}$$
(7)

It was proved in [1] that, for a trajectory starting in \(\mathscr {Z}\) (i.e., \({\mathrm {x}}(0)\in \mathscr {Z}\) ), the following inequalities hold

$$\begin{aligned} V_i\leqslant \liminf _{t\rightarrow \infty } x_i(t)\leqslant \limsup _{t\rightarrow \infty } x_i(t)\leqslant H_i,\quad i=1,2,3.\nonumber \\ \end{aligned}$$
(8)

Therefore, \(\mathscr {Z}\) is an invariant set under Eq. (3).

For \({{\mathscr {C}}}^m ({\mathrm {x}}(t), t_n)\), consider also the set

$$\begin{aligned} \mathcal{T}=\left\{ \theta \in {\mathbb {R}}:\,\,\,\, 0\leqslant \theta \leqslant T_{\varSigma }\right\} , \end{aligned}$$

where \(T_{\varSigma }=\sum \nolimits _{i=0}^{m-1}T_i\). Obviously, \(T_{\varSigma }\) is the least period of the m-cycle being estimated. Therefore, the space \(\mathcal{D}=\mathcal{Z}\times \mathcal{T}\) (where \(\times \) is a Cartesian product) constitutes the (phase) subspace of feasible initial conditions for the observer.

Introduce the continuous state estimation error \(r(t)={\mathrm {x}}(t)-\hat{\mathrm {x}}(t)\). For all values of t, where r(t) is continuous, it satisfies the differential equation

$$\begin{aligned} \dot{r}(t)=D\,r(t). \end{aligned}$$
(9)

The function r(t) undergoes jumps \(r(t^+)-r(t^-)=\lambda _nB\) at the points \(t=t_n\) and \(r(t^+)-r(t^-)=-{\hat{\lambda }}_nB\) at the points \(t={\hat{t}}_n\). Thus, when evolving in t, r(t) is subject to jumps induced both by the impulsive feedback in the plant and that of the observer.

In general, the continuous state estimation error r(t) can belong to:

  • an equilibrium point corresponding to a synchronous mode,

  • a periodic attractor that contains solutions with asynchronous firing of impulses in the plant and the observer,

  • a quasiperiodic attractor, or

  • a chaotic attractor.

Of the alternatives above, only the first one is acceptable when an accurate hybrid state estimate is desired. The second option in the list is an undesirable behavior featuring, for a certain values of K and \(k_d\), an p-periodic asynchronous mode with \(\hat{\mathrm {x}}_{n+p}\equiv \hat{\mathrm {x}}_n\), \(\hat{t}_{n}\ne t_n\), where \(p\geqslant 1\) is some integer (Fig. 1). If such asynchronous mode is locally stable, then, for certain initial conditions, the observer might enter this mode, instead of a synchronous one.

Fig. 1
figure 1

Illustration of a stable asynchronous 2-cycle of the observer: the continuous state estimate of the observer \(\hat{x}_1\) (in red) with respect to the actual one of the plant \(x_1\) (in blue). The observer does not give a correct estimate of the hybrid plant state. (Color figure online)

Full size image

To include the whole space of feasible initial conditions \(\mathcal D\) into the domain of attraction of the synchronous mode, the gain coefficients K and \(k_d\) have to be selected so that there are no other periodic modes of the observer, distinct from the synchronous one, or these modes are unstable. The conditions for the existence and stability of a periodic asynchronous mode are provided in the next section. Further, by choice of K and \(k_d\), the synchronous mode has to be rendered locally asymptotically stable and attractive on \(\mathscr {D}\) with a suitable convergence rate. This constitutes the observer design problem at hand.

5 Discrete mapping

Recall from [17] the discrete mapping capturing the propagation of the continuous observer states through the discrete cumulative (plant and observer) sequence of the feedback firing instants

$$\begin{aligned} Q: \begin{bmatrix} \hat{\mathrm {x}}_{n}\\ {\hat{t}}_{n} \end{bmatrix}\mapsto \begin{bmatrix} \hat{\mathrm {x}}_{n+1}\\ {\hat{t}}_{n+1} \end{bmatrix}. \end{aligned}$$
(10)

Define \( R=(1-k_d)\,C,\quad \alpha (\zeta ,\theta )=R\zeta +k_d z(\theta ). \) Introduce the set

$$\begin{aligned}&S_{k,s}=\{(\zeta ,\,\theta ):\,\,\, \zeta \in {\mathbb {R}}^3,\,\,\, \theta \in {\mathbb {R}},\,\,\,\, t_k\leqslant \theta<t_{k+1},\\&\quad t_s\leqslant \theta +\varPhi (\alpha (\zeta , \theta ))<t_{s+1}\}, \end{aligned}$$

and a piecewise-defined function \(P(\zeta ,\theta )=P_{k,s}(\zeta ,\theta )\) for \((\zeta ,\theta )\in S_{k,\,s}\) with

$$\begin{aligned}&P_{k,s}(\zeta ,\theta )= {\mathrm {e}}^{A(\theta +\varPhi (\alpha (\zeta , \theta ))-t_s)}{\mathrm {x}}(t_s^+)\\&\quad +\, {\mathrm {e}}^{D\varPhi (\alpha (\zeta , \theta ))}\left[ \zeta +F(C\zeta )B - {\mathrm {e}}^{A(\theta -t_k)}{\mathrm {x}}(t_k^+) \right] \\&\quad -\,\sum _{i=k+1}^s \lambda _i {\mathrm {e}}^{D(\theta +\varPhi (\alpha (\zeta , \theta ))-t_i)}B. \end{aligned}$$

Hence, each point of the observer hybrid state \((\hat{\mathrm {x}}_n, {\hat{t}}_n)\) belongs to one of the sets \(S_{k,s}\), i.e., to each \((\hat{\mathrm {x}}_n, {\hat{t}}_n)\) one can uniquely match two points \(({\mathrm {x}}_k, t_k)\) and \(({\mathrm {x}}_s, t_s)\) of the observed system (if \(k=s\), these points coincide) such that \(t_k\leqslant {\hat{t}}_n<t_{k+1}, \,\, t_s\leqslant {\hat{t}}_n+\varPhi (\alpha (\hat{\mathrm {x}}_n, {\hat{t}}_n))<t_{s+1}\). Now mapping Eq. (10) can be written as

$$\begin{aligned} \begin{bmatrix} \hat{\mathrm {x}}_{n+1}\\ {\hat{t}}_{n+1} \end{bmatrix}= Q(\hat{\mathrm {x}}_{n},\,{\hat{t}}_{n})= \begin{bmatrix} P(\hat{\mathrm {x}}_{n},\,{\hat{t}}_{n})\\ {\hat{t}}_{n}+\varPhi (\alpha (\hat{\mathrm {x}}_{n}, {\hat{t}}_{n})) \end{bmatrix} \end{aligned}$$
(11)

As proven in [17], the mapping \(Q(\zeta ,\theta )\) is smooth provided the functions \(\varPhi (\cdot )\) and \(F(\cdot )\) have continuous derivatives. Thus, the discrete observer dynamics admit linearization in the vicinity of \((\hat{\mathrm {x}}_n,\,{\hat{t}}_n)\), where local stability properties of observer solutions can be analyzed.

Disregarding for a moment the task of state observation, one can look upon observer Eqs. (4)–(6) as a hybrid dynamical system driven by the plant output \({\mathrm {y}}(t)\). Then, for a given plant model, each solution of the observer equations is completely defined by the initial conditions on the observer \(\hat{\mathrm {x}}(\hat{t}_0^-)\), the observer gains \(K, k_d\), and the time evolution of the plant output y(t). Therefore, in view of synchronous and asynchronous observer modes (e.g., as in Fig. 1), it is now possible to obtain general conditions for existence of a periodical solution in the observer.

Consider an m-cycle \(\mathscr {C}^m({\mathrm {x}}(t), t_n)\) of plant Eq. (3) that is characterized by a sequence of the jump points \({\mathrm {x}}_n\) and the intervals \(T_n=t_{n+1}-t_n\), \(n=0,\ldots ,m-1\), \(T_0=T_m\) between the subsequent firing times. Assume that there exists a p-cycle \({{\mathscr {C}}}^{p}(\hat{\mathrm {x}}(t), {\hat{t}}_n)\) of observer Eqs. (4)–(6), such that each point \((\hat{\mathrm {x}}_n, {\hat{t}}_n)\) (\(n=0,\ldots ,p-1\)) corresponds to two points \((\mathrm {x}_{k_n}, t_{k_n})\) and \((\mathrm {x}_{s_n}, t_{s_n})\) of the plant m-cycle where the subscripts \(k_n\) and \(s_n\) are determined by \(0\leqslant k_n\leqslant s_n\) and \(t_{k_n}\leqslant {\hat{t}}_n<t_{k_n+1}, \, t_{s_n}\leqslant {\hat{t}}_n+\varPhi (\alpha (\hat{\mathrm {x}}_n, \hat{t}_n))<t_{s_n+1}\).

Note that \(t_{i+m}=t_i+T_{\varSigma }\) for any \(i=0,1,\ldots \) and \(\sum _{i=0}^{p-1}{\hat{T}}_i=NT_{\varSigma }\), where \(N\geqslant 1\) is a integer. In order to simplify notation, without loss of generality, assume \(t_0=0\), \(N=1\) and denote \(\tau =\hat{t}_0-t_{k_0}\).

Theorem 1

A p-cycle \({{\mathscr {C}}}^{p}(\hat{\mathrm {x}}(t), {\hat{t}}_n)\) of observer equations (4)–(6) corresponding to an m-cycle \({{\mathscr {C}}}^m({\mathrm {x}}(t), t_n)\) of plant Eq. (3) is completely defined by the two sequences \(\hat{\mathrm {x}}_0, \ldots , \hat{\mathrm {x}}_{p-1}\), \({\hat{T}}_0, \ldots , \hat{T}_{p-2}\) and \(\tau \), whose values can be found by solving of the following system of transcendental equations:

$$\begin{aligned} {\hat{\mathrm {x}}_0}&= \,\, \,{\mathrm {e}}^{A\left( {\tau }+T_{\varSigma }-\varTheta _{s_{p-1}}\right) }\left[ {\mathrm {x}}_{k_0}+\lambda _{k_0}B\right] \nonumber \\&\quad +{\mathrm {e}}^{D\left( T_{\varSigma }-\sum _{i=0}^{p-2}{{\hat{T}}_i}\right) }\Big [{\hat{\mathrm {x}}_{p-1}} +F(C{\hat{\mathrm {x}}_{p-1}})B\nonumber \\&\quad -{\mathrm {e}}^{A\left( {\tau }+\sum _{i=0}^{p-2}{{\hat{T}}_i}-\varTheta _{k_{p-1}}\right) }\left[ {\mathrm {x}}_{k_{p -1}}+\lambda _{k_{p -1}}B\right] \Big ]\nonumber \\&\quad -\sum _{i=k_{p -1}+1}^{s_{p - 1}}\lambda _{i \bmod {m}} \,{\mathrm {e}}^{D\left( {\tau }+T_{\varSigma }-\varTheta _i\right) }B,\nonumber \\ {\hat{\mathrm {x}}_n} =&\,\, \, {\mathrm {e}}^{A\left( {\tau }+\sum _{i=0}^{n-1}{{\hat{T}}_i}-\varTheta _{s_{n-1}}\right) }\left[ {\mathrm {x}}_{s_{n-1}}+\lambda _{s_{n-1}}B\right] \nonumber \\&\quad +{\mathrm {e}}^{D{{\hat{T}}_{n-1}}}\Big [{\hat{\mathrm {x}}_{n-1}} +F(C{\hat{\mathrm {x}}_{n-1}})B\nonumber \\&\quad -{\mathrm {e}}^{A\left( {\tau }+\sum _{i=0}^{n-2}{{\hat{T}}_i}-\varTheta _{k_{n-1}}\right) }\left[ {\mathrm {x}}_{k_{n -1}}+\lambda _{k_{n -1}}B\right] \Big ]\nonumber \\&\quad -\sum _{i=k_{n -1}+1}^{s_{n - 1}}\lambda _{i}\,{\mathrm {e}}^{D\left( {\tau }+\sum _{i=0}^{n-1}{{\hat{T}}_i}-\varTheta _i\right) }B, \nonumber \\&\quad \quad \text{ for }\,\,\, n=1,\ldots , p -1,\nonumber \\ { {\hat{T}}_0}&= \,\, \, \varPhi \left( R{\hat{\mathrm {x}}_0}+k_d\,C\,{\mathrm {e}}^{A{\tau }}\left[ {\mathrm {x}}_{k_0}+\lambda _{k_0}B\right] \right) ,\nonumber \\ {{\hat{T}}_n}&= \,\, \, \varPhi \left( R{\hat{\mathrm {x}}_n}+k_d\,C\,{\mathrm {e}}^{A\left( {\tau }+\sum _{i=0}^{n-1}{\hat{T}_i}+t_{k_0}-t_{k_n}\right) }\right. \nonumber \\&\quad \left. \times \left[ {\mathrm {x}}_{k_n}+\lambda _{k_n}B\right] \right) ,\quad \text{ for } \,\, n=1,\ldots , p -2,\nonumber \\ T_{\varSigma }&= \sum _{I=0}^{P-2}{{\hat{T}}_I}+\varPhi \bigg (R{\hat{\mathrm {X}}_{P -1}}\nonumber \\&\quad +K_D\,C\,{\mathrm {e}}^{A\left( {\tau }+\sum _{I=0}^{P -2}{{\hat{T}}_I}+T_{K_0}-T_{K_{P -1}}\right) }\nonumber \\&\quad \times \left[ {\mathrm {x}}_{k_{p -1}}+\lambda _{k_{p -1}}B\right] \bigg ), \end{aligned}$$
(12)

where \(\varTheta _j=t_j-t_{k_0}=\sum _{i=k_0}^{j-1}T_i\) for \(j\geqslant k_0\) and \({i\bmod {m}}\) is the remainder of the division of i by m.

Proof

See “Appendix A”. \(\square \)

Note that system of equations (12) can possess multiple solutions and every distinct solution determines a different p-cycle. The plant parameters of Eq. (3) impose although limitations on the least period of the corresponding observer solution.

Remark 1

For a given m-cycle \({{\mathscr {C}}}^m({\mathrm {x}}(t), t_n)\) of the plant, bounds on the least period p of the corresponding observer cycle \({{\mathscr {C}}}^{p}(\hat{\mathrm {x}}(t), {\hat{t}}_n)\) can be derived from Eq. (2) as below

$$\begin{aligned} \left\lceil \dfrac{m\,\varPhi _1}{\varPhi _1+\varPhi _2}\right\rceil\leqslant & {} \left\lceil \dfrac{T_{\varSigma }}{\varPhi _1+\varPhi _2}\right\rceil \leqslant p\leqslant \left\lfloor \dfrac{T_{\varSigma }}{\varPhi _1}\right\rfloor \\\leqslant & {} \left\lfloor \dfrac{m\,(\varPhi _1+\varPhi _2)}{\varPhi _1}\right\rfloor , \end{aligned}$$

where the number \(\lceil r\rceil \) denotes the least integer greater than r and \(\lfloor r\rfloor \) is the largest integer not greater than r (i.e., the integer part, or floor, of r).

Next, consider a special case when \(p = m\), \(k_0=0\), \(t_0=0\) (hence, \(\tau ={\hat{t}}_0\)) and \(s_{n}=k_n+1\) for all \(n = 0,\ldots , m-1\). Since the solution \((\hat{\mathrm {x}}(t), {\hat{t}}_n)\) is m-periodic, it can be defined as \(\hat{\mathrm {x}}(t)=\hat{\mathrm {x}}(t+T_{\varSigma })\) for \(t\in [0,{\hat{t}}_0)\). Consider the continuous state estimation error r(t) in the interval \([0, {\hat{t}}_0+T_{\varSigma }]\) and denote \(r_n={\mathrm {x}}_n-\hat{\mathrm {x}}(t_n)\) and \({\hat{r}}_n={\mathrm {x}}({\hat{t}}_n)-\hat{\mathrm {x}}_n\).

Then, one concludes that, for each \(n=1,\ldots ,m-1\), it applies that

$$\begin{aligned} r_n={\mathrm {e}}^{D(t_n-{\hat{t}}_{n-1})}\left[ {\hat{r}}_{n-1}-\hat{\lambda }_{n-1}B\right] , \end{aligned}$$

and \(r_0={\mathrm {e}}^{D(T_{\varSigma }-{\hat{t}}_{m-1})}\left[ {\hat{r}}_{m-1}-\hat{\lambda }_{m-1}B\right] \). Similarly, for each \(n=0,\ldots ,m-1\), one has

$$\begin{aligned} {\hat{r}}_n={\mathrm {e}}^{D({\hat{t}}_n- t_n)}\left[ r_n+ \lambda _{n}B\right] . \end{aligned}$$

Therefore, for each \(n=1,\ldots ,m\), it follows that

$$\begin{aligned} {\hat{r}}_n= & {} {\mathrm {e}}^{D({\hat{t}}_n- {\hat{t}}_{n-1})}\left[ {\hat{r}}_{n-1}-{\hat{\lambda }}_{n-1}B\right] +\lambda _n\,{\mathrm {e}}^{D({\hat{t}}_n- t_n)}B{}\\= & {} {\mathrm {e}}^{D{\hat{T}}_{n-1}}\left[ {\hat{r}}_{n-1}-F\left( C\left( {\mathrm {e}}^{A\left( {\hat{t}}_0+\sum _{i=0}^{n-1}\left( {\hat{T}}_i-T_i\right) \right) }{\mathrm {x}}(t_n^+)\right. \right. \right. \\&\left. \left. \left. -{\hat{r}}_n\right) \right) B\right] +\lambda _n\,{\mathrm {e}}^{D\left( {\hat{t}}_0+\sum _{i=0}^{n-1}\left( {\hat{T}}_i-T_i\right) \right) }B, \end{aligned}$$

where \(r_m=r_0, T_m=T_0, {\hat{r}}_m={\hat{r}}_0, {\hat{T}}_m={\hat{T}}_0\).

Considering only cycles of the same periodicity in the observer as in the plant results in the following simplification.

Corollary 1

For the case \(p = m\), Eq. (12) are equivalent to the following:

$$\begin{aligned} \begin{aligned} {{\hat{r}}_n}&= \,\, \, {\mathrm {e}}^{D{{\hat{T}}_{n-1}}}\left[ {{\hat{r}}_{n-1}}-F\left( C\left( {\mathrm {e}}^{A\left( {{\hat{t}}_0}+\sum _{i=0}^{n-1}\left( {{\hat{T}}_i}-T_i\right) \right) }{\mathrm {x}}(t_n^+)\right. \right. \right. \\&\quad \left. \left. \left. -{{\hat{r}}_n}\right) \right) B\right] +\lambda _n\,{\mathrm {e}}^{D\left( {{\hat{t}}_0}+\sum _{i=0}^{n-1}\left( {{\hat{T}}_i}-T_i\right) \right) }B, \\ {{\hat{T}}_n}&= \,\, \, \varPhi \left( C\,{\mathrm {e}}^{A\left( {{\hat{t}}_0}+\sum _{i=0}^{n-1}\left( {{\hat{T}}_i}-T_i\right) \right) }{\mathrm {x}}(t_n^+)-R\,{{\hat{r}}_n}\right) ,\\ \end{aligned} \end{aligned}$$
(13)

for \(n=1,\ldots , m\).

Proof

Note that for \(n=m\) one has \(\sum _{i=0}^{n-1}\left( {\hat{T}}_i-T_i\right) =0\). Then, \({\hat{T}}_m=\hat{T}_0=\varPhi \left( C\,{\mathrm {e}}^{A {\hat{t}}_0}{\mathrm {x}}(t_0^+)-R\,\hat{r}_0\right) \). Also in Eq. (13) one can substitute \(\hat{T}_{m-1}=T_{\varSigma }-\sum _{i=0}^{m-2}{\hat{T}}_i\). As a result, the sequence \(\hat{\mathrm {x}}_0,\ldots , \hat{\mathrm {x}}_{m-1}\) can be reconstructed as follows:

$$\begin{aligned} \hat{\mathrm {x}}_n={\mathrm {e}}^{A\left( {\hat{t}}_0+\sum _{i=0}^{n-1}\left( {\hat{T}}_i-T_i\right) \right) }{\mathrm {x}}(t_n^+)-{\hat{r}}_n. \end{aligned}$$

\(\square \)

The situation covered by Corollary 1 is, for instance, encountered further in the paper and illustrated in Fig. 3a.

Given the results of [10], the scenarios of 1-cycle and 2-cycle featuring one or two GnRH pulses fired by the plant feedback in the least period of the solution are particularly relevant to the case of Te regulation and considered below.

  • \({\mathbf {1}}\)-cycle, \(p = m = 1\): The Eq. (13) take the following form:

    $$\begin{aligned} \begin{aligned} {{\hat{r}}_0}&= - F\left( C\left[ {\mathrm {e}}^{A{{\hat{t}}_0}}{\mathrm {x}}(t_0^+) - {{\hat{r}}_0}\right] \right) v_0 + \lambda _0M{\mathrm {e}}^{D{{\hat{t}}_0}}B, \\ T_0&= \varPhi \left( C {\mathrm {e}}^{A{{\hat{t}}_0}}{\mathrm {x}}(t_0^+)-R{{\hat{r}}_0}\right) , \end{aligned} \end{aligned}$$
    (14)

    where \(M = {(I - {\mathrm {e}}^{DT_0})}^{-1}\), \(v_0=M{\mathrm {e}}^{DT_0}B\) and \(x(t_0^+)={\mathrm {x}}_0+\lambda _0B\). The matrix M is always non-singular for a Hurwitz D but, as soon as \(\det D=0\) and the continuous observer dynamics are marginally stable, the inverse does not exist. Notably, non-singularity of M can always be secured by a proper choice of K since (A, C) is observable.

  • \({\mathbf {2}}\)-cycle, \(p=m=2\): Equation (13) are reduced to:

    $$\begin{aligned} \begin{aligned} {{\hat{r}}_0}&= {\mathrm {e}}^{D(T_{\varSigma }-{{\hat{T}}_0})}\left[ {{\hat{r}}_1} - F\left( C\left[ {\mathrm {e}}^{A{{\hat{t}}_0}}{\mathrm {x}}(t_0^+) - {{\hat{r}}_0}\right] \right) B\right] \\&\quad + \lambda _0{\mathrm {e}}^{D{{\hat{t}}_0}}B, \\ {{\hat{T}}_0}&= \varPhi \left( C {\mathrm {e}}^{A{{\hat{t}}_0}}{\mathrm {x}}(t_2^+)-R\,{{\hat{r}}_0}\right) ,\\ {{\hat{r}}_1}&= {\mathrm {e}}^{D{{\hat{T}}_0}}\left[ {{\hat{r}}_0} - F\left( C\left[ {\mathrm {e}}^{A({{\hat{t}}_0}+{{\hat{T}}_0} - T_0)}{\mathrm {x}}(t_1^+) \right. \right. \right. \\&\quad \left. \left. \left. - {{\hat{r}}_1}\right] \right) B\right] \\&\quad + \lambda _1{\mathrm {e}}^{D({{\hat{t}}_0}+{{\hat{T}}_0} - T_0)}B, \\ {{\hat{T}}_0}&= T_{\varSigma }-\varPhi \left( C {\mathrm {e}}^{A({{\hat{t}}_0}+{{\hat{T}}_0}-T_0)}{\mathrm {x}}(t_1^+)-R\,{{\hat{r}}_1}\right) , \end{aligned} \end{aligned}$$
    (15)

    where \(T_{\varSigma }=T_0+T_1\).

6 Stability of periodic observer solutions

Stability conditions for an m-cycle \({{\mathscr {C}}}^{m}(\hat{\mathrm {x}}(t), \hat{t}_n)\) of observer Eqs. (4)–(6) satisfying

$$\begin{aligned} (\hat{\mathrm {x}}_{0},\, {\hat{t}}_{0}+T_{\varSigma })=P^{(m)}(\hat{\mathrm {x}}_0,\,{\hat{t}}_0) \end{aligned}$$

can be obtained through analyzing the Jacobian of the pointwise map iterated m times \(\mathcal {F}_m=Q'^{(m)}\) evaluated at the fixed point of map Eq. (11). Then, the m-cycle is locally asymptotically stable if the Jacobian \(\mathcal {F}_m=Q'^{(m)}\) is Schur stable [15, 17]. The calculation of the Jacobian can be simplified by applying the chain rule, as

$$\begin{aligned} \mathcal {F}_{n+1}=\hat{J}_n\mathcal {F}_n, \quad n=0,1,\ldots ,m-1,\quad {\mathcal {F}_{0}=I,} \end{aligned}$$

where \(\hat{J}_n=Q'(\hat{\mathbf {x}}_n,\hat{t}_n)\).

Theorem 2

The Jacobian of Q at the point \((\hat{\mathrm {x}}_n,\,{\hat{t}}_n)\) is calculated as

$$\begin{aligned} Q'(\hat{\mathrm {x}}_n,\,{\hat{t}}_n)={\hat{J}}_n=\begin{bmatrix} \left( {\hat{J}}_n\right) _{11} &{}\quad \left( {\hat{J}}_n\right) _{12}\\ \left( {\hat{J}}_n\right) _{21} &{}\quad \left( {\hat{J}}_n\right) _{22} \end{bmatrix}, \end{aligned}$$

where

$$\begin{aligned} \left( {\hat{J}}_n\right) _{11}&= {\hat{\varPhi }}'_n {\mathrm {e}}^{ A({\hat{t}}_n+{\hat{\varPhi }}_n-t_s)} A {\mathrm {x}}^+_{s} R + {\mathrm {e}}^{ D{\hat{\varPhi }}_n} \left( I+ {\hat{F}}'_{n} B C\right) \\&\quad -{\hat{\varPhi }}'_n {\mathrm {e}}^{ D{\hat{\varPhi }}_n} D \left( {\mathrm {e}}^{ A({\hat{t}}_n-t_k)} {\mathrm {x}}^+_{k}-\hat{\mathrm {x}}_n-{\hat{F}}_nB\right) R\\&\quad -{\hat{\varPhi }}'_n D \sum _{i=k+1}^s \lambda _i {\mathrm {e}}^{D({\hat{t}}_n+{\hat{\varPhi }}_n-t_i)}BR,\\ \left( {\hat{J}}_n\right) _{12}&=\left( 1+{\hat{\varPhi }}'_nk_d C A \,{\mathrm {e}}^{ A({\hat{t}}_n-t_k)}{\mathrm {x}}^+_s\right) {\mathrm {e}}^{ A({\hat{t}}_n+{\hat{\varPhi }}_n-t_s)} A {\mathrm {x}}^+_{s}\\&\quad -{\hat{\varPhi }}'_n {\mathrm {e}}^{ D{\hat{\varPhi }}_n} D \left( {\mathrm {e}}^{ A({\hat{t}}_n-t_k)} {\mathrm {x}}^+_{k}-\hat{\mathrm {x}}_n-{\hat{F}}_nB\right) \\&\quad \times k_dC A{\mathrm {e}}^{ A({\hat{t}}_n-t_k)}{\mathrm {x}}^+_k -{\mathrm {e}}^{ D{\hat{\varPhi }}_n} {\mathrm {e}}^{ A({\hat{t}}_n-t_k)} A {\mathrm {x}}^+_{k}\\&\quad -\left( 1+{\hat{\varPhi }}'_nk_d C A \,{\mathrm {e}}^{ A({\hat{t}}_n-t_k)}{\mathrm {x}}^+_k\right) D\\&\quad \times \sum _{i=k+1}^s \lambda _i {\mathrm {e}}^{D({\hat{t}}_n+{\hat{\varPhi }}_n-t_i)}B,\\ \left( {\hat{J}}_n\right) _{21}&={\hat{\varPhi }}'_{n} R, \qquad \left( {\hat{J}}_n\right) _{22}=1+{\hat{\varPhi }}'_nk_d C A \,{\mathrm {e}}^{ A({\hat{t}}_n-t_k)}{\mathrm {x}}^+_k. \end{aligned}$$

Here, \({\hat{\varPhi }}_n\), \({\hat{F}}_n\), \({\hat{\varPhi }}'_n\) and \({\hat{F}}'_n\) denote \(\varPhi (\alpha (\hat{\mathrm {x}}_n, {\hat{t}}_n))\), \(F({\hat{x}}_n)\) and their derivatives, respectively, and \({\mathrm {x}}_i^+={\mathrm {x}}(t_i^+)\). The indices k and s obey the inequality \(t_k\leqslant {\hat{t}}_n<t_{k+1}, \, t_s\leqslant {\hat{t}}_n+{\hat{\varPhi }}_n<t_{s+1}\).

Proof

By direct calculations along the lines of the proof of Theorem 2 in [15]. \(\square \)

If \((\hat{\mathrm {x}}(t), {\hat{t}}_n)\) is a synchronous mode, i.e., \((\hat{\mathrm {x}}(t), {\hat{t}}_n)=({\mathrm {x}}(t), t_n)\), then the Jacobian of Q at the point \(({\mathrm {x}}_n,\,t_n)\) is calculated as

$$\begin{aligned} Q'({\mathrm {x}}_n,\,t_n)=J_n=\begin{bmatrix} \left( J_n\right) _{11} &{}\quad \left( J_n\right) _{12}\\ \left( J_n\right) _{21} &{}\quad \left( J_n\right) _{22} \end{bmatrix}, \end{aligned}$$
(16)

where

$$\begin{aligned} (J_n)_{11}&= \varPhi '(C{\mathrm {x}}_n) A x_{n+1} R\\&\quad + {\mathrm {e}}^{ D\varPhi (C{\mathrm {x}}_n)}\left( I+F'(C{\mathrm {x}}_n) B C\right) , \\ (J_n)_{12}&= A {\mathrm {x}}_{n+1}(1+\varPhi '(C{\mathrm {x}}_n) k_d C A {\mathrm {x}}_n)\\&\quad -{\mathrm {e}}^{D\varPhi (C{\mathrm {x}}_n)}A({\mathrm {x}}_{n}+\lambda _{n}B),\\ (J_n)_{21}&= \varPhi '(C{\mathrm {x}}_n) R, \quad \\ (J_n)_{22}&=1+\varPhi '(C{\mathrm {x}}_n)k_d C A {\mathrm {x}}_n. \end{aligned}$$

Local asymptotic stability implies that if the point \((\hat{\mathrm {x}}_n, {\hat{t}}_n)\) is in a sufficiently small neighborhood of the point \(({\mathrm {x}}_n, t_n)\) then, after a firings of the observer discrete feedback, the point \((\hat{\mathrm {x}}_{n+a}, {\hat{t}}_{n+a})\) will be in a smaller neighborhood of the point \(({\mathrm {x}}_{n+a}, t_{n+a})\), for some \(a\geqslant 1\). Yet, in [22], it was shown that the basin of attraction of a synchronous mode in the vicinity of the point \(({\mathrm {x}}_n, t_n)\) is considerably asymmetrical relative to the jump instant \(t_n\). Even small overestimates of the plant feedback firing time (i.e., \({\hat{t}}_n>t_n\)) interrupt and postpone the convergence. The term ”overjump” will be used to denote a situation when the estimated firing time \({\hat{t}}_{n+1}\) lies in a right neighborhood of \(t_{n+1}\), while \({\hat{t}}_n\) belongs to a left neighborhood of \(t_n\). Since the function \(\varPhi (\cdot )\) is increasing, the overjumps are generally more likely to occur for high values of \(k_d\). This may lead to the appearance of undesired high-periodic or chaotic modes of the observer that can be revealed and investigated by bifurcation analysis; see Sect. 7.

After finding a feasible set of the gains K and \(k_d\) for which the synchronous mode is attractive in the whole \(\mathcal D\), one has to determine the suitable values of K and \(k_d\) ensuring the highest achievable convergence rate. Since the greatest challenge for the observation problem at hand is the unknown initial firing time \(t_0\) (and therefore all the following instants \(t_n\)) of the system, the observer convergence rate can be characterized by the first time instant when \({\hat{t}}_n\) comes into \(\varepsilon _f\)-neighborhood of \(t_n\) and never leaves it, i.e.,

$$\begin{aligned}&{{\mathcal {P}}}(\varepsilon _f)={\hat{t}}_{n^*},\quad \nonumber \\&\quad n^*=\min \{k: \left| {\hat{t}}_N-t_N \right| <\varepsilon _f\,\,\forall N>k\}. \end{aligned}$$
(17)

7 Bifurcation analysis

The normal stationary operation regime for the observer is that of synchronous mode. All other modes have to be excluded by design, while the convergence to a synchronous mode has to be guaranteed from any point of the plant initial condition set \(\mathcal D\) at, preferably, the fastest achievable rate.

Fig. 2
figure 2

Three-dimensional phase portrait for the considered stable 2-cycle in the plant with \(t_0=0\), \(T_0=119.47, T_1=111.05, T_{\varSigma }=230.52\)

Full size image
Fig. 3
figure 3

a The stable 2-cycle (\(k_d=-72\)) of the observer, distinct from the synchronous one. The firings in the plant do not match the firings in the observer. The red vertical lines of height \(-{\hat{\lambda }}_n\) positioned at \({\hat{t}}_n\) correspond to the observer firing sequence. The pulse modulation of the plant is shown by blue lines of height \(\lambda _n\) positioned at \(t_n\) (with \(t_0=0\)). b Transients in the continuous components of the state observation error. Stable asynchronous 2-cycle (\(k_d=-72\)). Note that since the plant and the observer each have two impulses in the least period, the observation error has four impulses in its least period

Full size image

In the present section, the nonlinear dynamics of the observer at hand are investigated specifically with respect to variation in the observer gain \(k_d\). As the analysis below demonstrates, there is a well-defined interval of the gain values that correspond to a synchronous mode of the observer with sufficient basin of attraction and convergence rate. The existence of this interval is guaranteed by the fact that the hybrid state estimation error asymptotically vanishes for a sufficiently large value of the continuous gain K with \(k_d=0\) if the following condition holds (see Theorem 4 in [15]):

$$\begin{aligned} -1<\prod _{i=0}^{m-1}(\varPhi '(C{\mathrm {x}}_i)CA{\mathrm {x}}_{i+2}+1)<1. \end{aligned}$$
(18)

The necessary condition above reminds once again that the design of observer Eqs. (4)–(6) is performed with respect of to a certain solution of the plant rather than with respect to the model. It also hints to the conclusion that plants with a steep frequency modulation function are more difficult to deal with. Notice also that condition Eq. (18) applies only under \(k_d=0\) thus specifying what plant solutions can be reconstructed by the observer without a feedback to the discrete state estimate. When Eq. (18) is not satisfied, the search for a suitable \(k_d\) should start with a nonzero gain value.

In order to discern the nonlinear dynamical phenomena in the observer by means of bifurcation analysis, assume the following parameter values: \(b_1=0.018\), \(b_2=0.15\), \(b_3=0.1\), \(g_1=2.8\), \(g_2=1.5\), \(\varPhi _1=40.0\), \(\varPhi _2=80.0\), \(F_1=0.05\), \(F_2=5.0\), \(h=2.7\), and \(p=2\). For the selected parameter values, plant Eq. (3) has a stable 2-cycle depicted in Fig. 2 and inequality Eq. (18) holds.

Figure 3a and b demonstrates an example of the stable asynchronous mode arising for \(k_d=-72\). The figures depict firing mismatch in the discrete state variable (Fig. 3a) as well as nonzero error in the estimates of the continuous plant states (Fig. 3b).

The hybrid observer dynamics are described by Eqs. (4)–(6). Consider the gain matrix K of the following form:

$$\begin{aligned} K= {k_c}\begin{bmatrix} 0 &{}\quad 0\\ 1&{}\quad 0\\ 0 &{}\quad 1 \end{bmatrix}, \end{aligned}$$
(19)

where \({k_c}>0\) and renders the matrix D Hurwitz stable. The motivation for restricting the structure of K and the performance consequences of it are discussed in detail in [17]. Here, it suffices to note that, under this restriction, the observer demonstrates good performance [15, 17]. The guidelines for selecting \({k_c}\) are given in Sect. 8. Here, \({k_c}=1\) is assumed. The choice of the discrete gain \(k_d\) directly impacts the discrete dynamics of the observer and is, therefore, more significant.

7.1 Discrete gain

In order to discern the mechanisms of the transition from asynchronous to synchronous mode, select \(k_d\) as the bifurcation parameter.

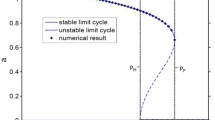
Figure 4 displays the results of one-dimensional bifurcation analysis for \(-150.0<k_d<100.0\). Figure 4a shows the bifurcation diagram obtained through direct simulation and by means of continuation techniques using transcendental Eq.  (15). These equations allow to determine not only the stable cycles but as well the unstable ones. The two horizontal lines denoted by number 1 in Fig. 4a represent the observed 2-cycle of the plant. Figure 4b, c illustrates the variation of multipliers of the asynchronous and synchronous 2-cycles.

For the values of the gain factor \(k_d < k_d^{\mathrm {sn}}\), mapping Eq. (11) shows a pair of asynchronous 2-cycles (Fig. 4a), one of which is stable (drawn in solid lines and denoted by number 3), while the other, drawn in dashed lines and denoted by number 2, is a saddle one.

As the gain \(k_d\) increases, the stable 2-cycle (denoted by number 3) merges with the saddle 2-cycle (2) and disappears in a saddle-node bifurcation at the point \(k_d^{\mathrm {sn}}\) (Fig. 4a). The variation of the multipliers \(\rho _{1,2}\) and \(\rho _1^\mathrm {u}\) for the stable and saddle asynchronous 2-cycles, respectively, is shown in Fig. 4b, c. To better illustrate the later transition, a magnified section of Fig. 4a outlined by the dashed rectangle is presented in Fig. 4c. As illustrated in this figure, with the increasing gain factor \(k_d\), the stable focus 2-cycle transforms into the stable node 2-cycle, as a pair of complex-conjugated multipliers \(\rho _{1,2}=\mu \pm i \omega \) for the stable 2-cycle become real \(\rho _1\) and \(\rho _2\) . At the saddle-node bifurcation point \(k_d^{\mathrm {sn}}\), the largest (in the absolute value) multipliers \(\rho _1\) and \(\rho _1^\mathrm {u}\) of the stable and saddle 2-cycles become equal to + 1.

Fig. 4
figure 4

a Bifurcation diagram illustrating the transition from a stable asynchronous 2-cycle to an attracting synchronous mode as the discrete gain \(k_d\) is increased, with subsequent transition to chaotic or high-periodic attractors. The domain between the points \(k_d^{\mathrm {h}}\) and \(k_d=100.0\) is a region of bistability, where the stable synchronous 2-cycle coexists with chaotic or high-periodic attractors. Here, \(k_d^{\mathrm {sn}}\) and \(k_d^{\mathrm {sn}*}\) are the saddle-node bifurcation points. The point \(k_d^{*}\) defines the value of the gain \(k_d\) in which the saddle synchronous 2-cycle merges with the stable asynchronous 2-cycle. This transition leads to the appearance of a stable synchronous 2-cycle. Note that this bifurcation can be considered as a modification of the transcritical bifurcation. Here, the transition does not involve the appearance of an unstable asynchronous 2-cycle. The green dashed lines mark the saddle asynchronous 2-cycles. b, c Multiplier diagrams for the stable asynchronous and synchronous 2-cycles. The red lines denote the imaginary parts of complex-conjugated multipliers. d The two largest Lyapunov exponents \(\varLambda _{1,2}\) as functions of the gain factor \(k_d\) for the interval \(-150.0< k_d < 100.0\). e Magnified part of the Lyapunov exponents outlined by the rectangle in (d). f Magnified part of the bifurcation diagram outlined by the rectangle in (a). Line 4 denotes a stable synchronous 2-cycle and 2 a saddle 2-cycle one. (Color figure online)

Full size image
Fig. 5
figure 5

a Coexistence of a stable synchronous 2-cycle (denoted by \(\mathcal {C}_2\)) and a stable 31-cycle (denoted by \(\mathcal {C}_{31}\)). b Two-dimensional projection of the basins of attraction for coexisting 2- and 31-cycles. Here, \(\mathcal {B}_2\) and \(\mathcal {B}_{31}\) denote the basins of attraction for 2- and 31-cycles, respectively. \(k_d=84.5\)

Full size image

When the gain factor \(k_d\) passes the value \(k_d=k_d^{\mathrm {sn}}\), an abrupt transition to chaos takes place, as evidenced by Fig. 4a, c, and the observer does not exhibit stable periodic dynamics in the interval between the points \(k_d^{\mathrm {sn}}\) and \(k_d^{\mathrm {sn}*}\). In the region \(k_d^{\mathrm {sn}}<k_d< k_d^{\mathrm {sn}*}\), the largest Lyapunov exponent \(\varLambda _1\) becomes positive, signaling the development of chaotic dynamics (Fig. 4d). The second Lyapunov exponent \(\varLambda _2\), on the other hand, is negative everywhere in the considered interval \(-150.0<k_d<100.0\).

With the further increase in \(k_d\), the system enters the 2-cycle window. The saddle-node bifurcation at the left edge \(k_d^{\mathrm {sn}*}\) of the region \(k_d^{\mathrm {sn}}<k_d<k_d^{\mathrm {sn*}}\) produces the saddle and stable asynchronous 2-cycles, drawn in dashed line and denoted by number 3, and drawn in solid line and denoted by number 2, respectively. When crossing the point \(k_d^{\mathrm {*}}\) with increasing \(k_d\), the stable asynchronous 2-cycle merges with the saddle synchronous 2-cycle in a “transcritical”-like bifurcation: at the point \(k_d^{\mathrm {*}}\), one of the multipliers \(\rho _1^*\) and \(\rho _1^{**}\) of the saddle synchronous and stable asynchronous 2-cycles, respectively, becomes equal to + 1 (Fig. 4b, c). After this bifurcation, the saddle synchronous 2-cycle transforms into a stable one (denoted by number 4). The variation of the multipliers for the synchronous \((\rho _{1,2}^*)\) and asynchronous \((\rho _{1,2}^{**})\) 2-cycles is shown in Fig. 4b. The considered bifurcation is similar to the classical transcritical bifurcation. However, dissimilar to the transcritical bifurcation, this transition does not involve the appearance of an unstable asynchronous 2-cycle.

As illustrated in Fig. 4b, when crossing the point \(k_d^{\mathrm {c}*}\) with increasing gain parameter \(k_d\), the stable node synchronous 2-cycle turns into stable focus (the real multipliers \(\rho _{1,2}^*\) become complex \(\rho _{1,2}^* =\mu ^*\pm i \omega ^*)\). The domain that falls to the right of the point \(k_d^{\mathrm {h}}\) is a region of bistability, where the stable synchronous 2-cycle coexists with chaotic or high-periodic attractors. In the domain of chaotic dynamics, there exists a usual dense set of periodic windows (Fig. 4a). Figure 4e depicts the magnified part of the diagram presented in Fig. 4d of the largest Lyapunov exponent \(\varLambda _1\) in the region \(k_d>k_d^{\mathrm {h}}\). As illustrated in Fig. 4e, the largest Lyapunov exponent \(\varLambda _1\) is positive in most of the considered interval, and this Lyapunov exponent becomes negative in the windows of periodicity.

Fig. 6
figure 6

Variation of the absolute value of the largest multipliers for the synchronous 2-cycle. As illustrated in Fig. 4b, when passing through the value \(k_d^{\mathrm {c}*}\), the largest (in the absolute value) real multiplier of the 2-cycle becomes equal to another one, which gives rise to a pair of complex-conjugated multipliers

Full size image

It can be concluded that the basins of attraction of the coexisting motions are delineated by the stable manifold of the saddle asynchronous 2-cycle denoted by number 2 in Fig. 4a, which appears at the point \(k_d^{\mathrm {sn}}\) in a saddle-node bifurcation. Figure 4f displays the magnified part of the bifurcation diagram that is outlined by the rectangle in Fig. 4a. Inspection of Fig. 4a, f reveals that, as the parameter \(k_d\) increases, the saddle asynchronous 2-cycle approaches the stable synchronous 2-cycle, when of the gain factor \(k_d\) changes the sign.

In the region of bistability \(k_d>k_d^\mathrm {h}\), the stable synchronous and saddle asynchronous 2-cycles are very close to each other. Here, the system may choose different motions depending on initial conditions. In particular, if a certain ratio between the radii of basins of attractions and the magnitude of random disturbances takes place, then either chaotic or high-periodic dynamics occurs. It also becomes possible for the system to exhibit a hard transition from a stable synchronous 2-cycle to a chaotic or high-periodic attractor and vice versa.

Figure 5a depicts a three-dimensional phase space projection of the coexisting stable synchronous 2-cycle (denoted by \(\mathcal {C}_2\)) and stable 31-cycle (denoted by \(\mathcal {C}_{31}\)) for \(k_d=84.5\). Figure 5b illustrates a two-dimensional projection of the basins of attraction for coexisting 2- and 31-cycles. Here, \(\mathcal {B}_2\) and \(\mathcal {B}_{31}\) denote the basins of attraction for 2- and 31-cycles, respectively.

7.2 Basin of attraction for the synchronous mode

As mentioned earlier, it is important to guarantee the observer convergence to the synchronous mode from all admissible initial estimates, i.e., in the whole set \(\mathcal D\). For the numerical example at hand, according to Eq. (7), the bounds on the hybrid states of the plant are \(V_1=0.065\), \(V_2=0.1217\), \(V_3=1.8275\), \(H_1=9.84\), \(H_2=183.7\), \(H_3=2755\), i.e.,

$$\begin{aligned} \mathcal{D}=\left\{ 0.065\leqslant x_1(0)\leqslant 9.84,\quad 0.1217\leqslant x_2(0)\leqslant 183.7,\right. \\ \left. 1.8275\leqslant x_3(0)\leqslant 2755,\quad 0\leqslant t_0\leqslant 230.52 \right\} . \end{aligned}$$

An analysis of the basin of attraction of the synchronous mode in the four-dimensional initial conditions space reveals that it includes all the points within \(\mathcal D\), for the selected value of K and \(-49.5=k^*_d \leqslant k_d \leqslant k^h_d=38.5\).

As illustrated in Figs. 4a, b and 5, the synchronous mode is locally asymptotically stable for \(k_d\geqslant k^*_d\). Figure 6 shows the absolute value of the largest multipliers \(\rho \) for the synchronous 2-cycle. This value will be referred to as the spectral radius \(\rho (\mathcal {F}_{2})\) of the Jacobian \(\mathcal {F}_{2}\).

In Fig. 6, one can see that the synchronous mode is still locally stable for \(k_d>k^h_d\) since \(\rho (\mathcal {F}_{2})<1\). However, these values of \(k_d\) are not suitable for the observer since the basin of attraction for the synchronous mode is too small, and the synchronous 2-cycle either coexists with stable high-periodic asynchronous modes or with a chaotic attractor (Figs. 4 and 5).

7.3 Convergence rate to the synchronous mode

When it is guaranteed that the observer estimates converge to the synchronous mode from all the points of \(\mathcal D\) for \(k^*_d \leqslant k_d \leqslant k^h_d\), it is reasonable to select the gain value that ensures fastest observer convergence. The greatest challenge for the hybrid observation problem at hand is the unknown initial firing time \(t_0\). Then, a suitable gain \(k_d\) from the interval \(\left( k^*_d,k^h_d\right) \) should be chosen to minimize the settling time \(\mathcal {P}(\varepsilon _f)\) defined in Eq. (17), for all initial times \({\hat{t}}_0\) from \(\mathcal{T}=\left\{ \theta \in {\mathbb {R}}:\,\,\,\, 0\leqslant \theta \leqslant T_{\varSigma }\right\} \). From Fig. 7, it can be concluded that for the fastest convergence of the observer to the synchronous mode from all possible initial instants \({\hat{t}}_0\) one should select a value of \(k_d\) close to the upper bound of the feasible interval, i.e., \(k^h_d\).

Fig. 7
figure 7

The contour plot illustrating the dependence of settling time \(\mathcal {P}(\varepsilon _f)\) on \({\hat{t}}_0\) and \(k_d\) for \(\varepsilon _f=1\). The vertical colorbar represents the mapping of values of \(\mathcal {P}(\varepsilon _f)\) into the corresponding colors. (Color figure online)

Full size image

Since initial values of the unmeasurable components of the system state \({\mathrm {x}}\) cannot be related to \({\hat{t}}_0\), one has to select them independently of \({\hat{t}}_0\), e.g., \(\hat{\mathrm {x}}_0 = \left[ {\hat{x}}_{1,0}, {\hat{x}}_{2,0}, \hat{x}_{3,0}\right] ^\top \). Notice that the initial condition for the measurable component estimate \({\hat{x}}_{3,0}={\hat{z}}({\hat{t}}_0)\) has the greatest impact on the convergence, since it is the modulation parameter and defines the value of \({\hat{T}}_0\). Figure 8 illustrates the settling time \(\mathcal {P}(\varepsilon _f)\) depending on \({\hat{t}}_0\) and \({\hat{x}}_{3,0}\) for \(k_d=38\), from which one can conclude that choosing \({\hat{x}}_{3,0}\) as \(z({\hat{t}}_0)\) (measured value of the system at time \({\hat{t}}_0\)) is a feasible solution. The values of \({\hat{x}}_{1,0}\) and \({\hat{x}}_{2,0}\) can be chosen arbitrarily small but positive.

Fig. 8
figure 8

The contour plot illustrating the dependence of the settling time \(\mathcal {P}(\varepsilon _f\)) on \({\hat{t}}_0\) and \({\hat{x}}_{3,0}\) for \(\varepsilon _f=1\). Finite values of settling time imply asymptotic convergence to synchronous mode. The red line depicts the measured values \(z({\hat{t}}_0)\) of the system with \(t_0=0\) and provided for reference. Observe the drastic increase in the convergence time immediately after the firing time and a drop in it before the firing. The vertical colorbar represents the mapping of values of \(\mathcal {P}(\varepsilon _f)\) into the corresponding colors

Full size image

8 Observer design algorithm

In this section, an algorithm for finding the values of the observer gains K and \(k_d\) rendering the synchronous mode attractive for all the points of \(\mathcal D\) with an appropriate convergence rate is presented.

Let the structure of K be defined by Eq. (19). First of all, notice that local stability of the synchronous mode is a necessary condition for attractivity of \(\mathcal D\). Since Eq. (18) holds, for \(k_d=0\), one can find a value \(k_\mathrm {max}\) such that, for any \({k_c}>k_\mathrm {max}\), the spectral radius \(\rho \) of the Jacobian \(\mathcal {F}_{2}\) calculated at the points of the synchronous mode differs no more than \(\varepsilon >0\) from \(\rho (\mathcal {F}_{2})\) for \(k_c=k_\mathrm {max}\).

Figure 9 shows the dependence of \(\rho (\mathcal {F}_{2})\) on the gains \({k_c}\) and \(k_d\). For a fixed \({k_c}\) (\(0<{k_c}<k_\mathrm {max}\)), denote by \(\mathcal{K}({k_c})\) the interval of \(k_d\) for which the synchronous mode is locally asymptotically stable (\(\rho (\mathcal {F}_{2})<1)\). For example, in Fig. 9, the intervals \(\mathcal{K}(0.5)=(-14.9,90.1)\) and \(\mathcal{K}(1)=(-49.5,288.7)\) are highlighted by the red horizontal line segments. One can see that \(\mathcal{K}({k_c})\) grows with increasing \({k_c}\). Moreover, since inequality Eq. (18) holds, the spectral radius \(\rho (\mathcal {F}_{2})\rightarrow \rho _\mathrm {const}<1\) as \({k_c}\rightarrow \infty \), for any fixed \(k_d\). However, the observer convergence rate is low for large values of \({k_c}\), whereas one can see from Fig. 9 that, for small \({k_c}\), there are values of \(k_d\) for which \(\rho (\mathcal {F}_{2})<<\rho _\mathrm {const}\).

Fig. 9
figure 9

The contour plot illustrating the dependence of the spectral radius of the Jacobian \(\rho (\mathcal {F}_{2})\) on \({k_c}\) and \(k_d\). A higher value of \({k_c}\) allows for a wider range of suitable \(k_d\), as highlighted by the red dashed lines. The vertical colorbar represents the mapping of values of \(\mathcal {P}(\varepsilon _f)\) into the corresponding colors. (Color figure online)

Full size image

If \({\hat{t}}_0\) is far from \(t_0\), then the observer may not approach the synchronous mode at all, e.g., for small \({k_c}\), the interval of suitable \(k_d\) becomes very small and settling time increases (Fig. 10).

Fig. 10
figure 10

The contour plot illustrating the dependence of settling time \(\mathcal {P}(\varepsilon _f)\) on \({k_c}\) an \(k_d\) for \(\varepsilon _f=1\) and \({\hat{t}}_0=120\)

Full size image

Denote by \(\mathcal{K}_2({k_c})\subseteq \mathcal{K}({k_c})\) the interval \(k_d\) for which the whole subspace of feasible initial conditions \(\mathcal D\) is within the basin of attraction of the synchronous mode. The interval \(\mathcal{K}_2({k_c})\) can be found by bifurcation analysis. For \({k_c}=1\), the interval is evaluated to \(\mathcal{K}_2({k_c})=(-49.5, 38.5)\) (Fig. 4). Notice that it can be sufficient to determine the interval \(\mathcal{K}_3({k_c})\subseteq \mathcal{K}_2({k_c})\) that consists of those \(k_d\) that satisfy \(\mathcal {P}(\varepsilon _f)<\mathcal {P}_*\) for all initial conditions in \(\mathcal D\), where \(P_*\) is some large number. Figure 10 shows the dependence of \(\mathcal {P}(\varepsilon _f)\) on \({k_c}\) an \(k_d\) for \(\varepsilon _f=1\) and \({\hat{t}}_0=120\), where the two red horizontal line segments are the intervals of \(k_d\) such that \(\mathcal {P}(\varepsilon _f)<8000\) for \({k_c}=1\) and \({k_c}=2\), respectively. For \({k_c}=1\), it was found that \(\mathcal{K}_3(1)=(-25.7, 38.3)\).

From Fig. 10, one can conclude that, for large \({k_c}\), the interval of \(k_d\), for which the observer converges to the synchronous mode, increases. However, the interval \(\mathcal{K}_3({k_c})\) is bounded, since overjumps may occur for some values of \({\hat{t}}_0\) and large \(k_d\). Figure 10 shows that, for each large \({k_c}\), one can choose \(k_d\) ensuring fast convergence (i.e., the values in the dark blue area). Yet, with a large \(k_d\), convergence cannot be achieved for all possible initial \(\hat{t}_0\in \mathcal{T}\) due to overjumps. Therefore, it is reasonable to choose some moderate value of \({k_c}\) that yields a sufficiently large interval of suitable \(k_d\) such that the synchronous mode is attractive for all \({\hat{t}}_0\in \mathcal{T}\). Finally, after finding such a value of \({k_c}\), a suitable \(k_d\) that minimizes \(\mathcal {P}({\varepsilon _f})\) over \({\hat{t}}_0\in \mathcal{T}\) can be chosen from \(\mathcal{K}_3({k_c})\).

Fig. 11
figure 11

Transients in the continuous states of the observer due to different initial conditions mismatches with respect to the corresponding plant states (blue dashed lines, \(t_0 = 0\)). Red lines initial conditions \({\hat{t}}_0=80, \hat{\mathrm {x}}_{0}=[0.04\,\,\, 1\,\,\, 7]^\top \). Yellow lines initial conditions \({\hat{t}}_0=30, \hat{\mathrm {x}}_{0}=[0.4\, 1\, 100]^\top \). Green lines initial conditions \(\hat{t}_0=100, \hat{\mathrm {x}}_{0}=[0.001\,\,\, 0.01\,\,\, 0.01]^\top \). (Color figure online)

Full size image

Recapitulating, the following bifurcation analysis-based iterative algorithm for finding the gains K and \(k_d\) for a given periodic mode in the plant is proposed. For non-periodic (chaotic, quasi-periodic) modes in the plant, the design procedure will be the same, but one has to use the Lyapunov exponents instead of the spectral radius of the Jacobian.

Initialization::

Select the step \(\varDelta =k_{\max }/N, N>> 1\). For \(k_d=0\), find the value \(k_{\max }\).

do::

Starting with \({k_c}=k_\mathrm {max}\) and decreasing \({k_c}\) with some step \(\varDelta \) do the following (for each fixed \({k_c}\))

Step 1::

determine the interval of \(k_d\) for which the synchronous mode is locally stable, i.e., the spectral radius of the Jacobian is less than one (or the largest Lyapunov exponent is negative) and denote it \(\mathcal{K}\);

Step 2::

exclude the values of \(k_d\) for which the stable synchronous mode, according to bifurcation analysis, coexists with other stable modes, as a result obtain the set \(\mathcal{K}_1\subseteq \mathcal{K}\);

Step 3::

find a subset \(\mathcal{K}_2\subseteq \mathcal{K}_1\) such that the whole subspace of feasible initial conditions \(\mathcal D\) is within the basin of attraction of the synchronous mode;

Step 4::

find the interval \(\mathcal{K}_3\subseteq \mathcal{K}_2\) containing the values of \(k_d\) for which the settling time \(\mathcal {P}(\varepsilon _f)<\mathcal {P}_*\) for all initial conditions from \(\mathcal D\);

Step 5::

finally, select \(k_d\) from \(\mathcal{K}_3\) that minimizes the criterion \(\mathcal {P}({\varepsilon _f})\).

As a suitable gain \({{{\bar{k}}}_c}\) choose the one, for which the value of \(\mathcal {P}(\varepsilon _f)\) found in Step 5 and averaged over all \({\hat{t}}_0\in \mathcal{T}\) is minimal. The corresponding value of the gain \({\bar{k}}_d\) should be taken as suitable \(k_d\).

9 Design example

The main intended application area for the developed observer is the processing of endocrine data where it is supposed to complement or substitute the deconvolution techniques. Naturally, to be implemented, the observer demands a complete plant model. Such individualized models have been obtained from experimental data in [10]. At that stage, no consistent theory for design of the observer was available and pure simulation of the estimated model was performed to demonstrate the fidelity. System identification is not considered in this work, and therefore, the observer is not run on biological data but only on synthetic such.

For the example considered in Sect. 7, one obtains, with \(\varepsilon =0.02\), that \(k_{\max }=3\). Decreasing \(k_c\) with the step \(\varDelta =0.1\) (i.e., \(N=30\)), the calculations specified by Step 1–Step 5 of the proposed observer design algorithm are performed, for each value of \(k_c\). As a result, one obtains \({k_c}=1, k_d=38.3\) as suitable observer gains.

To illustrate Step 1–Step 5 of the algorithm in Sect. 7, the results of one cycle of it for \(k_c=1\) are provided below:

Step 1::

the interval \(\mathcal{K}=(-49.5,288.7)\); see Figs. 6 and 9;

Step 2::

the interval \(\mathcal{K}_1=(-49.5,k_d^h)=(-49.5,38.5)\); see Fig. 4a;

Step 3::

an analysis of the basin of attraction of the synchronous mode in the four-dimensional initial conditions space reveals that it includes all the points within \(\mathcal D\) for the interval \(\mathcal{K}_2=\mathcal{K}_1\);

Step 4::

for \(P_*=8000\), one can conclude from Fig. 10 that the interval \(\mathcal{K}_3=(-25.7,38.3)\);

Step 5::

the averaged over \({\hat{t}}_0\in \mathcal{T}\) minimum value of \(\mathcal {P}(\varepsilon _f)\) for \(\varepsilon _f=1\) is achieved for \(k_d=38.2\); see Fig. 7.

The value of \(\mathcal {P}(\varepsilon _f)\) for \({k_c}=1\) obtained on Step 5 is minimal for all \(0<{k_c}\leqslant 3\), so \({k_c}=1\) and \(k_d=38.2\) are selected as suitable gain values.

Figure 11 contains time-domain illustrations of the designed observer performance starting from different initial conditions. Note that the convergence rate of the designed observer is not much dependent on the initial conditions. In fact, this is also seen in Fig. 10, where the rate of convergence practically does not change depending on the components of the state \( \hat{\mathrm {x}}_{0}\), since large initial deviations are quickly compensated by an exponential decrease in the first intervals of continuity. Therefore, the initial state of \(\hat{\mathrm {x}}\) does not really matter. The rate of convergence is affected mostly by the discrete component \({\hat{t}}_0\), namely the distance to \(t_0\) (especially, for cycles of low periodicity, e.g., 1-cycles and 2-cycles, here the influence of \(k_d\) is preeminent) and the occurrence of a jump after the first pulse.

10 Conclusions

A systematic design procedure for a hybrid observer reconstructing the state variables of the impulsive Goodwin’s oscillator is proposed. It is based on the numerical bifurcation analysis of a discrete mapping capturing the observer state transition from one firing of the cumulative impulsive sequence of the observer and plant feedback to another one. The design procedure produces the values of the observer continuous and discrete gains that guarantee the asymptotic convergence of the hybrid state estimation error to zero from all feasible initial conditions at a highest possible rate.

The problem of evaluating periodic solutions in the observer is reduced to solving a system of analytically derived transcendental equations with respect to the points of the periodic orbit of the discrete mapping. This allows to not only evaluate the stable cycles but as well the unstable ones.

A detailed investigation of the bifurcation phenomena in transition from asynchronous to synchronous observer mode with respect to the discrete gain is presented. In particular, the transition from a stable asynchronous \(2-\)cycle to a stable synchronous 2-cycle can occur through a “transcritical”-like bifurcation in which the saddle synchronous 2-cycle transforms into a stable one. However, unlike to the transcritical bifurcation, this transition does not involve the appearance of an unstable asynchronous 2-cycle. For higher values of gain, the system displays a region of bistability, where the stable synchronous 2-cycle coexists with chaotic or high-periodic attractors. Since the stable coexisting synchronous and saddle asynchronous 2-cycles are very close to each other, the observer is sensitive to noise this region. An arbitrarily small level of noise may cause a sudden and unpredictable transition between the attractors.

The design procedure is illustrated by a simulation example that confirms efficacy of the observer.