Skip to main content
SpringerLink
Log in

Nonlinear vibration absorption of laminated composite beams in complex environment

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

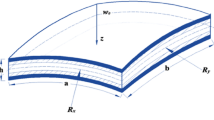
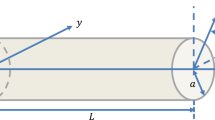
Nonlinear vibration absorption of a laminated composite beam is investigated with the account of complex environment (moisture and temperature). A passive efficient nonlinear energy sink (NES) vibration absorber is used to control the transverse vibration. The generalized Hamilton principle is applied to derive a dynamic model of the laminated composite beam coupled with the NES. Numerical simulations reveal the effects of temperature, moisture, and laying angle on natural frequencies. It is numerically found that the NES can rapidly reduce the vibration amplitude. Then, approximate analytical solutions are sought via the harmonic balance method. The approximate analytical solutions are confirmed by the numerical solutions. Amplitude–frequency response curves show that the NES can reduce the amplitude to very low values for various temperatures, moisture levels, and laying angles. In a certain ranges of the NES parameters, different control effects are determined via an approximate analysis. It is demonstrated that the NES is a promising approach to control vibration of a laminated composite beam in complex environment.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Alidoost, H., Rezaeepazhand, J.: Flutter of multi-cracked laminated composite beams subjected to a non-conservative compressive load. Eng. Fract. Mech. 199, 1–12 (2018)

    Google Scholar 

  2. Nguyen, T.K., Nguyen, N.D., Vo, T.P., Thai, H.T.: Trigonometric-series solution for analysis of laminated composite beams. Compos. Struct. 160, 142–151 (2017)

    Google Scholar 

  3. Song, Z.G., Li, F.M.: Active aeroelastic flutter analysis and vibration control of supersonic composite laminated plate. Compos. Struct. 94(2), 702–713 (2012)

    Google Scholar 

  4. Mohammad-Abadi, M., Daneshmehr, A.R.: Modified couple stress theory applied to dynamic analysis of composite laminated beams by considering different beam theories. Int. J. Eng. Sci. 87, 83–102 (2015)

    Google Scholar 

  5. Sun, B.H., Huang, D.: Vibration suppression of laminated composite beams with a piezo-electric damping layer. Compos. Struct. 53(4), 437–447 (2001)

    Google Scholar 

  6. Djojodihardjo, H., Jafari, M., Wiriadidjaja, S., Ahmad, K.A.: Active vibration suppression of an elastic piezoelectric sensor and actuator fitted cantilevered beam configurations as a generic smart composite structure. Compos. Struct. 132, 848–863 (2015)

    Google Scholar 

  7. Gohari, S., Sharifi, S., Vrcelj, Z.: A novel explicit solution for twisting control of smart laminated cantilever composite plates/beams using inclined piezoelectric actuators. Compos. Struct. 161, 477–504 (2017)

    Google Scholar 

  8. Hwu, C., Chang, W.C., Gai, H.S.: Vibration suppression of composite sandwich beams. J. Sound Vib. 272(1–2), 1–20 (2004)

    Google Scholar 

  9. Yuvaraja, M., Senthilkumar, M.: Comparative study on vibration characteristics of a flexible GFRP composite beam using SMA and PZT actuators. Procedia Eng. 64, 571–581 (2013)

    Google Scholar 

  10. Kang, Y.K., Park, H.C., Kim, J., Choi, S.B.: Interaction of active and passive vibration control of laminated composite beams with piezoceramic sensors/actuators. Mater. Des. 23(3), 277–286 (2002)

    Google Scholar 

  11. Zhang, S.Q., Schmidt, R., Müller, P.C., Qin, X.S.: Disturbance rejection control for vibration suppression of smart beams and plates under a high frequency excitation. J. Sound Vib. 353, 19–37 (2015)

    Google Scholar 

  12. Asadi, H., Kiani, Y., Shakeri, M., Eslami, M.R.: Exact solution for nonlinear thermal stability of hybrid laminated composite Timoshenko beams reinforced with SMA fibers. Compos. Struct. 108, 811–822 (2014)

    Google Scholar 

  13. Rahmani, B., Shenas, A.G.: Robust vibration control of laminated rectangular composite plates in hygrothermal and thermal environment. Compos. Struct. 179, 665–681 (2017)

    Google Scholar 

  14. Jiang, B.K., Xu, J., Li, Y.H.: Flapwise vibration analysis of a rotating composite beam under hygrothermal environment. Compos. Struct. 117, 201–211 (2014)

    Google Scholar 

  15. Gendelman, O., Manevitch, L., Vakakis, A.F.: Energy pumping in nonlinear mechanical oscillators: part I—dynamics of the under lying Hamiltonian systems. J. Appl. Mech. 68(1), 34–42 (2001)

    MathSciNet  MATH  Google Scholar 

  16. Vakakis, A.F., Gendelman, O.V., Bergman, L.A., Mcfarland, D.M., Kerschen, G.: Nonlinear Targeted Energy Transfer in Mechanical and Structural Systems. Springer, Netherlands (2009)

    MATH  Google Scholar 

  17. Savadkoohi, A.T., Vaurigaud, B., Lamarque, C.H., Pernot, S.: Targeted energy transfer with parallel nonlinear energy sinks, part II: theory and experiments. Nonlinear Dyn. 67(1), 37–46 (2013)

    MathSciNet  MATH  Google Scholar 

  18. Haris, A., Motato, E., Theodossiades, S., Rahnejat, H., Kelly, P.: A study on torsional vibration attenuation in automotive drivetrains using absorbers with smooth and non-smooth nonlinearities. Appl. Math Model. 46, 674–690 (2016)

    MathSciNet  MATH  Google Scholar 

  19. Habib, G., Romeo, F.: The tuned bistable nonlinear energy sink. Nonlinear Dyn. 89(1), 1–18 (2017)

    Google Scholar 

  20. Yan, Z., Ragab, S.A., Hajj, M.R.: Passive control of transonic flutter with a nonlinear energy sink. Nonlinear Dyn. 91(1), 1–14 (2017)

    Google Scholar 

  21. Bichiou, Y., Hajj, M.R., Nayfeh, A.H.: Effectiveness of a nonlinear energy sink in the control of an aeroelastic system. Nonlinear Dyn. 86(4), 1–17 (2016)

    MathSciNet  Google Scholar 

  22. Oliva, M., Barone, G., Navarra, G.: Optimal design of Nonlinear Energy Sinks for SDOF structures subjected to white noise base excitations. Eng. Struct. 145, 135–152 (2017)

    Google Scholar 

  23. Tripathi, A., Grover, P., Kalmár-Nagy, T.: On optimal performance of nonlinear energy sinks in multiple-degree-of-freedom systems. J. Sound Vib. 388, 272–297 (2017)

    Google Scholar 

  24. Chen, J.E., He, W., Zhang, W., Yao, M.H., Liu, J., Sun, M.: Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks. Nonlinear Dyn. 91(2), 885–904 (2018)

    Google Scholar 

  25. Georgiades, F., Vakakis, A.F.: Dynamics of a linear beam with an attached local nonlinear energy sink. Commun. Nonlinear Sci. Numer. Simul. 12(5), 643–651 (2007)

    MATH  Google Scholar 

  26. Gendelman, O., Manevitch, L.I., Vakakis, A.F., Closkey, R.M.: Energy pumping in nonlinear mechanical oscillators: part I-dynamics of the underlying Hamiltonian systems. J. Appl. Mech. 68, 34–41 (2001)

    MathSciNet  MATH  Google Scholar 

  27. Vakakis, A.F., Gendelman, O.: Energy pumping in coupled mechanical oscillators II: resonance capture. J. Appl. Mech. 68(1), 42–48 (2001)

    MathSciNet  MATH  Google Scholar 

  28. Luongo, A., Zulli, D.: Nonlinear energy sink to control elastic strings: the internal resonance case. Nonlinear Dyn. 81(1–2), 425–435 (2015)

    MathSciNet  MATH  Google Scholar 

  29. Zhang, Y.W., Yuan, B., Fang, B., Chen, L.Q.: Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink. Nonlinear Dyn. 87(2), 1159–1167 (2016)

    Google Scholar 

  30. Haris, A., Motato, E., Mohammadpour, M., Theodossiades, S., Rahnejat, H.: On the effect of multiple parallel nonlinear absorbers in palliation of torsional response of automotive drivetrain. Int. J. Nonlinear Mech. 96, 22–35 (2017)

    Google Scholar 

  31. Motato, E., Haris, A., Theodossiades, S., Mohammadpour, M., Rahnejat, H.: Targeted energy transfer and modal energy redistribution in automotive drivetrains. Nonlinear Dyn. 87(1), 169–190 (2017)

    Google Scholar 

  32. Costa, S.N.J., Hassmann, C.H.G., Balthazar, J.M., Dantas, M.J.H.: On energy transfer between vibrating systems under linear and nonlinear interactions. Nonlinear Dyn. 57(1–2), 57–67 (2008)

    MathSciNet  MATH  Google Scholar 

  33. Zhang, Y.W., Zang, J., Yang, T.Z., Fang, B., Wen, X.: Vibration suppression of an axially moving string with transverse wind loadings by a nonlinear energy sink. Math. Probl. Eng. 2013, 1–7 (2013)

    MathSciNet  MATH  Google Scholar 

  34. Yang, T.Z., Yang, X.D., Li, Y.H., Fang, B.: Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity. J. Vib. Control. 20(9), 1293–1300 (2014)

    MathSciNet  Google Scholar 

  35. Gourc, E., Michon, G., Seguy, S., Berlioz, A.: Targeted energy transfer under harmonic forcing with a vibro-impact nonlinear energy sink: analytical and experimental developments. J. Vib. Acoust. 137(3), 1–7 (2015)

    Google Scholar 

  36. Chen, J.E., Zhang, W., Yao, M.H., Liu, J., Sun, M.: Vibration reduction in truss core sandwich plate with internal nonlinear energy sink. Compos. Struct. 193, 180–188 (2018)

    Google Scholar 

  37. Zhang, Y.W., Zhang, H., Hou, S., Xu, K.F., Chen, L.Q.: Vibration suppression of composite laminated plate with nonlinear energy sink. Acta Astronaut. 123, 109–115 (2016)

    Google Scholar 

  38. Ghayesh, M.H., Amabili, M.: Steady-state transverse response of an axially moving beam with time-dependent axial speed. Int. J. Nonlinear Mech. 49, 40–49 (2013)

    Google Scholar 

  39. Ding, H.: Periodic responses of a pulley-belt system with one-way clutch under inertia excitation. J. Sound Vib. 353, 308–326 (2015)

    Google Scholar 

  40. Ghayesh, M.H., Amabili, M.: Nonlinear dynamics of axially moving viscoelastic beams over the buckled state. Compos. Struct. 112–113, 406–421 (2012)

    Google Scholar 

  41. Ding, H., Tan, X., Dowell, E.H.: Natural frequencies of a super-critical transporting Timoshenko beam. Eur. J. Mech. A Solids 66, 79–93 (2017)

    MathSciNet  MATH  Google Scholar 

  42. Rao, S.S.: Vibration of Continuous Systems. Wiley, Hoboken (2007)

    Google Scholar 

  43. Kani, M., Khadem, S.E., Pashaei, M.H., Dardel, M.: Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn. 83, 1–22 (2016)

    MathSciNet  Google Scholar 

  44. Zang, J., Chen, L.Q.: Complex dynamics of a harmonically excited structure coupled with a nonlinear energy sink. Acta Mech. Sin. 33(4), 801–822 (2017)

    MathSciNet  MATH  Google Scholar 

  45. Ding, H., Zhu, M., Chen, L.Q.: Nonlinear vibration isolation of a viscoelastic beam. Nonlinear Dyn. 92(2), 325–349 (2018)

    Google Scholar 

  46. Zang, J., Zhang, Y.W., Ding, H., Yang, T.Z., Chen, L.Q.: The evaluation of a nonlinear energy sink absorber based on the transmissibility. Mech. Syst. Signal Process. 125, 99–122 (2019)

    Google Scholar 

  47. Ding, H., Jean, W.Z.: Steady-state responses of pulley-belt systems with a one-way clutch and belt bending stiffness. J. Vib. Acoust. 136(4), 63–69 (2014)

    Google Scholar 

  48. Ding, H., Li, D.P.: Static and dynamic behaviors of belt-drive dynamic systems with a one-way clutch. Nonlinear Dyn. 78(2), 1553–1575 (2014)

    MathSciNet  Google Scholar 

  49. Viguié, R., Kerschen, G.: Nonlinear vibration absorber coupled to a nonlinear primary system: a tuning methodology. J. Sound Vib. 326, 780–793 (2009)

    Google Scholar 

  50. Zang, J., Yuan, T.C., Lu, Z.Q., Zhang, Y.W., Ding, H., Chen, L.Q.: A lever-type nonlinear energy sink. J. Sound Vib. 437, 119–134 (2018)

    Google Scholar 

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Project Nos. 11772205, 11872159), the Scientific Research Fund of LiaoNing Provincial Education Department (No. L201703), and LiaoNing Revitalization Talents Program (XLYC1807172).

Author information

Authors and Affiliations

  1. College of Aerospace Engineering, Shenyang Aerospace University, Shenyang, 110136, China

    Ye-Wei Zhang, Shuai Hou, Jian Zang, Zhi-Yu Ni & Ying-Yuan Teng

  2. Science and Technology on Reliability and Environment Engineering Laboratory, Beijing Institute of Structure and Environment Engineering, Beijing, 100076, China

    Zhong Zhang

  3. Department of Mechanics, Harbin Institute of Technology, Shenzhen, 518055, China

    Li-Qun Chen

Authors
  1. Ye-Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Shuai Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhong Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jian Zang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Zhi-Yu Ni
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Ying-Yuan Teng
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Li-Qun Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Li-Qun Chen.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

The nonlinear ordinary differential equations with different N.

For \(N=1\)

$$\begin{aligned}&M_1 \ddot{q}_1 +C_1 \dot{q}_1 +K_1 q_1 +S_1 q_1 ^{3}-A_1 \sin (\omega \bar{{t}})\nonumber \\&\quad -\left( {k(\bar{{y}}-\phi _1 (d_1 )q_1 )^{3}+c(\dot{\bar{{y}}}-\phi _1 (d_1 )\dot{q}_1 )} \right) \phi _1 (d_1 )=0 \end{aligned}$$
(A1a)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}+k(\bar{{y}}-\phi _1 (d_n )q_1 )^{3}+c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 )=0 \end{aligned}$$
(A1b)
$$\begin{aligned}&M_1 =\int _0^1 {\phi _1 (\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _1 ^{\prime \prime }(\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_1 =\eta \int _0^1 {\phi _1 (\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&K_1 =\bar{{M}}\int _0^1 {\phi _1 ^{\prime \prime }(\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}}+\int _0^1 {\phi _1 ^{(4)}(\bar{{x}})\phi _1 (\bar{{x}})d} \bar{{x}} \nonumber \\&S_1 =-\frac{3}{2}\bar{{P}}\int _0^1 {\left( {\phi _1 ^{\prime }(\bar{{x}})} \right) } ^{3}\phi _s (\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&A_1 =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _1 (d_0 )} \phi _1 (\bar{{x}})\mathrm{d}x \end{aligned}$$
(A1c)

For \(N=2\)

$$\begin{aligned}&M_{11} \ddot{q}_1 +C_{11} \dot{q}_1 +K_{11} q_1 +S_{11} q_1 ^{3}\nonumber \\&\quad +\,R_{11} q_2 ^{2}q_1 -A_{11} \sin (\omega \bar{{t}})\nonumber \\&\quad -\, \left( k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 ) \right) \phi _1 (d_n )=0 \end{aligned}$$
(A2a)
$$\begin{aligned}&M_{22} \ddot{q}_2 +C_{22} \dot{q}_2 +K_{22} q_2 +S_{22} q_2 ^{3}+R_{22} q_1 ^{2}q_2 \nonumber \\&\quad -\, \left( k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 ) \right) \phi _2 (d_n )=0 \end{aligned}$$
(A2b)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}+k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 )^{3}\nonumber \\&\quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 )=0 \end{aligned}$$
(A2c)
$$\begin{aligned}&M_{11} =\int _0^1 {\phi _1 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _1 } (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{22} =\int _0^1 {\phi _2 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _2 (\bar{{x}})} \phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&C_{11} =\eta \int _0^1 {\phi _1 (\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{22} =\eta \int _0^1 {\phi _2 (\bar{{x}})\phi _2 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&K_{11} =\bar{{M}}\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{22} =\bar{{M}}\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&R_{11} =-\frac{3}{2}\bar{{P}}\int _0^1 {\phi _1 } (\bar{{x}})\left( \phi _1 ^{\prime \prime }(\bar{{x}})\phi _2 ^{\prime 2}(\bar{{x}})\right. \nonumber \\&\left. \quad \quad +\,2\phi _1 ^{\prime }(\bar{{x}})\phi _2 ^{\prime }(\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}}) \right) \mathrm{d}\bar{{x}} \nonumber \\&R_{22} =-\frac{3}{2}\bar{{P}}\int _0^1 {\phi _2 } (\bar{{x}})\left( \phi _1 ^{\prime 2}(\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}})\right. \nonumber \\&\left. \quad \quad +\,2\phi _1 ^{\prime }(\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\phi _2 ^{\prime }(\bar{{x}}) \right) \mathrm{d}\bar{{x}}\nonumber \\&S_{11} =-\frac{3}{2}\bar{{P}}\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{\prime 2}(\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}} \nonumber \\&S_{22} =-\frac{3}{2}\bar{{P}}\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{\prime 2}(\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}} \nonumber \\&A_{11} =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _1 (d_0 )} \phi _1 (\bar{{x}})\mathrm{d}x \end{aligned}$$
(A2d)

For \(N=3\)

$$\begin{aligned}&M_{11} \ddot{q}_1 +C_{11} \dot{q}_1 +K_{11} q_1 +S_{11} (q_1 ^{3}+3q_1 ^{2}q_2 \nonumber \\&\quad +\,8q_1 q_2 ^{2}+18q_1 q_3 ^{2}+12q_2 ^{2}q_3 )-A_{11} \sin (\omega \bar{{t}}) \nonumber \\&\quad -\,\left( k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 -\phi _3 (d_n )q_3 )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 -\phi _3 (d_n )\dot{q}_3 ) \right) \phi _1 (d_n )=0 \nonumber \\ \end{aligned}$$
(A3a)
$$\begin{aligned}&M_{22} \ddot{q}_2 +C_{22} \dot{q}_2 +K_{22} q_2 +S_{22} (2q_2 ^{3}\nonumber \\&\quad +\,9q_2 q_3 ^{2}+q_2 q_1 ^{2}+3q_1 q_2 q_3 )\nonumber \\&\quad - \,\left( k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 -\phi _3 (d_n )q_3 )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 -\phi _3 (d_n )\dot{q}_3 ) \right) \phi _2 (d_n )=0 \nonumber \\ \end{aligned}$$
(A3b)
$$\begin{aligned}&M_{33} \ddot{q}_3 +C_{33} \dot{q}_3 +K_{33} q_3 +S_{33} (81q_3 ^{3}+72q_3 q_2 ^{2}\nonumber \\&\quad +\,12q_1 q_2 ^{2}+18q_1 ^{2}q_3 +q_1 ^{3})-A_{33} \sin (\omega \bar{{t}}) \nonumber \\&\quad -\,\left( k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 -\phi _3 (d_n )q_3 )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 -\phi _3 (d_n )\dot{q}_3 ) \right) \phi _3 (d_n )=0 \nonumber \\ \end{aligned}$$
(A3c)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}+k(\bar{{y}}-\phi _1 (d_n )q_1 -\phi _2 (d_n )q_2 -\phi _3 (d_n )q_3 )^{3}\nonumber \\&\quad +\,c(\dot{\bar{{y}}}-\phi _1 (d_n )\dot{q}_1 -\phi _2 (d_n )\dot{q}_2 -\phi _3 (d_n )\dot{q}_3 )=0 \end{aligned}$$
(A3d)
$$\begin{aligned}&M_{11} =\int _0^1 {\phi _1 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _1 } (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{22} =\int _0^1 {\phi _2 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _2 (\bar{{x}})} \phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{33} =\int _0^1 {\phi _3 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _3 (\bar{{x}})} \phi _3 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&C_{11} =\eta \int _0^1 {\phi _1 (\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{22} =\eta \int _0^1 {\phi _2 (\bar{{x}})\phi _2 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{33} =\eta \int _0^1 {\phi _3 (\bar{{x}})\phi _3 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&K_{11} =\bar{{M}}\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{22} =\bar{{M}}\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{33} =\bar{{M}}\int _0^1 {\phi _3 (\bar{{x}})\phi _3 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _3 (\bar{{x}})\phi _3 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&A_{11} =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _1 (d_0 )} \phi _1 (\bar{{x}})\mathrm{d}x \nonumber \\&A_{33} =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _3 (d_0 )} \phi _3 (\bar{{x}})\mathrm{d}x \nonumber \\&S_{11} =\frac{9L\pi ^{4}}{h^{2}},\quad S_{22} =\frac{72L\pi ^{4}}{h^{2}},\quad S_{33} =\frac{9L\pi ^{4}}{h^{2}} \end{aligned}$$
(A3e)

For \(N =4\)

$$\begin{aligned}&M_{11} \ddot{q}_1 +C_{11} \dot{q}_1 +K_{11} q_1 +S_{11} (q_1 ^{3}+3q_1 ^{2}q_3 \nonumber \\&\quad +\,8q_1 q_2 ^{2}+16q_1 q_2 q_4 +18q_1 q_3 ^{2}+32q_1 q_4 ^{2}+12q_2 ^{2}q_3 \nonumber \\&\quad +\, 48q_2 q_3 q_4 )-A_{11} \sin (\omega \bar{{t}})-\left( k(\bar{{y}}-\,\sum _{r=1}^4 {\phi _r (d_n )q_r } )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\sum _{r=1}^4 {\phi _r (d_n )\dot{q}_r } ) \right) \phi _1 (d_n )=0 \end{aligned}$$
(A4a)
$$\begin{aligned}&M_{22} \ddot{q}_2 +C_{22} \dot{q}_2 +K_{22} q_2 +S_{22} (q_1 ^{2}q_2 +q_1 ^{2}q_4 +3q_1 q_2 q_3\nonumber \\&\quad +\,6q_1 q_3 q_4 +2q_2 ^{3}+9q_2 q_3 ^{2}+16q_2 q_4 ^{2}\nonumber \\&\quad + \,9q_3 ^{2}q_4 )-\left( k(\bar{{y}}-\sum _{r=1}^4 {\phi _r (d_n )q_r } )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\sum _{r=1}^4 {\phi _r (d_n )\dot{q}_r } ) \right) \phi _2 (d_n )=0 \end{aligned}$$
(A4b)
$$\begin{aligned}&M_{33} \ddot{q}_3 +C_{33} \dot{q}_3 +K_{33} q_3 +S_{33} (q_1 ^{3}+18q_1 ^{2}q_3 +12q_1 q_2 ^{2}\nonumber \\&\quad +\,48q_1 q_2 q_4 +72q_2 ^{2}q_3 +144q_2 q_3 q_4 +81q_3 ^{3}\nonumber \\&\quad +\,288q_3 q_4 ^{2})-A_{33} \sin (\omega \bar{{t}})-\left( k(\bar{{y}}-\sum _{r=1}^4 {\phi _r (d_n )q_r } )^{3}\right. \nonumber \\&\left. \quad +\,c(\dot{\bar{{y}}}-\sum _{r=1}^4 {\phi _r (d_n )\dot{q}_r } ) \right) \phi _3 (d_n )=0 \end{aligned}$$
(A4c)
$$\begin{aligned}&M_{44} \ddot{q}_4 +C_{44} \dot{q}_4 +K_{44} q_4 +S_{44} (q_1 ^{2}q_2 +4q_1 ^{2}q_4 \nonumber \\&\quad +\,6q_1 q_2 q_3 +16q_2 ^{2}q_4 +9q_2 q_3 ^{2}+36q_3 ^{2}q_4 +32q_4 ^{3}) \nonumber \\&\quad -\,\left( k(\bar{{y}}-\sum _{r=1}^4 {\phi _r (d_n )q_r } )^{3}\right. \nonumber \\&\quad \left. +\,c(\dot{\bar{{y}}}-\sum _{r=1}^4 {\phi _r (d_n )\dot{q}_r } ) \right) \phi _4 (d_n )=0 \end{aligned}$$
(A4d)
$$\begin{aligned}&\varepsilon \ddot{\bar{{y}}}+k(\bar{{y}}-\sum _{r=1}^4 {\phi _r (d_n )q_r } )^{3}+c(\dot{\bar{{y}}}-\sum _{r=1}^4 {\phi _r (d_n )\dot{q}_r } )=0 \end{aligned}$$
(A4e)
$$\begin{aligned}&M_{11} =\int _0^1 {\phi _1 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _1 } (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{22} =\int _0^1 {\phi _2 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _2 (\bar{{x}})} \phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{33} =\int _0^1 {\phi _3 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _3 (\bar{{x}})} \phi _3 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&M_{44} =\int _0^1 {\phi _4 ^{2}(\bar{{x}})} \mathrm{d}\bar{{x}}-\bar{{m}}\int _0^1 {\phi _4 (\bar{{x}})} \phi _4 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}} \nonumber \\&C_{11} =\eta \int _0^1 {\phi _1 (\bar{{x}})\phi _1 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{22} =\eta \int _0^1 {\phi _2 (\bar{{x}})\phi _2 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{33} =\eta \int _0^1 {\phi _3 (\bar{{x}})\phi _3 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&C_{44} =\eta \int _0^1 {\phi _4 (\bar{{x}})\phi _4 (\bar{{x}})} \mathrm{d}\bar{{x}} \nonumber \\&K_{11} =\bar{{M}}\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _1 (\bar{{x}})\phi _1 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{22} =\bar{{M}}\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _2 (\bar{{x}})\phi _2 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{33} =\bar{{M}}\int _0^1 {\phi _3 (\bar{{x}})\phi _3 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _3 (\bar{{x}})\phi _3 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} } \nonumber \\&K_{44} =\bar{{M}}\int _0^1 {\phi _4 (\bar{{x}})\phi _4 ^{\prime \prime }(\bar{{x}})\mathrm{d}\bar{{x}}+\int _0^1 {\phi _4 (\bar{{x}})\phi _4 ^{(4)}(\bar{{x}})\mathrm{d}\bar{{x}}} }\nonumber \nonumber \\&A_{11} =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _1 (d_0 )} \phi _1 (\bar{{x}})\mathrm{d}x \nonumber \\&A_{33} =\int _0^1 {f\delta (\bar{{x}}-d_0 )\phi _3 (d_0 )} \phi _3 (\bar{{x}})\mathrm{d}x \nonumber \\&S_{11} =\frac{9L\pi ^{4}}{h^{2}},\quad S_{22} =\frac{72L\pi ^{4}}{h^{2}},\nonumber \\&S_{33}=\frac{9L\pi ^{4}}{h^{2}},\quad S_{44} =\frac{72L\pi ^{4}}{h^{2}} \end{aligned}$$
(A4f)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhang, YW., Hou, S., Zhang, Z. et al. Nonlinear vibration absorption of laminated composite beams in complex environment. Nonlinear Dyn 99, 2605–2622 (2020). https://doi.org/10.1007/s11071-019-05442-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05442-3

Keywords

Search

Navigation