Free vibration characteristics of stiffened sandwich plates with auxetic core and functionally graded piezoelectric face sheet

Abstract

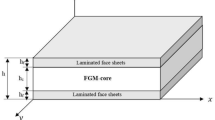
In this paper, the free vibration characteristics of stiffened sandwich plates with auxetic core and functionally graded piezoelectric face sheet are investigated. The sandwich plate configuration comprises three distinct layers: a top layer consisting of functionally graded piezoelectric material (FGPie), a core layer composed of auxetic material exhibiting a negative Poisson's ratio, and a bottom layer made of functionally graded material (FGM). The sandwich plate is reinforced by isotropic stiffeners along the x and y directions. A novel model is established based on the four-variable shear deformation refined plate theory and the pb2-Ritz method. This model offers the flexibility to analyze plates with diverse mechanical boundary conditions and supports two types of electrical boundary conditions: closed circuit and open circuit. The accuracy and convergence of the proposed model are validated through comparative analyses against published results, thereby confirming the reliability when analyzing the vibration characteristics of this complex sandwich structure. Furthermore, some new investigations are carried out to explore the influence of various parameters on the vibrational characteristics of the stiffened piezoelectric auxetic sandwich (SA-FGPie) plates. The results suggest that the properties of the reinforcing stiffeners, such as quantity or dimensions, alter the free vibration characteristics of the SA-FGPie plates significantly. In addition, parameters such as the volume fraction indexes of the FGPie and FGM layers, electrical boundary conditions or FGPie layer thickness, as well as geometric parameters of the auxetic unit cell also have a significant influence on the vibration response of SA-FGPie plates. However, the influence of these parameters depends on the specific boundary conditions.

Appendix A

$$\overline{k}^{{s_{1} s_{1} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{{a^{2} b^{2} }}\left( {b^{2} A_{11} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \varsigma }\frac{{\partial {\overline{\mathbf{U}}}^{T} }}{\partial \varsigma } + a^{2} A_{66} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \vartheta }\frac{{\partial {\overline{\mathbf{U}}}^{T} }}{\partial \vartheta }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{1} s_{2} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{ab}\left( {A_{12} \frac{{\partial {\overline{\mathbf{U}}}}}{\varsigma }\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\vartheta } + A_{66} \frac{{\partial {\overline{\mathbf{U}}}}}{\vartheta }\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\varsigma }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{1} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{ - 16}{{ab^{2} }}\left( {{\mkern 1mu} \frac{{b^{2} }}{{a^{2} }}B_{11} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \varsigma }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \varsigma^{2} }} + B_{12} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \varsigma }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \vartheta^{2} }} + 2B_{66} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial \vartheta }} \right)} d\varsigma d\vartheta } ;$$

$$\overline{k}^{{s_{1} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{ - 16}{{ab^{2} }}\left( {\frac{{b^{2} }}{{a^{2} }}\left( {B_{11}^{s} + \frac{{B_{12}^{s} }}{2}{\mkern 1mu} } \right)\frac{{\partial {\overline{\mathbf{U}}}}}{\partial \varsigma }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \varsigma^{2} }} + 2B_{66}^{s} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial \vartheta } + \frac{{B_{12}^{s} }}{2}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{{\partial \vartheta^{2} }}\frac{{\partial {\overline{\mathbf{U}}}^{T} }}{\partial \varsigma }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{1} s_{5} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{2}{a}\left( {\left( {P_{3} - A_{pie} } \right)\frac{{\partial {\overline{\mathbf{U}}}}}{\partial \varsigma }{\overline{{\Phi }}}^{T} } \right)d\varsigma d\vartheta } } ; \, \overline{k}^{{s_{2} s_{1} }} = \left( {\overline{k}^{{s_{1} s_{2} }} } \right)^{T} ;$$

$$\overline{k}^{{s_{2} s_{2} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{{a^{2} b^{2} }}\left( {a^{2} A_{22} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial \vartheta }\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\partial \vartheta } + b^{2} A_{66} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial \varsigma }\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\partial \varsigma }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{2} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{ - 16}{{a^{2} b}}\left( {{\mkern 1mu} B_{12} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }}\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\partial \vartheta } + \left( \frac{a}{b} \right)^{2} B_{22} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \vartheta^{2} }}\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\partial \vartheta } + 2B_{66} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial \varsigma }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial \vartheta }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{2} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{ - 16}{{a^{3} b^{3} }}\left( {ab^{2} B_{12}^{s} + a^{3} B_{22}^{s} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \vartheta^{2} }} + {\mkern 1mu} 2ab^{2} B_{66}^{s} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial \varsigma }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial \vartheta }} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{2} s_{5} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{2}{a}\left( {\left( {P_{3} - A_{pie} } \right)\frac{{\partial {\overline{\mathbf{V}}}}}{\partial \vartheta }{\overline{{\Phi }}}^{T} } \right)d\varsigma d\vartheta } } ; \, \overline{k}^{{s_{3} s_{1} }} = \left( {\overline{k}^{{s_{1} s_{3} }} } \right)^{T} ; \, \overline{k}^{{s_{3} s_{2} }} = \left( {\overline{k}^{{s_{2} s_{3} }} } \right)^{T} ;$$

$$\overline{k}^{{s_{3} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{32}{{a^{4} b^{4} }}\left( \begin{gathered} b^{4} D_{11} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \varsigma^{2} }} + 2a^{2} b^{2} D_{12} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \vartheta^{2} }} + \hfill \\ a^{4} D_{22} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \vartheta^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{{\partial \vartheta^{2} }} + 4a^{2} b^{2} D_{66} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \varsigma \partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial \vartheta } \hfill \\ \end{gathered} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{3} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{16}{{a^{2} b^{2} }}\left( \begin{gathered} \left( {{\mkern 1mu} \left( \frac{b}{a} \right)^{2} \left( {2D_{11}^{s} + {\mkern 1mu} D_{12}^{s} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \varsigma^{2} }}} \right) \hfill \\ + 2\left( {D_{12}^{s} + \frac{1}{2}D_{22}^{s} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \vartheta^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \varsigma^{2} }} \hfill \\ + D_{12}^{s} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \vartheta^{2} }} + 8D_{66} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \varsigma \partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial \vartheta } \hfill \\ + \left( \frac{a}{b} \right)^{2} D_{22}^{s} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \vartheta^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \vartheta^{2} }} \hfill \\ \end{gathered} \right)d\varsigma d\vartheta } } ;$$

$$\begin{gathered} \overline{k}^{{s_{3} s_{5} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{16}{{a^{2} b^{2} }}\left( {\left( {B_{bp}^{b} - P_{4} } \right)\left( {\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \varsigma^{2} }} + \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{{\partial \vartheta^{2} }}} \right){\overline{{\Phi }}}^{T} } \right)d\varsigma d\vartheta } } ; \, \overline{k}^{{s_{4} s_{1} }} = \left( {\overline{k}^{{s_{1} s_{4} }} } \right)^{T} ; \hfill \\ \overline{k}^{{s_{4} s_{2} }} = \left( {\overline{k}^{{s_{2} s_{4} }} } \right)^{T} ; \, \overline{k}^{{s_{4} s_{3} }} = \left( {\overline{k}^{{s_{3} s_{4} }} } \right)^{T} ; \hfill \\ \end{gathered}$$

$$\overline{k}^{{s_{4} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{{a^{2} b^{2} }}\left( \begin{gathered} {\mkern 1mu} \left( \frac{b}{a} \right)^{2} \left( {4\left( {H_{11}^{s} + {\mkern 1mu} H_{12}^{s} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{{\partial \vartheta^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \varsigma^{2} }}} \right) \hfill \\ + 4\left( {H_{12}^{s} + 2H_{22}^{s} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{{\partial \vartheta^{2} }}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{{\partial \varsigma^{2} }} \hfill \\ + b^{2} A_{55}^{s} \frac{{\partial {\overline{\mathbf{W}}}_{s} }}{\partial \varsigma }\frac{{\partial {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma } + a^{2} A_{44}^{s} \frac{{\partial {\overline{\mathbf{W}}}_{s} }}{\partial \vartheta }\frac{{\partial {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \vartheta } \hfill \\ + 16H_{66}^{s} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{\partial \varsigma \partial \vartheta }\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial \vartheta } \hfill \\ \end{gathered} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{4} s_{5} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{4}{{a^{2} b^{2} }}\left( \begin{gathered} b^{2} \left( {B_{pie}^{s} - P_{5} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{{\partial \varsigma^{2} }}{\overline{{\Phi }}}^{T} + a^{2} \left( {B_{pie}^{s} - P_{5} } \right)\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{{\partial \vartheta^{2} }}{\overline{{\Phi }}}^{T} \hfill \\ + \left( {P_{1} - A_{pie}^{s} } \right)\left( {a^{2} \frac{{\partial {\overline{\mathbf{W}}}_{s} }}{\partial \vartheta }\frac{{\partial {\overline{{\Phi }}}^{T} }}{\partial \vartheta } + b^{2} \frac{{\partial {\overline{\mathbf{W}}}_{s} }}{\partial \varsigma }\frac{{\partial {\overline{{\Phi }}}^{T} }}{\partial \varsigma }} \right) \hfill \\ \end{gathered} \right)d\varsigma d\vartheta } } ;$$

$$\overline{k}^{{s_{5} s_{5} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2\left( {\frac{{P_{2} }}{{a^{2} }}\frac{{\partial {\overline{{\Phi }}}}}{\partial \varsigma }\frac{{\partial {\overline{{\Phi }}}^{T} }}{\partial \varsigma } + \frac{{P_{2} }}{{b^{2} }}\frac{{\partial {\overline{{\Phi }}}}}{\partial \vartheta }\frac{{\partial {\overline{{\Phi }}}^{T} }}{\partial \vartheta } + P_{6} {\mathbf{\overline{\Phi }\overline{\Phi }}}^{T} } \right)d\varsigma d\vartheta } } ;$$

$$m^{{s_{1} s_{1} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2I_{0} \frac{{\partial {\overline{\mathbf{U}}}}}{\partial t}\frac{{\partial {\overline{\mathbf{U}}}^{T} }}{\partial t}d\varsigma d\vartheta } } ; \, m^{{s_{1} s_{2} }} = 0; \, m^{{s_{1} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{{ - 4I_{1} }}{a}\frac{{\partial {\overline{\mathbf{U}}}}}{\partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial t}d\varsigma d\vartheta } } ;$$

$$m^{{s_{1} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{{ - 4I_{2} }}{a}\frac{{\partial {\overline{\mathbf{U}}}}}{\partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial t}d\varsigma d\vartheta } } ;$$

$$m^{{s_{2} s_{1} }} = 0; \, m^{{s_{2} s_{2} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2I_{0} \frac{{\partial {\overline{\mathbf{V}}}}}{\partial t}\frac{{\partial {\overline{\mathbf{V}}}^{T} }}{\partial t}d\varsigma d\vartheta } } ; \, m^{{s_{2} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{{ - 4I_{1} }}{b}\frac{{\partial {\overline{\mathbf{V}}}}}{\partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \vartheta \partial t}d\varsigma d\vartheta } } ;$$

$$m^{{s_{2} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{{ - 4I_{2} }}{b}\frac{{\partial {\overline{\mathbf{V}}}}}{\partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \vartheta \partial t}d\varsigma d\vartheta } } ; \, m^{{s_{3} s_{1} }} = m^{{s_{1} s_{3} }} ; \, m^{{s_{3} s_{2} }} = m^{{s_{2} s_{3} }} ;$$

$$m^{{s_{3} s_{3} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2I_{0} \frac{{\partial {\overline{\mathbf{W}}}_{b} }}{\partial t}\frac{{\partial {\overline{\mathbf{W}}}_{b}^{T} }}{\partial t}d\varsigma d\vartheta } } + \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{{8I_{4} }}{{a^{2} b^{2} }}\left( {b^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \varsigma \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \varsigma \partial t} + a^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \vartheta \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{b}^{T} }}{\partial \vartheta \partial t}} \right)d\varsigma d\vartheta } } ;$$

$$m^{{s_{3} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2{\mkern 1mu} I_{0} \frac{{\partial {\overline{\mathbf{W}}}_{b} }}{\partial t}\frac{{\partial {\overline{\mathbf{W}}}_{s}^{T} }}{\partial t}d\varsigma d\vartheta } } + \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{{a^{2} b^{2} }}{\mkern 1mu} I_{3} \left( {b^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \varsigma \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial t} + a^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{b} }}{\partial \vartheta \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \vartheta \partial t}} \right)d\varsigma d\vartheta } } ;$$

$$m^{{s_{4} s_{1} }} = \left( {m^{{s_{1} s_{4} }} } \right)^{T} ; \, m^{{s_{4} s_{2} }} = \left( {m^{{s_{2} s_{4} }} } \right)^{T} ; \, m^{{s_{4} s_{3} }} = \left( {m^{{s_{3} s_{4} }} } \right)^{T} ;$$

$$m^{{s_{4} s_{4} }} = \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {2{\mkern 1mu} I_{0} \frac{{\partial {\overline{\mathbf{W}}}_{s} }}{\partial t}\frac{{\partial {\overline{\mathbf{W}}}_{s}^{T} }}{\partial t}d\varsigma d\vartheta } } + \frac{ab}{4}\int\limits_{0}^{1} {\int\limits_{0}^{1} {\frac{8}{{a^{2} b^{2} }}I_{5} \left( {b^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{\partial \varsigma \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \varsigma \partial t} + a^{2} \frac{{\partial^{2} {\overline{\mathbf{W}}}_{s} }}{\partial \vartheta \partial t}\frac{{\partial^{2} {\overline{\mathbf{W}}}_{s}^{T} }}{\partial \vartheta \partial t}} \right)d\varsigma d\vartheta } }$$