Skip to main content

Advertisement

SpringerLink
Log in

Spectro-spatial analyses of a nonlinear metamaterial with multiple nonlinear local resonators

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

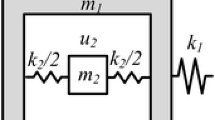
Recent focus has been given to spectro-spatial analysis of nonlinear metamaterials since they can predict interesting nonlinear phenomena not accessible by spectral analysis (i.e., dispersion relations). However, current studies are limited to a nonlinear chain with single linear resonator or linear chain with nonlinear resonator. There is no work that examines the combination of nonlinear chain with nonlinear resonators. This paper investigates the spectro-spatial properties of wave propagation through a nonlinear metamaterials consisting of nonlinear chain with multiple nonlinear local resonators. Different combinations of softening and hardening nonlinearities are examined to reveal their impact on the traveling wave features and the band structure. The method of multiple scales is used to obtain closed-form expressions for the dispersion relations. Our analytical solution is validated via the numerical simulation and results from the literature. The numerical simulation is based on spectro-spatial analysis using signal processing techniques such as spatial spectrogram, wave filtering, and contour plots of 2D Fourier transform. The spectro-spatial analysis provides a detailed information about wave distortion due to nonlinearity and classify the distortion into different features. The observations suggest that nonlinear chain with multiple nonlinear resonators can affect the waveform at all wavelength limits. Such nonlinear metamaterials are suitable for broadband vibration control and energy harvesting, as well as other applications such as acoustic switches, diodes, and rectifiers, allowing wave propagation only in a pre-defined direction.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Hussein, Mahmoud I., Leamy, Michael J, Ruzzene, Massimo: Dynamics of phononic materials and structures: historical origins, recent progress, and future outlook. Appl. Mech. Rev. 66(4), 040802 (2014)

    Article  Google Scholar 

  2. Cai, Wenshan, Shalaev, Vladimir M: Optical Metamaterials, Volume 10. Springer, Berlin (2010)

    Book  Google Scholar 

  3. Achaoui, Younes, Laude, Vincent, Benchabane, Sarah, Khelif, Abdelkrim: Local resonances in phononic crystals and in random arrangements of pillars on a surface. J. Appl. Phys. 114(10), 104503 (2013)

    Article  Google Scholar 

  4. Bertoldi, Katia, Vitelli, Vincenzo, Christensen, Johan, van Hecke, Martin: Flexible mechanical metamaterials. Nat. Rev. Mater. 2(11), 17066 (2017)

    Article  Google Scholar 

  5. Sigalas, Michael M., Economou, Eleftherios N.: Elastic and acoustic wave band structure. J. Sound Vib. 158, 377–382 (1992)

    Article  Google Scholar 

  6. Sigalas, M., Economou, Eleftherios N.: Band structure of elastic waves in two dimensional systems. Solid State Commun. 86(3), 141–143 (1993)

    Article  Google Scholar 

  7. Kushwaha, Manvir S., Halevi, Peter, Dobrzynski, Leonard, Djafari-Rouhani, Bahram: Acoustic band structure of periodic elastic composites. Phys. Rev. Lett. 71(13), 2022 (1993)

    Article  Google Scholar 

  8. Kushwaha, Manvir S., Halevi, P., Martinez, G., Dobrzynski, Leonard, Djafari-Rouhani, Bahram: Theory of acoustic band structure of periodic elastic composites. Phys. Rev. B 49(4), 2313 (1994)

    Article  Google Scholar 

  9. Vasseur, J.O., Djafari-Rouhani, B., Dobrzynski, L., Kushwaha, M.S., Halevi, P.: Complete acoustic band gaps in periodic fibre reinforced composite materials: the carbon/epoxy composite and some metallic systems. J. Phys. Condens. Matter 6(42), 8759 (1994)

    Article  Google Scholar 

  10. Kushwaha, Manvir S.: Classical band structure of periodic elastic composites. Int. J. Modern Phys. B 10(09), 977–1094 (1996)

    Article  Google Scholar 

  11. Liu, Zhengyou, Zhang, Xixiang, Mao, Yiwei, Zhu, Y.Y., Yang, Zhiyu, Chan, Che Ting, Sheng, Ping: Locally resonant sonic materials. Science 289(5485), 1734–1736 (2000)

    Article  Google Scholar 

  12. Liu, Liao, Hussein, Mahmoud I: Wave motion in periodic flexural beams and characterization of the transition between Bragg scattering and local resonance. J. Appl. Mech. 79(1), 011003 (2012)

    Article  Google Scholar 

  13. Huang, G.L., Sun, C.T.: Band gaps in a multiresonator acoustic metamaterial. J. Vib. Acoust. 132(3), 031003 (2010)

    Article  Google Scholar 

  14. Zhu, R., Liu, X.N., Hu, G.K., Sun, C.T., Huang, G.L.: A chiral elastic metamaterial beam for broadband vibration suppression. J. Sound Vib. 333(10), 2759–2773 (2014)

    Article  Google Scholar 

  15. Kivshar, Yuri S., Flytzanis, Nikos: Gap solitons in diatomic lattices. Phys. Rev. A 46(12), 7972 (1992)

    Article  Google Scholar 

  16. Nadkarni, Neel, Daraio, Chiara, Kochmann, Dennis M: Dynamics of periodic mechanical structures containing bistable elastic elements: from elastic to solitary wave propagation. Phys. Rev. E 90(2), 023204 (2014)

    Article  Google Scholar 

  17. Liang, Bin, Yuan, Bo, Cheng, Jian-chun: Acoustic diode: rectification of acoustic energy flux in one-dimensional systems. Phys. Rev. Lett. 103(10), 104301 (2009)

    Article  Google Scholar 

  18. Manimala, James M., Sun, C.T.: Numerical investigation of amplitude-dependent dynamic response in acoustic metamaterials with nonlinear oscillators. J. Acoust. Soc. Am. 139(6), 3365–3372 (2016)

    Article  Google Scholar 

  19. Nayfeh, Ali H.: Introduction to Perturbation Techniques. Wiley, Hoboken (2011)

    MATH  Google Scholar 

  20. Nayfeh, Ali H., Mook, Dean T.: Nonlinear Oscillations. Wiley, Hoboken (2008)

    MATH  Google Scholar 

  21. Narisetti, Raj K., Leamy, Michael J., Ruzzene, Massimo: A perturbation approach for predicting wave propagation in one-dimensional nonlinear periodic structures. J. Vib. Acoust. 132(3), 031001 (2010)

    Article  Google Scholar 

  22. Manktelow, Kevin, Leamy, Michael J., Ruzzene, Massimo: Multiple scales analysis of wave-wave interactions in a cubically nonlinear monoatomic chain. Nonlinear Dyn. 63(1–2), 193–203 (2011)

    Article  MathSciNet  Google Scholar 

  23. Lazarov, Boyan Stefanov, Jensen, Jakob Søndergaard: Low-frequency band gaps in chains with attached non-linear oscillators. Int. J. Non-Linear Mech. 42(10), 1186–1193 (2007)

    Article  Google Scholar 

  24. Khajehtourian, Romik, Hussein, Mahmoud I.: Dispersion characteristics of a nonlinear elastic metamaterial. AIP Adv. 4(12), 124308 (2014)

    Article  Google Scholar 

  25. Hussein, M.I., Khajehtourian, R.: Nonlinear Bloch waves and balance between hardening and softening dispersion. Proc. R. Soc. A Math. Phys. Eng. Sci. 474(2217), 20180173 (2018)

    Article  MathSciNet  Google Scholar 

  26. Liang, B., Guo, X.S., Tu, J., Zhang, D., Cheng, J.C.: An acoustic rectifier. Nat. Mater. 9(12), 989 (2010)

    Article  Google Scholar 

  27. Xue-Feng Li, Xu, Ni, Liang Feng, Ming-Hui, Lu, He, Cheng, Chen, Yan-Feng: Tunable unidirectional sound propagation through a sonic-crystal-based acoustic diode. Phys. Rev. Lett. 106(8), 084301 (2011)

    Article  Google Scholar 

  28. Ma, Chu, Parker, Robert G., Yellen, Benjamin B.: Optimization of an acoustic rectifier for uni-directional wave propagation in periodic mass-spring lattices. J. Sound Vib. 332(20), 4876–4894 (2013)

    Article  Google Scholar 

  29. Boechler, Neil, Theocharis, Georgios, Daraio, C.: Bifurcation-based acoustic switching and rectification. Nat. Mater. 10(9), 665 (2011)

    Article  Google Scholar 

  30. Moore, Keegan J., Bunyan, Jonathan, Tawfick, Sameh, Gendelman, Oleg V, Li, Shuangbao, Leamy, Michael, Vakakis, Alexander F: Nonreciprocity in the dynamics of coupled oscillators with nonlinearity, asymmetry, and scale hierarchy. Phys. Rev. E 97(1), 012219 (2018)

    Article  Google Scholar 

  31. Ganesh, R., Gonella, Stefano: Spectro-spatial wave features as detectors and classifiers of nonlinearity in periodic chains. Wave Motion 50(4), 821–835 (2013)

    Article  Google Scholar 

  32. Zhou, W.J., Li, X.P., Wang, Y.S., Chen, W.Q., Huang, G.L.: Spectro-spatial analysis of wave packet propagation in nonlinear acoustic metamaterials. J. Sound Vib. 413, 250–269 (2018)

    Article  Google Scholar 

  33. Bukhari, M.A., Barry, O.R.: Nonlinear metamaterials with multiple local mechanical resonators: Analytical and numerical analyses. In: NODYCON 2019 The First International Nonlinear Dynamics Conference. (Accepted) (2019)

  34. Bukhari, M., Barry, O.: On the spectro-spatial wave features in nonlinear metamaterials with multiple local resonators. In: ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers (2019)

Download references

Acknowledgements

This work was supported by the start-up grant provided by the Department of Mechanical Engineering at Virginia Tech.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Virginia Tech, Blacksburg, Virginia, 24061, USA

    Mohammad Bukhari & Oumar Barry

Authors
  1. Mohammad Bukhari
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Oumar Barry
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Oumar Barry.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Bukhari, M., Barry, O. Spectro-spatial analyses of a nonlinear metamaterial with multiple nonlinear local resonators. Nonlinear Dyn 99, 1539–1560 (2020). https://doi.org/10.1007/s11071-019-05373-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05373-z

Keywords

Search

Navigation