1 Introduction

The first proposal of implementing a mechanical resonator to mitigate vibrations dates back to 1883, when Philip Watt [1, 2] proposed to adopt a rectangular water tank placed aboard a ship to reduce rolling. The idea was further developed by Frahm [3], whose invention (a U-shaped tank partially filled with water) found also a fair success in the ship industry [4]. The problem was formalized in more rigorous terms by Den Hartog and Ormondroyd [5], Den Hartog [6] and Brock [7], who developed tuning rules that formed the basis of the so-called Den Hartog’s equal-peak method. The vibration absorber considered in [5,6,7], usually called tuned mass damper (TMD), consists in a small mass attached to the primary system to be controlled through a spring and a damper. Their proper tuning enables to engage the TMD in a 1:1 modal interaction with the primary system, triggering a significant dissipation of vibration energy from the primary system.

Thanks to its simplicity, effectiveness and fully passive mode of operation, the TMD is today extensively used in real-life applications. Its main fields of application include civil structures, such as long-span bridges [8, 9], skyscrapers [10] and slender towers [11], aircraft engines [12] and helicopter rotors [13, 14], structures subject to human-induced vibrations [15] and production machines [16]. Several different designs for the TMD exist, as detailed in [17].

The fundamental drawback of the TMD is that it generally works in a relatively narrow frequency band. For instance, this limits its implementation to suppress vibrations of slender structures, whose natural frequency is usually not constant with respect to the oscillation amplitude [18]. To overcome this limitation, besides adopting semi-active solutions [19,20,21], several authors proposed the introduction of an intentional nonlinearity in the absorber, in order to expand its operational frequency band. Thanks to this new approach, a number of nonlinear vibration absorber was developed. One of the most famous is the nonlinear energy sink (NES), which, in its original design, consists of a small mass attached to the primary system through a damper and an essentially nonlinear spring [22, 23]. Possessing a nonlinear restoring force, the NES is able to interact with the primary structure virtually at any frequency [24,25,26]. Similarly, vibro-impact [27, 28], visco-hysteretic [29], rotational [30, 31], bistable [32,33,34] and other variants of vibration absorbers [35] exploit analogous phenomena, obtaining a broadband energy dissipation. Most of these vibration absorbers share the drawback that their performance strongly depends on the energy level of the system. In general, for low energy level they experience a drop in efficiency (although some of the mentioned vibration absorbers partially overcome this limitation [31, 34]).

Another approach to address the variation of the natural frequency of a primary system was recently proposed in [36, 37]. Instead of generally enlarging the frequency band of operation, the restoring force of the absorber should be designed such that a modal interaction between the primary system and the absorber is triggered both in the linear and in the nonlinear domain. This is obtained adopting the so-called principle of similarity [38], which consists in using for the absorber restoring force equations similar to those of the primary system. In some sense, this represents a nonlinear extension of Den Hartog’s original equal-peak rule. Based on this principle, an analytical tuning for this vibration absorber, termed the nonlinear tuned vibration absorber (NLTVA), was obtained in [38]. Its performance and robustness were investigated via bifurcation tracking in [39], and it was studied adopting a different analytical method in [40]. It was later applied for the suppression of self-excited oscillations in [41]. Addressing specific engineering problems, it was applied for flutter suppression in a pitch and plunge aeroelastic model [42] and chatter mitigation in turning machining [43]. NLTVA performance’s were improved by the addition of a properly designed fifth-order nonlinearity in [44], by suppressing a detrimental detached resonance curve previously observed [39]. A series of experimental validations were performed by different research groups, exploiting a 3D-printed doubly-clamped beam [45, 46], movable magnets [47, 48] or geometrical nonlinearities [49]. The same idea was extended to passive piezoelectric vibration absorbers, first theoretically [50] and then experimentally [51]. Recently, it was proposed to couple the NLTVA with an energy harvester [52].

Despite the significant number of studies about NLTVA, its performance for the suppression of impulsive excitations was only partially investigated [48]. The main objective of this study is to fill this gap. As better detailed in Sect. 2, the system under study consists of an undamped hardening Duffing oscillator, coupled to a light mass through a linear damper, a linear and a cubic spring. Imposing an initial displacement to the system, the ability of the light attachment to rapidly dissipate energy is numerically evaluated in Sect. 3. Then, in Sect. 4, adopting an analytical procedure which combines harmonic balance with a straightforward expansion [53], the so-called slow invariant manifolds of the system are identified, providing further insight into the transient dynamics of the system. Finally, in Sect. 5 a parametric analysis is performed in order to define the optimal tuning of the absorber parameters.

2 Governing equations

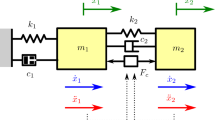
We model the primary structure as an undamped single degree-of-freedom (DoF) Duffing oscillator, possessing a linear and cubic elastic force characteristic (Fig. 1). The primary structure has an attached NLTVA, also possessing a linear and cubic elastic force characteristic, according to the design proposed in [37,38,39]. The system dynamics is governed by the following equations of motion

$$\begin{aligned}&m_1x''_{1}+k_1x_1+k_{nl1}x_1^3+c_2\left( x'_{1}-x'_{2}\right) \nonumber \\&\quad +k_2\left( x_1-x_2\right) +k_{nl2}\left( x_1-x_2\right) ^3=0\nonumber \\&m_2x''_{2}+c_2\left( x'_{2}-x'_{1}\right) +k_2\left( x_2-x_1\right) \nonumber \\&\quad +k_{nl2}\left( x_2-x_1\right) ^3=0, \end{aligned}$$
(1)

where prime \('\) indicates differentiation with respect to time t, \(m_1\) and \(m_2\) are the masses of the primary system and of the absorber, respectively, \(k_1\) and \(k_2\) are the linear elastic coefficients of the primary system and of the absorber, respectively, \(k_{nl1}\) and \(k_{nl2}\) are the cubic elastic coefficients of the primary system and of the absorber, respectively, and \(c_2\) is the absorber linear damping coefficient. Addressing practical constraints, we assume \(m_2\ll m_1\). All coefficients are assumed non-negative (which implies that nonlinearities are of hardening type). The objective of the absorber is to minimize the dissipation time of the vibration energy in the primary system.

Fig. 1
figure 1

Mechanical model

Full size image

Adopting a standard non-dimensionalization procedure, we reduce the system to

$$\begin{aligned}&\ddot{y}_{1}+y_1+y_1^3+\varepsilon \left( 2\zeta _2\left( \dot{y}_{1}-\dot{y}_{2}\right) +\lambda ^2\left( y_1-y_2\right) \right. \nonumber \\&\quad +\left. \delta \left( y_1-y_2\right) ^3\right) =0\nonumber \\&\ddot{y}_{2}+2\zeta _2\left( \dot{y}_{2}-\dot{y}_{1}\right) +\lambda ^2\left( y_2-y_1\right) +\delta \left( y_2-y_1\right) ^3=0, \end{aligned}$$
(2)

where over-dot indicates derivation with respect to the dimensionless time \(\tau =\sqrt{k_1/m_1}t\), \(\varepsilon =m_2/m_1\) is the mass ratio, \(\lambda ^2=k_2m_1/(m_2k_1)\) is the natural frequency ratio, \(\zeta _2=c_2/\sqrt{4m_2k_1\varepsilon }\) is the absorber’s relative damping, \(\delta =k_{nl2}/(\varepsilon k_{nl1})\) is the cubic stiffness ratio, \(y_1=x_1\sqrt{k_{nl1}/k_1}\) and \(y_2=x_2\sqrt{k_{nl1}/k_1}\) are the dimensionless displacement of the primary system and of the absorber, respectively.

3 Preliminary numerical analysis

In order to rapidly provide a general picture of the system behavior, we perform a series of numerical simulations of the system, aiming at identifying the optimal absorber parameters. Optimization is performed with respect to the minimal time required to dissipate 70% of the initial energy of the system. Although this value is chosen arbitrarily, as it will be shown later, the choice of the percentage of energy to be dissipated has limited impact on the results obtained.

3.1 Linear optimization

As a first step, we analyze the underlying linear system and identify the optimal natural frequency ratio \(\lambda \) and damping ratio \(\zeta _2\) of the absorber, for various values of the mass ratio \(\varepsilon \). Therefore, nonlinear stiffness coefficients \(k_{nl1}\) and \(k_{nl2}\) are fixed to zero, making the system linear. Initial conditions are fixed at \(y_1(0)=y_2(0)=1\), \(\dot{y}_2(0)=\dot{y}_2(0)=0\) (amplitude is not relevant, since the system is linear at this stage). Extensive numerical simulations provided the results depicted by the black lines in Fig. 2. They show that optimal \(\lambda \) values are close to 1 and slowly decrease for increasing mass ratio \(\varepsilon \), damping ratio \(\zeta _2\) has an opposite trend, increasing with \(\varepsilon \), while the dissipation time (time required to dissipate 70% of the system initial energy) decreases for increasing mass ratio. These results are not surprising, since they qualitatively match with the optimal parameter values obtained analytically in [54] (although computed for nonzero initial velocity and zero initial displacement). These are depicted by blue dashed lines in Fig. 2. Even though the optimal natural frequency ratio and damping value are not exactly the same for the two cases (Fig. 2a, b), Fig. 2c illustrates that the dissipation time is practically identical. In Fig. 2c, both curves refer to the same initial conditions with nonzero displacement and zero velocity.

Fig. 2
figure 2

Optimal values of \(\lambda \) (a) and \(\zeta _2\) (b) calculated for each \(\varepsilon \); c dissipation time corresponding to optimal \(\lambda \) and \(\zeta _2\) values. Initial conditions are \(y_1(0)=y_2(0)=1\), \(\dot{y}_1(0)=\dot{y}_2(0)=0\). Blue dashed lines refer to the tuning rule given in [54]

Full size image
Fig. 3
figure 3

Dissipation time for various \(\delta \) values and initial conditions; \(\varepsilon =0.02\), \(\lambda =0.98\), \(\zeta _2=0.15\), \(\dot{y}_1(0)=\dot{y}_2(0)=0\), \(y_1(0)=y_2(0)=y_0\). a and b provide two different views of the same diagram

Full size image

3.2 Nonlinear optimization

We now perform a numerical analysis of the system behavior in the nonlinear regime. The term \(y_1^3\) is reinstated in the system and mass ratio \(\varepsilon \) is fixed at 0.02. \(\zeta _2\) is fixed at 0.15, that is a larger value than the one obtained from linear optimization, utilized because it gives more robustness to the absorber, as it will be shown in Sect. 5. Conversely, \(\lambda \) is set at 0.98, according to the value obtained from the linear optimization. In fact, a relatively accurate tuning of \(\lambda \) is required in order to make the absorber work properly in a large amplitude range, going continuously from linear to strongly nonlinear regime.

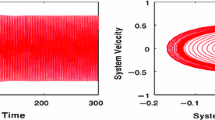
A series of direct numerical simulations provided the results illustrated in Fig. 3, which depicts the dissipation time for various \(\delta \) values and initial conditions. As expected, for low initial energy, the effect of \(\delta \) is practically negligible, since the system is in the linear domain. Figure 4a illustrates a time series for initial displacement \(y_1(0)=y_2(0)=1\) and \(\delta =0.03\). The figure clearly shows that energy is rapidly dissipated, despite the relatively small value of \(\delta \).

Fig. 4
figure 4

Time series for parameter values \(\varepsilon =0.02\), \(\lambda =0.98\), \(\zeta _2=0.15\), \(\delta =0.03\) (a, b) and 0.1 (c), initial conditions \(y_1(0)=y_2(0)=1\), \(\dot{y}_1(0)=\dot{y}_2(0)=0\) (a) and \(y_1(0)=y_2(0)=5\), \(\dot{y}_1(0)=\dot{y}_2(0)=0\) (b, c)

Full size image

For higher values of the initial displacement, the system has higher initial energy and nonlinearities become dominant over the system dynamics. Figure 3 shows that, in this case, the value of \(\delta \) is critical for the system behavior. In particular, it seems that for \(\delta \approx 0.093\) there is a complete change of the absorber performance, corresponding to a jump in dissipation time from about 90 to 15 time units. Figure 4b, c depicts time series for \(y_1(0)=y_2(0)=5\) and \(\delta =0.03\) and 0.1, respectively. A comparison of the two time series illustrates the different behavior of the absorber in the two cases. For \(\delta =0.03\), the \(y_1-y_2\) amplitude (that is the quantity responsible for the energy dissipation) is much smaller than for \(\delta =0.1\), which is clearly related to the different dissipation energy performance. The abrupt change of behavior suggests that a qualitative difference exists between the two cases. However, time simulations do not shed light on the mechanism leading to this difference.

The dashed line in Fig. 3b indicates the optimal \(\delta \) value for the case of forced oscillations of this system, as identified numerically and analytically in [37, 38]. It is remarkable that this value (given by the function \(k_{nl2}=k_{nl1}2\varepsilon ^2/(1+3.5\varepsilon )\) for the case of cubic nonlinearity [38]) lies deeply inside the region with poor performance, which means that the NLTVA requires much stronger nonlinearity if it is employed for impulsive vibration rather than for forced vibration mitigation. However, we notice that in [37, 38] moderate levels of nonlinearity are considered, while in this work we refer to highly nonlinear systems (natural frequency shift of the primary system is more than 100% larger than its value in the linear regime).

4 Analytical investigation of the transient dynamics

Considering the unclear scenario provided by the numerical analysis performed, an analytical investigation of the system dynamics seems necessary to provide a better understanding of the system behavior.

The only term related to the dissipation of energy in the system is \(2\varepsilon \zeta _2\left( \dot{y}_1-\dot{y}_2\right) \), which is proportional to the difference of the velocity between the primary system and the absorber. It is therefore convenient to operate the change of variable \(z=y_1-y_2\), which transforms the equations of motion in

$$\begin{aligned} \ddot{y}_{1}+y_1+y_1^3+\varepsilon \left( 2\zeta _2\dot{z}+\lambda ^2 z+\delta z^3\right)&=0\nonumber \\ \varepsilon \left( \ddot{z}-\ddot{y}_1+2\zeta _2 \dot{z}+\lambda ^2 z+\delta z^3\right)&=0. \end{aligned}$$
(3)

Exploiting the assumption that \(\varepsilon \ll 1\) and with the objective of studying the slow dynamics of the system, we neglect terms of order \(\varepsilon ^1\) or higher, reducing the equations of motion to

$$\begin{aligned}&\ddot{y}_{1}+y_1+y_1^3 \approx 0\nonumber \\&\ddot{z}-\ddot{y}_1+2\zeta _2 \dot{z}+\lambda ^2 z+\delta z^3 =0. \end{aligned}$$
(4)

The first equation of (4), which is independent of the second one, is an undamped unforced Duffing oscillator, while the second one is a damped Duffing oscillator, forced by the term \(-\ddot{y}_1\). Therefore, we expect that its solution is periodic, with frequency and superharmonic content increasing for growing amplitude of oscillation (which depends uniquely on the initial conditions). Obviously, the original system in Eq. (3) has no periodic solution and for \(t\rightarrow \infty \) it always tends to 0 (unless \(\zeta _2=0\) or \(\varepsilon =0\)). However, dissipation terms of the first equation of (3) are of order \(\varepsilon \), therefore they are not caught by a first-order approximation.

Initially, we solve the first equation of (4). Although its exact solution can be found adopting elliptic functions [55], according to the hypothesis that the majority of the energy is dissipated by a 1:1 resonance, it is more practical to identify a single harmonic approximate solution. We approximate its solution by

$$\begin{aligned} y_1\approx Ae^{i\omega t}+\bar{A}e^{-i\omega t}, \end{aligned}$$
(5)

where A is a complex variable and the overbar indicates complex conjugate. Inserting Eq. (5) into Eq. (4a) and dropping terms related to higher harmonics we obtain

$$\begin{aligned} -\omega ^2A+A+3A^2\bar{A}+\text {c.c.}=0, \end{aligned}$$
(6)

where c.c. indicates complex conjugate terms. Defining A as

$$\begin{aligned} A=\frac{1}{2}ae^{i\alpha }, \end{aligned}$$
(7)

where a and \(\alpha \) are real variables, we obtain

$$\begin{aligned} -\omega ^2+1+\frac{3}{4}a^2=0\quad \Rightarrow \quad \omega =\sqrt{1+\frac{3}{4}a^2}, \end{aligned}$$
(8)

which indicates the variation of the system vibration frequency with respect to its amplitude.

We now insert the approximate solution of Eq. (4a) into Eq. (4b) and approximate its solution by

$$\begin{aligned} z=Be^{i\omega t}+\bar{B}e^{-i\omega t}, \end{aligned}$$
(9)

where \(B=1/2be^{i\beta }\). Neglecting harmonic terms higher than the first order, we attain

$$\begin{aligned} -\omega ^2B+\omega ^2A+i2\zeta _2\omega B+\lambda ^2B+3\delta B^2\bar{B}+\text {c.c.}=0 \end{aligned}$$
(10)

or

$$\begin{aligned}&-\frac{1}{2}\omega ^2be^{i\beta }+\frac{1}{2}\omega ^2ae^{i\alpha }+i\zeta _2 b\omega e^{i\beta }+\frac{1}{2}\lambda ^2be^{i\beta }\nonumber \\&\quad +\frac{3}{8}\delta b^3e^{i\beta }+\text {c.c.}=0. \end{aligned}$$
(11)

Separating real and imaginary parts we have

$$\begin{aligned} -\omega ^2a\cos \alpha&=\left( -\omega ^2+\lambda ^2+\frac{3}{4}\delta b^2\right) b\cos \beta \nonumber \\&\quad -2\zeta _2 b\omega \sin \beta \nonumber \\ -\omega ^2a\sin \alpha&=\left( -\omega ^2+\lambda ^2+\frac{3}{4}\delta b^2\right) b\sin \beta \nonumber \\&\quad +2\zeta _2 b\omega \cos \beta . \end{aligned}$$
(12)

We then sum up the squares of these two equations obtaining

$$\begin{aligned} \omega ^4a^2=b^2\left( \lambda ^2-\omega ^2+\frac{3}{4}\delta b^2\right) ^2+4\zeta _2^2b^2 \omega ^2. \end{aligned}$$
(13)

Recalling the dependence of \(\omega \) on a expressed in Eq. (8), we impose \(\omega ^2=1+3/4a^2\), obtaining an equation of the third order in \(a^2\), which can therefore be easily solved in closed form with computer algebra. Its solutions are

$$\begin{aligned} a_1=&\left( \frac{1}{18} \left( 6 b^2-\frac{2 \root 3 \of {2} \left( 9 b^4 (6 \delta -1)+24 b^2 \left( 3 \lambda ^2-6 \zeta _2^2-1\right) -16\right) }{\chi _1}+2^{2/3} \chi _1-16\right) \right) ^{1/2}\nonumber \\ a_2=&\Bigg (\frac{1}{324} \Bigg (36 \left( 3 b^2-8\right) +\frac{18 \root 3 \of {2} \left( 1+i \sqrt{3}\right) \left( 9 b^4 (6 \delta -1)+24 b^2 \left( 3 \lambda ^2-6 \zeta _2^2-1\right) -16\right) }{\chi _1}+9\ 2^{2/3} i \left( \sqrt{3}+i\right) \chi _1\Bigg )\Bigg )^{1/2}\nonumber \\ a_3=&\Bigg (\frac{1}{324} \Bigg (36 \left( 3 b^2-8\right) +\frac{18 \root 3 \of {2} \left( 1-i \sqrt{3}\right) \left( 9 b^4 (6 \delta -1)+24 b^2 \left( 3 \lambda ^2-6 \zeta _2^2-1\right) -16\right) }{\chi _1}-9\ 2^{2/3} \left( 1+i \sqrt{3}\right) \chi _1\Bigg )\Bigg )^{1/2}, \end{aligned}$$
(14)

where

$$\begin{aligned} \chi _1=&\Big (128 + 27 b^6 \left( 2 - 18 \delta + 27 \delta ^2\right) \nonumber \\&\quad + 216 b^4 \left( 1 - 3 \lambda ^2 + \delta (-3 + 9 \lambda ^2) + 6 \zeta _2^2\right) \nonumber \\&\quad +144 b^2 \left( 2 - 6 \lambda ^2 + 9 \lambda ^4 + 12 \zeta _2^2\right) + \chi _2\Big )^{1/3} \end{aligned}$$
(15)

and

$$\begin{aligned} \chi _2=&\Big (4 \left( 9 b^4 (6 \delta -1)+24 b^2 \left( 3 \lambda ^2-6 \zeta _2^2-1\right) -16\right) ^3\nonumber \\&+\Big (27 b^6 \left( 27 \delta ^2-18 \delta +2\right) \nonumber \\&\quad +216 b^4 \left( \delta \left( 9 \lambda ^2-3\right) -3 \lambda ^2+6 \zeta _2^2+1\right) \nonumber \\&\quad +144 b^2 \left( 9 \lambda ^4-6 \lambda ^2+12 \zeta _2^2+2\right) +128\Big )^2\Big )^{1/2}. \end{aligned}$$
(16)
Fig. 5
figure 5

Slow invariant manifolds for \(\lambda =0.98\), \(\zeta _2=0.15\) and \(\delta \) as indicated in the different plots. Black lines refer to the results obtained analytically, while the red dots are obtained from numerical simulations

Full size image

Figure 5 illustrates the variations of a as a function of b for \(\lambda =0.98\), \(\zeta _2=0.15\) and various \(\delta \) values (ratio between the absorber and the primary system nonlinear stiffness coefficients), according to Eq. (14) (black solid lines). The curves depicted in the figure are usually referred to as slow invariant manifolds (SIMs) of the system and they describe its slow dynamics. For each value of a, which represents the amplitude of the primary system oscillation, at least one value of b, representing the difference of amplitude between the primary system and the absorber, is given. Considering that the energy dissipated is proportional to oscillation amplitude b, the SIMs give clear indications about the absorber performance: the larger is b, the faster is the energy dissipation.

For variations of \(\delta \), Fig. 5 shows interesting variations of the manifold. For \(\delta <0.0530\), there is one lower branch for any a value, on top of which a folded branch exists and descends as \(\delta \) increases. The lower branch corresponds to a locus of stable solutions, while the topper one corresponds to couples of stable and unstable solutions. For \(\delta =0.0530\), the two branches intersect with each other and for \(\delta >0.0530\) a folded branch lays below the straight one. The intersection of the two branches corresponds to a simple bifurcation according to the classical nomenclature adopted in singularity theory [56]. The \(\delta \) value for which they intersect can be easily found analytically, by computing the derivative of Eq. (13) with respect to a and b and equating them to zero [44, 56]. Although the expression indicating \(\delta \) at the intersection point is too long to be written here, its value for \(\lambda =0.98\), \(\zeta _2=0.15\) is \(\delta =0.05299\), as illustrated in Fig. 5d.

The red dots in Fig. 5 indicate instantaneous vibration amplitudes obtained from direct numerical simulations of the full system, by collecting the amplitude vibration peaks of \(y_1\) and of \(y_1-y_2\). In particular, the dots in Fig. 5b, f refer to time series in Fig. 4b, c, respectively. After a short transient, the red dots quite precisely overlap the manifold (black lines); this confirms the accuracy of the analytical procedure.

Considering the manifold structure, we suppose that the absorber has good behavior if it reaches the topper attractor. On the contrary, if the system converges to the lower attractor, much worst performance is awaited. Accordingly, we expect that for \(\delta <0.093\) (see Fig. 3), the lower attractor is reached and the topper one for \(\delta >0.093\). This is confirmed by the red dots shown in Fig. 5, only in Fig. 5f the dots lie on the top branch.

Fig. 6
figure 6

a Frequency response of z variable referring to Eq. (4); corresponding SIM; parameter values \(\lambda =0.98\), \(\zeta _2=0.15\) and \(\delta =0.03\)

Full size image

The main idea of the procedure to obtain the SIM is graphically explained in Fig. 6. Figure 6a illustrates the frequency response of the z variable (limited to the first harmonic) with respect to the second equation of (4), for different values of the excitation amplitude \(y_1\) (or a). The excitation amplitude corresponds to the vibration amplitude of the primary system. For each value of a, only a specific frequency should be considered, as expressed by Eq. (8). This means that specific points of the frequency response curve should be selected, as those marked by red dots in Fig. 6a. These points are already part of the SIM, but in the \(\omega ,b\) space. To bring the manifold in the a, b space, the \(\omega (a)\) relation of Eq. (8) should be considered again, which will lead us to the SIM depicted in Fig. 6b. This graphical representation may help to understand the reshaping of the manifold illustrated in Fig. 5.

Besides vibration amplitude, the computed manifold can be directly used to estimate the absorber dissipation power. In fact, instantaneous dissipation power is given by \(P_i=2\varepsilon \zeta _2\dot{z}^2\), which, averaged over one period and considering that \(z\approx z_0\cos (\omega \tau )\), gives \(P=\varepsilon \zeta _2\omega ^2z_0^2\). According to the used formalism, this quantity is approximated by \(P\approx \varepsilon \zeta _2\omega ^2b^2\). Considering Eq. (14), dissipation power can be easily plotted as a function of the primary system vibration amplitude a, as illustrated in Fig. 7 for the case of \(\varepsilon =0.02\), \(\lambda =0.98\), \(\zeta _2=0.15\) and \(\delta =0.03\), 0.08 and 0.1. In the figure, the black lines refer to the analytical results, while the red dots are obtained from direct numerical simulations. The good matching between the two confirms the validity of the procedure and the predictive character of the analytical development.

Fig. 7
figure 7

Absorber dissipation power for \(\lambda =0.98\), \(\zeta _2=0.15\) and \(\delta \) as indicated in the different plots. Black lines refer to the results obtained analytically, while the red dots are obtained from numerical simulations

Full size image

Despite the good agreement between analytical and numerical results, both analyses are unable to explain the critical \(\delta \) value, separating good and poor performance, which is instead related to the basins of attractions of the two branches of solutions, as it will be shown later. Furthermore, although the topology of the manifold exhibits a bifurcation at a specific \(\delta \) value (\(\delta =0.0529863\)), this seems to be irrelevant with respect to the absorber performance.

4.1 Basins of attraction of transient dynamics

The system in Eq. (2) has only the trivial steady-state solution, it is therefore meaningless to talk about basins of attraction of the solution of the system (which includes all possible initial conditions). However, neglecting terms of order \(\varepsilon ^1\) or higher  [Eq. (4)], the system does not converge to zero, but it rather has periodic steady-state solutions, which are approximated by the manifold discussed above. Therefore, studying the basins of attraction of these periodic solutions allows us to estimate in which conditions the system converges to the topper or to the lower manifold branch. Indeed, this is directly related to the performance of the absorber and indicates the dynamic path the system undertakes to reach the zero.

Basins of attraction are computed performing direct numerical simulations of the system in Eq. (4), imposing initial conditions \(y_1(0)=5\), \(\dot{y}_1(0)=0\) and for varying z(0) and \(\dot{z}(0)\). Parameter values are fixed at \(\lambda =0.98\) and \(\zeta _2=0.15\), while several values of \(\delta \) are considered. We notice that Eq. (4) (and so the basins of attraction obtained) does not depend on \(\varepsilon \). For each \(\delta \) value, 500\(\times \)500 simulations were performed.

Results of the computation are presented in Fig. 8. Black areas refer to the lower attractor (bad dissipation performance), while white areas to the topper (good dissipation performance). The red dot in the center of each plot indicates initial conditions utilized in Figs. 3 (for \(y_0=5\)) and 4b, c. Figure 8a illustrates that, for \(\delta =0.01\), for the whole considered domain the system converges to the lower manifold branch. For \(\delta =0.03\) (Fig. 8b) some white areas are already visible. Increasing further the value of \(\delta \), it can be recognized how the black region shrinks, meaning that the lower manifold branch robustness decreases. However, for \(\delta =0.08\) (Fig. 8d) the center is still in the black area, which explains the poor performance obtained for this \(\delta \) value according to Fig. 3. Figure 8e shows that for \(\delta =0.1\) the red dot is finally in the white area, which corresponds to good absorber performance. This confirms the results shown in Figs. 4c and 5f. Higher values of \(\delta \) further reduce the extension of the black area until it finally disappears for \(\delta =0.14\) (not shown here).

Fig. 8
figure 8

Basins of attraction in the \(z(0),\dot{z}(0)\) space, for Eq. (4) with parameter values \(\lambda =0.98\) and \(\zeta _2=0.15\) (\(\delta \) indicated in the plots). Initial conditions \(y_1(0)=5\) and \(\dot{y}_1(0)=0\). Black: bottom attractor; white: top attractor

Full size image

The scenario just discussed explains the sharp edge separating good and poor behavior of Fig. 3. However, it also illustrates that having a \(\delta \) value larger than 0.093 does not necessarily mean that the absorber will work efficiently, neither that having a smaller \(\delta \) value will surely provide poor performance, in fact, z(0) and \(\dot{z}(0)\) are not necessarily zero, but they may vary even significantly. Besides, the basins of attraction shown here refer to specific initial conditions of the primary system, which consist in an initial displacement and zero velocity, while in real cases they are a combination of the two. A full analysis of the basins of attraction requires to start numerical simulations on a four-dimensional grid of values, which involves a high computational cost and it is therefore out of the scope of this paper. Nevertheless, these results suggest that the efficiency of the absorber, in a real application, should have a probabilistic basis, that is, for a specific set of admissible initial conditions, the probability of obtaining poor or good performance should be evaluated.

With respect to the low predictability of the system behavior, it is emblematic the fuzzy structure exhibited by Fig. 3, approximately for \(\delta \in (0.055,0.093)\) and \(y_0>7.5\). This is directly related to the fractal shape that the basin of attraction of the manifold solutions assumes in this area. This is clearly illustrated in Fig. 9a for \(\delta =0.077\) and \(y_1(0)=9\). Such a structure makes it practically impossible to predict the performance of the system, which can have very different behavior even for two very close initial conditions. Figure 9b, c depicts the time series obtained for the same parameter values and initial conditions \(\mathbf {y}(0)=\left[ y_1(0),\dot{y}_1(0),z(0),\dot{z}(0)\right] =[9,0,0,-0.7]\) and \(\mathbf {y}(0)=[9,0,0,-0.8]\), respectively. While in the first case a lot of time is required to dissipate energy, in the second one the dissipation is much faster.

Fig. 9
figure 9

a Basin of attraction for \(\lambda =0.98\), \(\zeta _2=0.15\), \(\delta =0.077\), \(y_1(0)=9\) and \(\dot{y}_1(0)=0\). b, c Time series for the same parameter values and \(z(0)=0\), \(\dot{z}(0)=-0.7\) (b) and \(\dot{z}(0)=-0.8\) (c)

Full size image

For the sake of completeness, we notice that in Fig. 3 there are some areas, within the region of poor performance, where the absorber behaves slightly better, such as for \(\delta \approx 0.025\) and \(y_0>6\). The different behavior is due to superharmonic resonances, which improve the performance of the absorber. This is shown in Fig. 10, where the time series and the corresponding wavelet transformation illustrate that the absorber has a 3:1 resonance with the primary system. As far as the superharmonic resonance persists (\(\tau \approx 150\)), the performance of the absorber is enhanced. This phenomenon cannot be captured by the analytical framework adopted, since only one harmonic is taken into account.

Fig. 10
figure 10

Time series (a) for \(\lambda =0.98\), \(\zeta _2=0.15\), \(\delta =0.025\), \(\mathbf {y}(0)=[8,0,0,0]\) and corresponding wavelet transformations (b)

Full size image

5 Parametric analysis with respect to absorber performance

In the previous section, the analysis of the NLTVA in the nonlinear domain was performed for fixed values of \(\lambda \), \(\zeta _2\) and \(\varepsilon \). In this section, we partially investigate the effect of variations of those parameters on the system dynamics. Furthermore, in order to verify if the results obtained have a general validity, we analyze the effect of introducing a small damping in the primary system or changing the threshold of energy dissipated, fixed at 70% in the rest of the paper.

Fig. 11
figure 11

Dissipation time calculated for various parameter values. Unless indicated in the different subplots, parameter values are \(\lambda =0.98\), \(\zeta _2=0.15\) and \(\varepsilon =0.02\) and initial conditions \(\mathbf {y}(0)=\left[ y_0,0,0,0\right] \)

Full size image

5.1 Variations of mass and natural frequency ratios

The parametric analysis consists in performing numerical simulations for various \(\delta \) values and initial conditions, as in Fig. 3, varying either the mass ratio \(\varepsilon \), the natural frequency ratio \(\lambda \) or the absorber damping ratio \(\zeta _2\).

Fig. 12
figure 12

Invariant manifolds for \(\delta =0.1\) and \(\zeta _2=0.15\); \(\lambda =0.5\), 1 and 1.5, as indicated in the subplots. Black lines and red dots refer to analytical and numerical results, respectively

Full size image

Figure 11a illustrates dissipation times for mass ratios \(\varepsilon =0.01\), 0.02, 0.03 and 0.04, for \(\lambda =0.98\) and \(\zeta _2=0.15\). It can be immediately recognized that increasing the mass ratio the dissipation time is reduced. This result is not surprising and corresponds to what, in general, happens with dynamic vibration absorbers of any kind, that is a larger mass of the absorber enhances performance. Furthermore, Fig. 11a shows that the \(\delta \) value separating good and poor performance does not change significantly for variations of \(\varepsilon \). This means that the basins of attraction, depicted in Fig. 8 for \(\varepsilon =0\), would not significantly change if \(\varepsilon \ne 0\) (for \(\varepsilon \ne 0\), they are understood as attractors of a transient solution, which is not mathematically rigorous, but engineering meaningful). Figure 11a also illustrates that, for large \(\varepsilon \) values, \(\delta \) becomes much less relevant with respect to the system performance, which suggests that, in real applications, if it is possible to use a relatively large mass it is not very important to perform a fine tuning. With respect to the analytical results carried out in the previous section, we notice that the SIMs were obtained assuming a small value of \(\varepsilon \) and they are independent of the actual \(\varepsilon \) value. Therefore, that analysis cannot be used to investigate the effect of variations of \(\varepsilon \).

Figure 11b illustrates dissipation times for \(\lambda =0\), 0.5, 1 and 1.5, while \(\zeta _2=0.15\) and \(\varepsilon =0.02\). The case of \(\lambda =1\), which practically gives identical results as for \(\lambda =0.98\) in Fig. 3, is the only one which exhibits good performance at low amplitude. This was expected, considering that at low amplitude the primary system is practically linear and the absorber behaves like a TMD. Therefore, detuning \(\lambda \) makes the absorber lose modal interaction. Comparing the cases of \(\lambda =0.5\) and \(\lambda =1.5\), it can be noticed that the increase in the natural frequency ratio is more detrimental than its decrease. For \(\lambda =0\), the absorber is practically an NES and it presents the well-known energy threshold, below which its performance is poor. For large amplitudes, the effect of variation of \(\lambda \) is negligible, since the cubic stiffness term is much larger than the linear one. Overall, Fig. 11b clearly illustrates that, in order to have an absorber able to work in a wide energy range (starting from low energy), it is necessary to properly tune both the linear and the nonlinear stiffness coefficients, \(\lambda \) and \(\delta \). While mistuning \(\delta \) might cause poor performance at high energy levels, mistuning \(\lambda \) deteriorates performance at low energy.

The scenario just described could be predicted through the SIMs. In Fig. 12, the SIMs are depicted for \(\lambda =0.5\), 1 and 1.5. Despite the topology of the manifolds is not the same in the three cases, at large amplitude (for instance at \(a=5\)) the top branches of the three manifolds have more or less the same b values (18.1, 17.9 and 17.5, respectively), which means that they provide similar dissipation power. At low amplitude, for instance at \(a=0.5\), the b value in the three cases are 0.61, 1.8 and 0.52. Since dissipation power is proportional to the square of b (it can be easily proven that \(P\approx \varepsilon \zeta _2\omega ^2b^2\)), this implies that in the case of \(\lambda =1\) dissipation power is approximately 8.7 times larger than for \(\lambda =0.5\) and 12 times larger than for \(\lambda =1.5\). The red dots in Fig. 12 confirm the predictive character of the SIMs.

Fig. 13
figure 13

Invariant manifolds and dissipation power for \(\lambda =0.98\), \(\delta =0.1\) and \(\zeta _2=0.4\) and 0.8, as indicated in the different plots. Black lines refer to the results obtained analytically, while the red dots are obtained from numerical simulations

Full size image

5.2 Variations of absorber damping

Figure 11c depicts the dissipation time for \(\lambda =0.98\), \(\varepsilon =0.02\) and \(\zeta _2=0.05\), 0.1, 0.15 and 0.2. Interestingly, the figure suggests that, in the nonlinear regime, the larger is the damping, the fastest is the energy dissipation, with no apparent limitation within the range considered (other numerical simulations, not presented here, showed that this is valid also for larger \(\zeta _2\) values, up to \(\zeta _2\approx 1\)). This is in contrast with what happens in the case of linear absorbers for linear primary systems, where increasing damping ratio above a certain optimum value, performance decreases.

This effect can be explained considering that dissipation power is linearly proportional to damping ratio and quadratically to the oscillation amplitude of the absorber (with respect to the primary system). Linear vibration absorbers rely on the fact that the absorber is at resonance during optimal behavior. For a linear system near resonance, vibration amplitude decreases almost linearly with the damping ratio, therefore, in general, increasing damping dissipation power decreases, until an optimum is reached for a relatively low damping value. Of course, a minimal damping ratio value is required to have dissipation, but in general it should be small.

In the case under study (at large amplitude), the scenario is very different. As illustrated in Fig. 6a, the points of the manifold (in red) do not correspond to resonances. Far from resonance, increasing damping ratio causes only small amplitude reduction (sometimes it even increases oscillation amplitude), therefore, it is convenient to increase damping in order to increase the dissipation power.

This phenomenon can be explained through the invariant manifolds. These are plotted for \(\zeta _2=0.4\) and 0.8 in Fig. 13. Figure 13a, b shows that the lower branch of the manifold is practically identical, although the damping ratio is doubled. On the contrary, dissipation power is significantly increased for larger damping, as it can be noticed from Fig 13c, d. Dissipation time for the two cases is 37.9 and 24.9 time units, respectively.

Another effect of variations of the damping ratio is that, increasing damping, the value of \(\delta \) marking the transition between poor and good performance increases as well (this is hardly recognizable from the figure, because of the prospective adopted). This can be explained considering that, for lower damping, the absorber undergoes larger oscillations further activating nonlinearities.

Fig. 14
figure 14

Dissipation time for various values of \(\delta \) and initial oscillation amplitude \(y_0\). Parameter values are \(\lambda =0.98\) and \(\zeta _2=0.15\). a The primary system has a relative damping of 0.02, b, c dissipation time corresponds to dissipation of 90 and 30% of initial energy, respectively

Full size image

5.3 Damped primary system or different energy threshold

All the analysis carried out in the paper refers to an undamped primary system. Although this assumption is clearly not realistic, it is justified by the fact that vibration absorbers are implemented in lightly damped systems and neglecting a small damping term is usually conservative for vibration mitigation purposes [30, 57]. Nevertheless, it is worth verifying, at least numerically, the validity of this assumption. Figure 14a depicts the dissipation time for various initial amplitude \(y_0\) and \(\delta \), other parameter values are \(\lambda =0.98\) and \(\zeta _2=0.15\). In the primary system a linear damping term is included, having relative damping ratio 0.02. Practically, Fig. 14a is analogous to Fig. 3, except for the additional damping term of the primary system.

Comparing the two figures, it can be recognized that the main features are still present: poor absorber performance for high initial amplitude and low \(\delta \) values, which suddenly improves for a specific value of \(\delta \) (that is practically unchanged). Further increase of \(\delta \) slowly reduces system performance. The main quantitative difference between the two figures is observed in the region of poor behavior, where dissipation time has only a moderate increase. This is clearly due to the fact that, even if the absorber is ineffective, the linear damping of the primary system still dissipates energy. Indeed, the primary system without absorber and with 0.02 relative damping has a dissipation time of 23 time units, only slightly larger than the worst case of Fig. 14a.

Figure14b, c depicts dissipation time for the same conditions of Fig. 3, but counting the dissipation time when initial energy is reduced by 90% or 30%, respectively. The three figures are qualitatively and quantitatively very similar, except for the dissipation time, which is obviously different in the three cases. This suggests that the energy percentage for computing dissipation time is not particularly relevant for the analysis. In order to reduce computational time, it might be convenient to use a lower percentage and reduce simulation time.

6 Conclusions

The objective of this study was to analyze the performance of the NLTVA for dissipating impulsive vibrations in a Duffing oscillator. A combination of direct numerical simulations and an analytical approach provided a relatively clear picture of the overall system dynamics and absorber performance. For low amplitudes, when the nonlinearity of the primary system is barely activated, the NLTVA has practically identical performance as the classical TMD. Increasing the energy level of the system, the TMD rapidly becomes unable to provide acceptable performance and the additional nonlinearity of the NLTVA becomes essential for obtaining good performance. Interestingly, our results show that a sharp limit on the value of the absorber nonlinear stiffness coefficient separates good and poor behavior of the absorber. The setting of the nonlinear stiffness below or above that value can change the performance of the absorber of even 700%.

The analytical identification of slow invariant manifolds, describing the slow dynamics of the system, enabled us to explain this behavior, which is related to the coexistence of two dynamical paths (two different branches of the manifolds) which enable either a slow or a fast energy dissipation. The numerical identification of the basins of attraction of these two branches allowed us to explain the existence of the sharp edge characterizing the performance of the absorber, which is strictly related to the initial conditions of the system. This result suggests that, for the design of a similar absorber in a real system, it is necessary to adopt a probabilistic approach with respect to the admissible initial conditions that the system might assume.

A parametric analysis of the system displayed an interesting aspect of the NLTVA, for this specific application. While for most of dynamic vibration absorbers an optimal damping value exists, the results obtained in this work illustrate that, in general, the larger is the damping ratio, the better are the performance of the absorber. Considering the similarity of the NLTVA and the NES at high energy level, most probably this is valid also for the NES.

The majority of the results illustrated in the paper refer to high energy levels and to a strongly nonlinear primary system, which are conditions rarely reached in real applications. Furthermore, we notice that, although the assumption that the primary system is undamped is conservative with respect to the system integrity, it was shown that the introduction of even a small damping into the primary system has non-negligible quantitative effect. These two considerations should be taken into account if the results of this paper are directly used for a real engineering application.