Nonlinear vibrations of a rotating thin-walled composite piezo-beam with circumferentially uniform stiffness (CUS)

Abstract

A rotating system comprising a hub and a thin-walled laminate cantilever beam with embedded nonlinear piezoelectric layers is analysed in the paper. The reinforcing fibres set-up in composite material conforms to circumferentially uniform stiffness lamination scheme. This configuration exhibits the mutual bending couplings in two orthogonal planes. Nonlinear analytical model of a piezoelectric material embedded onto the beam walls is postulated by considering the higher-order constitutive relations with respect to electric field variable. Moreover, to properly model electromechanical structural behaviour, the full two-way coupling piezoelectric effect is considered. To this aim, the assumption of a spanwise electric field variation is postulated in the mathematical model of the structure. Based on previous authors’ research, the system of mutually coupled nonlinear equations of motion is formulated. In the numerical analysis the forced response of the system under zero and nonzero mean value harmonic torque excitation is considered. In particular, the influence of hub inertia, excitation amplitude and mean rotating speed on system dynamics is investigated. The results are presented in the form of appropriate frequency response plots and bifurcation diagrams.

1 Introduction

The continuous development of composite materials offers a great potential for modern structural systems that can take advantage of unique composite material properties as well as material tailoring technology. Historically, this later idea is exploited since late 1980s and relies on proper laminae stacking sequence and orientation of unidirectional (UD) reinforcing fibres. The main objective of this technology is to reduce weight of the structure, improve its stiffness and maintain static strength under compressive loads [10]. Other applications of the material tailoring technology in aerospace industry include the drag reduction [43], gust response [13] and optimum aeroelastic behaviour and flutter characteristics [1]. One of the most prominent demonstrators of this technology was the test programme of the forward swept wing experimental fighter Grummann X-29 [3]. Further progress within the material tailoring technology is the tow-steering technique, where the fibres orientations within a ply follow a predefined curvilinear path; thus the ply stiffness vary continuously through the plane of each ply. It has been demonstrated that these fibre paths can be optimized to increase the structural performance of a laminate beyond that of an equivalent regular UD laminate [26, 32, 38].

Further improvement in system performance and enhancement in its capabilities can be achieved by incorporating multifunctional materials into structural design. This technology offers, along with other concurrent abilities, advantages of active control, sensing, self-healing and thermal functionality of the structure. Typical applications of multifunctional designs range from civil structures, marine systems and automobiles, through machine tools and fine mechanics to aerospace and aeronautics systems and structures. Representative examples of active aerospace designs might be inflatable and deployable space structures such as solar panels or space antennas and mirrors that often undergo large controlled rotations and positioning when expanding from an initially compact configuration to a final geometry [25]. Referring to other aeronautical systems like fixed-wing aircraft, applications cover active control of flutter and handling qualities improvement. In particular, the potential of using piezoceramic transducers to suppress or delay the onset of panel aeroelastic instability has been studied. The conducted research have shown the possibility to increase the flutter speed up to 50% combined with reduction of the power-spectral density of response. Moreover, the potential savings in control effort resulting from optimal positioning of active elements on the wings and ailerons have been confirmed [34]. Further applications areas of piezoceramic materials cover structural health monitoring and interior/exterior noise reduction. The technology of smart material-based SHM sensors enhances the system flight safety and reliability, but also results in savings in operational and maintenance/inspection costs and extends the life cycle of an ageing aircraft [44]. For rotary-wing aircrafts the embedded smart material sensors can be used for rotor tracking and head health monitoring, while active material actuators may induce changes in airfoil shape, which in turn help to control static and dynamic aeroelastic problems [6]. Numerous studies and comprehensive research programs run in recent years have demonstrated the feasibility of piezo-composite materials for a helicopter active rotor design and tilt rotor vehicles. Active twisting of blades with embedded piezoceramic transducers and shape memory alloy actuated tabs and flaps systems have been examined in order to actively control vibration and blade-vortex-induced noise. Results have shown reductions of vibratory loads of about 80%, as well as reductions up to 6 dB in blade-vortex interaction and in-plane noise. Moreover, the impact of the active flap on rotor performance, rotor smoothing, and control power has been demonstrated [4, 33]. Tests performed by Boeing on V-22 tilt rotor aircraft have revealed the potential of active flow control to minimize hover download-lift during takeoff conditions and to improve the payload lift and angle-of-attack capability [4, 11]. When compared to fixed-wing aircraft, helicopters appear to show much higher potential for a major payoff with the application of smart structures technology. The given above numerous examples of piezo-composite beam-like structures confirm the current relevance and timeliness of this subject matter and give a great stimulus and motivation to continue research in this area.

While currently there are many types of active materials available, like shape memory alloys, electrostrictives, and magnetorheological fluids etc. piezoelectric materials remain the most widely used ”smart” ones. This is primarily due to their strong voltage-dependent actuation viability. Secondly, piezoceramics are capable of interacting with dynamic systems at high frequencies ranging up to even 1 MHz. Finally, the crucial feature of piezoceramic materials is their large energy density. Therefore, they can be effectively adapted to, e.g. energy-harvesting devices that can generate high electric potentials or may be used to supply power to wireless sensors and low-power electronics [20].

Composite materials are perfect candidates for implementing the concept of structural functionality because of their multiphase nature, suitable manufacturing technology, low density and inherent directional mechanical properties [6, 28, 39]. Studies on multifunctional structures started in late 1980s/early 1990s from modelling isotropic material systems followed next by the research on piezoelectric laminated composite materials. Smith et al. [31] proposed the constituent equations representing the behaviour of piezoelectric bimorphs for arbitrary mechanical boundary conditions. Weinberg [42] studied the piezoelectric multimorph for sensing and actuation by means of the Euler–Bernoulli beam model. Closed-form solutions for force, displacement and charge developed in piezoelectric beams were derived. His work was later extended by Tadmor and Kósa [36] by accounting for the effect of strain on the electric field in the active material domain. This was done by a simple correction factor to the moment of inertia of the piezoelectric layers. A review of different theories used for modelling and analysis of piezoelectric laminates at that time was published by Gopinathan et al. [9].

It is interesting to note the most papers studying structural behaviour of piezoelectric materials and their possible applications to multifunctional structures are focused on the classical $d_{33}$ or $d_{31}$ piezoelectric effects. This trend comes from the fact these phenomena are easily observed and can be directly exploited in axial and transverse deformations modes of structures. However, in some piezoceramics, the $d_{15}$ piezoelectric shear coefficient is much higher than the $d_{33}$ and $d_{31}$ ones. Therefore, transducers based on these materials should be operated in shear deformation modes since the electromechanical coupling coefficient of the piezoelectric material is one of the most significant parameters affecting energy conversion. Studies on this topic were done, e.g. by Dietl et al. [7]. Authors developed a mathematical model of a piezoelectric sensor based on the Timoshenko beam theory. Next, it was used to examine the frequency response of vibration-based energy harvesters; finally the obtained results were compared to ones coming from the classical Euler–Bernoulli model. Also Malakooti and Sodano [23] studied the shear deformation modes of piezoelectric materials. The proposed model was used to predict the electric power output from a cantilever piezoelectric sandwich beam under base excitations. It was shown that the energy harvester operating in the shear mode was able to generate up-to 50% more power if compared to the standard transverse mode operating one. Capabilities of shearable beam with embedded piezoelectric actuation for beam shape control were studied also by Voß and Scherpen [41]. Also mixed theories adopting the geometrically linear Bernoulli–Euler hypothesis for the mechanical components and a first-order theory for the electrical variable can be found in the recent literature [15, 35].

Conclusions summarizing these papers indicate that the Euler–Bernoulli beam model severely over-predicts the structural behaviour of tested functional structures, especially at low frequencies and low length-to-width aspect ratios. This over-prediction is of particular importance in case of composite materials that exhibit relatively low shear stiffness when compared to classical isotropic materials.

Another important aspect in proper modelling the piezoelectric functional structures is mutual interaction of mechanical and electrical domains of the system. The initial studies did not consider the field coupling effects thus both mechanical and electrical domains were treated independently. Within this framework, the mechanical properties of the hybrid structure resulted solely from the combination of stiffnesses of two constituent materials. The functional nature of the structure was captured by introducing dynamic loading acting at the requested position on the structure. This simplified approach provides only approximate results, and therefore, in some cases like high frequency vibrations or thick piezoelectric material layers, significant errors arise [37].

The coupled electromechanical model of the smart composite materials was proposed by Mitchell et al. [24]. Authors presented a method of enhancing plate theory to account for the charge equations of electrostatics. Further studies on coupled domain models of piezoelectric composite plates were done by Li et al. [21] and Zhou et al. [45]. Chattopadhyay et al. [5] elaborated a higher-order displacement field model of a plate to investigate the behaviour of smart helicopter rotor blades. However, the proposed theory was based on a three-dimensional approach so the final equations were too complicated to be solved analytically and the finite element method was used to get the solution. Later, authors extended their model by addressing the nonlinear electromechanical coupling effect. To this aim, the polarization versus electric field hysteresis was taken into account and a new material constant was introduced to explicitly formulate the nonlinear constitutive governing equations of the structure.

Fig. 1

Model of the rotating piezoelectric composite beam structure (a); clamping to the rigid hub at presetting angle $\theta$ (b); geometrical parameters of the specimen cross section (c)

This paper is a continuation of the previous authors’ research on dynamics of thin-walled composite beams. In particular, in reference [18] by Latalski et al. where the general partial differential equations of motion of a thin-walled composite beam clamped to the rigid hub were derived, the nonclassical effects like material anisotropy, rotary inertia, transverse shear, arbitrary pitch angle, and hub inertia were considered. The ordinary differential equations were formulated together with the associated orthogonality condition for the specific case of circumferential asymmetric stiffness (CAS) of the cross section.

In the following research [16], Latalski proposed a mathematical model of a beam with integrated piezoelectric layer accounting for both full electromechanical coupling effects as well as the higher-order constitutive relations. The detailed derivation procedure by means of Hamilton least action principle was presented. With respect to former research a new governing equation was formulated representing the electric field distribution within the piezoceramic domain. It has been shown the electromechanical coupling in the structure comes from the shear deformation in flapwise bending plane. This model has been adopted in later research for the analysis of a rotating thin-walled composite beam with embedded piezoelectric layer [17]. In studies, a specific case of circumferentially asymmetric stiffness lamination scheme that exhibits flapwise bending and twist mode elastic coupling was considered. Numerical results for system free vibrations were obtained to investigate the natural mode shapes and the electrical field spatial distribution depending on the system rotation speed and laminae fibre orientation angle.

In this research, the same fully coupled mathematical model of functional structure is adopted to study the dynamics of a rotating composite beam featuring bending to bending coupling. This dynamical behaviour is achieved by adopting the circumferentially uniform stiffness (CUS) along the profile cross section. In the formulation, the higher-order constitutive relations with respect to electric field variable are considered. In the numerical analysis, the forced responses of the system under zero and nonzero mean value harmonic excitation are investigated. Regarding the referenced papers and to the best of authors knowledge, these aspects of CUS laminated multifunctional beams with nonlinear piezoelectrics have not been studied in detail yet.

2 Structural model and problem formulation

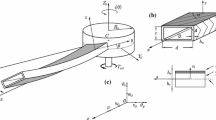
Let us consider an elastic single-cell thin-walled beam with box-shaped cross section. The beam is clamped to the rigid hub at an arbitrary presetting angle $\theta$—see Fig. 1a, b. The hub has radius $R_0$ and is driven by the external torque $T_{{\mathrm{ext}},z}$ resulting in rotation of a structure about fixed vertical axis $CZ_0$.

The considered beam is made of unidirectional fibre-reinforced composite material obeying Hook law. Apart from regular UD material plies, two additional structural layers of transversely isotropic piezoceramic material are embedded onto the beam. These ones are placed on the outer faces of the two beam walls that are perpendicular to the flapwise bending plane (i.e. the plane of lower specimen stiffness—the $\langle {}xz\rangle$ one of the local coordinate system $\langle {}xyz\rangle$, see Fig. 1c), and cover the full span of the beam. Moreover, it is assumed the active piezoelectric material is poled in the thickness direction. Thus, this configuration is a typical geometry corresponding to ’3-1’ mode operating transducers based on active piezoelectric materials. Moreover, in the performed analysis, it is assumed that the piezoceramic layers are not covered by electrodes and the poles of the piezoceramics are considered to be open-circuited.

2.1 Piezoelectric material model

The equations of motion of the structure are derived following the extended Hamilton principle of the least action

$$\begin{aligned} \delta J=\int _{t_{1}}^{t_{2}} \big ( \delta T-\delta U+\delta W_{\mathrm{ext}} \big )\mathrm {d}t=0 \end{aligned}$$

(1)

where J is the action, T is the kinetic energy, U is the potential energy including mechanical ($U_\mathrm{m}$) and electrical components ($U_\mathrm{e}$), and the work done by the external loads (driving torque $T_{{\mathrm{ext}},z}$) is given by the $W_{\mathrm{ext}}$ term.

Fig. 2

Laminate circumferentially uniform stiffness (CUS) ply angle configuration in thin-walled beam

Detailed derivation procedure of a six-DOF model of the beam with an arbitrary presetting angle $\theta$ and any circumferential lamination scheme has been presented in former authors papers [17] and [18]. These papers include also the list of adopted kinematic and structural assumptions to the mathematical model as well as the discussion on their significance. In particular, the second paper provides an efficient approach to properly model the full two-way electromechanical coupling interaction observed in piezoelectric structures. The relevance and suitability of this mathematical formulation is further enhanced by postulating the higher-order constitutive relations with respect to electric field

$$\begin{aligned} \varvec{\sigma }&= {\mathbf {C}}\varvec{\varepsilon } - \mathbf {e} \mathbf {E} - \hat{\mathbf {b}} \; \mathrm {sgn}(E_3)\mathbf {E}^2\nonumber \\ \mathbf {D}&= \mathbf {e} \varvec{\varepsilon } + \varvec{\xi } \mathbf {E} + \varvec{\chi } \mathrm {sgn}(E_3)\mathbf {E}^2 \end{aligned}$$

(2)

In the above relations ${\mathbf {C}}$ stands for the second-order piezoceramic elasticity tensor at constant electric field, $\mathbf {e}$ is the tensor of piezoelectric coefficients, $\varvec{\xi }$ is second-order permittivity tensor, $\hat{\mathbf {b}}$ is effective electrostrictive constants tensor, $\varvec{\chi }$ is third-order electric susceptibility tensor. Moreover, the variables $\varvec{\sigma }$, $\varvec{\varepsilon }$ and $\mathbf {D}$ stand for stress and strain tensors and electric displacement vector, respectively. Finally, the electric field vector is denoted by $\mathbf {E}$, and it contains just one component $E_3$ as results from the transducer topology and the posed assumption on piezoceramic material poling through the layer thickness. To capture the two-way electromechanical coupling effect, the electric field variable $E_3$ is assumed to be a spatially dependent one $E_3=E_3(x)$. More details on the mathematical modelling of piezoceramic two-way coupling effect can be found in [37, 45], as well as in previous study [16].

The considered constitutive equations postulate second-order nonlinearities expressed in electric field magnitude, rather than the electric field itself. Moreover, a third-order nonlinearities are not taken into account. In this way, the proposed model is capable to predict a softening/hardening curves with their peaks changing linearly with the excitation magnitude. This comes from the fact the linear change in peak response frequency with increased excitation level has been observed in experimental research on both stiff and soft piezoelectric materials—note papers by Usher and Sim [40], Mahmoodi et al. [22] and Leadenham and Erturk [19] among others.

2.2 CUS laminate configuration

One of the crucial features of structures made of fibre-reinforced laminates is the ability to tailor their mechanical properties to meet specific design requirements. This aim can be achieved by adjusting the orientation of the fibres in the composite material or/and through the use of the variable stiffness concept. This later idea implies the stiffness properties of the structure vary spatially throughout its volume. In case of thin-walled beam elements, this usually corresponds to changes in material thickness or laminate properties along the specimen span or along the cross-section midline (e.g. different orientation of reinforcing fibres in the subsequent segments of the cross section). When considering this second case, two designs are most typically adopted–they are referred to as circumferentially uniform stiffness (CUS) and circumferentially asymmetric stiffness (CAS) configurations [30]. For a thin-walled beam of arbitrary but rectangular cross section, the CUS lamination scheme can be generated by skewing the ply angles in the top and bottom walls (flanges) according to the formula $\alpha (z) = \alpha (-z)$ and in the lateral walls (webs) as $\alpha (y) = \alpha (-y)$, respectively. The reinforcing fibres orientation angle $\alpha$ is measured with respect to the in-plane axis (e.g. s) of a wall related coordinate system $\langle sxn \rangle$; note Fig. 2 for reference.

Accepting the discussed circumferentially uniform stiffness lamination scheme causes the general system of six (three translations and three rotations) fully coupled governing equations of the beam to be split into two independent subsystems. One of these subsystems describes the coupled in-plane and out-of-rotation plane shearable bendings of the blade. The second governing subsystem represents the coupled axial (specimen extension) and torsional dynamics of the beam. It should be noted that the circumferentially uniform stiffness ply angle configuration is preferred in the design of helicopter blades and tilt rotor aircraft [14].

2.3 Equations of motion

Presuming the discussed above circumferentially uniform stiffness of the profile as well as beam presetting angle $\theta =-\tfrac{\pi }{2}$ the system of partial differential governing equations for the structure under consideration is as follows

• the hub

  $$\begin{aligned}&J_\mathrm{h}\ddot{\psi }(t)+ (B_{22} + B_4 l)\ddot{\psi }(t)\nonumber \\&\quad +\int _0^{l}\, b_1 (R_{0}+x)\,\left[ 2 u_0 \ddot{\psi }(t)+2 \dot{u}_0 \dot{\psi }(t)+\ddot{w}_0 \right] \mathrm {d}x \nonumber \\&\quad - T_{{\mathrm{ext}},z}(t) = 0 \end{aligned}$$

  (3)

• lateral displacement $v_0$ (i.e. out-of-rotation plane)

  $$\begin{aligned} b_1 \ddot{v}_0 - a_{44}(v_0^{\prime \prime } +\vartheta _z^\prime ) - a_{34} \vartheta _y^{\prime \prime } - b_1\dot{\psi }^2[R_x(x) v_0^\prime ]^\prime = 0 \end{aligned}$$

  (4)

  with boundary conditions

  $$\begin{aligned} v_0 \Big |_{x=0} = 0,\qquad [a_{44}(v_0^{\prime }+\vartheta _z) + a_{34} \vartheta _y^{\prime }] \Big |_{x=l} = 0 \end{aligned}$$

• lateral shear $\vartheta _z$

  $$\begin{aligned}&B_5 \ddot{\vartheta _z} - B_5\dot{\psi }^2\vartheta _z- a_{22}\vartheta _z^{\prime \prime } + a_{44}(v_0^{\prime } + \vartheta _z) \nonumber \\&\quad -\,a_{25}(w_0^{\prime \prime } + \vartheta _y^{\prime }) + a_{34}\vartheta _y^{\prime } = 0 \end{aligned}$$

  (5)

  with boundary conditions

  $$\begin{aligned} \vartheta _z\Big |_{x=0} = 0,\qquad [a_{22}\vartheta _z^{\prime } + a_{25}(w_0^{\prime } + \vartheta _y)] \Big |_{x=l} = 0 \end{aligned}$$

• lead-lag displacement $w_0$ (i.e. in the plane of rotation)

  $$\begin{aligned}&b_1 \ddot{w}_0 + 2 b_1 \dot{u}_0 \dot{\psi }- b_1 \dot{\psi }^2w_0 + b_1 (R_0 + x) \ddot{\psi }\nonumber \\&\quad - a_{55} (w_0^{\prime } - \vartheta _y)^\prime - a_{25} \vartheta _z^{\prime \prime } - b_1 \dot{\psi }^2[R_x(x)w_0^\prime ]^\prime = 0 \end{aligned}$$

  (6)

  with boundary conditions

  $$\begin{aligned} w_0 \Big |_{x=0} = 0,\qquad [a_{55}(w_0^{\prime }+\vartheta _y) + a_{25} \vartheta _z^{\prime }] \Big |_{x=l} = 0 \end{aligned}$$

• lead–lag plane shear $\vartheta _y$

  $$\begin{aligned}&B_4 \ddot{\vartheta _y} - B_4\dot{\psi }^2\vartheta _y- a_{33}\vartheta _y^{\prime \prime } + a_{55}(w_0^{\prime } + \vartheta _y) \nonumber \\&\quad - a_{34}(v_0^{\prime \prime } + \vartheta _z^{\prime }) + a_{25}\vartheta _z^{\prime } \nonumber \\&\quad - a_{3e}E_3^\prime - a_{3b} [\mathrm {sgn}(E_3)E_3^2]^\prime - a_{3f}(E_3^3)^\prime = 0 \end{aligned}$$

  (7)

  with boundary conditions

  $$\begin{aligned}&\vartheta _y\Big |_{x=0} = 0,\qquad [a_{33}\vartheta _y^{\prime } + a_{34}(v_0^{\prime } + \vartheta _z) +a_{3e}E_3\\&\qquad \qquad +\,a_{3b}\,\mathrm {sgn}(E_3)E_3^2+a_{3f}E_3^3] \Big |_{x=l} = 0 \end{aligned}$$

• electrostatic equation ${E}_3$

  $$\begin{aligned} a_{E3}\vartheta _y^{\prime } - a_{Ee} E_3 - a_{Eb}\, \mathrm {sgn}(E_3) (E_3)^2 - a_{Ef} E_3^3 = 0 \end{aligned}$$

  (8)

where $R_x(x)=R_0(l-x)+\tfrac{1}{2}(l^2-x^2)$.

In the above equations, variables $v_0$ and $w_0$ represent displacements of the beam cross-section origin O along the y and z axes in the local coordinate system $\langle xyz \rangle$—see Fig. 1b, while $\vartheta _y, \vartheta _z$ are the corresponding rotations. Moreover, the coefficients $b_1$, $B_4$ and $B_5$ are translational ($b_1$) and rotational inertias ($B_4, B_5$), respectively. Terms $a_{ij}$ represent different stiffness coefficients of the specimen. In particular, the pair $a_{22}, a_{44}$ represents chordwise (local $\langle {}xy\rangle$ plane) and pair $a_{33}, a_{55}$ flapwise (local $\langle {}xz\rangle$ plane) bending and shear stiffnesses, respectively. Moreover, there are two additional stiffness coefficients $a_{25}$ and $a_{34}$ that lead to mutual coupling of beam bending deformations. The term $a_{25}$ is chordwise bending to flapwise transverse shear and $a_{34}$ is flapwise bending to chordwise transverse shear coupling stiffness. The last Eq. (8) of the system represents the distribution of the electric field along the span of the beam, and it is directly related to the lead–lag plane shear variable $\vartheta _y$ Eq. (7).

Commenting on the given above equations of motion, it is worth to emphasize the mutual coupling within the system of beam governing equations is achieved by both shear deformation angles $\vartheta _y$ and $\vartheta _z$. Therefore, within the framework of simplified unshearable beam theory (like Euler–Bernoulli one), not only the shear deformation Eqs. (5) and (7) vanish but the remaining displacements ones get decoupled. The relations are as follows:

• lateral displacement $v_0$

  $$\begin{aligned} b_1 \ddot{v}_0 - B_{5} \ddot{v}_0^{\prime \prime } + a_{22} v_0^{\prime \prime \prime \prime } + B_{5} \dot{\psi }^2v_0^{\prime \prime } - b_{1} \dot{\psi }^2[R_x(x) v_0^\prime ]^\prime = 0 \end{aligned}$$

  (9)

  with boundary conditions

  $$\begin{aligned} v_0 \Big |_{x=0} {=v_0^\prime \Big |_{x=0} }= 0,\qquad v_0^{\prime \prime }\Big |_{x=l} {= v_0^{\prime \prime \prime }\Big |_{x=l}} = 0 \end{aligned}$$

• lead–lag displacement $w_0$

  $$\begin{aligned}&b_{1} \ddot{w}_0 - B_{4} \ddot{w}_0^{\prime \prime } + a_{33} w_0^{\prime \prime \prime \prime } + 2 b_1 \dot{u}_0 \dot{\psi }+ B_{4} \dot{\psi }^2w_0^{\prime \prime } \nonumber \\&\quad - b_{1} \dot{\psi }^2w_0 - b_1 \dot{\psi }^2[R_x(x)w_0^\prime ]^\prime \nonumber \\&\quad + b_1 (R_0 + x) \ddot{\psi }- a_{3e}E_3^{\prime \prime } - a_{3b} [\mathrm {sgn}(E_3)E_3^2]^{\prime \prime } \nonumber \\&\quad - a_{3f}(E_3^3)^{\prime \prime } =0 \end{aligned}$$

  (10)

  with boundary conditions

  $$\begin{aligned}&w_0 \Big |_{x=0} = {w_0^\prime \Big |_{x=0}=\ } 0,\qquad [-\,a_{33}w_0^{\prime \prime } + a_{3e}E_3 \\&\qquad \qquad +\, a_{3b}\,\mathrm {sgn}(E_3)E_3^2 + a_{3f}E_3^3] \Big |_{x=l} {= w_0^{\prime \prime \prime }\Big |_{x=l}}= 0 \end{aligned}$$

This formulation is derived by extracting $a_{44}(v_0^{\prime }+\vartheta _z)$ and $a_{55}(w_0^{\prime } - \vartheta _y)^\prime$ from Eqs. (4) and (6), respectively, replacing these expressions in the remaining equations of motion Eqs. (5) and (7) and finally substituting $\vartheta _y=-w_0^\prime$ and $\vartheta _z=-v_0^\prime$.

The definitions and ultimate formulas of the individual stiffness coefficients are given as follows

$$\begin{aligned} a_{22} =&\int _c \left[ K_{11}\,y^{2} + 2K_{14}\frac{\hbox {d}z}{\hbox {d}s}y + K_{44}\left( \frac{\hbox {d}z}{\hbox {d}s}\right) ^{2}\right] \mathrm {d}s \nonumber \\ =&\frac{1}{2} K_{11}^{(\mathrm{w})} c d^2 + 2 K_{44}^{(\mathrm{w})} c + \frac{1}{6} K_{11}^{(\mathrm{f})} d^3\nonumber \\ a_{33} =&\int _c \left[ K_{11}\,z^{2} - 2K_{14}\frac{\hbox {d}y}{\hbox {d}s}z + K_{44}\left( \frac{\hbox {d}y}{\hbox {d}s}\right) ^{2} \right] \mathrm {d}s \nonumber \\ =&\frac{1}{2} K_{11}^{(\mathrm{f})} c^2 d + 2 K_{14}^{(\mathrm{f})} c d + 2 K_{44}^{(\mathrm{f})} d + \frac{1}{6} K_{11}^{(\mathrm{w})} c^3\nonumber \\ a_{44} =&\int _c \left[ K_{22}\left( \frac{\hbox {d}y}{\hbox {d}s} \right) ^{2} + A_{44}\left( \frac{\hbox {d}z}{\hbox {d}s}\right) ^{2}\right] \mathrm {d}s = 2 K_{22}^{(\mathrm{f})} d + 2 A_{44}^{(\mathrm{w})} c\nonumber \\ a_{55} =&\int _c \left[ K_{22}\left( \frac{\hbox {d}z}{\hbox {d}s}\right) ^{2} + A_{44}\left( \frac{\hbox {d}y}{\hbox {d}s} \right) ^{2} \right] \mathrm {d}s = 2 K_{22}^{(\mathrm{w})} c + 2 A_{44}^{(\mathrm{f})} d\nonumber \\ a_{25} =&\int _c \left[ K_{12}\frac{\hbox {d}z}{\hbox {d}s}y + K_{24}\left( \frac{\hbox {d}z}{\hbox {d}s}\right) ^{2} \right] \mathrm {d}s = K_{12}^{(\mathrm{w})} c d\nonumber \\ a_{34} =&\int _c \left[ K_{12}\frac{\hbox {d}y}{\hbox {d}s}z - K_{24}\left( \frac{\hbox {d}y}{\hbox {d}s}\right) ^{2}\right] \mathrm {d}s - K_{12}^{(\mathrm{f})} c d - 2 K_{24}^{(\mathrm{f})} d \end{aligned}$$

(11)

In the above expressions, the additional superscripts $(\mathrm {w})$ or $(\mathrm {f})$ at K stiffnesses correspond to the part of the cross-section perimeter belonging to the web or to the flange, respectively.

The coefficients $K_{ij}$ are expressed in terms of reduced two dimensional stiffnesses A, B, and D of the classical laminate theory

$$\begin{aligned} \begin{alignedat}{2} K_{11} =&\left( A_{22}-\frac{A_{12}A_{12}}{A_{11}} \right)&\qquad K_{12} =&\left( A_{26}-\frac{A_{12}A_{16}}{A_{11}} \right) \\ K_{14} =&\left( B_{22}-\frac{A_{12}B_{12}}{A_{11}} \right)&K_{22} =&\left( A_{66}-\frac{A_{16}A_{16}}{A_{11}} \right) \\ K_{24} =&\left( B_{26}-\frac{A_{16}B_{12}}{A_{11}} \right)&K_{44} =&\left( D_{22}-\frac{B_{12}B_{12}}{A_{11}} \right) \\ \end{alignedat} \end{aligned}$$

(12)

It should be observed for the sections of the perimeter corresponding to lateral walls (webs) that the coefficient $K_{44}$ reduces just to bending stiffness $D_{22}$, and two other ones, namely $K_{14}$ and $K_{24}$, vanish. This is the result of material symmetry with respect to the wall midline that forces $B_{12}=B_{22}=B_{26}=0$. However, in case of flanges, the present outer piezoelectric layers break the wall cross-section symmetry and thus respective membrane-bending coupling stiffnesses $B_{ij}$ are different from zero.

The magnitudes of stiffness coefficients depend on reinforcing fibres orientation in UD laminae. In case of the bending stiffnesses $a_{22}$ and $a_{33}$ the relation is straightforward. They increase monotonically when the fibre orientation angle approaches the beam span direction. However, in case of the shear stiffnesses $a_{44}$ and $a_{55}$ as well as the coefficients $a_{25}$ and $a_{34}$ accounting for in-plane/out-of-plane shearable bendings coupling the relations are more complicated; see Fig. 3.

Fig. 3

Governing equations stiffness coefficients with respect to reinforcing fibre orientation angle $\alpha$ (measured from circumferential axis direction s—see Fig. 2). Data used for this analysis correspond to specimen data used in numerical studies given in Sect. 4

Both shear deformation coefficients $a_{44}$ and $a_{55}$ exhibit very similar behaviour with respect to reinforcing fibre orientation. Initially, their magnitude increases until $\alpha \approx 54^\circ$ and $\approx 68^\circ$, respectively. Next, the curves decrease rapidly reaching global minimum at $\alpha =\tfrac{\pi }{2}$—i.e. when fibres are oriented along the beam span.

Regarding the coefficient of chordwise bending to flapwise transverse shear coupling ($a_{25}$), one observes it reaches its global extrema at orientations $\alpha \approx 74^\circ$ or $\alpha \approx 106^\circ$ and stays antisymmetric with respect to beam span direction. For limit cases of fibres oriented along the cross-section circumference or along the beam spam, it reaches zero value. However, the qualitative behaviour of the second coupling coefficient $a_{34}$ (flapwise bending to chordwise transverse shear) is different. Apart from global extrema corresponding to angles $28^\circ$ and $152^\circ$ and zero values at the limits $0^\circ$ and $90^\circ$, one can spot two additional roots corresponding to $\alpha \approx 16^\circ$ and $\alpha \approx 114^\circ$. It means, at this specific orientations, the bending of the specimen in the plane of rotation, namely lead-lag bending, do not contribute to shear deformation in the orthogonal plane. The qualitative difference of the $a_{34}$ curve if compared to $a_{25}$ one can be explained by the presence of the piezoceramics within the flanges of the cross section breaking the symmetry of material distribution with respect to these walls midline. Due to this fact, additional local membrane–bending couplings arise ($B_{12}, B_{22}, B_{26}\ne 0$) contributing to the global specimen behaviour.

3 Solution procedure

To facilitate the solution and extend the generality of the problem formulation one starts from rewriting the original equations of the system (4)–(8) into their dimensionless form. To this aim, a dimensionless spanwise abscissa $\eta ={x}/{l}$ ($\eta \in \langle 0,1\rangle$) is introduced as well as dimensionless time $\tau = \omega t$, where t is physical time and $\omega = \sqrt{{a_{33}(0)}/{b_1 l^4}}$. The parameter $a_{33}(0)$ corresponds to the flapwise bending stiffness presuming that the laminate fibres are oriented at $\alpha =0^\circ$ with respect to profile circumferential axis s.

Next, the reformulated system of governing equations is transformed into ordinary differential form. To this aim the Extended Galerkin Method is used. At the first stage the simplified linear model of a non-rotating beam without piezoceramic layer is considered and the corresponding eigenvalue problem is solved. Within this procedure, the consistent admissible functions which have to fulfil all the geometric boundary conditions while not violating complementary boundary conditions [2, 29] were used. Based on previous authors’ studies [18], Duncan polynomials modified by Karanamoorthy have been adopted to approximate the displacements $v_0$, $w_0$ and subsequent $\sin (\tfrac{2 i-1}{2}\pi \eta )$, $i=1\ldots k$, functions to represent the rotations $\vartheta _y$ and $\vartheta _z$. As a solution of the eigenvalue problem, a series of complex mode shapes $V(\eta )$, $W(\eta )$, $Y(\eta )$, $Z(\eta )$ and corresponding natural frequencies have been determined. These mode shapes have been used to represent the original problem unknown variables by separating space and time dependent functions, respectively

$$\begin{aligned}&v_0(\eta ,\tau ) = \sum _{j=1}^{N}V_j(\eta )\,q_j(\tau ) \quad \vartheta _y(\eta ,\tau ) = \sum _{j=1}^{N}Y_j(\eta )\,q_j(\tau )\nonumber \\&w_0(\eta ,\tau ) = \sum _{j=1}^{N}W_j(\eta )\,q_j(\tau ) \quad \vartheta _z(\eta ,\tau ) = \sum _{j=1}^{N} Z_j(\eta )\,q_j(\tau )\nonumber \\&E_3(\eta ,\tau ) = \sum _{j=1}^{N}\epsilon _j(\eta )\,q_j(\tau ) \end{aligned}$$

(13)

In the above relations, j stands for the mode order and the variables $q_j(\tau )$ are the corresponding generalized coordinates representing time dependent system behaviour, N is the number of mode shapes obtained from the eigenproblem.

The accuracy of this solution method, and the proposed analytical model has been verified in the previous authors’ research [18] by comparing the analytically obtained natural frequencies to the outcomes of the FE analysis. For the discussed therein case of CAS lamination configuration, the margin of error was less than 5%.

Having found the individual components of beam modes shapes, the reduction in the system of partial differential equations to ordinary ones can be done. Combining all five equations representing the dynamics of the beam (subsystem of Eqs. (4)–(8)) and making use of the derived orthogonality condition

$$\begin{aligned}&\left( \omega _{m}^2 - \omega _{n}^2\right) \int _0^1 \Big [ b_{1} l^2 V_{m}(\eta ) V_{n}(\eta ) + B_{5} Z_{m}(\eta )Z_{n}(\eta )\nonumber \\&\quad + b_{1} l^2 W_{m}(\eta )W_{n}(\eta ) + B_{4} Y_{m}(\eta )Y_{n}(\eta )\Big ] \, d\eta = 0 \end{aligned}$$

(14)

one finally arrives at the system of two dimensionless equations

$$\begin{aligned}&\left( 1 + \widehat{J}_\mathrm{h} + \alpha _{\mathrm{h}i2} q_i\right) \ddot{\psi } + \alpha _{\mathrm{h}i1} \ddot{q}_i + \varsigma _{\mathrm{h}}\dot{\psi } + \alpha _{\mathrm{h}i3} \dot{q}_i\dot{\psi } = \mu \nonumber \\&\ddot{q}_i + \varsigma _{i}\dot{q}_i + \alpha _{i2} \ddot{\psi } + \left( \alpha _{i1} + \alpha _{i3}\dot{\psi }^2\right) q_i + \alpha _{i4}q_i\dot{q}_i\dot{\psi } \nonumber \\&\quad + \alpha _{i5}\mathrm {sgn}(q_i){q}_i^2 = 0 \end{aligned}$$

(15)

where $\mu$ is dimensionless driving torque supplied to the hub and symbol $\widehat{J}_\mathrm{h}$ denotes the relative mass moment of inertia of the hub calculated with respect to the beam inertia. In the general case, the torque is expressed as a sum of a constant component $\mu _0$ and a periodic function of time t. Thus

$$\begin{aligned} \mu (t)=\mu _0+\rho \cos \omega t \end{aligned}$$

(16)

where $\rho$ and $\omega$ are the amplitude and the frequency of the excitation, respectively.

Moreover, the factors $\zeta _\mathrm{h}$ and $\zeta _i$ are hub and beam viscous damping coefficients and their magnitude has been estimated during test-stand experiments. The subscript i of the generalized coordinate $q_i$ indicates the mode order to be considered in the performed analysis.

The geometric characteristics of the rotating beam as well as composite and piezoceramic material data used in the subsequent numerical simulations are collected in Table 1. For the composite, the subscripts 1, 2 and 3 refer to parallel and transverse to the fibre directions respectively (the standard classical laminate theory assignment). The embedded active element is made of PZT-3203HD ceramic material and its properties are collected from the papers by Rao et al. [27] and by Kapuria et al. [12].

Table 1 System geometric data and materials as used in numerical simulations

Table 2 Dimensionless coefficients of the rotating structure, $40^\circ$ CUS configuration, mode 1

4 Numerical results

Numerical analysis of the rotating piezo-composite blades is performed around selected resonance zones of the rotating hub–beam system. By neglecting in Eqs. (15) the nonlinear terms, we can determine the first linear natural frequency of the structure. Therefore, the fundamental frequency of the linearized hub–blade system is approximated as

$$\begin{aligned} \omega _0= \sqrt{\frac{\alpha _{11}+\alpha _{13} \dot{\psi }^2}{1- {\alpha _{12} \alpha _{\mathrm{h}11}}/({1 + \widehat{J}_\mathrm{h}})}} \end{aligned}$$

Studying this relation, one may notice in the limit case of hub mass moment of inertia $\widehat{J}_\mathrm{h}$ approaching infinity the natural frequency of the rotor tends to $\omega _{0}=\sqrt{\alpha _{11}+\alpha _{13} \dot{\psi }^2}$. In particular case when there is no rotation it simplifies to $\omega _{0} = \sqrt{\alpha _{11}}$ which corresponds to the natural frequency of a regular cantilever beam.

We investigate dynamics of the system imposing periodic torque $\mu$ to the hub. Solutions of the reduced model are obtained numerically; a continuation method together with bifurcation analysis is performed for selected system parameters [8].

Table 3 Dimensionless coefficients of the rotating structure, $40^\circ$ CUS configuration, mode 2

Table 4 Dimensionless coefficients of the rotating structure, $70^\circ$ CUS configuration, mode 1

Table 5 Dimensionless coefficients of the rotating structure, $70^\circ$ CUS configuration, mode 2

For the analysis two configurations of the laminate corresponding to reinforcing fibres orientations $\alpha =40^\circ$ and $\alpha =70^\circ$ ale selected; see Fig. 2 for notation of fibre direction. For each layout, the reduction to single mode is performed and dynamics of the system around the fundamental (mode 1) and the second (mode 2) natural frequency is investigated. The values of dimensionless coefficients obtained for both configurations after a system reduction are presented in Tables 2, 3, 4 and 5. Moreover, the shapes of investigated modes coming from the eigenvalue problem solution are presented in Fig. 4 with separation of individual components contribution.

Fig. 4

Individual components ($v,w,\vartheta _y, \vartheta _z$ and $E_3$) of free vibration modes for thin-walled composite beam with integrated piezoelement; CUS configuration and fibre angle $\alpha =40^\circ$

Fig. 5

Individual components ($v,w,\vartheta _y, \vartheta _z$ and $E_3$) of free vibration modes for thin-walled composite beam with integrated piezoelement; CUS configuration and fibre angle $\alpha =70^\circ$

4.1 Fundamental frequency

At first we consider a case when the structure is excited periodically by torque with constant component equal to zero, $\mu _0=0$ (note Eq. (16) for reference). This scenario corresponds to the case of non-fully rotating structure but performing oscillations around its zero position due to zero mean value excitation $\mu (\tau )=\rho \cos \omega \tau$. The response of the blade $q_1$ and the angular velocity of the hub $\dot{\psi }$ are computed for different torque amplitudes $\rho$ and varied frequency $\omega$ in the neighbourhood of the resonance zone.

Results of the analysis for configuration corresponding to $\alpha =40^\circ$ when the mode 1 is excited are presented in Fig. 6a, b. The values of coefficients used in numerical simulation are given in Table 2.

Fig. 6

Resonance curves of the blade (a) and the hub (b) for selected values of excitation amplitude $\rho =0.1$ (black), $\rho =0.2$ (blue), $\rho =0.4$ (green), laminate configuration with fibres orientation $\alpha =40^\circ$, numerical data given in Table 2. (Color figure online)

One can clearly observe the softening phenomenon near the resonance zone due to the nonlinear characteristics of the PZT layers. It should be noted the backbone curve reveals change in peak response frequency with increased excitation level. As commented in Section 2, this effect is related to the presence of second-order nonlinearities expressed in variables magnitude, rather than the variables itself. The softening effect occurs both for the beam Fig. 6a and for the hub Fig. 6b, despite the fact that active layers giving rise to system nonlinearity are embedded into the beam only. This layout of the composite reinforcing gives significant nonlinear effect observed even for relatively small excitation level $\rho =0.1$ (black curve) and is increasing if torque amplitude is enlarged ($\rho =0.2$—blue curve and $\rho =0.4$—green curve).

Changing the composite configuration into $\alpha =70^\circ$ layout (values of the corresponding coefficients are collected in Table 4) a similar set of fundamental resonance curves has been obtained—see Fig. 7. However, one notices the nonlinear softening effect is now much less pronounced comparing to the previous case $\alpha =40^\circ$. To observe the nonlinear phenomenon the excitation amplitude has to be increased up to $\rho =0.4$ (green curve); for the record also $\rho =0.5$ (red curve) $\rho =0.6$ (magenta curve) cases are plotted. This observation can be easily explained by the significant difference in flapwise bending (in lead-lag direction, i.e. rotation plane) stiffness $a_{33}$ of the beam for these two specific cases—refer to Fig. 3. Moreover, at the orientation $\alpha =70^\circ$, there is a much stronger coupling of flapwise bending to the chordwise one (out-of-plane bending)—note coefficient $a_{34}$ when compared to $\alpha =40^\circ$ case. This is accompanied by the similar strong reverse coupling ($a_{25}$ coefficient), but this modal component is barely present—see Figs. 4 and 5.

Fig. 7

Resonance curves of the blade (a) and the hub (b); values of excitation amplitude $\rho =0.1$ (black), $\rho =0.2$ (blue), $\rho =0.4$ (green), $\rho =0.5$ (red), $\rho =0.6$ (magenta), laminate configuration with fibres orientation $\alpha =70^\circ$, numerical data given in Table 4. (Color figure online)

When analysing hub responses in both fibre configurations one can notice a zone where the hub vibrations are close to zero ($\omega =3.85$ on the Fig. 6 and $\omega =5.07$ on the Fig. 7). This phenomenon is apparently occurring for all studied levels of excitation $\rho$. It corresponds to dynamic absorption of hub vibrations when the total oscillation energy is directed to the blade and keeping the hub at rest. Detailed analysis reveals the effect occurs at the excitation frequency corresponding to the natural frequency of the cantilever beam $\omega _0=\sqrt{\alpha _{11}}$.

The direct comparison of both CUS $40^\circ$ and CUS $70^\circ$ layout variants is shown in Fig. 8. Changing the orientation of composite reinforcing fibres from $40^\circ$ to $70^\circ$ results in the shift of the resonance zone towards higher frequencies (i.e. to the right). Moreover, this stiffening effect is manifested in reduction of the resonance curve inclination and the magnitude of amplitudes as well.

Fig. 8

Comparison of resonance curves of the blade (a) and the hub (b) for CUS $40^\circ$—green curve (data in Table 2) and CUS $70^\circ$—blue curve (data in Table 4); amplitude of excitation $\rho =0.4$, $\mu _0=0$. (Color figure online)

In order to check the influence of the hub on the structure dynamics, we computed resonance curves for different magnitudes of hub mass moment of inertia $\widehat{J}_\mathrm{h}$. In Fig. 9, we present resonance curves for mode 1 and CUS $70^\circ$ configuration taking into account the relatively light hub (mass moment of inertia $\widehat{J}_\mathrm{h}=5$ – black curve), next the cases of $\widehat{J}_\mathrm{h}=20$—blue curve and $\widehat{J}_\mathrm{h}=50$—green curve, and finally for the very heavy one $\widehat{J}_\mathrm{h}=100$—red curve. One can observe the increase in the hub mass moment of inertia leads to shifting of the resonance zone into lower frequencies presuming the driving torque magnitude imposed to the hub is constant. The sharp decrease in the vibration amplitude is to be noted and–in consequence–the reduction in the nonlinearity effect. However, the already mentioned phenomenon of hub absorbtion is still present and occurs independently of the hub mass moment of inertia (Fig. 9b) and at the same frequency corresponding to natural vibrations of the cantilever beam.

Fig. 9

Resonance curves of the blade (a) and the hub (b) for selected values of mass moment of inertia $\widehat{J}_h=5$ (black), $\widehat{J}_h=20$ (blue), $\widehat{J}_h=50$ (green), $\widehat{J}_h=100$ (red), excitation amplitude $\rho =0.6$, $\mu _0=0$, mode 1 of CUS $70^\circ$ configuration. (Color figure online)

Fig. 10

Influence of relative mass moment of hub inertia $\widehat{J}_h$ on the response of the blade (a) and the hub (b) obtained for fixed excitation amplitude $\rho =0.6$ and selected excitation frequency external torques; $\omega =5.2$ (black), $\omega =5.4$ (blue), $\omega =5.6$ (green), $\omega =6.0$ (red), $\omega =6.5$ (magenta), $\omega =9.0$ (orange), $\mu _0=0$, mode 1 of CUS $70^\circ$ configuration. (Color figure online)

Now let us consider just for reference the black resonance curve (Fig. 9) computed for $\widehat{J}_\mathrm{h}=5$ and the excitation amplitude $\rho =0.6$. We intend to study the response of the system against $\widehat{J}_\mathrm{h}$ parameter for frequencies before, inside and after the resonance zone corresponding to this curve. To this aim, the response plots for the cases $\omega =5.2$ corresponding to sub-resonance zone, $\omega =5.4$ and $\omega =5.6$ inside the resonance zone as well as $\omega =6.0$, $\omega =6.5$, $\omega =9.0$ after the resonance have been computed. Appropriate plots are presented in Fig. 10. We note that the dynamics of the system changes qualitatively passing from the softening to hardening nature when the $\widehat{J}_\mathrm{h}$ parameter is decreased. Moreover, the amplitudes of hub response (Fig. 10b) are higher for lower $\widehat{J}_\mathrm{h}$ values and also if excitation frequencies are higher. In the case of beam response (Fig. 10a), the tendency is slightly different. Beam amplitudes increase as well, but for very low hub inertia, the tendency is opposite (orange curve in Fig. 10a).

4.2 Second natural frequency

The next mode of our interest is the second mode (mode 2). Coefficients of the discretised equations of motion corresponding to the $\alpha =40^\circ$ layout are gathered in Table 3 and for $70^\circ$ configuration in Table 5.

Fig. 11

Resonance curves of the blade (a) and the hub (b) for selected values of excitation amplitude $\rho =0.1$ (black), $\rho =0.2$ (blue), $\rho =0.4$ (green), $\rho =0.6$ (red), $\rho =1.1$ (magenta); CUS $40^\circ$ configuration, numerical data given in Table 3. (Color figure online)

We start the analysis from plotting the response curves for five different driving torque amplitudes, namely $\rho =0.1$, $\rho =0.2$, $\rho =0.4$, $\rho =0.6$ and also for the highest one $\rho =1.1$. The curves are presented in Fig. 11 for layout CUS $\alpha =40^\circ$ and in Fig. 12 for CUS $70^\circ$ case. It can be easily observed the amplitudes for the second mode are a few orders of magnitude smaller then those obtained for mode 1. Furthermore, the resonance curves demonstrate tendency to hardening effect which can be visible for very large, although non-realistic, external excitations which are not plotted here. Moreover, the dynamic absorption effect characteristic for fundamental frequency is not present any more since the resonate curves of the hub response decline monotonically.

Fig. 12

Resonance curves of the blade (a) and the hub (b) for selected values of excitation amplitude $\rho =0.1$ (black), $\rho =0.2$ (blue), $\rho =0.4$ (green), $\rho =0.6$ (red), $\rho =1.1$ (magenta), CUS $70^\circ$ configuration, numerical data given in Table 5. (Color figure online)

Comparison of the mode 2 resonance curves generated for CUS $40^\circ$ and CUS $70^\circ$ configurations is presented in Fig. 13. Since this mode can be activated in system response for higher excitation frequencies, therefore, in order to have comparison with fundamental mode 1, the analysis is performed for the same excitation level $\rho =0.6$. In contrast to the similar comparison prepared for mode 1 in the resonance zone of mode 2, amplitudes are higher for CUS $70^\circ$ configuration. This behaviour can be explained by studying the mode plots in Figs. 4 and 5. For both configurations, the dominating deformation is related to out-of-plane bending ($v(\eta )$ and $\vartheta _z(\eta )$), and thus the normalization of mode shapes to 1 has been done with respect to $\vartheta _z$ in both cases. However, for the layout corresponding to $\alpha =70^\circ$, there is an additional component coming from lead–lag bending that is barely present for $\alpha =40^\circ$ set-up. When comparing the response of the hub, both configurations reveal almost the same behaviour, and the curves overlap as presented in Fig. 13b.

Fig. 13

Comparison of resonance curves of the blade (a) and the hub (b) for CUS $40^\circ$—green curve (data in Table 3) and CUS $70^\circ$—blue curve (data in Table 5); amplitude of excitation $\rho =0.6$, $\mu _0=0$. (Color figure online)

4.3 Influence of rotating speed: full rotation case

Fig. 14

Resonance curves of the blade (a) and the hub (b) for selected values of constant torque component $\mu _0=0$ (black), $\mu _0=0.2$ (blue), $\mu _0=0.4$ (green), $\mu _0=1.0$ (red); a CUS $40^\circ$ configuration, b CUS $70^\circ$ configuration; $\rho =0.1$, mode 1. (Color figure online)

In all the analysis performed so far the rotor has been excited by periodic torque with zero mean value. To capture a full rotation impact, we add the constant component $\mu _0$ which results with an increase of mean value of angular speed. The resonance curves of the blade for selected angular velocities $\mu _0=0$, $\mu _0=2$, $\mu _0=0.4$ and $\mu _0=1.0$ are presented in Fig. 14. Commenting these plots, one observes the evident centrifugal stiffening effect resulting in shift of resonance curves to the right. Moreover, due to the nonlinear properties of the PZT layers, the resonance curves still demonstrate a softening effect; however, it is less pronounced at higher rotating speeds (higher $\mu _0$ value), again due to centrifugal stiffening of the blade. The softening, however, is much better demonstrated for mode 1 and CUS $40^\circ$ configuration and as expected less visible for CUS $70^\circ$ configuration.

The change of nature of constant component $\mu _0$ and for fixed amplitude $\rho$ and excitation $\rho$ are shown in Fig. 15a for beam response and in Fig. 15b for angular velocity of the hub. The increased value of constant component $\mu _0$ makes a shift of the response; however, the nonlinear nature of the solution is clearly demonstrated.

Fig. 15

Influence of constant torque component $\mu _0$ on dynamics the rotor with piezo-blade; a blade and b hub response, $\omega =5.2$ (black), $\omega =5.4$ (blue),$\omega =5.5$ (green), $\omega =5.8$ (red), $\omega =8.0$ (magenta); CUS $70^\circ$ configuration. (Color figure online)

5 Conclusions

The analysed model of the rotating hub with the composite thin-walled beam with embedded nonlinear piezoelectric layer demonstrates softening effect near its resonance zones. The nonlinear phenomenon is observed for the beam as well as for hub response due to the coupling of the hub to the blade by inertia terms. The intensity of the nonlinearity depends on the studied mode and the layout of reinforcing fibres within the discussed CUS configuration framework. Referring to the fundamental resonance zone the nonlinear nature of the response curve is much more pronounced for CUS $40^\circ$ layout than for the CUS $70^\circ$ case. This discrepancy comes from the significant difference in specimen bending/shear stiffness. In case of the second resonance zone, the oscillations are a few orders smaller if referred to fundamental resonance response. Furthermore, for the second mode, a small stiffening effect is observed with larger oscillation for CUS $70^\circ$ configuration, in contrast to the results obtained for first mode. The mass moment of hub inertia changes the dynamics of the rotating system. Depending on the excitation frequency response of the beam and hub as a function of hub inertia may vary from softening to hardening as presented in Fig. 10.

Another interesting phenomenon observed for the first mode and both configurations is the absorption of hub oscillations by beam motion. This dynamic absorption takes place for frequency equal to natural frequency of cantilever beam $\omega \approx \sqrt{\alpha _{11}}$. In this singular zone oscillations of the hub are close to zero with vibration localized in the beam. For the second mode, the absorption is not present. The presented reduced model allows fast and efficient parametric analysis and optimal design of the rotating composite structure with active blades comparing to for example high-computational cost and time consuming finite element studies.