Abstract
The nonlinear dynamics of towed wheels is analysed with the help of the brush tyre model. The time delay in the tyre–ground contact and the non-smooth nature of the system caused by contact friction are considered simultaneously. Firstly, the centre manifold reduction is performed on the infinite-dimensional system transforming the governing equations into a normal form containing linear and piecewise-smooth second-order terms. Then, this normal form is used to establish the stability of the non-hyperbolic equilibria of the system and to give an estimation of the limit cycles emerging at the linear stability boundary. This way, it is demonstrated how subcritical Hopf bifurcations in the non-smooth delayed system generate bistable parameter ranges, which are left undetected by standard tyre models.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
The self-excited vibration of towed wheels is one of the oldest and most thoroughly studied phenomena in vehicle dynamics. This can be explained by the fact that in case of road vehicles, the contact between the vehicle and the road surface is realised by elastic tyres. Consequently, there is a great need to understand the mechanism behind the force generation of the dynamically deformed tyres in vehicle modelling [25]. This is a challenging task due to the fact that the deformed shape of the tyre travelling backwards in the contact region is subject to the effect of partial sticking and sliding governed by friction laws. This is the reason why this task is approached mainly by large-scale numerical studies often using complex tyre models such as the FTire [9], the RMOD-K [22] and finite element-based models [12, 14], while limited analytical results are available.
Tyre models can be classified based on their complexity in terms of the physical representation of the tyre–ground contact. The simplest version of these models considers the wheel as a rigid body that has a single contact point at the ground [33, 40]. These models are reasonable in case of the rigid wheels of shopping carts, baby strollers or rolling suitcases [8, 23], and they provide a relatively simple formulation of the nonlinear governing equations. In these cases, one can consider various friction laws leading to a large variety of behaviours as shown for the example of a rolling rigid disc in [27].
A more sophisticated representation of the contact is possible by considering nonzero contact area between the interacting bodies. In such cases, when the shape of the contact area is well defined (e.g. elliptic [15]), these models were effectively used to study the dynamics of fundamental mechanical examples like the billiard ball or the Celtic stone (see [16, 17]).
In case of tyres, the so-called physical tyre models, such as the brush and the stretched string models, are originated in a similar assumption: a contact region of finite area is considered and tyre deformation is represented with the help of spring elements distributed along the contact patch. These models are often simplified by assuming quasi-steady-state deformation. By introducing the side-slip angle calculated from vehicle kinematics, the lateral tyre force and the self-aligning moment characteristics can be derived [25]. This initiated the introduction of semi-empirical tyre models, among others the widely used Magic Formula [26], which capture the tyre force and moment characteristics with shape functions based on extensive experiments. If viscous damping is also considered in the system, these tyre models can provide even quantitatively good results for the linear stability of the rectilinear motion of a caster–wheel system.
However, there are essential discrepancies in the description of the nonlinear behaviour of the tyres in case of the semi-empirical and the physical tyre models. The source of the problem is related to the force characteristics derived by means of a Coulomb-like friction law that leads to non-smooth governing equations.
Note that a Coulomb-like friction law between two rigid bodies usually results in a so-called Filippov system with discontinuous governing equations. These systems may feature bifurcations characteristic only to them (see [30]), and they often exhibit chaos, as shown, for example, for the stick-slip phenomenon in [1, 2].
In case of the tyre, however, friction has a direct effect on the lateral deformation, which is integrated along the contact length to calculate the lateral force and the self-aligning moment. Thus, we obtain piecewise-smooth continuous functions in the governing equations where the discontinuity appears in the nonlinear terms only. While this type of discontinuity in a higher derivative is clearly weaker than the discontinuity in case of Filippov systems, it still causes a significant difference compared to smooth systems in the way the limit cycles (self-excited vibrations) emerge at the linear stability boundary [19, 29, 30]. One difference is that while for a classical Hopf bifurcation in a smooth system, its sub- or supercriticality is decided by the second- and the third-order terms, then in the non-smooth case, the discontinuous second-order terms alone are decisive. This difference is also visible in the corresponding normal forms. If second-order terms are present in a smooth system (i.e. the nonlinearity is non-symmetric), one can eliminate them with a nonlinear near-identity transformation. On the contrary, this is not possible in the non-smooth case: the second-order terms already show odd symmetry and no unique nonlinear transformation exists that is capable to eliminate them in the normal form for both sides of the switching boundary. A further consequence is that with the piecewise-smooth characteristics, one can see a conical structure in the bifurcation diagrams as shown in [7], while using the smooth characteristics of the Magic Formula provides parabolae as expected for classical Hopf bifurcations [11].
Nevertheless, neither model can provide bistable parameter domains in the one degree of freedom model of towed wheels, which were otherwise experimentally presented in [5, 24, 39]. Additional dry friction at the king pin can be one explanation [24]. However, such parameter regions can also appear as a result of subcritical Hopf bifurcations leading to the coexistence of a stable rectilinear motion and stable self-excited oscillation of the towed wheel. This means that a so-called unsafe parameter region may exist where, depending on the initial conditions, either decaying vibrations or large amplitude oscillations can be experienced for the same set of parameters. Note that using multi-degrees of freedom models considering the compliance of the wheel suspension, subcritical Hopf bifurcations can be detected in narrow parameter regions even with the classical quasi-steady-state tyre models as shown in [41, 42] for an aircraft landing gear.
If the assumption of the quasi-steady-state tyre deformation is relaxed and the lateral deformation in the contact zone is described by the governing partial differential equation (PDE), a travelling wave solution can be identified introducing the so-called delayed tyre model [36, 38]. In the present paper, we use this dynamically varying tyre deformation in the contact region, which leads to the demonstration of a qualitatively correct nonlinear dynamical behaviour: a subcritical Hopf bifurcation of the straight-line motion is detected, and as a result, bistable parameter domains are explored. A further goal of our analysis is to present how the contact delay and dry friction contribute to the complex structure of the stable and unstable rectilinear and periodic motions in the system. With this aim, we perform the bifurcation analysis of the rectilinear motion of the non-smooth system [7] by studying the characteristic normal form [21]. In order to carry out closed-form analytical calculations, the simple brush tyre model is used, where the deformation at the sliding regions can be calculated directly. Although the brush model is less accurate compared to the stretched string models, the analytical results are still relevant either as test examples for advanced numerical codes or as qualitative examples for nonlinear tyre dynamics.
The rest of the paper is organised as follows. In Sect. 2, as a motivation of our study, experimental results are presented to demonstrate the appearance of bistable parameter domains and the strong effect of the tyre–ground contact friction on the dynamics of towed wheels. In Sect. 3, the mechanical model of a towed wheel of elastic tyre and its non-smooth equation of motion are presented. In Sect. 4, we expand the governing equations into a power-series form around the rectilinear motion up to the piecewise-smooth second-order terms. Then, in Sect. 5, critical parameters are presented as a result of linear stability analysis. At these critical parameters, Hopf bifurcations occur, which are analysed by means of centre manifold reduction and normal form transformation. The normal form is studied in Sect. 6 in order to determine the nature of the vibrations that occur around the rectilinear motion close to the critical parameters corresponding to loss of stability. In Sect. 7, the global dynamics of the system is presented by means of both analytical and numerical results, while the conclusions of the paper are summarised in Sect. 8.
2 Motivation
Measurements were carried out on a caster–wheel system running on a treadmill (see Fig. 1). The fork in which the bicycle wheel rotates is fixed to the caster which is mounted to the rack such that it can rotate around the king pin. It can be shown by means of the Galilean transformation that this configuration is identical to the scenario when the wheel is towed in a straight line with a given speed V. During the measurements, a bistable speed domain was explored by applying different force impulses on the caster. These impulses correspond to equivalent initial angular velocities \(\varOmega \) as shown in Fig. 2. Then, observing whether the system converges to stable large amplitude vibrations or to the stable rectilinear motion, we can estimate the angular velocity corresponding to the separatrix between the two stable solutions, which is used as an approximation of the amplitude of an (otherwise undetectable) unstable limit cycle (see red dashed line in Fig. 2). Performing this for different speeds V in the bistable region, the branch of the unstable limit cycles was continued until the point where the mechanical noise from the treadmill and the wheel unbalance resulted large amplitude vibrations without any additional impact hammer excitation. The root mean square (RMS) of the noise characteristic to the experiment is indicated by the dotted horizontal line in Fig. 2. The measurement results are compared with a theoretical bifurcation diagram showing a subcritical non-smooth Hopf bifurcation in the upper panel of Fig. 2. It can be observed that the unstable limit cycle appears to emerge in a conical structure rather than a paraboloid one that is characteristic to Hopf bifurcations in smooth dynamical systems. This indicates that, indeed, the non-smooth nature of the system, caused by dry friction in the tyre–ground contact, has an essential effect on the way the limit cycles develop.
Top panel: theoretical bifurcation diagram. The arrows indicate where the solutions converge to. Bottom panel: measurement results. Initial angular velocities (filled markers) and steady-state velocity amplitudes (empty markers) are plotted for different towing speeds. The cases when the system converged to the rectilinear motion are marked by circles, while those cases when persistent large amplitude vibrations occurred are marked with stars. The red dashed line estimates the likely locations of unstable limit cycles
3 Mechanical model
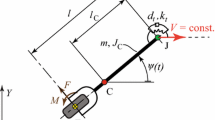
The nonlinear dynamics around a straight-line rolling of a towed wheel is analysed with the mechanical model shown in Fig. 3. The connection of the caster–wheel system to the towing vehicle is realised by a rotational joint at A. The rigid caster is towed along the X-direction by a prescribed constant velocity of V. This can be described by the geometric constraints \(X_\text {A}(t) = V t\) and \(Y_\text {A}(t) \equiv 0\), where \(X_\text {A}(t)\) and \(Y_\text {A}(t)\) refer to the X and Y coordinates of the king pin A, respectively. The distance of the wheel centroid T from the joint A is denoted by l, while the distance of the centre of gravity C of the caster and the joint A is \(l_\text {C}\). The mass of the caster–wheel system is m, while its mass moment of inertia with respect to the centre of gravity C is \(J_\text {C}\). One can use the angle \(\psi \) as a generalised coordinate to determine the orientation of the caster in the (X, Y) plane. The resultant of the lateral tyre deformation is considered in the form of the lateral force F and the self-aligning moment M, while the effects of longitudinal deformation and longitudinal sliding are assumed to be negligible. This is a standard simplification for the analysis of wheel shimmy when the wheel is towed with constant speed [24]. While it is justified by the good correlation between the theoretical and experimental results, this assumption is not acceptable when the wheel is subject to strong acceleration/deceleration.
3.1 Tyre model
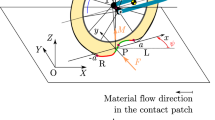
The deformation of the elastic tyre is described by means of the brush tyre model [25] shown in Fig. 4. It is assumed that tiny tread elements are distributed along the circumference of the wheel, which can be deformed normal to the wheel centre plane. The corresponding linear elasticity of these elements is characterised by the parameter k that stands for the lateral stiffness distributed along the longitudinal direction with unit N/\(\hbox {m}^2\).
3.1.1 Sticking region
Depending on the vertical load and the deformation of the tyre particles in contact, they can either stick to or slide on the ground. If the elastic elements are considered to stick to the ground, their velocity in the ground-fixed (X, Y, Z) coordinate system is zero, which can be expressed as the kinematic constraint
As explained in details in [36, 37], this can be used to derive the nonlinear PDE
which describes the lateral deformation q(x, t) of the centre line. Prime refers to differentiation with respect to the space coordinate x attached to the caster. To this equation, the boundary condition \(q(a,t) = 0\) is attached, where we use the standard assumption for brush models, namely that the leading point of the contact line always sticks to the ground with zero lateral deformation [25].
For this problem, one can construct the travelling wave solution:
by introducing the time delay \(\tau (x)\) distributed along the contact length x, whereas we also obtained a formula:
which gives the position along the x axis. Clearly, in linear approximation, the solution of (4) is
which is the time needed for a particle to travel from the leading position L to the actual position P at x.
3.1.2 Sliding region
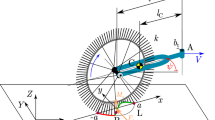
To model the partial sliding of the tyre in the lateral direction, we consider a parabolic vertical force distribution in the contact region, which can be used to define two parabolic deformation boundaries due to the independent deformation of the tyre particles [25]. For a compact formulation, we introduce them as
for \(x \in [-\,a,a]\) where \(N^{\pm }\) refers to the magnitude of the limiting parabolae, which also depends on the resultant vertical load \(F_z\) on the tyre and the contact friction coefficient \(\mu \). If \(N^\pm \) is considered to be positive, the formula above provides the upper boundary, while a negative value gives the lower boundary.
In what follows, it is assumed that sliding occurs only at the rear end of the contact, which is a reasonable assumption for small vibrations around the rectilinear motion \(\psi (t) \equiv 0\).
3.2 Governing equations
The equation of motion of the towed wheel can be obtained by means of Lagrange’s equation of the second kind as
where the mass moment of inertia of the caster–wheel system with respect to the king pin axis at A is \(J_\text {A} = J_\text {C} + m l^2_{\text {C}}\), while \(b_\text {t}\) is the torsional viscous damping factor in the joint.
Based on the brush tyre model, the resultant lateral tyre force F and the self-aligning moment M can be calculated by the integral formulae
and
Thus, substituting into Eq. (7), the governing equations of the mechanical system can be expressed as
where \(\varOmega \) is the angular velocity of the caster. The integral formulae that provide the lateral tyre force and the self-aligning moment are divided into two parts as defined in Eq. (11). \(I_1\) corresponds to the sticking part of the contact where the travelling wave solution (3) applies. Thus, instead of coordinate x, the distributed time delay \(\tau \) can be used for integration by substitution. This means that the limits are changed as \(x = a \Leftrightarrow \tau = 0\) and \(x = x^*\Leftrightarrow \tau = \tau ^ *\), where \(x^*\) and \(\tau ^*\) refer to the actually unknown boundary between the sticking and sliding regions. The derivative \(\text {d} x/ \text {d} \tau \) used for the integral transformation is based on the travelling wave solution (4) and reads as
The integral \(I_2\) includes the lateral force and self-aligning moment generated in the sliding part of the contact. In case of sliding, the deformation is known from the parabolic limits in Eq. (6); this is why we keep the coordinate x as integration variable.
4 Power-series expansion of the tyre force and self-aligning moment
4.1 Sticking region
To carry out the local bifurcation analysis of the rectilinear motion, we have to expand the system into a power-series form up to the second-order terms. Note that for Hopf bifurcations in smooth systems, one has to consider the third-order terms as well while the second-order terms can be eliminated by a near-identity transformation [18]. This cannot be performed in the non-smooth case due to the piecewise-defined nature of the second-order terms, which are in this sense ‘stronger’ than the third-order terms as they already determine the vague stability of the non-hyperbolic equilibria of the system [19].
The rectilinear motion can be expressed as \(\psi (t) \equiv 0\), \(\varOmega (t) \equiv 0\) and \(q (x,t) \equiv 0\). For the coordinate x, we get \(x = a - V \tau \) since the whole contact region sticks to the ground in this case. This means that the ‘boundary’ between the sticking and sliding regions is exactly at the rear edge, i.e. \( x^*= -a \Leftrightarrow \tau ^*= \frac{2a}{V} =: \tau _0^*\).
In the integral formula \(I_1\) in Eq. (11), both the coordinate x and the lateral deformation q(x, t) are multiplied by the derivative \(\text {d} x/ \text {d} \tau \). Consequently, in the non-smooth system, it is sufficient to consider them up to the linear terms:
as follows from Eqs. (3), (4) and (12). Using the ansatz \(\vartheta = -\tau \), the second-order approximation of the resultant moment at joint A from the tyre force F and the self-aligning moment M in the sticking region reads as
where the time delay \(\tau ^*\) at the boundary between the sticking and sliding regions is state dependent [28]: \(\tau ^*(t) = \tau ^*(\psi (t), \varOmega (t), q(x,t))\). After the elimination of q(x, t) by means of the travelling wave solution, this can be transformed into \(\tau ^*(t) = \tau ^*(\psi _t, \varOmega _t)\) where the continuous functions \(\psi _t(\vartheta ) := \psi (t+\vartheta )\) and \(\varOmega _t(\vartheta ) := \varOmega (t+\vartheta )\), \(\vartheta \in [-\tau ^*,0]\) represent the infinite-dimensional state-space coordinates of the time-delayed system. Consequently, one can approximate the time delay \(\tau ^*\) by the implicit integral formula
which can be regarded as a generalised power-series expansion up to the linear terms. The coefficient functions \(f_1(\vartheta )\) and \(f_2(\vartheta )\) will be determined in the subsequent section.
4.2 Sticking–sliding boundary
The boundary of the sticking and sliding regions appears where the travelling wave solution (3) crosses one of the parabolic deformation boundaries in (6). With the above-explained linear approach, this can be expressed as
Substituting the linearised formula for coordinate x into Eq. (14) to obtain
Keeping the linear terms only, this equation can be expanded as
Comparing the coefficients of \(\psi (t+\vartheta )\) and \(\varOmega (t+\vartheta )\), the functions \(f_1 (\vartheta )\) and \(f_2 (\vartheta )\) can be expressed as
where \(\delta \) denotes the Dirac delta function. Thus, for the time delay \(\tau ^*\) at the sticking–sliding boundary, we obtain the implicit formula
Consequently, the explicit form of this power series can be expressed as
where
Based on this, also the integral formula \(I_1\) can be expressed in the power-series form
where the second subscripts refer to the order of the dependence on the infinite-dimensional state-space variables \(\psi _t\) and \(\varOmega _t\). This calculation provides
and
4.3 Sliding region
For the sliding region, the closed-form calculation of the integral \(I_2\) leads to
Then, the sticking–sliding boundary \(x^*\) can be expanded similarly as it was performed for the time delay \(\tau ^*\):
Substituting this result into Eq. (31), the integral formula \(I_2\) is considered in the power-series form
where
where the approximation \(\tau ^*\approx \tau _0^*= 2a/V\) is sufficient here for the time delay at the sticking–sliding boundary. This indicates that sliding does not have an effect on the linear stability of the system, which validates the former calculations in [36, 37] where pure rolling is considered in the tyre–ground contact during the linear stability analysis.
The power-series expansion of the non-smooth governing Eqs. (2), (10)–(12) can be summarised in the form of the following system of nonlinear delay differential equations (DDEs):
where \(\tau _1^*\) is expressed in (26) and \(N^\pm \) can be found in (6).
5 Centre manifold reduction
In order to analyse the dynamics of the above-described non-smooth system, first the stability analysis of the rectilinear motion is carried out, which is followed by a detailed and rigorous Hopf bifurcation calculation. Since the system of DDEs (36), (37) is defined in the infinite-dimensional state space of the continuous functions \(\psi _t, \; \varOmega _t\), this system is transformed to the operator differential equation form (see [31])
where \({\mathbf {y}}_t\) is defined by the shift \({\mathbf {y}}_t = {\mathbf {y}} (t+\vartheta )\) for \(\vartheta \in \left[ -2a/V,0 \right] \), while \({\mathbf {y}}\) represents the vector of the caster angle and angular velocity:
The operator \({\mathscr {A}}\) stands for the linear part, while \({\mathscr {F}}\) corresponds to the nonlinear part of the system. The linear operator \({\mathscr {A}}\) is defined as (see [10])
for any \(\varvec{\chi }: \left[ -2a/V,0 \right] \rightarrow {\mathbb {C}}^2\) where the coefficient matrices \({\mathbf {A}}_0\) and \({\mathbf {A}}_\tau \) are calculated form the linear part of the DDE (37):
The nonlinear operator \({\mathscr {F}}\) in (38) is approximated till second order by
where the vector function \({\mathbf {f}}_2\) is calculated from the nonlinear part of the DDE (37) [see also (30), (35)] as
5.1 Stability analysis
The eigenvalue–eigenfunction problem for the linear operator \({\mathscr {A}}\) can be formulated as
where \(\lambda \in {\mathbb {C}}\) is the eigenvalue and \(\varvec{\phi }\) is the right eigenfunction of the operator defined above \(\left[ -2a/V, 0 \right] \ni \vartheta \). Based on (40), this equation can be expressed as the ordinary differential equation (ODE)
with the boundary condition
The general solution of ODE (46) has the exponential form
where \({\mathbf {c}} \in {\mathbb {C}}^2\) is a constant vector. Substituting this into the boundary condition (47), we obtain
This leads to the characteristic function \(D(\lambda )\) and the characteristic equation
where \({\mathbf {I}}\) refers to the identity matrix while \({\mathbf {A}}_0\) and \({\mathbf {A}}_\tau \) are given in (41) and (42), respectively. The characteristic Eq. (50) is identical to the one that is obtained after substituting the exponential trial solution
into the system of DDEs (36), (37). After performing the integration and expanding the determinant, the characteristic function in (50) can be expressed as
The characteristic equation can be used to study the linear stability of the rectilinear motion: all the real parts of the infinitely many characteristic exponents are negative in case of exponential stability. Based on this, a necessary stability condition \(l > -a\) can be derived. This critical caster length corresponds to saddle-node bifurcation, i.e. a real characteristic exponent crosses the imaginary axis at the stability boundary (\(\lambda = 0 \)). In practice, however, the stability boundaries related to oscillatory loss of stability are the essential ones, that is, when a pure imaginary pair of characteristic exponents crosses the imaginary axis (\(\lambda = \pm \text {i} \omega \)). These boundaries can be found by the D-subdivision method [38]. Calculating the real and imaginary parts of the characteristic function \(D(\text {i} \omega )\) provides the equations
respectively. For the undamped system (\(b_{\text {t}} = 0\)), the stability boundaries can be calculated analytically as shown also in [36, 38]. On the one hand, \(l = a\) satisfies both (53) and (54) with the frequency of \(\omega = 2 a \sqrt{2ka / (3 J_{\text {A}})}\). On the other hand, one can derive formulae for the critical towing speed \(V_{\text {cr}}\) and caster length \(l_{\text {cr}}\) by introducing the dimensionless frequency \(\alpha : = 2 a \omega / V_{\text {cr}}\) as a parameter in the formulae
Equations (55) and (56) provide the stability boundaries that divide the parameter space into linearly stable and unstable domains. The sense of the different parameter regions can be determined by methods presented in [32]. Stability charts constructed this way in the plane of the towing velocity V and the caster length l are shown in Figs. 6 and 9 in Sect. 7. In Fig. 6, the critical vibration frequencies \(\omega \) in (57) at the stability boundaries are also presented.
5.2 Tangent space of centre manifold
The Hopf bifurcation calculation requires the determination of the tangent space of the centre manifold at the critical parameters corresponding to the oscillatory loss of stability. Accordingly, consider the case of the pure imaginary pair of characteristic exponents \(\lambda _{1,2} = \pm \text {i} \omega \) corresponding to the Hopf bifurcation of the rectilinear motion, where \(\omega \) denotes the critical angular frequency of the system. Then, the characteristic exponent \(\lambda _1 = \text {i} \omega \) satisfies Eq. (45) with the eigenfunction \(\varvec{\phi }_1\):
Substituting it back into Eq. (50), we obtain
from where the two eigenvectors in the ODE (46) can be expressed as
and the corresponding eigenfunction of the linear part of the operator differential Eq. (38) is
Note that \(\varvec{\phi }_2 = \overline{\varvec{\phi }_1}\), where the overbar refers to complex–conjugate. The real and imaginary parts of the eigenfunction \(\varvec{\phi }_1\) provide a basis of the centre eigensubspace of the system. We represent them in the matrix function
In order to reduce the system to the centre manifold, one has to calculate the adjoint basis as well using the left eigenfunctions of the linear operator \({\mathscr {A}}\). The adequate eigenvalue problem can be expressed as
where \(\varvec{\psi }\) is the left eigenfunction. Alternatively, we can use the adjoint operator \({\mathscr {A}}^*\) as
where \({\mathscr {A}}^*\) is defined as
for any \(\varvec{\rho }: \left[ 0,2a/V \right] \rightarrow {\mathbb {C}}^2\) with \({\mathbf {A}}_0^*\) and \({\mathbf {A}}_{\tau }^*\) as transposed matrices. Substituting into the eigenvalue problem in Eq. (64) at the critical characteristic exponent \({\overline{\lambda }}_1 = - \text {i} \omega \), it leads to ODE
with boundary condition
The general solution of this ODE for the left critical eigenfunction \(\varvec{\psi }_1\) of the operator \({\mathscr {A}}\) can be expressed in the exponential form
where \({\mathbf {d}}_1 \in {\mathbb {C}}^2\) is a constant vector. The boundary condition (67) leads to
which has the solution
and similarly, \({\mathbf {d}}_2 = \overline{{\mathbf {d}}_1}\). With the help of the real and imaginary parts of the eigenfunction \(\varvec{\psi }_1\), the adjoint basis is formed, which is represented by the matrix
5.3 Bilinear form
In order to set an orthonormal basis \(\varvec{\Phi }\) and adjoint basis \(\varvec{\Psi }\) of the tangent space of the centre manifold, we need the scalar product defined by the bilinear form [10]
where the new basis
of the left eigenfunctions is introduced with the constant multiplier matrix \({\mathbf {K}} \in {\mathbb {R}}^{2 \times 2}\). This coefficient matrix is to be determined from the orthonormality condition
Based on this, the inverse transpose of the matrix \({\mathbf {K}}\) can be given as
The elements of this matrix are given as \(\kappa _{jk} \; j,k \in \lbrace 1,2 \rbrace \), where
With the help of Eq. (54), one can show that at the stability boundaries \(\kappa _{22} = -\kappa _{11}\). Introducing the notation
the constant matrix \({\mathbf {K}}\) in (73) that normalises the tangent basis of the centre manifold can be given as
5.4 Decomposition and reduction to centre manifold
Using the bases \(\varvec{\Phi }\) and \(\varvec{\Psi }\), an arbitrary solution \({\mathbf {y}}_t\) is decomposed as
where \({\mathbf {u}}\) is the vector of the state variables in the centre manifold:
while \({\mathbf {w}}_t\) refers to the rest of the state variables in the infinite-dimensional complementer space. As a result, the functions of the deflection angle \(\psi _t\) and the angular velocity \(\varOmega _t\) are approximated in the centre manifold by harmonic functions:
Thus, the reduced system can be expressed in the form
where \({\mathbf {w}}_t\) depends on the second-order terms of \(u_1\) and \(u_2\) in the centre manifold. Since the operator \({\mathscr {F}}_2\) includes second-degree terms only, the approximation \({\mathbf {w}}_t \approx 0\) can be considered, which leads to
with coefficients
6 Second-order non-smooth normal form
Equation (85) obtained from the centre manifold reduction is the specific case of the general form
where the real part \(\mu \) of the critical eigenvalues is zero for the non-hyperbolic equilibrium [as given in (85)], and \({\mathbf {h}}_2\) contains the non-smooth second-order terms. These can be given as
where the coefficients \(c_{jk} (0)\) and \(d_{jk} (0)\) for \(j,k \in \left\{ 1,2 \right\} \) are given as
The function H stands for the switching manifold, which is defined with the help of the limiting parabolae (6). Since we assumed that sliding occurs only at the rear section of the contact region, it follows that a transition from the upper parabola to the lower one can take place only at the rear edge R (at \(x = -a\)) as the sliding region shrinks to that single point. This means that for the time instant \({\tilde{t}}\) of switching, the whole contact region is sticking to the ground, that is, \(x^*= -a\) and \(q (x^*, {\tilde{t}}) = 0\). Consequently, the travelling wave solution (3) related to the sticking region can be used at \(x = -a\) to express the switching condition. Since in (91) it is satisfactory to have its linear approximation only, the switching condition can be expressed with the linearised travelling wave solution (13) by projecting the state variables \(\psi \) and \(\varOmega = {\dot{\psi }}\) to the centre manifold with \(u_1\) and \(u_2\) as given in Eq. (82):
This expression is calculated at the stability boundary for the critical towing speed \(V_{\text {cr}}\) when \(\mu = 0\) in (90).
Equations (90) and (91) define the normal form of the local bifurcation of the rectilinear motion. This reduced system is thoroughly examined in [7], to which we rely on in the present study. The introduction of the polar coordinates \(r, \, \varphi \) with \(u_1 = r \cos \varphi \) and \(u_2 = r \sin \varphi \) in (90), (91) leads to the non-smooth ODE
where the coefficient of the second-order terms can be expressed as
while \(\varphi _0\) refers to the orientation angle of the switching line H (see Fig. 5):
For the angle \(\varphi \), the polar coordinate transformation in (90), (91) leads to the approximation \({\dot{\varphi }} \approx - \omega \).
Using the odd symmetry of the flow, one can compose a map of consecutive intersections of the switching line and a trajectory corresponding to an initial condition \(r_0\) as shown in Fig. 5. The non-hyperbolic equilibrium at \(\mu = 0\) is stable if \(r_{k+1} < r_k\) for any \(k \in {\mathbb {N}}\). It can be shown [7] that its stability is decided by the integral
Namely, the equilibrium is stable (unstable) if \(\delta <0\) (\(\delta >0\)). The substitution of (96) into the integral (98) leads to the Poincarè–Lyapunov constant \(\delta \) of the non-smooth Hopf bifurcation in the form
where, by abuse of notation, \(c_{jk} = c_{jk}(0)\) and \(d_{jk} = d_{jk}(0)\).
As in case of the classical Hopf bifurcation theorem [18], the stability of the non-hyperbolic equilibrium is topologically extrapolated to the arising limit cycles. The approximate amplitude \(r_0\) for \(\mu \ne 0\) can be derived as the nonzero trivial (constant in time) solution of (90), which is approximated with the help of formula (98):
This indicates that if the non-hyperbolic equilibrium is asymptotically stable due to the nonlinear terms (\(\delta < 0\)), then the non-smooth Hopf bifurcation is supercritical and the emerging periodic solutions are orbitally asymptotically stable, and similarly, if the non-hyperbolic equilibrium is unstable (\(\delta > 0\)), then the bifurcation is subcritical and the limit cycles are unstable.
Formula (100) of the vibration amplitude also represents a common feature of piecewise-smooth systems [19]: the limit cycles emerge in a conical structure at non-smooth Hopf bifurcations instead of the paraboloid structure at classical Hopf bifurcations of smooth dynamical systems [18].
In practical examples, bifurcation parameters are selected, which help to visualise the structure of the emerging periodic solutions as a function of some relevant physical parameters. In case of the DDE model (36) and (37) of the shimmying wheel, a natural choice for this bifurcation parameter is the towing speed V since this parameter can be varied in the simplest way in experiments. The real part of the critical characteristic exponents \(\lambda _{1,2} (V) = \mu (V) \pm \text {i} \omega (V)\) depends on the towing speed V and \(\mu (V_{\text {cr}}) = 0\) at the stability boundary. The root tendency
can be calculated by means of the implicit derivation of the characteristic function \(D (\mu +\text {i} \omega )\) in (52). The bifurcation diagrams are constructed by transforming (100) with respect to the bifurcation parameter in the form
7 Results
Top panel: critical frequencies at the stability boundaries. Bottom panel: Stability chart of the rectilinear motion in the undamped system. The white domains are linearly stable, while the light red domains are unstable. The linear stability boundaries are coloured by means of their nonlinear stability considering the second-order terms. The blue curves are stable, the red ones are unstable, while the black one is neutral in this sense
Bifurcation diagram for a small caster length \((l = 0.02\) m) of the undamped system (10), (11). The thick curves are results of numerical collocation, while the thin straight lines represent the results of the analytical bifurcation calculation (102). Red and blue colours refer to unstable and stable branches, respectively
Bifurcation diagram for a large caster length \((l = 0.2\) m) of the undamped system (10), (11). The thick curves are results of numerical collocation, while the thin straight lines represent the results of the analytical bifurcation calculation (102). Red and blue colours refer to unstable and stable branches, respectively
Before investigating the nonlinear behaviour of the system, the linear stability analysis of the rectilinear motion has to be performed. Stability charts are created in the plane of the towing speed V and the caster length l. Figure 6 shows the stability chart and the critical frequencies (57) for the case when no damping is considered at the king pin (\(b_{\text {t}} = 0\)). The rest of the system parameters are listed in Table 1. The stability boundaries (55), (56), all corresponding to Hopf bifurcation, divide the (V, l) parameter plane into linearly stable and unstable parameter domains. One can use semi-discretisation [13] to establish the stability of the rectilinear motion for each domain. Thus, linearly stable and unstable parameter domains are obtained alternating in a chessboard-like structure. For large caster lengths, the unstable parameter boundaries shrink to asymptotes corresponding to \(l \rightarrow \infty \) which can be given as
In the undamped case, for \(V \rightarrow 0\), an infinite number of linear stability boundaries exists which behaviour is typical in delay differential equations. After establishing linear stability, the stability of the non-hyperbolic equilibria is investigated with the help of the non-smooth second-order terms as explained in Sect. 6. We found that by varying the towing speed V, the nonlinearly stable (shown in blue) and unstable (shown in red) non-hyperbolic equilibria also appear in an alternating structure in Fig. 6. The line \(l = a\) was found to be ‘neutral’ (\(\delta = 0\)) for the second-order terms; therefore, its stability could be decided by the higher-order terms. Note that in previous studies [34], using a quasi-steady-state tyre model, this line proved to be unstable due to the third-order terms. There are also points in the (V, l) parameter plane where two linear stability boundaries intersect each other. At such points, two complex–conjugate pairs of characteristic exponents cross the imaginary axis resulting possible quasi-periodic in oscillations having two frequencies. For an analytical investigation of these ‘double-Hopf’ points (see [20, 35]) an extension of the presented algorithm is needed, which is beyond the scope of this study together with the numerical analysis of the further possible bifurcations of the periodic motions emerging from the presented primary bifurcations.
Stability chart of the rectilinear motion with viscous damping considered at the king pin. The white domains are linearly stable, while the light red domains are unstable. The linear stability boundaries are coloured by means of their nonlinear stability considering the second-order terms. The blue curves are stable, the red ones are unstable, while the black one is neutral in this sense. The thin curves correspond to the linear stability boundaries of the undamped system
As one can observe, for each linearly unstable domain, the left boundary relates to subcritical bifurcation, while the right boundary corresponds to supercritical bifurcation. Thus, at each unstable domain, both branches of the arising limit cycles are tilted to the left (i.e. to smaller velocities). Figures 7 and 8 show two examples of the structure of the periodic solutions for small (\(l = 0.02\) m) and large (\(l = 0.2 \) m) caster length. In these bifurcation diagrams, the branches of limit cycles are calculated using numerical collocation [4, 6] while their tangent lines at the bifurcation points are determined by considering the non-smooth second-order terms according to expression (102). It can be seen that the numerical collocation and the semi-analytical approximation are in good agreement with each other for small amplitudes in the vicinity of the bifurcation points. For both small and large caster lengths, bistable parameter domains occur where stable rectilinear motion and periodic oscillation coexist with domains of attraction separated by unstable limit cycles. This behaviour is already predicted by the second-order terms, though our semi-analytical calculation does not capture the numerically observed saddle-node bifurcation of the periodic orbits (see the folds in Figs. 7 and 8 ).
As it is denoted in Fig. 7 for short caster (\(l = 0.02\) m), the vibration amplitudes may reach \(\pi /2\) in the unstable parameter region of \(V \approx 0.35\) m/s. At this point, the mathematical model has a singularity and it cannot describe those motions where the wheel is rotating in the opposite direction. In other cases, the amplitudes remain below \(5\times 10^{-3}\) rad, e.g. in the long caster case. While these so-called ‘micro-shimmy’ vibrations [39] are unlikely to cause structural vibrations and accidents, they are still undesirable due to the related energy loss, high tyre wear and noise generation.
Bifurcation diagram for a small caster length \((l = 0.02\) m) with viscous damping \(b_\text {t} = 0.61\) Nms considered at the king pin. The thick curves are results of numerical collocation, while the thin straight lines represent the results of the analytical bifurcation calculation (102). Red and blue colours refer to unstable and stable branches, respectively
If viscous damping \(b_t\) is considered at the king pin, the stability boundaries can only be found numerically, for example, with the multidimensional bisection method [3]. In Fig. 9, we present how the stability boundaries change if an increasing value of damping is added to the system. As one would expect, the unstable parameter domains shrink and for large enough damping only the rightmost unstable domains survive. In the meantime, the nonlinear analysis revealed that the damped system largely preserves the structure of the nonlinearly stable and unstable boundaries. In Fig. 10, the bifurcation diagram is shown for \(l = 0.02\) m and \(b_t = 0.61\,\)Nms where the system also features a bistable parameter domain.
8 Conclusions
In this paper, local bifurcation analysis was performed with respect to the rectilinear motion of a towed wheel. It was confirmed analytically that the simultaneous presence of time delay and partial sliding in the tyre–ground contact leads to an alternating structure of supercritical and subcritical bifurcations in the undamped system. If viscous damping at the king pin is considered, this structure breaks down to unstable islands in the parameter plane. Another, yet theoretically relevant, result is that discarding the side-slip in linear stability analysis is correct even if time delay is considered in the brush tyre model.
The experimental, analytical and numerical results all confirmed the existence of subcritical bifurcations of the rectilinear motion, which presents bistable parameter domains for certain towing speeds. These are undetected by simple quasi-steady-state tyre models. The results follow the rule of thumb that time delay tends to destabilise dynamical systems not only in terms of linear stability but also in the nonlinear domain by inducing subcritical bifurcations. Moreover, the results also underline why the consideration of the contact memory effect could give us a better understanding of the tyre deformation dynamics and help to develop more accurate tyre models.
The unique analytical calculations in this infinite-dimensional and non-smooth problem were possible because it was shown that the evaluation of the second-order terms only is satisfactory for the Hopf bifurcation analysis. In future work, this could be followed by considering the third-order terms, which would give an estimation for the saddle-node bifurcation of the periodic orbits; this defines the fold boundary of the bistable parameter domain. Another topic of further studies should be the application of the presented technique for the stretched string tyre model. As presented in [36] for linear stability analysis, the brush and the stretched string tyre models are qualitatively identical and it is expected that their behaviour in the nonlinear domain is similar, too. Although these future extensions cause further difficulties in both the analytical and the numerical calculations, the results are expected to be close to the experimental ones not just quantitatively but also qualitatively.
Change history
02 September 2019
In the initial online version of the article, the poor alignment in the typeset matrices in Equations (44), (60), (61), (62), (70), (71), (81), (84), (85), (86), and (90) may have caused misinterpretation as vectors.
References
Awrejcewicz, J., Sendkowski, D.: How to predict stick-slip chaos in R4. Phys. Lett. A 330, 371–376 (2004)
Awrejcewicz, J., Olejnik, P.: Occurrence of stick-slip phenomenon. J. Theoret. Appl. Mech. 45(1), 33–40 (2007)
Bachrathy, D., Stepan, G.: Bisection method in higher dimensions and the efficiency number. Period. Polytech. Mech. Eng. 56(2), 81–86 (2012)
Barton, D.A.W., Krauskopf, B., Wilson, E.: Collocation schemes for periodic solutions of neutral delay differential equations. J. Differ. Equ. Appl. 12, 1087–1101 (2006)
Beregi, S., Takács, D.: Analysis of the tyre-road interaction with a non-smooth delayed contact model. In: Proceedings of the EUROMECH Colloquium578 in Rolling Contact Mechanics for Multibody System Dynamics (2017)
Beregi, S., Takács, D., Barton, D.A.W.: Hysteresis effect in the nonlinear stability of towed wheels. In: Print Proceedings of the ASME 2017 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference Nonlinear Dynamics, and Control (MSNDC) (2017)
Beregi, S., Takács, D., Stépán, G.: Nonlinear analysis of a shimmying wheel with contact-force characteristics featuring higher-order discontinuities. Nonlinear Dyn. 90, 877–888 (2017)
Facchini, G., Sekimoto, K., du Pont, S.C.: The rolling suitcase instability: a coupling between translation and rotation. In: Proceedings of the Royal Society A, MAthematical Phycical and Engineering Sciences (2017). https://doi.org/10.1098/rspa.2017.0076
Gipser, M.: FTire– the tire simulation model for all applications related to vehicle dynamics. Veh. Syst. Dyn. 45(Supplement 1), 139–151 (2007)
Hale, J.: Theory of Functional Differential Equations. Springer, New York (1977)
Holmes, J., Guckenheimer, P.: Nonlinear Oscillations Dynamical Systems and Bifurcations of Vector Fields. Springer, New York (2002)
Hölscher, H., Tewes, M., Botkin, N., Löhndorf, M., Hoffmann, K., Quandt, E.: Modeling of pneumatic tires by a finite element model for the development a tire friction remote sensor. Comput. Struct. (2004)
Insperger, T., Stépán, G.: Semi-Discretization for Time-Delay Systems–Stability and Engineering Applications. Springer, Berlin (2011)
Korunovic, N., Trajanovic, M., Stojkovic, M., Misic, D., Milovanovic, J.: Finite element analysis of a tire steady rolling on the drum and comparison with experiment. J. Mech. Eng. 57, 888–897 (2011)
Kudra, G., Awrejcewicz, J.: Approximate modelling of resulting dry friction forces and rolling resistance for elliptic contact shape. Eur. J. Mech. A. Solids 42, 358–375 (2013)
Kudra, G., Awrejcewicz, J.: Application and experimental validation of new computational models of friction forces and rolling resistance. Acta Mech. 226(9), 2831–2848 (2015)
Kudra, G., Szewc, M., Wojtunik, I., Awrejcewicz, J.: On some approximations of the resultant contact forces and their applications in rigid body dynamics. Mech. Syst. Signal Process. 79, 182–191 (2016)
Kuznetsov, Y.: Elements of Applied Bifurcation Theory. Springer, New York (2004)
Leine, R.: Bifurcations of equilibria in non-smooth continuous system. Physica D 223, 121–137 (2006)
Molnar, T.G., Dombovari, Z., Insperger, T., Stepan, G.: On the analysis of the double Hopf bifurcation in machining processes via center manifold reduction. Proc. R. Soc. A Math. Phys. Eng. Sci. 473, 20170502 (2017). https://doi.org/10.1098/rspa.2017.0502
Neild, S.A., Champneys, A.R., Wagg, D.J., Hill, T.L., Cammarano, A.: The use of normal forms for analysing nonlinear mechanical vibrations. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 373(2051), 20140404 (2015). https://doi.org/10.1098/rsta.2014.0404. http://rsta.royalsocietypublishing.org/content/373/2051/20140404
Oertel, C., Fandre, A.: Ride comfort simulations and steps towards life time calculations: RMOD-K and ADAMS. In: International ADAMS Users’ Conference. Berlin, Germany (1999)
O’Reilly, O.M., Varadi, P.: A travelers woes: some perspectives from dynamical systems. In: Moon, F.C. (ed.) IUTAM Symposium on New Applications of Nonlinear and Chaotic Dynamics in Mechanics, pp. 397–406. Kluwer Academic, Dordrecht (1999)
Pacejka, H.B.: The wheel-shimmy phenomenon: a theoretical and experimental investigation with particular reference to the non-linear problem. Phd thesis, Delft University of Technology (1966)
Pacejka, H.B.: Tyre and Vehicle Dynamics. Elsevier Butterworth-Heinemann, Oxford (2002)
Pacejka, H.B., Bakker, E.: The magic formula tyre model. Veh. Syst. Dyn. 21, 1–18 (1991)
Saux, C.L., Leine, R., Glocker, C.: Dynamics of a rolling disk in the presence of dry friction. J. Nonlinear Sci. 15, 22–61 (2005)
Sieber, J.: Local bifurcations in differential equations with state-dependent delay. Chaos Interdiscip. J. Nonlinear Sci. 27(114326), 114326 (2017)
Simpson, D.J.W.: Bifurcations in Piecewise-Smooth Continuous Systems. World Scientific Publishing Co. Pte. Ltd, Singapore (2010)
Simpson, D.J.W., Meiss, J.D.: Andronov-Hopf bifurcations in planar, piecewise-smooth, continuous flows. Phys. Lett. A 371(3), 213–220 (2007)
Stépán, G.: Great delay in predator-prey model. Nonlinear Anal. Theor. Methods Appl. 10(9), 913–929 (1986)
Stépán, G.: Retarded Dynamical Systems: Stability and Characteristic Functions. Longman Scientific and Technical, Essex (1989)
Stepan, G.: Chaotic motion of wheel. Veh. Syst. Dyn. 20(6), 241–351 (1991)
Stépán, G.: Nonlinear modelling of shimmying wheels. In: Christiansen P.L., Eilbeck J.C., Parmentier R.D. (eds) Future Directions of Nonlinear Dynamics in Physical and Biological Systems. NATO ASI Series (Series B: Physics), vol. 312. Springer, Boston, MA (1993)
Stépán., G., Haller, G.: Quasiperiodic oscillations in robot dynamics. Nonlinear Dyn. 8(4), 513–528 (1995)
Takács, D., Orosz, G., Stépán, G.: Delay effects in shimmy dynamics of wheels with stretched string-like tyres. Eur. J. Mech. A/Solids 28, 516–525 (2009)
Takács, D., Stépán, G.: Dynamic contact problem of rolling elastic wheels. In: Proceedings of ICGF 2006 (2006)
Takács, D., Stépán, G.: Experiments on quasiperiodic wheel shimmy. J. Comput. Nonlinear Dyn. 4(3), 031007 (2009)
Takács, D., Stépán, G.: Micro-shimmy of towed structures in experimentally uncharted unstable parameter domain. Veh. Syst. Dyn. 50(11), 1613–1630 (2012). https://doi.org/10.1080/00423114.2012.691522
Takács, D., Stépán, G., Hogan, S.J.: Isolated large amplitude periodic motions of towed rigid wheels. Nonlinear Dyn. 52(1–2), 27–34 (2008)
Terkovics, N., Neild, S., Lowenberg, M., Krauskopf, B.: Bifurcation analysis of a coupled nose-landing-gear-fuselage system. J. Aircr. 51(1), 259–272 (2014)
Thota, P., Krauskopf, B., Lowenberg, M.: Interaction of torsion and lateral bending in aircraft nose landing gear shimmy. Nonlinear Dyn. 57(3), 455–467 (2008)
Acknowledgements
Open access funding provided by Budapest University of Technology and Economics (BME).
Funding
This research was funded by the National Research, Development and Innovation Office under Grant No. NKFI-128422.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The original version of this article has been revised: The matrices in Equations (44), (60), (61), (62), (70), (71), (81), (84), (85), (86), and (90) have been re-aligned to prevent misinterpretation as vectors.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Beregi, S., Takacs, D. & Stepan, G. Bifurcation analysis of wheel shimmy with non-smooth effects and time delay in the tyre–ground contact. Nonlinear Dyn 98, 841–858 (2019). https://doi.org/10.1007/s11071-019-05123-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-019-05123-1