1 Introduction

Position control is a fundamental task in mechatronic systems. In such tasks, the aim of the control system is to maintain a desired position of the mechanical subsystem. The desired position can include a specified position or tracking a trajectory defined as a series of positions in time. Many applications of position control are typically related to robotic systems where state feedback is used in the control algorithm. For example, in case of industrial robots steady-state position control and trajectory tracking are very common. In those applications, the main objectives are high accuracy and high speed. The gains are usually tuned to values that guarantee best performance in terms of the primary objectives.

For such applications, comprehensive studies [1,2,3] are available on digital control theory. In classic control theory, phase and/or gain margins are used to design the controllers, while another basic design method is the so-called pole placement. This method determines the control gains of the feedback matrix in order to modify the characteristic roots or poles of the uncontrolled system to achieve the desired motion. In case of discrete-time control [4,5,6], the characteristic roots are described in continuous time, and they are transformed back to discrete-time domain with a given sampling time in order to get the control gains for the discrete-time case.

On the other hand, in force-feedback haptic systems [7], position control serves a different purpose. In such systems, the difference between desired and actual positions is seen as the deflection of a virtual spring, and the proportional control gain is the stiffness coefficient of the virtual spring. These generate the force/torque values that are fed back to the human user from the virtual environment through the haptic device. Therefore, the value of proportional gain is very important in such applications since it determines how soft or hard the user feels the virtual environment. For these systems, the sampling frequency often cannot be increased to high enough values [8], and the time discretization effects become very visible leading to stability problems.

A discrete-time position control with a proportional gain only is always unstable [9, 10], and the level of instability, the rate of divergence depends on the sampling rate; the higher it is, the slower the system position diverges away from the desired value. To stabilize a discrete-time position controlled system, some physical or virtual dissipation is needed. For high sampling rates, often the inherent physical dissipation of the mechanical system can be sufficient. But, such dissipation can also be added via derivative feedback that acts as a virtual viscous damping element. The other source of physical dissipation can come through Coulomb friction.

Little is known about the dynamic effects of Coulomb friction in haptic systems. It is typically neglected in order to achieve a linearized, worst-case system model for stability analysis [11]. Considering time discretization, delay, quantization, and Coulomb effects, a passivity condition is given in [8]. But, other papers mostly consider viscous damping that is necessary to achieve/maintain passivity [11, 12].

The analysis of the effect of sampling requires the handling of infinite dimensional mathematical models. The complexity of the mathematical treatment is further increased by the non-smooth property of dry friction [13, 14]. In order to simplify the analysis and/or the control design, the effect of dry friction is often neglected. This can be justified by considering friction compensation [15], or aiming for designing a robust controller with conservative stability conditions [16].

Although the above simplifications can be reasonable from the engineering point of view, precise control and the explanation of some intricate vibration phenomena require the use of more accurate models. As it was demonstrated in [17, 18], when Coulomb friction compensates for the possible instability caused by the sampling, decreasing vibrations occur with concave envelope. In these two papers, the only considered source of physical dissipation was Coulomb friction. As was demonstrated in a sampled-data setting, Coulomb friction can act as an important dissipative phenomenon; however, it can cause intricate dynamic effect.

In [19], the effect of the additional viscous damping was investigated while this current paper focuses on how the effect of virtual damping can modify the dynamic behavior of sampled-data systems. The main objective of this paper is not related to traditional controller design approaches, i.e., how to tune the gains to achieve best performance. We rather intend to show the complex dynamic effects that can arise due to virtual damping and Coulomb friction. These can be important in applications such as haptic systems where sampling rates often cannot be increased to high values, and the control gains themselves can carry physical meaning.

The paper is organized as follows. In Sect. 2, the mathematical model of a sampled-data system is introduced where the effect of dry friction is considered as the main source of physical dissipation. As a reference, stability and dynamic analysis of the corresponding sampled-data system with negligible dry friction is presented in Sects. 3 and 4 . The nonlinear vibrations induced by sampling and friction effects are presented in Sect. 5. Section 6 concludes the paper.

2 Model of position control

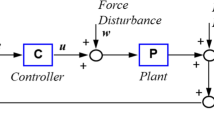
To illustrate the combined effect of sampling and dry friction on positioning, a single degree-of-freedom mechanical model is considered [20]. The mechanical system is positioned into the zero reference position by a discrete-time state-feedback controller in the presence of friction. In this model, zero-order hold is used to reconstruct the discrete-time control force into a continuous-time signal that results in a piecewise-constant function of time. The corresponding equation of motion is

$$\begin{aligned} m \ddot{q}(t) = f_{\mathrm {u}}(t_j) - f_{\mathrm {fr}}(t) \quad \text{ for } \quad t \in \left[ t_j, t_j + \tau \right) , \end{aligned}$$
(1)

where q(t) represents the generalized coordinate as a function of time t, which corresponds to the modeled degree of freedom, m denotes the generalized mass corresponding to the generalized coordinate q, and dot refers to differentiation with respect to time. In addition, \(f_{\mathrm {u}}\) is the generalized control force, \(f_{\mathrm {fr}}\) is the generalized friction force, and \(t_j = j \tau \) denotes the jth sampling instant, where \(\tau \) is the sampling time.

The generalized friction force is considered by the Coulomb friction law assuming that the magnitudes of static and kinetic friction forces are equal. Thus,

$$\begin{aligned} f_{\mathrm {fr}}(t) = {\left\{ \begin{array}{ll} f_{\mathrm {C}} \, \mathrm {sgn} \left( {\dot{q}}(t) \right) &{}\quad \text{ if } \quad {\dot{q}}(t) \ne 0 \\ \left[ -f_{\mathrm {C}} , f_{\mathrm {C}} \right] &{}\quad \text{ if } \quad {\dot{q}}(t) = 0 \end{array}\right. }, \end{aligned}$$
(2)

where \(f_{\mathrm {C}} = \mu f_{\mathrm {N}}\) denotes the magnitude of dry friction force, \(\mu \) is the kinetic friction coefficient and \(f_{\mathrm {N}}\) denotes the magnitude of normal contact force.

As it can be seen in Eq. (2), the friction force is a multivalued function at zero velocity. If the velocity is zero and \(|f_{\mathrm {fr}}| \ge |f_{\mathrm {u}}|\) at \(t\ne 0\), then the motion will stop within finite time in a so-called sticking region \(\left[ -\Delta , \Delta \right] \) generated around the desired position. With initial positions outside \(\left[ -\Delta , \Delta \right] \) and with zero initial velocity, motion takes place in the opposite direction before the velocity becomes zero resulting local extrema in the position signal. Therefore, during the analysis of motion, the friction force can be taken into account as

$$\begin{aligned} f_{\mathrm {fr}}(t) = f_{\mathrm {C}} \, \mathrm {sgn} \left( {\dot{q}}(t) \right) . \end{aligned}$$
(3)

Based on the discrete-time state feedback, the control force is determined by the linear combination of the sampled position and velocity as

$$\begin{aligned} f_{\mathrm {u}}(t_j) = - k_{\mathrm {p}} q(t_j) - k_{\mathrm {d}} {\dot{q}}(t_j), \end{aligned}$$
(4)

where the constant parameters \(k_{\mathrm {p}}\) and \(k_{\mathrm {d}}\) are the feedback gains.

In order to obtain a compact discrete-time model with reduced number of free parameters, the dimensionless time \(T = t/\tau \) is introduced. Thus, the dimensionless sampling instant is \(T_j = j\). Based on these, the equation of motion can be rewritten as

$$\begin{aligned}&\tfrac{m}{\tau ^2} q''(T) + f_{\mathrm {C}} \, \mathrm {sgn} \left( q'(T) \right) \nonumber \\&\quad = -\, k_{\mathrm {p}} q(T_j) - \tfrac{k_{\mathrm {d}}}{\tau } q'(T_j) \quad \text{ for } \quad T \in \left[ j, j + 1 \right) ,\nonumber \\ \end{aligned}$$
(5)

where prime denotes the differentiation with respect to the dimensionless time.

By assuming that the direction of motion does not change between two consecutive sampling instants, the piecewise linear system presented in Eq. (5) can be solved analytically for the discrete state variables collected in \(\mathbf {x}_j = [q_j \, v_j]^\mathrm {T}\), where the discrete states are \(q(T_j) = q_j\) and \(q'(T_j) = v_j\).

By integrating Eq. (5) over the given time interval \(T \in \left[ j, j + 1 \right) \), the following switched discrete mapping can be derived

$$\begin{aligned} \mathbf {x}_{j+1} = \mathbf {A} \mathbf {x}_j - \mathbf {a} \, \mathrm {sgn} \left( q'(T) \right) , \end{aligned}$$
(6)

where

$$\begin{aligned} \mathbf {A} = \begin{bmatrix} 1-\tfrac{p}{2}&1-\tfrac{d}{2} \\ -p&1-d \end{bmatrix} \quad \text{ and } \quad \mathbf {a} = \begin{bmatrix} \tfrac{\sigma }{2}\\ \sigma \end{bmatrix} \end{aligned}$$
(7)

with

$$\begin{aligned} p = \tfrac{k_{\mathrm {p}} \tau ^2}{m}, \quad d = \tfrac{k_{\mathrm {d}} \tau }{m} \quad \text{ and } \quad \sigma = \tfrac{f_{\mathrm {C}} \tau ^2}{m}. \end{aligned}$$
(8)

This mapping is valid between velocity reversals, and by detecting the zero crossings in the velocity, it can be used to numerically calculate the solution without directly integrating Eq. (5). For further details see [18].

3 Stability analysis with negligible friction

First, the case is investigated when the effect of dry friction is neglected, i.e., \(\sigma = 0\). The corresponding results can serve as reference to examine the effect of friction on system stability. Consequently, Eq. (6) simplifies to the linear map \(\mathbf {x}_{j+1} = \mathbf {A} \mathbf {x}_j\).

Fig. 1
figure 1

Stability chart in the frame of dimensionless control parameters p–d (left) and the location of characteristic multipliers in the complex plane z (right). (Color figure online)

Full size image
Fig. 2
figure 2

Numerical simulation without the effect of friction. The control parameters are selected to be \(p=3.5\) and \(d=1.935\), and the initial conditions are \(x_0=6.25\), \(v_0=0\). (Color figure online)

Full size image

Using this linear map, the time series of the discrete states can be determined for any initial conditions \(\mathbf {x}_0\) which forms a generalized, or multidimensional geometric series, called Neumann series [16]. The convergence of this series is equivalent to \(\rho (\mathbf {A}) < 1\) where \(\rho \) denotes spectral radius. Thus, the eigenvalues of matrix \(\mathbf {A}\) determine the asymptotic stability of the system, which is stable if, and only if, the eigenvalues are inside the complex unit disk [4], i.e., \(|z_n| < 1\) with \(n = 1,2\).

The characteristic equation of matrix \(\mathbf {A}\) can be given in the from

$$\begin{aligned} z^2 - \left( 2-d-\tfrac{p}{2}\right) z + 1-d+\tfrac{p}{2} = 0. \end{aligned}$$
(9)

If the Möbius transformation \(z = (w+1)/(w-1)\) with \(w \in {\mathbb {C}}\) is applied, the complex unit disk is transformed into the left half of the complex plane and the stability condition is also reformulated to

$$\begin{aligned} |z_n|<1, \, n=1,2 \quad \Leftrightarrow \quad \mathrm {Re}\{w_n\}<0, \, n=1,2. \end{aligned}$$
(10)

Using the Routh–Hurwitz stability criterion for w, the stability condition yields

$$\begin{aligned} p> 0, \quad d>\tfrac{p}{2} \quad \text{ and } \quad d<2 \end{aligned}$$
(11)

for the control parameters. The corresponding stable domain is illustrated in the plane of the dimensionless control gains p and d as a shaded triangular area in the left panel of Fig. 1.

Since the possible maximum steady-state error is \(\Delta = \sigma / p\), the proportional gain needs to be selected as high as possible [16] to improve the precision of positioning. As an example, consider the case of \(p=3.5\) and \(d=1.935\), which selection results in somewhat unexpected multi-frequency oscillations in the frictionless case. Such oscillations are plotted in black in both panels of Fig. 2.

This behavior can be explained by considering the higher harmonics associated with the time domain transformation of the eigenvalues of the transition matrix \(\mathbf {A}\), which is presented in detail in Sect. 4. The effect of higher harmonics can also be seen in Fig. 3. In this figure, the power spectrum is calculated by using the same time history of vibration which is presented using the black line in Fig. 2.

Fig. 3
figure 3

Power spectrum of the result of the numerical simulation without the effect of friction. The control parameters are selected to be \(p=3.5\) and \(d=1.935\), and the initial conditions are \(x_0=6.25\), \(v_0=0\)

Full size image

4 Dynamic analysis with negligible friction

The coefficients of the monomials of the characteristic polynomial in Eq. (9) and the discriminant of Eq. (9) determine the location of the characteristic roots, or the so-called characteristic multipliers \(z_{1,2}\) in the complex plane z. It follows that these conditions result in three separation curves in the stable domain by

$$\begin{aligned} {\mathcal {T}}:= & {} \mathrm {tr} (\mathbf {A}) = 0 \quad \Leftrightarrow \quad d = 2 - \tfrac{p}{2}, \end{aligned}$$
(12)
$$\begin{aligned} {\mathcal {D}}:= & {} \det (\mathbf {A}) = 0 \quad \Leftrightarrow \quad d= 1 + \tfrac{p}{2}, \end{aligned}$$
(13)
$$\begin{aligned} \delta:= & {} {\mathcal {T}}^2-4{\mathcal {D}} = 0 \quad \Leftrightarrow \quad d = -\tfrac{p}{2} \pm 2 \sqrt{p} \,. \end{aligned}$$
(14)

In the left panel of Fig. 1, the red, green and blue dashed lines obtained from the expressions in Eqs. (12)–(14) correspond to the sub-domain boundaries. These lines divide the stable domain into six regions where the different locations of the characteristic multipliers are demonstrated by blue dots in the right panel of Fig. 1 where the small black crosses represent \({\mathcal {T}}/2\).

The location of the characteristic multipliers determines the different types of possible motions. Thus, these roots have to be transformed by using inverse \({\mathcal {Z}}\) transformation that is given, in general, as \(s = \ln (z)/\tau \). This transformation rule is presented in Fig. 4, and it further simplifies to \(s = \ln (z)\) due to the introduction of dimensionless time.

Fig. 4
figure 4

Transformations between the domains of s and z. The parameters \(\rho \) and \(\vartheta \) are defined in Eq. (17). Furthermore \(\beta =\ln (\rho )/\tau \), \(\omega _0 = \vartheta /\tau \) and \(\omega _{\mathrm {s}} = 2 \pi /\tau \)

Full size image

Based on the characteristic equation in Eq. (9), the characteristic multipliers can be expressed as

$$\begin{aligned} z_{1,2} =\tfrac{{\mathcal {T}}}{2} \pm \tfrac{\sqrt{\delta }}{2} =\tfrac{4-2d-p}{4} \pm \tfrac{\sqrt{(2d+p)^2 - 16p}}{4}. \end{aligned}$$
(15)

In order to apply the inverse \({\mathcal {Z}}\) transformation in the easiest way, these characteristic multipliers in Eq. (15) are reformulated into the complex exponential form as \(z = \rho \mathrm {e}^{i \vartheta }\), where \(\rho \) and \(\vartheta \) denote the magnitude and the argument of z. It is important to note that z is also a rotating vector which means \(\vartheta \) is periodic and \(\vartheta + 2k \pi \), \(k \in {\mathbb {Z}}\). If the transformation is applied, then the resulting infinite number of characteristic roots in the domain of s are called characteristic exponents.

As an example, Fig. 4 also presents the location of the characteristic multipliers associated with the sub-domain \(\#\)5 and also the corresponding characteristic exponents. In this sub-domain, \({\mathcal {T}}<0\), \({\mathcal {D}}>0\) and \(\mathcal {\delta }<0\) results in \(z_{1,2} \in {\mathbb {C}}\) with negative real part and nonzero imaginary part. Based on these properties

$$\begin{aligned} z_1 = \rho \mathrm {e}^{i (\vartheta + 2k \pi )} \quad \text{ and } \quad z_2 = \rho \mathrm {e}^{-i(\vartheta - 2k \pi )} \end{aligned}$$
(16)

where

$$\begin{aligned} \rho = \sqrt{1 - d + p/2} \quad \text{ and } \quad \tan \vartheta = \tfrac{\sqrt{16 p - (2d+p)^2}}{4-2d-p}.\nonumber \\ \end{aligned}$$
(17)

After the application of the inverse \({\mathcal {Z}}\) transformation, the characteristic exponents are

$$\begin{aligned} s_1 = \tfrac{\ln (\rho )}{\tau } + i \tfrac{\vartheta + 2k \pi }{\tau } \quad \text{ and } \quad s_2 = \tfrac{\ln (\rho )}{\tau } - i \tfrac{\vartheta - 2k \pi }{\tau }.\nonumber \\ \end{aligned}$$
(18)
Fig. 5
figure 5

Numerical simulations without and with the effect of friction. The control parameters are selected to be \(p=0.95\) and \(d=0.36\), and the initial conditions are \(x_0=9.4\), \(v_0=0\) with \(\sigma = 0.8\). (Color figure online)

Full size image
Fig. 6
figure 6

Numerical simulation with and without the effect of friction. The control parameters are selected to be \(p=3.74\) and \(d=1.77\), and the initial conditions are \(x_0=5\), \(v_0=0\) with \(\sigma = 1.1\)

Full size image

If only the dominant characteristic exponents are taken into account, the position x(T) can be given as

$$\begin{aligned} x(T) = \mathrm {e}^{\beta T} \left( c_1 \cos (\omega _0 T) + c_2 \sin (\omega _0 T)\right) , \end{aligned}$$
(19)

where \(\beta =\ln (\rho )/\tau \) and \(\omega _0 = \vartheta /\tau \). The constants \(c_1\) and \(c_2\) come from the initial conditions \(x(0)=x_0\) and \(x'(0) = v_0\). Based on this, the given oscillation is presented in blue in the left panel of Fig. 2. On the other hand, if the higher harmonics corresponding to \(k=-1\) are also taken into account, x(T) can be characterized as

$$\begin{aligned} x(T)= & {} \mathrm {e}^{\beta T} \left( c_1 \cos (\omega _0 T) +\,c_2 \sin (\omega _0 T) \right. \nonumber \\&\left. +\, c_3 \cos (\omega _1 T) + c_4 \sin (\omega _1 T)\right) , \end{aligned}$$
(20)

where \(\omega _1 = \omega _{\mathrm {s}} - \omega _0\) with \( \omega _{\mathrm {s}} = 2 \pi /\tau \). The constants \(c_1\), \(c_2\), \(c_3\) and \(c_4\) come also from initial conditions, but, based on the original system, only two conditions \(x(0)=x_0\) and \(x'(0) = v_0\) are known. The other necessary equations can be given from the properties of the original system: due to the applied zero-order holder, the initial acceleration is constant, i.e., \(x''(0) = - p x_0 - d v_0\) and therefore the initial jerk is \(x'''(0) =0\). Based on this, the given oscillation is presented as the dashed red curve in the right panel of Fig. 2. As it can also be seen, this red curve shows good agreement with the simulated black one of the full system.

Accordingly, without considering the effect of higher harmonics corresponding to \(k=-1\), the dominant motions cannot be characterized correctly. This consequence is also valid for the characterization of the typical motions in sub-domains \(\#\)2, \(\#\)3 and \(\#\)4 where the common property is that one of the characteristic multipliers lies in the left half of the complex plane z.

5 Nonlinear vibrations induced by sampling and friction effects

When Coulomb friction can stabilize an otherwise unstable motion, the resulting motions may have concave envelope [17, 18]. If the control gains are selected from the lower region of the stability map, the motion is exponentially unstable with one dominant frequency. It is presented as black curve in the left panel of Fig. 5. When the friction stabilizes the motion, the predicted concave envelope is presented as red curve in the right panel of Fig. 5.

This concave envelope is also observed when the effect of friction stabilizes such kind of unstable motions that can be characterized by two dominant vibration frequencies. This is presented in the left panel of Fig. 6. In these cases, due to the effects of two dominant frequencies, it results in the vibrations exhibit double concave envelope as shown in the right panel of Fig. 6.

As it was mentioned above, the stabilization effect of Coulomb friction is sensitive to the initial conditions resulting unstable limit cycle around the zero desired position. In case of the presented examples, when the motions are initiated with zero velocity at \(x_0 = 5.8\) instead of \(x_0 = 5\), or at \(x_0 = 9.8\) instead of \(x_0 = 9.4\) the motions become unstable due to the presence of an unstable oscillation.

6 Conclusions

In this paper, the main characteristics of position controlled mechanical systems were investigated by considering dry friction as the primary source of physical dissipation. For the analysis of the effect of sampling with dry friction, a detailed analysis was presented for the frictionless system. It was demonstrated that even a single degrees-of-freedom mechanical system can have multi-frequency vibrations when it is positioned by a discrete-time state-feedback controller. The observed vibrations can be explained by the higher harmonics in the solution which correspond to the periodicity of the eigenvalues of the transition matrix. When the effect of dry friction is also taken into account, it was also shown that the position controlled systems with discrete-time state feedback can become sensitive to the initial conditions, and unstable oscillations may appear around the desired position.