1 Introduction

The tasks of human motion control can be classified in many different ways. One of the simplest categorizations can be represented with the help of the basic single-degree-of-freedom (DoF) mechanical model

$$\begin{aligned} m\ddot{q} + k q = Q(q,\dot{q},\ddot{q}), \end{aligned}$$
(1)

where m and k refer to the inertia and the stiffness of the controlled mechanical system, respectively, which may be the model of certain parts of the human body, while Q refers to the control force of certain muscles, which is actuated as a function of the sensed position q, velocity \(\dot{q}\) and/or acceleration \(\ddot{q}\) with dot referring to time derivatives.

The position control task corresponds to the case when the mass is not in contact with the environment, that is, the stiffness is zero: \(k=0\). Force control is represented by the case of positive stiffness \(k>0\) that models the elastic contact between the mass m and the environment. Finally, stabilization of otherwise unstable positions refers to the case of \(k < 0\), since these systems would be unstable without any control force Q due to the negative stiffness in the structure. Human balancing during standing still belongs to this class of problems.

Clearly, many further combinations of these basic control tasks can appear, like hybrid position/force control, or following prescribed paths while balancing, or tasks with many DoF involved. These basic models are established in classical robotics papers [1, 2] and books like [3]. Biomechanics often uses these models for the mathematical description of human motion, although there are many obvious differences. One of these is related to the time delay that appears in the human motion control. The delays are originated in the processing time of the sensory signals in the neural system and also in the reaction time of the muscles. These time delays of 0.1–1 s are orders of magnitudes larger than the ones that appear in robotics related to the sampling times of the digital controllers. The digital effects related to sampling and zero-order hold in time were considered in several studies on force control [4,5,6,7], but it is less investigated in case of analogous time delays that are essential elements of models in human motion control [8], human force control [9, 10] or human balancing [11,12,13,14]. Remote force control tasks of telemanipulation [15,16,17] and physical contacts between robots and humans via force control are actual research topics of haptic systems [18,19,20,21], specifically in rehabilitation robotics [22,23,24].

This paper investigates the basic models of force control in the presence of human reaction time delays from nonlinear vibrations viewpoint similarly to the Hopf bifurcation analyses in delayed oscillators [25,26,27], predator–prey population models [28,29,30] or delayed networks in transportation, biological and neural systems [31,32,33]. These calculations are usually based on the center manifold reduction and normal form theory summarized in [34], which are then combined with the infinite dimensional representation of delay differential equations [35]. The corresponding algorithm of the Hopf bifurcation analysis in delay systems was published in [36]. While this algorithm has a rigorously proven theoretical background, the application of the method of multiple scales (MMS) can make shortcuts in the lengthy algebraic manipulation [37]. A relevant single-authored paper [38] of Nayfeh discussed the comparison of the two approaches in the presence of delay parameters, and since then, MMS has become equally popular in the nonlinear analysis of delay systems.

The structure of the paper is as follows. The simplest possible force control strategy is considered with proportional gains while the saturation of the control force is taken into account as the relevant nonlinearity. The corresponding mechanical models are presented in Sect. 2, where the equations of motion are derived for different locations of the force sensors: first, called non-collocated case, when the contact force is sensed between the rigid environment and the mass, and second, called collocated case, when it is sensed between the mass and the actuator. In the non-collocated case, in Sect. 3, the stability analysis of the steady-state desired contact force is presented together with the Hopf bifurcation calculation done by the method of multiple scales extended for nonlinear delay differential equations. The same calculations are presented for the collocated configuration in Sect. 4. The analytical results and conclusions are summarized in Sect. 5.

2 Mechanical models of basic force control concepts

Consider the basic task of force control when a block of mass m is in contact with the rigid environment through a spring of stiffness \(k_1\) along a horizontal axis as shown in Fig. 1. The actual contact force is measured by means of a serially connected spring of large stiffness \(k_2(\gg k_1)\). In Fig. 1a, the so-called non-collocated configuration is presented where the force sensor is at the contact point to the rigid environment and its signal is fed back to the control force Q of the actuator, while Fig. 1b is the sketch of the collocated configuration with contact force measured at the actuator force.

Fig. 1
figure 1

Mechanical models with non-collocated (a) and collocated (b) force sensor configurations. The stiffness \(k_2\) of the force sensor is an order of magnitude larger than the stiffness \(k_1\) of the actuator. P refers to proportional gain; \(\tau \) stands for time delay

Full size image

2.1 Modeling the non-collocated configuration

In case of Fig. 1a, the Newtonian equations assume the form

$$\begin{aligned}& m\ddot{q}_1=Q-k_1(q_1-q_2) \nonumber \\& 0= k_1(q_1-q_2)-k_2 q_2, \end{aligned}$$
(2)

where the selected generalized coordinates \(q_1\) and \(q_2\) are the absolute positions of the block and the end point of the spring that senses the force, respectively. The actuator force Q depends on the force error

$$\begin{aligned} F_{\mathrm{e}}=F_{\mathrm{m}}-F_{\mathrm{d}}, \end{aligned}$$
(3)

which is the difference in the actual measured force

$$\begin{aligned} F_{\mathrm{m}}=k_2q_2 \end{aligned}$$
(4)

and the constant desired force \(F_{\mathrm{d}}\). Consider the simplest possible linear control strategy using a single (dimensionless) proportional gain P for the force error \(F_{\mathrm{e}}\) while adding the actual measured force (see [3]):

$$\begin{aligned} Q=-P(F_{\mathrm{m}}-F_{\mathrm{d}}) + F_{\mathrm{m}}. \end{aligned}$$
(5)

The reaction time \(\tau \) of the human actuation can be taken into account with the delayed values \(F_{\mathrm{m}}(t-\tau )\) of the measured force in (4), and the additional parameter \(F_{\mathrm{s}}\) can describe the level of the actuator force saturation approximated by means of the tangent hyperbolic function \(\mathrm{tanh}\). This way, the actual control force Q at the time instant t is given by

$$\begin{aligned} Q(t)= & {} -F_{\mathrm{s}}\;\mathrm{tanh}\left( {\frac{1}{F_{\mathrm{s}}}} P\bigl (k_2q_2(t-\tau )-F_{\mathrm{d}}\bigr ) \right) \nonumber \\&+ \,k_2q_2(t-\tau ). \end{aligned}$$
(6)

The equations of motion (2) with the nonlinear delayed control force (6) have an equilibrium at the trivial solution

$$\begin{aligned} q_{10}={\frac{k_1+k_2}{k_1k_2}}F_{\mathrm{d}},\quad q_{20}={\frac{1}{k_2}}F_{\mathrm{d}}. \end{aligned}$$
(7)

The perturbation x around the equilibrium of the block at \(q_{10}\) with \(q_1(t)=q_{10}+x(t)\) is introduced. If the approximation \(k_2\!\gg \!k_1\) is used for the angular natural frequency \(\omega _{\mathrm{n}}\) of the uncontrolled system, and if the dimensionless perturbed block position \(\tilde{x}\) is scaled to the static saturation level \(F_{\mathrm{s}}/k_1\) and the dimensionless time \(\tilde{t}\) is scaled to the delay \(\tau \), then we have

$$\begin{aligned} \omega _{\mathrm{n}} \approx \sqrt{k_1/m},\quad \tilde{x}=x/(F_{\mathrm{s}}/k_1),\quad \tilde{t}=t/\tau , \end{aligned}$$
(8)

where, by abuse of notation, we will drop the tilde from the dimensionless variables. Substituting all these into the Newtonian equation (2) and eliminating the state variable \(q_2\), we obtain the nonlinear delay differential equation (DDE) of retarded type in the dimensionless form of

$$\begin{aligned} \ddot{x}(t)+(\omega _{\mathrm{n}}\tau )^2x(t)= & {} (\omega _{\mathrm{n}}\tau )^2x(t-1)\nonumber \\&-(\omega _{\mathrm{n}}\tau )^2\;\mathrm{tanh}\left( P x(t-1)\right) \end{aligned}$$
(9)

with trivial solution at zero. Note that the dimensionless parameter \(\omega _{\mathrm{n}}\tau =2\pi (\tau /T)\) can also be expressed with the ratio of the reaction time \(\tau \) and the time period T of the free oscillation of the uncontrolled system.

2.2 Modeling the collocated configuration

When the collocated configuration is considered as shown in Fig. 1b, the Newtonian equations assume the form

$$\begin{aligned}& m\ddot{q}_1=k_2q_2-k_1q_1 \nonumber \\& 0=Q-k_2q_2, \end{aligned}$$
(10)

where the generalized coordinates \(q_1\) and \(q_2\) now stand for the absolute position of the block of mass m and the position of the end of the spring of stiffness \(k_2\) relative to the position of the block. This choice of coordinates means that the measured force \(F_{\mathrm{m}}\) can be expressed in the same way as in (4) and the saturated and delayed actuator force can be expressed as given in (6).

The equations of motion (10) with the control force (6) have a trivial solution at

$$\begin{aligned} q_{10}={\frac{1}{k_1}}F_{\mathrm{d}},\quad q_{20}={\frac{1}{k_2}}F_{\mathrm{d}}. \end{aligned}$$
(11)

If the perturbation x is introduced again around the equilibrium \(q_{10}\) of the block in the same way as in the case of the non-collocated configuration, and the same dimensionless quantities are used as in (8), then the elimination of the coordinate \(q_2\) from the equations of motion (10) leads to the nonlinear DDE of neutral type

$$\begin{aligned}& \ddot{x}(t)+(\omega _{\mathrm{n}}\tau )^2x(t)= \ddot{x}(t-1)+(\omega _{\mathrm{n}}\tau )^2x(t-1)\nonumber \\&\quad -(\omega _{\mathrm{n}}\tau )^2\;\mathrm{tanh}\left( P\Bigl (\frac{1}{(\omega _{\mathrm{n}}\tau )^2}\ddot{x}(t-1) + x(t-1)\Bigr )\right) .\nonumber \\ \end{aligned}$$
(12)

This equation of motion is similar to Eq. (9) of the non-collocated case, but there is an essential difference due to the appearance of the delayed acceleration terms \(\ddot{x}(t-1)\). While (9) has the standard form of a retarded DDE, the neutral DDE (12) has an implicit form that generally cannot be expressed in the standard explicit form as required for the application of fundamental theorems for neutral DDEs (see, e.g., in [35, 39]). In this case, however, it is easy to recognize that the implicit neutral DDE (12) can be transformed into the explicit scalar nonlinear difference equation

$$\begin{aligned} y(t)=y(t-1)-\mathrm{tanh}\left( Py(t-1)\right) \end{aligned}$$
(13)

by means of the new variable

$$\begin{aligned} y=\frac{1}{(\omega _{\mathrm{n}}\tau )^2}\ddot{x}+ x. \end{aligned}$$
(14)

The physical meaning of this transformation is clear: The dynamics of the block and the spring of stiffness \(k_1\) has no effect on the dynamics of the actuator force that is determined by the delayed force \(k_2q_2(t-\tau )\) sensed at the actuator. In other words, the second algebraic equation of (10) with the delayed and saturated control force expression in (6) can be transformed into the same nonlinear difference Eq. (13) by selecting \(y=k_2q_2-F_{\mathrm{d}}\).

3 Analysis of non-collocated configuration

The third-order Taylor series approximation of the nonlinear retarded DDE (9) assumes the form

$$\begin{aligned}& \ddot{x}(t) + ({\omega _{\mathrm{n}}}\tau )^2x(t)\nonumber \\&\quad =({\omega _{\mathrm{n}}}\tau )^2\left( (1-P)x(t-1)+\frac{1}{3}P^3x^3(t-1)\right) .\nonumber \\ \end{aligned}$$
(15)

First, the linear part is used to determine the stable domains in the parameter plane \(\omega _{\text{ n }}\tau \) and P, and then, the Hopf bifurcation calculations are presented for the above third-order approximation by means of the methods of multiple scales.

3.1 Stability

The local stability is analyzed by means of the characteristic function

$$\begin{aligned} D(\lambda )=\lambda ^2+({\omega _{\mathrm{n}}}\tau )^2(1+(P-1)\mathrm{e}^{-\lambda }) \end{aligned}$$
(16)

of the linear part of (15). At the limit of stability, the decomposition of the characteristic function (16) with substitution of the critical pure imaginary characteristic root \(\lambda _{\mathrm{c}}=\mathrm{i}\omega _{\mathrm{c}}\) yields:

$$\begin{aligned} \mathop {\mathrm{Re}}(D({\text {i}}\omega _{{\text {c}}}))= & {} ({\omega _{\mathrm{n}}}\tau )^2(P-1)\cos \omega _{{\text {c}}} +({\omega _{\mathrm{n}}}\tau )^2-{\omega _{{\text {c}}}}^2, \nonumber \\ \end{aligned}$$
(17)
$$\begin{aligned} \mathop {\mathrm{Im}}(D({{\text {i}}}\omega _{{\text {c}}}))= & {} ({\omega _{\mathrm{n}}}\tau )^2(1-P)\sin \omega _{{\text {c}}}. \end{aligned}$$
(18)

The equations \(\mathop {\mathrm{Re}}(D({{\text {i}}}\omega _{\text {c}}))=0\) and \(\mathop {\mathrm{Im}}(D({{\text {i}}}\omega _{{\text {c}}}))=0\) give critical values for the gain P and the dimensionless critical angular frequency \(\omega _{{\text {c}}}\):

$$\begin{aligned} P = \left\{ {\begin{array}{*{20}{cl}} {1,} &{} \,{{\omega _c} = {\omega _n}\tau },\\ 2-\frac{(2k-1)^2\pi ^2}{{({\omega _n}\tau )}^2}, &{} \,{{\omega _c} = (2k - 1)\pi },\\ {{{\frac{{(2k{\pi })^2 }}{{({\omega _n}\tau )^2 }}} }}, &{} \,{{\omega _c} = 2k\pi }, \end{array}} \right. \end{aligned}$$
(19)

with \(k=1,2,\ldots \) . This leads to the stability chart in the parameter plane of \((P,\omega _{\text {n}}\tau )\) for the case of non-collocated force control, as shown in Fig. 2. For certain given values of the gain P, the critical delay parameters \(\tau _\text {c}\) can be obtained from

$$\begin{aligned} \omega _{\text {n}}\tau _{\text {c},j} =&\frac{j}{\sqrt{2-P}}\pi ,\quad \text {for}\ j=2k-1, \end{aligned}$$
(20)
$$\begin{aligned} \omega _{\text {n}}\tau _{\text {c},j} =&\frac{j}{\sqrt{P}}\pi ,\quad \quad \text {for}\ j=2k, \end{aligned}$$
(21)

where \(k=1,2,\ldots \), and the critical angular oscillation frequency is given by \(\omega _{\text {c},j}=j\pi \) corresponding to the stability limit at \(\tau _{\text {c},j}\). Some numerical values for the critical delays \(\tau _{\text {c},j}\) and vibration frequencies \(\omega _{\text {c},j}\) are summarized in Table 1 for the specific gains \(P=0.6, 0.9, 1.2\) and 1.5 in the subsequent subsection where the Hopf bifurcations are analyzed at the critical delays (20) and (21). The stability boundaries in Fig. 2 are numbered according to the sequential numbers j of the critical delays, but for the sake of simplicity, the sequential subscripts j for the values of the critical delay \(\tau _{\text {c}}\) and vibration frequency \(\omega _{\text {c}}\) are dropped later.

Table 1 Critical delay values (see black dots in Fig. 2), dimensionless critical angular frequencies and senses of Hopf bifurcations for different feedback gains P
Full size table
Fig. 2
figure 2

Stability chart in the parameter plane \((P,\omega _{\text {n}}\tau )\) for non-collocated force control. Shaded regions refer to stability. Black stability boundaries refer to supercritical and red ones to subcritical Hopf bifurcations

Full size image

As it is shown in Fig. 2, the maximal gain value can be calculated at the intersection of the first and second stability boundary curves. The calculation is based on the second and third equations of (19) for \(k=1\), and it gives \(P_{\text {max}}=8/5\) at the critical delay \(\tau _{\text {c},1}=\tau _{\text {c},2}=\sqrt{5/2\,}\pi /\omega _{\mathrm{n}}\).

3.2 Hopf bifurcation

In order to analyze the effect of varying the delay parameter, the dimensionless bifurcation parameter \(\mu \) is chosen as

$$\begin{aligned} \omega _\text {n}\tau =\omega _\text {n}\tau _\text {c}+\mu \end{aligned}$$
(22)

in the subsequent calculations, where the critical dimensionless parameter values \(\omega _\text {n}\tau _\text {c}\) corresponding to the critical delay \(\tau _{{\text {c}}}\) can be determined from (19) for any fixed value of the gain P. To study small amplitude oscillations, let

$$\begin{aligned} x(t) = \sqrt{\varepsilon } \bar{x}(t),\quad \mu =\varepsilon \bar{\mu }, \end{aligned}$$
(23)

where \(\varepsilon \) is a small non-dimensional bookkeeping parameter, i.e., \(0\!<\!\varepsilon \! \ll \! 1\), and \(\bar{\mu }={{\text {O}}}(1)\) is the detuning parameter (see [37, 38] or Appendix 2 in [40]). Then Eq. (15) can be transformed in the form

$$\begin{aligned}& \ddot{x}(t)+(\omega {_\text{ n }}\tau _{\text{ c }}+\varepsilon {\mu })^2x(t)=(\omega {_\text{ n }}\tau _{\text{ c }}+\varepsilon {\mu })^2(1-P)x(t-1)\nonumber \\&\quad +\frac{1}{3}\varepsilon (\omega {_\text{ n }}\tau _{\text{ c }}+\varepsilon {\mu })^2P^3x^3(t-1), \end{aligned}$$
(24)

where, by abuse of notation, the over-lines are dropped immediately from \(\overline{x}\) and \(\overline{\mu }\). The multiple timescales are defined as \(T_k=\varepsilon ^k t,\ k=0,1,2,\ldots \). To study the Hopf bifurcation, a two-scale expansion of the solution is assumed as

$$\begin{aligned} x(t) = {x_0}({T_0},{T_1}) + \varepsilon {x_1}({T_0},{T_1}) + {\text {O}}({\varepsilon ^2}). \end{aligned}$$
(25)

By means of the differential operators defined as [38]

$$\begin{aligned} \begin{array}{l} \frac{{\text {d}}}{{{\text {d}}t}} = \frac{\partial }{{\partial {T_0}}} + \varepsilon \frac{\partial }{{\partial {T_1}}} + \text {O}({\varepsilon ^2}) =: {\text {D}_0} + \varepsilon {\text {D}_1} + \text {O}({\varepsilon ^2}),\\ \frac{{{\text {d}^2}}}{{\text {d}{t^2}}} =: \text {D}_0^2 + 2\varepsilon {\text {D}_0}{\text {D}_1} + \text {O}({\varepsilon ^2}), \end{array} \end{aligned}$$
(26)

the delayed state can be expressed as

$$\begin{aligned} x(t - 1 )= & {} {x_0}({T_0} - 1 ,{T_1} - \varepsilon ) + \varepsilon {x_1}({T_0} - 1,{T_1} - \varepsilon ) + \text {O}({\varepsilon ^2})\nonumber \\= & {} {x_0}({T_0} - 1 ,{T_1}) + \varepsilon ({x_1}({T_0} - 1 ,{T_1})\nonumber \\&-{D_1}{x_0}({T_0} - 1 ,{T_1})) + \text {O}({\varepsilon ^2}). \end{aligned}$$
(27)

Substituting Eqs. (25), (26) and (27) into Eq. (24), and equating the same powers of \(\varepsilon \), a set of linear partial differential equations are obtained in the form

$$\begin{aligned}& \text {D}_0^2{x_0}+(\omega {_\text{ n }}\tau _{\text{ c }})^2\bigl ((P-1)x_{0\tau }+x_0\bigr ) = 0, \nonumber \\& \text {D}_0^2{x_1}+(\omega {_\text{ n }}\tau _{\text{ c }})^2\bigl ((P-1)x_{1\tau }+x_1\bigr )\nonumber \\&\quad = -2\text {D}_0\text {D}_1x_0 +(P-1)(\omega {_\text{ n }}\tau _{\text {c}})^2\text {D}_1x_{0\tau } \nonumber \\&\qquad -2{\mu }(\omega {_\text {n}}\tau _{\text{ c }})\bigl (x_0 +(P-1)x_{0\tau }\bigr ) +\frac{1}{3}P^3(\omega {_\text{ n }}\tau _{\text{ c }})^2x^3_{0\tau },\nonumber \\ \end{aligned}$$
(28)

where the notations \(x_k:=x_k(T_0, T_1)\), \(x_{k\tau }:=x_k (T_0-1, T_1)\) are introduced.

At the stability boundary, one pair of pure imaginary characteristic roots \(\pm \mathrm{i} \omega _{\mathrm{c}}\) exists, while all the other infinitely many eigenvalues have negative real parts. All the solution terms related to these negative real eigenvalues decay with time. Thus, to study the long-time behavior of the system, the solution of the first equation of (28) is assumed as

$$\begin{aligned} x_0(T_0,T_1)=R(T_1){\mathrm{e}}^{{\mathrm{i}}\omega _{\mathrm{c}} T_0}+\overline{R}(T_1)\mathrm{e}^{-\mathrm{i}\omega _{\mathrm{c}} T_0}\, \end{aligned}$$
(29)

with the complex amplitude R and with \(\overline{R}\) denoting its complex conjugate, \({\mathrm{i}}^2=-\,1\). Substituting Eq. (29) into the second equation of (28), the secular term can be found, which must be zero:

$$\begin{aligned}& \left( 2\,\mathrm{i}\,\omega _{\mathrm{c}}-({\omega _{\mathrm{n}}}{\tau _{\mathrm{c}}})^2 (P-1)\mathrm{e}^{-\mathrm{i}\omega _{\mathrm{c}}}\right) \overset{\,\circ }{R}(T_{1})\nonumber \\&\quad +2\mu {\omega _{\mathrm{n}}}{\tau _{\mathrm{c}}}\left( 1+(P-1)\mathrm{e}^{-\mathrm{i}\omega _{\mathrm{c}}}\right) R(T_1)\nonumber \\&\quad -({\omega _{\mathrm{n}}}{\tau _{\mathrm{c}}})^2 P^3 \mathrm{e}^{-\mathrm{i}\omega _{\mathrm{c}}} R^2(T_1){\overline{R}}(T_1)=0, \end{aligned}$$
(30)

where over-circle stands for the derivative w.r.t. the slow time: \(\overset{\,\circ }{R}=\mathrm{d}R/\mathrm{d}T_1\). This can be arranged into the complex normal form

$$\begin{aligned} \overset{\,\circ }{R}=\gamma \mu R+\delta {{R}^2\bar{R}}, \end{aligned}$$
(31)

with

$$\begin{aligned} \gamma= & {} -\frac{2\omega _{{\mathrm{n}}}\tau _{{\mathrm{c}}}(P-1+{\mathrm{e}^{\mathrm{i}\omega _{\mathrm{c}}}}) }{2\,{\text {i}}\,\omega _{{\mathrm{c}}}{\mathrm{e}^{\mathrm{i}\omega _{\mathrm{c}}}}-({\omega _{\mathrm{n}}}{\tau _{{\text {c}}}})^2 \left( P-1 \right) } , \end{aligned}$$
(32)
$$\begin{aligned} \delta= & {} \frac{{\omega _{{\text {n}}}}^{2} {\tau _{{\text {c}}}}^{2}{P}^{3}}{2\,{\text {i}}\,\omega _{{\mathrm{c}}}{\mathrm{e}^{\mathrm{i}\omega _{\mathrm{c}}}}-({\omega _{\mathrm{n}}}{\tau _{{\text {c}}}})^2 \left( P-1 \right) }. \end{aligned}$$
(33)

The sign of the Poincaré–Lyapunov constant \({\text {Re}}\,\delta \) determines the sense of Hopf bifurcation: It is supercritical or subcritical if \({\text {Re}}\,\delta <0\) or \({\text {Re}}\,\delta >0\), respectively, i.e., the bifurcated periodic motions are stable or unstable, respectively. Here for the non-collocated case, we have

$$\begin{aligned} {\text {Sgn}}\,{\text {Re}}\,\delta ={\text {Sgn}}\,(1-P) , \end{aligned}$$
(34)

which indicates that the Hopf bifurcation is supercritical (or subcritical) for \(P>1\) (or \(0<P<1\)). These results are also indicated in case of the numerical values in Table 1. Note that there are degenerate Hopf bifurcations along the stability boundary \(P=1\) at the Bautin points \(\omega _{\text {n}}\tau =j\pi \), \(j=1,2,\ldots \), where not only the sense of the Hopf bifurcations, but also the stability of the equilibrium change to opposite in the same time. In this respect, these Bautin points are special ones.

The bifurcating periodic motions are approximated by the dimensionless form

$$\begin{aligned} x(T_0)={r}\cos (\omega _{\mathrm{c}}T_0) \end{aligned}$$
(35)

that can be obtained from (29) when the phase is eliminated by the appropriate selection of the initial time instant. The dimensionless vibration amplitude \({r}=2\vert R\vert \) and the dimensionless angular frequency \(\omega _{\mathrm{c}}\) satisfy (31) with \({\overset{\,\circ }{R}}\equiv 0\) and \(R\ne 0\), that is,

$$\begin{aligned} \gamma \mu +\delta \vert R\vert ^2=0. \end{aligned}$$
(36)

Its real and imaginary parts lead to the equations

$$\begin{aligned}& -2(P-1+\cos \omega _{\mathrm{c}})\mu +\omega _{\mathrm{n}}\tau _{\mathrm{c}}P^3\vert R\vert ^2 = 0, \end{aligned}$$
(37)
$$\begin{aligned}& \sin \omega _{\mathrm{c}}= 0. \end{aligned}$$
(38)

The second Eq. (38) is satisfied at the stability boundaries given in (19) by \(\omega _{\mathrm{c}}=j\pi \), \((j=1,2,\ldots )\). The substitution of \(\cos \omega _{\mathrm{c}}=(-1)^j\) into (37) gives \(\vert R\vert \), the double of which gives the dimensionless vibration amplitude

$$\begin{aligned} {r}=\frac{2\sqrt{2}}{P}\sqrt{\frac{P-1+(-1)^j}{\omega _{{\text {n}}} \tau _{{\text {c}}}P}\mu \,} \, \end{aligned}$$
(39)

in the approximation of the periodic solutions (35). This means that the branches bifurcating from the first, third, fifth, \(\ldots \) stability boundary curves (for \(j=2k-1\)) have amplitudes

$$\begin{aligned} {r}=\frac{2\sqrt{2}}{P}\sqrt{\frac{P-2}{P}\frac{\mu }{\omega _{{\text {n}}} \tau _{{\text {c}}}}\,} , \end{aligned}$$
(40)

while for the bifurcating branches from the second, fourth, sixth, \(\ldots \) boundary curves (for \(j=2k)\) are defined by

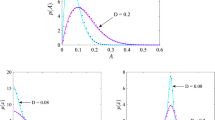
$$\begin{aligned} {r}=\frac{2\sqrt{2}}{P}\sqrt{\frac{\mu }{\omega _{{\text {n}}}\tau _{{\text {c}}}}\,} \,, \end{aligned}$$
(41)

and they are all unstable for \(0<P<1\) and stable for \(1<P<2\). The corresponding bifurcated branches are presented in Fig. 3 by means of the above algebraic formulas, and these are also checked by numerical solutions of the original nonlinear Eq. (9) obtained with a collocation method [41] combined with path following.

Fig. 3
figure 3

Theoretical and numerical bifurcation diagrams for various gains P in case of non-collocated force control

Full size image

Transforming these results back to the time and space with dimensions according to (8), approximation (35) gives the periodic contact force oscillations bifurcating from the jth stability boundary in the form:

$$\begin{aligned} F_j(t)= & {} F_{\mathrm{d}}+F_{\mathrm{s}}\frac{2\sqrt{2}}{P}\sqrt{\left( 1+\frac{(-1)^j-1}{P}\right) \left( \frac{\tau }{\tau _{{\mathrm{c}},j}}-1\right) \,}\nonumber \\&\times \cos \left( j\frac{\pi }{\tau }t\right) , \end{aligned}$$
(42)

with \(j=1,2,\ldots \); these are all unstable for \(0<P<1\) and stable for \(1<P<2\). In this formula, the jth critical delays \(\tau _{{\text {c}},j}\) are given in (20), (21) and the delay parameter \(\tau \) is ‘close enough’ to one of these. Recall that in formula (42), \(F_{\text {d}}\) is the desired contact force and \(F_{\text {s}}\) is the force saturation level of the actuator. The comparison of the numerical and analytical results in Fig. 3 shows that the algebraic approximations obtained by MMS are acceptable in engineering applications for delay parameters \(\tau \) within 15% of their corresponding critical values.

The Hopf bifurcations can also be studied with the same methodology along the stability boundary \(P=1\) given in (19), too. In this case, the modified definition of the bifurcation parameter \(\mu \) is necessary along the gain parameter P in the form

$$\begin{aligned} P=P_{\mathrm{c}}+\mu ,\quad P_{\mathrm{c}}=1. \end{aligned}$$
(43)

Since the linear system does not include any delay term in the critical parameter case \(\mu =0\), the calculations with MMS are simpler than the ones above. For the sign of the Poincaré–Lyapunov constant, one gets

$$\begin{aligned} {{\text {Sgn}}}\,{\text {Re}}\,\delta ={{\text {Sgn}}}\,(-\sin (\omega _{\text {n}}\tau )) . \end{aligned}$$
(44)

This means that along the stability boundary \(P=1\), there are supercritical Hopf bifurcations for \(2j\pi /\omega _{\text {n}}<\tau <(2j+1)\pi /\omega _{\text {n}}\), \(j=0,1,\ldots \), while the bifurcations are subcritical for \((2h-1)\pi /\omega _{\text {n}}<\tau <2h\pi /\omega _{\text {n}}\), \(h=1,2,\ldots \). This result is consistent with the above-discussed special Bautin points where the criticality of the Hopf bifurcations and the stability of the equilibrium swap at the same parameter points (see also the colored stability boundaries in Fig. 2).

4 Analysis of collocated configuration

When the collocated force control configuration is analyzed, the relevant difference Eq. (13) is considered with the third-order polynomial approximation

$$\begin{aligned} y(t)=(1-P)y(t-1)+\frac{1}{3}P^3y^3(t-1)+{\mathrm{h.o.t.}}. \end{aligned}$$
(45)

Since this is a simple scalar nonlinear difference equation, the stability and bifurcations of the zero solution can easily be obtained based on the normal form of scalar discrete maps [34].

4.1 Stability

The stability of the linear part of (45) is equivalent to the convergence of the geometric series of quotient \((1-P)\), which is the characteristic multiplier of the corresponding scalar linear map. The stability condition assumes the form

$$\begin{aligned} \vert 1-P\vert<1\quad \Leftrightarrow \quad 0<P<P_{\mathrm{c}}=2, \end{aligned}$$
(46)

which means that the stability of the collocated configuration does not depend on the delay, and the maximal proportional gain that can be achieved without losing stability is \(P_{\mathrm{max,c}}=P_{\mathrm{c}}=2\) as opposed to the non-collocated configuration where the maximal gain \(P_{\mathrm{max,nc}}=1.6\) can be achieved at \(\tau =\sqrt{5/2\,}\,\pi /\omega _{\mathrm{n}}\) only.

4.2 Period-doubling bifurcation

At the critical gain \(P_{\mathrm{c}}\), the characteristic multiplier is \(-\,1\), that is, the nonlinear mapping (45) has a period-doubling (or flip) bifurcation here. Since only the gain parameter is responsible for the loss of stability in this case, the bifurcation parameter \(\mu \) is now defined by

$$\begin{aligned} P=P_{\mathrm{c}}+\mu \,,\quad P_{\mathrm{c}}=2, \end{aligned}$$
(47)

and the normal form of the corresponding mapping is given as

$$\begin{aligned} y_{k}=(-1-\mu )y_{k-1}+\delta y^3_{k-1},\quad \delta =\frac{1}{3}P^3_{\mathrm{c}}. \end{aligned}$$
(48)

Since \(\delta =8/3>0\), the period-doubling bifurcation is supercritical, that is, stable period-2 oscillations appear in (45) and similarly in (13) for \(\mu >0\), that is, for \(P>P_{\mathrm{c}}\). The amplitude r of this oscillation is expressed by

$$\begin{aligned} r=\sqrt{\frac{\mu }{\delta }\,}\quad \Rightarrow \quad r=\sqrt{\frac{3}{8}(P-2)\,}. \end{aligned}$$
(49)

After transforming this result back to the real contact force in the real time, it means that for proportional gains P somewhat larger than the critical value \(P_{\mathrm{c}}\), stable self-excited contact force oscillation occurs around the desired value with frequency \(1/(2\tau )\) that corresponds to the basic critical dimensionless angular frequency \(\omega _{\mathrm{c}}=\pi \) related to the critical characteristic multiplier at \(\exp (\mathrm{i}\omega _{\mathrm{c}})=-1\):

$$\begin{aligned} F(t)=F_{\mathrm{d}}+F_{\mathrm{s}}\sqrt{\frac{3}{8}(P-2)\,}\cos \left( \frac{\pi }{\tau }t\right) . \end{aligned}$$
(50)

5 Conclusions

Basic single-degree-of-freedom mechanical models of force control with collocated and non-collocated force sensor arrangements were constructed and the governing delay differential equations (DDE) were derived when the relevant nonlinearity is the actuator saturation and time delay appears in the feedback loop. These models are similar to those of position control with collocated and non-collocated position sensors [42], but the equations of motion are more complex due to the unilateral elastic connection of the controlled object and the environment.

The mathematical model of the non-collocated force control is a retarded DDE that belongs to the class of delayed oscillators. The stability properties show alternating stable and unstable regions for both the delay and the gain parameter (see Fig. 2). The maximization of the gain P in the feedback loop within the stable parameter region has relevance when there is dry friction in the mechanical structure. The maximum gain \(P_{\mathrm{max}}=1.6\) can be achieved only at the critical delay \(\tau _{\mathrm{c}}=\sqrt{5/2\,}\pi /\omega _{\mathrm{n}}\) where \(\omega _{\mathrm{n}}\) is the angular natural frequency of the uncontrolled system. At the stability boundaries, subcritical Hopf bifurcations occur for proportional gains \(P<1\), while these are supercritical for \(P>1\). At loss of stability, the vibration frequency and the vibration amplitude of the contact force are well approximated with the simple algebraic formula (42).

The mathematical model of the collocated force control is an implicit neutral DDE that can be transformed into a simple nonlinear difference equation. Its dynamic properties are much simpler: The system is stable for all gains \(0<P<2\), and the Hopf bifurcation is always supercritical at the gain \(P_{\mathrm{max}}=2\). This maximal gain can be achieved for any time delay, which means that the system is robust against the delay parameter. In practice, however, the accuracy of this control strategy is worse due to the fact that the sensor is not exactly at the position of the contact between the object and the environment. The approximation of the emerging stable oscillations for \(P>2\) is presented again by the simple formula (50).

The closed-form analytical expressions for the stable parameter domains are useful for the preliminary parameter estimation during the design of force controlled structures. The formulas for the frequencies and amplitudes of emerging vibrations support the identification of experimentally detected unwanted vibrations and also the parameter estimations regarding the critical ratios of the time delays and the time periods of the natural oscillations of the uncontrolled system.

There are several open questions even in these simple models of force control, especially in the non-collocated case. The numerical results show that the bifurcated branches leaning against each other between subsequent stability boundaries remain separate as it is shown, for example, by the rightmost unstable branches in Fig. 3 for \(P=0.9\). These periodic solutions are probably ‘separated’ by the insets and outsets of quasiperiodic oscillations embedded in the infinite-dimensional phase space. The structure of these could be explored with the methods presented in [34, 43, 44] for the analysis of codimension-2 Hopf bifurcations that emerge at the cross sections of subsequent Hopf stability boundaries shown also in Fig. 2. Among these, the one at the peak of the stability chart in Fig. 2, where the gain P is maximal, requires even more careful handling since this codimension-2 Hopf bifurcation occurs with the specific 1:2 resonant frequencies.

The gains \(0<P<1\) seem to guarantee exponential stability for very short time delays and/or for very soft connections between the controlled object and the environment. However, the subcriticality of the Hopf bifurcation at the first bifurcation point for the delay shows that the force control can still exhibit increasing vibrations for large enough perturbation. There are no attractors identified outside these unstable branches, and no large-amplitude stable oscillations are identified for increased values of the delay either (see the bifurcation diagrams for \(P=0.6\) and 0.9 in Fig. 3). In these cases, another relevant nonlinearity has to be included and analyzed in the model: The increasing large-amplitude oscillations are limited by the loss of contact between the controlled object and the environment. Such large-scale nonlinearities originated in the unilateral constraints are relevant in cases of transitions between position and force control (see, e.g., [45, 46]), but the study of these global nonlinearities in the non-collocated force control model for \(0<P<1\) is the task of future research.

Another possible extension of the research work is the study of the effect of viscous damping in the model. It is expected that the disjunct stable domains of the non-collocated case become simply connected, the stable region gets larger via a smooth variation of the stability boundaries with increasing damping, the special Bautin points disappear, while the double Hopf bifurcation points still survive. In the collocated case, the separated oscillator becomes physically damped, too. However, the algebraic calculations become so intricate that the effect of the parameters on the nonlinear system behavior cannot be summarized in simple closed formulas anymore.