Skip to main content
SpringerLink
Log in

Magnetoelastic axisymmetric multi-modal resonance and Hopf bifurcation of a rotating circular plate under aerodynamic load

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

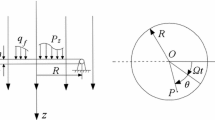
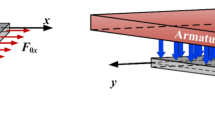
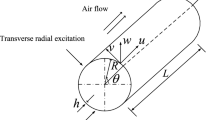
In this article, an investigation of magnetoelastic axisymmetric multi-mode interaction and Hopf bifurcations of a circular plate rotating in air and uniform transverse magnetic fields is presented. The expressions of electromagnetic forces and an empirical aerodynamic model are applied in the derivation of the dynamical equations, through which a set of nonlinear differential equations for axisymmetric forced oscillation of the clamped circular plate are deduced. The method of multiple scales combined with the polar coordinate transformation is employed to solve the differential equations and achieve the phase–amplitude modulation equations for the interaction among the first three modes under primary resonance. Then, the frequency response equation for the single-mode vibration, the steady-state response equations for three-mode resonance and the corresponding Jacobian matrix are obtained by means of the modulation equations. Numerical examples are presented to show the dependence of amplitude solutions as a function of different parameters in the cases of single mode and three-mode response. Furthermore, a Hopf bifurcation can be found in three-mode equilibrium by choosing appropriate parameters, where a limit cycle occurs and then evolves into chaos after undergoing a series of period-doubling bifurcations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  1. Chona, S., Jiang, Z.W., Shyu, Y.J.: Stability analysis of a 2” floppy disk drive system and the optimum design of the disk stabilizer. J. Vib. Acoust. 114(2), 283–286 (1992)

    Article  Google Scholar 

  2. Hoska, H.C., Randall, S.: Self-excited vibrations of a flexible disk rotating on an air film above a surface. Acta Mech. 3, 115–127 (1992)

    Google Scholar 

  3. Renshaw, A.A., Mote, C.D.: Absence of one nodal diameter critical speed modes in an axisymmetric rotating disk. J. Appl. Mech. 59(3), 687–688 (1992)

    Article  MATH  Google Scholar 

  4. Renshaw, A.A., D’Angelo, C., Mote, C.D.: Aerodynamically excited vibration of a rotating disk. J. Sound Vib. 177(5), 577–590 (1994)

    Article  MATH  Google Scholar 

  5. Renshaw, A.A.: Critical speeds for floppy disks. J. Appl. Mech. 65(1), 116–120 (1998)

    Article  Google Scholar 

  6. Kim, H.R., Renshaw, A.A.: Aeroelastic flutter of circular rotating disks: a simple predictive model. J. Sound Vib. 256(2), 227–248 (2002)

    Article  Google Scholar 

  7. Yasuda, K., Torii, T., Shimizu, T.: Self-excited oscillations of a circular disk rotating in air. JSME Int. J. Ser. III. 35(3), 347–352 (1992)

    Google Scholar 

  8. Kim, B.C., Raman, A., Mote, C.D.: Prediction of aeroelastic flutter in a hard disk drive. J. Sound Vib. 238(2), 309–325 (2000)

    Article  Google Scholar 

  9. Hansen, M.H., Raman, A., Mote, C.D.: Estimation of nonconservative aero-dynamic pressure leading to flutter of spinning disks. J. Fluids Struct. 15(1), 39–57 (2005)

    Article  Google Scholar 

  10. Wang, X.Z., Huang, X.Y.: A simple modeling and experiment on dynamic stability of a disk rotating in air. J. Struct. Stab. Dyn. 8(1), 41–60 (2008)

    Article  Google Scholar 

  11. Huang, X.Y., Wang, X., Yap, F.F.: Feedback control of rotating disk flutter in an enclosure. J. Fluids Struct. 19(7), 917–932 (2004)

    Article  Google Scholar 

  12. Li, X.Y., Ding, H.J., Chen, W.Q.: Three-dimensional analytical solution for functionally graded magneto-electro-elastic circular plates subjected to uniform load. Compos. Struct. 83(4), 381–90 (2008)

    Article  Google Scholar 

  13. Dai, H.L., Dai, T., Yang, L.: Free vibration of a FGPM circular plate placed in a uniform magnetic field. Meccanic 48(10), 2339–2347 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  14. Hu, Y.D., Wang, T.: Nonlinear resonance of a rotating circular plate under static loads in magnetic field. Chin. J. Mech. Eng. 28(6), 1277–1284 (2015)

    Article  Google Scholar 

  15. Hu, Y.D., Wang, T.: Nonlinear free vibration of a rotating circular plate under the static load in magnetic field. Nonlinear Dyn. 85(3), 1825–1835 (2016)

    Article  MathSciNet  Google Scholar 

  16. Hu, Y.D., Li, Z., Du, G.J., Wang, Y.N.: Magneto-elastic combination resonance of rotating circular plate with varying speed under alternating load. Int. J. Struct. Stab. Dyn. 18(3), 1850032 (2017)

    MathSciNet  Google Scholar 

  17. Hu, Y.D., Piao, J.M., Li, W.Q.: Magneto-elastic dynamics and bifurcation of rotating annular plate. Chin. Phys. B 26(9), 269–279 (2017)

    Google Scholar 

  18. Hu, Y.D., Li, W.Q.: Study on primary resonance and bifurcation of a conductive circular plate rotating in air-magnetic fields. Nonlinear Dyn. 93(2), 671–687 (2018)

    Article  Google Scholar 

  19. Touzé, C., Thomas, L.O., Chaigne, A.: Asymmetric non-linear forced vibrations of free-edge circular plates. Part I: theory. J. Sound Vib. 258(4), 649–676 (2002)

    Article  Google Scholar 

  20. Touzé, C., Thomas, L.O., Chaigne, A.: Asymmetric non-linear forced vibrations of free-edge circular plates. Part II: experiments. J. Sound Vib. 265(5), 1075–1101 (2003)

    Article  Google Scholar 

  21. Camier, C., Touzé, C., Thomas, O.: Non-linear vibrations of imperfect free-edge circular plates and shells. Euro. J. Mech. A-Solids 28(2), 500–515 (2009)

    Article  MATH  Google Scholar 

  22. Touzé, C., Thomas, O., Amabili, M.: Transition to chaotic vibrations for harmonically forced perfect and imperfect circular plates. Int. J. Nonlinear Mech. 46(1), 234–246 (2011)

    Article  Google Scholar 

  23. Sridhar, S., Mook, D.T., Nayfeh, A.H.: Nonlinear resonances in the forced responses of plates. Part I: symmetric response of circular plates. J. Sound Vib. 41(3), 359–373 (1975)

  24. Hadian, J., Nayfeh, A.H.: Modal interaction in circular plates. J. Sound Vib. 142(2), 279–292 (1990)

    Article  MathSciNet  Google Scholar 

  25. Chin, C.M., Nayfeh, A.H.: Three-to-one internal resonances in hinged-clamped beams. Nonlinear Dyn. 12(2), 129–154 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  26. Chin, C.M., Nayfeh, A.H.: Three-to-one internal resonances in parametrically excited hinged-clamped beams. Nonlinear Dyn. 20(2), 131–158 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  27. Feng, Z.H., Hu, H.Y.: Largest Lyapunov exponent and almost certain stability analysis of slender beams under a large linear motion of basement subject to narrowband parametric excitation. J Sound Vib. 257(4), 733–752 (2002)

    Article  Google Scholar 

  28. Feng, Z.H., Hu, H.Y.: Principal parametric and three-to-one internal resonances of flexible beams undergoing a large linear motion. Acta Mech. Sinica 19(4), 355–364 (2003)

    Article  Google Scholar 

  29. Sahoo, B., Panda, L.N., Pohit, G.: Two-frequency parametric excitation and internal resonance of a moving viscoelastic beam. Nonlinear Dyn. 82(4), 1721–1742 (2015)

    Article  MathSciNet  Google Scholar 

  30. Nowinski, J.L.: Nonlinear transverse vibrations of a spinning disk. J. Appl. Mech. 31(1), 72–78 (1961)

    Article  Google Scholar 

  31. Liang, D.S., Wang, H.J., Chen, L.W.: Vibration and stability of rotating polar orthotropic annular disks subjected to a stationary concentrated transverse load. J. Sound. Vib. 250(5), 795–811 (2002)

    Article  Google Scholar 

  32. Norouzi, H., Younesian, D.: Forced vibration analysis of spinning disks subjected to transverse loads. Int. J. Struct. Stab. Dyna. 15(3),1450049(2015)

  33. Ambarcumian, S.A., Bagdasarin, G.E., Belubekian, M.V.: Magneto-elastic of thin shell and plate. Science, Moscow (1977)

  34. Moon, F.C.: Magneto-Solid Mechanics. Wiley, New York (1984)

    Google Scholar 

  35. John, K.D.: Electromagnetic. McGraw-Hill, New York (1984)

    Google Scholar 

  36. Dowell, E.H.: Aeroelasticity of plates and shells. Noordhoff International Publishing, Leyden (1975)

    MATH  Google Scholar 

  37. Chu, H.N.: Influence of large amplitudes on flexural vibrations of a thin circular cylindrical shell. J. Aerosp. Sci. 28(9), 685–692 (1961)

    Article  MathSciNet  Google Scholar 

  38. Reddy, J.N.: Theory and analysis of elastic plates and shell. Taylor & Francis, New York (2007)

    Google Scholar 

  39. Nayfeh, A.H., Mook, D.T.: Nonlinear Oscillations. Wiley, New York (1995)

    Book  MATH  Google Scholar 

  40. Korenev, B.G.: Bessel Functions and Their Applications. Taylor & Francis Inc, Landon and New York (2002)

    MATH  Google Scholar 

  41. Leissa, A.W.: Vibration of Plates. United States Government Printing Office, Washington, D. C. (1969)

    Google Scholar 

  42. Joncs, D.G.: Handbook of Viscoelastic Vibration Damping. Wiley, New York (2001)

    Google Scholar 

Download references

Acknowledgements

This project was supported by the National Natural Science Foundation of China (No. 11472239), Hebei Provincial Natural Science Foundation of China (No. A2015203023), Hebei Provincial Graduate Innovation Foundation of China (No. CXZZBS2018058) and Hebei Provincial Yanshan University Graduate Innovation Foundation of China (No. CXZS201908).

Author information

Authors and Affiliations

  1. School of Civil Engineering and Mechanics, Yanshan University, Qinhuangdao, 066004, China

    Y. D. Hu & W. Q. Li

  2. Hebei Key Laboratory of Mechanical Reliability for Heavy Equipments and Large Structures, Yanshan University, Qinhuangdao, 066004, China

    Y. D. Hu & W. Q. Li

Authors
  1. Y. D. Hu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. Q. Li
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Y. D. Hu.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix

Appendix

$$\begin{aligned}& \hat{{\alpha }}_{e0} =\frac{3}{2}\left( {3{\phi }'_{e0} {\phi }'_{e0} {\phi }''_{e0} +\frac{1}{r}{\phi }'_{e0} {\phi }'_{e0} {\phi }'_{e0} } \right) \\& \hat{{\alpha }}_{x0e0} =\left( {3{\phi }'_{e0} {\phi }'_{x0} {\phi }''_{x0} +\frac{1}{r}{\phi }'_{e0} {\phi }'_{x0} {\phi }'_{x0} } \right) \\&\, +\left( {\frac{3}{2}{\phi }'_{x0} {\phi }'_{x0} {\phi }''_{e0} +\frac{1}{2r}{\phi }'_{x0} {\phi }'_{x0} {\phi }'_{e0} } \right) \\& \hat{{\alpha }}_3 =\left( {\frac{3}{2}{\phi }'_{10} {\phi }'_{10} {\phi }''_{00} +\frac{1}{2r}{\phi }'_{10} {\phi }'_{10} {\phi }'_{00} } \right) \\&\, +\left( {3{\phi }'_{10} {\phi }'_{00} {\phi }''_{10} +\frac{1}{r}{\phi }'_{10} {\phi }'_{00} {\phi }'_{10} } \right) \\& \hat{{\alpha }}_4 =\left( {3{\phi }'_{20} {\phi }'_{10} {\phi }''_{10} +\frac{1}{r}{\phi }'_{20} {\phi }'_{10} {\phi }'_{10} } \right) \\&\, +\left( {\frac{3}{2}{\phi }'_{10} {\phi }'_{10} {\phi }''_{20} +\frac{1}{2r}{\phi }'_{10} {\phi }'_{10} {\phi }'_{20} } \right) \\& \hat{{\alpha }}_5 =\left( {3{\phi }'_{00} {\phi }'_{10} {\phi }''_{20} +\frac{1}{r}{\phi }'_{00} {\phi }'_{10} {\phi }'_{20} } \right) \\&\, +\left( {3{\phi }'_{10} {\phi }'_{20} {\phi }''_{00} +\frac{1}{r}{\phi }'_{10} {\phi }'_{20} {\phi }'_{00} } \right) \\& +\left( {3{\phi }'_{20} {\phi }'_{00} {\phi }''_{10} +\frac{1}{r}{\phi }'_{20} {\phi }'_{00} {\phi }'_{10} } \right) \end{aligned}$$

\(\delta _{je} \) is the Kronecker delta which satisfies \(\delta _{je} =\left\{ {\begin{array}{ll} 0 &{}\,\, j\ne e \\ 1 &{}\,\, j=e \\ \end{array}} \right. \), \(e=0\), 1, 2

$$\begin{aligned} \vartheta _{e0}= & {} \int _0^1 {\frac{1}{r}} \left( {{\phi }'_{e0} +r{\phi }''_{e0} } \right) \phi _{e0} r\hbox {d}r\\ Q_{e0}= & {} \int _0^1 {q_0 \phi _{e0} r\hbox {d}r}\\ \varGamma _{e0}= & {} \int _0^1 {\hat{{\alpha }}_{e0} \phi _{e0} r\hbox {d}r}\\ \varGamma _{x0e0}= & {} \int _0^1 {\hat{{\alpha }}_{x0e0} \phi _{e0} r\hbox {d}r}\\ \varGamma _{3e0}= & {} \int _0^1 {\hat{{\alpha }}_3 \delta _{e2} \phi _{e0} r\hbox {d}r}\\ \varGamma _{4e0}= & {} \int _0^1 {\hat{{\alpha }}_4 \delta _{e0} \phi _{e0} r\hbox {d}r}\\ \varGamma _{5e0}= & {} \int _0^1 {\hat{{\alpha }}_5 \delta _{e1} \phi _{e0} r\hbox {d}r}\\ \mu _{00}= & {} \frac{1}{2}C_d -\frac{\sigma B_{0z}^2 }{24}\vartheta _{00}\\ \mu _{10}= & {} \frac{1}{2}C_d -\frac{\sigma B_{0z}^2 }{24}\vartheta _{10}\\ \mu _{20}= & {} \frac{1}{2}C_d -\frac{\sigma B_{0z}^2 }{24}\vartheta _{20}\\ \hat{{B}}_1= & {} \frac{1}{288}\left( \frac{\omega _{00}^2 +\varOmega ^{2}}{\omega _{00} }\vartheta _{00} \right. \\&\left. +2\frac{\omega _{10}^2 +\varOmega ^{2}}{\omega _{10} }\vartheta _{10} -\frac{\omega _{20}^2 +\varOmega ^{2}}{\omega _{20} }\vartheta _{20} \right) \\ \hat{{C}}_1= & {} \frac{1}{8}\left( {\frac{\varGamma _{00} }{\omega _{00} }+\frac{4\varGamma _{0010} }{\omega _{10} }-\frac{2\varGamma _{0020} }{\omega _{20} }} \right) \\ \hat{{D}}_1= & {} \frac{1}{8}\left( {\frac{2\varGamma _{10} }{\omega _{10} }+\frac{2\varGamma _{1000} }{\omega _{00} }-\frac{2\varGamma _{1020} }{\omega _{20} }} \right) \\ \hat{{E}}_1= & {} \frac{1}{8}\left( {\frac{\varGamma _{20} }{\omega _{20} }-\frac{2\varGamma _{2000} }{\omega _{00} }-\frac{4\varGamma _{2010} }{\omega _{10} }} \right) \\ \hat{{B}}_2= & {} \frac{1}{288}\frac{\omega _{20}^2 +\varOmega ^{2}}{\omega _{20} }\vartheta _{20}\\ \hat{{C}}_2= & {} \frac{\varGamma _{0020} }{4\omega _{20} }\\ \hat{{D}}_2= & {} \frac{\varGamma _{1020} }{4\omega _{20} }\\ \hat{{E}}_2= & {} \frac{\varGamma _{20} }{8\omega _{20} }\\ G_1= & {} \frac{1}{{X}_{00} }\left[ \sigma _1 -\sigma \right. \\&+\frac{1}{288}\left( {\frac{\omega _{00}^2 +\varOmega ^{2}}{\omega _{00} }\vartheta _{00} +2\frac{\omega _{10}^2 +\varOmega ^{2}}{\omega _{10} }\vartheta _{10} } \right) \\&-\frac{3}{8}{X}_{00}^2 \left( {\frac{\varGamma _{00} }{\omega _{00} }+\frac{4\varGamma _{0010} }{\omega _{10} }} \right) \\&-\frac{1}{8}{X}_{10}^2 \left( {\frac{2\varGamma _{10} }{\omega _{10} }+\frac{2\varGamma _{1000} }{\omega _{00} }} \right) \\&- \frac{1}{8}{X}_{20}^2 \left( {\frac{2\varGamma _{2000} }{\omega _{00} }+\frac{4\varGamma _{2010} }{\omega _{10} }} \right) \\&\left. -\frac{4}{8}\frac{\varGamma _{510} }{\omega _{10} }{X}_{00} {X}_{20} \cos {H}_1 \right] \\&+\frac{1}{{X}_{20} }\left[ \frac{1}{8\omega _{20} }\left( 4{X}_{00} {X}_{20} \varGamma _{0020} \right. \right. \\&\left. \left. +{X}_{10}^2 \varGamma _{320} \cos {H}_1 \right) \right] \\ G_2= & {} \frac{1}{{X}_{00} }\left[ -\frac{1}{8}2{X}_{10} {X}_{00} \left( {\frac{2\varGamma _{10} }{\omega _{10} }+\frac{2\varGamma _{1000} }{\omega _{00} }} \right) \right. \\&\left. -\frac{1}{8}2{X}_{10} {X}_{20} \frac{2\varGamma _{400} }{\omega _{00} }\cos {H}_1 \right] \\&+\frac{1}{{X}_{20} }\left[ \frac{1}{8\omega _{20} }\left( 4{X}_{10} {X}_{20} \varGamma _{1020} \right. \right. \\&\left. \left. +2\varGamma _{320} {X}_{00} {X}_{10} \cos {H}_1 \right) \right] \\ G_3= & {} \frac{1}{{X}_{00} }\left[ -\frac{1}{8}\left( {\frac{2\varGamma _{2000} }{\omega _{00} }+\frac{4\varGamma _{2010} }{\omega _{10} }} \right) 2{X}_{20} {X}_{00}\right. \\&\left. -\frac{1}{8}\left( {\frac{\varGamma _{400} }{\omega _{00} }{X}_{10}^2 +\frac{2\varGamma _{510} }{\omega _{10} }{X}_{00}^2 } \right) \cos {H}_1 \right] \\&+\frac{1}{{X}_{20} }\left[ \sigma -\frac{1}{288}\frac{\omega _{20}^2 +\varOmega ^{2}}{\omega _{20} }\vartheta _{20}\right. \\&+\frac{1}{8\omega _{20} }\left( 2{X}_{00}^2 \varGamma _{0020}\right. \\&\left. \left. +2{X}_{10}^2 \varGamma _{1020} +3{X}_{20}^2 \varGamma _{20} \right) \right] \\ G_4= & {} \left\{ \frac{1}{{X}_{00} }\left[ {\frac{1}{8}\left( {\frac{\varGamma _{400} }{\omega _{00} }{X}_{10}^2 {X}_{20} +2\frac{\varGamma _{510} }{\omega _{10} }{X}_{00}^2 {X}_{20} } \right) } \right] \right. \\&\left. +\frac{1}{{X}_{20} }\left[ {-\frac{1}{8}\frac{\varGamma _{320} }{\omega _{20} }{X}_{00} {X}_{10}^2 } \right] \right\} \sin {H}_1\\ G_5= & {} -\frac{1}{{X}_{20} }\frac{Q_{20} }{\omega _{20} }\sin {H}_2\\ J_1= & {} \frac{1}{8{X}_{20} \omega _{20} }\left( {4{X}_{00} {X}_{20} \varGamma _{0020} +{X}_{10}^2 \varGamma _{320} \cos {H}_1 } \right) \\ J_2= & {} \frac{1}{8{X}_{20} \omega _{20} }\left( 4\varGamma _{1020} {X}_{10} {X}_{20} \right. \\&\left. +2\varGamma _{320} {X}_{00} {X}_{10} \cos {H}_1 \right) \\ J_3= & {} \frac{1}{{X}_{20} }\left[ \sigma -\frac{1}{288}\frac{\omega _{20}^2 +\varOmega ^{2}}{\omega _{20} }\vartheta _{20} \right. \\&+\frac{1}{8\omega _{20} }\left( 2{X}_{00}^2 \varGamma _{0020} \right. \\&\left. \left. +2{X}_{10}^2 \varGamma _{1020} +3{X}_{20}^2 \varGamma _{20} \right) \right] \\ J_4= & {} -\frac{1}{8{X}_{20} }\frac{\varGamma _{320} }{\omega _{20} }{X}_{00} {X}_{10}^2 \sin {H}_1\\ J_5= & {} -\frac{1}{{X}_{20} }\frac{Q_{20} }{\omega _{20} }\sin {H}_2\\ \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hu, Y.D., Li, W.Q. Magnetoelastic axisymmetric multi-modal resonance and Hopf bifurcation of a rotating circular plate under aerodynamic load. Nonlinear Dyn 97, 1295–1311 (2019). https://doi.org/10.1007/s11071-019-05049-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05049-8

Keywords

Search

Navigation