Skip to main content
SpringerLink
Log in

Primary and secondary resonance analyses of a cantilever beam carrying an intermediate lumped mass with time-delay feedback

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

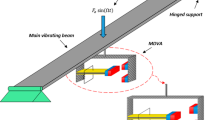
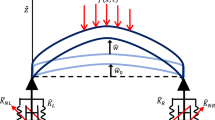
Time-delay displacement and velocity feedback of different types of active control in a cantilever beam carrying an lumped mass is investigated in this paper. Based on Euler–Bernoulli beam theory, the nonlinear governing equation is studied with damping, harmonic distribution, displacement delay, velocity delay and two time delays. The multiple scales perturbation method is applied to obtain the frequency response equations near primary, superharmonic and subharmonic resonances. A thorough study on the stability is proposed, with a particular emphasis on delay feedback. The results show that the hardening and softening behaviors of the system depend on the location of lumped mass. Furthermore, the displacement feedback gain coefficient only makes the peak amplitude move to the low frequency, yet velocity feedback coefficient and their time delays can be used to effectively enhance the stability and quench the nonlinear vibration of the cantilever beam. Thus, reasonable selection of the control system parameters can effectively improve the level of vibration control for the mechanical system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Kevin, M.H., Earl, D.: Nonlinear responses of inextensible cantilever and free-free beams undergoing large deflections. J. Appl. Mech. 85(5), 051008 (2018)

    Article  Google Scholar 

  2. Dwivedy, S.K., Kar, R.C.: Nonlinear dynamics of a cantilever beam carrying an attached mass with 1:3:9 internal resonances. Nonlinear Dyn. 31(1), 49–72 (2003)

    Article  MATH  Google Scholar 

  3. Kar, R.C., Dwivedy, S.K.: Non-linear dynamics of a slender beam carrying a lumped mass with principal parametric and internal resonances. Int. J. Nonlinear Mech. 34(3), 515–529 (1999)

    Article  MATH  Google Scholar 

  4. Navadeh, N., Hewson, R.W., Fallah, A.S.: Dynamics of transversally vibrating non-prism Timoshenko cantilever beams. Eng. Struct. 166, 511–525 (2018)

    Article  Google Scholar 

  5. Pratiher, B., Bhowmick, S.: Nonlinear dynamic analysis of a Cartesian manipulator carrying an end effector placed at an intermediate position. Nonlinear Dyn. 69(1–2), 539–553 (2012)

    Article  MathSciNet  Google Scholar 

  6. Ercoli, L., Laura, P.A.A.: Analytical and experimental investigation on continuous beams carrying elastically mounted masses. J. Sound Vib. 114, 519–533 (1987)

    Article  Google Scholar 

  7. Gürgöze, M.: On the eigen-frequencies of a cantilever beam with attached tip mass and a spring-mass system. J. Sound Vib. 190(2), 149–162 (1996)

    Article  Google Scholar 

  8. Kanaka, R.K., Venkateswara, R.G.: Towards improved evaluation of large amplitude free-vibration behaviour of uniform beams using multi-term admissible functions. J. Sound Vib. 282, 1238–1246 (2005)

    Article  Google Scholar 

  9. Kazemi-Lari, M.A., Fazelzadeh, S.A.: Flexural-torsional flutter analysis of a deep cantilever beam subjected to a partially distributed lateral force. Acta Mech. 226(5), 1379–1393 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  10. Rhoads, J.F., Shaw, S.W., Turner, K.L.: The nonlinear response of resonant microbeam systems with purely parametric electrostatic actuation. J. Micromech. Microeng. 16, 890–899 (2006)

    Article  Google Scholar 

  11. Nayfeh, A.H., Younis, M.I.: Dynamics of MEMS resonators under superharmonic and subharmonic excitations. J. Micromech. Microeng. 15, 1840–1847 (2005)

    Article  Google Scholar 

  12. Ekici, H., Boyaci, H.: Effects of non-ideal boundary conditions on vibrations of microbeams. J. Vib. Control 13(9–10), 1369–1378 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  13. Mehran, S., Davood, Y., Ebrahim, E.: Nonlinear harmonic vibration and stability analysis of a cantilever beam carrying an intermediate lumped mass. Nonlinear Dyn. 84, 1667–1682 (2016)

    Article  MathSciNet  Google Scholar 

  14. Eftekhari, S.A., Bakhtiari-Nejad, F., Dowell, E.H.: An investigation on the sensitivity of limit cycle oscillations for detecting damage in an aeroelastic panel. Appl. Mech. Mater. 110–116, 4424–4432 (2012)

    Google Scholar 

  15. Eftekhari, S.A., Bakhtiari-Nejad, F., Dowell, E.H.: Damage detection of an aeroelastic panel using limit cycle oscillation analysis. J. Non-Linear Mech. 58, 99–110 (2014)

    Article  Google Scholar 

  16. Oveissi, S., Toghraie, D., Ali Eftekhari, S.: Investigation the effect of axially moving carbon nanotube and nano-flow on the vibrational behavior of the system. Int. J. Fluid Mech. Res. 45(2), 171–186 (2018)

    Article  Google Scholar 

  17. Toghraie, D., Ali Eftekhari, S., Oveissi, S.: Analysis of transverse vibration and instabilities of the axially moving carbon nanotube conveying fluid. Int. J. Fluid Mech. Res. 44(2), 115–129 (2017)

    Article  Google Scholar 

  18. Nayfeh, A.H., Younis, M.I.: Dynamics of MEMS resonators under super-harmonic and sub-harmonic excitations. J. Micromech. Microeng. 15, 1840–1847 (2005)

    Article  Google Scholar 

  19. Younis, M.I., Nayfeh, A.H.: A study of the nonlinear response of a resonant micro-beam to an electric actuation. Nonlinear Dyn. 31, 91–117 (2003)

    Article  MATH  Google Scholar 

  20. Eftekhari, M., Ziaei-Rad, S., Mahzoon, M.: Vibration suppression of a symmetrically cantilever composite beam using internal resonance under chord wise base excitation. Int. J. Non-Linear Mech. 48, 86–100 (2013)

    Article  Google Scholar 

  21. Abdel-Rahman, E.M., Younis, M.I., Nayfeh, A.H.: Characterization of the mechanical behavior of an electrically actuated micro-beam. J. Micromech. Microeng. 12, 759–766 (2002)

    Article  Google Scholar 

  22. Kuang, J.H., Chen, C.J.: Dynamic characteristics of shaped micro-actuators solved using the differential quadrature method. J. Micromech. Microeng. 14, 647–655 (2004)

    Article  Google Scholar 

  23. Amer, Y.A., El-Sayed, A.T., El-Bahrawy, F.T.: Torsional vibration reduction for rolling mill’s main drive system via negative velocity feedback under parametric excitation. J. Mech. Sci. Technol. 29(4), 1581–1589 (2015)

    Article  Google Scholar 

  24. Khaled, A., Majed, A.: Free vibrations control of a cantilever beam using combined time delay feedback. J. Vib. Control 18(5), 609–621 (2011)

    MathSciNet  MATH  Google Scholar 

  25. Seyed, H.M., Amir, M.K., Amir, H.G.: Optimizing time delay feedback for active vibration control of a cantilever beam using a genetic algorithm. J. Vib. Control 22(19), 4047–4061 (2016)

    Article  MathSciNet  Google Scholar 

  26. Cai, G.P., Yang, S.X.: A Discrete optimal control method for a flexible cantilever beam with time delay. J. Vib. Control 12(5), 509–526 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  27. Mustafa, Y.: Direct and parametric excitation of a nonlinear cantilever beam of varying orientation with time delay state feedback. J. Sound Vib. 324, 892–902 (2009)

    Article  Google Scholar 

  28. Hu, H., Dowell, E.H., Virgin, L.N.: Resonances of a harmonically forced Duffing oscillator with time delay state feedback. Nonlinear Dyn. 15, 311 (1998)

    Article  MATH  Google Scholar 

  29. Hu, H.Y., Wang, Z.H.: Nonlinear dynamics of controlled mechanical systems with time delays. Prog. Nat. Sci. 10, 801 (2000)

    MathSciNet  Google Scholar 

  30. Amer, Y.A., El-Sayed, A.T., Kotb, A.A.: Nonlinear vibration and of the Duffing oscillator to parametric excitation with time delay feedback. Nonlinear Dyn. 85(4), 2497–2505 (2016)

    Article  MathSciNet  Google Scholar 

  31. Kirrou, I., Belhaq, M.: On the quasi-periodic response in the delayed forced Duffing oscillator. Nonlinear Dyn. 84, 2069–2078 (2016)

    Article  MathSciNet  Google Scholar 

  32. El-Gohary, H.A., El-Ganaini, W.A.: Vibration suppression of a dynamical system to multi-parametric excitations via time-delay absorber. Appl. Math. Model. 36, 35–45 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  33. Saeed, N.A., El-Ganini, W.A., Eissa, M.: Nonlinear time delay saturation-based controller for suppression of nonlinear beam vibrations. Appl. Math. Model. 37, 8846–8864 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  34. Zhang, L., Huang, L., Zhang, Z.: Stability and Hopf bifurcation of the maglev system with delayed position and speed feedback control. Nonlinear Dyn. 57, 197–207 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  35. Wang, H., Li, J., Zhang, K.: Non-resonant response, bifurcation and oscillation suppression of a non-autonomous system with delayed position feedback control. Nonlinear Dyn. 51, 447–464 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  36. Zhao, Y.Y., Xu, J.: Using the delayed feedback control and saturation control to suppress the vibration of the dynamical system. Nonlinear Dyn. 67, 735–753 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  37. Daqaq, M.F., Alhazza, K.A., Qaroush, Y.: On primary resonances of weakly nonlinear delay systems with cubic nonlinearities. Nonlinear Dyn. 64, 253–277 (2011)

    Article  MathSciNet  Google Scholar 

  38. Alhazza, K.A., Daqaq, M.F., Nayfeh, A.H., Inman, D.J.: Nonlinear vibrations of parametrically excited cantilever beams subjected to non-linear delayed-feedback control. Int. J. Non-Linear Mech. 43, 801–812 (2008)

    Article  MATH  Google Scholar 

  39. Alhazza, K.A., Nayfeh, A.H., Daqaq, M.F.: On utilizing delayed feedback for active-multimode vibration control of cantilever beams. J. Sound Vib. 319, 735–752 (2009)

    Article  Google Scholar 

  40. Alhazza, K.A., Majeed, M.A.: Free vibrations control of a cantilever beam using combined time delay feedback. J. Vib. Control. 18(5), 609–621 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  41. Daqaq, M.F., Alhazza, K.A., Arafat, H.N.: Non-linear vibrations of cantilever beams with feedback delays. Int. J. Non-Linear Mech. 43, 962–978 (2008)

    Article  MATH  Google Scholar 

  42. Ji, J.C.J., Zhang, N.: Suppression of the primary resonance vibrations of a forced nonlinear system using a dynamic vibration absorber. J. Sound Vib. 329, 2044–2056 (2010)

    Article  Google Scholar 

  43. Ji, J.C., Leung, A.Y.T.: Resonances of a non-linear sdof system with two time-delays in linear feedback contror. J. Sound Vib. 253(5), 985–1000 (2002)

    Article  MATH  Google Scholar 

  44. Hamdan, M.N., Shabaneh, N.H.: On the large amplitude free vibrations of a restrained uniform beam carrying an intermediate lumped mass. J. Sound Vib. 199(5), 711–736 (1997)

    Article  Google Scholar 

  45. Xu, J., Pei, L.J.: Advances in dynamics for delayed systems. Adv. Mech. 36, 17–30 (2006)

    Google Scholar 

Download references

Acknowledgements

The work described in this paper is funded by the research Grant from the Natural Science Foundation of China (Grant Nos. 11662006 and 11172115). The authors are grateful for their financial support.

Author information

Authors and Affiliations

  1. Department of Engineering Mechanics, Kunming University of Science and Technology, Kunming, 650500, Yunnan, People’s Republic of China

    Chun-Xia Liu, Yan Yan & Wen-Quan Wang

Authors
  1. Chun-Xia Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yan Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wen-Quan Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to Yan Yan or Wen-Quan Wang.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendix A

Appendix A

$$\begin{aligned}&\varepsilon ^{1}:\,\,D_0^2 u_1 +u_1 =+e^{-5i\Omega T_0 }\left( {-\alpha _2 \Lambda ^{5}+2\Lambda ^{5}\beta _2 \Omega ^{2}} \right) \nonumber \\&\qquad +\,e^{5i\Omega T_0 }\left( {-\alpha _2 \Lambda ^{5}+2\Lambda ^{5}\beta _2 \Omega ^{2}} \right) +e^{-5iT_0 }\left( {-\alpha _2 A^{5}+2A^{5}\beta _2 } \right) \nonumber \\&\qquad +\,e^{5iT_0 }\left( {-\alpha _2 A^{5}+2A^{5}\beta _2 } \right) \nonumber \\&\qquad +\,e^{-3i\Omega T_0 }\left( {\begin{array}{l} -\alpha _1 \Lambda ^{3}-20A\bar{{A}}\alpha _2 \Lambda ^{3}-5\alpha _2 \Lambda ^{5}+2\beta _1 \Omega ^{2}\Lambda ^{3}+12A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,6\beta _2 \Lambda ^{5}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{3i\Omega T_0 }\left( {\begin{array}{l} -\alpha _1 \Lambda ^{3}-20A\bar{{A}}\alpha _2 \Lambda ^{3}-5\alpha _2 \Lambda ^{5}+2\beta _1 \Omega ^{2}\Lambda ^{3}+12A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,6\beta _2 \Lambda ^{5}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2}+6A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-i\Omega T_0 }\left( {\begin{array}{l} -\,6A\bar{{A}}\alpha _1 \Lambda -30A^{2}\bar{{A}}^{2}\alpha _2 \Lambda -3\alpha _1 \Lambda ^{3}-60A\bar{{A}}\alpha _2 \Lambda ^{3}-10\alpha _2 \Lambda ^{5} \\ +\,2A\bar{{A}}\beta _1 \Lambda \Omega ^{2}+2\beta _1 \Lambda ^{3}\Omega ^{2}+6A^{2}\bar{{A}}^{2}\beta _2 \Lambda \Omega ^{2}+30A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,8\beta _2 \Lambda ^{5}\Omega ^{2}+2A\bar{{A}}\beta _1 \Lambda +18A^{2}\bar{{A}}^{2}\beta _2 \Lambda +18A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{i\Omega T_0 }\left( {\begin{array}{l} -\,6A\bar{{A}}\alpha _1 \Lambda -30A^{2}\bar{{A}}^{2}\alpha _2 \Lambda -3\alpha _1 \Lambda ^{3}-60A\bar{{A}}\alpha _2 \Lambda ^{3}-10\alpha _2 \Lambda ^{5} \\ +\,2A\bar{{A}}\beta _1 \Lambda \Omega ^{2}+2\beta _1 \Lambda ^{3}\Omega ^{2}+6A^{2}\bar{{A}}^{2}\beta _2 \Lambda \Omega ^{2}+30A\bar{{A}}\beta _2 \Lambda ^{3}\Omega ^{2} \\ +\,8\beta _2 \Lambda ^{5}\Omega ^{2}+2A\bar{{A}}\beta _1 \Lambda +\,18A^{2}\bar{{A}}^{2}\beta _2 \Lambda +18A\bar{{A}}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{4iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}+2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ +e^{-i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}-2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-4iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}+2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ +\,e^{-i\Omega T_0 }\left( {-5A^{4}\alpha _2 \Lambda +A^{4}\beta _2 \Lambda \Omega ^{2}-2A^{4}\beta _2 \Lambda \Omega +7A^{4}\beta _2 \Lambda } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{3iT_0 }\left( {\begin{array}{l} -A^{3}\alpha _1 -5A^{4}\bar{{A}}\alpha _2 -20A^{3}\alpha _2 \Lambda ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega ^{2}+2A^{3}\beta _1 +6A^{4}\bar{{A}}\beta _2 \\ +\,18A^{3}\beta _2 \Lambda ^{2} \\ +e^{2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ +e^{-2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}-6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-3iT_0 }\left( {\begin{array}{l} -A^{3}\alpha _1 -5A^{4}\bar{{A}}\alpha _2 -20A^{3}\alpha _2 \Lambda ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega ^{2}+2A^{3}\beta _1 +6A^{4}\bar{{A}}\beta _2 \\ +\,18A^{3}\beta _2 \Lambda ^{2} \\ +e^{2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}+6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ +e^{-2i\Omega T_0 }\left( {-10A^{3}\alpha _2 \Lambda ^{2}+5A^{3}\Lambda ^{2}\beta _2 \Omega ^{2}-6A^{3}\beta _2 \Lambda ^{2}\Omega +9A^{3}\beta _2 \Lambda ^{2}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{iT_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \bar{{A}}-10A^{3}\bar{{A}}^{2}\alpha _2 -6A\alpha _1 \Lambda ^{2}-60A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-30A\alpha _2 \Lambda ^{4}+2A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +\,18A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+18A\Lambda ^{4}\beta _2 \Omega ^{2}+2A^{2}\bar{{A}}\beta _1 +2A\Lambda ^{2}\beta _1 +8A^{3}\bar{{A}}^{2}\beta _2 \\ +\,30A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \omega _0^2 +6A\Lambda ^{4}\beta _2 +g_p Ae^{-i\tau _1 }+ig_d Ae^{-i\tau _2 } \\ +e^{4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ +e^{-4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{iT_0 }e^{2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2}+15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2} \\ 16A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\Lambda ^{2}\beta _1 \Omega +6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega +4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \end{aligned}$$
$$\begin{aligned}&\qquad +\,e^{iT_0 }e^{-2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2}+15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2} \\ 16A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\Lambda ^{2}\beta _1 \Omega -6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega -4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }\left( {\begin{array}{l} -3A^{2}\alpha _1 \bar{{A}}-10A^{3}\bar{{A}}^{2}\alpha _2 -6A\alpha _1 \Lambda ^{2}-60A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-30A\alpha _2 \Lambda ^{4} \\ +\,2A\Lambda ^{2}\beta _1 \Omega ^{2}+18A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+18A\Lambda ^{4}\beta _2 \Omega ^{2}+2A^{2}\bar{{A}}\beta _1 \\ +\,2A\Lambda ^{2}\beta _1 +8A^{3}\bar{{A}}^{2}\beta _2 +30A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +6A\Lambda ^{4}\beta _2 \\ +e^{4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ +e^{-4i\Omega T_0 }\left( {-5A\alpha _2 \Lambda ^{4}+7A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\beta _2 \Lambda ^{4}\Omega +A\beta _2 \Lambda ^{4}} \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }e^{2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+16A\Lambda ^{4}\beta _2 \Omega ^{2}+2A\Lambda ^{2}\beta _1 \Omega \\ +6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega +4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +\,15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-iT_0 }e^{-2i\Omega T_0 }\left( {\begin{array}{l} -\,3A\alpha _1 \Lambda ^{2}-30A^{2}\bar{{A}}\alpha _2 \Lambda ^{2}-20A\alpha _2 \Lambda ^{4}+3A\Lambda ^{2}\beta _1 \Omega ^{2} \\ +15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega ^{2}+16A\Lambda ^{4}\beta _2 \Omega ^{2}-2A\Lambda ^{2}\beta _1 \Omega \\ -\,6A^{2}\bar{{A}}\Lambda ^{2}\beta _2 \Omega -4A\Lambda ^{4}\beta _2 \Omega +A\Lambda ^{2}\beta _1 \\ +15A^{2}\bar{{A}}\Lambda ^{2}\beta _2 +4A\Lambda ^{4}\beta _2 \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{2iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+2A^{2}\beta _1 \Lambda \Omega +4A^{3}\bar{{A}}\beta _2 \Lambda \Omega +6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{-i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-2A^{2}\beta _1 \Lambda \Omega -4A^{3}\bar{{A}}\beta _2 \Lambda \Omega -6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ +e^{-3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ \end{array}} \right) \nonumber \\&\qquad +\,e^{-2iT_0 }\left( {\begin{array}{l} e^{i\Omega T_0 }\left( {\begin{array}{l} -\,3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+2A^{2}\beta _1 \Lambda \Omega +4A^{3}\bar{{A}}\beta _2 \Lambda \Omega +6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{-i\Omega T_0 }\left( {\begin{array}{l} -3A^{2}\alpha _1 \Lambda -20A^{3}\bar{{A}}\alpha _2 \Lambda -30A^{2}\alpha _2 \Lambda ^{3}+A^{2}\beta _1 \Lambda \Omega ^{2}+4A^{3}\bar{{A}}\beta _2 \Lambda \Omega ^{2} \\ +\,15A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-2A^{2}\beta _1 \Lambda \Omega -4A^{3}\bar{{A}}\beta _2 \Lambda \Omega -6A^{2}\Lambda ^{3}\beta _2 \Omega \\ +\,3A^{2}\beta _1 \Lambda +16A^{3}\bar{{A}}\beta _2 \Lambda +15A^{2}\beta _2 \Lambda ^{3} \\ \end{array}} \right) \\ +e^{3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}+6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ +e^{-3i\Omega T_0 }\left( {-10A^{2}\alpha _2 \Lambda ^{3}+9A^{2}\Lambda ^{3}\beta _2 \Omega ^{2}-6A^{2}\Lambda ^{3}\beta _2 \Omega +5A^{2}\Lambda ^{3}\beta _2 } \right) \\ \end{array}} \right) \end{aligned}$$
(32)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, CX., Yan, Y. & Wang, WQ. Primary and secondary resonance analyses of a cantilever beam carrying an intermediate lumped mass with time-delay feedback. Nonlinear Dyn 97, 1175–1195 (2019). https://doi.org/10.1007/s11071-019-05039-w

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05039-w

Keywords

Search

Navigation