1 Introduction

Atomic force microscopy (AFM) has become one of the most prominent characterization tools in modern science. It is ubiquitously used to characterize and manipulate surface properties of materials down to atomic resolution in both air and liquid environments [1]. Among the various AFM operational modes, tapping mode AFM (TM-AFM) [2] also known as amplitude modulation AFM (AM-AFM) [3] is one of the most extensively used techniques to obtain high-resolution images of wide variety of samples. Owing to reduced lateral forces and high-phase sensitivity, TM-AFM is widely popular in soft matter [4], biological samples [5] and polymer [6] applications.

TM-AFM is based on the near-resonant excitation of a microcantilever with a sharp tip at its free end that is vibrating in the vicinity of the sample. The vibrations in the cantilever are influenced by the tip–sample interaction forces, which modifies the beam dynamics. In general, the tip–sample interaction is nonlinear and comprises long-range attractive Van der Waals forces, short-range quantum mechanical repulsive forces, adhesive and contact forces. The nonlinear response due to tip–sample interaction is even more involved in the presence of electrostatic and capillary forces [7]. In the existence of such complex nonlinearities, a comprehensive understanding of the multi-stable response is crucial, since these nonlinearities can be efficiently utilized for extracting several nanomechanical properties of the sample [3, 8,9,10]. Furthermore, the accuracy of imaging and nanomechanical characterization of sample surfaces from measured data depends crucially on the deconvolution of data with appropriate models.

In recent years, the underlying dynamics of AFM cantilever and its exploitation have been investigated by many authors [11,12,13,14,15,16,17,18]. The vast majority of these studies have been dedicated to study the microcantilever dynamics by utilizing a simplified single-degree-of-freedom point mass model [16,17,18]. In this approach, first a static analysis is performed to determine the cantilever stiffness and then the equivalent mass is calculated based on the experimentally evaluated fundamental resonance frequency. Furthermore, the excitation is modelled as an external force acting on the point mass [16,17,18]. Such a lumped parameter model does not represent the conditions encountered in reality, where the microcantilever is subjected to base excitation at the clamped end by means of a piezoelectric actuator. The base excitation induces linear and nonlinear parametric excitations that are typically not captured by the lumped parameter model, thus failing to accurately describe the dynamics of the microcantilever [13, 14].

Continuous beam models on the contrary have proven to predict the nonlinear aspects of AFM cantilever dynamics accurately [12,13,14,15]. These models are able to provide precise and deeper insights into the physics behind the nonlinear phenomena such as amplitude jumps, period-doubling, and grazing bifurcations [14, 19]. Therefore, in spite of the complexities involved in modelling of the AFM cantilever as a continuous beam, it allows for capturing the overall nonlinear aspects of the AFM dynamics [20].

In practical operation, the dynamics of AFM cantilever is influenced by several operating parameters such as tip radius, excitation amplitude, excitation frequency, and feedback values. The real-time variation of these parameters during an AFM operation can lead to unwanted dynamical phenomena such as bifurcations and unstable and aperiodic motions, which can decrease the reliability of results and strictly limit the operating ranges of the AFM. The dynamic models as well as the feedback strategies implemented in standard AFM systems tend to focus on governing the local dynamics of the system, leaving the impact on the global dynamics largely unknown. Therefore, in order to predict and control these dynamical events as well as preserving the stability of operation in TM-AFM, it is important to study and understand the nonlinear responses from a global perspective.

Currently, there are no detailed works on global dynamics of TM-AFM, which (i) evaluate the escape boundaries, (ii) estimate dynamical integrity, and (iii) perform detailed analysis of bifurcations. Existing literature has focused on the dynamical integrity and bifurcation scenarios of non-contact AFM [19, 21]. But basins of attraction and erosion process of basin portraits in TM-AFM are lacking in the literature. The erosion of uncorrupted basins of attraction surrounding each main solution as a function of AFM operation parameters is of paramount importance from both theoretical and experimental perspective.

In this article, we elucidate the global dynamics and robustness of attractors in TM-AFM. Differently from existing works, which are based on limited analysis on the local dynamical behaviour, this work makes systematic use of bifurcation diagrams to highlight the appearance and disappearance of steady-state solutions. The latter offers an overall interpretation of the dynamic response with respect to operational parameters, namely excitation frequency and forcing amplitude. Additionally, we show that, by changing the operation parameters, a microcantilever initially in the primary resonant branch can escape from its local potential well and get captured by a second coexisting local potential well close to the sample surface. This regime of oscillation close to the sample surface, referred in this article as ‘in-contact’ attractor, is unexplored in the literature. In this work, we examine its evolution and robustness properties with frequency response curves and basins of attraction. Furthermore, the envelopes of local bifurcation boundaries are built to understand the escape scenarios of the solutions. Finally, integrity analysis is performed to quantify the steady-state solutions associated with all the attractors present in TM-AFM.

Based on these motivations, the article is organized as follows: the modelling of the system is discussed briefly in Sect. 2. This is followed by a detailed analysis of frequency response of the system, bifurcation charts and response scenarios including escape of solutions in an excitation parameter space in Sect. 3. Particular attention is paid to the frequency response analysis of the in-contact attractor around its primary and parametric resonance. The results of this section are then utilized to build basins of attraction and dynamical integrity curves for the main attractors present in the system in Sect. 4.

Fig. 1
figure 1

Schematic of the AFM cantilever in a static deflection configuration and b configuration at which AFM cantilever exhibits oscillations around the nonlinear static equilibrium. The sample is at \(\bar{\eta }_1 = 1\)

Full size image

2 Numerical model

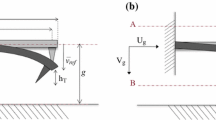
The classical beam theory, based on the Euler–Bernoulli assumptions, is used to obtain the continuous model for the AFM microcantilever shown in Fig. 1. The nomenclature used to describe the equations in this article is identical to the one described by Ruetzel et al. [12]. The deflection of the cantilever towards the sample is treated as positive, and the rest position of the cantilever is taken as reference. The considered microcantilever has a length L, mass density \(\rho \), Young’s modulus E, area moment of inertia I, and cross-sectional area A. The beam is clamped at \(x = 0\) and free at \(x = L\). The tip–sample separation distance in the reference configuration is denoted by Z, and the total deflection of the microcantilever w(x, t) can be expressed as \(w(x,t) = u(x,t)+ w^*(x) + y(t)\), where u(x, t) is the deflection of the microcantilever relative to a non-inertial reference frame attached to the base and \(w^*(x)\) is the static deflection towards the sample due to tip–sample interaction. The base excitation is generated by a dither piezo and is assumed to be harmonic, i.e. \(y(t) = Y \mathrm{sin}(\varOmega t)\), where Y and \(\varOmega \) are the amplitude and frequency of excitation, respectively.

2.1 Tip–sample interaction

In TM-AFM, the microcantilever oscillates in close proximity to the sample surface. In our work, we use the Lennard–Jones (LJ) potential to describe the tip–sample interactions [22]. Although the model doesn’t take into account the real contact mechanics encountered in TM-AFM, it represents a generic tip–surface interaction potential which mimics qualitatively, the more detailed and computationally expensive models [13]. The LJ potential models the non-retarded dispersive Van der Waals forces as well as the short-range repulsive exchange interactions between two molecules. Assuming a spherical tip apex with radius R and a flat sample surface, the interaction potential and the force are:

$$\begin{aligned} U_\mathrm{LJ}= & {} \frac{A_1 R}{1260 z^7}-\frac{A_2 R}{6 z}, \end{aligned}$$
(1a)
$$\begin{aligned} P_\mathrm{LJ}= & {} -\frac{\partial {U}}{\partial {z}}=\frac{A_1 R}{180 z^8}-\frac{A_2 R}{6 z^2}, \end{aligned}$$
(1b)

where z is the instantaneous tip–sample separation gap. A\(_{\text {1}}\) and A\(_{\text {2}}\) are the Hamaker constants for the repulsive and attractive potentials, respectively. A positive interaction force implies repulsion. The Hamaker constants are A\(_{\text {1}}\) \(=\) \(\pi \)\(^{\text {2}}\)\(\rho _1\rho _2\)c\(_{\text {1}}\) and A\(_{\text {2}}\) \(=\) \(\pi \)\(^{\text {2}}\)\(\rho _1\rho _2\)c\(_{\text {2}}\), where \(\rho _1\) and \(\rho _2\) are the number densities of molecules in the interacting media and c\(_{\text {1}}\) and c\(_{\text {2}}\) are the interaction coefficients of intermolecular pair potential [22].

2.2 Equation of motion

The nonlinear static deflection of the microcantilever in the absence of base excitation is computed by solving for the equilibrium gap between the tip and the sample shown in Fig. 1. The static equilibrium gap \(\eta ^*\) at the free end is calculated as a function of the approach distance Z through static balancing of the cantilever restoring force and the tip–sample interaction forces.

The dynamic equation of motion of the tip deflection u(x, t) about its nonlinear equilibrium subjected to base harmonic motion is then derived through a single mode discretization of the Euler–Bernoulli beam equation. The interaction forces given by Eq. (1b) are assumed to be acting on the free end of the cantilever and are mathematically achieved through the use of Kronecker delta (\(\delta \)) function. Writing the equation of motion of the vibrating cantilever with respect to a non-inertial frame of reference leads to the following governing equation,

$$\begin{aligned}&\rho A \ddot{u}(x,t) + EI (u^{\prime \prime \prime \prime }(x,t)+w^{*\prime \prime \prime \prime }(x))\nonumber \\&\quad =F_i(Z-w(L,t))\delta (x-L) + \rho A \varOmega ^2 Y \mathrm{sin}(\varOmega t),\nonumber \\ \end{aligned}$$
(2)

where

$$\begin{aligned}&F_i(Z-w(L,t))\nonumber \\&\quad =-\frac{A_1 R}{180(Z-w^*(L)-u(L,t)-Y\mathrm{sin}(\varOmega T)^8}\nonumber \\&\qquad +\frac{A_2 R}{6(Z-w^*(L)-u(L,t)-Y\mathrm{sin}(\varOmega T)^2}. \end{aligned}$$
(3)

Equation (2) is a non-autonomous and nonlinear equation. The equation is discretized by projecting the dynamics onto the system’s linear modes of vibration. The natural modes and frequencies are obtained using the Galerkin approach [12, 23]. The frequency range of the analyses in this paper spans around the neighbourhood of the fundamental resonance, where the contribution of higher modes is substantially negligible. Based on this assumption, a single-degree-of-freedom model is used. Assuming \(u(x,t)=\phi _1(x) q_{\text {1}}(t)\) (where \(\phi _1\) is the first approximate eigenfunction around the static deflected configuration) and using the Galerkin approach, the following nonlinear equation can be derived [12]:

$$\begin{aligned} \ddot{\bar{\eta }}_1= & {} -d_1\dot{\bar{\eta }}_1 -\bar{\eta }_1 +B_1 + \frac{C_{11}}{(1-\bar{\eta }_1 - \bar{y}\mathrm{sin}(\bar{\varOmega }t))^8}\nonumber \\&+ \frac{C_{12}}{(1-\bar{\eta }_1 - \bar{y}\mathrm{sin}(\bar{\varOmega }t))^2} + \bar{y} \bar{\varOmega }^2 E_1 \mathrm{sin}(\bar{\varOmega } t). \end{aligned}$$
(4)

The dimensionless variables and the corresponding coefficients are described in “Appendix”. The microcantilever tip deflection towards the sample is denoted by \(\bar{\eta }_1\). In addition, the equation is made dimensionless with respect to equilibrium gap width (\(\eta ^*\)) and the fundamental frequency of the free microcantilever (\(\omega _1\)) in the absence of tip–sample interaction forces. The amplitude of the dither piezoelectric actuator is denoted by \(\bar{y}\). The dotted quantities represent derivatives with respect to rescaled time \(\tau \) (\(\tau =\omega _1 t\)). Finally, the modal damping \(d_{1}\) is explicitly introduced in Eq. (4) and is related to the quality factor Q of the cantilever by the relation \(Q=1/d_{\text {1}}\).

3 Numerical analysis

In order to investigate the dynamical behaviour of the TM-AFM, the simulations of the model given by Eq. (4) are performed in this section. The entire analysis is carried out for the interaction of a soft monocrystalline silicon microcantilever with the (111) face of flat silicon sample. The cantilever and interaction properties are listed in Table 1. Furthermore, the analysis is performed for tip–sample gap (\(\eta ^*\)) in the bi-stable region of nonlinear elastostatic equilibrium curve. Thus, a value of \(\eta ^*=6.542\,\hbox {nm}\)Footnote 1 is chosen for the rest of the analysis in this article. However, a similar analysis can be carried out for any other tip–sample gap values.

Table 1 Properties and dimensions of the cantilever [12]
Full size table
Fig. 2
figure 2

Frequency response curve and basin portrait of the system for fixed parameters \(\bar{y}=0.006\) and \(R=150\) nm. The parameters are obtained from the monostable region of nonlinear elastostatic equilibrium curve. a Frequency response shows softening and hardening behaviour corresponding to the attractive and repulsive tip–sample forces. Continuous and dotted lines indicate stable and unstable branches of the solution. Red and blue circles indicate period-doubling and saddle-node bifurcation points, respectively. The natural frequency of the system is \(\bar{\varOmega }_0=0.94\). b Basins of attraction taken at section \(\bar{\varOmega }=0.8\). The positive displacement implies movement of the tip closer to the sample. The details on basin colour and the corresponding attractor/solution description are given in Table 4. (Color figure online)

Full size image
Fig. 3
figure 3

Frequency response curve and basin portrait of the system for fixed parameter \(\bar{y}=0.020\) and \({R}={150}\,\hbox {nm}\). The parameters are obtained from the bi-stable region of nonlinear elastostatic equilibrium curve. a Frequency response of the system showing both attractive (lower curve) and in-contact (upper curve) main solutions. Continuous and dotted lines indicate stable and unstable branches of the solution. Red and blue circles indicate period-doubling and saddle-node bifurcation points, respectively. b Basins of attraction of the system are obtained at section \(\bar{\varOmega }=0.8\). The details on basin colour and the corresponding attractor/solution description are given in Table 4. (Color figure online)

Full size image
Fig. 4
figure 4

Frequency response curve and basins of attraction for the in-contact attractor. a Frequency response of in-contact attractor for fixed parameter \(\bar{y}=0.005\) and \(R={150}\,\hbox {nm}\). Continuous and dotted lines indicate stable and unstable branches of solution. Red and blue circles indicate period-doubling and saddle-node bifurcation points, respectively. b, c Basins of attraction of in-contact attractor obtained at sections, \(\bar{\varOmega }=0.5\) and \(\bar{\varOmega }=2.96\), respectively, in the frequency response curve. The details on basin colour and the corresponding attractor/solution description are given in Table 4. (Color figure online)

Full size image

Numerical simulations are performed by using a pseudo-arc-length continuation technique [24]. We also make use of basins of attraction (phase space) in order to illustrate the presence of various attractors (steady-state solutions). A basin of attraction is a set of possible initial conditions about an equilibrium point in phase space that assures a specific response from the cantilever. In other words, any chosen initial condition within the phase space will be ‘attracted’ to a particular steady-state motion of the cantilever. Unless specified, the basins are evaluated in a phase-space grid of \(\bar{\eta }_1=[-0.9, 0.9]\) and \(\dot{\bar{\eta }}_1=[-0.9, 0.9]\) as it contains all the main attractors involved in the system potential well.

3.1 Frequency response and bifurcation scenarios

The interaction between tip and sample gives rise to different nonlinear frequency responses depending on the tip–sample separation distance. The response displayed in Fig. 2a shows an initial softening behaviour when the tip is far away from the sample. This region is dominated by attractive Van der Waals forces. However, when the tip–sample separation reaches the order of the interatomic distance, the response exhibits hardening behaviour and this region is dominated by repulsive forces (see Fig. 2a). Figure 2b shows the corresponding basin portrait associated with the frequency response at \(\bar{\varOmega }=0.8\). The blue and crimson basins together form the attractive region, while the purple basin belongs to the repulsive region.

The nonlinear frequency response shown in Fig. 2a is well known and studied extensively by many authors [10, 12, 25]. However, there exists another overlooked steady-state response when the cantilever escapes the local potential well and gets trapped by a subsequent attractor very close to the sample. Figure 3a shows the frequency response for the model given by Eq. (4), and Fig. 3b shows the position of the in-contact attractor in the basin portrait. Note that Fig. 3a is made up of two different solutions belonging to the attractive (lower frequency response curve) and the in-contact attractor (upper frequency response curve). The two solutions can be obtained by using different initial conditions in the numerical integration. In the next section, the detailed analysis of the in-contact attractor’s frequency response and corresponding bifurcation scenarios is presented parametrically.

3.2 Frequency response curves

Local dynamic analysis is performed using frequency response curves together with the bifurcation charts. The analysis offers a complete overview into the bifurcations and escape scenarios of the system. Furthermore, the unstable solution branches shown in the frequency response curves are not discussed in detail but are reported for the sake of completeness.

Fig. 5
figure 5

Frequency response curve of the in-contact attractor for fixed parameter values \(\bar{y}=0.020\) and \({R}= 150\,\hbox {nm}\). Continuous and dotted lines indicate stable and unstable branches of the solution, respectively. Red and blue circles indicate period-doubling and saddle-node bifurcation points, respectively. (Color figure online)

Full size image

Figures 4 and 5 show the evolution of frequency response of the in-contact attractor as a function of the excitation amplitude, \(\bar{y}=0.005\) and 0.020, respectively. In both figures, red and blue circles indicate period-doubling and saddle-node bifurcation points, respectively. Although the dimensionless natural frequency of the system oscillating in attractive regime is found to be \(\bar{\varOmega }_0=0.83\) (\(\bar{\varOmega }_0\) is the natural frequency affected by the system potential well), it can be observed in Fig. 4 that the first natural frequency of the system oscillating in the in-contact regime is \(\bar{\varOmega }_0=3.72\) with corresponding parametric resonance at 2\(\bar{\varOmega }_0=7.44\). This shift in resonance frequency is due to the presence of strong repulsive forces which act as a hard spring connecting the cantilever to the sample. This can be visualized as a change in the boundary conditions of the cantilever similar to that of a clamped–clamped beam. Interestingly, the system also exhibits softening nonlinearity in spite of the presence of repulsive forces. This is due to the fact that the cantilever is oscillating in the potential well with a duration of oscillation longer in the attractive regime. In addition, multi-stability can be observed with different solutions overlapping in several discrete ranges of frequencies (see Fig. 4a). At lower values of forcing frequency \(\bar{\varOmega } \le 1.85\), the system has only one non-resonant low-amplitude solution (LP\(_{\text {1}}\)). The corresponding basin associated with LP\(_{\text {1}}\) solution at \(\bar{\varOmega }=0.5\) is shown in light brown colour in Fig. 4b. The figure illustrates the low-amplitude attractor being the dominant solution in the in-contact regime at low-frequency values. The LP\(_{\text {1}}\) solution eventually gives rise to a superharmonic branch (Su\(_{\text {1}}\)HP\(_{\text {1}}\)) at \(\bar{\varOmega }=1.85\) via saddle-node bifurcation, and later a resonant high-amplitude solution (HP\(_{\text {1}}\)) at \(\bar{\varOmega }=3.3\). Figure 4c reports the orange basin belonging to HP\(_{\text {1}}\) solution arising from the boundaries of Su\(_{\text {1}}\)HP\(_{\text {1}}\) solution (green basin) in the in-contact regime.

Furthermore, the HP\(_{\text {1}}\) branch in Fig. 4a destabilizes with the inception of a pair of period-2 branches via flip/period-doubling bifurcations. One of the period-doubling bifurcation occurs close to the low-frequency saddle-node bifurcation at \(\bar{\varOmega }=0.3\), while the other period-doubling bifurcations occur at \(\bar{\varOmega }=1.56\) (zoomed part of Fig. 4a). This behaviour is similar to the nonlinear cantilever response seen in attractive regime as illustrated earlier in Fig. 3a. Moreover, in Fig. 4a the period-2 branch continuation shows stable motion over a short frequency range before undergoing further period-doubling bifurcation cascade. The subharmonic response associated with the period-doubling bifurcation can be observed around the principal parametric resonance frequency of 2\(\bar{\varOmega }_0=7.44\). The stable large amplitude period-2 solution (referred to as Pa-P\(_{\text {2}}\) in Fig. 4a), arising from one of the period-doubling points, is found to be stable over a wide range of excitation frequency (\(\bar{\varOmega }\in [4.8, 7.7]\)). In addition to the above analysis, referring to Fig. 5, at larger excitation amplitudes (\(\bar{y} \ge 0.0118\)), the softening behaviour in the nonlinear response of the system increases along with a larger field of existence of the superharmonic response (Su\(_{\text {1}}\)HP\(_{\text {1}}\)). Furthermore, a second superharmonic branch (Su\(_{\text {2}}\)HP\(_{\text {1}}\)) bifurcates through a saddle-node at \(\bar{\varOmega }=1.79\). Here, four forced period-1 solutions coexist out of which only two are stable (Su\(_{\text {2}}\)HP\(_{\text {1}}\) and Su\(_{\text {1}}\)HP\(_{\text {1}}\)) and two are unstable. The superharmonic branch for larger excitations eventually joins the main branch of the in-contact response via the saddle-node at \(\bar{\varOmega }=2.83\). In addition, the Su\(_{\text {1}}\)HP\(_{\text {1}}\) branch is destabilized over narrow frequency ranges, \(\bar{\varOmega }\in [0.92, 0.95]\) and \(\bar{\varOmega }\in [2.41, 2.42]\), by the occurrence of period-doubling bifurcations.

Fig. 6
figure 6

In-contact attractor bifurcation and response chart focusing on the region below the primary resonance frequency (\(\bar{\varOmega }_0=3.721\) indicated by the vertical dashed line). The first and second superharmonic frequencies are indicated at \(\bar{\varOmega }=1.851\) and \(\bar{\varOmega }=1.24\) by dashed–dotted lines. Blue lines are the saddle-node bifurcation loci on period-1 solution branches, red lines are the period-doubling/flip bifurcation loci on period-1 solution branches, and green lines are the period-doubling/flip bifurcation loci on period-2 solution branches. The details on individual bifurcation envelope description and the corresponding solution regions are summarized in Tables 2 and 3, respectively. Refer to “Appendix” for detailed instruction on how to read the bifurcation chart. (Color figure online)

Full size image

It is observed in Fig. 5 that the low-frequency period-doubling point (\(\bar{\varOmega }=0.94\)) has a stable period-2 solution over a short frequency range (see zoomed part of the figure) and the high-frequency period-doubling (\(\bar{\varOmega }=2.42\)) presents mostly an unstable bifurcated period-2 solution except for few initial continuation points that are stable. These few stable points are not shown in the frequency response curves but are described in the bifurcation maps. In an analogous way, a period-doubling bifurcation at \(\bar{\varOmega }=2.90\) is observed on the HP\(_{\text {1}}\) branch having a stable period-2 solution limited in frequency range \(\bar{\varOmega }\in [2.7, 2.9]\). Moreover, period-doubling cascades are present in both stable period-2 solutions arising from Su\(_{\text {1}}\)HP\(_{\text {1}}\) and HP\(_{\text {1}}\) branches. This period-doubling cascade can lead to chaos in a similar fashion as encountered in standard TM-AFM systems [26].

Fig. 7
figure 7

In-contact attractor bifurcation and response map focusing on the region near the neighbourhood of parametric resonance frequency (\(2\bar{\varOmega }_0=7.44\) indicated by the vertical dashed line). The details on individual bifurcation envelope description and the corresponding solution regions are summarized in Tables 2 and 3, respectively

Full size image
Table 2 Bifurcation envelope data
Full size table

3.3 Bifurcation chart, response scenarios and escape threshold

Figures 6 and 7 provide an overview of the various bifurcation scenarios and escape thresholds occurring for a wide range of excitation amplitudes and frequencies. In these figures, local bifurcation envelope (loci) is constructed by following the variation of the bifurcation point (saddle-node or period-doubling) with respect to operating parameters, namely \(\bar{\varOmega }\) and \(\bar{y}\). Furthermore, by assembling all the local bifurcation envelopes together, the global response and behaviour map of the entire system in the excitation amplitude and frequency control space are obtained. The bifurcation map has been obtained numerically for the in-contact attractor over a wide range of frequencies which includes the fundamental (\(\bar{\varOmega }_0\)) and principal parametric resonances (\(2\bar{\varOmega }_0\)). Thus, it is convenient to analyse the global dynamics by dividing the bifurcation map into two separate regions: the first region focuses around the fundamental resonance frequency \(\bar{\varOmega }_0 =3.72\) illustrated in Fig. 6, whereas the second region analyses the principal parametric resonance frequency \(\bar{\varOmega }_0=7.44\) as shown in Fig. 7. In addition, Table 2 outlines the data concerning the various bifurcation envelopes of Figs. 6 and 7. Furthermore, Table 3 summarizes the various dynamic regions formed by these envelopes and the corresponding solutions involved. From an experimental perspective, the response scenario map provides qualitative information on the form of cantilever response expected for the chosen set of excitation amplitude and excitation frequency.

3.3.1 Analysis of the bifurcation map around the fundamental resonance

Around the fundamental resonance frequency of the in-contact attractor, the dynamics is more involved than in the case of the attractive region [19]. The period-doubling/flip bifurcations appear not only on the main branch of the solution (HP\(_{\text {1}}\) branch in Fig. 5), but also on the first superharmonic branch (Su\(_{\text {1}}\)HP\(_{\text {1}}\) branch in Fig. 5). This drastically increases the possibility of global escape through crisis and also chaotic behaviour through period-doubling cascade. In an analogous way, the saddle-node bifurcations that arise from the superharmonic branch increase the complexity of the response.

Table 3 Correlation data between the dynamic regions and corresponding solutions
Full size table
Table 4 Correlation data between the basin colours and corresponding attractors
Full size table

Figure 6 reports all the possible regions of motions for the cantilever in the range of frequencies surrounding the fundamental resonance. The different regions are named with pink labels and accordingly numbered. For both low-amplitude excitations and frequencies up to \(\bar{y}=0.004\) and \(\bar{\varOmega } < 1.85\), there exists only the LP\(_{\text {1}}\) motion indicated by region R1 in Fig. 6. Hereafter, with the increase in \(\bar{\varOmega } \ge 1.85\), the response consists of both the HP\(_{\text {1}}\) and superharmonic high-amplitude (Su\(_{\text {1}}\)HP\(_{\text {1}}\)) solutions bound by loci HP\(_{\text {1}}\)-SPF as shown in the region R2 of Fig. 6. Moving to even larger values of excitation frequency, the solution HP\(_{\text {1}}\) governs the behaviour of the system (R9). In particular, special attention should be given to the regions bounded by SPF (red) and SPF\(_{\text {2}}\) (green) loci. These regions exist over a narrow frequency range and invade into other period-1 regions resulting in new multi-stable regions which consist of both period-1 and period-2 solutions. Similarly, in addition to the discussion of aforementioned regions, the presence of other response scenarios and dynamic regions data is tabulated in Table 3. Moreover, in contrast to the various stable responses seen in Fig. 6, the bifurcation analysis of in-contact attractor shows the presence of multiple strange attractors leading to crisis scenarios and global escape. The operating parameters leading to escape are depicted by grey regions (R11) in Fig. 6. The crisis scenario also highlights appearance of several rare attractors (period-5 and above) along with period-doubling cascades, which lead the solution to escape from the local potential well.

The detailed instructions on reading the bifurcation chart together with an example are provided in “Appendix B”.

3.3.2 Analysis of the bifurcation map around the principal parametric resonance

Figure 7 shows that, below the parametric resonance frequency, \(\bar{\varOmega } < 7.44\) , only HP\(_{\text {1}}\) solution exists (R9) until the Pa-P\(_{\text {2}}\) solution from the parametric resonance (2\(\bar{\varOmega }_0=7.44\)) overlaps with the region R9 resulting in two coexisting period-1 (HP\(_{\text {1}}\)) and period-2 (Pa-P\(_{\text {2}}\)) responses as shown in region R9 \(+\) R12. In between the classic parametric instability tongue (V-shaped region near \(\bar{\varOmega }=7.44\)) formed by the parametric subcritical (Pa-SBF) and supercritical (Pa-SPF) bifurcations, the HP\(_{\text {1}}\) solution becomes unstable and there exists only period-2 (Pa-P2) solution (R12). As expected in any of the archetypal parametric oscillators, the system requires a minimum excitation threshold to achieve parametric resonance. This is indicated by the lifting of the instability tongue (V-shaped region) along the \(\bar{y}\) axis and in our system the critical threshold is at \(\bar{y}=0.00014\). Finally, for excitation frequency \(\bar{\varOmega } > 7.44\), only HP\(_{\text {1}}\) solution is present as shown in region R9.

4 Dynamical integrity and robustness of attractors

In the previous section, we provided insight into diverse solutions and bifurcation scenarios including escape thresholds. However, the analysis did not furnish details on the various instability paths and eventual escape of the steady-state solutions. The information on the instability path (escape from local potential well, cross-well chaos) taken by the cantilever response is of utmost importance in practical applications of AFM. This helps to disentangle image artefacts from factual data.

From an experimental perspective, if the system perturbations can be quantized, then basins of attraction provide insight into the evolution of various steady-state responses (system attractors) and instabilities (erosion profiles) occurring in the system. Furthermore, measures of the basin portraits, the dynamical integrity of the system, are able to quantify the robustness of different attractors. This can be realized through various scalar integrity measures [27]. These integrity measures provide information on the strength of such quantized perturbations required to destabilize the corresponding system response. Therefore, basin portraits together with integrity measures provide a means to track the basin erosion process with respect to changes in operating parameters. Hence, in order to advance the dynamical analysis of the AFM cantilever in the in-contact regime of oscillation, this section focuses on the global topology analysis by means of basins of attraction [28, 29].

There have been multiple integrity measures introduced in the literature [30], and this section makes use of two integrity indicators to measure the evolution of phase-space topology, namely local integrity measures (LIM) [27] and integrity factor [31] (IF). The LIM is defined as the normalized radius of the largest hypersphere (circle in 2D), centred on the safe attractor and entirely belonging to the safe basin. It is used to analyse the robustness of the attractor of interest against perturbations. On the other hand, the IF is defined as the normalized radius of the largest circle entirely belonging to the compact part of safe basin. The IF is suitable to study the dynamical integrity of the attractors subject to perturbation around its initial equilibrium condition. The reason to choose these measures with respect to others such as global integrity measures (GIM) relies on the fact that IF and LIM can disentangle the fractality of basin since they focus only on its compact part [27]. In our case this is a serious advantage since the homoclinic tangling of the saddle results in fractalization of the low-amplitude attractive regime basin.

Fig. 8
figure 8

Variation of integrity measures (LIM, IF), basin portraits and frequency response curves as a function of tip radius (R), for fixed parameter values of \(\bar{y}=0.005\) and \(\bar{\varOmega }=0.85\). a Integrity profiles of the attractive region containing non-resonant low-amplitude (crimson) and resonant high-amplitude solution (blue) attractors. b Integrity profiles of repulsive region attractor. c Integrity profiles of the in-contact region consisting of non-resonant low-amplitude (light brown) and resonant high-amplitude solution (orange) attractors. The continuous and dotted lines indicate the LIM and IF integrity measures, respectively. d–f show the basin portraits at specific radius values of \(114\,\hbox {nm}\), \(117\,\hbox {nm}\), and \(197\,\hbox {nm}\), respectively. The details on basin colour and the corresponding attractor/solution description are given in Table 4. g Frequency response of microcantilever with radius \(R=105\,\hbox {nm}\) and \(R={182}\,\hbox {nm}\) oscillating with initial condition in attractive region. h Frequency response of microcantilever with radius \(R={136}\,\hbox {nm}\) and \(R={182}\,\hbox {nm}\) oscillating with initial condition in the in-contact region. (Color figure online)

Full size image
Fig. 9
figure 9

Phase-space topology evolution with respect to tip radius (R) from 105 to \(225\,\hbox {nm}\), at fixed excitation amplitude and frequency of \(\bar{y}=0.020\), \(\bar{\varOmega }=0.8\), respectively

Full size image

4.1 Basin portraits and evolution as a function of tip radius

One of the common causes for image artefacts during AFM scanning operation is the degradation of tip radius R due to repetitive impacts with the sample surface [32]. Furthermore, the correct and reliable operation of the AFM is dependent on the status of the probe tip, since it is responsible for resolving the topography of the sample [10]. The change in radius value during the aforementioned scanning operation thus causes a sensible variation in the system response and corresponding global integrity values. Therefore, in this section, we make an effort to elucidate the variation of system integrity via basin portraits by considering the AFM tip radius (R) as the corresponding varying parameter.

Figure 8 outlines the variation of dynamical integrity of system attractors as a function of AFM cantilever tip radius R. The numerical simulations are performed for tip radius ranging from 105 to \(225\,\hbox {nm}\) in steps of \(3\,\hbox {nm}\), with excitation frequency \(\bar{\varOmega }=0.85\) being close to resonance, and excitation amplitude \(\bar{y}=0.005\). Figure 8a–c reports the integrity variation trend as a function of tip radius, and Fig. 8d–f reveals the snapshot of basin portrait at several crucial radius values, namely \(114\,\hbox {nm}\), \(117\,\hbox {nm}\), and \(197\,\hbox {nm}\), respectively. The continuous and dotted lines in Fig. 8a–c belong to LIM and IF measures, respectively.

It is observed in Fig. 8a that in the attractive regime around the radius value \(R=114\,\hbox {nm}\), there is a sharp increase in the high-amplitude resonant solution (shown in Fig. 8g as A-HP\(_{\text {1}}\)) and the integrity of low-amplitude non-resonant solution (shown in Fig. 8g as A-LP\(_{\text {1}}\)) rapidly decreases to zero, indicating the complete erosion of its basin from the system. This phenomenon is observed in the basin portrait of Fig. 8d, where the blue basin representing A-HP\(_{\text {1}}\) solution completely dominates the attractive region. Physically, the disappearance of A-LP\(_{\text {1}}\) solution marks the transition from a bi-stable to a monostable cantilever response in the attractive regime. Interestingly, in Fig. 8a, by considering an even blunter tip, with radius in the range of \({R \in [114, 117]\,\hbox {nm}}\), the robustness of A-HP\(_{\text {1}}\) suddenly drops, due to the appearance of a novel competing attractor in the system. The new attractor is indicated by the light brown basin in Fig. 8e. This novel attractor, which is the in-contact attractor, has a smaller growth rate at lower radius values and does not affect the erosion of the A-HP\(_{\text {1}}\) solution rapidly. This is observed in Fig. 8a by a steady increase in the integrity measure of A-HP\(_{\text {1}}\) solution between radius values \({R \in [117, 185]}\,\hbox {nm}\). With the further increase in the blunting of the tip, the A-HP\(_{\text {1}}\) basin is eroded along its boundaries smoothly by the in-contact attractor as seen in Fig. 8f. The robustness characteristics shown by LIM and IF measures for attractive regime follow similar trend. However, the IF safe basin measure is larger in magnitude compared to LIM which is due to the smooth erosion of the basin without in-well fractality at low excitation amplitudes (\(\bar{y} < 0.015\)).

The repulsive attractor, unlike attractive, shows a steady growth in basin size for increasing radius values as shown in Fig. 8b. This trend of increasing basin size is due to the fact that an increase in radius value will increase the area over which repulsive forces are perceived by the system. However, it is worth to observe in Fig. 8d–f that the size of the purple basin (strength of integrity measure) associated with repulsive attractor is very small compared to the attractive and the in-contact regimes. Thus, at low \(\bar{y}\), the repulsive attractor although resilient to changes in radius has a smaller influence on the basin erosion process as compared to other two attractors. Moreover, at low radius values, a perturbation inside the attractive regime (blue basin) can lead the system towards the repulsive attractor leading to hardening behaviour as illustrated in Fig. 8g. In this case, for a cantilever oscillating initially in the attractive region, the system frequency response shows both softening due to attractive forces and hardening due to repulsive forces as shown in Fig. 8g (black frequency response curve). However, with a further increase in radius values, the attractive and repulsive basins are separated and the system oscillates purely in attractive regime showing only softening nonlinearity (green frequency response curve in Fig. 8g).

The robustness characteristics displayed by the in-contact attractor in Fig. 8c are unique, and present features are not observed in the other two attractors. For low radius values, e.g. \(R < 117\,\hbox {nm}\), the in-contact attractor does not exist as seen in Fig. 8c and further illustrated by the absence of light brown basin in Fig. 8d. This highlights the existence of a critical radius value for the manifestation of the in-contact attractor. This critical radius value for our system is at \(R=117\,\hbox {nm}\). Around this radius value, there is a sudden appearance of the in-contact attractor (shown in Fig. 8e as light brown basin) and it grows steadily with the increase in the value of R. Interestingly, the critical radius value remains the same for higher excitation amplitudes and excitation frequencies. Furthermore, from Fig. 8c it is observed that, the growth rate of low-amplitude solution (LP\(_{\text {1}}\)) is not as steep as the attractive and repulsive attractors, but at large radii, the in-contact attractor eventually becomes dominant with no in-well fractality or boundary erosion.

Figure 9 illustrates the evolution of the basin portrait with respect to the tip radius. The LIM integrity measure is utilized to characterize the robustness of the attractors and track the changes in the basin portraits as the tip deteriorates. The basin portraits are analysed for constant parameters \(\bar{y}=0.020\) and \(\bar{\varOmega }=0.8\). The figure reinforces the previous discussion pictorially. It depicts the disappearance of A-LP\(_{\text {1}}\) basin, fractalization of the attractive regime triggering the erosion process and finally the requirement of critical radius for manifestation of the in-contact attractor.

Fig. 10
figure 10

Variation of LIM as a function of excitation frequency (\(\bar{\varOmega }\)) for fixed parameter values of \(\bar{y}=0.005\), \(\bar{y}=0.010\), \(\bar{y}=0.020\) and \({R}={150}\,\hbox {nm}\). a Integrity profiles for the attractive region consisting of non-resonant low-amplitude (crimson) and resonant high-amplitude branch attractors (blue). b Integrity profiles for repulsive region attractor (purple). c Integrity profiles for the non-resonant low-amplitude (light brown) attractor in the in-contact region. d Integrity profiles for the first superharmonic branch attractor in the in-contact region. e Integrity profiles for the resonant high-amplitude branch (orange) attractor in the in-contact region. (Color figure online)

Full size image
Fig. 11
figure 11

Variation of basin portraits as a function of excitation frequency (\(\bar{\varOmega }\)) for fixed parameter values of \(\bar{y}=0.005\), \(\bar{y}=0.020\) and \(R={150}\,\hbox {nm}\). The analysis is focused around the fundamental resonance frequencies of respective system attractors. The circle inside the basin portrait indicates the LIM. a–c Basins portraits at \(\bar{y}=0.005\) and specific \(\bar{\varOmega }\) values of 0.6, 0.8, 0.9, respectively. d–f Basins portraits at \(\bar{y}=0.020\) and specific \(\bar{\varOmega }\) values of 0.7, 1.8, 1.9, respectively. g–i Basins portraits at \(\bar{y}=0.005\) and specific \(\bar{\varOmega }\) values of 2.5, 2.9, 3.4, respectively. The details on basin colour and the corresponding attractor/solution description are given in Table 4

Full size image

4.2 Basin erosion as a function of excitation frequency and excitation amplitude

In Sect. 4.1, the evolution of phase-space topology as a function of radius was showcased. Accordingly, in this section the dynamical integrity analysis aims at quantifying the extent and evolution of the basins along with their erosion process as a function of the excitation amplitude (\(\bar{y}\)) and excitation frequency (\(\bar{\varOmega }\)). This is established in Fig. 10 for excitation amplitudes \(\bar{y}=0.005\), \(\bar{y}=0.010\) and \(\bar{y}=0.020\), respectively, whereas Figs. 11 and 12 report the snapshots of basin portraits at crucial excitation frequencies (\(\bar{\varOmega }\)) near the neighbourhood of fundamental and principal parametric resonance frequencies, respectively.

All simulations are performed at a constant radius value of \(R=150\,\hbox {nm}\) and finally, LIM and IF measures are calculated for the aforementioned data. However, we observed that the strength of LIM and IF measure as a function of \(\bar{\varOmega }\) remain approximately the same. Thus, we can argue that the excitation frequency in the selected interval does not modify the global shape of the portrait and we do not experience a significant subdivision of the basin. Therefore, in order to simplify the analysis, only LIM is used to quantify the robustness of dominant attractors present in the system.

4.2.1 Analysis of basin erosion profiles around the fundamental resonance frequency

The fundamental ideology of TM-AFM is based on the near-resonant excitation of the microcantilever. Therefore, it is of significant interest to study the system topology with regard to basin erosion profiles since, these profiles are indicative of solution instabilities. In this respect, the following section utilizes the integrity measures shown in Fig. 10 to discuss the various system attractors in the neighbourhood of their respective resonance frequencies. In addition, to further delineate the behaviours observed in the integrity profiles, the basin portraits are reported in Fig. 11 at specific frequencies.

The integrity profiles of attractive regime attractors are illustrated in Fig. 10a and, similar to Sect. 4.1, the crimson and blue colours belong to the low-amplitude non-resonant solution (A-LP\(_{\text {1}}\)) and the high-amplitude resonant solution (A-HP\(_{\text {1}}\)), respectively. Figure 10a shows that the attractive regime is dominated by A-LP\(_{\text {1}}\) non-resonant solution at low excitation frequencies \(\bar{\varOmega } < 0.77\). This is illustrated through the basin portrait of Fig. 11a in which the crimson basin corresponding to A-LP\(_{\text {1}}\) is the dominant solution. By further increasing the excitation frequency value above \(\bar{\varOmega } > 0.77\), the A-LP\(_{\text {1}}\) solution exhibits a sharp decrease in its integrity value (illustrated in Fig. 10a). The sharp decline is attributed to the sudden appearance of the A-HP\(_{\text {1}}\) resonant attractor from inside the local potential well via saddle-node bifurcation. The appearance of saddle-node triggers the erosion process of the A-LP\(_{\text {1}}\) basin from outside its boundaries. The appearance of A-HP\(_{\text {1}}\) (blue basin) inside the A-LP\(_{\text {1}}\) local potential well (crimson basin) is shown in Fig. 11b. Any further increment in excitation frequency causes the complete erosion of the low-amplitude attractive (A-LP\(_{\text {1}}\)) solution as seen in Fig. 11c, leaving large amplitude oscillations of A-HP\(_{\text {1}}\) as the dominant solution in the attractive potential well. Hereafter, the A-HP\(_{\text {1}}\) solution remains largely stable as illustrated in Fig. 10a, and its robustness is mainly affected when the excitation frequency reaches the in-contact fundamental resonance or when the system is driven with an excitation amplitude above the parametric threshold of the system. This trend of solution instabilities observed around the fundamental resonance frequency remains unaffected irrespective of excitation amplitudes.

Contrary to the above discussion on attractive regime, where steady-state solutions exist over a large range of frequencies, the repulsive basin (purple) exists in a narrow frequency range around the fundamental resonance frequency and shows sharp increase/decrease as we move closer/farther away from resonance. This is illustrated in Fig. 10b for \(\bar{y}=0.005\), \(\bar{y}=0.010\) and \(\bar{y}=0.020\), respectively. Moreover, the repulsive basin size is small compared to other two attractors in case of \(\bar{y}=0.005\) as shown in Fig. 11c. But it displays a sharp increase in size for higher values of \(\bar{y}\) as seen in Fig. 11d for \(\bar{y}=0.020\). This is due to the fact that the harder the cantilever is driven, the deeper the oscillations penetrate into the repulsive regime, and the time period of oscillations spent in repulsive regime increases. Therefore, contrary to the observation in Sect. 4.1, the repulsive basin at higher excitation amplitudes significantly constricts the attractive regime basin in the neighbourhood of the fundamental resonance frequency.

On the other hand, the in-contact regime solution displays rich nonlinear behaviour absent in the case of the attractive and repulsive regimes. Figure 10c–e illustrates the integrity profiles of various solution branches namely LP\(_{\text {1}}\), Su\(_{\text {1}}\)-HP\(_{\text {1}}\), and HP\(_{\text {1}}\) that are observed in the in-contact regime. Similar to Sect. 4.1 and summarized in Table 4, the light brown colour corresponds to non-resonant LP\(_{\text {1}}\) solution branch, the green colour belongs to Su\(_{\text {1}}\)HP\(_{\text {1}}\) solution branch and orange colour belongs to HP\(_{\text {1}}\) resonant solution branch. The appearance and disappearance of several rare attractors, together with period-2 responses appearing not only on HP\(_{\text {1}}\) solution branch but also on Su\(_{\text {1}}\)HP\(_{\text {1}}\) superharmonic solution causes the robustness of in-contact attractor to vary rapidly. This behaviour can be observed in the integrity profiles of Fig. 10d, e in the form of sharp peaks and valleys as the excitation amplitude is increased.

At low excitation frequencies \(\bar{\varOmega }<1.5\), the in-contact basin is dominated by LP\(_{\text {1}}\) solution as shown in Fig. 10c. This is further demonstrated in the basin portrait of Fig. 11a where only the light brown basin dominates the in-contact region. Further increasing \(\bar{\varOmega }>1.5\), we observe the drop in integrity of LP\(_{\text {1}}\) solution due to the appearance of Su\(_{\text {1}}\)HP\(_{\text {1}}\) attractor. This is visualized by comparing Fig. 10c, d between frequency ranges \(\bar{\varOmega }\in [1, 2]\). The drop in integrity is sharp for small values of \(\bar{y}\) and slowly smoothens with increasing \(\bar{y}\) amplitudes. This effect is due to the increased softening effect of the in-contact response which causes the Su\(_{\text {1}}\)HP\(_{\text {1}}\) branch to overlap with LP\(_{\text {1}}\) branch over larger \(\bar{\varOmega }\) values. Along with the increased overlapping effect, at higher amplitudes of excitation \(\bar{y} > 0.00118\), the Su\(_{\text {1}}\)HP\(_{\text {1}}\) solution grows more robust. The appearance of Su\(_{\text {1}}\)HP\(_{\text {1}}\) attractor (green basin) from within the LP\(_{\text {1}}\) basin for \(\bar{y}=0.020\) is shown in Fig. 11e, f.

Fig. 12
figure 12

Variation of basin portraits as a function of excitation frequency (\(\bar{\varOmega }\)) for fixed parameter values of \(\bar{y}=0.005\), \(\bar{y}=0.020\) and \(R={150}\,\hbox {nm}\). The analysis is focused around the principal parametric resonance frequencies of respective system attractors. The circle inside the basin portrait indicates the LIM. a–c Basin portraits at \(\bar{y}=0.020\) and specific \(\bar{\varOmega }\) values of 1.4, 1.6, 1.7, respectively. d–f Basin portraits at \(\bar{y}=0.005\) and specific \(\bar{\varOmega }\) values of 6.6, 6.7, 7.1, respectively. The details on basin colour and the corresponding attractor/solution description are given in Table 4

Full size image

Furthermore, with \(\bar{\varOmega }\) growing closer to resonance (i.e. \(\bar{\varOmega } = 3.72\)), the high-amplitude resonant solution (HP\(_{\text {1}}\)) appears via saddle-node bifurcation and grows in dominance as depicted in Fig. 10e. In a similar fashion to the attractive regime, the saddle-node triggers the erosion of the previously dominant Su\(_{\text {1}}\)HP\(_{\text {1}}\) solution from outside the boundary. This is observed in basin portraits from Fig. 11g–i where the orange basin belonging to HP\(_{\text {1}}\) solution is growing along the periphery of green basin. Interestingly, at low amplitudes of excitation, \(\bar{y}< 0.010\) the erosion of Su\(_{\text {1}}\)HP\(_{\text {1}}\) basin is smooth with no influence of rare attractors on its robustness. After the complete erosion of Su\(_{\text {1}}\)HP\(_{\text {1}}\) basin (see Fig. 11i), the in-contact response is completely dominated by HP\(_{\text {1}}\) solution until \(\bar{\varOmega }\) reaches close to parametric resonance frequency. This is illustrated by the gradual drop in robustness measure in Fig. 10e for values of \(\bar{\varOmega } >3.7\) . The increase in \(\bar{y}\) has a peculiar effect on the HP\(_{\text {1}}\) solution since the robustness decreases in contrast to the expected increasing trend. This is due to the large number of rare attractors which tend to appear at higher excitation amplitudes. This peculiarity makes the experimental investigation of the in-contact attractor a challenging task.

4.2.2 Analysis of basin erosion profiles around the principal parametric resonance frequency

The aforementioned discussion was focused on the robustness and erosion profiles of system attractors for excitation amplitudes below the parametric threshold and excitation frequencies around the fundamental resonance. However, the system excited parametrically exhibits different dynamics that are not observed through direct excitation. In addition, the theoretical analysis of parametrically driven AFM has shown the added benefits such as high quality factor, lower imaging forces and reduced cantilever transients [33]. These advantages, if harnessed, can be of significant interest in areas such as soft polymers and biological specimens. Therefore, the current section focuses on the basin erosion profiles of system attractors in the neighbourhood of respective principal parametric resonance frequencies. Similar to the previous section, the analysis utilizes integrity measures illustrated in Fig. 10 to discuss the evolution of system responses, whereas Fig. 12 is used to understand the metamorphoses of basin erosion graphically.

Considering the attractive force regime, an excitation amplitude of \(\bar{y}=0.020\) is utilized to study the robustness of attractors oscillating near the parametric resonance frequency. The chosen excitation amplitude is above the required threshold amplitude of \(\bar{y}=0.01515\) needed to excite the system parametrically. The solution belonging to \(\bar{y}=0.020\) case is drawn by dotted lines in Fig. 10a. From Fig. 10a there is a sudden decline in the A-HP\(_{\text {1}}\) attractor’s integrity value around the parametric resonance frequency of \(\bar{\varOmega }~\in ~[1.4, 1.75]\). This sudden decrease in robustness is promoted by the appearance of period-2 attractor (A-Pa-P\(_{\text {2}}\)) within the compact part of A-HP\(_{\text {1}}\) basin. This is illustrated in the basin portraits of Fig. 12a–c, where the A-Pa-P\(_{\text {2}}\) attractors shown by dark red basin are surrounding the A-HP\(_{\text {1}}\) blue basin. The rate of erosion of A-HP\(_{\text {1}}\) basin is directly proportional to the nearness of \(\bar{\varOmega }\) to the principal parametric resonance frequency. For values of \(\bar{\varOmega }\) away from the parametric resonance the A-HP\(_{\text {1}}\) integrity shows a steady increase back to its original value. Hereafter, the A-HP\(_{\text {1}}\) solution remains almost independent of \(\bar{\varOmega }\) until the in-contact resonance frequency is reached.

In case of the in-contact regime, the parametric threshold amplitude is found to be as low as \(\bar{y}=0.00014\). The low threshold amplitude also suggests the potential application of stochastic resonance of cantilever oscillating in the in-contact regime. However, in order to facilitate the study, an excitation amplitude of \(\bar{y}=0.005\) is utilized. The corresponding integrity profile is illustrated in Fig. 10e by the continuous line, and the relative basin portraits are shown in Fig. 12d, e. By considering Fig. 10e, the integrity measure of HP\(_{\text {1}}\) solution displays a steady decline as \(\bar{\varOmega }\) is brought close to principal parametric resonance frequency (\(\bar{\varOmega }=7.44\)). Finally, around \(\bar{\varOmega }=7.1\) the HP\(_{\text {1}}\) basin completely disappears, indicating that the system is in the parametric instability region. The appearance of parametric period-2 attractors (Pa-P\(_{\text {2}}\)) in the basin portrait is indicated by the dark red basin in Fig. 12d, e. The figures illustrates the appearance of period-2 attractors (dark red) from the compact part of HP\(_{\text {1}}\) basin (orange) along with period-6 rare attractors (dark blue). Finally, the erosion process of HP\(_{\text {1}}\) solution is non-smooth with the interacting basins featuring severe fractality.

5 Conclusions

The global dynamics of TM-AFM has been investigated with the aim of evaluating the robustness and dynamical integrity of coexisting attractors of the system. Extensive numerical analyses have been carried out to show the existence and the properties of the in-contact attractor. The frequency response curves and basin portraits are obtained, showing that the in-contact attractor is highly sensitive to the main driven parameters with large amplitude superharmonic branches appearing for small excitation amplitudes.

In order to unveil the entire bifurcation scenario of the so-called in-contact attractor around the primary and parametric resonance, several local bifurcation envelopes are combined together to build global bifurcation maps. Utilizing the bifurcation maps, the escape thresholds along with various response scenarios in the excitation parameter space are analysed in detail around the direct and parametric resonance frequency. The outcome of the analysis shows new routes to crisis, escape scenarios via appearance of strange attractors and multiple period-doubling cascades. In addition, the robustness of attractors has been analysed by making use of basins of attraction and integrity measures such as local integrity measure (LIM) and integrity factor (IF). The analysis has focused on the basin erosion with respect to variation in excitation frequency, excitation amplitude and the AFM probe tip radius. The results highlight the appearance of in-contact attractor for a critical radius value. In addition, the parametric resonance and its effect on basin erosion via fractalization are discussed for both attractive and in-contact attractors. It is seen that the period-2 attractors arising from parametric resonance decrease the robustness of attractive regime in a smooth fashion, whereas in case of in-contact attractor the period-2 solution together with higher-order strange attractors, erodes the basin through fractalization. In conclusion, our analysis of basins of attraction, global bifurcation charts and integrity profiles provides a method to study the complex dynamics involved in TM-AFM.