Optimal cascaded control of mobile manipulators

Abstract

In this study, the solution to the kinematically optimal control problem of the mobile manipulators is proposed. Both dynamic equations are assumed to be uncertain, and globally unbounded disturbances are allowed to act on the mobile manipulator when tracking the trajectory by the end effector. We propose a computationally efficient class of cascaded control algorithms, which are based on an extended Jacobian transpose matrix. Our controllers involve two new non-singular terminal sliding mode manifolds defined by nonlinear integral equalities of both the second order with respect to the task space tracking error and the first order with respect to reduced mobile manipulator acceleration. Using the Lyapunov stability theory, we prove that the proposed Jacobian transpose cascaded control schemes are finite time stable provided that some practically reasonable assumptions are fulfilled during the mobile manipulator movement. The numerical examples carried out for mobile manipulators [consisting of a non-holonomic platform of type (2, 0) and holonomic manipulators of 2 and 3 revolute kinematic pairs], which operate in two-dimensional and three-dimensional work spaces, respectively, illustrate both the trajectory tracking performance of the proposed control schemes and simultaneously their minimising property for some practically useful objective function.

1 Introduction

Mobile manipulators are robotic systems, for which the range in the work space of the non-holonomic mobile platforms is, in fact, unbounded. The holonomic manipulator, rigidly attached to the platform, makes it possible to accomplish different manipulation tasks by the end effector, e.g. tracking a desired trajectory given in the task space. Modern control systems for such mechanisms require both extremely high precision and stability of the trajectory tracking. On account of the fact that desired trajectories are most often expressed in task (Cartesian) coordinates, the application of the joint space control techniques first requires solving the inverse kinematics problem. The process of kinematic inversion is both time-consuming (there does not exist, in general, an analytic form of inverse mapping) and becomes very complicated when the Cartesian trajectory generates kinematic and/or algorithmic singularities [1]. Thus, controllers to be designed should accurately track desired end effector trajectory despite possible singularities met on this trajectory, uncertain dynamic equations, unknown payload to be transferred by the end effector and external disturbances. On account of the fact that mobile manipulators become usually redundant mechanisms when accomplishing the end effector tasks, designed control algorithms should also provide steering signals optimising some useful goals (singularity and/or collision avoidance, posture control, etc.). Moreover, in order to avoid undesirable effect of chattering, such controllers have to generate at least absolutely continuous control signals (torques). Due to the challenges posed to modern controllers in the context of their design, many researchers have proposed different approaches to the control problem of mobile manipulators. Among them, we mainly focus on the three major ones.

The first approach, analysed in works [2,3,4,5,6,7,8,9,10,11,12,13], utilises the formulation of extended (augmented) task space (including also input–output linearisation techniques) in the inverse kinematics problem. It is based on extending the dimension of the task space by incorporating as many additional constraints as the degree of the redundancy. These additional constraints are obtained based on, e.g. various types of optimisation criteria. Consequently, the resulting system becomes non-redundant. The control formulations based on the augmented task space technique have some disadvantages. The controllers proposed in [2,3,4,5,6,7,8] require inverse of the extended Jacobian matrix that can potentially consist of algorithmic and/or kinematic singularities [1] and as a consequence can produce the control inputs to become unbounded even though the mobile manipulator is not in a singular configuration. Moreover, the dimensionality of the inverse kinematics problem associated with the extended Jacobian matrix increases. Furthermore, control algorithms from [2,3,4,5,6,7,8] require full knowledge of the dynamic equations. The controllers offered in [9,10,11,12,13,14] need the knowledge of desired trajectories for both the end effector and non-holonomic platform and are not optimal in any sense. Steering signals generated in works [10,11,12,13,14] are discontinuous and require the knowledge of the holonomic manipulator and platform velocities. Using both fuzzy logic system to compensate for modelling uncertainties and a robust term to ensure system stability, a trajectory tracking controller has been proposed in work [12], which, however, generates also discontinuous steering signals. An adaptive robust trajectory tracking controller for a mecanum-wheeled mobile robot has been offered in [13]. To make the system robust, the authors in [13] have designed a second-order sliding mode law providing also discontinuous steering signals.

The second approach, discussed in the works [15,16,17,18,19,20,21,22,23,24,25,26], is based on the application of the (generalised) pseudo-inverse of the mobile manipulator Jacobian matrix in the control formulation. Control algorithms developed from the pseudo-inverse of the Jacobian matrix are attractive and further examined by many researchers; they also have some disadvantages. That is to say, the controls thus obtained supply only sub-optimal (and not optimal) solutions. The adaptive control law proposed in [25] needs the knowledge of both holonomic manipulator and platform velocities. The control scheme from [25] involves all the adaptive terms multiplied by the regression matrix that seems to be complex to implement and very time-consuming. In the basic monograph [26], the authors have proposed an adaptive robust control of mobile manipulators. Nevertheless, the control laws from [26] require an explicit form of the inverse/pseudo-inverse of the Jacobian matrix as well as desired trajectories of both the end effector and the mobile platform. Moreover, generated torques/forces belong only to a class of bounded mappings which tend in a limit to discontinuous functions. As was shown in works [27, 28], pseudo-inverse control strategies are not, in general, repeatable. This inconvenience prevents accomplishment of an important class of cyclic technological operations (cyclic kinematic tasks) by this approach. Moreover, due to explicit inverse matrix operations, computation of the pseudo-inverses of the Jacobian matrix is computationally time-consuming. A technique of damped least squares has been proposed in works [29, 30] to tackle the singular configurations in lieu of the pseudo-inverses. Nonetheless, this technique generates the tracking errors due to a long-term numerical integration drift. Furthermore, the control algorithms mentioned before give only at most asymptotic stability which may be insufficient for completing the tasks that require the extremely high precision.

The third approach presented in several papers [31,32,33] is based on the use of the gradient of some potential function. Algorithms from [31,32,33] solve a regulation problem in a task space. Involving a Filippov solution, works [31,32,33] may result in discontinuous right-hand side of motion equations, which may induce the undesirable effect of chattering.

From the literature survey focusing on the mobile manipulator control, one follows that almost all control schemes demand inverse or pseudo-inverse of a Jacobian matrix. This significant inconvenience may cause numerical instabilities of the control algorithms due to (possible) kinematic and/or algorithmic singularities, which may be met on the mobile manipulator trajectory. Moreover, all those algorithms are not able to generate continuous controls resulting in finite-time stability when dynamic equations are uncertain and (globally unbounded) disturbances act on the mobile manipulator.

This paper presents a significant generalisation of the results previously published in works [34,35,36,37]. Namely, works [34,35,36,37] solve the finite-time control problem in the task (Cartesian) space for only holonomic uncertain dynamic systems, in particular, for stationary robotic manipulators. On the other hand, the present study introduces a new class of controllers being finite time stable for mobile manipulators (with uncertain dynamics) whose mobile platforms are subject to non-holonomic constraints. In order to eliminate the shortcomings of the control algorithms known from the literature, two kinds of non-singular terminal sliding manifolds are introduced in this paper. They are defined by nonlinear integral equalities of the second order with respect to the task tracking errors and the first order with respect to reduced mobile manipulator acceleration, respectively. The manifolds introduced make it possible to simultaneously join the first-order sliding mode, possessing the ability of the finite-time control, with the second-order sliding techniques generating at least absolutely continuous steering signals. The controller proposed in the paper has a cascaded structure consisting of the two sub-controllers which utilise the introduced integral manifolds. The task of the first sub-controller, using the transpose Jacobian matrix, is to track the desired end effector trajectory with simultaneous minimisation of some criterion function reflecting a given kinematic characteristics. In turn, the task of the second sub-system, which takes into account uncertain dynamics and unknown disturbances, is a dynamic compensation of the error appearing between the actual reduced acceleration of the mobile manipulator and the reference acceleration obtained from the first sub-controller. Both controllers use (also introduced in the paper) a new dynamic version of the classic (static) computed torque known from the literature [38, 39]. By fulfilment of reasonable assumption regarding the rank of the Jacobian matrix, the proposed combined control scheme is shown to be finite time stable. Moreover, it generates at least absolutely continuous controls (torques/forces) thus avoiding the undesirable chattering effects. Furthermore, this study is an essential generalisation of the result given in [40] which only deals with kinematics of the mobile manipulator subject to non-holonomic constraints. It is also worth to note that our transpose Jacobian controller is able to stably attain the origin in a finite time. The remainder of the study is organised as follows. Section 2 formulates the kinematically optimal finite-time trajectory tracking control problem. A new class of kinematically optimal cascaded controllers, which solve the trajectory tracking problem in a finite time, is proposed in Sect. 3. Section 4 presents numerical simulation results carried out for a mobile manipulator (consisting of a non-holonomic platform of type (2, 0) and a holonomic manipulator of two revolute kinematic pairs) operating in a two-dimensional work space whose task is to track a desired end effector trajectory and simultaneously to minimise some practically useful objective function. Finally, some concluding remarks are drawn in Sect. 5. Throughout this paper, $\lambda _{\min }(\cdot )$, $\lambda _{\max }(\cdot )$ denote the minimal and maximal eigenvalues of the matrix $(\cdot )$.

2 Problem formulation

Consider a mobile manipulator composed of a non-holonomic platform and a holonomic manipulator. Location of the platform is described by the vector of generalised coordinates $x \in {\mathbb {R}}^l$ (platform posture $x_{1,c}\ x_{2,c},\ \theta$—see Fig. 1, where $\theta$ is the orientation angle of the platform with respect to a global coordinate system $Ox_1x_2$; $x_{1,c},\ x_{2,c}$ stand for coordinates of the platform centre; $\phi _1$, $\phi _2$ are angles of driving wheels; 2W denotes platform width; 2L is the platform length; R stands for the radius of the wheel; $(\text {a},\text {b})$ denotes the point at which the holonomic manipulator base is fasten to the platform), where $l \ge 2$. The posture of a holonomic manipulator mounted on the platform is described by the vector of joint coordinates $y=(y_1,\ldots ,y_n)^{\mathrm{T}} \in {\mathbb {R}}^n$, where n is the number of its kinematic pairs. During the operation of the mobile manipulator in the work space, non-holonomic constraints related to the platform motion are induced. They are usually expressed in the so-called Pfaffian form

$$\begin{aligned} A(x){\dot{x}}=0, \end{aligned}$$

(1)

where A(x) stands for the $k \times l$ matrix of the full rank (that is, $\text{ rank }(A(x))=k$) depending on x analytically; $1 \le k < l$. Let $\text{ Ker }(A(x))$ denote a linear subspace generated by vector fields $a_1(x),\ldots ,a_{l-k}(x)$. Hence, the kinematic constraint (1) can be equivalently described by an analytic drift-less dynamic system

$$\begin{aligned} {\dot{x}}=N(x) \alpha , \end{aligned}$$

(2)

where $N(x)=[a_1(x),\ldots ,a_{l-k}(x)]$; $\text{ rank }(N(x))=l-k$ and $\alpha =\left( \alpha _1,\ldots ,\alpha _{l-k}\right) ^{\mathrm{T}}$ stands for quasi-velocity of the platform (introduced in [41]).

The kinematic equations of the mobile manipulator relate the position and orientation of the end effector in the global coordinate system with vector variables x and y as follows

$$\begin{aligned} p_e=f_e(q), \end{aligned}$$

(3)

where $q=\left( \begin{array}{l} x\\ y \end{array}\right)$ is the configuration of the mobile manipulator; $p_e \in {\mathbb {R}}^m$ denotes the end effector coordinates; $f_e : {\mathbb {R}}^l\times {\mathbb {R}}^n \longrightarrow {\mathbb {R}}^m$ stands for the m-dimensional mapping (usually nonlinear with respect to q); and $m \le n$ is the dimension of the task space.

The consequence of inequality $l+n > m+k$ (one can observe that mobile manipulator considered herein is a redundant mechanism) is the possibility to augment the end effector conventional trajectory tracking (primary task) with additional user-specified useful task coordinates $p_a \in {\mathbb {R}}^{l+n-m-k}$ (secondary task) of the following general form:

$$\begin{aligned} p_a=f_\mathrm{a}(q), \end{aligned}$$

(4)

where $f_\mathrm{a}:{\mathbb {R}}^{l+n} \longrightarrow {\mathbb {R}}^{l+n-m-k}$ stands for a given at least triply differentiable mapping with respect to q. It is practically desirable to generate joint trajectory $q=q(t)$ in such a way as to minimise an objective (kinematic) function ${\mathcal {F}}(q)$. Based on ${\mathcal {F}}(q)$, which is assumed to be at least four times differentiable with respect to q, the general form for $f_\mathrm{a}$, proposed, e.g. in work [1] for holonomic systems and generalised in [8] for the non-holonomic ones, may be expressed as

$$\begin{aligned} f_\mathrm{a}={\mathcal {N}}(q)\frac{\partial {\mathcal {F}}(q)}{\partial q}, \end{aligned}$$

(5)

where ${\mathcal {N}}$ stands for the $(l+n-m-k)\times (l+n)$ orthogonal complementary matrix to

$$\begin{aligned} \jmath (q)=\left[ \begin{array}{c} \jmath _1(q)\\ .\\ .\\ \jmath _{m+k}(q) \end{array} \right] =\left[ \begin{array}{ll} \qquad \frac{\partial f_e(q)}{\partial q} \\ A &{} 0_{k\times n} \end{array} \right] , \end{aligned}$$

(6)

i.e. $\jmath {\mathcal {N}}^{\mathrm{T}}=0$, $0_{k\times n}$ is the $k\times n$ zero matrix. Let us note that $\jmath (q)$ denotes an auxiliary Jacobian matrix which is related to necessary condition of minimum of objective function ${\mathcal {F}}$ subject to both holonomic constraints (3) and non-holonomic ones (1) (see [8] for details). Consequently, $f_\mathrm{a}={\mathcal {N}}(q)\frac{\partial {\mathcal {F}}(q)}{\partial q}=0$ presents $n+l-m-k$ transversality conditions which together with (3) and (1) make it possible to uniquely determine optimal mobile manipulator configuration q corresponding to a current end effector location $p_e$.

In further analysis, we shall employ a simple and practically useful optimisation criterion for redundancy resolution with a cost function

$$\begin{aligned} {\mathcal {F}}(q)=\frac{c_{{\mathcal {F}}}}{2} \langle q-q_{\mathrm{rest}},\ K_{{\mathcal {F}}}(q-q_{\mathrm{rest}})\rangle , \end{aligned}$$

(7)

where $q_{\mathrm{rest}}$ means some rest (preferred) posture; $\langle \ , \ \rangle$ denotes the scalar product of vectors; $c_{{\mathcal {F}}}$ is a positive constant; $K_{{\mathcal {F}}}$ is a positive definite diagonal weighting matrix.

Let us observe that, involving criterion function (7) into optimisation problem with equality constraints (1), (3) results in fulfilment of sufficient condition for a local (in general) optimality of trajectory $q=q(t)$, $t \ge 0$. If this is the case, the Hessian H for ${\mathcal {F}}$ given by (7) and constraints $f_e(q)-p_e=0$ and $A(x){\dot{x}}=0$ equals $H={\mathcal {N}}\left( c_{{\mathcal {F}}}K_{{\mathcal {F}}}+\sum _{i=1}^{m+k} l_i \frac{\partial \jmath _i(q)}{\partial q} \right) {\mathcal {N}}^{\mathrm{T}}$, where $l_i$ denote the Lagrange multipliers for regular (by assumption) constrained optimisation problem (1), (3) and (7), $i=1,\ldots ,m+k$. Let us note that for sufficiently large value of $c_{{\mathcal {F}}}$, matrix $c_{{\mathcal {F}}}K_{{\mathcal {F}}}+\sum _{i=1}^{m+k} l_i \frac{\partial \jmath _i(q)}{\partial q}$ becomes symmetric and positive definite. Consequently, taking into account the assumed regularity of constraints $f_e(q)-p_e=0$, $A(x){\dot{x}}=0$ (full rank of matrix $\jmath$ and hence full rank of ${\mathcal {N}}$), we deduce that matrix H is symmetric and positive definite too, what implies (local) optimality of trajectory q(t).

Let us notice that for $q_{\mathrm{rest}}=q(0)$, minimisation of (7) avoids sudden changes of configurations and enables the mobile manipulator to reduce the values of controls in $L_2$ norm by appropriate weighting of joints closer to the mobile platform, as the computer simulations given in Sect. 4 will show.

Differentiating q once and then twice with respect to time and taking into account (2) result in the following relations:

$$\begin{aligned} {\dot{q}}=Cz, \quad \ddot{q}=C{\dot{z}}+{\dot{C}}z, \end{aligned}$$

(8)

where $C=\left[ \begin{array}{cc} N(x) &{} 0 \\ 0 &{} {\mathbb {I}}_{n} \end{array} \right]$; $z=\left( \begin{array}{c} \alpha \\ {\dot{y}} \end{array} \right) \in {\mathbb {R}}^{l+n-k}$ is the vector of reduced velocities; ${\mathbb {I}}_{n}$ denotes $n \times n$ identity matrix.

By combining $f_e(q)$ with $f_\mathrm{a}(q)$, one obtains the general kinematic and differential mappings between q and extended task coordinates $p=\left( \begin{array}{l}p_e\\ p_a\end{array}\right)$

$$\begin{aligned} p=f(q),\qquad {\dot{p}}=Jz, \end{aligned}$$

(9)

where $f=\left( \begin{array}{l}f_e\\ f_\mathrm{a} \end{array}\right)$ and $J=\frac{\partial f}{\partial q}C$ is the $(l+n-k)\times (l+n-k)$ extended Jacobian matrix.

The task of the mobile manipulator is to track both desired trajectory $p^e_d(t) \in {\mathbb {R}}^m$ by the end effector and simultaneously user-specified trajectory $p^a_d(t) \in {\mathbb {R}}^{l+n-k-m}$ which equals $p^a_d(t)=0$ for $f_\mathrm{a}$ given by expression (5). Functions $p^e_d(\cdot )$ and $p^a_d(\cdot )$ are assumed to be at least triply differentiable with respect to time. By introducing the task tracking error e equal to $e=\left( \begin{array}{l} e^e\\ e^a \end{array} \right) =f(q)-p_d(t)$, where $p_d=\left( \begin{array}{l} p^e_d\\ p^a_d \end{array} \right)$, $e^e=f_e-p^e_d$; $e^a=f_\mathrm{a}-p^a_d$, the kinematically optimal finite-time control problem in the task space may be formally expressed as follows

$$\begin{aligned}&\lim _{t \rightarrow T}e(t)=0,\ \lim _{t \rightarrow T} {\dot{e}}(t)=0,\nonumber \\&\quad \lim _{t \rightarrow T} \ddot{e}(t)=0, \end{aligned}$$

(10)

where $0 \le T$ denotes a finite time of convergence of f(q) to $p_d(t)$ and $e(t)={\dot{e}}(t)=\ddot{e}(t)=0$ for $t \ge T$. Let us observe that the left sided equality of (10), i.e. $f_e(q)-p_d^e(t)=0$, ${\mathcal {N}}\frac{\partial {\mathcal {F}}(q)}{\partial q}=0$, and equality (1) present for a current $t \ge T$ the necessary and sufficient condition for constraint regular minimum of criterion function ${\mathcal {F}}$ [see comments regarding necessary and sufficient condition of minimum between formulas (6) and (8)]. In the sequel, extended Jacobian matrix J is assumed to be of the full rank in a (closed) operation region of the end effector, i.e.

$$\begin{aligned} \text {rank}(J(q))=l+n-k. \end{aligned}$$

(11)

From (11), it follows that there exists a real number $a > 0$ such that

$$\begin{aligned} 0 < a \le \lambda _{\min }(JJ^{\mathrm{T}}). \end{aligned}$$

(12)

The control scheme, which will be proposed in next section, may be applicable to non-holonomic mechanical systems comprising particularly mobile manipulators analysed in our study. The dynamics of such mechanisms expressed in reduced coordinates is given by the following differential equations [21,22,23,24]:

$$\begin{aligned} M(q){\dot{z}}+P(q,\ z) z + G(q) + D(t,\ q,\ z)=Bv, \end{aligned}$$

(13)

where M denotes the $(l+n-k)\ \times (l+n-k)$ symmetric positive definite reduced inertia matrix; P is the $(l+n-k)$-dimensional reduced vector representing centrifugal and Coriolis forces; G stands for the mobile manipulator reduced gravity forces; D means the $(l+n-k)$-dimensional external disturbance signal whose time derivative ${\dot{D}}$ is (by assumption) a locally bounded Lebesgue measurable mapping; B denotes the $(l+n-k)\ \times (l+n-k)$ matrix describing the configuration variables of the platform and holonomic manipulator which are directly driven by the actuators and v represents the $(l+n-k)$-dimensional vector of controls (torques/forces). Without loss of generality, ||D|| and $||{\dot{D}}||$ are assumed to be upper estimated as follows

$$\begin{aligned} ||D|| \le \alpha _0(t,\ q,\ z), \qquad ||{\dot{D}}|| \le \alpha _1(t,\ q,\ z), \end{aligned}$$

(14)

where $\alpha _0$ and $\alpha _1$ stand for the time-dependent known non-negative and locally bounded Lebesgue measurable functions, respectively.

In further considerations, useful properties of kinematic equations (9) are given below, which will be utilised by designing our controllers. For revolute kinematic pairs of the holonomic manipulator and function ${\mathcal {F}}$ given by expression (9), the following inequalities hold true:

$$\begin{aligned}&||J||_F,\quad \ \left| \left| \frac{\partial J}{\partial q} \right| \right| _F, \nonumber \\&\left| \left| \frac{\partial ^2 J}{\partial q^2} \right| \right| _F \le w_1+w_2||q-q_{\mathrm{rest}}||, \end{aligned}$$

(15)

where $||\ ||_F$ is the Frobenius (Euclidean) norm of the matrix; $w_1$ and $w_2$ are known positive scalar coefficients (construction parameters of the mobile manipulator). The aim is to determine at least absolutely continuous control vector v, for which the corresponding trajectory $q=q(t)$ as being the solution of differential equations (13) accomplishes the control task (10). For this purpose, let us differentiate both expressions (8), (13) once with respect to time and the error equation $e=f(q)-p_d(t)$ triply by time thus obtaining the following system of differential equations:

$$\begin{aligned} \begin{array}{l} \frac{\mathrm{d}^3 q}{\mathrm{d}t^3}=C\ddot{z}+2{\dot{C}}{\dot{z}}+{\ddot{C}}z,\\ \frac{\mathrm{d}^3e}{\mathrm{d}t^3}=J\ddot{z}+2{\dot{J}}{\dot{z}}+{\ddot{J}}z- \frac{\mathrm{d}^3 p_d}{\mathrm{d}t^3},\\ M\ddot{z}=B{\dot{v}}+{\dot{B}} v-{\dot{M}}{\dot{z}}- \frac{\mathrm{d}}{\mathrm{d} t} \left( P z+G + D \right) . \end{array} \end{aligned}$$

(16)

Using the Lyapunov stability theory, expressions (16) will be used in the next section to the solution of control problem (10).

3 Cascaded sliding control of the mobile manipulator

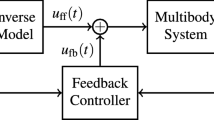
The idea of the proposed control law utilises two sub-systems cooperating with each other. Both sub-controllers involve suitable non-singular sliding manifolds introduced in the work which are defined for the first sub-system by nonlinear integral equation of the second order with respect to the task tracking error e and for the second sub-system by integral equation of the first order with respect to reduced acceleration ${\dot{z}}$ of the mobile manipulator, respectively. The first sub-system is a kinematic controller whose task is to determine reference (desired) acceleration $v_{\mathrm{ref}}$ satisfying relations (10). Next, using both $v_{\mathrm{ref}}$ provided by the kinematic controller and actual reduced acceleration ${\dot{z}}$ of the mobile manipulator, the task of the second (dynamic) sub-system is to compensate (uncertain) dynamics of the non-holonomic mechanism. This compensation is based on the determination of the controls v in such a way as to reduce the error between $v_{\mathrm{ref}}$ and ${\dot{z}}$ to zero in a finite time.

3.1 Kinematically optimal sub-controller

The proposed first sub-system uses two upper equations of (16) suitably reformulated to the following forms:

$$\begin{aligned}&\frac{\mathrm{d}^3 q}{\mathrm{d}t^3}=C{\dot{v}}_{\mathrm{ref}}+2{\dot{C}}v_{\mathrm{ref}}+{\ddot{C}}z,\nonumber \\&\frac{\mathrm{d}^3e}{\mathrm{d}t^3}=J{\dot{v}}_{\mathrm{ref}}+2{\dot{J}}v_{\mathrm{ref}}+{\ddot{J}}z-\frac{\mathrm{d}^3 p_d}{\mathrm{d}t^3}, \end{aligned}$$

(17)

where $v_{\mathrm{ref}}={\dot{z}}$ denotes reduced reference acceleration to be determined, for which Eq. (10) is satisfied. In order to find it, non-singular terminal sliding vector variable $s=(s_1,\ldots ,s_{l+n-k})^{\mathrm{T}} \in {\mathbb {R}}^{l+n-k}$, expressed in task coordinates, is introduced below

$$\begin{aligned} s(t)=\ddot{e}+\int ^t_0 \left( \lambda _2\ddot{e}^{3/5}\!+\!\lambda _2\lambda _1^{3/5}({\dot{e}}^{9/7}+\lambda _0^{9/7}e)^{1/3} \right) \mathrm{d}\tau , \!\!\!\!\!\!\!\nonumber \\ \end{aligned}$$

(18)

where $\lambda _0=\hbox {diag}(\lambda _{0,1},\ldots ,\lambda _{0,l+n-k})$; $\lambda _1=\hbox {diag}(\lambda _{1,1},$$\ldots ,\lambda _{1,l+n-k})$; $\lambda _2= \hbox {diag}(\lambda _{2,1},\ldots ,\lambda _{2,l+n-k})$; $\lambda _{i,j}$ stand for positive coefficients (controller gains); $i=0{:}2$; $j=1{:}l+n-k$. Partly inspired by the methodology of dynamically computed torque introduced in our works [34,35,36] for stationary robotic manipulators, we now propose determination of $v_{\mathrm{ref}}$ from the following differential equation:

$$\begin{aligned} {\dot{v}}_{\mathrm{ref}}=J^{\mathrm{T}}u_{\mathrm{ref}}, \end{aligned}$$

(19)

where $u_{\mathrm{ref}} \in {\mathbb {R}}^{l+n-k}$ is a new reference acceleration to be found. Inserting the right-hand side of (19) into the lower equation of (17) results in the task error dynamic equation which is dependent of $u_{\mathrm{ref}}$ as follows

$$\begin{aligned} \frac{\mathrm{d}^3e}{\mathrm{d}t^3}=JJ^{\mathrm{T}} u_{\mathrm{ref}}+2{\dot{J}}v_{\mathrm{ref}}+{\ddot{J}}z -\frac{\mathrm{d}^3 p_d}{\mathrm{d}t^3}. \end{aligned}$$

(20)

In order to find $u_{\mathrm{ref}}$ and as a consequence to fulfil equality constraints (10), the following kinematically optimal control law with respect to ${\mathcal {F}}$ given by (7) is proposed below:

$$\begin{aligned}&u_{\mathrm{ref}}(t,\ q,\ z,\ v_{\mathrm{ref}},\ e,\ s)\\&\quad =\left\{ \begin{array}{ll} -\frac{c}{a} \frac{s}{||s||}({\mathcal {W}}+c_0) &{} \quad \text {for }s \ne 0\nonumber \\ 0 &{} \quad \text {otherwise}, \nonumber \\ \end{array} \right. \end{aligned}$$

(21)

where c and $c_0$ are positive constant controller gains to be specified further on; ${\mathcal {W}}=||\lambda _2\ddot{e}^{3/5}+\lambda _2\lambda _1^{3/5}({\dot{e}}^{9/7}+\lambda _0^{9/7}e)^{1/3}-\frac{\mathrm{d}^3 p_d}{\mathrm{d}t^3}||+ (w_1+w_2||q-q_{\mathrm{rest}}||) (w_3^k ||v_{\mathrm{ref}}|| ||z||$$+w_4^k ||z||^3 )$; $w_3^k$ and $w_4^k$ denote known positive scalar coefficients (construction parameters of the mobile manipulator). Based on (19) and (21), one can determine $v_{\mathrm{ref}}$ as being at least absolutely continuous vector function of time by solving (in the Filippov sense [42]), the following differential equation:

$$\begin{aligned} {\dot{v}}_{\mathrm{ref}}=J^{\mathrm{T}}u_{\mathrm{ref}}(t,\ q,\ z,\ v_{\mathrm{ref}},\ e,\ s). \end{aligned}$$

(22)

The existence of the solution of differential equation (22) was shown in work [36]. On account of the fact that the right-hand side of (22) is not a Lipschitz mapping (it is even a discontinuous one), the solution of (22) is assumed to be unique in further considerations. The aim is to give conditions on controller gains $\lambda _0$, $\lambda _1$, $\lambda _2$, c and $c_0$, which guarantee the fulfilment of equalities (10).

Theorem 1

If extended Jacobian matrix J fulfils inequality (12) along desired trajectory $p_d$ of the end effector and $\lambda _0$, $\lambda _1$, $\lambda _2$, $c_0 > 0$, $c \ge 1$ then control scheme (21)–(22) enables the mobile manipulator stable convergence in a finite time of the task tracking errors $(e,\ {\dot{e}},\ \ddot{e})$ to the origin, i.e. $(e,\ {\dot{e}},\ \ddot{e})=(0,\ 0,\ 0)$. Moreover, controller (21)–(22) is kinematically (locally) optimal.

Proof

The proof of Theorem 1 is a small modification of the proof of Theorem 1 from [36]. Therefore, it will be omitted.$\square$

Taking into account kinematically optimal control law (21)–(22) and Theorem 1, a few remarks may be made below.

• Remark 1 Although the proof of Theorem 1 is similar to that given in work [36], Theorem 1 presents a significant generalisation of the results published in [36]. In particular, work [36] deals with the finite-time control problem for only holonomic uncertain dynamic systems (stationary robotic manipulators). On the other hand, Theorem 1 provides conditions on controller gains which guarantee finite-time stability for mobile manipulators with uncertain dynamics whose platforms are subject to non-holonomic constraints.

• Remark 2 If the task of the control is only to track desired end effector trajectory $p^e_d$ (without objective function ${\mathcal {F}}$), then mobile manipulator becomes strictly redundant, i.e. $l+n > m$. If this is the case, we can define the task space TSM manifold $s^e$ as $s^e=\ddot{e}^e+\int ^t_0 (\lambda _{2,e}(\ddot{e}^e)^{3/5}+\lambda _{2,e}\lambda _{1,e}^{3/5}(({\dot{e}}^e)^{9/7}+ \lambda _{0,e}^{9/7}e^e)^{1/3} ) d\tau$, where $\lambda _{0,e}$, $\lambda _{1,e}$, $\lambda _{2,e}$ stand for the controller gains. Thus, control law (21)–(22) may be expressed in the following form:

  $$\begin{aligned} {\dot{v}}^e_{\mathrm{ref}}=B^{-1}(j^e)^{\mathrm{T}}u^e_{\mathrm{ref}}(t,\ q,\ z^e,\ v^e_{\mathrm{ref}},\ e^e), \end{aligned}$$

  (23)

  where $j^e=\frac{\partial f_e}{\partial q}C$ and

  $$\begin{aligned} u^e_{\mathrm{ref}}=\left\{ \begin{array}{ll} -\frac{c_e}{a_e} \frac{s^e}{||s^e||}({\mathcal {W}}_e+c_0^e) &{}\quad \text {for }s^e \ne 0\\ 0 &{}\quad \text {otherwise}, \end{array} \right. \end{aligned}$$

  (24)

  ${\mathcal {W}}_e=||\lambda _{2,e}(\ddot{e}^e)^{3/5}+\lambda _{2,e}\lambda _{1,e}^{3/5}(({\dot{e}}^e)^{9/7}+\lambda _{0,e}^{9/7}e^e)^{1/3}$$-\frac{d^3p_d^e}{dt^3}||+w_3^k||v^e_{\mathrm{ref}}||||z||+w_4^k||z||^3$; $c_e >1$ and $c_0^e$ are positive constant gains; $a_e$ stands for the estimation of the minimal eigenvalue of matrix $j^e(j^e)^{\mathrm{T}}$.

• Remark 3 Let us note that for a special form of auxiliary kinematic function $f_\mathrm{a}$ equal to

  $$\begin{aligned} f_\mathrm{a}(q)= W(q) q, \end{aligned}$$

  (25)

  where $W(\cdot )$ stands for a given $(l+n-m-k) \times (l+n)$ weighting matrix whose elements may (generally) depend on q, the Frobenius norm of the Jacobian $\frac{\partial }{\partial q} \left( (f_e(q))^{\mathrm{T}},\ (W(q) q)^{\mathrm{T}} \right) ^{\mathrm{T}}$ fulfils inequality (14). Consequently, an auxiliary function (25) provides the same controller as that given by expressions (21)–(22) with $e=\left( \begin{array}{l} f_e(q)-p_d^e(t)\\ W(q) q - p_d^a(t) \end{array} \right)$.

• Remark 4 Let us observe that formulas (21)–(22) describe a transposed Jacobian controller. The use of the transpose of the Jacobian is a well-known technique for controlling the robotic systems. In such a context, there exist a few papers [43,44,45,46,47] which take into account stability analysis of the transposed Jacobian controllers. Nevertheless, works [43,44,45,46,47] deal with stability analysis for the set point control problems. Alternatively, Theorem 1 provides stability analysis for the trajectory tracking problems of the non-holonomic dynamic systems. Moreover, the transposed Jacobian controller (21)–(22) is capable of attaining the stable equilibrium $(e,{\dot{e}},\ddot{e})=(0,0,0)$ in a finite time. In such a context, it is worth to note the fact that the authors from works [48, 49] were among the first who have also shown finite-time convergence of their controller using, however, the inverse of the Jacobian matrix. Furthermore, transposed Jacobian controller (21)–(22) provides (locally) optimal solution using the sliding mode control technique. In such a context, there are several papers [9,10,11,12,13,14] which also involve sliding variables in the control laws. However, controllers offered in [9,10,11,12,13,14] are not optimal in any sense and in most cases provide discontinuous steering signals.

3.2 Dynamic sub-controller of the mobile manipulator

The aim of the dynamic sub-system is to compensate both uncertain dynamics of the mobile manipulator and unknown external disturbances acting on it in such a way as to make the origin $(E,\ {\dot{E}})=(0,\ 0)$ finite time stable, where tracking errors E, ${\dot{E}}$ are defined below

$$\begin{aligned}&E=z-\int ^t_{0} \ v_{\mathrm{ref}} \mathrm{d}\tau , \nonumber \\&{\dot{E}}={\dot{z}}- v_{\mathrm{ref}}. \end{aligned}$$

(26)

Let us note that tracking errors E, ${\dot{E}}$ equal identically zero when neglecting the mobile manipulator dynamics [see equality $v_{\mathrm{ref}}-{\dot{z}}=0$ immediately after formula (17)]. On the other hand, both the uncertain dynamics and unknown external disturbances acting on the mobile manipulator when accomplishing its task result in nonzero errors (26). The task is to find at least absolutely continuous control vector v reducing E, ${\dot{E}}$ to zero in finite time. For this purpose, lower equation of (16) is reformulated to the following compact form:

$$\begin{aligned} \ddot{z}=M^{-1}B{\dot{v}}+{\mathcal {R}}(t,\ q, \,z,\ v), \end{aligned}$$

(27)

where ${\mathcal {R}}=M^{-1} \left( {\dot{B}} v-{\dot{M}}{\dot{z}}-\frac{d}{d t} \left( P z+G + D \right) \right)$. Inspired by the control methodology borrowed from the theory of holonomic systems (see our recent work [37]), we propose now the following dynamically computed torque vector ${\dot{v}}$ of the form

$$\begin{aligned} {\dot{v}}=B^{-1}u, \end{aligned}$$

(28)

where $u \in {\mathbb {R}}^{l+n-k}$ is a new control to be determined. Let us note that for the non-holonomic platforms of the type $(2,\ 0)$, considered in the study (see Fig. 1), actuation matrix B in (13) is diagonal with positive elements. Consequently, $B^{-1}$ exists, too. Replacing ${\dot{v}}$ in (27) by the right-hand side of (28) results in the expression dependent of u

$$\begin{aligned} \ddot{z}=M^{-1} u +{\mathcal {R}}. \end{aligned}$$

(29)

Let A be a positive number, which fulfils the following inequalities (matrix $M^{-1}$ is symmetric and positive definite):

$$\begin{aligned} 0 < A \le \lambda _{\min }(M^{-1}). \end{aligned}$$

(30)

The aim is to find input signal u(t) and the corresponding control v such that vector z of actual reduced velocity exactly tracks $\int _0^t v_{\mathrm{ref}} \mathrm{d} \tau$ after a finite time. Therefore, error equation $E=z-\int _0^t v_{\mathrm{ref}} \mathrm{d} \tau$ is twofold differentiated with respect to time thus obtaining

$$\begin{aligned} {\ddot{E}}=\ddot{z}-{\dot{v}}_{\mathrm{ref}}=\ddot{z}-J^{\mathrm{T}} u_{\mathrm{ref}}. \end{aligned}$$

(31)

Replacing $\ddot{z}$ in (31) by the right-hand side of (29) results in the equation of the error dynamics dependent on u

$$\begin{aligned} {\ddot{E}}=M^{-1} u +{\mathcal {R}}-J^{\mathrm{T}} u_{\mathrm{ref}}. \end{aligned}$$

(32)

In order to find control law reducing E and ${\dot{E}}$ to zero in a finite time, the following non-singular vector sliding variable $S=(S_1,\ldots ,S_{l+n-k}) \in {\mathbb {R}}^{l+n-k}$ is introduced below:

$$\begin{aligned} S={\dot{E}}+\int ^t_0 \left( \varLambda _0 E^{\alpha _1}+\varLambda _1 ({\dot{E}})^{\alpha _2} \right) \mathrm{d}\tau , \end{aligned}$$

(33)

where $\alpha _1=\frac{n_1}{n_2}$; $n_1$ and $n_2$ are odd natural numbers satisfying the inequalities $n_1< n_2 < 2n_1$; $\varLambda _0=\hbox {diag}(\varLambda _{0,1},\ldots , \varLambda _{0,l+n-k})$; $\varLambda _1=\hbox {diag}(\varLambda _{1,1},\ldots ,$$\varLambda _{1,l+n-k})$; $\alpha _2=\frac{2 \alpha _1}{1 + \alpha _1}$; $\varLambda _{i,j}$ denote positive coefficients (controller gains); $i=0,1$; $j=1,2,\ldots ,l+n-k$. In the sequel, useful result is given [34].

Lemma 1

If $S=0$ for $t \ge T^{\prime }$, where $0 \le T^{\prime } < \infty$, then tracking errors $(E,\ {\dot{E}})$ stably converge in a finite time to the origin $(E,\ {\dot{E}})=(0,\ 0)$.

Differentiating S in (33) with respect to time and then replacing ${\ddot{E}}$ by the right-hand side of (32) result in the expression

$$\begin{aligned} {\dot{S}}=M^{-1} u + {\mathcal {U}}(t,\ q,\ z,\ v,\ u_{\mathrm{ref}},\ E), \end{aligned}$$

(34)

where ${\mathcal {U}}={\mathcal {R}}-J^{\mathrm{T}}u_{\mathrm{ref}}+\varLambda _0 E^{\alpha _1}+\varLambda _1 ({\dot{E}})^{\alpha _2}$. In further analysis, we find an upper estimate on $||{\mathcal {U}}||$.

For this purpose, ${\mathcal {R}}$ from (27) is reformulated as follows

$$\begin{aligned} {\mathcal {R}}= & {} M^{-1}[{\dot{B}} v-{\dot{M}} (M^{-1}Bv\nonumber \\&-\,M^{-1}Pz-M^{-1}G-M^{-1}D)\nonumber \\&-\,({\dot{P}}z+P{\dot{z}}+{\dot{G}}+{\dot{D}})]. \end{aligned}$$

(35)

As is known (see, for example, [26]), matrices $M^{-1}$, B, P and gravity vector G from dynamic equations (13) fulfil the following relations: $||M^{-1}||_F \le \varLambda$, $c_1 \ge ||\frac{\partial B}{\partial q}C||_F$, $c_2 \ge ||\frac{\partial M}{\partial q}C||_F$, $||B||_F \le c_3$, $||P||_F \le c_4 ||z||$, $||G|| \le c_5$, $||\frac{\partial P}{\partial q}C||_F \le c_6 ||z||$, $||\frac{\partial P}{\partial z}||_F \le c_7$ and $||\frac{\partial G}{\partial q}C||_F \le c_8$, where $\varLambda$, $c_1,\ldots ,c_8$ are positive coefficients (construction parameters of the mobile manipulator). Moreover, based on the above inequalities, it is easy to show that $||{\dot{P}}||_F \le c_6||z||^2 +c_7 ||{\dot{z}}||$. Hence, the norm of ${\mathcal {R}}$ may be upper estimated as follows

$$\begin{aligned} ||{\mathcal {R}}||\le & {} \varLambda [(c_1+\varLambda c_2c_3)||v|| ||z||+(\varLambda c_2c_4+c_6)||z||^3\nonumber \\&+\,(c_4+c_7)||z|| ||{\dot{z}}||\nonumber \\&+\,(c_2c_5+c_2\alpha _0+c_8)||z||+\alpha _1]. \end{aligned}$$

(36)

By introducing new coefficients $w_3,\ldots ,w_7$, defined as follows $w_3=\varLambda (c_1+\varLambda c_2c_3)$, $w_4=\varLambda (\varLambda c_2c_4+c_6)$, $w_5=\varLambda (c_4+c_7)$, $w_6=\varLambda \max \{c_2c_5+c_8, c_2 \}$, $w_7=\varLambda$, we finally obtain the following upper estimation on ${\mathcal {U}}$:

$$\begin{aligned} ||{\mathcal {U}}|| \le \chi (t,\ q,\ z,\ v,\ u_{\mathrm{ref}},\ E), \end{aligned}$$

(37)

where $\chi =w_3||v|| ||z||+w_4||z||^3+w_5 ||z|| ||{\dot{z}}|| +w_6(||z||+\alpha _0||z||)+w_7\alpha _1+||\varLambda _0 E^{\alpha _1}+\varLambda _1 ({\dot{E}})^{\alpha _2}-J^{\mathrm{T}}u_{\mathrm{ref}}||$; $w_3,\ldots ,w_7$ denote positive coefficients (construction parameters of the mobile manipulator). In order to fulfil equality $(E,\ {\dot{E}})=(0,\ 0)$ in a finite time, the following dynamic controller is proposed:

$$\begin{aligned}&u(t,\ q,\ z,\ u_{\mathrm{ref}},\ v,\ E,\ S)\nonumber \\&\quad =\left\{ \begin{array}{ll} -\frac{C^d}{A} \frac{S}{||S||}(\chi +C_0) &{} \quad \text {for }S \ne 0\\ 0 &{} \quad \text {otherwise}, \end{array} \right. \end{aligned}$$

(38)

where $C^d$ and $C_0$ are positive controller gains to be specified further on. Based on (38) and (28), one can find absolutely continuous (by time) control vector v by solving (in the Filippov sense [42]) the following differential equation:

$$\begin{aligned} {\dot{v}}=B^{-1}u(t,\ q,\ z,\ u_{\mathrm{ref}},\ v,\ E,\ S). \end{aligned}$$

(39)

The aim of further considerations is to give conditions on controller gains $\varLambda _0$, $\varLambda _1$, $C^d$, and $C_0$ which guarantee fulfilment of equality $(E,\ {\dot{E}})=(0,\ 0)$ in a finite time. Applying the Lyapunov stability theory, we offer the following result.

Theorem 2

If $\varLambda _0$, $\varLambda _1$, $C_0 > 0$ and $C^d \ge 1$, then control scheme (38)–(39) provides stable convergence in a finite time of the tracking errors $(E,\ {\dot{E}})$ to the origin $(E,\ {\dot{E}})=(0,\ 0)$.

Proof

Consider a Lyapunov function candidate given below

$$\begin{aligned} V=\frac{1}{2} \langle S,\ S \rangle . \end{aligned}$$

(40)

Computing the time derivative of (40) along trajectory (34) results in the expression

$$\begin{aligned} {\dot{V}}= \langle S,\ M^{-1}u+{\mathcal {U}} \rangle . \end{aligned}$$

(41)

By inserting the right-hand side of (38) in (41), one obtains

$$\begin{aligned} {\dot{V}}=\left\langle S,\ -M^{-1}\frac{C^d}{A} \frac{S}{||S||}(\chi +C_0) \right\rangle +\langle S,\ {\mathcal {U}} \rangle . \end{aligned}$$

(42)

Based on inequalities (30), we get

$$\begin{aligned} {\dot{V}} \le -C^d ||S||(\chi +C_0) +\langle S,\ {\mathcal {U}} \rangle . \end{aligned}$$

(43)

The next step is to upper estimate scalar product $\langle S,\ {\mathcal {U}} \rangle$ in (43). On account of inequality (37), we have

$$\begin{aligned} \langle S,\ {\mathcal {U}} \rangle \le ||S|| \chi . \end{aligned}$$

(44)

Hence, applying the assumption $C^d \ge 1$ from Theorem 2, it is easy to obtain the following inequalities:

$$\begin{aligned} {\dot{V}} \le -C^d ||S||(\chi +C_0) +||S|| \chi \le -C^dC_0 ||S||. \end{aligned}$$

(45)

Let us notice that $C^d C_0>0$. Consequently, inequality (45) proves that TSM manifold $S=0$ is stably attainable in a finite time less or equal to $\frac{\sqrt{2V(0)}}{C^d C_0}$. Finally, from Lemma 1, it follows that the origin $(E,\ {\dot{E}})=(0,\ 0)$ can be achieved in a finite time.$\square$

Theorems 1 and 2 imply the following result.

Theorem 3

By fulfilment of the assumptions from both Theorems 1 and 2, control schemes (21)–(22), (38)–(39) provide stable convergence in a finite time of the task tracking errors $(e,\ {\dot{e}},\ \ddot{e})$ to the origin $(e,\ {\dot{e}},\ \ddot{e})=(0,\ 0,\ 0)$.

Proof

Application of controller (38)–(39) implies fulfilment of equalities $E={\dot{E}}=0$ after a finite time $0 \le T_d < \infty$. Hence, ${\dot{z}}=v_{\mathrm{ref}}$ for $t \ge T_d$. As a result, for $t \ge T_d$, control law (21)–(22) is implemented, which implies, according to Theorem 1, stable convergence in finite time $0 \le T_k < \infty$ of the task tracking errors $(e,\ {\dot{e}},\ \ddot{e})$ to the origin. Consequently, the tracking errors $(e,\ {\dot{e}},\ \ddot{e})$ stably converge to the origin in a finite time less or equal to the sum of $T_k$ and $T_d$, i.e. $0 \le T_k+T_d < \infty$.$\square$

Let us observe that controllers (21)–(22), (38)–(39) require the knowledge of the following quantities: q, $z=\left( \begin{array}{l} \alpha \\ {\dot{y}} \end{array} \right)$, ${\dot{z}}=\left( \begin{array}{l} {\dot{\alpha }}\\ \ddot{y} \end{array} \right)$, e, ${\dot{e}}$ and $\ddot{e}$, respectively, to generate suitable torques/forces. Hence, reconstructions of auxiliary velocity $\alpha$, auxiliary acceleration ${\dot{\alpha }}$, joint velocity ${\dot{y}}$ and joint acceleration $\ddot{y}$ of the holonomic manipulator, task error e, task error velocity ${\dot{e}}$, and task error acceleration $\ddot{e}$ are needed to apply controllers (21)–(22), (38)–(39) in practice. Most often in practice, real mobile manipulators are equipped with encoders which measure angular displacements of the wheels of the platform and angles in the kinematic pairs of the holonomic manipulator. Let us note that for the mobile platforms belonging to a class of $(2,\ 0)$, auxiliary velocities $\alpha$ are equal to scaled angular velocities ${\dot{\phi }}=\left( \begin{array}{l} {\dot{\phi }}_1\\ {\dot{\phi }}_2 \end{array} \right)$ of the platform wheels (see Fig. 1), i.e. $\alpha =\frac{R}{2}{\dot{\phi }}$. As a result, $z=\frac{\mathrm{d}}{\mathrm{d} t}\left( \left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right)$; ${\dot{z}}=\frac{\mathrm{d}^2}{\mathrm{d} t^2}\left( \left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right)$ and their reconstruction is equivalent to reconstruction of ${\dot{\phi }}$, $\ddot{\phi }$, ${\dot{y}}$ and $\ddot{y}$, respectively ($\phi$ and y are available from mobile manipulator encoders). Moreover, many commercial sensors are available for measurement of the end effector position $p_e$, such as vision systems, electromagnetic measurement systems, position sensitive detectors, or laser tracking systems. Consequently, task error e appearing in the proposed controllers is also assumed to be available from measurements. There exist many approaches in the literature to reconstruct quantities z, ${\dot{z}}$, ${\dot{e}}$, and $\ddot{e}$, respectively (see, for example, our recent works [35, 36], in which different kinds of state observers were analysed). Although the observers known from the literature are able to reliably reconstruct mobile manipulator state (both reduced velocity and acceleration) based on position measurement, almost all of them have to satisfy the so-called separation principle [50]. Let us observe that control laws (21)–(22), (38)–(39) are discontinuous. Consequently, separation principle is not fulfilled for our controllers. A computationally efficient approach based on the uniform robust exact finite-time differentiation has been recently proposed in works [51, 52] to numerically find derivatives of absolutely continuous functions. The separation principle is trivially fulfilled for differentiators (model-free observers) from [51, 52]. Assuming that angles $\phi$ and y and task error e are known (measurable), one can exactly reconstruct reduced velocity z(t), reduced acceleration ${\dot{z}}(t)$, task error velocity ${\dot{e}}(t)$, and task error acceleration $\ddot{e}(t)$ (by neglecting the measurement noise of the devices) after finite times of transient processes, say $T^{\prime }_z,\ T^{\prime }_e>0$, respectively. The second-order uniform robust exact differentiators for reconstruction of both z, ${\dot{z}}$ and ${\dot{e}}$, $\ddot{e}$, respectively, take in our case the following forms:

$$\begin{aligned} {\dot{z}}_0= & {} z_1-{\hat{\lambda }}_2^z L_z(t)^{1/3} \left| \left| z_0-\left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right| \right| ^{2/3}\nonumber \\&\times \,\text {sign}\left( z_0-\left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right) ,\nonumber \\ {\dot{z}}_1= & {} z_2-{\hat{\lambda }}_1^z L_z(t)^{2/3} \left| \left| z_0-\left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right| \right| ^{1/3}\nonumber \\&\times \, \text {sign}\left( z_0-\left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right) ,\nonumber \\ {\dot{z}}_2= & {} -{\hat{\lambda }}_0^z L_z(t) \nonumber \\&\times \,\text {sign} \left( z_0-\left[ \begin{array}{cc} \frac{R}{2}{\mathbb {I}}_2 &{} 0\\ 0 &{} {\mathbb {I}}_n \end{array} \right] \left( \begin{array}{l} \phi \\ y \end{array} \right) \right) \end{aligned}$$

(46)

and

$$\begin{aligned} \begin{array}{l} {\dot{\eta }}_0=\eta _1-{\hat{\lambda }}_2^e L_e(t)^{1/3}||\eta _0-e||^{2/3} \text {sign}(\eta _0-e),\\ {\dot{\eta }}_1=\eta _2-{\hat{\lambda }}_1^e L_e(t)^{2/3}||\eta _0-e||^{1/3} \text {sign}(\eta _0-e),\\ {\dot{\eta }}_2=-{\hat{\lambda }}_0^e L_e(t) \text {sign}(\eta _0-e), \end{array} \end{aligned}$$

(47)

where ${\hat{\lambda }}_0^z$, ${\hat{\lambda }}_1^z$, ${\hat{\lambda }}_2^z$, ${\hat{\lambda }}_0^e$, ${\hat{\lambda }}_1^e$, ${\hat{\lambda }}_2^e$ are diagonal matrices with positive constants whose numerical values were suggested in [51, 52]; $z_1$, $z_2$, $\eta _1$, $\eta _2$ denote the outputs of differentiators (46)–(47) reconstructing exactly reduced velocity z(t), reduced acceleration ${\dot{z}}(t)$, task error velocity ${\dot{e}}(t)$, and task error acceleration $\ddot{e}(t)$, respectively, i.e. $z(t)=z_1(t)$, ${\dot{z}}(t)=z_2(t)$ for $t \ge T^{\prime }_z$, ${\dot{e}}(t)=\eta _1(t)$, $\ddot{e}(t)=\eta _2(t)$ for $t \ge T^{\prime }_e$. $L_z(t)$ and $L_e(t)$ stand for positive continuous functions which take [based on (16), (21) and (38)] the forms $L_z(t)=\lambda _{\max }(M^{-1}) [C^d/A(\chi +C_0)+w_3 ||v||||z_1|| +w_4 ||z_1||^3+w_5||z_1||||z_2||+w_6(||z_1||+\alpha _0||z_1||)+w_7\alpha _1 ]$ and $L_e(t)=|\lambda _{\max }(J)| L_z(t)+w_4 ||z_1||^3+w_5||z_1||||z_2||+||\frac{\mathrm{d}^3 p_d}{\mathrm{d}t^3}||$. The quantities $L_z(t)$, $L_e(t)$ represent physically upper estimates of the norms of $\ddot{z}$, $\frac{\mathrm{d}^3 e}{\mathrm{d}t^3}$ (both reduced jerk and task error jerk). Let us define concatenating control $v_c=(v_{c,1},\ldots ,v_{c,l+n-k})^{\mathrm{T}}$ as follows

$$\begin{aligned} v_c=\left\{ \begin{array}{ll} v^{\prime }(t), &{}\quad t \in [0,\ \max \{T^{\prime }_z,\ T^{\prime }_e\}],\\ v(t), &{} \quad t \ge \max \{T^{\prime }_z,\ T^{\prime }_e\}, \end{array} \right. \end{aligned}$$

(48)

where $v^{\prime }(t)$ is arbitrary absolutely continues mapping of time t (e.g. $v^{\prime }(t)=0$); v(t) is given by (38)–(39) with $z=z_1$, ${\dot{z}}=z_2$, ${\dot{e}}=\eta _1$, $\ddot{e}=\eta _2$ for $t \ge \max \{T^{\prime }_z,\ T^{\prime }_e$}. Based on (38)–(39) and (46)–(47), we are now in position to give the following theorem.

Theorem 4

If $\phi$, y, e are only available from measurements and the assumptions from Theorem 3 are fulfilled, then control scheme (46)–(48) guarantees stable convergence in a finite time of the task space tracking errors $(e,\ {\dot{e}},\ \ddot{e})$ to the origin $(e,\ {\dot{e}},\ \ddot{e})=(0,\ 0,\ 0)$.

Proof

Inserting $v^{\prime }$ into dynamic equations (13) results in measured angles $\phi =\phi (t)$, $y=y(t)$ and task errors $e=e(t)$ which serve as inputs to differentiators (46)–(47). For $t > \max \{T^{\prime }_z,\ T^{\prime }_e\}$, one obtains $z(t)=z_1(t)$, ${\dot{z}}(t)=z_2(t)$, ${\dot{e}}(t)=\eta _1(t)$ and $\ddot{e}(t)=\eta _2(t)$, respectively. Hence, control v(t) defined by (38)–(39) can be applied with the initial conditions $v(T^{\prime })=v^{\prime }(T^{\prime })$, $z(T^{\prime })=z_1(T^{\prime })$, ${\dot{z}}(T^{\prime })=z_2(T^{\prime })$, ${\dot{e}}(T^{\prime })=\eta _1(T^{\prime })$ and $\ddot{e}(T^{\prime })=\eta _2(T^{\prime })$ to track $p_d$, where $T^{\prime } \ge \max \{T^{\prime }_z,\ T^{\prime }_e\}$. Consequently, from Theorem 3, it follows that the origin $(e,\ {\dot{e}},\ \ddot{e})=(0,\ 0,\ 0)$ is attained in a finite time less or equal to $0 \le T^{\prime }+T_d+T_k < \infty$.$\square$

4 Numerical examples

Based on chosen mobile manipulator tasks, this section demonstrates the performance of controllers proposed in the paper. Two different mobile manipulator structures will be considered herein. The first aim is to numerically compare the performances of kinematically optimal controller involving the objective function ${\mathcal {F}}$ with non-optimal controller which utilises task coordinates $p_a$ to eliminate redundancy of the mobile manipulator. Therefore, two basic controllers given by equations (5)–(7), (46)–(48) and (25), (46)–(48) will be tested further on for the first mobile manipulator schematically shown in Fig. 1. In all numerical simulations, the SI units of radians, seconds, metres, etc., are used. The holonomic part (a SCARA type stationary manipulator) with two revolute kinematic pairs ($n=2$) operating for simplicity of computations in two-dimensional task space ($m=2$) is mounted on the platform which is assumed to be physically driven by two wheels of angular velocities $({\dot{\phi }}_1,\ {\dot{\phi }}_2)^{\mathrm{T}}$.

The platform is subject to the following non-holonomic constraints ($k=3$ and $l=5$):

$$\begin{aligned} \begin{array}{l} \sin \theta \cdot {\dot{x}}_{1,c}-\cos \theta \cdot {\dot{x}}_{2,c}=0,\\ \cos \theta \cdot {\dot{x}}_{1,c}+\sin \theta \cdot {\dot{x}}_{2,c}+W \dot{\theta }-R \cdot {\dot{\phi }}_1=0,\\ \cos \theta \cdot {\dot{x}}_{1,c}+\sin \theta \cdot {\dot{x}}_{2,c}-W \dot{\theta }-R \cdot {\dot{\phi }}_2=0. \end{array} \end{aligned}$$

(49)

The corresponding matrix N(x) equals

$$\begin{aligned} N(x)=\left[ \begin{array}{cc} \cos \theta &{} \cos \theta \\ \sin \theta &{} \sin \theta \\ \frac{1}{W} &{} -\frac{1}{W} \\ \frac{2}{R} &{} 0 \\ 0 &{} \frac{2}{R} \end{array} \right] , \end{aligned}$$

(50)

where $x=(x_{1,c},\ x_{2,c},\ \theta ,\ \phi _1,\ \phi _2)^{\mathrm{T}}$. The kinematic equations of the mobile manipulator equal

$$\begin{aligned}&f_e(q)\nonumber \\&\quad =\left( \begin{array}{c} c \theta \left( \text {a}+l_1 c y_1+l_2 c y_{12}\right) -s\theta \left( \text {b}+l_1 s y_1+l_2 s y_{12} \right) +x_{1,c}\\ s \theta \left( \text {a}+l_1 c y_1+l_2 c y_{12}\right) +c\theta \left( \text {b}+l_1 s y_1+l_2 s y_{12} \right) +x_{2,c} \end{array}\right) , \nonumber \\ \end{aligned}$$

(51)

where $c\theta =\cos \theta$, $s\theta =\sin \theta$, $c y_1=\cos y_1$, $c y_{12}=\cos (y_1+y_2)$, $s y_1=\sin y_1$, $s y_{12}=\sin ( y_1+y_2)$, $l_1=0.4=l_2$ stand for the link lengths of its holonomic part; $\text {a}=0.85$, $\text {b}=0.2$; $2W=0.5$; $2L=1.8$; $y_1$, $y_2$ denote joint coordinates of the holonomic manipulator. Hence, vector q of the generalised coordinates takes the form $q=\left( x_{1,c},\ x_{2,c},\ \theta ,\ \phi _1,\ \phi _2,\ y_1,\ y_2 \right) ^{\mathrm{T}}$. Matrix C is equal to

$$\begin{aligned} C=\left[ \begin{array}{cc} N(x) &{} 0\\ 0 &{} {\mathbb {I}}_2 \end{array} \right] ; \end{aligned}$$

(52)

reduced velocity z equals $z=(\alpha _1\ \alpha _2\ {\dot{y}}_1,\ {\dot{y}}_2)^{\mathrm{T}}$ and control $v=(v_1,\ldots ,v_4)^{\mathrm{T}}$, respectively. The task of the mobile manipulator is to make the end effector follow desired circle trajectory $p_d^e=(2+\cos (t),\ 3+\sin (t))^{\mathrm{T}}$ (see the solid circle in Fig. 1). On account of the fact that $l+n-m-k=2$, the mobile manipulator becomes redundant mechanism. Auxiliary matrix $\jmath (q)$ takes the following form for the mobile manipulator from Fig. 1:

$$\begin{aligned} \jmath =\left[ \begin{array}{ccccccc} 1 &{}{} 0 &{}{} \jmath _{13} &{}{} 0 &{}{} 0 &{}{} \jmath _{14} &{}{} \jmath _{15}\\ 0 &{}{} 1 &{}{} \jmath _{23} &{}{} 0 &{}{} 0 &{}{} \jmath _{24} &{}{} \jmath _{25}\\ -s \theta &{}{} c \theta &{}{} 0 &{}{} 0 &{}{} 0 &{}{} 0 &{}{} 0\\ c \theta &{}{} s \theta &{}{} W &{}{} - R &{}{} 0 &{}{} 0 &{}{} 0\\ c \theta &{}{} s \theta &{}{} -W &{}{} 0 &{}{} -R &{}{} 0 &{}{} 0\\ \end{array} \right] , \end{aligned}$$

(53)

where $\jmath _{13}=-s \theta (a+l_1cy_1+l_2cy_{12})-c\theta (b+l_1 sy_1+l_2 sy_{12})$; $\jmath _{14}=c\theta (-l_1sy_1-l_2 sy_{12})-s\theta (l_1 cy_1+l_2 cy_{12})$; $\jmath _{15}=c\theta (-l_2 sy_{12}) -s\theta l_2 cy_{12}$; $\jmath _{23}=c\theta (a+l_1 cy_1+l_2 cy_{12})-s\theta (b+l_1sy_1 +l_2 sy_{12})$; $\jmath _{24}=s\theta (-l_1sy_1 -l_2 sy_{12}) +c\theta (l_1cy_1+l_2 cy_{12})$; $\jmath _{25}=s\theta (-l_2 sy_{12}) + c\theta l_2 cy_{12}$.

Fig. 1

A kinematic scheme of the mobile manipulator in the absolute coordinate system and the tracking task to be accomplished

Hence, the corresponding orthogonal complementary matrix ${\mathcal {N}}$ may be expressed after time-consuming but simple calculations in the form given below

$$\begin{aligned} {\mathcal {N}}=[{\mathcal {N}}_1(q)\ {\mathcal {N}}_2(q)]^{\mathrm{T}}, \end{aligned}$$

(54)

where ${\mathcal {N}}_1\!=\!({\mathcal {N}}_{11},\ldots ,{\mathcal {N}}_{17})^{\mathrm{T}}$; ${\mathcal {N}}_2=({\mathcal {N}}_{21},\ldots ,{\mathcal {N}}_{27})^{\mathrm{T}}$; ${\mathcal {N}}_{11}=0$; ${\mathcal {N}}_{12}=0$; ${\mathcal {N}}_{14}=0$; ${\mathcal {N}}_{15}=0$; $\left( \begin{array}{l} {\mathcal {N}}_{13}\\ {\mathcal {N}}_{16}\\ {\mathcal {N}}_{17} \end{array} \right) =\left( \begin{array}{l} \jmath _{13}\\ \jmath _{14}\\ \jmath _{15} \end{array} \right) \times \left( \begin{array}{l} \jmath _{23}\\ \jmath _{24}\\ \jmath _{25} \end{array} \right)$; $\times$ denotes vector product; $\left( \begin{array}{l} {\mathcal {N}}_{21}\\ {\mathcal {N}}_{22} \end{array} \right) =\left( \begin{array}{l} c \theta \\ s \theta \end{array} \right) \cdot \text{ det }({\mathcal {M}}{\mathcal {M}}^{\mathrm{T}})$; ${\mathcal {M}}=\left[ \begin{array}{ccc} -\jmath _{13} &{} -\jmath _{14} &{} - \jmath _{15}\\ -\jmath _{23} &{} -\jmath _{24} &{} - \jmath _{25} \end{array} \right]$; ${\mathcal {N}}_{24}={\mathcal {N}}_{25}=\frac{\text{ det }({\mathcal {M}}{\mathcal {M}}^{\mathrm{T}})}{R}$; $\left( \begin{array}{l} {\mathcal {N}}_{23}\\ {\mathcal {N}}_{26}\\ {\mathcal {N}}_{27} \end{array} \right) ={\mathcal {M}}^{\mathrm{T}} \text{ adj }({\mathcal {M}}{\mathcal {M}}^{\mathrm{T}}) \left( \begin{array}{l} c \theta \\ s \theta \end{array} \right)$; $\text{ adj }(\cdot )$ stands for adjoint matrix of $(\cdot )$. Consequently, the user-specified function $f_\mathrm{a}(q)$ equals

$$\begin{aligned} f_\mathrm{a}=c_{{\mathcal {F}}}[{\mathcal {N}}_1(q)\ {\mathcal {N}}_2(q)]^{\mathrm{T}}K_{{\mathcal {F}}}(q-q_{\mathrm{rest}}). \end{aligned}$$

(55)

The components of the nominal dynamic equations of the mobile manipulator take the following values: platform mass $m_{\mathrm{p}}=94$; wheel mass $m_\mathrm{w}=5$; platform moment of inertia $I_{\mathrm{p}}=6.609$; the masses of the links of the holonomic manipulator equal $m_1=m_2=4$, respectively, and $G(q)=0$. Initial configuration q(0), reduced velocity z(0), and control v(0) equal $q(0)=(-0.4\ 0\ 0\ 0\ 0\ 0\ 0)^{\mathrm{T}}$; $z(0)=(0\ 0\ 0\ 0)^{\mathrm{T}}$, $v(0)=(0\ 0\ 0\ 0)^{\mathrm{T}}$, respectively, in all the simulations. Moreover, $q_{\mathrm{rest}}$ takes the form $q_{\mathrm{rest}}=(0\ 0\ 0\ 0\ 0\ \pi /4\ \pi /4)^{\mathrm{T}}$. The non-singular actuation matrix B is equal to

$$\begin{aligned} B=\left[ \begin{array}{cccc} \frac{2}{R} &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{2}{R} &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 1\end{array} \right] . \end{aligned}$$

(56)

The estimates of the constants $w_1,\ldots ,w_7$ which depend only on configuration q can be determined based both on the numerical solution of the following system of algebraic and differential equations:

$$\begin{aligned} \left( \begin{array}{c} f_e(q)-p_d^e(t)\\ f_\mathrm {a}(q)-p_d^a(t)\\ \sin \theta \cdot {\dot{x}}_{1,c}-\cos \theta \cdot {\dot{x}}_{2,c}\\ \cos \theta \cdot {\dot{x}}_{1,c}+\sin \theta \cdot {\dot{x}}_{2,c}+W\dot{\theta }-R \cdot {\dot{\phi }}_1\\ \cos \theta \cdot {\dot{x}}_{1,c}+\sin \theta \cdot {\dot{x}}_{2,c}-W\dot{\theta }-R \cdot {\dot{\phi }}_2 \end{array} \right) =0\nonumber \\ \end{aligned}$$

(57)

and the knowledge of the components of the nominal dynamic equations. Nevertheless, in order to simplify the computations, rough conservative estimates of a, A, $w_i$, $i=1,\ldots ,7$, $w_3^k$ and $w_4^k$ have been assumed for controllers (5)–(7), (46)–(48) and (25), (46)–(48). Hence, they were chosen as follows $a=A=0.1$; $w_1=1.5$; $w_2=0.001$; $w_3=w_3^k=2$; $w_4=w_4^k=3$; $w_5=0.001$; $w_6=4$; $w_7=0$; $\lambda _{\max }(M^{-1})=64$. In order to observe the effects of acting both the discontinuous disturbing signal and measurement noise on the performance of the proposed controllers as well as to attain the convergence of task errors $e^e$ less or equal to $10^{-3}$ in approximately the same time, possibly small numeric value of control gain $C^d$ has been chosen in the simulations. Therefore, the numeric values of gain coefficients for both controllers are assumed to be equal to: $c=C^d=2$; $c_0=C_0=1$; $\lambda _0=1$; $\lambda _1=11$; $\lambda _2=6$; $\varLambda _0=11$; $\varLambda _1=6$; $c_{{\mathcal {F}}}=1.$; $K_{{\mathcal {F}}}=\text{ diag }(0.01\ 0.01\ 0.01\ 0.01\ 1.5)$.

To speed up the convergence process of differentiators (46)–(47), we have chosen good initial guesses $z_1(0)$, $z_2(0)$, $\eta _0(0)$, $\eta _1(0)$, $\eta _2(0)$ in the numerical examples (which imply relation $T^{\prime }\simeq \max \{T^{\prime }_z,\ T^{\prime }_e\}\simeq 0$—see the proof of Theorem 4) based on the nominal values of our dynamic model. Consequently, differentiators (46)–(47) were run with the following initial values: $z_1(0)=z(0)=0$, $z_2(0)=0$, $\eta _0(0)=(-1.75,\ -2.8,\ 0.18,\ 0.15)^{\mathrm{T}}$, $\eta _1(0)=(0,\ 1,\ 0,\ 0)^{\mathrm{T}}$, $\eta _2(0)=(1,\ 0,\ 0,\ 0)^{\mathrm{T}}$ , $v(0)=(0,\ 0,\ 0,\ 0)^{\mathrm{T}}$ and parameters ${\hat{\lambda }}^e_0=156$; ${\hat{\lambda }}^e_1=40.5$; ${\hat{\lambda }}^e_2=10.8$; ${\hat{\lambda }}^z_0=71.5$; ${\hat{\lambda }}^z_1=22.6$; ${\hat{\lambda }}^z_2=5.1$, respectively. Due to conservative nature of estimates $L_z$ and $L_e$ in (46)–(47), they are assumed for simplicity of computations to be equal, i.e. $L_e(t)=L_z(t)$ in all the simulations.

The first task is to track $p^e_d$ by means of non-optimal controller (25), (46)–(48) with $f_\mathrm{a}=W q$, where $W=\left[ \begin{array}{ccccccc} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1\end{array} \right]$ and $p_d^a(t)=(\pi /4,\ \pi /4)^{\mathrm{T}}$ (see Remark 2). The mobile manipulator is assumed not to be disturbed in this simulation, i.e. $D=0$ and hence $\alpha _0=\alpha _1=0$. The results of the first simulation are depicted in Figs. 2, 3, 4, 5, 6 and 7 which show finite-time convergence of the errors $e^e$ and $e^a$ to the origin (Figs. 2 and 3). Moreover, as shown in Figs. 4, 5, 6 and 7, controller (25), (46)–(48) generates at least absolutely continuous steering signals $v_c$ with the integral norm $\overline{||v_c||}=55.2$ (defined in $L_2[0,\ 6]$ norm as $\overline{||v_c||}=\sqrt{\int _0^6 \langle v_c,\ v_c \rangle \mathrm{d}t}$).

Fig. 2

Euclidean norm of task errors $e^e$ for controller (25), (46)–(48) versus time

Fig. 3

Euclidean norm of task errors $e^a$ for controller (25), (46)–(48) versus time

Fig. 4

Torque $v_{c,1}$ for controller (25), (46)–(48) versus time

Fig. 5

Torque $v_{c,2}$ for controller (25), (46)–(48) versus time

Fig. 6

Torque $v_{c,3}$ for controller (25), (46)–(48) versus time

Fig. 7

Torque $v_{c,4}$ for controller (25), (46)–(48) versus time

Fig. 8

Euclidean norm of task errors $e^e$ for kinematically optimal controller (5)–(7), (46)–(48)

In the second task, the same desired trajectory $p_d^e$ is tracked. However, controller (5)–(7), (46)–(48) involves now auxiliary function $f_\mathrm{a}$ given by eqn (55). Mobile manipulator is also not disturbed in this simulation, i.e. $\alpha _0=\alpha _1=0$. The results of the second simulation are given in Figs. 8, 9, 10, 11, 12 and 13 which show finite-time convergence of $e^e$ and $e^a$ to the origin (see Figs. 8 and 9).

Fig. 9

Euclidean norm of task errors $e^a$ for kinematically optimal controller (5)–(7), (46)–(48)

Fig. 10

Torque $v_{c,1}$ for kinematically optimal controller (5)–(7), (46)–(48)

Fig. 11

Torque $v_{c,2}$ for kinematically optimal controller (5)–(7), (46)–(48)

Fig. 12

Torque $v_{c,3}$ for kinematically optimal controller (5)–(7), (46)–(48)

Fig. 13

Torque $v_{c,4}$ for kinematically optimal controller (5)–(7), (46)–(48)

From Figs. 8–9, it is also seen that for $t \ge 4$ controller (5)–(7), (46)–(48) generates kinematically optimal absolutely continuous torques (see Figs. 10, 11, 12 and 13). The integral torque norm $\overline{||v_c||}$ equals in this case $\overline{||v_c||}=47.1$ and is clearly smaller than that obtained in the first experiment.

The aim of the next two simulations is to numerically show that non-optimal controller (25), (46)–(48) and the kinematically optimal one (5)–(7), (46)–(48) are robust against both disturbance signal $D \ne 0$ and a measurement noise. For this purpose, nonlinear discontinuous friction term of the form $D=2 z+5 \text{ sign }(z)+5 \exp (-0.2 ||z||^2 \text{ sign }(z)$ exhibiting viscous, the Coulomb and Stribeck effects [53, 54] has been added to mobile manipulator dynamic equations. The numerical coefficients at the discontinuous terms were chosen as relatively large to show the effects of the performance of the controllers under the conditions of discontinuity. Let us note that ${\dot{D}}$ is not locally bounded Lebesgue measurable function. Consequently, the same control laws as those from the first and second experiments with the same controller gains have been applied in the next two simulations. Moreover, both measured angles $\phi$ and y and task error $e^e$ obtained from encoders have been additionally contaminated by a measurement noise $\zeta _i(t)$ with relatively large normalised magnitude of a Brownian motion of the form $\mathrm{d}\zeta _i(t)=10^{-5}\sqrt{t} X(t)\mathrm{d}t$; $X(t)\sim N(0,\ 1)$, $i=1,2,3,4,5,6$.

The third task is also to track $p^e_d$ by means of the non-optimal controller (25), (46)–(48) under the conditions of acting both disturbance signal D and measurement noise $\zeta _i$, $i=1,2,3,4,5,6$ on the mobile manipulator. The results of this simulation are given in Figs. 14, 15, 16, 17, 18 and 19 which indicate a good tracking performance of controller (25), (46)–(48) (see Figs. 14 and 15). As was expected, the measurement noise with greater normalised magnitude (which is proportional to $\sqrt{t}$) generates greater norms of task errors for greater time moments (see Figs. 14 and 15). The corresponding torques $v_c$ are depicted in Figs. 16, 17, 18 and 19. Sudden increases or decreases in $v_{c,3}$ and $v_{c,4}$ in the time interval $[4.2,\ 4.9]$ are a result of the Coulomb and Stribeck discontinuous friction term D (see Figs. 18 and 19). Nevertheless, transient impetuous variations in $v_c$ in neighbourhood of zero reduced velocity z still present absolutely continuous functions of time. Moreover, controller (25), (46)–(48) provides $\overline{||v_c||}$ equal to $\overline{||v_c||}=93.7$.

Fig. 14

Euclidean norm of task errors $e^e$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

Fig. 15

Euclidean norm of task errors $e^a$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

Fig. 16

Torque $v_{c,1}$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

Fig. 17

Torque $v_{c,2}$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

Fig. 18

Torque $v_{c,3}$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

Fig. 19

Torque $v_{c,4}$ for controller (25), (46)–(48) with both disturbance signal and measurement noise

The aim of the fourth simulation is to numerically show that controller (5)–(7), (46)–(48) is both robust against disturbance signal $D \ne 0$ and the measurement noise and also provides optimal solution. The results of the fourth simulation are given in Figs. 20, 21, 22, 23, 24, and 25 which seem to indicate better tracking performance of controller (5)–(7), (46)–(48) as compared with that given by (25), (46)–(48) (see Figs. 14–15 and 20–21). The corresponding absolutely continuous torques $v_c$ are presented in Figs. 22, 23, 24 and 25 with the norm $\overline{||v_c||}$ equal to $\overline{||v_c||}=82.1$, which is also clearly smaller than that obtained in the third simulation. Sudden increases and decreases in $v_{c,4}$ in time interval $[0,\ 1.4]$ (see Fig. 25) are result of discontinuous friction term D. Similarly, rapid variations in $v_{c,3}$ and $v_{c,4}$ in time interval $[3,\ 6]$ (see Figs. 24 and 25) are result of both friction term D and measurement noise $\zeta _i$. Nevertheless, $v_{c,3}$ and $v_{c,4}$ still present absolutely continuous functions of time.

Fig. 20

Euclidean norm of task errors $e^e$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

Fig. 21

Euclidean norm of task errors $e^a$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

Fig. 22

Torque $v_{c,1}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

Fig. 23

Torque $v_{c,2}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

Fig. 24

Torque $v_{c,3}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

Fig. 25

Torque $v_{c,4}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise

The aim of the fifth simulation is to show that a slight increase only of the controller gain $C^d$ practically reduces the task errors $e^e$, $e^a$ (caused by the measurement noise and disturbance signal—see Figs. 20 and 21 for $t \ge 4.7$) to zero and simultaneously significantly decreases the $L_2$ norm of $v_c$ as compared to the previous experiment. For this purpose, we increase now $C^d$ to value equal to $C^d=20$. All other controller gains remain unchanged in this simulation. The results of the fifth simulation are presented in Figs. 26, 27, 28, 29, 30 and 31 which indicate accurate finite-time convergence of $e^e$ and $e^a$ to the origin (see Figs. 26 and 27). Absolutely continuous steering signals $v_c$ are depicted in Figs. 26, 27, 28, 29, 30 and 31. The $L_2$ norm of $v_c$ equals in this case $\overline{||v_c||}=51$ and is significantly smaller than that obtained in the previous simulation.

Fig. 26

Euclidean norm of task errors $e^e$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Fig. 27

Euclidean norm of task errors $e^a$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Fig. 28

Torque $v_{c,1}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Fig. 29

Torque $v_{c,2}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Fig. 30

Torque $v_{c,3}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Fig. 31

Torque $v_{c,4}$ for kinematically optimal controller (5)–(7), (46)–(48) with both disturbance signal and measurement noise as well as increased C

Finally, we have carried out additional computations in conditions closely related to the experiment (the second aim of this section). For this purpose, the second mobile manipulator operating in a three-dimensional work space and shown in Fig. 32 has been utilised in this ‘real case’. Kinematic and dynamic data correspond to KUKA youBot mobile platform and holonomic manipulator. However, in the computations carried out herein, the platform is assumed to be of the non-holonomic (2, 0) type (the same as that considered in the previous computations) and the holonomic manipulator has only three revolute kinematic pairs ($n=3$) (the last three links of the original KUKA holonomic arm form the single link of the manipulator utilised in the computations). Consequently, kinematic equations of the mobile manipulator from Fig. 32 take the form

$$\begin{aligned} f_e(q)=\left( \begin{array}{c} \text {a} c \theta +l_1 c_{\theta 1}+\frac{l_2}{2} c_{\theta 1 2}+ \frac{l_3}{2} c_{\theta 1 2 3} +x_{1,c}\\ \text {a} s \theta -l_1 s_{\theta 1}-\frac{l_2}{2} s_{\theta 1 2}- \frac{l_3}{2} s_{\theta 1 2 3} +x_{2,c}\\ \text {c}-l_2sy_2-l_3 sy_{23}+x_{3,c} \end{array}\right) , \nonumber \\ \end{aligned}$$

(58)

where $(x_{1,c}, x_{2,c}, x_{3,c})^{\mathrm{T}}$ stand for coordinates of the platform centre, $c_{\theta 1}=\cos (-\theta +y_1)$, $c_{\theta 1 2}=\cos (-\theta +y_1+y_2)+\cos (\theta -y_1+y_2)$, $c_{\theta 1 2 3}=\cos (-\theta +y_1+y_2+y_3)+\cos (\theta -y_1+y_2+y_3)$, $s_{\theta 1}=\sin (-\theta +y_1)$, $s_{\theta 1 2}=\sin (-\theta +y_1+y_2)-\sin (\theta -y_1+y_2)$, $s_{\theta 1 2 3}=\sin (-\theta +y_1+y_2+y_3)-\sin (\theta -y_1+y_2+y_3)$, $(\text {a}, 0,\text {c})^{\mathrm{T}}$ denotes the point at which the holonomic manipulator is fasten to the platform; $l_1$, $l_2$, $l_3$ are the lengths of the arm. Hence, vector q equals $q=(x_{1,c},\ x_{2,c},\ \theta ,\ \phi _1,\ \phi _2,\ y_1,\ y_2,\ y_3)^{\mathrm{T}}$. Taking into account the above assumptions and the KUKA youBot documentation [55], the kinematic parameters of the mobile manipulator from Fig. 32 take the following numeric values: $(\text {a}, 0,\text {c})^{\mathrm{T}}=(0.167,\ 0,\ 0.161)^{\mathrm{T}}$, $x_{3,c}=0.084$, $l_1=0.033$, $l_2=0.155$, $l_3=0.342$, $W=0.158$, and $R=0.05$, respectively.

Fig. 32

A kinematic scheme of the youBot mobile manipulator with platform of (2, 0) type in the absolute coordinate system and the tracking task to be accomplished

Matrix C is equal to

$$\begin{aligned} C=\left[ \begin{array}{cc} N(x) &{} 0\\ 0 &{} {\mathbb {I}}_3 \end{array} \right] , \end{aligned}$$

(59)

where N(x) is given by formula (50). The task is both to track the end effector desired trajectory $p^e_d=(2+\cos (t),\ 3+\sin (t),\ 0.35)^{\mathrm{T}}$ and to fulfil equality $y_2(t)-\frac{\pi }{9}=0$, respectively, $t \ge T$ ($m=4$). Hence, $l+n-m-k=1$ and auxiliary matrix $\jmath (q)$ equals

$$\begin{aligned} \jmath =\left[ \begin{array}{cccccccc} 1 &{} 0 &{} \jmath _{13} &{} 0 &{} 0 &{} \jmath _{14} &{} \jmath _{15} &{} \jmath _{16}\\ 0 &{} 1 &{} \jmath _{23} &{} 0 &{} 0 &{} \jmath _{24} &{} \jmath _{25} &{} \jmath _{26}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} \jmath _{35} &{} \jmath _{36}\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0\\ -s \theta &{} c \theta &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ c \theta &{} s \theta &{} 0 &{} -R &{} 0 &{} 0 &{} 0 &{} 0\\ c \theta &{} s \theta &{} 0 &{} 0 &{} -R &{} 0 &{} 0 &{} 0\\ \end{array} \right] , \end{aligned}$$

(60)

where $\jmath _{13}=-\text {a}s \theta +l_1 s_{\theta 1}+\frac{l_2}{2}s_{\theta 1 2}+\frac{l_3}{2}s_{\theta 1 2 3}$; $\jmath _{14}=-l_1 s_{\theta 1}-\frac{l_2}{2}s_{\theta 1 2}-\frac{l_3}{2}s_{\theta 1 2 3}$; $\jmath _{15}=\frac{l_2}{2}(-\sin (-\theta +y_1+y_2)-\sin (\theta -y_1+y_2))+\frac{l_3}{2}(-\sin (-\theta +y_1+y_2+y_3)-\sin (\theta -y_1+y_2+y_3))$; $\jmath _{16}=\frac{l_3}{2}(-\sin (-\theta +y_1+y_2+y_3)-\sin (\theta -y_1+y_2+y_3))$; $\jmath _{23}=\text {a}c \theta +l_1 c_{\theta 1}+\frac{l_2}{2}c_{\theta 1 2}+\frac{l_3}{2}c_{\theta 1 2 3}$; $\jmath _{24}=-l_1 s_{\theta 1}-\frac{l_2}{2}c_{\theta 1 2}-\frac{l_3}{2}c_{\theta 1 2 3}$; $\jmath _{25}=-\frac{l_2}{2}(\cos (-\theta +y_1+y_2)-\cos (\theta -y_1+y_2))-\frac{l_3}{2}(\cos (-\theta +y_1+y_2+y_3)-\cos (\theta -y_1+y_2+y_3))$; $\jmath _{26}=\frac{l_3}{2}(\cos (-\theta +y_1+y_2+y_3)-\cos (\theta -y_1+y_2+y_3))$; $\jmath _{35}=-l_2cy_2-l_3cy_{23}$; $\jmath _{36}=-l_3cy_{23}$. The corresponding orthonormal complementary vector ${\mathcal {N}}$ is given below

$$\begin{aligned} {\mathcal {N}}=({\mathcal {N}}_1,\ldots ,{\mathcal {N}}_8)^{\mathrm{T}}, \end{aligned}$$

(61)

where ${\mathcal {N}}_7=0$, ${\mathcal {N}}_8=0$, ${\mathcal {N}}_3=-(s\theta \jmath _{13}-c\theta \jmath _{23})$, ${\mathcal {N}}_6=s\theta \jmath _{13} -c \theta \jmath _{23}$, ${\mathcal {N}}_1=-{\mathcal {N}}_3 \jmath _{13}-{\mathcal {N}}_6 \jmath _{14}$, ${\mathcal {N}}_2=-{\mathcal {N}}_3 \jmath _{23}-{\mathcal {N}}_6 \jmath _{24}$, ${\mathcal {N}}_4=\frac{c\theta {\mathcal {N}}_1+s \theta {\mathcal {N}}_2 }{R}$ and ${\mathcal {N}}_5=-\frac{c\theta {\mathcal {N}}_1+s \theta {\mathcal {N}}_2 }{R}$. Consequently, $f_\mathrm{a}(q)$ takes the form

$$\begin{aligned} f_\mathrm{a}=c_{{\mathcal {F}}}\langle {\mathcal {N}},\ K_{{\mathcal {F}}}(q-q_{\mathrm{rest}})\rangle , \end{aligned}$$

(62)

with $c_{{\mathcal {F}}}=5$ and $K_{{\mathcal {F}}}=\text {diag}(0.0002, 0.0002, 0.0002,$1, 1, 0.0002, 0.2, 0.2), respectively. The components of the nominal dynamic equations are equal to: platform mass $m_{\mathrm{p}}=19.803$; wheel mass $m_\mathrm{w}=1.4$; masses of the holonomic manipulator links equal $m_1=1.39$, $m_2=1.318$ and $m_3=2.496$, respectively. The remaining dynamic parameters of the robot are taken from KUKA youBot documentation [55]. In order to obtain more realistic conditions of computations, the following friction term is adopted: $D=0.002\text {sgn}(z)+0.2 z$. Consequently, $\alpha _0=0.202$. On account of the fact that ${\dot{D}}$ is not locally bounded Lebesgue measurable function, we assume $\alpha _1=0$ in controller (5)–(7), (46)–(48). Nevertheless, disturbing term D is added to dynamic equations of mobile manipulator. Moreover, measured quantities $\phi$, y and $e^e$ obtained from encoders have been additionally contaminated by a measurement noise $\zeta _i(t)$ with relatively large normalised magnitude of a Brownian motion of the form $\mathrm{d}\zeta _i(t)=10^{-5}\sqrt{t} X(t)\mathrm{d}t$; $X(t)\sim N(0,\ 1)$, $i=1,\ldots ,8$. Initial reduced velocity, control, and configuration equal $z(0)=(0,\ 0,\ 0,\ 0,\ 0)^{\mathrm{T}}$, $v(0)=(0,\ 0,\ 0,\ 0,\ 0)^{\mathrm{T}}$, $q(0)=(-0.4, 0, 0, 0, 0, 0, -\frac{\pi }{18}, \frac{\pi }{9})^{\mathrm{T}}$, respectively. Moreover, $q_{\mathrm{rest}}=q(0)$. Actuation matrix B takes the following form:

$$\begin{aligned} B=\left[ \begin{array}{ccccc} \frac{2}{R} &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} \frac{2}{R} &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1\end{array} \right] . \end{aligned}$$

(63)

In order to simplify the computations, rough conservative estimates of a, $w_3^k$, $w_4^k$, A and $w_i$, $i=1,\ldots ,7$ have been assumed for controller (5)–(7), (46)–(48). They were chosen as follows $a=A=0.2$; $w_1=1.5$; $w_2=0.001$; $w_3^k=2$; $w_4^k=3$; $w_3=24$; $w_4=36$; $w_5=24$; $w_6=48$; $w_7=1100$. To observe the effect of acting both the discontinuous disturbing signal D and measurement noise on the performance of the controllers, possibly small numeric value of $C^d$ has been chosen in the computations. Therefore, the values of gain coefficients for both controllers are assumed to be equal to: $c=2$, $C^d=20$, $c_0=C_0=1$, $\lambda _0=1$; $\lambda _1=11$; $\lambda _2=6$; $\varLambda _0=11$; $\varLambda _1=6$. In order to accelerate the convergence process of differentiators (46)–(47), we have chosen good initial guesses $z_1(0)$, $z_2(0)$, $\eta _0(0)$, $\eta _1(0)$, $\eta _2(0)$, based on the nominal values of our dynamic model. Consequently, differentiators (46)–(47) were run with the following initial values: $z_1(0)=z(0)=0$, $z_2(0)=(-0.08,\ -0.08,\ 0,\ 70,\ -70)^{\mathrm{T}}$, $\eta _0(0)=(-2.75,\ -3.,\ -0.14,\ 0.,\ 0)^{\mathrm{T}}$, $\eta _1(0)=(0,\ -1,\ 0,\ 0,\ 0)^{\mathrm{T}}$, $\eta _2(0)=(2.75,\ 0,\ -10,\ 0,\ 70)^{\mathrm{T}}$ and parameters ${\hat{\lambda }}^e_0=55$; ${\hat{\lambda }}^e_1=20.4$; ${\hat{\lambda }}^e_2=7.6$; ${\hat{\lambda }}^z_0=\text {diag}(22,\ 22,\ 2200,\ 2200,\ 2200)$; ${\hat{\lambda }}^z_1=\text {diag}(11,\ 11,\ 237,\ 237,\ 237)$; ${\hat{\lambda }}^z_2=\text {diag}(5.6,\ 5.6,\ 26,$$\ 26,\ 26)$, respectively. Due to conservative nature of estimates $L_z$ and $L_e$ in (46)–(47), they are assumed to be equal in this ‘real case’, i.e. $L_e(t)=L_z(t)$.

The results for this ‘real case’ are given in Figs. 33, 34, 35, 36, 37, 38 and 39, which indicate a good tracking performance of kinematically optimal controller (5)–(7), (46)–(48) (see Figs. 33 and 34). As was expected, both disturbing signal D and measurement noises $\zeta _i$ with greater magnitude generate greater task error norms for greater time moments. Let us observe (Figs. 33 and 34) that for $t \ge 4$ mobile manipulator accomplishes (locally) optimal movement. The corresponding torques $v_{c}$ are depicted in Figs. 35, 36, 37, 38 and 39. Rapid variations in $v_{c}$ in time interval $[0.5,\ 7]$ (see Figs. 37, 38 and 39) are result of both friction term D and measurement noises $\zeta _i$. Nevertheless, torques $v_{c}$ are still absolutely continuous functions of time.

Although finite-time controllers (5)–(7), (46)–(48) provide, at least theoretically, zero tracking errors and generated trajectories are also (locally) optimal, the practical implementation of control laws (5)–(7), (46)–(48) to an actual system does not seem to be a trivial task. The reason is that the right-hand sides of Eqs. (22) and (39) are locally bounded Lebesgue measurable functions. Numerical integration of such class of mappings by using standard Runge–Kutta solvers of the 45 order requires a small value of integration step (whom a high sampling frequency corresponds) to obtain finite-time stability of the control law (5)–(7), (46)–(48). In practice, the integration step should take the values in interval $[10^{-5},\ 10^{-4}]$ what forces fast computations in real time. Otherwise, greater values of integration step may lead to unstable work of controller (5)–(7), (46)–(48). Our computations carried out with integration step equal to $10^{-3}$ have led to unstable work of controllers (5)–(7), (46)–(48). Moreover, on account of finite integration step corresponding to a finite sampling frequency in computations by solving differential equations (22), (39), task errors e, ${\dot{e}}$ and $\ddot{e}$ do not equal (theoretically) zero for $t \ge T$ but take very small values (of the order of $10^{-4}$).

Fig. 33

Euclidean norm of task errors $e^e$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 34

Euclidean norm of task errors $e^a$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 35

Torque $v_{c,1}$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 36

Torque $v_{c,2}$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 37

Torque $v_{c,3}$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 38

Torque $v_{c,4}$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

Fig. 39

Torque $v_{c,5}$ for kinematically optimal controller (5)–(7), (46)–(48) of youBot robot with both disturbance signal and measurement noise

5 Conclusions

The new kinematically optimal class of the cascaded controllers, intended for the end effector trajectory tracking in the task space, has been presented. The main advantage of the proposed control algorithms is the elimination of the inverse or a pseudo-inverse of the mobile manipulator Jacobian matrix from the trajectory tracking problem. Instead, a simple class of the transpose Jacobian controllers has been proposed. Moreover, the offered control scheme generates at least absolutely continuous steering signals. Applying the Lyapunov stability theory, it was shown in the work that the proposed control strategies are finite time stable provided that some practically reasonable assumption regarding the rank of the extended Jacobian matrix is fulfilled. Numerical examples have also shown that kinematically optimal cascaded controller generates smaller steering signals (in the $L_2$ norm) as compared to the control scheme (25), (46)–(48). The proposed approach to the trajectory tracking control problem may be directly applicable to many cooperating mobile manipulators operating in a six-dimensional task space.