Skip to main content
SpringerLink
Log in

Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

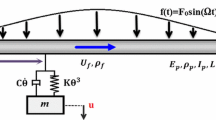
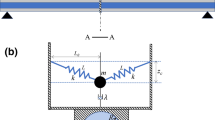
Different from the both-end supported pipe conveying fluid as a conservative system, the cantilevered fluid-transporting pipe is a non-conservative system and its dynamic behavior is more complex with flutter instabilities when the flow velocity is beyond the critical value. Indeed, controlling such a flutter system is always challenging in engineering applications. This study presents nonlinear vibrations of cantilevered pipe conveying fluid passively controlled via a nonlinear energy sink (NES). Based on the Hamilton principle, the nonlinear dynamic equations coupling with the NES are derived and discretized using high-order Galerkin method. It is indicated that increasing the mass and damping of NES results in an increase in critical flow velocity. Importantly, the optimal placed position of NES where the critical flow velocity is highest has a strong relationship with the pipe’s flutter mode. In the following, the nonlinear analysis shows the dynamic controlling effect on vibration amplitude of the pipe can be classified to three suppression regions with increasing the flow velocity. Varying the mass, damping and stiffness of NES is followed by variations of the suppression regions which are associated with controlling effects and dynamic behaviors of the pipe system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Paidoussis, M.P.: Fluid–Structure Interactions: Slender Structures and Axial Flow. Academic Press, London (1998)

    Google Scholar 

  2. Paidoussis, M.P., Issid, N.T.: Dynamic stability of pipes conveying fluid. J. Sound Vib. 33, 267–294 (1974)

    Article  Google Scholar 

  3. Semler, C., Li, G.X., Paidoussis, M.P.: The non-linear equations of motion of pipes conveying fluid. J. Sound Vib. 169, 577–599 (1994)

    Article  MATH  Google Scholar 

  4. Benjamin, T.B.: Dynamics of a system of articulated pipes conveying fluid. I. Theory. Proc. R. Soc. Lond. A 261, 57–86 (1961)

    MathSciNet  Google Scholar 

  5. Gregory, R.W., Paidoussis, M.P.: Unstable oscillation of tubular cantilevers conveying fluid. I. Theory. Proc. R. Soc. Lond. A 293, 12–27 (1966)

    Google Scholar 

  6. Sinha, J.K., Singh, S., Rao, A.R.: Finite element simulation of dynamic behaviour of an open-ended cantilever pipe conveying fluid. J. Sound Vib. 240, 189–194 (2001)

    Article  Google Scholar 

  7. Ryu, S.U., Sugiyama, Y., Ryu, B.J.: Eigenvalue branches and modes for flutter of cantilevered pipes conveying fluid. Comput. Struct. 80, 1231–1241 (2002)

    Article  Google Scholar 

  8. Olsonl, G., Jamison, D.: Application of a general purpose finite element method to elastic pipes conveying fluid. J. Fluids Struct. 11, 207–222 (1997)

    Article  Google Scholar 

  9. Païdoussis, M.P.: The canonical problem of the fluid-conveying pipe and radiation of the knowledge gained to other dynamics problems across applied mechanics. J. Sound Vib. 310, 462–492 (2008)

    Article  Google Scholar 

  10. Païdoussis, M.P., Li, G.X.: Pipes conveying fluid: a model dynamical problem. J. Fluids Struct. 7, 137–204 (1993)

    Article  Google Scholar 

  11. Seiranyan, A.P.: Collision of eigenvalues in linear oscillatory systems. J. Appl. Math. Mech. 58, 805–813 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  12. Zhou, X., Dai, H.L., Wang, L.: Dynamics of axially functionally graded cantilevered pipes conveying fluid. Compos. Struct. 190, 112–118 (2018)

    Article  Google Scholar 

  13. He, F., Dai, H.L., Huang, Z., Wang, L.: Nonlinear dynamics of a fluid-conveying pipe under the combined action of cross-flow and top-end excitations. Appl. Ocean Res. 62, 199–209 (2017)

    Article  Google Scholar 

  14. Paidoussis, M.P., Semler, C., Wadham-Gagnon, M., Saaid, S.: Dynamics of cantilevered pipes conveying fluid—part 2: dynamics of the system with intermediate spring support. J. Fluids Struct. 23, 569–587 (2007)

    Article  Google Scholar 

  15. Jin, J.D.: Stability and chaotic motion of a restrained pipe conveying fluid. J. Sound Vib. 208, 427–439 (1997)

    Article  Google Scholar 

  16. Demir, M.H., Yesildirek, A., Yigit, F.: Control of a cantilever pipe conveying fluid using neural network. In: The 6th International Conference on Modeling, Simulation, and Applied Optimization (ICMSAO) (2015)

  17. Yau, C.H., Bajaj, A.K., Nwokah, O.D.I.: Active control of chaotic vibration in a constrained flexible pipe conveying fluid. J. Fluids Struct. 9, 99–122 (1995)

    Article  Google Scholar 

  18. Doki, H., Hiramoto, K., Skelton, R.E.: Active control of cantilevered pipes conveying fluid with constraints on input energy. J. Fluids Struct. 12, 615–628 (1998)

    Article  Google Scholar 

  19. Tsai, Y.K., Lin, Y.H.: Adaptive modal vibration control of a fluid-conveying cantilever pipe. J. Fluids Struct. 11, 535–547 (1997)

    Article  Google Scholar 

  20. Dai, H.L., Wang, L., Ni, Q.: Dynamics of a fluid-conveying pipe composed of two different materials. Int. J. Eng. Sci. 73, 67–76 (2013)

    Article  MATH  Google Scholar 

  21. Wang, L., Dai, H.L.: Vibration and enhanced stability properties of fluid-conveying pipes with two symmetric elbows fitted at downstream end. Arch. Appl. Mech. 82, 155–161 (2012)

    Article  MATH  Google Scholar 

  22. Firouz-Abadia, R.D., Askariana, A.R., Kheiri, M.: Bending-torsional flutter of a cantilevered pipe conveying fluid with an inclined terminal nozzle. J. Sound Vib. 332, 3002–3014 (2013)

    Article  Google Scholar 

  23. Yu, D., Wen, J., Zhao, H., Liu, Y., Wen, X.: Vibration reduction by using the idea of phononic crystals in a pipe-conveying fluid. J. Sound Vib. 318, 193–205 (2008)

    Article  Google Scholar 

  24. Rechenberger, S., Mair, D.: Vibration control of piping systems and structures using tuned mass dampers. In: Proceedings of the ASME Pressure Vessels and Piping Conference, Waikoloa, Hawaii, USA (2017)

  25. Yu, D.L., Païdoussis, M.P., Shen, H.J., Wang, L.: Dynamic stability of periodic pipes conveying fluid. J. Appl. Mech. 81(1), 011008 (2013)

    Article  Google Scholar 

  26. Vakakis, A.F.: Inducing passive nonlinear energy sinks in vibrating systems. J. Vib. Acoust. 123, 324–332 (2001)

    Article  Google Scholar 

  27. Gendelman, O.V.: Transition of energy to a nonlinear localized mode in a highly asymmetric system of two oscillators. Nonlinear Dyn. 25, 237–253 (2001)

    Article  MATH  Google Scholar 

  28. Lee, Y.S., Vakakis, A.F., Bergman, L.A., Mcfarland, D.M., Kerschen, G., Nucera, F., Tsakirtzis, S., Panagopoulos, P.N.: Passive non-linear targeted energy transfer and its applications to vibration absorption: a review. Proc. Inst. Mech. Eng. K J. Multi Body Dyn. 222, 322–329 (2008)

    Google Scholar 

  29. Vakakis, A.F., Manevitch, L.I., Gendelman, O., Bergman, L.: Dynamics of linear discrete systems connected to local, essentially non-linear attachments. J. Sound Vib. 264, 559–577 (2003)

    Article  Google Scholar 

  30. Starosvetsky, Y., Gendelman, O.V.: Response regimes of linear oscillator coupled to nonlinear energy sink with harmonic forcing and frequency detuning. J. Sound Vib. 315, 746–765 (2008)

    Article  Google Scholar 

  31. Yan, Z., Ragab, S.A., Hajj, M.R.: Passive control of transonic flutter with a nonlinear energy sink. Nonlinear Dyn. 91, 577–590 (2018)

    Article  Google Scholar 

  32. Pacheco, D.R.Q., Marques F.D., Ferreira, A.J.M.: Panel flutter suppression with nonlinear energy sinks: numerical modeling and analysis. Int. J. Nonlinear Mech. (2018). https://doi.org/10.1016/j.ijnonlinmec.2018.08.009

  33. Zhang, Y.W., Hou, S., Xu, K.F., Yang, T.Z., Chen, L.Q.: Forced vibration control of an axially moving beam with an attached nonlinear energy sink. Acta Mech. Solida Sin. 30, 674–682 (2017)

    Article  Google Scholar 

  34. Zhang, Y.W., Yuan, B., Fang, B., Chen, L.Q.: Reducing thermal shock-induced vibration of an axially moving beam via a nonlinear energy sink. Nonlinear Dyn. 87, 1159–1167 (2017)

    Article  Google Scholar 

  35. Dai, H.L., Abdelkefi, A., Wang, L.: Vortex-induced vibrations mitigation through a nonlinear energy sink. Commun. Nonlinear Sci. 42, 22–36 (2017)

    Article  Google Scholar 

  36. Georgiades, F., Vakakis, A.F.: Dynamics of a linear beam with an attached local nonlinear energy sink. Commun. Nonlinear Sci. 12, 643–651 (2007)

    Article  MATH  Google Scholar 

  37. Yang, T.Z., Yang, X.D., Li, Y., Fang, B.: Passive and adaptive vibration suppression of pipes conveying fluid with variable velocity. J. Vib. Control 20, 1293–1300 (2013)

    Article  MathSciNet  Google Scholar 

  38. Mamaghani, A.E., Khadem, S.E., Bab, S.: Vibration control of a pipe conveying fluid under external periodic excitation using a nonlinear energy sink. Nonlinear Dyn. 86, 1761–1795 (2016)

    Article  MATH  Google Scholar 

  39. Darabi, A., Michael, J.L.: Clearance-type nonlinear energy sinks for enhancing performance in electroacoustic wave energy harvesting. Nonlinear Dyn. 87(4), 2127–2146 (2017)

    Article  Google Scholar 

  40. Kong, X., Li, H., Chen, W.: Dynamics of 1-dof and 2-dof energy sink with geometrically nonlinear damping: application to vibration suppression. Nonlinear Dyn. 91(1), 733–754 (2018)

    Article  Google Scholar 

  41. Chen, J.E., He, W., Zhang, W., Yao, M., Liu, J., Sun, M.: Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks. Nonlinear Dyn. 91(2), 885–904 (2018)

    Article  Google Scholar 

  42. Snowdon, J.C.: Vibration and Shock in Damped Mechanical Systems. Wiley, New York (1968)

    Google Scholar 

  43. Paidoussis, M.P., Semler, C.: Nonlinear dynamics of fluid-conveying cantilevered pipe with an intermediate spring support. J. Fluids Struct. 7, 295–298 (1993)

    Google Scholar 

  44. García-Vallejo, D., Mayo, J., Escalona, J.L.: Efficient evaluation of the elastic forces and the Jacobian in the absolute nodal coordinate formulation. Nonlinear Dyn. 35, 313–329 (2004)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

The authors acknowledge the support provided by Science and Technology on Reactor System Design Technology Laboratory, Fundamental Research Funds for the Central Universities, HUST (2017KFYXJJ135), Natural Science Foundation of Hubei Province (2017CFB429) and National Natural Science Foundation of China (Nos. 11602090, 11672115 and 11872060).

Author information

Authors and Affiliations

  1. Department of Mechanics, Huazhong University of Science and Technology, Wuhan, 430074, China

    K. Zhou, H. L. Dai, H. Yan, L. Wang & Q. Ni

  2. Hubei Key Laboratory for Engineering Structural Analysis and Safety Assessment, Wuhan, 430074, China

    K. Zhou, H. L. Dai, H. Yan, L. Wang & Q. Ni

  3. Science and Technology on Reactor System Design Technology Laboratory, Nuclear Power Institute of China, Chengdu, 610213, China

    F. R. Xiong & N. B. Jiang

Authors
  1. K. Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. F. R. Xiong
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. N. B. Jiang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. H. L. Dai
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. H. Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. L. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Q. Ni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. L. Dai.

Ethics declarations

Conflict of interest

They have no conflict of interest.

Ethical standard

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki Declaration and its later amendments or comparable ethical standards.

Human and animal rights

This article does not contain any studies with animals performed by any of the authors.

Informed consent

Informed consent was obtained from all individual participants included in the study.

Appendix

Appendix

In this part, we offer the elements of matrices written in Sect. 3 in detail and also introduce a kind of algebraic relationship to simplify the derived nonlinear damping and stiffness matrices. Firstly, through some further manipulations, the mass, linear damping, nonlinear damping, linear stiffness and nonlinear stiffness matrices can be written as follows:

$$\begin{aligned} M= & {} \int _0^1 {\varvec{\varphi }}^\mathrm{T}{{\varvec{\varphi }}\mathrm{d}\xi } ,\nonumber \\ C_L= & {} \alpha \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{{{{\varvec{\varphi }}}}''''}}}\mathrm{d}\xi } \nonumber \\&+\, 2u\sqrt{\beta }\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi }} }'}\mathrm{d}\xi } \nonumber \\ K_L= & {} \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{{{{\varvec{\varphi }} }''''}}}}\mathrm{d}\xi }\nonumber \\&+\, {u}^{2}\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{{\varvec{\varphi }} }''}}\mathrm{d}\xi } \nonumber \\ C_N= & {} \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi }} }'{\varvec{q}}{\dot{{\varvec{q}}}}}^\mathrm{T}\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\&-\, 2u\sqrt{\beta }\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'{\varvec{qq}}}^\mathrm{T}\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\&-\, \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{q}}{\dot{{\varvec{q}}}}}^\mathrm{T}\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \mathrm{d}\xi } \right) \mathrm{d}\xi } \nonumber \\&+\, 2u\sqrt{\beta }\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) \mathrm{d}\xi } \nonumber \\&-\, 2u\sqrt{\beta }\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}\left( {\int _\xi ^1 {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\ K_N= & {} 2u\sqrt{\beta }\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'{\dot{{\varvec{q}}}}{\varvec{q}}}^\mathrm{T}{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi }\nonumber \\&+\,{u}^{2}\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } \nonumber \\&+\,3\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'{\varvec{qq}}}^\mathrm{T}{{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{\varvec{\varphi }} }'''}}}\mathrm{d}\xi } \nonumber \\&+\,\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}{{{\varvec{\varphi } }''}}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } \nonumber \\&-\, u^{2}\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'{\varvec{qq}}}^\mathrm{T}\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{{{\varvec{\varphi }} }'''}}}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\&+\, \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'{\varvec{qq}}}^\mathrm{T}\left( {\int _0^\xi {{{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{{\varvec{\varphi '}}}}'''}}}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\&+\,\, u^{2}\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{ {{{{\varvec{\varphi }} }'''}}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) \mathrm{d}\xi } \nonumber \\&-\, \int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}\left( {\int _\xi ^1 {\int _0^\xi {{{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{{\varvec{\varphi }} }''''}}}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) \mathrm{d}\xi } \nonumber \\&-\,u^{2}\int _0^1 {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}{\varvec{qq}}}^\mathrm{T}\left( {\int _\xi ^1 {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \right) \mathrm{d}\xi } \nonumber \\&-\, \int _0^1 {\varvec{\varphi }}^\mathrm{T}{{{{\varvec{\varphi }} }''}{\varvec{qq}}}^\mathrm{T}\left( \int _\xi ^1 {{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{\varvec{\varphi } }'''}}}\mathrm{d}\xi } \right) \mathrm{d}\xi \end{aligned}$$
(A.1)

It is noted that the nonlinear damping and stiffness matrices are as a function of \({{\varvec{q}}}\) and \({{\dot{{\varvec{q}}}}}\), which will bring a large number of integrals in each step and hence a high calculation consumption. Thus, in this work, we introduce the following algebraic relationship to solve this calculation problem [44]:

$$\begin{aligned} \left( {{{\varvec{Aqp}}}^{{{\varvec{T}}}}{{\varvec{B}}}} \right) _{ij}= & {} \sum _k \sum _l A_{ik} q_k p_l B_{lj} \nonumber \\= & {} \sum _k {\sum _l {q_k \left( {{\varvec{A}}} \right) _{ik} \left( {{\varvec{B}}} \right) _{lj} p_l } } \nonumber \\= & {} {{\varvec{q}}}^\mathrm{T}{{\varvec{C}}}^{ij}{{\varvec{p}}} \end{aligned}$$
(A.2)

where matrix \({{\varvec{C}}}^{ij}\) is built as follows:

$$\begin{aligned} {{\varvec{C}}}^{ij}={{\varvec{A}}}_i ^\mathrm{T}\left( {{{\varvec{B}}}^\mathrm{T}} \right) _j \end{aligned}$$
(A.3)

in which \({{\varvec{A}}}\) and \({{\varvec{B}}}\) are two arbitrary square matrices, \({{\varvec{q}}}\) and \({{\varvec{p}}}\) are two arbitrary array. Equations. (A.2) and (A.3) indicate that the products of form \({{\varvec{Aqp}}}^{{{\varvec{T}}}}{{\varvec{B}}}\) are matrices whose components can be written in the form of \({{\varvec{q}}}^\mathrm{T}{{\varvec{C}}}^{ij}{{\varvec{p}}}\). \({{\varvec{C}}}^{ij}\) is a matrix as the product of the transposition of row i of matrix \({{\varvec{A}}}\) and row j of matrix \({{\varvec{B}}}^\mathrm{T}\).

Using Eqs. (A.2) and (A.3), we can get the components of nonlinear damping and stiffness matrices in Eq. (A.1) as follows:

$$\begin{aligned}&\left( {{{\varvec{C}}}_{{\varvec{N}}} } \right) _{ij} ={{\varvec{q}}}^\mathrm{T}\left( {{{\varvec{C}}}_{{{\varvec{N1}}}} ^{ij}-{{\varvec{C}}}_{{{\varvec{N3}}}} ^{ij}} \right) {{\dot{{\varvec{q}}}}}\nonumber \\&\quad +\,{{\varvec{q}}}^\mathrm{T}\left[ {2u\sqrt{\beta }\left( {-{{\varvec{C}}}_{{{\varvec{N2}}}} ^{ij}+{{\varvec{C}}}_{{{\varvec{N4}}}} ^{ij}-{{\varvec{C}}}_{{{\varvec{N5}}}} ^{ij}} \right) } \right] {{\varvec{q}}} \nonumber \\&\left( {{{\varvec{K}}}_{{\varvec{N}}} } \right) _{ij} ={{\dot{{\varvec{q}}}}}^\mathrm{T}2u\sqrt{\beta }{{\varvec{K}}}_{{{\varvec{N1}}}} ^{ij}{{\varvec{q}}}\nonumber \\&\quad +\,{{\varvec{q}}}^\mathrm{T}\left( {{\begin{array}{l} {{u}^{2}{{\varvec{K}}}_{{{\varvec{N2}}}} ^{ij}+3{{\varvec{K}}}_{{{\varvec{N3}}}} ^{ij}+{{\varvec{K}}}_{{{\varvec{N4}}}} ^{ij}-{u}^{2}{{\varvec{K}}}_{{{\varvec{N5}}}} ^{ij}} \\ {+{{\varvec{K}}}_{{{\varvec{N6}}}} ^{ij}+{u}^{2}{{\varvec{K}}}_{{{\varvec{N7}}}} ^{ij}-{{\varvec{K}}}_{{{\varvec{N8}}}} ^{ij}-{u}^{2}{{\varvec{K}}}_{{{\varvec{N9}}}} ^{ij}-{{\varvec{K}}}_{{{\varvec{N1}}}0} ^{ij}} \\ \end{array} }} \right) {{\varvec{q}}}\nonumber \\ \end{aligned}$$
(A.4)

where

$$\begin{aligned} {{\varvec{C}}}_{{{\varvec{N1}}}} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{C}}}_{{{\varvec{N2}}}}^{ij}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } \nonumber \\ {{\varvec{C}}}_{{{\varvec{N3}}}} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \mathrm{d}\xi } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{C}}}_{{{\varvec{N4}}}} ^{ij}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } \nonumber \\ {{\varvec{C}}}_{{{\varvec{N5}}}} ^{ij}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } ,\nonumber \\ {{\varvec{K}}}_{{{\varvec{N1}}}} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}} \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi \nonumber \\ {{\varvec{K}}}_{{{\varvec{N2}}}} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {{\varvec{\varphi }'}^\mathrm{T}{\varvec{\varphi }'}} \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{K}}}_{{{\varvec{N3}}}} ^{{{\varvec{ij}}}}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {{{{\varvec{\varphi } }''}}^\mathrm{T}{ {{{{\varvec{\varphi }} }'''}}}} \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } \nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}4} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {{{{\varvec{\varphi } }''}}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}5} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{{{\varvec{\varphi }} }'''}}}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi \nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}6} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{\varvec{\varphi }'}} \right) _i ^\mathrm{T}\left( {\left( {\int _0^\xi {{{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{{\varvec{\varphi }} }''''}}}}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}7} ^{ij}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {\int _0^\xi {{\varvec{\varphi }'}^\mathrm{T}{{{{{{\varvec{\varphi }}} }'''}}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } \nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}8} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {\int _0^\xi {{{{\varvec{\varphi } }''}}^\mathrm{T}{{{{{{\varvec{\varphi }} }''''}}}}\mathrm{d}\xi } } \mathrm{d}\xi } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi ,\nonumber \\ {{\varvec{K}}}_{{{\varvec{N}}}9} ^{ij}= & {} \int _0^1 {\left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {{\varvec{\varphi }'}^\mathrm{T}{{{\varvec{\varphi } }''}}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi } \nonumber \\ {{\varvec{K}}}_{{{\varvec{N1}}}0} ^{ij}= & {} \int _0^1 \left( {{\varvec{\varphi }}^\mathrm{T}{{{\varvec{\varphi } }''}}} \right) _i ^\mathrm{T}\left( {\left( {\int _\xi ^1 {{{{\varvec{\varphi } }''}}^\mathrm{T}{ {{{{\varvec{\varphi }} }'''}}}\mathrm{d}\xi } } \right) ^{\mathrm {T}}} \right) _j \mathrm{d}\xi \end{aligned}$$
(A.5)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhou, K., Xiong, F.R., Jiang, N.B. et al. Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink. Nonlinear Dyn 95, 1435–1456 (2019). https://doi.org/10.1007/s11071-018-4637-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4637-8

Keywords

Search

Navigation