1 Introduction

Gyroscopes are present in a broad range of engineering systems such as air vehicles, automobiles, and satellites to track their orientation and control their path. Besides the directional gyroscopes, there are variety of gyroscopes (e.g., mechanical, optical and vibrating) that are being used to measure the angular velocity. The critical part of the conventional mechanical gyroscope is a wheel spinning at a high speed. Therefore, conventional gyroscopes although accurate are bulky and very expensive and they are applicable mainly in the navigation systems of large vehicles, such as ships, airplanes, space crafts, etc.

Micromechanical gyroscopes and angular rate sensors allow for signification miniaturization in contrary to solid-state gyroscopes, laser ring and fiber optic gyroscopes.

Progress in micromachining technology embraces the development of the miniaturized gyroscopes with improved performance and low power consumption that allow the integration with electronic circuits. Their manufacturing cost is also significantly lower [1, 2]. Such type of gyroscopes belongs to broad class of microelectromechanical systems (MEMS). Practically, any device fabricated using photo-lithography-based techniques with micrometer scale features that utilizes both electrical and mechanical functions could be considered as MEMS.

The operating principle of vibrating gyroscopes is based on the transfer of the mechanical energy among two vibrations modes via the Coriolis effect which occurs in the presence of a combination of rotational motions about two orthogonal axes. The drive mode is mainly generated employing the electrostatic actuation mechanism.

However, it is widely recognized that miniaturization achieved via fabrication technologies requires detailed studies from a point of view of nonlinear dynamical systems in order to understand and control of sometimes unexpected behavior of microcomponents, micromachines and MEMS/NEMS, and in particular of micromechanical gyroscopes. Reliable modeling of the micromechanical vibratory gyroscopes allows for improvement in sensitive elements and circuit design, and hence, it has an important impact on achieving high performances of the mentioned micromechanical systems. In other words the micro- and nanotechnologies require support of theoretical approaches based on theory of vibrations and nonlinear phenomena. In what follows, we briefly describe state of the art of the recent achievement in modeling and analysis on some chosen MEMS/NEMS and micro-/nanogyroscopes.

Tuner et al. [3] pointed out importance of parametric resonances in a micromechanical system. Lifshitz and Cross [4] investigated a response of the microring gyroscope under combined external forcing and parametric excitation to achieve required parametric amplification.

Gallacher et al. [5] proposed a control scheme for a MEMS electrostatic resonant gyroscope subjected to both harmonic forcing and parametric excitation.

Nayfeh and Younis [6] investigated dynamics of MEMS resonators under superharmonic/subharmonic excitations.

Kacem et al. [7] improved the performance of NEMS sensors based on employment of theoretical approaches of modeling nonlinear dynamics of nanomechanical beam resonators.

Lestev and Tikhonov [8] analyzed nonlinear dynamical behavior of micromechanical gyroscopes using the method of averaging. They pointed out that even though the parameters of the microstructural components are chosen in a way to provide a linear response, it cannot be achieved due to the fabrication errors. They investigated stable steady-state modes of vibratory micromechanical gyroscopes, and they presented the corresponding resonance curves.

Nonlinear dynamics and chaos of electrostatically actuated MEMS resonators under two-frequency external and parametric excitations were analyzed by Zhang et al. [9]. In particular, they illustrated effects of nonlinear square damping on the frequency response. Resonance frequencies and nonlinear dynamic characteristics were also reported. However, their investigation concerned relatively simple model consisting of a mass–spring–damper system.

Martynenko et al. [10] studied nonlinear phenomena of a vibrating micromechanical gyroscope with a ring resonator flexibly supported. The Krylov–Bogolubov averaging method was employed to predict fabrication errors, unstable branches of resonance curves, and quenching phenomenon.

Sang Won Yoon et al. [11] modeled vibratory ring gyroscopes by four vibration models (two flexural and two translation). The developed model consisted of the ring structure, the support-string structure, and the electrodes. It was shown that the developed model becomes vibration sensitive in the presence of both non-proportional damping and the sense electrodes capacitive nonlinearity.

Matheny et al. [12] studied nonlinear mode-coupling in nanomechanical systems. They demonstrated measurement protocol and design rules for getting accurate in situ characterization of nonlinear properties of NEMS resonators. In particular, the employment of the Euler–Bernoulli beam model was validated through the carried out laboratory measurements.

Ovchinnikova et al. [13] developed a model of micromechanical gyroscope using inertia properties of standing elastic waves providing maximum vibration amplitude with minimum control. The employed schemes of stabilization of the excited amplitude reduced nonlinear transformation characteristics. The method allowed for computation of the envelope of the fundamental mode of vibration of the governing two second-order ODEs yielded by the Bubnov–Galerkin approach.

Yoon et al. [14] studied a micromechanical vibrating ring gyroscope under high shocks based on mathematical analysis supported by the finite element method. They suggested employment of the developed vibrating ring gyroscope in navigation systems when both performance and high shock resistance are crucial in getting proper measurements.

Lestev [15] investigated combination resonances of sensitive elements of micromechanical gyros under translational and angular motions of the platform. The governing nonlinear ODEs were derived and the obtained results were validated experimentally.

Nitzan et al. [16] considered parametric amplification of a micromechanical resonating disk gyroscope taking into account of self-induced parametric excitation and Coriolis forces. The parametric self-induced amplification was yielded by nonlinear stiffness coupling between degenerate orthogonal vibration modes in a high-quality-factor micromechanical resonator.

Defoort et al. [17] analyzed occurrence of synchronization between two degenerate resonance modes of a microdisk resonator gyroscope. The carried out consideration were based on two second-order ODEs including a geometric nonlinearity of a cubic type. They demonstrated how mutual synchronization between modes was robust over temperature variation.

An impact of a cubic nonlinearity on the operation of a rate-integrating gyroscope was studied by Nitzan et al. [18]. It was shown how below the bifurcation threshold of cubic nonlinearity a splitting of angle-depending frequency between two resonant gyroscope modes occurred which impacted angle-dependent bias, quadrature error and controller efficacy. The method of compensating for angle-dependent frequency error was proposed and was experimentally validated.

A useful overview of gyroscopic technology including mechanical and optical at macro- and microscale was given by Passaro et al. [19].

In the present work, we conduct an analysis of dynamics of a MEMS gyroscope. This microdevice is a torsional resonator. Resonance is the desirable state of work of this sensor, so the elastic properties should be appropriately matched. Designing the resonator, only linear elasticity is taken into account. There arises the question what is the significance of the nonlinear properties of resilient resonator elements. Therefore, we propose the mathematical model describing motion of the MEMS gyroscope taking into account the nonlinear effects generated by the elastic properties of the suspension elements [20]. The main objective of the paper is to obtain and to examine the resonant responses of the considered system.

The paper is organized in the following way. Section 2 deals with a description of the further studied micromechanical gyroscope. Equations of motion are derived in Sect. 3. Section 4 reports the analytically obtained approximate solutions to the governing two second-order nonlinear ODEs in the case of non-resonant vibrations. Resonant vibrations are studied analytically and numerically in Sect. 5. Section 6 is devoted to investigation of steady-state gyroscope responses. Concluding remarks are given in Sect. 7.

Fig. 1
figure 1

Micromechanical gyroscope suspended on a set of two pivoted and mutually orthogonal pivot axes; 1—anchor, 2—gimbal, 3—sensing plate

Full size image
Fig. 2
figure 2

The angles of rotation \(\varPhi \) and \(\varTheta \): a the rotation of \(F_{1}\) by \(\varPhi \) about \({x}_{0}\)-axis; b the superposition of two rotations: \(F_{1}\) by \(\varPhi \) about \({x}_{0}\)-axis and \(F_{2}\) by \(\varTheta \) around \(y_{1}\)

Full size image

2 Description of micromechanical gyroscope

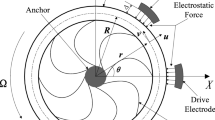
Dynamics of the torsional micromechanical gyroscope used to measure one component of the angular velocity is the subject of the paper. The Cardan suspension idea is applied to connect the sensing plate with the substrate whose angular velocity is measured. A diagram of the MEMS gyroscope is presented in Fig. 1. The sensing element “3” connects to the intermediate gyroscope part, i.e., the gimbal “2” via two torsional joints having a common axis called the sense axis. Two torsional joints link the gimbal with the anchors “1” mounted on the substrate which can be movable in the general case. These connectors are also aligned along a common straight line designating the drive axis. The gimbal is loaded by the external harmonically changing torque. The sense and drive axes around which the sensing plate and the gimbal can rotate independently are mutually orthogonal. In the system, there is the coupling effect. When the gyroscope is subjected to a rotation about z-axis caused by the substrate motion the sinusoidal Coriolis torque at the frequency of drive-mode oscillations is induced in the sense direction. The Coriolis torque excites the proof-mass to oscillate around the sense axis. This response, caused by the Coriolis effect and proportional to the angular velocity being measured, is registered by the detection electrodes. In order to attain the maximum response of the proof-mass, the desirable work regime of the micromechanical system is the resonance around both sense and drive axes. This state is achieved at the designing stage what especially involves the proper choice of the inertial properties of the MEMS parts and the elastic features of the torsional joints. It seems to be advisable to consider the influence of the nonlinear elastic properties of the torsional connectors on the micromechanical system operation. Including into consideration these nonlinearities can increase the working precision of the gyroscope.

Assuming the gimbal and the sensing plate are the rigid bodies, we model the torsional gyroscope as a two degrees-of-freedom (2-DOF) mass–spring–damper system with one sensing axis, so it is designed to measure one coordinate of the angular velocity of the substrate.

When describing the movement of MEMS parts, it is helpful to introduce three reference frames shown in Fig. 2. These frames have the common origin at the point O. Point O is also the center of mass of the whole gyroscope. In the frame \(F_{0}\) with the Cartesian coordinate system \({\textit{Ox}}_{0}y_{0}z_{0}\) the anchors and thus also the substrate whose angular velocity is measured are motionless. The frame \(F_{1}\) with the coordinate system \({\textit{Ox}}_{1}y_{1}z_{1}\) is fixed to the gimbal, whereas the frame Fin which it is assumed the coordinate system Oxyz is rigid connected with the sensing plate. At stable equilibrium position of the MEMS presented in Fig. 1, the axes of all these frames overlap with each other. Each of the introduced frames is non-inertial. The frame \(F_{1}\) which can oscillate about the drive axis \(x_{0}\) is presented in Fig. 2a in the position rotated by \(\varPhi \) counterclockwise. In Fig. 2b, the frame F oscillating around the sense axis \(y_{1}\) is depicted in the position being a result of the rotation by \(\varTheta \), also counterclockwise, and the rotation of the frame \(F_{1}\) associated to the gimbal. The anchors and the substrate can rotate about a fixed pivot axis. Let us assume that its absolute angular velocity \({\varvec{\Omega }}_{z}\) projected on the axes of the frame \(F_{0}\) is \({\varvec{\Omega }}_z =[0,0,\varOmega _z ]^{T}\), where \(\varOmega _z\) is to be measured.

The absolute gimbal angular velocity \({\varvec{\Omega }}_{1}\) is a superposition of the substrate rotation and own rotation about the drive axis. When projecting it onto the axes of the frame \(F_{1}\), we obtain

$$\begin{aligned} {\varvec{\Omega }}_1 =\left[ {\dot{\varPhi },\varOmega _z \sin \varPhi ,\varOmega _z \cos \varPhi } \right] ^{T}. \end{aligned}$$
(1)

The absolute angular velocity \({\varvec{\Omega }}\) of the sensing plate written in the reference frame F and being a result of the substrate motion, gimbal rotation and own rotation about y-axis is

$$\begin{aligned} {\varvec{\Omega }}= & {} \left[ -\varOmega _z \cos \varPhi \sin \varTheta +\cos \varTheta \dot{\varPhi },\varOmega _z \sin \varPhi \right. \nonumber \\&\left. +\, \dot{\varTheta },\varOmega _z \cos \varPhi \cos \varTheta +\dot{\varPhi }\sin \varTheta \right] ^{T}. \end{aligned}$$
(2)

3 Equations of motion

The considered micromechanical system has two degrees of freedom in its motion relative to the substrate. The rotation angles \(\varPhi (t)\) and \(\varTheta (t)\) are assumed to be the general coordinates. The point O that is the mass center both of the sensing plate and the gimbal is constantly at rest. Due to assumed symmetry, the axes of reference frames \(F_{1}\) and F are the principal axes of inertia of the gimbal and the sensing plate, respectively. Therefore, the inertia tensors of each of the gyroscope parts related to their own principal axes have the diagonal form independently of the current system configuration. Let \(I_x, I_y\) and \(I_z\) denote moments of inertia of the gimbal about its principal inertia axes, whereas \(J_x , \;J_y ,\;J_z \) stand for the principal moments of inertia of the senor plate with respect to the axes x, y and z. So, we can write the inertia tensors of both gyroscope parts as

$$\begin{aligned} \hat{\mathbf{I}}={{\hbox {diag}}}(I_x ,I_y ,I_z ), \quad \hat{\mathbf{J}}={{\hbox {diag}}}(J_x ,J_y ,J_z ). \end{aligned}$$
(3)

From the viewpoint of the absolute observer, the kinetic energy of the whole system is a sum of two bilinear forms

$$\begin{aligned} T=\frac{1}{2}\left( {{\varvec{\Omega }} }_1^T \cdot { \hat{\mathbf{I}}} \cdot {{\varvec{\Omega }}}_1 +{{\varvec{\Omega }}}^{\mathbf{T}} \cdot {\hat{\mathbf{J}}}\cdot {{\varvec{\Omega }}} \right) , \end{aligned}$$
(4)

where symbol \(\cdot \) denotes the inner product.

Substituting formulas (1)–(3) into Eq. (4), we get

$$\begin{aligned} T= & {} \frac{1}{2}I_x \dot{\varPhi }^{2}+\frac{\varOmega _z^2 }{2}\left( {I_z \cos ^{2}\varPhi +I_y \sin ^{2}\varPhi } \right) \nonumber \\&+\frac{J_y }{2}\left( {\varOmega _z \sin \varPhi +\dot{\varTheta }} \right) ^{2} \nonumber \\&+\frac{J_x }{2}\left( {\varOmega _z \cos \varPhi \;\sin \varTheta -\;\dot{\varPhi }\;\cos \varTheta } \right) ^{2}\nonumber \\&+\frac{J_z }{2}\left( {\varOmega _z \cos \varPhi \;\cos \varTheta +\;\dot{\varPhi }\;\sin \varTheta } \right) ^{2} \end{aligned}$$
(5)

There are assumed cubic nonlinear properties of soft type for all torsional joints. Taking into account that the mass center O of the whole micromechanical system remains constantly immovable, we can write the potential energy as follows

$$\begin{aligned} V=\frac{1}{2}k_{11} \varPhi ^{2}-\frac{1}{4}k_{12} \varPhi ^{4}+\frac{1}{2}k_{21} \varTheta ^{2}-\frac{1}{4}k_{22} \varTheta ^{4}, \end{aligned}$$
(6)

where \(k_{11}, k_{12}\) and \(k_{21}, k_{22}\) are elastic coefficients of the torsional joints, respectively, for the anchors-gimbal and gimbal-sensing plate connections.

Primary role in damping mechanism play the viscous effects of gas flow which occurs between the rotating surfaces and the immovable ones. As it was mentioned, the system is excited by the driving electrostatic torque \(M_0\hbox { sin}\left( {P t} \right) \) applied to the gimbal. The external loading and damping moments are introduced into motion equations as the generalized forces.

The equations of motion derived using the Lagrange equations of the second kind are as follows

$$\begin{aligned}&\frac{1}{2}\left( {2I_x +J_x +J_z +(J_x -J_z )\cos (2\varTheta )} \right) \ddot{\varPhi }\nonumber \\&\quad +\, C_1 \dot{\varPhi }+k_{11} \varPhi -k_{12} \varPhi ^{3} +\left( {J_z -J_x } \right) \sin (2\varTheta )\dot{\varPhi }\dot{\varTheta } \nonumber \\&\quad +\, \frac{\varOmega _z^2 }{4}\left( 2I_z -2I_y +J_x -2J_y +J_z\right. \nonumber \\&\quad \left. +(J_z -J_x )\cos (2\varTheta ) \right) \sin (2\varPhi ) \nonumber \\&\quad -\, \varOmega _z \dot{\varTheta }\left( J_y +(J_x -J_z )\right. \nonumber \\&\quad \left. \times \,\cos (2\varTheta ) \right) \cos \varPhi =M_0 \sin (P t), \end{aligned}$$
(7)
$$\begin{aligned}&J_y \ddot{\varTheta }+C_2 \dot{\varTheta }+k_{21} \varTheta -k_{22} \varTheta ^{3}\nonumber \\&\quad +\, \varOmega _z^2 \;(J_z -J_x )\cos \varTheta \;\sin \varTheta \cos ^{2}\varPhi \nonumber \\&\quad +\, \varOmega _z \dot{\varPhi }\left( {J_y +(J_x -J_z )\cos (2\varTheta )} \right) \cos \varPhi \nonumber \\&\quad -\, \left( {J_z -J_x } \right) \dot{\varPhi }^{2}\cos \varTheta \;\sin \varTheta =0, \end{aligned}$$
(8)

where \(C_{1}\) and \(C_{2}\) are the damping coefficients.

Expecting the elements of the system vibrate in very small ranges values of angles \(\varPhi \) and \(\varTheta \), so we carry out the linear approximation of trigonometric functions of these angles. It makes the equations of motion much simpler. It is convenient to transform the governing equations into non-dimensional form. For this purpose, we introduce the dimensionless time \(\tau =t \omega _1\) and the following dimensionless parameters:

$$\begin{aligned} p= & {} \frac{P}{\omega _1 }, \quad \omega _z =\frac{\varOmega _z }{\omega _1 }, \quad w=\frac{\omega _2 }{\omega _1 }, \quad c_1 =\frac{C_1 }{(I_x +J_x )\omega _1 },\nonumber \\ c_2= & {} \frac{C_2 }{J_y \omega _1 }, \quad \alpha _1 =\frac{k_{12} }{(I_x +J_x )\omega _1^2 }, \quad \alpha _2 =\frac{k_{22}}{J_y \omega _1^2 }, \nonumber \\ j_1= & {} \frac{I_z +J_z -I_y -J_y }{I_x +J_x }, \quad j_2 =\frac{J_z -J_x }{I_x +J_x },\nonumber \\ j_3= & {} \frac{J_y }{I_x +J_x }, \quad j_4 =\frac{J_z -J_x }{J_y }, \quad f_0 =\frac{M_0 }{(I_x +J_x )\omega _1^2 },\nonumber \\ \end{aligned}$$
(9)

where \(\omega _1 =\sqrt{\frac{k_{11} }{I_x +J_x }}\), \(\omega _2 =\sqrt{\frac{k_{21} }{J_y }}\).

The governing equations take the following dimensionless form

$$\begin{aligned}&\ddot{\varphi }+\left( {1+j_1 \omega _z^2 } \right) \varphi -\alpha _1 \varphi ^{3}+\left( {c_1 +2j_2 \vartheta \dot{\vartheta }} \right) \dot{\varphi }\nonumber \\&\quad +\, \left( {j_2 -j_3 } \right) \omega _z \dot{\vartheta }-f_0 \sin (p\tau )=0, \end{aligned}$$
(10)
$$\begin{aligned}&\ddot{\vartheta }+\left( {w^{2}+j_4 \omega _z^2 -j_4 \dot{\varphi }^{2}} \right) \vartheta -\alpha _2 \vartheta ^{3}\nonumber \\&\quad +\, c_2 \dot{\vartheta }+(1-j_4 )\omega _z \dot{\varphi }=0, \end{aligned}$$
(11)

where \(\varphi (\tau ), \;\vartheta (\tau )\) correspond to the dimensional general coordinates \(\varPhi (t)\) and \(\varTheta (t)\) and are functions of the non-dimensional time. Hereafter, the dots over symbols denote derivatives respecting to dimensionless time \(\tau \).

Equations (10)–(11) are supplemented with the proper initial conditions

$$\begin{aligned} \varphi (0)=\varphi _0 ,\dot{\varphi }(0)=\omega _0 ,\vartheta (0)=\vartheta _0 ,\quad \dot{\vartheta }(0)=\omega _{\vartheta 0}, \end{aligned}$$
(12)

where \(\varphi _0 ,\;\omega _{\varphi 0} ,\;\vartheta _0 ,\;\omega _{\vartheta 0}\) being known numbers describe the initial kinematic state of the gyroscope.

4 Approximate analytical solution for non-resonant case

The approximate analytical solution of the initial value problem (10)–(12) is obtained using multiple scales method (MSM) [21]. In accordance with MSM, the system evolution in time is described using several variables of time nature. These variables are related to each other by the so-called small parameter \(\varepsilon \). We introduce three time variables in the following manner: \(\tau _0 =\tau \) is the “fast” time, whereas \(\tau _1 =\varepsilon \tau \) and \(\tau _2 =\varepsilon ^{2}\tau \) play role of the “slow” times. Automatically, all functions dependent on time become the functions of the new time variables, and derivatives with respect to the original time \(\tau \) are replaced by the following partial differential operators

$$\begin{aligned} \frac{\hbox {d}}{\hbox {d}\tau }= & {} \frac{\partial }{\partial \tau _0 }+\varepsilon \frac{\partial }{\partial \tau _1 }+\varepsilon ^{2}\frac{\partial }{\partial \tau _2 }, \end{aligned}$$
(13)
$$\begin{aligned} \frac{\hbox {d}^{2}}{\hbox {d} \tau ^{2}}= & {} \frac{\partial ^{2}}{\partial \tau _0^2 }+2 \varepsilon \frac{\partial ^{2}}{\partial \tau _0 \partial \tau _1 }\nonumber \\&+\,\varepsilon ^{2}\left( {\frac{\partial ^{2}}{ \partial \tau _1^2 }+2\frac{\partial ^{2}}{\partial \tau _0 \partial \tau _2 }} \right) +O\left( {\varepsilon ^{4}} \right) . \end{aligned}$$
(14)

The solution of the initial value problem (10)–(12) is sought in the form of the power series of the small parameter \(\varepsilon \)

$$\begin{aligned} \varphi \left( {\tau ;\varepsilon } \right)= & {} \sum _{k=1}^{k=3} {\varepsilon ^{k}\phi _k \left( {\tau _0 ,\tau _1 ,\tau _2 } \right) +O(\varepsilon ^{4})} ,\nonumber \\ \vartheta \left( {\tau ;\varepsilon } \right)= & {} \sum _{k=1}^{k=3} {\varepsilon ^{k}\theta _k \left( {\tau _0 ,\tau _1 ,\tau _2 } \right) +O(\varepsilon ^{4})} . \end{aligned}$$
(15)

Moreover, several parameters describing the micromechanical system and its loading are assumed to be small, what using the small parameter \(\varepsilon \) can be written as follows

$$\begin{aligned} c_1 =\tilde{c}_1 \varepsilon ^{2},\quad c_2 =\tilde{c}_2 \varepsilon ^{2},\quad \omega _z =\tilde{\omega }_z \varepsilon \quad f_0 =\tilde{f}_0 \varepsilon ^{3}. \end{aligned}$$
(16)

When making assumptions (15), we take into account that the substrate angular velocity is much smaller than the frequencies of the movable gyroscope elements.

Relations (13)–(16) are then substituted into equations of motion (10)–(11). As a result, in the equations the small parameter \(\varepsilon \) appears in the different powers. It is required each of equations to be satisfied for any value of \(\varepsilon \). After arranging the components of both equations according to the powers of the small parameter, this requirement is realized by equating to zero all coefficients standing at the succeeding powers of \(\varepsilon \). Then, the obtained system of equations is solved recursively [22,23,24].

Fig. 3
figure 3

Time histories of the forced vibration in non-resonant conditions

Full size image

At every step of the solving process, the secular terms have to be removed. In this way, arise an initial value problem which is associated with the basic equations set. Solution of this problem, which often is named the modulation problem, present the slow evolution of vibration amplitudes and phases in time. The essential aspects regarding the recursive solving is presented in more detail in Sect. 5 where the resonant solution is sought.

The approximate solution of initial value problem (10)–(12) which is obtained using MSM has the following form

$$\begin{aligned} \varphi= & {} a_1 \cos (\tau +\psi _1 )-\frac{1}{32}\alpha _1 a_1^3 \cos (3\tau +3\psi _1 )\nonumber \\&+\,\frac{j_2 a_1 a_2^2 \cos (\tau -2w\tau +\psi _1 -2\psi _2 )}{8(w-1)} \nonumber \\&-\,\frac{j_2 a_1 a_2^2 \cos (\tau +2w\tau +\psi _1 +2\psi _2 )}{8(w+1)}\nonumber \\&+\, \frac{(j_3 -j_2 )w \omega _z a_2 \sin (w\tau +\psi _2 )}{w^{2}-1}+\frac{f_1 \sin (p\tau )}{1-p^{2}} , \end{aligned}$$
(17)
$$\begin{aligned} \vartheta= & {} a_2 \cos (\tau +\psi _2 )-\frac{j_4 a_1^2 a_2 \cos (2\tau -w\tau +2\psi _1 -\psi _2 )}{16(w-1)}\nonumber \\&+\, \frac{j_4 a_1^2 a_2 \cos (2\tau +w\tau +2\psi _1 +\psi _2 )}{16(w+1)}\nonumber \\&-\, \frac{\alpha _2 a_2^3 \cos (3w\tau +3\psi _2 )}{32w^{2}}-\frac{(j_4 -1)\omega _z a_1 \sin (\tau +\psi _1 )}{w^{2}-1}.\nonumber \\ \end{aligned}$$
(18)

The functions \(a_1 (\tau ), a_2 (\tau ), \psi _1 (\tau ), \psi _2 (\tau )\) are solutions of the modulation problem and have form

$$\begin{aligned} a_1= & {} a_{10} \;\exp \left( {-\frac{c_1 \tau }{2}} \right) , \end{aligned}$$
(19)
$$\begin{aligned} \psi _1= & {} \psi _{10} -\frac{3a_{10}^2 \left( {1-\exp \left( {-c_1 \tau } \right) } \right) \alpha _1 }{8c_1 }\nonumber \\&+\frac{1}{2}\left( {j_1 -\frac{(j_2 -j_3 )(j_4 -1)}{w^{2}-1}} \right) \tau \omega _z^2 , \end{aligned}$$
(20)
$$\begin{aligned} a_2= & {} a_{20} \;\exp \left( {-\frac{c_2 \tau }{2}} \right) \end{aligned}$$
(21)
$$\begin{aligned} \psi _2= & {} \psi _{20} -\frac{a_{10}^2 \left( {1-\exp \left( {-c_1 \tau } \right) } \right) j_4 }{4c_1 w}\nonumber \\&-\frac{3a_{20}^2 \left( {1-\exp \left( {-c_2 \tau } \right) } \right) \alpha _2 }{8c_2 w} \nonumber \\&+\frac{(j_3 -j_2 )w^{2}+j_4 ((1+j_2 -j_3 )w^{2}-1)}{2w(w^{2}-1)}\tau \omega _z^2\nonumber \\ \end{aligned}$$
(22)

where initial values of the amplitudes and the phases \(a_{10} , a_{20} , \psi _{10} , \psi _{20} \)are known and compatible with the initial values \(\varphi _0 ,\;\omega _{\varphi 0} ,\;\vartheta _0 ,\;\omega _{\vartheta 0} \) occurring in conditions (12).

It is worth to emphasize that the solution although approximated have however an analytical form. It describes the forced vibration of the mechanical gyroscope caused by the harmonic torque acting about the drive axis. Excluding the case when w = 0, the solution given by formulas (17)–(22) fails when p =1 or w = 1 because some denominators are then equal to zero. That are cases of main and internal resonances, respectively. These two cases determine the zone of the main and internal resonance, respectively. Therefore, solution (17)–(22) is useful to describe the gyroscope behavior in conditions being far from the resonance. The time histories of the generalized coordinates \(\varphi \) and \(\vartheta \) given by (17)–(18) together with (19)–(22) are presented in Fig. 3. The calculations were carried out for the following fixed values of parameters (several values of the parameters are taken from the paper [25])

$$\begin{aligned}&p = 0.021, \quad w = 0.8, \quad f_{0} = 0.0043662, \quad \alpha _{1} = 2,\\&\alpha _{2 }= 2, \quad {c}_{1} = 0.0000575531, \quad {c}_{2} = 0.0000575531, \\&\omega _{z} = 0.0000575531, j_{1} = 0, \quad j_{2} = 0, \quad j_{3} = 1, \quad j_{4} = 0,\\&a_{10}= 0.009, \quad a_{20}= 0.009, \quad \psi _{10}= 0, \quad \psi _{20}= 0. \end{aligned}$$

In Fig. 3 the beginning of the motion of both gyroscope parts is presented. We can observe slow modulation of the gimbal oscillations due to external loading. In fact, on each of these two graphs are depicted two curves representing the approximate solution of initial value problem (10)–(12). One of them present the solution obtained analytically according to (17)–(22), and the second the solution obtained numerically. The difference between these curves is unnoticeable.

The accuracy evaluation of the approximate solution is estimated using the measures

$$\begin{aligned} \delta _1= & {} \frac{1}{\tau _{\max } }\int \limits _0^{\tau _{\max } } \left| {G_1 (\varphi _a ,\vartheta _a )} \right| \hbox {d}\tau ,\nonumber \\ \delta _2= & {} \frac{1}{\tau _{\max } }\int \limits _0^{\tau _{\max } } {\left| {G_2 (\varphi _a ,\vartheta _a )} \right| \hbox {d}\tau } , \end{aligned}$$
(23)

where \(G_1 (\varphi _a ,\vartheta _a )\) and \(G_2 (\varphi _a ,\vartheta _a )\) stand for the differential operators, i.e., the left sides of motion equations (10)–(11), \(\varphi _a ,\vartheta _a\) are approximate solutions obtained using MMS or numerically, and \(\tau _{\max }\) is the total time. Proposed measures (23) evaluate the error of fulfillment of the governing equations of the simulation duration. The functions \(\varphi _a ,\vartheta _a\), irrespective of the way of their obtainment, satisfy the motion equations (10)–(11) only approximately.

For the approximate solution presented in Fig. 3 and obtained using MSM, the values of error are

$$\begin{aligned} \delta _{1} = 6.414247\cdot 10^{-7}, \quad \delta _{2} = 3.371118\cdot 10^{-9 }. \end{aligned}$$
(24)

The values of error of the fulfillment of the governing equations by the approximate solutions obtained numerically using NDSolve method implemented in Mathematica 11.1 are

$$\begin{aligned} \delta _{1} = 2.562360\cdot 10^{-7}, \quad \delta _{2} = 6.434821\cdot 10^{-8}. \end{aligned}$$
(25)

The solutions obtained using MSM satisfy the second of the motion equations with a significantly smaller error.

5 Resonant vibration

As it appears from equations (17)–(22), the frequencies of main and internal resonances are equal to each other. This characteristic feature of considered type of MEMS gyroscope results from its structure and geometry. Using non-dimensional parameters, we can write that resonances occur when \(p\approx \) 1 and \(w\approx \) 1. In view of assumptions (16), the substrate angular velocity do not affect significantly the resonance frequencies. Desirable work regime of the micromechanical system is the simultaneous resonance around both sense and drive axes. In order to achieve the state of coincidence of main and internal resonances, the system should be designed like that the both eigenfrequencies to be equal.

Assuming that the permanent equalizing the eigenfrequencies at the design stage is unobtainable in the nonlinear systems, we take into account the following resonance conditions

$$\begin{aligned} p=1+\sigma _1 , \quad w=1+\sigma _2 , \end{aligned}$$
(26)

where \(\sigma _1\) and \(\sigma _2\) play role of the detuning parameters. Additionally, we assume that \(\sigma _1 =\tilde{\sigma }_1 \varepsilon ,\;\sigma _2 =\tilde{\sigma }_2 \varepsilon \).

In order to solve the initial value problem near resonance, assumptions (26) and (16) are introduced into governing equations (10)–(11). Approximate solution is determined using MSM. We introduce three time variables. The “fast” time \(\tau _0 =\tau \), and the “slow” times \(\tau _1 =\varepsilon \tau \) and \(\tau _2 =\varepsilon ^{2}\tau \) replace the original time \(\tau \). According to MSM rules, we employ formulas (13)–(15) into motion equations (10)–(11), yielding appearance of the small parameter \(\varepsilon \) in various powers. After arranging the equations with respect to the powers of the small parameter, we realize the demand the motion equations to be satisfied for any value of \(\varepsilon \). We get a system of equations which have to be satisfied in order to guarantee satisfaction to the original equations. They are as follows:

  • the equations of the first-order approximation

    $$\begin{aligned}&\frac{\partial ^{2}\phi _1 }{\partial \tau _0^2 }+\phi _1 =0, \end{aligned}$$
    (27)
    $$\begin{aligned}&\frac{\partial ^{2}\theta _1 }{\partial \tau _0^2 }+\theta _1 =0, \end{aligned}$$
    (28)

  • the equations of the second-order approximation

    $$\begin{aligned}&\frac{\partial ^{2}\phi _2 }{\partial \tau _0^2 }+\phi _2 =\tilde{\omega }_z (j_3 -j_2 )\frac{\partial \theta _1 }{\partial \tau _0 }-2\frac{\partial ^{2}\phi _1 }{\partial \tau _0 \partial \tau _1 }, \end{aligned}$$
    (29)
    $$\begin{aligned}&\frac{\partial ^{2}\theta _2 }{\partial \tau _0^2 }+\theta _2 =-2\tilde{\sigma }_2 \theta _1 +\tilde{\omega }_z (j_4 -1)\frac{\partial \phi _1 }{\partial \tau _0 }-2\frac{\partial ^{2}\theta _1 }{\partial \tau _0 \partial \tau _1 },\nonumber \\ \end{aligned}$$
    (30)

  • the equations of the third-order approximation

    $$\begin{aligned} \frac{\partial ^{2}\phi _3 }{\partial \tau _0^2 }+\phi _3= & {} f_0 \sin (\tau _0 +\varepsilon \tau _{0 } \tilde{\sigma }_1 )-j_1 \tilde{\omega }_z^2 \phi _1 \nonumber \\&+\, \alpha _1 \phi _1^3 +(j_3 -j_2 )\tilde{\omega }_z \left( {\frac{\partial \theta _1 }{\partial \tau _1 }+\frac{\partial \theta _2 }{\partial \tau _0 }} \right) \nonumber \\&-\, \tilde{c}_1 \frac{\partial \phi _1 }{\partial \tau _0 }-\frac{\partial ^{2}\phi _1 }{\partial \tau _1^2 }-2j_2 \theta _1 \frac{\partial \theta _1 }{\partial \tau _0 }\frac{\partial \phi _1 }{\partial \tau _0 }\nonumber \\&-\, 2\frac{\partial ^{2}\phi _1 }{\partial \tau _0 \partial \tau _2 }-2\frac{\partial ^{2}\phi _2 }{\partial \tau _0 \partial \tau _1 }, \end{aligned}$$
    (31)
    $$\begin{aligned} \frac{\partial ^{2}\theta _3 }{\partial \tau _0^2 }+\theta _3= & {} -\left( {\tilde{\sigma }_2^2 +j_4 \tilde{\omega }_z^2 } \right) \theta _1 +\alpha _2 \theta _1^3 \nonumber \\&-\, 2\tilde{\sigma }_2^2 \theta _2 +(j_4 -1)\tilde{\omega }_z \left( {\frac{\partial \phi _1 }{\partial \tau _1 }+\frac{\partial \phi _2 }{\partial \tau _0 }} \right) \nonumber \\&-\, \tilde{c}_2 \frac{\partial \theta _1 }{\partial \tau _0 }-\frac{\partial ^{2}\theta _1 }{\partial \tau _1^2 }+j_4 \theta _1 \left( {\frac{\partial \phi _1 }{\partial \tau _0 }} \right) ^{2}\nonumber \\&-\, 2\frac{\partial ^{2}\theta _1 }{\partial \tau _0 \partial \tau _2 }-2\frac{\partial ^{2}\theta _2 }{\partial \tau _0 \partial \tau _1 }. \end{aligned}$$
    (32)

    The solution to equations (27)–(28) is as follows

    $$\begin{aligned} \phi _1= & {} B_1 (\tau _1 ,\tau _2 ) \exp ({i}\tau _0 )+\bar{{B}}_1 (\tau _1 ,\tau _2 ) \exp (-{i}\tau _0 ), \end{aligned}$$
    (33)
    $$\begin{aligned} \theta _1= & {} B_2 (\tau _1 ,\tau _2 ) \exp ({i}\tau _0 )+\bar{{B}}_2 (\tau _1 ,\tau _2 ) \exp (-{i}\tau _0 ),\nonumber \\ \end{aligned}$$
    (34)

where \(B_1 (\tau _1 ,\tau _2 )\), \(B_2 (\tau _1 ,\tau _2 )\)are unknown complex-valued functions of slow time scales, and i denotes the imaginary unit.

The equations system (27)–(32) are solved recursively, i.e., solutions (33)–(34) are substituted into equations (29)–(30), then their solution into equations (31)–(32). Linear differential operators of the equations system (27)–(32) are the same on each level of approximation. Therefore, it is inevitable that among solutions of equations (29)–(32) the secular terms appear. In vibration case, both generalized coordinates have to be bounded; hence, all secular terms should be eliminated from each of equations (29)–(32) after introducing into them the solutions of equations of lower levels approximation.

After introducing solutions (33)–(34) into equations (29)–(30) and rejection of the secular terms, one gets

$$\begin{aligned}&\frac{\partial ^{2}\phi _2 }{\partial \tau _0^2 }+\phi _2 =0, \end{aligned}$$
(35)
$$\begin{aligned}&\frac{\partial ^{2}\theta _2 }{\partial \tau _0^2 }+\theta _2 =0. \end{aligned}$$
(36)

The general solutions of homogeneous equations (35)–(36) are unknown functions of slow time variables like in the case of solutions (33)–(34). So, it is possible to omit these solution without lost the generality. The particular solutions are obviously equal to zero and do not induce any secular terms.

Inserting solutions (33)–(34) into equations (31)–(32) and elimination of the secular terms leads to the following equations

$$\begin{aligned} \frac{\partial ^{2}\phi _3 }{\partial \tau _0^2 }+\phi _3= & {} (\alpha _1 B_1^2 +2j_2 B_2^2 )B{ }_1\exp (3{i}\tau _0 )\nonumber \\&+\left( \alpha _1 \bar{{B}}_1^2 +2j_2 \bar{{B}}_2^2 \right) \bar{{B}}{ }_1\exp (-3{i}\tau _0 ), \end{aligned}$$
(37)
$$\begin{aligned} \frac{\partial ^{2}\theta _3 }{\partial \tau _0^2 }+\theta _3= & {} (\alpha _2 B_2^2 -j_4 B_1^2 )B_2 \exp (3{i}\tau _0 )\nonumber \\&+\left( \alpha _2 \bar{{B}}_2^2 -j_4 \bar{{B}}_1^2 \right) \bar{{B}}_2 \exp (-3{i}\tau _0 ).\nonumber \\ \end{aligned}$$
(38)

Without detracting from generality, we omit the general solutions of equations (37)–(38). The particular solutions are

$$\begin{aligned} \phi _3= & {} -\frac{1}{8}(\alpha _1 B_1^2 +2j_2 B_2^2 )B{ }_1\exp (3{i}\tau _0 )\nonumber \\&-\frac{1}{8}\left( \alpha _1 \bar{{B}}_1^2 +2j_2 \bar{{B}}_2^2 \right) \bar{{B}}{ }_1\exp (-3{i}\tau _0 ), \end{aligned}$$
(39)
$$\begin{aligned} \frac{\partial ^{2}\theta _3 }{\partial \tau _0^2 }+\theta _3= & {} -\frac{1}{8}(\alpha _2 B_2^2 -j_4 B_1^2 )B_2 \exp (3{i}\tau _0 )\nonumber \\&-\frac{1}{8}(\alpha _2 \bar{{B}}_2^2 -j_4 \bar{{B}}_1^2 )\bar{{B}}_2 \exp (-3{i}\tau _0 ).\nonumber \\ \end{aligned}$$
(40)

The solutions of the recursive system contain two unknown complex-valued functions \(B_1 (\tau _1 ,\tau _2), B_2 (\tau _1 ,\tau _2 )\) and their complex conjugates \(\bar{{B}}_1 (\tau _1 ,\tau _2 ), \bar{{B}}_2 (\tau _1 ,\tau _2)\).

Elimination of the secular terms in the process of solving equation system (31)–(34) results in getting the so-called solvability conditions

$$\begin{aligned}&{i}(j_3 -j_2 )\tilde{\omega }_z B_2 -2{i}\frac{\partial B_1 }{\partial \tau _1 }=0, \end{aligned}$$
(41)
$$\begin{aligned}&{-\,i}(j_3 -j_2 )\tilde{\omega }_z \bar{{B}}_2 +2{i}\frac{\partial \bar{{B}}_1 }{\partial \tau _1 }=0, \end{aligned}$$
(42)
$$\begin{aligned}&{i}(j_4 -1)\tilde{\omega }_z B_1 -2\tilde{\sigma }_2 B_2 -2{i}\frac{\partial B_2 }{\partial \tau _1 }=0, \end{aligned}$$
(43)
$$\begin{aligned}&-\,i(j_4 -1)\tilde{\omega }_z \bar{{B}}_1 -2\tilde{\sigma }_2 \bar{{B}}_2 +2{i}\frac{\partial \bar{{B}}_2 }{\partial \tau _1 }=0, \end{aligned}$$
(44)
$$\begin{aligned}&-\frac{1}{2}{i} \tilde{f}_0 \exp ({i}\varepsilon \tilde{\sigma }_1 \tau _0 )+3\alpha _1 B_1^2 \bar{{B}}_1 \nonumber \\&\quad +\frac{B_1 }{4}\left( {-4{i} \tilde{c}_1 +(j_2 -j_3 -4j_1 -j_2 j_4 +j_3 j_4 )\tilde{\omega }_z^2 } \right) \nonumber \\&\quad -\, 2j_2 \bar{{B}}_1 B_2^2 -\frac{{i}}{2}\left( {(j_2 -j_3 )\tilde{\sigma }_2 \tilde{\omega }_z B_2 +4\frac{\partial B_1 }{\partial \tau _2 }} \right) =0, \end{aligned}$$
(45)
$$\begin{aligned}&\frac{1}{2}{i} \tilde{f}_0 \exp (-{i}\varepsilon \tilde{\sigma }_1 \tau _0 )+3\alpha _1 \bar{{B}}_1^2 B_1 +\frac{\bar{{B}}_1 }{4}\nonumber \\&\quad \times \,\left( {4{i} \tilde{c}_1 +(j_2 -j_3 -4j_1 -j_2 j_4 +j_3 j_4 )\tilde{\omega }_z^2 } \right) \nonumber \\&\quad -\, 2j_2 B_1 \bar{{B}}_2^2 +\frac{{i}}{2}\left( {(j_2 -j_3 )\tilde{\sigma }_2 \tilde{\omega }_z \bar{{B}}_2 +4\frac{\partial \bar{{B}}_1 }{\partial \tau _2 }} \right) =0, \end{aligned}$$
(46)
$$\begin{aligned}&(3\alpha _2 B_2^2 -j_4 B_1^2 )\bar{{B}}_2 +\frac{B_2 }{4}\nonumber \\&\quad \times \,\left( {-4{i} \tilde{c}_2 +(j_2 +j_3 (j_4 -1)-4j_4 -j_2 j_4 )\tilde{\omega }_z^2 } \right) \nonumber \\&\quad -2{i}\frac{\partial B_2 }{\partial \tau _2 }+2j_4 B_1 B_2 \bar{{B}}_1 -\frac{{i}}{2}(j_4 -1)\tilde{\sigma }_2 \tilde{\omega }_z B_1 =0, \end{aligned}$$
(47)
$$\begin{aligned}&(3\alpha _2 \bar{{B}}_2^2 -j_4 \bar{{B}}_1^2 )B_2 +\frac{\bar{{B}}_2 }{4}\left( 4{i} \tilde{c}_2 +(j_2 +j_3 (j_4 -1)\right. \nonumber \\&\quad \left. -\, 4j_4 -j_2 j_4 )\tilde{\omega }_z^2 \right) +2{i}\frac{\partial \bar{{B}}_2 }{\partial \tau _2 }\nonumber \\&\quad +\, 2j_4 B_1 \bar{{B}}_2 \bar{{B}}_1 +\frac{{i}}{2}(j_4 -1)\tilde{\sigma }_2 \tilde{\omega }_z \bar{{B}}_1 =0, \end{aligned}$$
(48)

The solvability conditions create the system of eight partial differential equations of the first order with unknown functions \(B_1 (\tau _1 ,\tau _2 )\), \(B_2 (\tau _1 ,\tau _2 )\), \(\bar{{B}}_1 (\tau _1 ,\tau _2 ),\bar{{B}}_2 (\tau _1 ,\tau _2 )\). It is convenient to represent these functions using the following exponential representation

$$\begin{aligned} B_1= & {} \tilde{a}_1 \exp ({i}\psi _1 ),\quad \bar{{B}}_1 =\tilde{a}_1 \exp (-{i}\psi _1 ),\nonumber \\ B_2= & {} \tilde{a}_2 \exp ({i}\psi _2 ),\quad {\bar{{B}}_2 =\tilde{a}_2 \exp (-{i}\psi _2 )}, \end{aligned}$$
(49)

where \(\tilde{a}_1 (\tau _1 ,\tau _2 ),\;\tilde{a}_1 (\tau _1 ,\tau _2 ),\;\psi _1 (\tau _1 ,\tau _2 ),\;\psi _2 (\tau _1 ,\tau _2)\) are real-valued functions.

After changing variables in (41)–(48) according to relationships (49), we get the system of equations containing the first-order partial derivatives of unknown functions \(\tilde{a}_1 (\tau _1 ,\tau _2 ),\;\tilde{a}_1 (\tau _1 ,\tau _2 ),\;\psi _1 (\tau _1 ,\tau _2 ),\;\psi _2 (\tau _1 ,\tau _2 )\). We solve it with respect to these derivatives, and then insert the solutions into Eq. (13) what make possible to transform the system of partial differential equations (41)–(48) onto equivalent system of four ordinary differential equations. Applying inversely assumptions (16), one gets

$$\begin{aligned} \dot{a}_1= & {} -\frac{f_0 }{2}\cos (\sigma _1 \tau -\psi _1 )\nonumber \\&-\frac{j_2 -j_3 }{4}(2+\sigma _2 )\omega _z a_2 \cos (\psi _1 -\psi _2 )-\frac{1}{2}c_1 a_1 \nonumber \\&+\frac{j_2 }{4}a_1 a_2^2 \sin (2(\psi _1 -\psi _2 )), \end{aligned}$$
(50)
$$\begin{aligned} \dot{a}_2= & {} -\frac{1}{4}(j_4 -1)(\sigma _2 -2)\omega _z a_1 \cos (\psi _1 -\psi _2 )-\frac{1}{2}c_2 a_2\nonumber \\&-\frac{1}{8}j_4 a_1^2 a_2 \sin (2(\psi _1 -\psi _2 )), \end{aligned}$$
(51)
$$\begin{aligned} a_1 \dot{\psi }_1= & {} -\frac{3}{8}\alpha _1 a_1^3 +\frac{4j_1 +(j_2 -j_3 )(j_4 -1)}{8}\omega _z^2 a_1 \nonumber \\&+\frac{j_2 }{4}a_1 a_2^2 \cos (2(\psi _1 -\psi _2 ))-\frac{f_0 }{2}\sin (\sigma _1 \tau -\psi _1 )\nonumber \\&+\frac{j_2 -j_3 }{4}(2+\sigma _2 )\omega _z a_2 \sin (\psi _1 -\psi _2 ), \end{aligned}$$
(52)
$$\begin{aligned} a_2 \dot{\psi }_2= & {} \sigma _2 a_2 -\frac{3}{8}\alpha _2 a_2^3 +\frac{\omega _z^2 }{8}\left( {j_3 -j_2 +(4+j_2 -j_3 )j_4 } \right) a_2 \nonumber \\&+\frac{j_4 }{8}a_1^2 a_2 (\cos (2(\psi _1 -\psi _2 ))-2)\nonumber \\&- \frac{j_4 -1}{4}(\sigma _2 -2)\omega _z a_1 \sin (\psi _1 -\psi _2 ), \end{aligned}$$
(53)

where \(a_1 =\varepsilon \tilde{a}_1 \;,a_2 =\varepsilon \tilde{a}_2 \).

The initial conditions supplementing equations (50)–(53) are

$$\begin{aligned} a_1 (0)= & {} a_{10} ,\quad \psi _1 (0)=\psi _{10} ,\nonumber \\ a_2 (0)= & {} a_{20} ,\quad \psi _2 (0)=\psi _{20} , \end{aligned}$$
(54)

where \(\;a_{10} ,a_{20} ,\psi _{10} ,\psi _{20}\) are that known quantities like that the initial conditions (11) and (54) are compatible each to other.

Rejection of the secular terms guarantee not only that solutions of vibration problem are bounded but also it gives a way to determine the unknown functions \(B_1 (\tau _1 ,\tau _2 ),B_2 (\tau _1 ,\tau _2 )\). It should be noticed that although differential equations (50)–(53) are written using derivatives with respect to the time \(\tau \), they describe the evolution of the functions \(a_1 (\tau _1 ,\tau _2 ),a_1 (\tau _1 ,\tau _2 ),\;\;\psi _1 (\tau _1 ,\tau _2 ),\;\psi _2 (\tau _1 ,\tau _2 )\) with respect to the slow times variables \(\tau _1\) and \(\tau _2\) because these functions a priori depend only on the slow times variables.

After solving initial value problem (50)–(54), we apply inversely formula (49) what allow to express the complex-valued functions \(B_1 (\tau _1 ,\tau _2 ),B_2 (\tau _1 ,\tau _2 )\) and their complex conjugates through the real-valued functions \(a_1 (\tau _1 ,\tau _2 ),\;a_1 (\tau _1 ,\tau _2 ),\;\;\psi _1 (\tau _1 ,\tau _2 ),\;\psi _2 (\tau _1 ,\tau _2 )\) in solutions of the equations system (27)–(32) . Next, taking into account Eq. (15) we can write the approximate solution of original problem (10)–(12) related to the simultaneously occurring main and internal resonances. The solution has the following analytical form

$$\begin{aligned} \varphi= & {} a_1 \cos (\tau +\psi _1 )-\frac{1}{32}\alpha _1 a_1^3 \cos (3\tau +3\psi _1 )\nonumber \\&-\frac{1}{16}j_2 a_1 a_2^2 \cos (3\tau +\psi _1 +2\psi _2 ) \end{aligned}$$
(55)
$$\begin{aligned} \vartheta= & {} a_2 \cos (\tau +\psi _2 )+\frac{1}{32}j_4 a_1^2 a_2 \cos (3\tau +2\psi _1 +\psi _2 )\nonumber \\&-\frac{1}{32}\alpha _2 a_2^3 \cos (3\tau +3\psi _2 ) . \end{aligned}$$
(56)

The quantities \(a_1 \;,a_2 \) and \(\psi _1 \;,\psi _2\) introduced into consideration by exponential representation (49) are functions of slow time variables and occur respectively as the amplitudes and the phases of the components of approximate solution (55)–(56). So, initial value problem (50)–(54) which is associated with basic equations set (27)–(32) determine the slow evolution of the vibration amplitudes and phases in time. For that reason, this issue is known as modulation problem. Contrary to the previously discussed case of the non-resonant vibration, initial value problem (50)–(54) cannot be solved in the analytical manner.

The time histories of the generalized coordinates in case of the doubled resonance are presented in Fig. 4. The values of parameters assumed in this simulation are as follows:

$$\begin{aligned} \sigma _{1}= & {} 0.01, \quad \sigma _{2} = 0.04167, \quad f_{0} = 0.0043662, \quad \alpha _{1} = 1,\\ \alpha _{2 }= & {} 1, \quad {c}_{1} = 0.0000575531, \quad {c}_{2} = 0.0000575531, \\ \omega _{z}= & {} 0.0000575531, j_{1} = 0.04, \quad j_{2} = 0, \quad j_{3} = 0.96, \quad j_{4} = 0,\\ a_{10}= & {} 0.008,\quad a_{20}= 0.008, \quad \psi _{10}= 0, \quad \psi _{20}= 0. \end{aligned}$$
Fig. 4
figure 4

Time histories in case of doubled resonance: a the generalized coordinate \(\varphi \) and amplitude \(a_{1}\); b the generalized coordinate \(\vartheta \) and amplitude \(a_{2}\)

Full size image

In Fig. 4a, the black solid line represent the amplitude \(a_{1}\) whereas the black line depicted in Fig. 4b is the image of the amplitude \(a_{2}\). Both curves envelop the graphs of fast changing oscillations. The non-dimensional value \(\tau _{\mathrm{max}} = 20{,}000\) denoting the duration of simulation correspond to about 1.08 s.

Similarly as in Sect. 4, in Fig. 4 are depicted the approximate solutions obtained using MSM and calculated numerically. The values of error (23) for the solutions derived using MSM are as follows

$$\begin{aligned} \delta _{1} = 1.400831\cdot 10^{-7}, \quad \delta _{2} = 8.920221\cdot 10^{-9}. \end{aligned}$$
(57)

For comparison, the values of error for the solutions obtained by the optimized numerical method in Mathematica 11.1 are

$$\begin{aligned} \delta _{1} = 2.562360\cdot 10^{-7},\quad \delta _{2} = 6.434821\cdot 10^{-8}. \end{aligned}$$
(58)

Both values of error measuring satisfaction of the governing equations by approximate solution are smaller in case of MSM solution.

6 Steady-state responses

Initial value problem (50)–(54) arose in process of solving motion equations (10)–(12) using MSM is a good basis for studying the steady-state forced vibration of the micromechanical gyroscope. For this purpose, it is convenient to introduce modified phases \(\varPsi _1(\tau )\) and \(\varPsi _2 (\tau )\) as follows

$$\begin{aligned} \psi _1 (\tau )=\sigma _1 \tau -\varPsi _1 (\tau ),\;\;\;\;\psi _2 (\tau )=\sigma _1 \tau -\varPsi _2 (\tau )\;. \end{aligned}$$
(59)

Applying expressions (59) transforms modulation problem (50)–(54) into an autonomous form that is suitable to analyze steady-state motion of the system. Oscillations of forced system can achieve the steady state when all transient processes disappear. The symptom of this state is fixing of the values of the amplitudes \(a_1 ,a_2\) and modified phases \(\psi _1 \;,\psi _2\). By zeroing of the derivatives of amplitudes and modified phases in modulation equations (50)–(53), we get the conditions of a steady state

$$\begin{aligned}&2f_0 \cos (\varPsi _1 )+(j_2 -j_3 )(2+\sigma _2 )\omega _z a_2 \cos (\varPsi _1 -\varPsi _2 )\nonumber \\&\quad +\, a_1 (2c_1 +j_2 a_2^2 \sin (2(\varPsi _1 -\varPsi _2 )))=0, \end{aligned}$$
(60)
$$\begin{aligned}&2(j_4 -1)(\sigma _2 -2)\omega _z a_1 \cos (\varPsi _1 -\varPsi _2 )\nonumber \\&\quad +\, 4a_2 c_2 -j_4 a_1^2 a_2 \sin (2(\varPsi _1 -\varPsi _2 ))=0, \end{aligned}$$
(61)
$$\begin{aligned}&- 8\sigma _1 a_1 -3\alpha _1 a_1^3 +a_1 \left( {(4j_1 +(j_2 -j_3 )(j_4 -1)} \right) \omega _z^2 \nonumber \\&\quad +\, 2j_2 a_2^2 \cos (2(\varPsi _1 -\varPsi _2 ))-4f_0 \sin (\varPsi _1 )\nonumber \\&\quad -\, 2(j_2 -j_3 )(2+\sigma _2 )\omega _z a_2 \sin (\varPsi _1 -\varPsi _2 )=0, \end{aligned}$$
(62)
$$\begin{aligned}&-8\sigma _1 a_2 +8a_2 \sigma _2 -3\alpha _2 a_2^3 \nonumber \\&\quad +a_2 \left( {j_3 -j_2 +(4+j_2 -j_3 )j_4 } \right) \omega _z^2 \nonumber \\&\quad +\, j_4 a_1^2 a_2 (\cos (2(\varPsi _1 -\varPsi _2 ))-2)\nonumber \\&\quad -\, 2(j_4 -1)(\sigma _2 -2)\omega _z a_1 \sin (\varPsi _1 -\varPsi _2 )=0. \end{aligned}$$
(63)

The solution of system of nonlinear equations (60)–(63) determine the values of amplitudes and modified phases of the gyroscope vibration in case of main and internal resonances that occur simultaneously.

Let us analyze resonant response of micromechanical gyroscope in the general case, i.e., without any additional assumptions about its properties. The following values of parameters are fixed

$$\begin{aligned}&\hbox {SET1} = \{{\sigma }_{2}=- 0.00333, \quad f_{0} = 0.0000011, \\&\alpha _{1} = 1.42, \quad \alpha _{2}= 2.174, \quad {c}_{1} = 0.000010127,\\&{c}_{2} =0.00001, \quad \omega _{z} = 0.000131656, \quad j_{1} = 0.0769,\\&j_{2} = 0, \quad j_{3} = 0.923, \quad j_{4} = 0\}. \end{aligned}$$

The value of the detuning parameter \(\sigma _{1}\) is increased regularly by 0.000015, starting from \(\sigma _{1} = -0.0065\). The resonant response curves are obtained solving equations (60)–(63) with help the procedure NSolve offered in Mathematica 11.1. The results are presented in Fig. 5.

Fig. 5
figure 5

Resonance curves: a for the gimbal vibration, b for the sensing element vibration; set of data: SET1

Full size image

The resonant answers of the system exhibit high coincidence with the numerical solution of the motion equations. The simulation was carried out assuming the same values of parameter. Additionally, it is assumed

$$\begin{aligned}&\sigma _{1} = -0.004,\quad a_{10}= 0.01,\quad a_{20}= 0.01,\\&\psi _{10}= 0,\quad \psi _{20}= 0. \end{aligned}$$

Time histories of the generalized coordinates for this data are given in Fig. 6. Both graphs present the vibration just before the end of simulation which was realized for \(\tau \in \left[ {0,\tau _{\max } } \right] \), where \(\tau _{\max } =20{,}000\) corresponds to about 1.32s.

Fig. 6
figure 6

Time histories of generalized coordinates for the set of data: SET1

Full size image

The values of error (23) for the approximate solution obtained using MSM are as follows

$$\begin{aligned} \delta _{1} = 1.456467\cdot 10^{-9},\quad \delta _{2} = 2.940916\cdot 10^{-9,} \end{aligned}$$
(64)

while the values of the error for the numerical results obtained using Mathematica Software are

$$\begin{aligned} \delta _{1} = 2.289364\cdot 10^{-7},\quad \delta _{2} = 2.316752\cdot 10^{-7}. \end{aligned}$$
(65)

Equations (60)–(63) allow for a complete analysis of the gyroscope steady-state response for various special case studies.

Case 1 \((\alpha _1 =0,\;\;\alpha _2 =0)\)

Let us consider the micromechanical gyroscope the torsional joints of which have strictly linear elastic characteristic. Inserting \(\alpha _1 =0,\;\;\alpha _2 =0\) into equations (60)–(63), one gets

$$\begin{aligned}&2f_0 \cos (\varPsi _1 )+(j_2 -j_3 )(2+\sigma _2 )\omega _z a_2 \cos (\varPsi _1 -\varPsi _2 )\nonumber \\&\quad +\, a_1 (2c_1 +j_2 a_2^2 \sin (2(\varPsi _1 -\varPsi _2 )))=0, \end{aligned}$$
(66)
$$\begin{aligned}&2(j_4 -1)(\sigma _2 -2)\omega _z a_1 \cos (\varPsi _1 -\varPsi _2 )+4a_2 c_2 \nonumber \\&\quad -j_4 a_1^2 a_2 \sin (2(\varPsi _1 -\varPsi _2 ))=0, \end{aligned}$$
(67)
$$\begin{aligned}&-8\sigma _1 a_1 +a_1 \left( {(4j_1 +(j_2 -j_3 )(j_4 -1)} \right) \omega _z^2 \nonumber \\&\quad +\, 2j_2 a_2^2 \cos (2(\varPsi _1 -\varPsi _2 ))-4f_0 \sin (\varPsi _1 )\nonumber \\&\quad -\, 2(j_2 -j_3 )(2+\sigma _2 )\omega _z a_2 \sin (\varPsi _1 -\varPsi _2 )=0, \end{aligned}$$
(68)
$$\begin{aligned}&-8\sigma _1 a_2 {+}8a_2 \sigma _2 {+}a_2 \left( {j_3 -j_2 {+}(4+j_2 -j_3 )j_4 } \right) \omega _z^2 \nonumber \\&\quad +j_4 a_1^2 a_2 (\cos (2(\varPsi _1 -\varPsi _2 ))-2)\nonumber \\&\quad -2(j_4 -1)(\sigma _2 -2)\omega _z a_1 \sin (\varPsi _1 -\varPsi _2 )=0. \end{aligned}$$
(69)

Assumption about vanishing nonlinear does not cause any significant simplifications. The modulation equations are still nonlinear and majority of the nonlinear terms is conditioned by the inertial properties of the sensing plate.

Case 2\(({\begin{array}{llll} {\alpha _1 =0,\;}&{} {\alpha _2 =0,}&{} {j_2 =0,}&{} {j_4 =0} \\ \end{array} })\) Observe that the steady-state equations become much simpler when \(j_2 =j_4 =0\). These relations are satisfied if the components \(J_x\) and \(J_z \) of the diagonal inertia tensor \({\hat{\mathbf{J}}}\) of the sense plate are equal to each other. Modulation equations take the following form

$$\begin{aligned}&2f_0 \cos (\varPsi _1 )-j_3 (2+\sigma _2 )\omega _z a_2 \cos (\varPsi _1 -\varPsi _2 )+2a_1 c_1 =0, \end{aligned}$$
(70)
$$\begin{aligned}&2(\sigma _2 -2)\omega _z a_1 \cos (\varPsi _1 -\varPsi _2 )-4a_2 c_2 =0, \end{aligned}$$
(71)
$$\begin{aligned}&-8\sigma _1 a_1 +4j_1 \omega _z^2 a_1 +j_3 \omega _z^2 a_1 \nonumber \\&\quad -4f_0 \sin (\varPsi _1 )+2j_3 (2+\sigma _2 )\omega _z a_2 \sin (\varPsi _1 -\varPsi _2 )=0, \end{aligned}$$
(72)
$$\begin{aligned}&-8\sigma _1 a_2 +a_2 (8\sigma _2 +j_3 \omega _z^2 )-2(\sigma _2 -2)\omega _z a_1 \sin (\varPsi _1 -\varPsi _2 )=0.\nonumber \\ \end{aligned}$$
(73)

The modified phases can be eliminated from equations (70)–(73) using trigonometric identities what allows to express explicitly the amplitude-frequency dependencies

$$\begin{aligned}&\frac{a_2^2 \left( {16c_2^2 +(8\sigma _2 -8\sigma _1 +j_3 \omega _z^2 )^{2}} \right) }{4a_1^2 (\sigma _2 -2)^{2}\omega _z^2 }=1, \end{aligned}$$
(74)
$$\begin{aligned}&\left( {4a_1 j_1 \omega _z^2 -8a_1 \sigma _1 +a_1 j_3 \omega _z^2 +\frac{a_2^2 j_3 (2+\sigma _2 )(8\sigma _2 -8\sigma _1 +j_3 \omega _z^2 )}{a_1 (\sigma _2 -2)}} \right) ^{2}\nonumber \\&\quad +\frac{16\left( {a_1^2 c_1 (\sigma _2 -2)-a_2^2 c_2 j_3 (2+\sigma _2 )} \right) ^{2}}{a_1^2 (\sigma _2 -2)^{2}}=16f_0^2 . \end{aligned}$$
(75)

We get the system of two algebraic equations of the 8-th order with respect to the unknown amplitudes \(a_{1}\) and \(a_{2}\).

The resonance curves obtained in result of solving system (74)–(75) for the following data of parameters

\(\hbox {SET2} = \{f_{0}=1.\times 10^{-7}\), \(\alpha _{1} = 0\), \(\alpha _{2 }= 0\), \({c}_{1}=5.\times 10^{-7}\), \({c}_{2}=5.\times 10^{-7}\), \(\omega _{z}=3.\times 10^{-6}\), \(j_{1} = 0.00826\), \(j_{3} = 0.9917\}\) are presented in Fig. 7.

Fig. 7
figure 7

Resonance curves; \(a_{1}\)—amplitude of the gimbal, \(a_{2}\) amplitude of the sensing plate

Full size image

The full symmetry of the graphs depicted in Fig. 7 is typical behavior of the considered two-degrees-of-freedom linear system.

The mentioned symmetry is disturbed when the system is not perfectly tuned to the internal resonance, i.e., when \(\sigma _2 \ne 0\). The angular velocity of the substrate has also crucial influence on the resonant response. The influence on the resonant response of the detuning parameter \(\sigma _2 \ne 0\), which means that the system is not perfectly tuned, and with respect to the angular velocity \(\omega _z\) is presented in Fig. 8.

Fig. 8
figure 8

Resonance curves for various \(\omega _z\) and \(\sigma _2\) (set of data: SET2)

Full size image

Comparing several cases presented in Figs. 7 and 8, we can observe that resonant picks are moving away from each other when \(\omega _z\) increases. However, the increase of \(\sigma _2\) disturbs symmetry of the graphs.

Case 3 \((j_1 =j_2 =j_4 =0,\;j_3 =1)\)

In this case, we assume that moments of inertia of the gimbal are assumed as negligible and that the tensor of inertia of the sensor element is isotropic. Inserting the assumptions \(j_1 =j_2 =j_4 =0,\;j_3 =1\) into modulation equations (60)–(63), we get

$$\begin{aligned}&2f_0 \cos (\varPsi _1 )+(2+\sigma _2 )\omega _z a_2 \cos (\varPsi _1 -\varPsi _2 )+2a_1 c_1 =0, \end{aligned}$$
(76)
$$\begin{aligned}&2(\sigma _2 -2)\omega _z a_1 \cos (\varPsi _1 -\varPsi _2 )-4a_2 c_2 =0, \end{aligned}$$
(77)
$$\begin{aligned}&-\, 8a_1 \sigma _1 -3\alpha _1 a_1^3 +a_1 \omega _z^2\nonumber \\&\quad -\, 4f_0 \sin (\varPsi _1 )+2(2+\sigma _2 )\omega _z a_2 \sin (\varPsi _1 -\varPsi _2 )=0, \end{aligned}$$
(78)
$$\begin{aligned}&-\, 8a_2 \sigma _1 +a_2 (-3\alpha _2 a_2^2 +8\sigma _2 +\omega _z^2 )\nonumber \\&\quad -\, 2(\sigma _2 -2)\omega _z a_1 \sin (\varPsi _1 -\varPsi _2 )=0. \end{aligned}$$
(79)

Considered here assumptions cause vanishing of trigonometric functions whose argument is difference of the modified phases multiplied by two. This circumstance allow to eliminate from (76)–(79) the other trigonometric functions of the modified phases. In this manner, the following implicit dependence between the amplitudes and frequencies in the resonance zone is obtained

$$\begin{aligned}&\frac{a_2^2 \left( {16c_2^2 +(-3\alpha _2 a_2^2 +8\sigma _2 -8\sigma _1 +\omega _z^2 )^{2}} \right) }{4a_1^2 (\sigma _2 -2)^{2}\omega _z^2 }=1, \end{aligned}$$
(80)
$$\begin{aligned}&\left( {-3\alpha _1 a_1^3 -8\sigma _1 a_1 +\omega _z^2 a_1 +\frac{a_2^2 (2+\sigma _2 )(-3\alpha _2 a_2^3 +8\sigma _2 -8\sigma _1 +\omega _z^2 )}{a_1 (\sigma _2 -2)}} \right) ^{2}\nonumber \\&\quad +\frac{16\left( {\;c_1 (\sigma _2 -2)a_1^2 -c_2 (2+\sigma _2 )a_2^2 } \right) ^{2}}{a_1^2 (\sigma _2 -2)^{2}}=16f_0^2 . \end{aligned}$$
(81)

Equations (80)–(81) form the algebraic set of 48-th order with respect to the unknown amplitudes \(a_{1}\) and \(a_{2}\), where amplitudes appear only in even powers. These equations allow to perform qualitative analysis of the resonance steady-state amplitudes versus detuning parameter \(\sigma _1\) for various parameters.

The analysis of the influence of the damping coefficient on the amplitudes is presented in Fig. 9. The assumed values of system parameters are:

$$\begin{aligned} \hbox {SET3}= & {} \{ f_{0}=4.3662\times 10^{-7}, \quad \alpha _{1} = 1, \\&\alpha _{2 }=1, \quad \omega _{z}=6.\times 10^{-5}, \quad \sigma _2 =0\} \end{aligned}$$
Fig. 9
figure 9

Resonance curves for: (1) \({c}_1 =c_2 =1\times 10^{-5}\), (2) \({c}_1 =c_2 =2\times 10^{-5}\), (3) \({c}_1 =c_2 =3\times 10^{-5}\), (4) \({c}_1 =c_2 =4\times 10^{-5}\)

Full size image

The influence of the amplitude \(f_0\) on the resonance curves, for the set of parameters SET3 and \({c}_1 =c_2 =4\times 10^{-5}\), is presented in Fig. 10.

Fig. 10
figure 10

Resonance curves for: (1) \(f_{0}=4.\times 10^{-7}\), (2) \(f_{0}=6.\times 10^{-7}\), (3) \(f_{0}=8.\times 10^{-7}\), (4) \(f_{0}=9.\times 10^{-7}\)

Full size image

The nonlinearity parameters \(\alpha _1\) and \(\alpha _2\) have also essential impact on the resonant characteristics for the set of parameters SET3 and \({c}_1 =c_2 =2.5\times 10^{-6}\), is presented in Fig. 11.

Fig. 11
figure 11

Resonance curves for: (1) \(\alpha _1 =\alpha _2 =1\), (2) \(\alpha _1 =\alpha _2 =2\), (3) \(\upalpha _1 =\alpha _2 =2.5\), (4) \(\alpha _1 =\alpha _2 =3\)

Full size image

The values of damping coefficients for which the resonance curves become unique can be estimated, in the way of numerical simulations, for the given microsystem and given loading. In the case of data values specified in SET3, coefficients \(c_1 =c_2 =0.000034\) fulfill this criterion.

Case 4 \((\omega _z =0)\)

In the case of immovable substrate the form of modulation equations is simplified to the following

$$\begin{aligned}&2f_0 \cos (\varPsi _1 )+2a_1 c_1 -j_2 a_1 a_2^2 \sin (2(\varPsi _2 -\varPsi _1 )))=0, \end{aligned}$$
(82)
$$\begin{aligned}&4a_2 c_2 -j_4 a_2 a_1^2 \sin (2(\varPsi _1 -\varPsi _2 ))=0, \end{aligned}$$
(83)
$$\begin{aligned}&-\, 8a_1 \sigma _1 -3\alpha _1 a_1^3 +2j_2 a_1 a_2^2 \cos (2(\varPsi _1 -\varPsi _2 ))\nonumber \\&\quad -\, 4f_0 \sin (\varPsi _1 )=0, \end{aligned}$$
(84)
$$\begin{aligned}&-\, 8a_2 \sigma _1 +8a_2 \sigma _2 -3\alpha _2 a_2^3 \nonumber \\&\quad -\, 2a_1^2 a_2 j_4 +a_1^2 a_2 j_4 \cos (2(\varPsi _1 -\varPsi _2 ))=0. \end{aligned}$$
(85)

The inertial parameters \(j_1 \) and \(j_3 \) do not appear in equations (82)–(85). The trigonometric identities again allow to eliminate the functions \(\varPsi _1 \) and \(\varPsi _2 \).

Case 5 \({\begin{array}{lll} {(\omega _z =0,\;}&{} {j_2 =0,}&{} {j_4 =0} \\ \end{array} })\)

Let us assume that the substrate is immovable and additionally \(J_x =J{ }_z\), so \(j_2 =j_4 =0\). The last assumption together with \(\omega _z =0\) leads to the conclusion that \(a_2 =0\). When the substrate is at rest, then the sensing plate does not oscillate. The forced vibration of the gimbal does not excite the sensor what confirms that the Coriolis torque is the main reason causing the sense plate to vibrate. Due to the substrate and the sensor plate are at rest, the equation describing the relationship amplitude–frequency for gimbal is completely uncoupled and has the following form

$$\begin{aligned} a_1^2 \left( {16c_1^2 +(3\alpha _1 a_1^2 +8\sigma _1 )^{2}} \right) =16f_0^2 . \end{aligned}$$
(86)

The family of resonance curves, obtained using Eq. (86), for various values of damping coefficient \(c_1\) is presented in Fig. 12. The values of parameters assumed in this simulation are

$$\begin{aligned}&\hbox {SET4}=\{\sigma _{2} = -0.0394, \quad f_{0}=4.\times 10^{-6},\\&\alpha _{1} = 10, \quad \alpha _{2}= 10, \quad {c}_{2}=0.000114,\\&j_{2} = 0, \quad j_{4} = 0\} \end{aligned}$$
Fig. 12
figure 12

Resonance curves for the gimbal when substrate is immovable

Full size image
Fig. 13
figure 13

Steady state vibration for the gimbal and the sensing plate

Full size image
Fig. 14
figure 14

Resonance curves. The amplitudes of the gimbal and the sensing plate versus \(\sigma _{2}\) for various values of the damping coefficients; (1) \({c}_1 =c_2 =6\times 10^{-5}\), (2) \({c}_1 =c_2 =8\times 10^{-5}\), (3) \({c}_1 =c_2 =12\times 10^{-5}\), (4) \({c}_1 =c_2 =3\times 10^{-5}\), (4) \({c}_1 =c_2 =20\times 10^{-5}\)

Full size image

Case 6 (identification of angular velocity)

The identification problem of substrate angular velocity requires an unambiguous character of each of the both resonance response curves. So, determination of the value of the damping coefficient which guarantee this unambiguity for given micromechanical gyroscope is of significant importance. It is also important to reduce the number of the measurement system parameters that can have influence on the identification. One of the earlier discussed cases leads to essential simplification of the equations of steady state. It is the case when the gimbal moments of inertia are sufficiently slight and the tensor of inertia of the sense plate is isotropic. These assumptions that simplify the steady state equations to form (76)–(79) can be written as follows \(j_1 =j_2 =j_4 =0,\;j_3 =1\). Equation (77) of this system is relatively simple and contains the smallest number of gyroscope parameters. Let us solve Eq. (77) for the angular velocity

$$\begin{aligned} \omega _z =\frac{2a_2 c_2 }{(\sigma _2 -2)a_1 \cos (\varPsi _1 -\varPsi _2 )}. \end{aligned}$$
(87)

When the system is perfectly designed, made and tuned, the detuning parameter \(\sigma _2\) is equal to zero. Thus it is enough to know the damping coefficient \(c_{2}\) and to measure the values of amplitudes \(a_{1}\) and \(a_{2}\) in the resonance. In the steady state, the difference of the modified phases should be set at value \(\pi \). Assuming all these circumstances, we can write

$$\begin{aligned} \omega _z =\frac{a_2 c_2 }{a_1 }. \end{aligned}$$
(88)

The following simulation is carried out in order to apply this identification way. We assume some values of parameters of gyroscope including the value of the substrate angular velocity, namely

$$\begin{aligned}&\hbox {SET5}=\{\sigma _{1} = 0, \quad \sigma _{2} = 0, \quad f_{0}=4.5\times 10^{-6},\\&\alpha _{1} = 1, \alpha _{2 }= 1, \quad {c}_{1}=0.0005, \quad {c}_{2}=0.0005, \\&\omega _{z} = 0.0008, \quad a_{10}= 0.005, \quad a_{20}= 0.005,\\&\psi _{10}= 0, \quad \psi _{10}= 0\}. \end{aligned}$$

Then, we find the approximate solution of initial value problem (10)–(12) and determine the both values of amplitudes, replacing real measurement by the reading the values from the graphs. The variability over time of the both generalized coordinates for the steady-state vibration is presented in Fig. 13. Using graphs, we determine

\({\begin{array}{ll} {a_1 \approx 0.000249,}&{} {a_2 \approx 0.004} \\ \end{array} }\), and hence \(\omega _z \approx 0.0008032\).

However, this procedure fails when due to any reason the assumptions concerning the coincidence of both resonances at the same resonant frequency (\(\sigma _{2} = 0\)) are not strictly satisfied. The higher value the parameter \(\sigma _{2}\) takes, the less accurate the angular velocity measurement is. In Fig. 14, there is shown the influence of parameter \(\sigma _{2}\) on the vibration amplitude of the both the gimbal and the sensing plate. This influence is especially spectacular when the damping is small and the resonance response curves are ambiguous. However, even for sufficiently large values of damping coefficients which make sure the curves are functions of the detuning parameter \(\sigma _{2}\), the values of the both amplitudes change significantly with \(\sigma _{2}\). The numerical simulation was carried out assuming the following fixed values of parameters

$$\begin{aligned}&\hbox {SET6}=\{\sigma _{1} = -10^{-5}, \quad f_{0}=4.5\times 10^{-6},\\&\alpha _{1} = 1, \quad \alpha _{2}= 1, \quad \omega _{z} = 0.0008\}. \end{aligned}$$

7 Concluding remarks

The equations of motion of micromechanical gyroscope of torsional type has been derived. The mathematical model includes nonlinear characteristics of the torsional links. According to actual work regime of this type micromechanical gyroscope, only harmonically changing torque acting about the gimbal axis has been assumed. The dynamical problem has been solved using the method of multiple time scales belonging to wide class of asymptotic methods. The significant advantage of the asymptotic methods consist in the analytical form of the approximate solutions. That gives the opportunity to both qualitative and quantitative analysis of the behavior of the system for wide range of its parameters.

The approximate solution of analytical form has been obtained firstly for non-resonant vibration what among other allow to detect the resonance conditions. The main and internal resonances simultaneously occurring have been the subject of our study. The characteristic feature of this type gyroscope is that the both resonance frequencies are equal to each other. The approximate solution has been obtained also for the resonant vibration. Initial value problem of the modulation strictly associated with the procedure of solving the governing equations using MSM gives the possibility to analyze the slow evolution of the amplitudes and phases.

Steady-state resonance oscillations are desired regime of work of the micromechanical gyroscope, so this situation has been analyzed in more detail. Moreover, some special cases have been investigated. For example, we simulated negligible inertia of gimbal and isotropic tensor of inertia of the sensor. Another case refers to situation when the torsional joints have strictly linear elastic characteristic, for both symmetric and non-symmetric moments of inertia. We have also shown that if substrate is immovable, the modulation equations are uncoupled and reduce to one equation describing vibration of a gimbal. In that case the sensing plate is motionless.

For all cases, the amplitude–frequency relationships have been derived. Resonance curves have been drawn illustrating influence of various parameters on their shape and uniqueness. Also an impact of damping coefficients and amplitude of the external excitation has been discussed.

The approximate analytical solution has been validated using the proposed measure of the error of fulfillment of the governing equations and also by comparison with the numerical simulation.