A numerical study of the dynamics of three-mass system on frictional tracks

Abstract

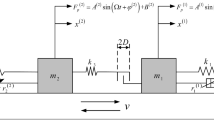
The study of dynamical systems subjected to friction force is of both fundamental and practical importance. In this work, the numerical investigation of the dynamics of a three-mass system where the middle mass slides on a moving track and the two other masses slide on stationary tracks is presented. Friction between the tracks and masses is considered. It is found that the all-stick state, where all masses stick to the tracks, plays a critical role in the qualitative behaviour of the unforced dynamics where period-adding and subcritical graze-sliding bifurcation are observed. The forced vibration due to a harmonic excitation is quasiperiodic in nature. Chaos emerges from large forcing amplitude via a likely Ruelle–Takens route and an exotic route evolved directly from a periodic orbit.

Appendices

Appendix A

The sticking region for the mass $m_{1,2}$ is defined by

$$\begin{aligned} -\Phi _{is}^-<\alpha q_i+\beta q_i^3<\Phi _{is}^+ \end{aligned}$$

(B.1)

and $\Phi _{is}^\pm =\pm \, F_{is}/kd$ for $i=1,2$. The boundary is therefore determined by

$$\begin{aligned} \alpha q_{i,ss}+\beta q_{i,ss}^3=\Phi _{is}, i=1,2 \end{aligned}$$

(B.2)

In general, there are two complex solutions and one real solution for (B.2). The real solution takes the form

$$\begin{aligned} q_{i,ss}={1\over 6}\left( {L\over \beta }\right) ^{1\over 3} - {2\alpha \over \left( L\beta ^2\right) ^{1\over 3}} \end{aligned}$$

(B.3)

and

$$\begin{aligned}&L=L(\alpha ,\beta ,\Phi _{is})\nonumber \\&\quad =12\sqrt{12\alpha ^3+81\beta \Phi _{is}^2\over \beta }+108\Phi _{is} \end{aligned}$$

(B.4)

It is important to note that the value of $q_{i,ss}$ determines the size of the intersection $\Sigma _{18}\cap \Sigma _{28}$. In this case, (B.4) implies that the size of the all-stick region is related to parameters $\alpha ,\beta$ and the static friction. In particular, $\mathrm{diam}(\Sigma _{18}\cap \Sigma _{28})\sim \Phi _{is}^{1/3}$. The size of the all-stick region is also determined by $\Sigma _{38}$ where the factor of $\Gamma$ will come into play. For $\Phi _{1s,2s}=0.105$, $q_{i,ss}=0.1326$ and, for $\Phi _ {1s,2s}=0.25$, $q_{i,ss}=0.3124$ (the case shown in Fig. 6).

Appendix B

The scientific computational package MATLAB is used to carry out the numerical simulation [20]. For the current system, a 3-digit array holding the value 0 or 1 was used to keep track of the transition between the slip/stick states defined by the 8 regions $S_{{\mathbb {N}}_\ell },\ell =1\ldots 8$. The integration routine ode45 in MATLAB is used where the potential transition is triggered by the event function: $\{y_1'=0\}\vee \{y_2'=0\}\vee \{y_3'-V_0=0\}$. The zero-crossing detection of the event function follows the false-position or regula falsi method (odezero). As it is set in MATLAB by default that the event function is called every time a successful integration is achieved, the simulation could potentially be slowed down significantly simply because of the velocity passes through zero. To circumvent this issue, additional codes were added in ode45 to check if the stick/slip transition actually occurs. The integration would be allowed to continue without interruption if the static friction force is overcome. It should be noted that ode45 is based on the, forward, explicit integration scheme. It is necessary to set small tolerances in order to find consistent result (typically in the range of $\le 10^{-8}$). All simulations were carried out for $t\le 15{,}000$, and the results are shown after transient period is skipped.