Abstract
This paper studies the issue of adaptive trajectory tracking control for an underactuated vibro-driven capsule system and presents a novel motion generation framework. In this framework, feasible motion trajectory is derived through investigating dynamic constraints and kernel control indexes that underlie the underactuated dynamics. Due to the underactuated nature of the capsule system, the global motion dynamics cannot be directly controlled. The main objective of optimization is to indirectly control the friction-induced stick–slip motions to reshape the passive dynamics and, by doing so, to obtain optimal system performance in terms of average speed and energy efficacy. Two tracking control schemes are designed using a closed-loop feedback linearization approach and an adaptive variable structure control method with an auxiliary control variable, respectively. The reference model is accurately matched in a finite-time horizon. The key point is to define an exogenous state variable whose dynamics is employed as a control input. The tracking performance and system stability are investigated through rigorous theoretic analysis. Extensive simulation studies are conducted to demonstrate the effectiveness and feasibility of the developed trajectory model and optimized adaptive control system.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Recently, a surge of attentions and contributions has been made towards the researches and applications of autonomous microrobotic systems from robotics and control communities. These systems have extensive applications that demand miniaturized structures working in a restricted space and vulnerable media and providing micro-manipulations, micro-positioning and micro-navigation with a wide mobility range and flexibility, for example, minimally invasive diagnosis and intervention [1], pipeline inspection [2], engineering diagnosis [3], seabed exploration [4] and disaster rescues [5].
Motion principle of the microrobotic systems is one of the crucial issues that determine the capabilities, performance, particularly energy consumption and degrees of autonomy. Some motion systems have been designed and utilized via mimicking the worm progression [6, 7], canoe paddling [8], friction drive [9] and magnetic field [10, 11], which feature complex mechanism structures and make the issue of motion control a challenging task. The vibro-impact capsule systems (e.g. [12,13,14]) employ motion generation principle based on interactions between internal impact force and external static friction. The main idea is so-called stick–slip effects that rectilinear locomotion can be achieved through an internally vibro-impact mass/inertia interacting with the main capsule body, overcoming the resistance forces acting at contacting surface. Additionally, the dynamics of vibro-impact capsule systems is governed by the underactuated configuration, which means the number of independent control inputs is less than the number of degrees-of-freedom (DOF) to be manipulated [15]. Generally speaking, underactuated systems are intractable to control because the conventional approaches are not directly applicable. Synthesis of the control systems for underactuated systems, according to the Brockett’s theorem [16], is always challenging due to the non-holonomic property, complicated internal dynamics and unavailability of feedback linearizability. It is worth mentioning that analytical studies on the dynamics of unactuated subsystem of the underactuated systems are still challenging. Therefore, it is necessary to consider the non-holonomic constraint dynamics between the system and the operating environment into the control system design; as such, the stick–slip effects can be effectively utilized to manipulate the locomotion of the system as a whole.
A number of the control systems have been designed for the underactuated systems with the purpose of reducing the complexity of the control problem through attempting to stabilize merely a subset of the system’s DOF. Several prevailing approaches have been proposed to achieve this objective, for instance, feedback linearization technique [17,18,19,20,21], sliding mode [22,23,24,25], inverse dynamics [26,27,28] and energy-based approaches [29,30,31,32]. It is also worth mentioning that most of the state-of-the-art studies on capsule systems mainly focus on the modelling and analysis of the dynamics and mechanics [12, 13], e.g. dynamic analysis of the system stability under variation of specific system parameters. However, the uncertainties lying in the system dynamics of underactuated systems are non-trivial problems and need to be addressed when designing the control system and planning the motion trajectory. The uncertainties include the time-varying external disturbances and the parametric system uncertainty that could not be known exactly beforehand. Towards this end, adaptive control system designs have attracted significant interests. To develop a roll stabilization system for a monohull ship, an adaptive linear quadratic compensator was designed in [33] to compensate the roll effect through a multilayer perceptron neural network. The trajectory generation and optimized adaptive control problems were studied in [34] for a class of wheeled inverted pendulum vehicle models. After separating the overall system into fully actuated and unactuated subsystems, a linear quadratic regulation optimization approach was employed to design an optimal reference model and an adaptive control scheme was developed in the presence of internal and external uncertainties. An adaptive control scheme was designed in [35] through decoupling of the system’s adaptation and control loops to allow for fast estimation rates and simultaneously to guarantee bounded deviation from a non-adaptive reference system. Fuzzy logic and hierarchical sliding model techniques were integrated into an adaptive control system design in [36] to cope with the unknown and single-input–multi-output systems in the presence of time-varying external disturbances. Towards a wheeled inverted pendulum vehicle with non-holonomic constraints, an error data-based trajectory planning and adaptive control scheme was proposed in [37]. The control problem was considered on kinematic and dynamic levels and approached by combination of indirect fuzzy control and variable structure technique. Generally speaking, these methods typically partition the overall underactuated system into two subsystems, where the first one is fully actuated and the other is unactuated. As such, the control objective is conventionally defined as the asymptotic stabilization of either subsystem to desired values.
In this paper, we consider the optimized adaptive tracking control and trajectory generation for an underactuated vibro-driven capsule system. By analytical investigation of the control indexes, the stick–slip motions and the dynamic constraints in collocated and non-collocated subsets, an optimized trajectory model is established. A closed-loop feedback controller is firstly developed through collocated partial linearization. By introducing an auxiliary control variable, a variable structure-based adaptive controller is constructed to establish the feedback loop in a non-collocated subset and to cope with the parametric uncertainty. The adaptive updating laws for the controller parameters are derived accordantly. Stability of the proposed adaptive control scheme is analysed rigorously and guaranteed by the Lyapunov theory, and the tracking error of the collocated subset can be reduced into a small range.
To sum up, the three main contributions of this paper consist of the following recapitulative aspects:
-
1.
An optimal motion generation model for the pendulum subsystem of the capsule system is derived using dynamic constraints to guarantee motion tracking and obtain optimal locomotion performance in terms of average robot velocity and energy efficacy;
-
2.
Kernel control indexes associated with the dynamic constraints in collocated and non-collocated subsets are designed and evaluated analytically;
-
3.
An auxiliary control variable is proposed to cope with the underactuated properties. This has an advantage to understand how to make appropriate control inputs from the original nonlinear system without partitioning the overall system into subsystems. A variable structure-based adaptive control scheme is developed in order to make the collocated dynamics to match the reference model dynamics in finite time in the presence of the parametric uncertainty.
The rest of this paper is organized as follows. In Sect. 2, the system dynamics and preliminary knowledge of the vibro-driven capsule system are presented. An optimized reference trajectory generator for the actuated subsystem is developed in Sect. 3 such that the stick–slip locomotion of the robot is indirectly manipulated with the satisfactions of the control indexes. Section 4 proposes two tracking control schemes. Extensive simulation studies are conducted in Sect. 5 to verify the effectiveness of the proposed approaches. Finally, concluding remarks and future works are given in Sect. 6.
2 System modelling and preliminaries
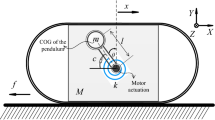
The considered vibro-driven capsule system shown in Fig. 1 contains a pendulum and a platform that merged with the rigid massless capsule shell. The actuator is mounted at the pivot to rotate the pendulum. The interaction between the actuator and the pendulum is described by a linear viscoelastic pair of torsional spring and viscous damper. The parameters of the system are defined as follows: M and m are the masses of the platform and the ball, respectively; l is the length from the pivot to the centre of mass (COM) of the ball; \(\mu \) is the friction coefficient between the platform and ground; k and c are elastic coefficient of the torsional spring and viscous coefficient of the damper, respectively; \(f_c \) denotes the horizontal sliding friction between the robot and the ground; f represents the motor viscous friction at the pivot; \(\theta \) is the angular displacement measured from the vertical; x is the displacement of the platform measured from the initial position; and \(\tau \) is the control torque applied to the pendulum through the actuator. In what follows, for the sake of brevity, \(s_\theta \), \(c_\theta \) and \(S_{\dot{x}}\) are employed to denote the trigonometric function \(\sin \theta \), \(\cos \theta \) and the signal function \(\hbox {Sign}\left( {\dot{x}}\right) \), respectively.
Assumption 1
The centre of gravity (COG) of the pendulum is centralized at the ball and the COM of the platform coincides with the pivot axis.
As shown in Fig. 1, the capsule system is different from the conventional cart and pendulum systems which have been extensively studied [25, 38, 39]. The inverted pendulum that actuated by the motor at the pivot is the driving mechanism of the system, and the motion of the platform is not directly controllable. As the capsule system is used as a mobile autonomous system through controlling the internal pendulum, their control problem is far challenging than the stabilization and swing-up control of the cart–pendulum systems whose cart is typically constrained on a guide rail.
The detailed working principle of the proposed robotic model can be found in our recent work [40]. The robot body is propelled over a surface rectilinearly via the interaction between the driving force and the horizontal sliding friction, generating sticking and slipping motions. Meanwhile, the elastic potential energy is stored and released alternatively in compatible with the contraction and relaxation of the torsional spring. The motion of the platform starts with static state, and it moves when the magnitude of resultant force applied on its body in the horizontal direction exceeds the maximal value of friction force. The definitions of the sticking phase and the slipping phase are given as follows:
Definition 1
The sticking phase is the moment when the magnitude of resultant force applied on the robot body in the horizontal direction is less than the maximal static friction force. The system keeps stationary in this phase.
Definition 2
The slipping phase is the instant when the magnitude of the resultant force applied on the system body in the horizontal direction is larger than the maximal static friction force. When this condition is met, the sticking phase is annihilated and the robot starts to move.
Let the centre of the robot be the origin of the coordinate. Using the Euler–Lagrangian’s method, the underactuated robot dynamics can be derived as
where \(q\left( t \right) =\left[ {\theta \quad x} \right] ^\mathrm{T}\) represents the system state vector. \(M\left( q \right) \in \mathcal{R}^{2\times 2}\) is the inertia matrix, \(C\left( {q,{\dot{q}}} \right) \in \mathcal{R}^{2\times 2}\) denotes the centripetal–Coriolis matrix, \(K\left( q \right) \in \mathcal{R}^{2\times 2}\) is the generalized stiffness matrix, \(\hbox {G}\left( \hbox {q} \right) \in \mathcal{R}^{2\times 1}\) represents the gravitational torques, \(B\in \mathcal{R}^{2\times 1}\) is the control input vector, \(F_d \left( t \right) \) denotes the frictional torques and \(u\in \mathcal{R}^{1}\) denotes the control input torque. Details of the variables are listed as follows: \(M\left( q \right) = \left[ {\begin{array}{cc} {m{l^2}}&{}{ - ml{c_\theta }}\\ { - ml{c_\theta }}&{}{\left( {M + m} \right) } \end{array}} \right] \), \(C\left( {q,\dot{q}} \right) = \left[ {\begin{array}{cc} 0&{}0\\ {ml{s_\theta }\dot{\theta }}&{}0 \end{array}} \right] \), \(K\left( q \right) =\left[ {{\begin{array}{cc} k&{} 0 \\ 0&{} 0 \\ \end{array} }} \right] \), \(G\left( q \right) =\left[ {-mgls_\theta \quad 0} \right] ^\mathrm{T}\), \(B=\left[ {1\quad 0} \right] ^\mathrm{T}\) and \({F_d}\left( t \right) = {\left[ {c\dot{\theta }\quad f} \right] ^\mathrm{T}}\). f denotes the sliding friction force. It is noted that the Coulomb friction model \(f=\mu \left( {M+F_y } \right) S_{{\dot{x}}} , \dot{x}\ne 0\) is assumed in this paper, with \(F_y\) being the internal reaction forces applied on the pendulum by the platform in the vertical direction, and \(g\in \mathcal{R}^{+}\) is the gravitational acceleration.
Remark 1
It is noted that the contact interface is anisotropic, and physical and structural inconsistency of the system parameters may induce asymmetry characteristic of the friction. The value of the stiction force falls into the threshold of the Coulomb friction, i.e. \(\left[ { - \mu \left( {M + {F_y}} \right) {S_{\dot{x}}},~\mu \left( {M + {F_y}} \right) {S_{\dot{x}}}~} \right] \). This is due to the sticking phase and largely relying on the magnitudes of the external forces.
The Lagrangian dynamics of the underactuated vibro-driven capsule system described by (1) has the following beneficial properties [34, 41, 42]:
Property 1
The inertia matrix \(M\left( {q,\alpha } \right) \) is symmetric and uniformly positive definite, and it has upper and lower boundaries satisfying the following inequalities
where \(M\left( {q,\alpha } \right) \) is the unknown inertia matrix of the system, \(\lambda _\mathrm{min} \left( \alpha \right) \) and \(\lambda _\mathrm{max} \left( \alpha \right) \) are two strictly positive constants denoting the minimum and the maximum eigenvalues of \(M\left( {q,\alpha } \right) \), \(\alpha \in \mathcal{R}^{p}\) is the vector of unknown parameters of the system mainly including the base initial parameters and possible loading parameters (p indicates the number of uncertain parameters) and \(\Vert \cdot \Vert \) denotes the standard Euclidean norm.
Property 2
The above matrixes \( M\left( {q,\alpha } \right) \) and \( C\left( {q,\dot{q},\alpha } \right) \) have the following particular skew-symmetric interconnection
under an appropriate definition of the unknown centripetal–Coriolis matrix \(C\left( {q,\dot{q},\alpha } \right) \). This property is a matrix version of energy conservation.
Property 3
The dynamic model (1) can be rewritten in a linear form with respect to an appropriate selection of initial estimation of the system’s base parameters and load parameters \(\alpha \) . Furthermore, there exist a regressor matrix \(Y\left( {q,\dot{q},\ddot{q}} \right) \) and a vector \(Y_0 \left( {q,\dot{q},\ddot{q}} \right) \) which contain known functions, which gives
3 Optimized trajectory model
3.1 Trajectory generation
To efficiently utilize the stick–slip effect and drive the capsule system move in one direction, a two-stage motion trajectory is designed. The definitions are firstly given as follows:
Definition 3
Progressive stage: driving the pendulum with higher angular acceleration incorporating with the release of the elastic energy stored in the torsional spring that leads the robot to overcome the maximal static friction to generate a slipping motion (\(\dot{x} \ne 0\)).
Definition 4
Restoring stage: returning the pendulum to initial position slowly to restore potential energy and prepare for the next cycle, the resultant force exerting on the robot body in the horizontal direction is less than the maximum dry friction, that is, the robot is kept in the sticking phase in this stage (\(\dot{x} = 0\)).
Definition 5
[43] The set of DOF of underactuated systems can be partitioned into two subsets, which referred to as collocated subset with its cardinality containing the actuated DOF and equalling to the number of control inputs; and non-collocated subset accounts for the remaining non-actuated DOF.
Based on practical control indexes and dynamic constraints associated with the stick–slip locomotion of the robot, the following principles are designed as objectives need to be achieved to establish an optimal motion trajectory model for the driving pendulum:
Principle 1
For each motion cycle, the pendulum is constrained to rotate within an advisable angle range; with this regard, the upper and lower boundaries are given as
where \(\theta _0 \) is the prescribed angle of the driving pendulum.
Principle 2
The angular velocity and angular acceleration of the driving pendulum need to be placed within bounded ranges, given by
where \(\fancyscript{{v}}_\theta \in \mathcal{{R}}^{+}\) and \({\fancyscript{a}}_\theta \in \mathcal{R}^{+}\) are the absolute boundary values of angular velocity and acceleration, respectively.
Principle 3
The robot is contacting with the sliding surface, and the contact force in the vertical direction has to be always greater than zero to maintain non-bounding motion, which gives
Principle 4
The robot has to be remained stationary after the progressive motion to wait for the pendulum’s return. In this occasion, the force of the driving pendulum applied on the robot in the horizontal direction has to be less than the maximal static friction, which yields
The forward motion of the unactuated subsystem cannot be directly controlled by the torque input but is directly affected by the pendulum dynamics. This inspires the authors to control the robot motion indirectly through the pendulum angular velocity reference trajectory.
Remark 2
Principles 1 and 2 are associated with the collocated subset of the overall DOF which is prone to control and can be achieved through conventional approaches. Nevertheless, Principles 3 and 4 are of vital importance for the non-collocated robot locomotion and energy efficacy. Therefore, in this paper, both of these principles are explicitly considered to establish the optimal trajectory model.
Consider the above design principles, a reference trajectory profile is generated for the actuated pendulum subsystem as shown in Fig. 2. Please refer to [21] for a detailed description of each phase and the overall profile.
The designed trajectory model can be described as
where \( P_1 \omega \) and \(P_3 \) are upper and lower trajectory boundaries, respectively. \(P_2 \) is the critical boundary when the robot keeps stationary, and \(\omega \) is the frequency of excitation.
3.2 Optimum selection of the trajectory parameters
Conventional approaches for robot motion planning are not directly applicable to the non-collocated subset; as a result, Principles 3 and 4 imposed on the robot locomotion need to be fully considered when planning an efficient nominal forced trajectory. The following lemmas are firstly given to characterize the constrained stick–slip motions.
Lemma 1
From the designed control index in Principle 3, the non-bounding motion of the robot can be achieved if the following inequality is satisfied
where \(\varpi =\frac{\left( {M+m} \right) g}{\sqrt{ml}}\).
Proof
The control index in Principle 3 can be reorganized to generate the following inequality
Enlarging the inequality in (11), a sufficient condition can be given based on the auxiliary angle formula, which yields
Subsequently, based on the AM–GM inequality theorem, we have
Therefore, the following inequality is obtained as
\(\square \)
Lemma 2
From the designed control index in Principle 4, the robot performs the sticking motion in the restoring stage if the following inequality is satisfied
where \(\varpi ^{\prime }=\frac{\left( {M+m} \right) g}{ml},\vartheta =\mu /\sqrt{\mu ^{2}+1}\).
Proof
The control index in Principle 4 can be reorganized by removing the absolute value and considering one side of the inequality, which gives
The above equation is reorganized as
Enlarging the inequality in Eq. (17), a sufficient condition can be given based on the auxiliary angle formula, which yields
Therefore, the following inequality is obtained as
The result proposed here is also applicable to the other side of the inequality. \(\square \)
Define the boundary conditions as \(\dot{x}{\left( t \right) _{\left| {t = {t_0},\mathrm{{~}}{t_3},{t_7}} \right. }} = 0\), \(\theta {\left( t \right) _{\left| {t = {t_0},{t_7}} \right. }} = - {\theta _0},~\theta {\left( t \right) _{\left| {t = {t_3}} \right. }} = {\theta _0},~\dot{\theta }{\left( t \right) _{\left| {t = {t_0}} \right. }} = 0\), we have
\( P_1 , P_2\) and \( P_3 \): integrating the robot dynamics (1) once along one full motion cycle, we have
Then, in the duration \(\left[ {0,t_3 } \right] \), \(P_2 \) can be obtained under the condition that \(mlc_{\theta _0 } +\mu mls_{\theta _0 } \ne 0\). We have
Based on the energy conservation principle, it gives
In order to optimally select the durations for each phase, Lemmas 1 and 2 towards the dynamic constraints are explicitly utilized.
\(t_1 \) and \(t_2 \): during Phase I and applying Lemma 1 at time \(t_1 \), the following inequality can be obtained as
where \(\dot{\theta }\left( {{t_1}} \right) = {P_1}\omega \) , \(\ddot{\theta }\left( {{t_1}} \right) = 0\) and \(\theta \left( {t_1 } \right) =P_1 \omega t_1 \).
As such, the upper boundary of the duration of Phase I is obtained as
The formulation for Phase II can be described as \(P_1 \omega s_{\omega t_3 -t_2 } =P_2 \); thus, the duration is obtained as
\( t_3 , t_4 \) and \( t_5 \): The motion trajectory is designed to reach the amplitude of the harmonic excitation at time \(\tau _1 \) and keep it till time \(\tau _2 \), and as such, the duration of this phase has to be half of the motion period of the excitation. In this regard, the duration Phase III can be yielded as
For the duration of Phase IV, the robot is controlled to perform a sticking motion and it is kept stationary, and the angular velocity of the driving pendulum gradually returns to zero. Applying Lemma 2 to Phases IV and V yields
where \(\theta \left( {t_3 } \right) =P_2 t_3 \), \(\dot{\theta } \left( {{t_3}} \right) = {P_2}\), \(\ddot{\theta }\left( {{t_3}} \right) = - {P_2}/\left( {{t_4} - {t_3}} \right) \); \(\ddot{\theta }\left( {{t_5}} \right) = 0\), \(\dot{\theta }\left( {{t_5}} \right) = {P_3}\), \( \theta \left( {t_5 } \right) =P_3 t_5 \).
Accordingly, we have
\( t_6 \) and \( t_7 \): A formulation can be achieved in the duration of \(\left[ {t_4 ,t_5 } \right] \) as
It is noted that the durations for Phase VI \(\left[ {\tau _4 ,\tau _5 } \right] \) and Phase VII \( \left[ {\tau _6 ,\tau _7 } \right] \) are accordant based on the design principles of the proposed trajectory, i.e. \(\tau _5 =\tau _7 -\tau _6 +\tau _4 \). Therefore, the durations for Phases VI and VII can be obtained through combination of Eq. (29) with Eq. (21), and we have
Remark 3
The proposed motion trajectory model can be adopted either as a motion pattern generator or as a motion pattern regulator in motion planning and control of underactuated or non-holonomic robotic systems, for example, in the manipulation robotic system mounted on a mobile platform for picking and grasping tasks. Also, the self-propelled robotic model can be potentially cascaded together in numbers to generate propagation of undulatory motions with flexible properties, and this may make sense to traverse and move/push the obstacles in cluttered environment. This will significantly enhance manoeuvrability and agility of the robot particularly when working in extreme scenarios such as nuclear facilities.
4 Tracking controller design
In this section, the objective of designing trajectory tracking controllers is twofold. Firstly, to verify the superior performance of the capsule system under the proposed trajectory planning approach and to make convenient comparison with a conventional approach, a closed-loop feedback control scheme is considered. On the other hand, an adaptive variable structure trajectory tracking control algorithm with an auxiliary control input is constructed to cope with the parametric uncertainty. It is noted that the duration of each motion phase is fixed; using equations of motion (1), the prior knowledge of desired robot trajectory for the progressive stage for each sampling time can be obtained by convenient computation.
4.1 Closed-loop feedback control
To verify the robot performance with the optimized trajectory model and to make comparisons with the conventional approach, a closed-loop feedback tracking control system is designed in this subsection. On the basis of the dynamic model in (1) and after some calculations, we have
Define the trajectory tracking error and its derivatives as
Substituting (33) into (32) and conducting appropriate mathematical manipulation, we have the following system dynamics
Then from (34), a feedback linearizing controller can be designed as
where \(K_v \) and \(K_p \) are positive control gains selected by the designer.
Substituting the tracking controller (35) into system (34), the closed-loop system error function can be obtained in the following form
Therefore, it is evident through the Routh–Hurwitz criterion that the system stability is guaranteed. Concretely, a linear combination of independent solutions for (36) gives the general solution of the trajectory tracking error \(\tilde{\theta }\left( t\right) \) as
where \(c_1 \) and \(c_2 \) are positive constant. Therefore, it can be concluded that the designed tracking controller (35) makes the tracking error \(\tilde{\varTheta }\left( t \right) \) converge to zero exponentially and drive the pendulum to follow the planned trajectory exponentially fast.
4.2 Variable structure-based adaptive controller with an auxiliary control variable
This subsection considers the circumstance when parametric uncertainty presents; in other words, the system base parameters are unknown. As stated, the main difficulty exists in the nonlinearity of the collocated inverse dynamics with respect to the base parameters, which makes the applications of conventional adaptive control algorithms not directly available. Therefore, an auxiliary control variable is designed in this paper to establish the non-collocated feedback loop.
In the following, new vector variables are defined as
where \(\delta \) denotes the filtered error signal and describes the measure of tracking accuracy, \(\varrho \) is referred to as vector of the reference trajectory and \({\varLambda }=\left[ {{\varLambda }_\theta { \varLambda }_x } \right] ^\mathrm{T}\) are positive constants selected by designers and denoting for the bandwidth of the first-order filter.
Alongside (37), two sliding variables \(\delta _\theta \) and \(\delta _x \) are designed for the collocated and non-collocated subsets, respectively. The error dynamics with respect to the defined sliding variables can be derived from (1) and (37) as
where \(N_\theta \left( t \right) \) and \(N_x \left( t \right) \) represent nonlinear functions with unknown base parameters detailed as follows:
Remark 4
The filtered error dynamics (38) satisfies Properties 3 and 4.
Accounting for the parametric uncertainty existing in \(Y_\theta \alpha _\theta \) and \(Y_x \alpha _x \) and based on the filtered error dynamics (38), the following theorem presents an adaptive variable structure control scheme with an auxiliary control variable that ensures asymptotic convergence of the collocated error signals.
Theorem 1
Consider the vibro-driven capsule system modelled by (1) with parametric uncertainty, if the following control system is applied to the underactuated robot system as
with the adaptation laws
where the subscripts “c” and “n” indicate the collocated and non-collocated, respectively. \(K_1, K_2 , K_3 \in \mathcal{R}^{1}\) are diagonal, constant positive definite matrices. \(\varGamma _1 \in \mathcal{R}^{1}\) and \(\varGamma _2 \in \mathcal{R}^{1}\) are positive definite matrices determining the rate of adaptation. \(\beta >0\) is a selected small constant. \(\eta \) is a designed auxiliary control variable. \(\tilde{\alpha }_\theta \left( t \right) = \hat{\alpha }_\theta \left( t \right) -\alpha _\theta \left( t \right) \) and \(\tilde{\alpha }_x \left( t \right) =\hat{\alpha } _x \left( t \right) -\alpha _x \left( t \right) \) are parameter estimation errors. Then, the following conclusions hold:
-
(1)
The system is globally asymptotically stabilized;
-
(2)
All signals in the closed-loop system are bounded and uniformly continuous;
-
(3)
The asymptotical convergence of the collocated error signals is guaranteed.
Proof
Consider the following Lyapunov function as
Differentiating both sides of (40) and substituting the control laws (39) yield
Adopting Properties 1 and 2 and substituting the auxiliary control variable in (39c) with its evolving law (39d), we have
From the definition of the Lyapunov function, V is lower bounded by zero and decreases for any nonzero \(\delta \) as shown from (41). It is evident from the above mathematical proof that the global uniform boundedness of the filtered tracking error of the collocated subset \(\delta _\theta \) and the non-collocated subset \(\delta _x \), the parameter estimation errors \(\tilde{\alpha }~ _\theta \) and \(\tilde{\alpha }~ _x \) are guaranteed. Note that the reference trajectory and its first- and second-order derivatives are well defined and bounded; then from the definition of filtered tracking error \(\delta \), it is evident that \(\delta \) is bounded. The boundedness of control input is obvious from (39). The uniform continuity of \({\dot{V}}\) can be checked through its derivative \(\ddot{{V}}\), which is concluded to be bounded. Hence, the uniformly continuity of \({\dot{V}}\) is guaranteed. We arrive that the collocated error signal \(\delta _\theta \in L_2^n \cap L_\infty ^n \), and it is also evident that \({\dot{\delta }}\in L_\infty ^n\) from (38); thus, application of Barbalat’s Lemma indicates that \(\delta _\theta \) is continuous and \(\delta _\theta \rightarrow 0\) as \(t\rightarrow \infty \), and \(\eta \in L_\infty \). From (39d), it is also shown that \(\tilde{\alpha }~ _\theta \in L_\infty ^p \). This in turns implies, based on Property 1 and (38), that the collocated error signals \({\dot{\delta }}\in L_\infty ^n\) and \( \tilde{\theta }~ \in L_\infty ^n \). Therefore, we can conclude that the collocated error \({\tilde{\theta }}\) is uniformly continuous and its convergence \(\tilde{\theta }\rightarrow 0\) as \(t\rightarrow \infty \). \(\square \)
5 Simulation studies
In this section, a number of numerical simulations are conducted to verify the performance and efficiency of the proposed trajectory planning scheme and the adaptive tracking control scheme. In particular, the advantages of the planned trajectory such as smooth transition in progressive stage, superior efficiency in progression and energy consumption are presented. In the simulation, the system parameters are configured as \(M=0.5\) kg, \(m=0.138\) kg, \(l=0.3\) m, \(g=9.81\, \hbox {m}/\hbox {s}^{2}\), \(\mu =0.01 \) N/ms and the system natural frequency \(\omega _n =5.7184\) rad/s. The control parameters are configured as \(k=0.36\) Nm/rad and \(c=0.0923 \,\hbox {kg\,m}^{2}/\hbox {s\,rad}\) to obtain optimal steady-state motion. The optimal selection of viscoelastic parameters will be reported in another paper. The initial conditions are set as \(\theta \left( 0 \right) =\theta _0 =\pi /3\), \({\dot{\theta }}(0)=0\), \(x\left( 0 \right) =0\) and \({\dot{x}}(0)=0\).
Firstly, in the absence of parametric uncertainty, comparative studies are performed with [20] (referred to as EPC system), in which a two-stage velocity trajectory is proposed using conventional approach with heuristically chosen control parameters. Control scheme (35) is employed to make convenient comparison. Based on the optimized trajectory model studied in Sect. 3, the parameters for the constructed trajectory (9) and the trajectory in [20] are detailed in Table 1.
The simulation results are presented in Figs. 3, 4 and 5. It can be clearly observed from Fig. 3 that the maximum angular velocity using the proposed scheme is about 7.8 rad/s, which is lower than the EPC system with 11 rad/s. The synchronized trajectory present better transient performance in terms of the overshoot and the maximum pendulum swing is about \(68.75^{\circ }\) (\(17.1^{\circ }\) smaller than the EPC system). These results have good agreements with the trajectory planning indexes and principles. The average velocity with the proposed trajectory calculated from Fig. 4 for the first five cycles is \(0.642\,\hbox {cm}/\hbox {s}\), whereas it is \(0.629\,\hbox {cm}/\hbox {s}\) for the EPC system. The transition functions inserted into progressive stage guarantee the smooth transition and thereafter a lower maximum input torques as shown in Fig. 5 (0.5367 Nm compared with 0.6246 Nm of EPC system). This directly demonstrates a superior performance in energy efficacy. The backward motions are sufficiently suppressed as shown in Fig. 4. The results conclude that the friction-induced stick–slip motions are precisely controlled through the proposed optimal trajectory model; as such, the superior performances are guaranteed.
Subsequently, the adaptive tracking control scheme in (39) is evaluated in the presence of parametric uncertainty. The mass of the robot body M and the friction coefficient \(\mu \) are assumed uncertain with known bounds, i.e. \(0.45\,\hbox {kg}\le M\le 0.55\,\hbox {kg}\) and \(0.009\,\hbox {N/ms}\le \mu \le 0.011\,\hbox {N/ms}\). This is under the consideration that the mass of robot body may vary when working in the environment with high degree of viscosity or humidity and the robot may be glued on environmental component such as water, mud and mucus. And the sliding friction coefficient is undergoing changes at different substrates. The bandwidth of the first-order filter is set as \(\varLambda =\left[ {\varLambda _\theta \quad \varLambda _x } \right] ^\mathrm{T}=\left[ {12\quad 30} \right] ^\mathrm{T}\). The control gains used in the simulation are chosen to be \(K_1 =1.3\), \(K_2 =10\) and \(K_3 =50\). As a result, the associated base parameters are \(\alpha _\theta =\left[ {0.01424,0.0414,0.36,0.0923,0.40527} \right] ^\mathrm{T}\) and \(\alpha _x =\left[ {0.0414, 0.638, 0.01, 0.0414} \right] ^\mathrm{T}\). The adaptation gains are chosen as \(\varGamma _1 =0.1\) and \(\varGamma _2 =0.1\). The simulation results of trajectory tracking performance using the adaptive control scheme (39) are shown in Figs. 6, 7 and 8. The planned collocated trajectory (9) (red dashed line), the simulated trajectory (black solid line) in Fig. 6 and the trajectory tracking error in Fig. 7 are portrayed. From Fig. 7, the angular velocity will eventually converge to zero as we desire. It can be observed that the driving pendulum tracks the planned trajectory accurately and the maximum angular velocity is about 7.9 rad/s. The control input torque is shown in Fig. 8. The figure illustrates the effectiveness of the designed control scheme. The sliding variables are considered as the difference between the system’s velocity and an exogenous state. Therefore, Fig. 9 clearly demonstrates the convergence towards zero of the collocated sliding variable \(\delta _\theta \). As clearly shown by the simulation results, in the presence of unknown system parameters, the proposed variable structure-based adaptive control scheme is able to guarantee exact tacking of the collocated (pendulum) subsystem. Therefore, the proposed control scheme is efficient in the presence of unknown nonlinear dynamic systems.
6 Conclusions
In this paper, the issues of optimal motion trajectory generation and adaptive tracking control of an underactuated vibro-driven capsule system have been studied. An optimized trajectory model has been proposed to efficiently manipulate the robot stick–slip motions with optimality in almost unidirectional progression and energy efficacy. By doing so, the dynamics of the actuated pendulum subsystem has been reshaped to indirectly control the forward motion of the unactuated robot subsystem. Two tracking control schemes are constructed with rigorous convergence analysis, wherein an auxiliary control variable is designed for the adaptive variable structure control of underactuated capsule systems in the presence of parametric uncertainties. Asymptotic stability of the proposed control systems and convergence of the collocated error signals for the system dynamics are shown by means of Lyapunov theory and illustrated through the simulation studies. Based on the current endeavours and achievements in trajectory optimization, advanced control and modelling and analysis of dynamic frictional interactions [40], the future work will be emphasized on the experimental tests, validations and further investigations of the findings in real environments.
References
Ergeneman, O., Chatzipirpiridis, G., Pokki, J., Marin-Suárez, M., Sotiriou, G.A., Medina-Rodriguez, S., Sánchez, J.F.F., Fernandez-Gutiérrez, A., Pane, S., Nelson, B.J.: In vitro oxygen sensing using intraocular microrobots. IEEE Trans. Biomed. Eng. 59, 3104–3109 (2012)
Wang, Z., Gu, H.: A bristle-based pipeline robot for Ill-constraint pipes. IEEEASME Trans. Mechatron. 13, 383–392 (2008)
Sitti, M.: Miniature devices: voyage of the microrobots. Nature 458, 1121–1122 (2009)
Fang, H.-B., Xu, J.: Controlled motion of a two-module vibration-driven system induced by internal acceleration-controlled masses. Arch. Appl. Mech. 82, 461–477 (2012)
Tang, Y., Chen, C., Khaligh, A., Penskiy, I., Bergbreiter, S.: An ultracompact dual-stage converter for driving electrostatic actuators in mobile microrobots. IEEE Trans. Power Electron. 29, 2991–3000 (2014)
Rashid, M.T., Frasca, M., Ali, A.A., Ali, R.S., Fortuna, L., Xibilia, M.G.: Artemia swarm dynamics and path tracking. Nonlinear Dyn. 68, 555–563 (2012)
Becker, T.C., Mahin, S.A.: Effect of support rotation on triple friction pendulum bearing behavior. Earthq. Eng. Struct. Dyn. 42, 1731–1748 (2013)
Kim, H.M., Yang, S., Kim, J., Park, S., Cho, J.H., Park, J.Y., Kim, T.S., Yoon, E.-S., Song, S.Y., Bang, S.: Active locomotion of a paddling-based capsule endoscope in an in vitro and in vivo experiment (with videos). Gastrointest. Endosc. 72, 381–387 (2010)
Eigoli, A.K., Vossoughi, G.R.: Dynamic analysis of microrobots with Coulomb friction using harmonic balance method. Nonlinear Dyn. 67, 1357–1371 (2012)
Ciuti, G., Valdastri, P., Menciassi, A., Dario, P.: Robotic magnetic steering and locomotion of capsule endoscope for diagnostic and surgical endoluminal procedures. Robotica 28, 199–207 (2010)
Yim, S., Gultepe, E., Gracias, D.H., Sitti, M.: Biopsy using a magnetic capsule endoscope carrying, releasing, and retrieving untethered microgrippers. IEEE Trans. Biomed. Eng. 61, 513–521 (2014)
Liu, Y., Wiercigroch, M., Pavlovskaia, E., Yu, H.: Modelling of a vibro-impact capsule system. Int. J. Mech. Sci. 66, 2–11 (2013)
Liu, Y., Pavlovskaia, E., Wiercigroch, M.: Experimental verification of the vibro-impact capsule model. Nonlinear Dyn. 83, 1029–1041 (2016)
Liu, P., Yu, H., Cang, S.: Geometric analysis-based trajectory planning and control for underactuated capsule systems with viscoelastic property. Trans. Inst. Meas. Control. 40, 2416–2427 (2017)
Ravichandran, M.T., Mahindrakar, A.D.: Robust stabilization of a class of underactuated mechanical systems using time scaling and Lyapunov redesign. IEEE Trans. Ind. Electron. 58, 4299–4313 (2011)
Brockett, R.W., et al.: Asymptotic stability and feedback stabilization. Differ. Geom. Control Theory 27, 181–191 (1983)
Li, H., Furuta, K., Chernousko, F.L.: Motion generation of the capsubot using internal force and static friction. In: Proceedings of the 45th IEEE Conference on Decision and Control, pp. 6575–6580. IEEE (2006)
Yu, H., Liu, Y., Yang, T.: Closed-loop tracking control of a pendulum-driven cart-pole underactuated system. Proc. Inst. Mech. Eng. Part J. Syst. Control Eng. 222, 109–125 (2008)
Huda, M.N., Yu, H.: Trajectory tracking control of an underactuated capsubot. Auton. Robots 39, 183–198 (2015)
Liu, P., Yu, H., Cang, S.: Modelling and control of an elastically joint-actuated cart-pole underactuated system. In: 2014 20th International Conference on Automation and Computing (ICAC), pp. 26–31. IEEE (2014)
Liu, P., Yu, H., Cang, S.: On periodically pendulum-diven systems for underactuated locomotion: a viscoelastic jointed model. Presented at the September (2015)
Xu, J.-X., Guo, Z.-Q., Lee, T.H.: Design and implementation of integral sliding-mode control on an underactuated two-wheeled mobile robot. IEEE Trans. Ind. Electron. 61, 3671–3681 (2014)
Yu, R., Zhu, Q., Xia, G., Liu, Z.: Sliding mode tracking control of an underactuated surface vessel. IET Control Theory Appl. 6, 461–466 (2012). https://doi.org/10.1049/iet-cta.2011.0176
Huang, J., Guan, Z.-H., Matsuno, T., Fukuda, T., Sekiyama, K.: Sliding-mode velocity control of mobile-wheeled inverted-pendulum systems. IEEE Trans. Robot. 26, 750–758 (2010)
Adhikary, N., Mahanta, C.: Integral backstepping sliding mode control for underactuated systems: swing-up and stabilization of the cart-pendulum system. ISA Trans. 52, 870–880 (2013)
Blajer, W., Dziewiecki, K., Kołlodziejczyk, K., Mazur, Z.: Inverse dynamics of underactuated mechanical systems: a simple case study and experimental verification. Commun. Nonlinear Sci. Numer. Simul. 16, 2265–2272 (2011)
Erez, T., Todorov, E.: Trajectory optimization for domains with contacts using inverse dynamics. In: 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 4914–4919. IEEE (2012)
Mistry, M., Buchli, J., Schaal, S.: Inverse dynamics control of floating base systems using orthogonal decomposition. In: 2010 IEEE International Conference on Robotics and Automation (ICRA), pp. 3406–3412. IEEE (2010)
Xin, X., Yamasaki, T.: Energy-based swing-up control for a remotely driven Acrobot: theoretical and experimental results. IEEE Trans. Control Syst. Technol. 20, 1048–1056 (2012)
Sun, N., Fang, Y., Zhang, X.: Energy coupling output feedback control of 4-DOF underactuated cranes with saturated inputs. Automatica 49, 1318–1325 (2013)
Albu-Schäffer, A., Petit, C.O.F.: Energy shaping control for a class of underactuated Euler–Lagrange systems. IFAC Proc. 45, 567–575 (2012)
Valentinis, F., Donaire, A., Perez, T.: Energy-based motion control of a slender hull unmanned underwater vehicle. Ocean Eng. 104, 604–616 (2015)
Fortuna, L., Muscato, G.: A roll stabilization system for a monohull ship: modeling, identification, and adaptive control. IEEE Trans. Control Syst. Technol. 4, 18–28 (1996)
Yang, C., Li, Z., Li, J.: Trajectory planning and optimized adaptive control for a class of wheeled inverted pendulum vehicle models. IEEE Trans. Cybern. 43, 24–36 (2013)
Nguyen, K.-D., Dankowicz, H.: Adaptive control of underactuated robots with unmodeled dynamics. Robot. Auton. Syst. 64, 84–99 (2015)
Hwang, C.-L., Chiang, C.-C., Yeh, Y.-W.: Adaptive fuzzy hierarchical sliding-mode control for the trajectory tracking of uncertain underactuated nonlinear dynamic systems. IEEE Trans. Fuzzy Syst. 22, 286–299 (2014)
Yue, M., An, C., Du, Y., Sun, J.: Indirect adaptive fuzzy control for a nonholonomic/underactuated wheeled inverted pendulum vehicle based on a data-driven trajectory planner. Fuzzy Sets Syst. 290, 158–177 (2016)
Ghosh, A., Krishnan, T.R., Subudhi, B.: Robust proportional–integral–derivative compensation of an inverted cart-pendulum system: an experimental study. IET Control Theory Appl. 6, 1145–1152 (2012)
Tao, C.W., Taur, J., Chang, J.H., Su, S.-F.: Adaptive fuzzy switched swing-up and sliding control for the double-pendulum-and-cart system. IEEE Trans. Syst. Man Cybern. Part B Cybern. 40, 241–252 (2010)
Liu, P., Yu, H., Cang, S.: Modelling and dynamic analysis of underactuated capsule systems with friction-induced hysteresis. In: 2016 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), pp. 549–554. IEEE (2016)
Pucci, D., Romano, F., Nori, F.: Collocated adaptive control of underactuated mechanical systems. IEEE Trans. Robot. 31, 1527–1536 (2015)
Fang, Y., Ma, B., Wang, P., Zhang, X.: A motion planning-based adaptive control method for an underactuated crane system. IEEE Trans. Control Syst. Technol. 20, 241–248 (2012)
Spong, M.W.: Underactuated mechanical systems. In: Siciliano, B., Valavanis, K.P. (eds.) Control Problems in Robotics and Automation, pp. 135–150. Springer, Berlin (1998)
Acknowledgements
This work was partially supported by European Commission Marie Skłodowska-Curie SMOOTH (Smart robots for fire-fighting) project (H2020-MSCA-RISE-2016-734875)—http://fusion-edu.eu/SMOOTH/, Royal Society International Exchanges Scheme (Adaptive Learning Control of a Cardiovascular Robot using Expert Surgeon Techniques) project (IE151224) and European Commission International Research Staff Exchange Scheme (IRSES) RABOT project (PIRSES-GA-2012-318902)—http://rabot.fusion-edu.eu/.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Liu, P., Yu, H. & Cang, S. Optimized adaptive tracking control for an underactuated vibro-driven capsule system. Nonlinear Dyn 94, 1803–1817 (2018). https://doi.org/10.1007/s11071-018-4458-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-018-4458-9