Skip to main content
SpringerLink
Log in

General high-order breathers, lumps in the \(\mathbf (2+1) \)-dimensional Boussinesq equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

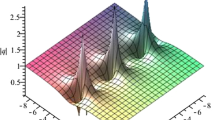
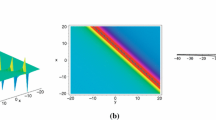
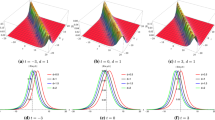
Under investigation in this work is a generalized \((2 + 1)\)-dimensional Boussinesq equation. By employing the Bell’s polynomials, bilinear formalism of this generalized \((2+1)\)-dimensional Boussinesq equation is succinctly derived. With the aid of the obtained bilinear formalism, general high-order breather solutions are constructed by using the Hirota’s bilinear method combined with the perturbation expansion. The breathers only periodically propagate along the x-direction. Taking a long-wave limit of the obtained breather solutions and then making further parameter constraints, general smooth rational solutions to the generalized \((2 + 1)\)-dimensional Boussinesq equation would be succinctly constructed. These smooth rational solutions are high-order lumps and mixed solutions comprising a line rogue wave and lumps. These results exhibit the dynamical behavior of the generalized \((2+1)\)-dimensional nonlinear wave fields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10

Similar content being viewed by others

References

  1. Wang, L., Zhang, J.H., Liu, C., Li, M., Qi, F.H.: Breather transition dynamics, Peregrine combs and walls, and modulation instability in a variable-coefficient nonlinear Schrödinger equation with higher-order effects. Phys. Rev. E. 93, 062217 (2016)

    Article  MathSciNet  Google Scholar 

  2. Wang, L., Li, M., Qi, F.H., Xu, T.: Modulational instability, nonautonomous breathers and rogue waves for a variable-coefficient derivative nonlinear Schrödinger equation in the inhomogeneous. Plasmas 22, 032308 (2015)

    Article  Google Scholar 

  3. Mihalache, D.: Multidimensional localized structures in optics and Bose–Einstein condensates: a selection of recent studies. Rom. J. Phys. 59, 295–312 (2014)

    Google Scholar 

  4. Bagnato, V.S., Frantzeskakis, D.J., Kevrekidis, P.G.: Bose–Einstein condensation: twenty years after. Rom. Rep. Phys. 67, 251–253 (2015)

    Google Scholar 

  5. Malomed, B., Torner, L., Wise, F., Mihalache, D.: On multidimensional solitons and their legacy in contemporary atomic, molecular and optical physics. J. Phys. B At. Mol. Opt. Phys. 49, 17 (2016)

    Article  Google Scholar 

  6. Kevrekidis, P.G., Frantzeskakis, D.J.: Solitons in coupled nonlinear Schrödinger models: a survey of recent developments. Rev. Phys. 1, 140–153 (2016)

    Article  Google Scholar 

  7. Bluman, G.W., Kumei, S.: Symmetries and Differential Equations. Springer, Berlin (1989)

  8. Matveev, V.B., Salle, M.A.: Darboux Transformation and Solitons. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  9. Gu, C.H., Hu, H.S., Zhou, Z.X.: Darboux Transformation in Soliton Theory and Geometric Applications. Shanghai Science and Technology Press, Shanghai (1999)

    Google Scholar 

  10. Ablowitz, M.J.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  11. Dickey, L.A.: Soliton Equations and Hamiltonian Systems. World Scientific, Singapore (2003)

    Book  MATH  Google Scholar 

  12. Matsuno, Y.: Bilinear Transformation Method. Academic, New York (1984)

    MATH  Google Scholar 

  13. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  14. Date, E., Kashiwara, M., Jimbo, M., Miwa, T.: Transformation groups for soliton equations. In: Jimbo, M., Miwa, T. (eds.) Nonlinear Integrable Systems—Classical Theory and Quantum Theory, p. 39C119. World Scientific, Singapore (1983)

    Google Scholar 

  15. Jimbo, M., Miwa, T.: Solitons and infinite dimensional Lie algebras. Publ. Res. Inst. Math. Sci. 19(3), 943–1001 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  16. Ohta, Y., Wang, D.S., Yang, J.: General N-dark–dark solitons in the coupled nonlinear Schrödinger equations. Stud. Appl. Math. 127(4), 345–371 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  17. Rao, J.G., Wang, L.H., Zhang, Y., He, J.S.: Rational solutions for the Fokas systems. Commun. Theor. Phys. 64(12), 605–618 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  18. Rao, J.G., Porsezian, K., He, J.S.: Semi-rational solutions of the third-type Davey–Stewartson equation. Chaos 27(8), 083115 (2017)

    Article  MathSciNet  Google Scholar 

  19. Rao, J.G., Cheng, Y., He, J.S.: Rational and semi-rational solutions of the nonlocal Davey–Stewartson equations. Stud. Appl. Math. 139, 568–598 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  20. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A. 379(36), 1975–1978 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ma, W.X., Qin, Z.Y., Lü, X.: Lump solutions to dimensionally reduced p-gKP and p-gBKP equations. Nolinear Dyn. 84(2), 923–931 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  22. Yang, J.Y., Ma, W.X.: Lump solutions to the BKP equation by symbolic computation. Int. J. Mod. Phys. B 30, 1640028 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  23. Kheybari, S., Darvishi, M.T., Wazwaz, A.M.: A semi-analytical algorithm to solve systems of integro-differential equations under mixed boundary conditions. Appl. Math. Comput. 317, 72–89 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  24. Darvishi, M.T., Najafi, M., Wazwaz, A.M.: Soliton solutions for Boussinesq-like equations with spatio-temporal dispersion. Ocean Eng. 130, 228–240 (2017)

    Article  Google Scholar 

  25. Wazwaz, A.M.: Abundant solutions of various physical features for the (2+1)-dimensional modified KdV-Calogero–Bogoyavlenskii–Schiff equation. Nolinear Dyn. 89, 1727–1732 (2017)

    Article  MathSciNet  Google Scholar 

  26. Kharif, C., Pelinovsky, E., Slunyaev, A.: Slunyaev, Rogue Waves in the Ocean. Springer, Berlin (2009)

    MATH  Google Scholar 

  27. Garett, C., Gemmrich, J.: Rogue waves. Phys. Today 62(6), 62–63 (2009)

    Article  Google Scholar 

  28. Pelinovsky, E., Kharif, C.: Extreme Ocean Waves. Springer, Berlin (2008)

    Book  MATH  Google Scholar 

  29. Osborne, A.R.: Nonlinear Ocean Waves and The Inverse Scattering Transform. Academic Press, New York (2010)

    MATH  Google Scholar 

  30. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Vector rogue waves in binary mixtures of Bose–Einstein condensates. Eur. Phys. J. Spec. Top. 185(1), 169–180 (2010)

    Article  Google Scholar 

  31. Bludov, Y.V., Konotop, V.V., Akhmediev, N.: Matter rogue waves. Phys. Rev. A. 80(2), 2962–2964 (2009)

    Article  Google Scholar 

  32. Montina, A., Bortolozzo, U., Residori, S., Arecchi, F.T.: Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys. Rev. Lett. 103(17), 173901 (2009)

    Article  Google Scholar 

  33. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature (London) 450(7172), 1054 (2007)

    Article  Google Scholar 

  34. Höhmann, R., Kuhl, U., Stöckmann, H.J., Kaplan, L., Heller, E.J.: Freak waves in the linear regime: a microwave study. Phys. Rev. Lett. 104(9), 093901 (2010)

    Article  Google Scholar 

  35. Ganshin, A.N., Efimov, V.B., Kolmakov, G.V., Mezhov-Deglin, L.P., McClintock, P.V.E.: Observation of an inverse energy cascade in developed acoustic turbulence in superfluid helium. Phys. Rev. Lett. 101(6), 065303 (2008)

    Article  Google Scholar 

  36. Moslem, W.M.: Langmuir rogue waves in electron–positron plasmas. Phys. Plasmas. 18(3), 032301 (2011)

    Article  Google Scholar 

  37. Bailung, H., Sharma, S.K., Nakamura, Y.: Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys. Rev. Lett. 107(25), 255005 (2011)

    Article  Google Scholar 

  38. Akhmediev, N., Ankiewicz, A., Taki, M.: Waves that appear from nowhere and disappear without a trace. Phys. Lett. A. 373, 675–678 (2009)

    Article  MATH  Google Scholar 

  39. Akhmediev, N., Ankiewicz, A., Soto-Crespo, J.M.: Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys. Rev. E. 80, 026601 (2009)

    Article  MATH  Google Scholar 

  40. Peregrine, D.H.: Water waves, nonlinear Schrödinger equations and their solutions. J. Austral. Math. Soc. Ser. B. 25, 16–43 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  41. Kibler, B., Fatome, J., Finot, C., Millot, G., Dias, F., Genty, G., Akhmediev, N., Dudley, J.M.: Observation of Kuznetsov–Ma soliton dynamics in optical fibre. Nat. Phys. 6, 790–795 (2010)

    Article  Google Scholar 

  42. Chabchoub, A., Hoffmann, N.P., Akhmediev, N.: Rogue wave observation in a water wave tank. Phys. Rev. Lett. 106, 204502 (2011)

    Article  Google Scholar 

  43. Ohta, Y., Yang, J.: General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc. R. Soc. Lond. Ser. A. 468(2142), 1716–1740 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  44. Ohta, Y., Yang, J.: Rogue waves in the Davey–Stewartson I equation. Phys. Rev. E. 86, 036604 (2012)

    Article  Google Scholar 

  45. Chen, S.: Twisted rogue-wave pairs in the Sasa–Satsuma equation. Phys. Rev. E. 5, 023202 (2013)

    Article  Google Scholar 

  46. Wang, X., Cao, J., Chen, Y.: Higher-order rogue wave solutions of the three-wave resonant interaction equation via the generalized Darboux transformation. Phys. Scr. 90, 105201 (2015)

    Article  Google Scholar 

  47. Mu, G., Qin, Z., Grimshaw, R.: Dynamics of rogue waves on a multi-soliton background in a vector nonlinear Schrödinger equation. SIAM J. Appl. Math. 75, 1–18 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  48. Ling, L., Guo, B., Zhao, L.C.: High-order rogue waves in vector nonlinear Schrödinger equations. Phys. Rev. E. 89, 041201 (2014)

    Article  Google Scholar 

  49. Chan, H.N., Malomed, B.A., Chow, K.W., Ding, E.: Rogue waves for a system of coupled derivative nonlinear Schrödinger equations. Phys. Rev. E. 93, 012217 (2016)

    Article  MathSciNet  Google Scholar 

  50. Dubard, P., Matveev, V.B.: Multi-rogue waves solutions: from the NLS to the KP-I equation. Nonlinearity 26, 93–108 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  51. Antonio, D., Fabio, B.: Rational solitons of wave resonant-interaction models. Phys. Rev. E. 88(4), 0529147 (2009)

    Google Scholar 

  52. Liu, Y.K., Li, B.: Rogue waves in the \((2+1)\)-dimensional nonlinear Schrödinger equation with a parity-time-symmetric potential. Chin. Phys. Lett. 34, 010202 (2017)

    Article  Google Scholar 

  53. Xu, T., Chen, Y., Lin, Y.: Localized waves of the coupled cubic-quintic nonlinear Schrödinger equations in nonlinear optics. Chin. Phys. B. 26, 120201 (2017)

    Article  Google Scholar 

  54. Xu, T., Chen, Y.: Localized waves in three-component coupled nonlinear Schrödinger equation. Chin. Phys. B 25, 090201 (2016)

    Article  Google Scholar 

  55. Wang, X., Yang, B., Chen, Y., Yang, Y.Q.: Higher-order localized waves in coupled nonlinear Schrodinger equations. Chin. Phys. Lett. 31, 090201 (2014)

    Article  Google Scholar 

  56. Chen, M.: Exact solutions of various Boussinesq systems. Appl. Math. Lett. 11, 45–49 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  57. Johnson, R.S.: A two-dimensional Boussinesq equation for water waves and some of its solutions. J. Fluid Mech. 323, 65–78 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  58. Triki, H., Chowdhury, A., Biswas, A.: Solitary wave and shock wave solutions of the variants of boussinesq equations. Univ. Pol. Bucharest Sci. Bull. Ser. A. 75, 39–52 (2013)

    MathSciNet  Google Scholar 

  59. Abazari, R., Jamshidzadeh, S., Biswas, A.: Solitary wave solutions of coupled boussinesq equation. Complexity 21, 151–155 (2016)

    Article  MathSciNet  Google Scholar 

  60. Adesanya, S.O., Mirzazadeh, M., Eslami, M., Biswas, A.: A note on the Bousinesq model for the propagation of pressure and velocity waves through arterial segment. J. Comput. Theor. Nanosci. 13(7), 4739–4748 (2016)

    Article  Google Scholar 

  61. Rao, J.G., Liu, Y.B., Qian, C., He, J.S.: Rogue waves and hybrid solutions of the Boussinesq equation. Z. Naturforsch. A. 72, 4–12 (2017)

    Google Scholar 

  62. Wang, X.B., Tian, S.F., Qin, C.Y., et al.: Characteristics of the breathers, rogue waves and solitary waves in a generalized \((2+ 1)\)-dimensional Boussinesq equation. Euro. Phys. Lett. 115(1), 10002 (2016)

    Article  Google Scholar 

  63. Korpel, A., Banerjee, P.: Proc. IEEE 72, 1109–1130 (1984)

    Article  Google Scholar 

  64. Liu, Y.K., Li, B.: Dynamics of rogue waves on multisoliton background in the Benjamin Ono equation. Pramana 88(4), 57 (2017)

    Article  Google Scholar 

  65. Fan, E.: Integrable System and Computer Algebra. Science Press, Beijing (2004)

    Google Scholar 

  66. Ma, H.C., Deng, A.P.: Lump solution of \((2+1)\)-dimensional Boussinesq equation. Commun. Theor. Phys. 65, 546–552 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  67. Gepreel, K.A.: Exact solutions for nonlinear integral member of Kadomtsev–Petviashvili hierarchy differential equations using the modified (\(\text{ w }/\text{ g }\))-expansion method. Comput. Math. Appl. 72(9), 2072–2083 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  68. Tu, J.M., Tian, S.F., Xu, M.J., et al.: On periodic wave solutions with asymptotic behaviors to a \((3 + 1)\)-dimensional generalized B-type Kadomtsev–Petviashvili equation in fluid dynamics. Comput. Math. Appl. 72(9), 2486–2504 (2016)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work is supported by the NSF of China under Grant Nos. 11775121, 11775116 and 11435005, and the K. C. Wong Magna Fund in Ningbo University.

Author information

Authors and Affiliations

  1. Ningbo City College of Vocational Technology, Ningbo, 315211, People’s Republic of China

    Yunkai Liu

  2. Department of Mathematics, Ningbo University, Ningbo, 315211, People’s Republic of China

    Biao Li

  3. College of Sciences, Nanjing Agricultural University, Nanjing, 210095, People’s Republic of China

    Hong-Li An

Authors
  1. Yunkai Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Biao Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hong-Li An
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yunkai Liu.

Ethics declarations

Conflict statement

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, Y., Li, B. & An, HL. General high-order breathers, lumps in the \(\mathbf (2+1) \)-dimensional Boussinesq equation. Nonlinear Dyn 92, 2061–2076 (2018). https://doi.org/10.1007/s11071-018-4181-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4181-6

Keywords

Search

Navigation