Online estimation and adaptive control for a class of history dependent functional differential equations

Abstract

This paper presents sufficient conditions for the convergence of online estimation methods and the stability of adaptive control strategies for a class of history-dependent, functional differential equations. The study is motivated by the increasing interest in estimation and control techniques for robotic systems whose governing equations include history-dependent nonlinearities. The functional differential equations in this paper are constructed using integral operators that depend on distributed parameters. As a consequence, the resulting estimation and control equations are examples of distributed parameter systems whose states and distributed parameters evolve in finite and infinite dimensional spaces, respectively. Well-posedness, existence, and uniqueness are discussed for the class of fully actuated robotic systems with history-dependent forces in their governing equation of motion. By deriving rates of approximation for the class of history-dependent operators in this paper, sufficient conditions are derived that guarantee that finite dimensional approximations of the online estimation equations converge to the solution of the infinite dimensional, distributed parameter system. The convergence and stability of a sliding mode adaptive control strategy for the history-dependent, functional differential equations is established using Barbalat’s lemma.

Appendices

Appendix A: Wavelets and approximation spaces over the triangular domain

We define the multiscaling functions

$$\begin{aligned} \phi _{j,k}(x) =1_{\Delta _{i_1,i_2,\ldots ,i_j}}(x)/\root \of {m(\Delta _{i_1,i_2,\ldots ,i_j})} \end{aligned}$$

in which

$$\begin{aligned} 1_{\Delta _{s}}(x)=\left\{ \begin{array}{lll} 1 &{} x \in \Delta _s\\ 0 &{} \text {otherwise} \end{array} \right. \end{aligned}$$

and $m(\Delta _{i_1,i_2,\ldots ,i_j})$ is the area of a triangle in the level j refinement. We have defined $(hf)(t)\circ \mu = \iint _\Delta \kappa (s,t,f)\mu (s)\mathrm{d}s.$ The approximation $(h_j f)(t)\circ \mu$ of this operator is given by

$$\begin{aligned} (h_j f)(t)\circ \mu = \iint _\Delta \sum _{l\in \Gamma _j} 1_{\Delta _{j,l}}(s) \kappa (\xi _{j,l},t,f) \mu (s)\mathrm{d}s, \end{aligned}$$

where $\xi _{j,l}$ is the quadrature point of number l triangle of grid level j. We approximate $\mu (s) \approx \sum _{m\in \Gamma _j} \mu _{j,m}\phi _{j,m}(s)$. Therefore,

$$\begin{aligned}&(h_j f)(t)\circ \mu _j\\&=\iint _S \left( \sum _{l\in \Gamma _j} 1_{\Delta _{j,l}}(s) \kappa (\xi _{j,l},t,f) \sum _{m\in \Gamma _j} \mu _{j,m}\phi _{j,m}(s)\right) \mathrm{d}s\\&=\sum _{l\in \Gamma _j}\sum _{m\in \Gamma _j}\kappa (\xi _{j,l},t,f) \left( \iint _S 1_{\Delta _{j,l}}(s) \phi _{j,m}(s) \mathrm{d}s\right) \mu _{j,m}\\&=\sum _{l\in \Gamma _j} \kappa (\xi _{j,l},t,f) \sqrt{m(\Delta _{j,l})}\mu _{j,l}. \end{aligned}$$

For an orthonormal basis $\left\{ \phi _k \right\} _{k=1}^\infty$ of the separable Hilbert space P, we define the finite dimensional spaces for constructing approximations as $P_n:=\text {span}\left\{ \phi _k\right\} _{k=1}^n$. The approximation error $E_n$ of $P_n$ is given by

$$\begin{aligned} E_n(f):= \inf _{g\in P_n} \Vert f-g\Vert _P. \end{aligned}$$

The approximation space $\mathcal {A}^\alpha _2$ of order $\alpha$ is defined as the collection of functions in P such that

$$\begin{aligned} \mathcal {A}^\alpha _2 := \biggl \{ f\in P \biggl | |f|_{\mathcal {A}^\alpha _2} := \left\{ \sum _{n=1}^\infty (n^\alpha E_n(f))^2 \frac{1}{n} \right\} ^{1/2} < \infty \biggr \}. \end{aligned}$$

For our purposes, the approximation spaces are easy to characterize: they consist of all functions $f \in P$ whose generalized Fourier coefficients decay sufficiently fast. That is, $f\in \mathcal {A}^\alpha _2$ if and only if

$$\begin{aligned} \sum _{k=1}^\infty k^{2\alpha }|(f,\phi _k)|^2 \le C \end{aligned}$$

for some constant C.

Appendix B: The projection operator $\Pi _{J\rightarrow j}$

The orthogonal projection operator $\Pi _{J\rightarrow j}: V_J\rightarrow V_j$ maps a distributed parameter $\mu _J$ to $\mu _j$ i.e., $\Pi _{J\rightarrow j}:\mu _J \mapsto \mu _j$ (Fig. 9).

Fig. 9

Projection operator $\Phi _{J\rightarrow j}:V_J\rightarrow V_j$

By exploiting the orthogonality property of the operator, we have

$$\begin{aligned}&\iint _\Delta \left( \sum _{m\in \Gamma _j} \mu _{j,m}\phi _{j,m}(s){-}\sum _{l\in \Gamma _J} \mu _{J,l}\phi _{J,l}(s)\right) \phi _{j,n}(s) \mathrm{d}s\\&\quad =0. \end{aligned}$$

Therefore, we can write

$$\begin{aligned}&\sum _{m\in \Gamma _j} \left( \iint _\Delta \phi _{j,m}(s)\phi _{j,n}(s) \mathrm{d}s \right) \mu _{j,m} \\&\quad =\sum _{l\in \Gamma _J} \left( \iint _\Delta \phi _{J,l}(s)\phi _{j,n}(s) \mathrm{d}s \right) \mu _{J,l}. \end{aligned}$$

Since orthogonality implies $\iint _\Delta \phi _{j,m}(s)\phi _{j,n}(s) \mathrm{d}s=\delta _{m,n},$ we conclude that

$$\begin{aligned} \mu _{j,n}=\sum _{l\in \Gamma _j} \left( \iint _\Delta \phi _{j,n}(s)\phi _{J,l}(s) \mathrm{d}s\right) \mu _{J,l}. \end{aligned}$$

From Theorem 1, we have

$$\begin{aligned} |(h_{j}f)(t)\circ \Pi _{j}\mu - (hf)(t)\circ \mu | \le \tilde{C}2^{-\alpha j}, \end{aligned}$$

with

$$\begin{aligned}&(hf)(t)\circ \mu = \iint _\Delta k(s,t,f)\mu (s)\mathrm {d}s,\\&(h_{j}f)(t)\circ \mu = \iint _\Delta \sum 1_{\Delta _j,l}(s)k(\zeta _{j,l},t,f)\mu (s)\mathrm {d}s, \end{aligned}$$

where $\mu \in P = L^{2}(\Delta )$ and we approximate $\mu (s) \approx \sum _{l\in \Gamma _J}\mu _{J,l}\phi _{J,l}(s) \in V_J$. To implement this for the finest grid J, we compute

$$\begin{aligned}&(h_J f)(t)\circ \mu _J = (h_j f)(t)\circ \Pi _J \mu _J,\\&\quad =\iint \left( \sum 1_{\Delta _J,l}(s)k(\zeta _{J,l},t,f)\sum _{m\in \Gamma _J}\mu _{J,m}\phi _{J,m}(s)\right) \mathrm {d}s,\\&\quad =\sum _{l\in \Gamma _J}\sum _{m\in \Gamma _J}k(\zeta _{J,l},t,f)\left( \iint 1_{\Delta _J,l}(s)\phi _{J,m}(s)\mathrm {d}s\right) \mu _{J,m},\\&\quad =\sum _{l\in \Gamma _J}\frac{k(\zeta _{J,l},t,f)\mu _{J,l}}{\left( \root \of {m(\Delta _{J,l}})\right) }, \end{aligned}$$

when $\root \of {m(\Delta _{J,l})}$ is the area of the corresponding triangle $\Delta _{J,l}$ in the grid having resolution level J.

Appendix C: Gronwall’s inequality

We employ the integral form of Gronwall’s inequality to obtain our final convergence result. Many forms of Gronwall’s inequality exist, and we will use a particularly simple version. See Section 3.3.4 in [17]. If the piecewise continuous function f satisfies the inequality

$$\begin{aligned} f(t) \le \alpha (t) + \int _0^t \beta (s) f(s) \mathrm{d}s \end{aligned}$$

with some piecewise continuous functions $\alpha ,\beta$ where $\alpha$ is nondecreasing, then

$$\begin{aligned} f(t) \le \alpha (t) e^{\int _0^t\beta (s)\mathrm{d}s}. \end{aligned}$$

Appendix D: Modeling of a prototypical wing section

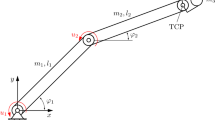
Figure 1 shows a simplified model of the wing. In the figure, we denote the center of mass by c.m., A is the aerodynamic center, and O is the elastic axis of the wing. The constants $K_h$ and $K_\theta$ are the linear and torsional stiffness, and h is the distance from origin to point O in the fixed reference frame. We denote by $x_\theta$ the distance between point O and center of mass, whereas $x_a$ is the distance between O and A. Point O is the origin for the body fixed reference frame.

We employ The Euler–Lagrange technique to derive the equation of motion for the depicted wing model. The function $L(\theta ,\dot{\theta })$ is the history-dependent lift force acting at the aerodynamic center, and $M(\theta ,\dot{\theta })$ is the history-dependent aerodynamic moment about point A. The variables $L_{\beta _1}$ and $L_{\beta _2}$ are the actuating forces acting at point D, and $\beta _1$, $\beta _2$ are the angles between the midchord of the wing and the trailing edge and leading edge flaps, respectively.

The position vector of the mass center is given as

$$\begin{aligned} \mathbf {r}_{c.m.} = h\hat{n}_1 - x_\theta \hat{b}_2, \end{aligned}$$

and therefore the corresponding velocity of point C is

$$\begin{aligned} \mathbf {\dot{r}}_{c.m.} = \dot{h}\hat{n}_1 + x_\theta \dot{\theta }\hat{b}_1. \end{aligned}$$

The rotation matrix for transformation between inertial frame of reference to body fixed frame of reference is

$$\begin{aligned} \begin{bmatrix} \hat{b}_1\\ \hat{b}_2 \end{bmatrix} = \begin{bmatrix} \cos \theta&\sin \theta \\ -\sin \theta&\cos \theta \end{bmatrix} \begin{bmatrix} \hat{n}_1\\ \hat{n}_2 \end{bmatrix}. \end{aligned}$$

The kinetic energy is computed to be

$$\begin{aligned} T= & {} \frac{1}{2}m(\mathbf {r}_{c.m.}.\mathbf {r}_{c.m.} ) + \frac{1}{2} I_\theta {\dot{\theta }^2},\\ T= & {} \frac{1}{2}m(\dot{h}^2+x_\theta ^2 \dot{\theta }^2 +2 x_\theta \dot{h} \dot{\theta } \cos {\theta }) + \frac{1}{2}I_\theta {\dot{\theta }^2}, \end{aligned}$$

and the corresponding potential energy is

$$\begin{aligned} V=\frac{1}{2}K_h h^2 + \frac{1}{2}K_\theta \theta ^2. \end{aligned}$$

therefore we can write Lagrangian as $L=T-V$. We apply Euler–Lagrange equations to write the equation of motion as follows

$$\begin{aligned}&\left[ \begin{array}{cc} m &{} m x_\theta \cos {\theta } \\ m x_\theta \cos {\theta } &{} m x_\theta ^2 + J\\ \end{array} \right] \left[ \begin{array}{l} \ddot{h} \\ \ddot{\theta }\\ \end{array} \right] \nonumber \\&\qquad + \left[ \begin{array}{lc} 0 &{} -m x_\theta \dot{\theta }\sin {\theta } \\ 0 &{} 0\\ \end{array} \right] \left[ \begin{array}{l} \dot{h} \\ \dot{\theta }\\ \end{array} \right] \nonumber \\&\qquad + \left[ \begin{array}{ll} K_h &{} 0 \\ 0 &{} K_{\theta }\\ \end{array} \right] \left[ \begin{array}{l} h \\ \theta \\ \end{array} \right] \nonumber \\&\quad = \left[ \begin{array}{l} L(\theta ,\dot{\theta }) \cos {\theta } \\ M(\theta ,\dot{\theta }) + x_a L(\theta ,\dot{\theta })\\ \end{array} \right] \nonumber \\&\qquad + \left[ \begin{array}{l} -L_{\beta _1} \cos {(\theta + \beta _1)} -L_{\beta _2} \cos {(\theta + \beta _2}) \\ -L_{\beta _1} (e_1 {+} d_1 \cos {\beta _1}){+}L_{\beta _2} (e_2 + d_2 \cos {\beta _2}).\\ \end{array} \right] \nonumber \\ \end{aligned}$$

(7.1)

The above equation is written in the form of a standard robotic equations of motion $M(q(t))\ddot{q}(t)+C(q(t),\dot{q}(t))\dot{q}(t)+K(q(t))=Q_a (t) + \tau (t)$, where $q = [h \, \theta ]^T$. We have discussed control applications for such systems in detail in Sect. 1. In addition, we employ a simplified version of this equation to validate our online identification and adaptive control strategy in Sect. 6.2.