On the dynamics of a nonlinear energy harvester with multiple resonant zones

Vibration energy harvesting is a relatively recent concept. Mechanical systems generally experience vibrations due to manufacturing or assembly imperfections [1], transient and impulsive loading [2] and wear/degradation. Although these causes have negative effects on the system structural integrity and ideal operation, the potential for energy harvesting from the vibratory modes has attracted much research [3, 4, 5]. It is envisaged that the otherwise dissipated energy can be supplied to devices of low power demand such as wireless sensors [3, 4, 6]. Besides improving the energy efficiency of the host structure, the compact design of a harvester would allow its positioning in confined and often hostile environments, such as in structural health monitoring [7], which pose difficult accessibility through traditional means with a power supply.

Most vibration energy harvesting concepts deal with ambient vibrations acting as translational base excitations for the harvesting attachment [8, 9]. Despite an overwhelming diversity of proposed concepts and designs, one can identify two major classes of vibration harvesters; cantilever beams with a tip mass in bending mode [10, 11, 12] (usually coupled with piezoelectric elements), or a base-excited seismic magnetic mass, oscillating in the proximity of an electric coil. The former class may also include continuous systems such as plates and beams with their deflections inducing voltage in piezoelectric elements [13], which may extend beyond mere vibration harvesting (e.g. fluid–structure interactions [14]). Stephen [4] considered direct mass and base excitation of a seismic mass, first proposed in [3], comprising a mass suspended from a linear spring. This concept was also used by Beeby et al. [5] for the development of a micro-generator. A common conclusion from all the analytical and experimental work has shown optimal device performance when operating in the vicinity of resonance. This finding points to the requirement for tuning of the harvester to the expected frequency of oscillations. However, ambient vibrations are subject to unpredictable variations, both in short- and long-term durations, rendering the tuning of a device unsuitable when the dominant frequency of oscillations shifts away from a tuned frequency. This problem occurs with systems under transient conditions as highlighted in [1, 2]. Therefore, complex and often expensive control methods are required to re-tune the harvester for an instantaneous prevailing condition. An alternative would be the use of multi-modal devices [15]. However, this approach can become impractical, given the design constraints often imposed with regard to any added weight and package space (compactness). Passive tuning has also been proposed, often related to frequency up-conversion [16] through impulsive interactions of the device with the instantaneous vibration response.

Another approach utilizes the system nonlinearities which lead to a broader frequency response. Mann and Sims [17] proposed the use of magnetic repulsion in order to impose strongly nonlinear restoring forces on a seismic magnetic mass. This concept has received much attention due to the novelty of an intentionally introduced nonlinearity. Barton et al. [18] suggested coupling between a magnetic tip mass and a ferrous coil core as a means of achieving nonlinear stiffness. Remick et al. [19] provided an investigation of dynamic instability of a strongly nonlinear harvester with repetitive impulsive excitation. These conditions occur in many mechanical systems such as in gear rattle, caused by impact of loose (unengaged) gearing [20]. A number of studies [21, 22] have explored the advantages of nonlinear harvesting over the classical linear approach, especially those related to the frequency range over which high quantities of energy can be captured.

A widely used model for systems with nonlinear forcing is based on the Duffing oscillator (cubic nonlinearity) [23]. The major advantage of nonlinear energy harvesting can be ascertained from the hardening spring influence upon the frequency response curve (FRC), in which an increase occurs in the response bandwidth [25]. This effect allows for a broader range of frequencies over which power can be generated efficiently, compared with a linear system. Duffing oscillators have long been studied because of their numerous applications in nonlinear engineering problems [23, 24, 25, 26]. Kovacic et al. [27, 28] studied the presence of a bias term in the harmonic excitation of a purely nonlinear Duffing system. It was found that this term can induce the frequency response to coincide with the hardening–softening characteristics, which has also been observed in the parametrically excited Duffing oscillators, along with branch detachments [29]. Increased complexity of the response (up to chaotic excursions) can be induced by the presence of strongly nonlinear terms (fast-slow mixed-modes, multi-stability etc. [30]). The large variation in dynamic behaviour necessitates detailed analysis of Duffing oscillators when employed in different environments and applications.

Although harvesting energy from translational oscillations has received much attention, there is a dearth of investigation of torsional systems which abound in powertrain and rotor dynamic applications. One can conceive the design of a piezogenerator, based on torsional stressing of its active elements [31, 32]. Furthermore, the piezoelectric cantilever design has been used for either torsional vibratory modes with piezoelectric attachments or in bending modes, extending radially from a shaft subjected to torsional oscillations [33].

In this paper, the magnetic levitation concept [17] is used for a torsional vibration energy harvester rigidly mounted onto a spinning shaft. The nonlinear restoring force pertains to the principle of energy harvesting within a broadband frequency response. The system is investigated with a constant shaft speed in order to reduce the complexity of the problem, thus enabling an analytical solution. The harmonic balance method is used to derive approximate analytical expressions for the system frequency response, which is validated against numerical integration of the system equations. The harvester is found to exhibit a complex dynamic behaviour when compared with other single-degree-of-freedom (SDOF) oscillators, mainly concerning the apparent coexistence of multiple backbone curves. This is potentially a significant contribution to the energy harvesting capabilities of the proposed concept, since it combines mono-stable with bi-stable dynamics over distinct frequency ranges for which significant energy levels can be attained. An estimation of the induced load power is also provided.

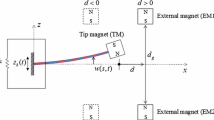
The proposed energy harvester comprises a levitating magnet which is free to move between two outer magnets, which are fixed to the device housing [17]. These repel the central levitating magnet as shown in Fig. 1. A coil is wrapped around the housing and the oscillating central magnet. The vibration energy is harvested from the levitating magnet through the induced voltage in the coil. The housing is attached to a rotating shaft, with the entire assembly rotating with it.

Open image in new window

It was also shown that the linear component of the stiffness can be tuned to a desired resonant frequency through changes in the initial separation of the magnets, \(d_0 \), without affecting the nonlinear stiffness, \(k_3 \) [17].

The FRCs of the proposed system are obtained based upon the derivations in the previous section for Eq. (). The approximate analytical results are compared with direct numerical integration of Eq. (4) or (8), where applicable, in order to examine the validity of the analysis. Numerical FRCs are constructed through sweep of excitation frequencies in incremental steps, whilst other system parameters remain unchanged. Every point of the FRC is computed based upon the time series of the numerical integration. The latter is performed within a small time step, \(\hbox {d}t=2\pi /\left( {100\varOmega } \right) \). Each time-domain solution is allowed to reach steady-state conditions prior to selection of the last few periods for the determination of the response characteristics. The values of the static displacement and harmonic amplitude are computed from the Fourier coefficients of the time series, whilst neglecting higher order harmonic contributions.

4.1 Behaviour charts

The graphical illustrations of the influence of varying system parameters upon the response amplitudes are presented using bifurcation diagrams. Applying the condition in Eq. (31) to Eq. (), the saddle-node bifurcation points can be calculated with respect to \(\left( {r,\varOmega } \right) \). The resulting boundaries are plotted in Fig. 2 for two values of the nonlinear stiffness coefficient \(k_3 \). In Fig. 2a, two main sets of branches are observed in the examined frequency range, along with a single detached bifurcation branch. These branches effectively discretize the parameter space into regions of different number of coexisting solutions (up to seven stable and unstable solutions for the examined range). Starting from the left-hand side of the figure, the bifurcation tongue ABC is found. Branch AB leads to three multiple solutions, before these converge into a single solution after a short frequency range, due to the crossing branch BC. This tongue extends approximately to value: \(r=0.011\,\hbox {m}\). Beyond this value, the system bifurcates when crossing branches DE or LK, again exhibiting three coexisting solutions. It is noted that for a very short range of r values just above point D, the response quickly returns to a single solution following the narrow DL branch. However, the number of coexisting solutions increases almost instantly into three with the crossing branch LK.

Open image in new window

The above structure indicates the rich dynamics of the examined system. Moving to higher frequencies, the system response solutions undergo a three-to-one saddle-node bifurcation on the branch EF, whereas multiple solutions exist on branches MK and FN. Below point F, a richer structure is evident. Branches KF and KJ induce the appearance of five coexisting solutions, which reduce to three in branch FG. Before that, a small area is found for the r parameter space enclosed by JGH, where seven solutions coexist, including the symmetric case (\(r=0)\). The final observed region occurs between GI and IH, defining a short range for five coexisting solutions.

With an increasing nonlinear stiffness coefficient, the same structure is generally maintained in the behaviour chart (Fig. 2b). Nevertheless, some notable changes are observed in branch ABC, now intersecting with branch DK, thus creating a region of five coexisting solutions in the low frequency range. Moreover, the region enclosed by branches JGH is expanded and as a result a wider area with seven coexisting solutions is present.

Figure 3 shows the FRCs of the static displacement \(x_0 \) for three cases selected from the behaviour chart of Fig. 2a. The FRCs confirm the coincidence of saddle-node bifurcations with the stability limits and jump frequencies. Figure 3a corresponds to the symmetric case (\(r=0.000)\) and as would be expected, up to seven multiple solutions are found in the narrow frequency range: \(f=21.6\text {--}22.1\,\hbox {Hz}\). In most of the frequency spectrum considered in Fig. 3a, three solutions coexist (in fact, for \(f>14.3\,\hbox {Hz})\). The small discrepancy between the analytical solutions and the forward numerical response around \(f=16\,\hbox {Hz}\) is due to the occurrence of a 1/3 sub-harmonic resonance which affects the static displacement. Further investigation of this interaction is beyond the scope of this paper.

Open image in new window

The behaviour chart of Fig. 2a predicts a narrow frequency range with three coexisting solutions within the ABC branch. Therefore, three coexisting solutions would be expected in Fig. 3a, b (crossing ABC). Indeed, in Fig. 3b there is a narrow region of coexisting solutions around 12 Hz. The same does not seem to be the case in Fig. 3a due to the coincidence of multiple solutions for \(x_0 =0\). This is caused by the symmetry of the system, which misleadingly appears to have a single solution around 12 Hz in Fig. 3a. Higher values of r give rise to distinct solutions in this frequency range, as it can be observed in Fig. 3b (for \(r=0.005)\). A finite value of r breaks the symmetry of the system leading to a biased response. This effect is further pronounced in Fig. 3c for \(r=0.013\) due to a higher centrifugal force. The response undergoes three bifurcations at branches DE, EF and FN (Fig. 2a), demonstrating the expected changes in the response. An interesting observation is that DE gives rise to a detached branch in the FRC, even though it only extends to a narrow frequency range (as it can be seen in the inset to Fig. 3c). The bifurcations observed in the system response have significant effect on the state of system equilibria. This can greatly affect the operation of the energy harvesting device, especially when the oscillation boundaries are of concern. However, the focus of this paper is on the harmonic response of the system.

Open image in new window

4.2 Backbone curves

The harmonic part of the response is important for vibration energy harvesting purposes. It is noteworthy that the obtained frequency response curves and the backbone curves emanate from the fundamental harmonic response and are not associated with secondary resonances (either the sub-harmonics or the super-harmonic) as the analytical approach disregards these. Figure 4 shows the backbone curves computed from Eq. (). The frequency response of the system is plotted for the same parameters and two different values of damping ratio (\(\zeta =0.03\) and \(\zeta =0.09\)). It can be seen that the value of damping ratio significantly influences the peak response amplitudes as one would expect. Due to the symmetry of the system (Fig. 4), several coexisting solutions appear as the amplitude corresponding to a positive static displacement equates to that of its negative equivalent. Therefore, there are only up to four distinct solutions instead of the predicted seven. A small discrepancy is also noted between the analytical and the numerically predicted responses (as is the case of the static response).

Open image in new window

A control parameter of significance is the linear stiffness of the oscillator, which is taken \(\omega _n =90\,\hbox {rad/s}\), or equivalently \(f_n =14.32\,\hbox {Hz}\). The first backbone curve given by Eq. () originates from frequencies lower than \(\omega _n \), whilst the second curve from Eq. () initiates at higher frequencies. This threshold separates the FRC into two distinct regions of single-well and double-well dynamics, respectively, as one may observe from the sign of the linear stiffness in Eq. (4). The presented backbone curves concentrate the different modes of oscillation of the considered system in the following manner: starting from low amplitude oscillations, the first backbone curve describes the nonlinear normal modes of a single-well Duffing oscillator (see Fig. 5, plot O1). These are an extension of the notion of linear normal modes to nonlinear systems, defined as synchronous periodic motions of all the material points of a conservative system [34]. As the amplitude increases, so does the frequency of the modes, resulting in a softer linear stiffness up to the point that it crosses the \(\omega _n \) threshold and becomes negative. At this point, the dynamics changes to a bi-stable system. The previously stable equilibrium \(x_0 =0\) is destabilized and the equilibria given by Eq. () are stabilized. It is well known that, subject to satisfactory input energy, bi-stable oscillators may perform cross-well oscillations, which have been shown to be favourable for vibration energy harvesting [35]. In fact, the continuation of the first backbone curve in the bi-stable regime comprises this type of cross-well oscillation modes, as Fig. 5 shows (plot O2). On the other hand, the second backbone curve which resides exclusively in the bi-stable frequency region (above \(\omega _n )\), corresponds to in-well oscillations of the system around each stable equilibrium (see Fig. 5, plot O3). Note that due to the symmetry of the currently considered layout, the harmonic properties of the response are identical for both equilibria. A notable difference with results previously reported in the literature is that these in-well oscillations are of hardening type that leads the bent backbone curve to cover a higher frequency range, compared with softening in-well oscillations. To summarize, the first backbone curve drives a transition from single-well dynamics to cross-well oscillations in the double-well range, whilst the second one describes in-well oscillations of the double-well version of the system, yet, of hardening type.

Open image in new window

Considering the damped dynamics of the system, the FRCs have an unusual structure as it can be seen for the case \(\zeta =0.03\). This exhibits strongly nonlinear behaviour with an increasing frequency. The low-energy branch, past the first backbone curve, is destabilized by a saddle-node bifurcation. This gives rise to another branch corresponding to the second backbone curve, the structure of which also replicates a hardening-type response. The emergence of this branch has a significant contribution to the system’s ability for vibration energy harvesting. It would normally be expected that the harmonic response of a regular Duffing-type oscillator with a single backbone curve asymptotically vanishes after the jump-down event with increasing frequency. However, the transition from single-well to double-well dynamics gives rise to the second backbone curve corresponding to in-well oscillations around each of the stabilized equilibria. Effectively, this behaviour induces a second resonant zone, leading to a high amplitude branch through a second high-energy stable path. Importantly, this second resonant zone is of hardening nature, allowing the harvester to cover higher frequency ranges with high response amplitudes. The two backbone curves (nonlinear regions) overlap only with insignificant damping, indicating that they may be exploited independently for energy harvesting purposes across the frequency spectrum. Nonetheless, even if the choice of system parameters leads to overlapping frequency ranges of the backbone curves, any jump-down from the first curve would land on the high-energy branch of the second, thus maintaining the beneficial contribution. Therefore, this system may act as two separate vibration energy harvesters working in a synergistic manner.

With any system (i.e. \(r\ne 0\)), the backbone curves are computed utilizing the conditions in Eq.s () and (). Figure 6 shows the backbone curves along with the frequency response of the harmonic amplitude obtained for the same system parameters as in Fig. 4, and \(r=0.002\,\hbox {m}\). This induces a breakage of the FRC at the point where the low-energy branch of the symmetric layout loses its stability. Therefore, a third backbone curve appears in the intermediate frequency range of the previously observed resonant zones in Fig. 4. The nonlinear branch, residing in the high frequency range (corresponding to the second backbone curve of the symmetric case), is now detached from the rest of the FRC, even though an overlap exists. In Fig. 3 it was shown that eccentricity leads to asymmetric frequency response, separating the multiple solutions for the static displacement to two distinct regions (in the positive and in the negative space). This observation points to the possibility of the levitating magnet oscillating closer to the top or the bottom static magnets. This behaviour is also observed in the FRC of the harmonic amplitude. Starting from the lowest frequency in Fig. 6a, one can observe a joint FRC shaped around the first two backbone curves. This FRC extends over the whole frequency range (diminishing in an asymptotic manner for \(f>25\,\hbox {Hz})\), corresponding to the positive static displacement seen in Fig. 6b. Furthermore, the region between the backbone curves, where only a single solution exists, connects the two local maxima. Since two local peaks exist for a single curve, then a local minimum also exists in the intermediate region. In fact, the maxima stem from the first condition used in the computations, Eq. (22a), whilst the minima are derived from the second condition, Eq. (22b). This allows for separate manipulation of these points, which in the context of energy harvesting requires the value of the local minimum to be as close as possible to the maxima, so that the response amplitude would retain high values in the intermediate region. On the other hand, the second FRC arising at \(f=19\,\hbox {Hz}\) corresponds to the negative static displacement in Fig. 6b. Thus, in order to fully exploit the potential of the harvester, one would have to impose a jump in the response from the positive space to the negative when the excitation frequency exceeds \(25\,\hbox {Hz}\).

The above observation becomes clearer when the basins of these coexisting attractors are plotted. Figure 7 shows the basins of the initial conditions, resulting in different solutions for the symmetric and asymmetric cases. It indicates that under certain conditions some attractors become dominant, whereas others demonstrate weaker attraction. This could potentially diminish the harvester’s capacity to operate with high vibration amplitudes, such as in Fig. 7b. The desired response (indicated as 3) occupies a narrow region of initial conditions, which renders it sensitive to even small sudden changes in the prevailing conditions. On the other hand, the basins of attractions point to a strategy for the integration of the multiple solutions in an optimized energy harvesting operation. For example, if the optimal response is no longer sustainable, a suitable strategy can be devised so that the response is attracted by the second best option, indicated as 1.

Open image in new window

Overall, as for the symmetric case, the onset of an additional backbone curve is equivalent to an additional nonlinear harvester, tuned to the frequency range where this curve would reside. It appears that a small eccentricity would bring beneficial influence on the usage of such a design for vibration energy harvesting, especially when the added curve covers a frequency range of otherwise relatively low response amplitudes.

Figure 6 shows that the backbone curves asymptotically tend to the vertical, as \(x_1 \rightarrow 0\). This is the typical shape of the backbone curves of oscillators with cubic nonlinearities. The physical interpretation is that of a linear-like behaviour of these oscillators when the excitation amplitude is sufficiently low. Even so, the separate backbone curves define multiple peaks in the shape of the FRC, with clear advantages for energy harvesting compared with a linear harvester, for which only a single resonant peak exists. Recalling the analysis in the previous section, it was shown that an intersection point of the backbone curves can exist. If the introduced eccentricity exceeds a critical value given by Eq. (23), then a real, non-negative solution exists for which the backbone curves intersect. Substituting the system parameters used in Fig. 6, it is found that: \(r_{crit} =0.0035\,\hbox {m}\). Thus, selecting higher values (\(r=0.004\,\hbox {m}\) and \(r=0.006\,\hbox {m})\) and repeating the steps to calculate the backbone curves, Fig. 8 shows that above the critical value of eccentricity the backbone curves merge, no longer defining multiple peaks in the FRC for every excitation amplitude. Instead, the merged part of the backbone curve resembles the structure of a typical nonlinear oscillator. Therefore, for relatively weak excitations the examined nonlinear harvester shows no advantage over a linear counterpart. In this respect, \(r_\mathrm{crit} \) is an important design parameter that can enhance the harvester’s adaptability to low excitation amplitudes. It is also noted that this curve results from merging the system’s extrema in a way that the locus of the local minima is now transformed to the locus of the peak amplitudes.

The above characteristics of the proposed examined system lead to a reduced frequency range for which resonant response is observed. In Fig. 9, the case for \(r=0.006\,m\) is considered, with the depicted results confined to the frequency range of the merging point. It can be seen that a low damping ratio of \(\zeta =0.03\) leads to multi-peak FRC, whereas an increased energy dissipation with \(\zeta =0.07\) forces the system to lower response amplitudes. The latter response due to the merging point of the backbone curves resembles the low-energy response of a single linear oscillator. Thus, apart from the classic dissipation resulting in lower amplitudes, increased damping can convert the two-peak FRC to a single-peak curve, essentially cancelling the “additional harvester” that the multiplicity of the backbone curves would offer. Nevertheless, this highlights the usefulness of Eq. (23). Should the eccentricity be lower than its critical value (e.g. as in Fig. 4), the FRC would still have a multi-peak structure regardless of the increased damping content. The merging points of the backbone curves can be computed, imposing both conditions in Eq. () on the system’s solution. Figure 10 shows the frequency and response amplitude of the intersection point for system parameters of Fig. 9 for \(\zeta =0.03\). As the eccentricity increases, the backbone curves merge at higher amplitudes and frequencies. This allows more space for the single backbone curve, thus deteriorating the overall energy harvesting opportunities.

Open image in new window

Open image in new window

4.3 Harvested energy

The electrical power of the circuit’s load is commonly considered as a measure of harvested electrical energy. With the employed assumptions, the power is proportional to the square of the response velocity. For a typical example comprising an N42 magnet of 0.02 kg weight, multilayer coil with 1600 turns, inner radius of 14.15 mm, outer radius of 20.25 and 15.5 mm length, the coupling constant is calculated to be \(\varTheta =6.75\,\hbox {Vs/m}\). Neglecting the coil’s resistance (for which \(R_\mathrm{i} \ll R_\mathrm{L} \) holds) and considering load resistance of \(1k\varOmega \), then: \(c_\mathrm{el} =0.0456\,\hbox {Ns/m}.\) Figure 11 shows the electrical power load averaged over a period of motion given by Eq. (10). The frequency response of the system is calculated from Eq. () (solid and dashed lines) and is compared with the numerical integration results, sweeping the excitation frequency forward (\(\circ )\) and backward (\(+\)). There is good agreement between the analytical and numerical results, which shows that the power follows the shape of the velocity frequency response. This example demonstrates the potential of the energy harvester in delivering tens of mW in a broad range of frequencies without suppressing resonant peaks as is the case with a linear harvester. In the latter case, broadband behaviour is achieved by increasing damping at the expense of severely truncated peak values.

Open image in new window

Open image in new window

The harmonic balance method is employed to analyse the dynamics of a vibration energy harvester with nonlinear magnetic restoring force. Due to the layout of the rotary system, the oscillating magnet is excited by the combined effect of centripetal force and gravity, resulting in a constant and a harmonic excitation component, respectively. The linear frequency of the system varies with the excitation frequency due to the action of the centripetal force. The aim of the analysis is to investigate the structure of the system’s dynamics. The overlapping boundaries of saddle-node bifurcations lead to the appearance of frequency regions with up to seven coexisting solutions, even when a small amount of eccentricity is present in the harvester. Most of these bifurcations result in limited changes in the amplitudes of oscillation with the frequency response dominated by stable branches. Jump phenomena account for the amplitude variations within a narrow frequency range only. Nevertheless, the possibility of a part of the FRC detaching from the main branches exists.

The FRC structure of the studied system is of particular interest. When the excitation is purely symmetric, the frequency response is dominated by two distinct backbone curves, which induce the corresponding resonant zones. The first curve concentrates the nonlinear normal modes, corresponding to oscillations in a single-well potential for frequencies below the \(\omega _n \) threshold. This incorporates a transition to cross-well oscillations when the threshold, leading to a double-well potential, is reached. The second curve describes the nonlinear modes of in-well hardening oscillatory characteristics. The damped response of the system is then determined by the combined influence of these modes. In regular bi-stable oscillators, in-well oscillations exhibit softening characteristics, resulting in interactions between the cross-well and in-well oscillations over a confined frequency range. In the case demonstrated here, the transition from single-well to double-well dynamics occurs with cross-well oscillations as the continuation of the first backbone curve, where the in-well oscillations follow hardening characteristics. The result is two resonant zones, covering relatively distinct frequency ranges, thus establishing a coexisting frame of effectively broadening frequency range of high response amplitudes. One can consider the analogy of two nonlinear harvesters, the responses of which cover different frequency ranges. With the proposed concept, this is achieved through a SDOF oscillator only. In fact, once the frequency is increased beyond the first FRC peak, the low-energy branch is destabilized and the response follows the higher-energy path, leading to the second peak.

In addition, the introduction of eccentricity in the system layout (triggering asymmetric forcing of the oscillator) results in the appearance of an additional backbone curve. This is induced by the loss of symmetry, yielding non-identical equilibria of in-well oscillations, unlike the previous case. A new multi-peak FRC is created that can be conceived synergistically, as the symmetric system was. Nevertheless, the response can return to a single-peak form if higher energy dissipation is attained. The appearance of additional resonant zones in the dynamics of this nonlinear system significantly enhances the energy harvesting capabilities. This is because high velocity response of the oscillating magnet can be sustained through passage over separate hardening resonant zones, thus resulting in broader spectra of power load output.