Skip to main content
SpringerLink
Log in

New exact solutions for a generalized KdV equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

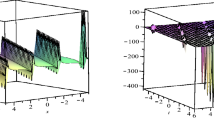
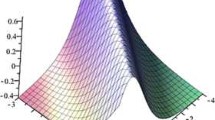
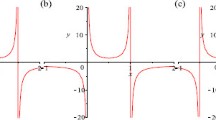
In this paper, we establish a triple-order complete discrimination system to derive the traveling wave solutions of the generalized KdV equation with high power nonlinearities, which consist of solitary patterns solutions, compactons solutions, periodic solutions and Jacobi elliptic functions solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Huang, Y.: New no-traveling wave solutions for the Liouville equation by Bäcklund transformation method. Nonlinear Dyn. 72, 87–90 (2013)

    Article  Google Scholar 

  2. Ibrahin, E., Yavuz, I.U., Hasan, B.: Auto-Bäcklund transformation for some nonlinear partial differential equation. Optik Int. J. Light Electron Opt. 127, 10780–10785 (2016)

    Article  Google Scholar 

  3. Chen, Y., Wang, Q.: Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic function solutions to (1+1)-dimensional dispersive long wave equation. Chaos Solitons Fractals 24, 745–757 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  4. Liu, S.K., Fu, Z.T., Liu, S.D.: Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations. Phys. Lett. A 289, 69–74 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  5. Parkes, E.J., Duffy, B.R., Abbott, P.C.: The Jacobi elliptic function method for finding periodic wave solutions to nonlinear evolution equations. Phys. Lett. A 295, 280–286 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  6. Tchier, F., Aslan, E.C., Inc, M.: Optical solitons in parabolic law medium: Jacobi elliptic function solution. Nonlinear Dyn. 85, 2577–2582 (2016)

    Article  MathSciNet  Google Scholar 

  7. Hirota, R.: Exact solution to the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27, 1456–1458 (1971)

    Article  MATH  Google Scholar 

  8. Wazwaz, A.M.: Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh-coth method. Appl. Math. Comput. 190, 633–640 (2007)

    MathSciNet  MATH  Google Scholar 

  9. Liu, H.Z., Li, J.B., Liu, L.: Painlevé analysis, Lie symmetries, and exact solutions for the time-dependent coefficients Gardner equations. Nonlinear Dyn. 59, 497–502 (2010)

    Article  MATH  Google Scholar 

  10. Malfliet, W., Hereman, W.: The tanh method: Exact solutions of nonlinear evolution and wave equations. Phys. Scr. 54, 563–568 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  11. Wang, Y.Y., Zhang, Y.P., Dai, C.Q.: Re-study on localized structures based on variable separation solutions from the modified tanh-function method. Nonlinear Dyn. 83, 1331–1339 (2016)

    Article  MathSciNet  Google Scholar 

  12. Wazwaz, A.M.: Kinks and solitons for the generalized KdV equation with two power nonlinearities. Appl. Math. Comput. 183, 1181–1189 (2006)

    MathSciNet  MATH  Google Scholar 

  13. Pelinovsky, D.E., Grimshaw, R.H.: An asymptotic approach to solitary wave instability and critical collapse in long-wave KdV-type evolution equations. Phys. D 98, 139–155 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  14. Pelinovsky, D.E., Afanasjev, V.V., Kivshar, Y.S.: Nonlinear theory of oscillating, decaying and collapsing solitons in the generalized nonlinear Schrodinger equation. Phys. Rev. E 53, 1940–1953 (1996)

    Article  Google Scholar 

  15. Osman, M.S., Wazwaz, A.M.: An efficient algorithm to construct multi-soliton rational solutions of the (2 + 1)-dimensional KdV equation with variable coefficents. Appl. Math. Comput. 321, 282–289 (2018)

    MathSciNet  Google Scholar 

  16. Klaus, M., Pelinovsky, D., Rothos, V.: Evans function for Lax operators with algebraically decaying potentials. J. Nonlinear. Sci. 16, 1–44 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  17. Lai, S.Y., Zhang, Y., Yin, J.: Solutions of distinct physical structures for two generalized KdV equations. Dyn. Contin. Dis. Ser. A. 16, 661–672 (2009)

    MathSciNet  MATH  Google Scholar 

  18. Yang, L., Hou, X.Y., Zeng, Z.B.: Complete discrimination system for polynomial. Sci. China. Ser. E. 39, 628–646 (1996)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Mathematics and Software Science, Sichuan Normal University, Chengdu, 610066, China

    Lingfei Li, Yingying Xie & Shihui Zhu

Authors
  1. Lingfei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yingying Xie
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shihui Zhu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yingying Xie.

Additional information

Supported by National Natural Science Foundation of P.R.China (11501395) and The Sichuan Province Fund for Distinguished Young Scholars (2014JQ0039).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, L., Xie, Y. & Zhu, S. New exact solutions for a generalized KdV equation. Nonlinear Dyn 92, 215–219 (2018). https://doi.org/10.1007/s11071-018-4050-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-018-4050-3

Keywords

Search

Navigation