A coupled-field model of a rotating composite beam with an integrated nonlinear piezoelectric active element

Abstract

The dynamics of a system consisting of a rotating rigid hub and a thin-walled composite beam with embedded active element is presented. The beam comprises of a generally orthotropic host made of an arbitrary laminate and an additional layer of a transversely isotropic piezoceramic material. The higher-order constitutive relations for piezoelectric are used to properly model its electromechanical structural behaviour when operated in near resonance conditions or subjected to strong electric fields. In the mathematical formulation of the problem, the full two-way coupling piezoelectric effect is considered by adopting the assumption of a spanwise electric field variation. To enhance the generality of the formulation, the model considers also the hub mass moment of inertia and a non-constant rotating speed case. A general nonlinear system of mutually coupled partial differential equations is derived using the Hamilton principle, and the Galerkin method is applied to reduce these governing equations to the ordinary differential ones. A specific case of CAS lamination scheme that exhibits flapwise bending and twist mode elastic coupling is discussed in detail. Numerical results for system free vibrations are obtained to investigate the natural mode shapes and electrical field spatial distribution depending on the system rotation speed and laminae fibre orientation angle. Next, a forced vibration case is studied by applying to the hub a periodic driving torque with zero mean value. Nonlinear frequency response curves for the combined beam–hub system together with time series plots are prepared for different driving torque scenarios.

1 Introduction

The development of composite structures and active materials technology offers a great potential for advanced structural systems that can benefit from synergistic interactions of anisotropic composite material tailoring and adaptive material properties. One of the most popular active materials is piezoelectric ones that are commonly employed as both actuators and sensors by taking advantage of direct and converse piezoelectric effects.

There are a number of approaches to modelling these advanced systems concerning problems of electric field distribution, deformations kinematics and constitutive relations. As regards actuator behaviour and electric field domain, the most popular formulations are based on the converse effect only. These models consider the impact of known electrical field on the mechanical one and neglect electric potential generated due to the actuator deformation (direct piezoelectric effect). This one-way coupling approach leads to further simplification that ignores in-plane electric field spatial variation. In consequence, for the cantilever structures where the piezoactuators are spread over the entire specimen span, the external electric excitation appears merely as an additional term present in the boundary conditions associated with bending. Besides, the equations of motion of the system modelled by the discussed one-way coupling approach are reduced just to mechanical ones and electric degree of freedom is not present. Therefore, within this framework, the structural control can be achieved via the boundary moment strategy only [1,2,3].

However, as reported by several researchers [4,5,6], these one-way coupling models are not sufficiently accurate since they tend to underestimate the material stiffness and natural frequencies of the structure. The improved models of piezoelectric active systems are formulated incorporating both converse and direct effects (two-way coupling) and assuming spatial distribution of the electric potential in the longitudinal/transversal direction of the piezoelectric actuator. Further reading on issues related to mathematical modelling of electroelastic systems can be found in a comprehensive overview by Erturk and Inman [7].

Initial research on fully coupled models of piezoelectric structures was done in mid-1990s by Anderson and Hagood [8] and by Mitchell and Reddy [9] who formulated the hybrid plate theory. More advanced approaches were presented in papers published in the next decade. Zhou and collaborators [4] investigated cantilever composite plates with surface-bonded piezoelectric actuators and sensors. The assumptions to the mathematical model took into account spatial variation of the electric field as well as its higher-order distribution through the thickness of piezoelectric layers. Moreover, a higher-order laminate theory was used to represent mechanical displacement fields of both composite and piezoelectric layers and to accurately model transverse shear deformation. Numerical results indicated that two-way coupling effects significantly affected the predicted structural deflection, stress distribution and electrical signal magnitude.

Next, Zhang et al. [10] proposed a mathematical model of a piezoelectric active element bonded to an elastic substrate taking into account interfacial shear and normal stresses. In the analysis the linear constitutive equations were used to accurately represent fully coupled electromechanical field effects. A set of differential and integro-differential static equilibrium equations in terms of force, moment and electric displacements was derived.

Also Thornburgh et al. [5] developed a coupled-field model of a smart composite plate structure. In the formulation an additional degree of freedom was added to incorporate any attached electrical circuitry dynamics. The equations of motion were formulated using the fully coupled linear piezoelectric relation and solved for strain and electric charge. In the performed analysis, transient responses of the cantilever beam with piezoelectric active elements and integrated simple LRC circuit were studied. A cross-check with the classical plate theory and uncoupled piezoelectric modelling techniques was made to illustrate the importance of the coupled-field approach. Comparison with experimental data confirmed the accurate estimation of sensor response during transient loading of adaptive structures.

Next, Chandiramani [11] proposed a mathematical model of a smart rotating thin-walled doubly tapered composite beam carrying a tip mass. In the proposed formulation a spanwise and thicknesswise variation of the electric field applied to actuators was considered. Stress–strain relations were based on the linear piezoelectric material constitutive equations. To improve model accuracy for medium–thick wall structures, the higher-order shear deformation theory (HSDT) was incorporated. The proposed model was used to perform parametric studies involving ply angle, rotation speed, beam taper, etc., and finally to study the optimal control of a thin-walled rotating beam. It was concluded that considering the fully coupled piezoelectric effect yielded an order-of-magnitude reduction in beam settling time and required control voltage while compared to the decoupled approach.

The problem of accurate modelling of smart composite beams was investigated also by Roy and Yu [12]. In contrast to the mentioned above papers, authors approach was not based on classical a priori kinematic assumptions but fell into the class of asymptotic models. Through a rigourous dimensional reduction of the original 3-D fully coupled electromechanical problem and using the variational asymptotic method, authors developed the model of a Timoshenko beam with embedded/surface mounted active layer. Presented results demonstrated good agreement with the research available in the literature and with the direct 3-D multiphysics ANSYS simulation. Moreover, the significance of electro- to mechanical coupling effects was disclosed through comparison with an uncoupled approach. Later on authors extended their model to take into account the beam pre-twist effect as well as initial curvature [13].

All the discussed above papers indicated that the two-way coupling electromechanical effects affected the predicted structural properties significantly and had to be taken into account in mathematical models.

A further improvement in modelling hybrid systems may be achieved by considering the inherent nonlinear effects. This is especially important in case of high-power systems often operated under extreme conditions or in near resonant regime. The observed nonlinear characteristics of flexible piezoelectric devices can be attributed, among others, to large amplitude oscillations (geometric nonlinearities) and the hysteresis between the electric field and polarisation as well as strain. The importance of geometric nonlinearities and nonlinear damping hysteresis in cantilever PZT beam energy harvesters has been examined by Yang and Upadrashta [14]. The studies let to estimate the threshold value of the ratio of tip deflection to beam length, below which the geometrical linearity is a valid assumption and beyond which modelling of geometric nonlinearity is necessary. Studies on transient responses of smart cantilever beams and plates in geometrically nonlinear regime have been presented also by Zhang and Schmidt [15].

Other sources of structural nonlinearities are higher-order terms present in piezoceramic constitutive formula. These terms might involve purely elastic ones, only electrical effects or higher-order electromechanical coupling [16, 17]. Finally, nonlinearities may also result from coupling interactions to an electrical circuit connected to piezoelement (power source or energy harvesting circuit)—see research by, for example, Stanton et al. [18]. An attempt to develop a unified nonlinear non-conservative framework considering the above given constitutive effects and interactions within the two-way coupling approach frame was made very recently by Leadenham and Erturk [19].

Regarding the electric field effect, the most common mathematical models are the linear ones. They provide a reasonable approximation of the characteristics of piezoelectric materials at low levels of applied voltages and stresses. Unfortunately, these relations become increasingly inaccurate as the magnitude of electric field and stress levels increase. This is manifested in numerous laboratory experiments on the piezoelectric materials and piezoelectric devices—see, for example, [20,21,22]. Besides, as reported by Wagner and Hagedorn [21], nonlinear effects can be observed even if the electric field remains small but the piezoceramic actuators are excited in resonance.

Advanced studies on strong electric field effects in smart piezoelectric flexible structures were started in very recent years. Kapuria et al. [23] derived a fully coupled mathematical model of a smart composite plate considering piezoelectric constitutive nonlinearity with respect to electric field. To represent hybrid system kinematics accurately, a layerwise zig-zag theory was employed. A set of governing equations including an electric degree of freedom was derived within the frame of finite element formulation. The dynamic response of the system controlled by a linear quadratic Gaussian (LQG) controller was tested. It was revealed that, considering piezoelectric nonlinearity, an efficient vibration control could be achieved at a much lower actuation potential than predicted by the fully coupled but the linear model.

The authors continued this topic in their subsequent paper [24] where the previously developed mathematical model was extended to consider piezoelectric nonlinearity on an active vibration suppression of smart cylindrical and spherical shells. The effects of actuator thickness, radius of curvature to span ratio and applied loading on the relative difference between linear and nonlinear predictions are illustrated for the shape and vibration control cases.

Also Rao et al. [25] studied the behaviour of laminated shells under large applied electric fields. In the mathematical model, the assumptions of small strains and second-order nonlinear constitutive equations were adopted to develop a nonlinear finite element formulation of the problem. Numerical simulations were performed to study the effect of material nonlinearity for piezoelectric bimorph and composite shells under static loading. The importance of the derived nonlinear model under strong electric fields was confirmed by a significant difference between the results obtained by the linear and nonlinear constitutive models.

Fig. 1

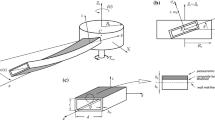
a Rotating thin-walled composite beam with electroded top/bottom surfaces referenced in global (inertial) ($X_0,Y_0,Z_0$) and local (x, y, z) coordinate systems; b beam profile cross section and associated coordinate system (n, s); c generalised displacements of a representative point 0 due to elastic deformation of the specimen

While analysing the above referenced literature one observes, there is no research on the integrated piezolaminated rotating composite beams involving the two-way coupled electromechanical theory. Also the electrically nonlinear piezoelectric constitutive relation has not been taken into account when studying the discussed structures. To bridge this gap, the present paper is given as an extension of recent author’s research [26], where the derivation of an analytical model for these types of hybrid systems was presented. In the proposed formulation the non-classical effects like material anisotropy, rotary inertia, first-order transverse shear deformation and warping restraint are incorporated. Moreover, the model considers an arbitrary beam pitch angle, the hub mass moment of inertia and a non-constant rotating speed case. In the proposed formulation the higher-order constitutive relations given by Joshi [16] and Tiersten [27] for small strains and large electric fields were used to take into account the effect of a nonlinear piezoceramic material behaviour.

In this research the previously developed set of nonlinear governing PDE equations is updated and solved for an unidirectional graphite–epoxy laminate and PZT-3203HD piezoceramic case. The results for system free vibrations are obtained to investigate the natural mode shapes and electrical field spatial distribution depending on the system rotation speed and laminae fibre orientation angle. Next, forced vibration cases are studied by applying to the hub a periodic driving torque with zero mean value. Nonlinear frequency response curves for the combined beam–hub system are presented, as well as bifurcation diagrams studying the system response with respect to excitation amplitude. Finally, time series plots are prepared for different driving torque scenarios. The observed differences between the responses of linear and nonlinear piezoceramic material models are discussed.

2 Problem formulation

Let us consider a slender, straight and elastic composite thin-walled smart beam clamped at the rigid hub of radius $R_0$ and inertia $J_\mathrm {h}$ rotating about a fixed frame axis $CZ_0$ as shown in Fig. 1. The hub current position is described by an angle $\psi (t)$ with respect to an inertial reference frame ($X_0,Y_0,Z_0$), and the rotational speed of the system $\dot{\psi }(t)$ is assumed to be arbitrary, i.e. not necessarily constant. The system is driven by an external torque $T_{\mathrm {ext}}$ applied to the hub.

The beam has a prismatic cross section, spanwise uniform (no taper) and no initial twist and curvature in its natural state.

In the analysis it is assumed the original shape of the cross section is maintained in its plane, but is allowed to warp out of the plane due to an elastic deformation of the beam. Presetting angle of the beam with respect to the plane of rotation ($X_0,Y_0$) is denoted by $\theta$—see Fig. 1b.

The composite material of the hosting beam is linearly elastic. Reinforcing fibres in individual laminas are set at an arbitrary angle $\alpha$ with respect to the cross-section circumferential axis s (see Fig. 1b). The number of layers as well as the their stacking sequence is arbitrary but preserving the profile thin-wall assumption, so the stresses in the wall transverse normal direction n can be neglected.

Apart from the fibre unidirectional layer, there are two additional piezoceramic layers of thickness $h_\mathrm {p}$ each. These are located on the outer surfaces of profile flanges and cover the full span of the beam. The active material is poled through its thickness and equipped with traditional surface electrodes. This is the typical geometry for (31) mode operating piezoelectric actuators and sensors.

For more details on all the imposed assumptions and discussion on their significance for the mathematical formulation of the problem, please refer to the previous author’s papers [28, 29].

3 Electromechanical governing equations

The mechanical equations of motion of the rotating beam and a charge equation of electrostatics are derived according to the extended Hamilton principle of the least action

$$\begin{aligned} \delta J=\int _{t_{1}}^{t_{2}} \left( \delta T-\delta U+\delta W_\mathrm {ext} \right) \hbox {d}t=0 \end{aligned}$$

(1)

where J is the action, T is the kinetic energy, U is the potential energy including mechanical ($U_\mathrm {m}$) and electrical components ($U_\mathrm {e}$), and the work done by the external loads is given by the $W_\mathrm {ext}$ term.

Following the kinematic assumptions given in the previous section and discussed in detail in [28, 29], the elastic displacements of an arbitrary point A of the cross section can be expressed in the local coordinates frame (0, x, y, z) as [29]

$$\begin{aligned} D_x&= u_0(x,t) + {\vartheta }_y(x,t) \left( z - n\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\right) \nonumber \\&\quad + {\vartheta }_z(x,t)\left( y + n\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}\right) -G(n,s)\varphi ^\prime \nonumber \\ D_y&= v_0\,(x,t) - \left( y + n\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}\right) \left( 1-\cos \varphi \right) \nonumber \\&- \left( z - n\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\right) \sin \varphi \nonumber \\&\approx v_0\,(x,t) - \tfrac{1}{2}\left( y + n\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}\right) \varphi ^2 - (z - n\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s})\varphi \nonumber \\ D_z&= w_0\,(x,t) + \left( y + n\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}\right) \sin \varphi \nonumber \\&\quad - \left( z - n\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\right) \left( 1-\cos \varphi \right) \nonumber \\&\approx w_0\,(x,t) + \left( y + n\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}\right) \varphi - \tfrac{1}{2}\left( z - n\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\right) \varphi ^2 \end{aligned}$$

(2)

In formulas (2) the variables $u_0$, $v_0$, $w_0$ are the displacements of the point 0 located on the beam axis and belonging to the same cross section as the discussed point A, $\varphi =\varphi (x,t)$ denotes rotation of the cross section about the Ox axis (profile twist)—see Fig. 1c. Angles ${\vartheta }_y(x,t)=\gamma _{xz} - w_0^\prime$ and ${\vartheta }_z(x,t) = \gamma _{xy} - v_0^\prime$ represent cross-section rotations about the respective local axes y and z and considering the shear effect. These six variables constitute a set of basic mechanical unknowns of the problem. Besides, the first equation in the above set includes warping effect due to the warping function term G(s, n), where n stands for the distance of the considered point A to the cross-section wall mid-line, and s is a circumferential coordinate—see Fig. 1b.

Strain formulas are as follows:

$$\begin{aligned} \varepsilon _{xx}&= \varepsilon _{xx}^{(0)} + n\varepsilon _{xx}^{(1)}=u_{0}^{\prime } + z{\vartheta }_y^{\prime } + y{\vartheta }_z^{\prime } - G^{(0)}(s)\varphi ^{\prime \prime } \nonumber \\&\quad + \tfrac{1}{2}\left( v_{0}^{\prime } - z\varphi ^{\prime }\right) ^2\nonumber \\&\quad + \tfrac{1}{2}\left( w_{0}^{\prime } + y\varphi ^{\prime }\right) ^2 \nonumber \\&\quad + n\left( \tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s}{\vartheta }_z^{\prime } -\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}{\vartheta }_y^{\prime } - G^{(1)}(s)\varphi ^{\prime \prime }\right) \nonumber \\ \gamma _{xs}&= \gamma _{xs}^{(0)} + n\gamma _{xs}^{(1)}=({\vartheta }_y+ w_{0}^{\prime })\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s} + ({\vartheta }_z+ v_{0}^{\prime })\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\nonumber \\&\quad + g^{(0)}(s)\varphi ^{\prime } + n g^{(1)}(s)\varphi ^{\prime }\nonumber \\ \gamma _{xn}&= \gamma _{xn}^{(0)} = -({\vartheta }_y+ w_{0}^{\prime })\tfrac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s} + ({\vartheta }_z+ v_{0}^{\prime } )\tfrac{\mathop {}\!\mathrm {d}z}{\mathop {}\!\mathrm {d}s} \end{aligned}$$

(3)

where the prime symbol corresponds to the differentiation with respect to space variable x, and the superscripts $(\centerdot )^{(0)}$ and $(\centerdot )^{(1)}$ denote the cross-section mid-line and off-mid-line components, respectively.

Although the mathematical model of the beam is limited to the linear case, higher-order terms associated with the lateral and transversal displacements in axial strain $\varepsilon _{xx}$ are taken into account. These terms play a crucial role in a proper modelling of the blade stiffening effect arising from the system rotation $\dot{\psi }(t)$. This approach is one of several methods that are used in linear models of rotating systems to capture these phenomena.

To write down the expressions for stresses in piezoceramic layer, its constitutive relations have to be used. For the specific case of an active material subjected to electric field in poling direction $x_3$ (thicknesswise) and limiting the analysis to linear strains and cubic nonlinearities in the electric field as well as plane stress condition, a set of reduced constitutive equations for the converse effect is [26]

$$\begin{aligned}&\begin{Bmatrix} \sigma _{ss}\nonumber \\ \sigma _{xx}\nonumber \\ \sigma _{xs}\nonumber \\ \end{Bmatrix}_{\!\!(\mathrm {p})} = \begin{bmatrix} \tilde{Q}_{11}&\quad \tilde{Q}_{12}&\quad 0\nonumber \\ \tilde{Q}_{12}&\quad \tilde{Q}_{11}&\quad 0\nonumber \\ 0&\quad 0&\quad \tilde{Q}_{66}\nonumber \\ \end{bmatrix} \begin{Bmatrix} \varepsilon _{ss}\nonumber \\ \varepsilon _{xx}\nonumber \\ \gamma _{ss}\\ \end{Bmatrix}- \begin{Bmatrix} \tilde{e}_{31} E_3\nonumber \\ \tilde{e}_{31} E_3\nonumber \\ 0 \end{Bmatrix}\\&\quad - \mathrm {sgn}(E_3)\begin{Bmatrix} \tilde{b}_{31} E_3^2\nonumber \\ \tilde{b}_{31} E_3^2\nonumber \\ 0 \end{Bmatrix}- \begin{Bmatrix} \tilde{f}_{31} E_3^3\nonumber \\ \tilde{f}_{31} E_3^3\nonumber \\ 0 \end{Bmatrix}\nonumber \\&\sigma _{{xn}_{(\mathrm {p})}} = \ \tilde{C}_{44} \gamma _{xn} \end{aligned}$$

(4)

where the reduced stiffnesses $\tilde{Q}_{ij}$ and appropriate constants are

$$\begin{aligned} \tilde{Q}_{11}= & {} \tilde{Q}_{22}=\tilde{C}_{11}-\frac{\tilde{C}_{13}^2}{\tilde{C}_{33}} \quad \tilde{Q}_{66} = \tilde{C}_{66} \nonumber \\ \tilde{Q}_{12}= & {} \tilde{C}_{12}-\frac{\tilde{C}_{13}^2}{\tilde{C}_{33}}\nonumber \\ \tilde{e}_{31}= & {} e_{31}-\frac{\tilde{C}_{13} e_{33}}{\tilde{C}_{33}} \quad \tilde{f}_{31} = f_{31}-\frac{\tilde{C}_{13} f_{33}}{\tilde{C}_{33}}\nonumber \\ \tilde{b}_{31}= & {} \hat{b}_{31}-\frac{\tilde{C}_{13} \hat{b}_{33}}{\tilde{C}_{33}} \end{aligned}$$

In the above expressions $\tilde{C}_{ij}$ stands for members of the second-order piezoceramic material elasticity tensor, $e_{13}$ and $e_{33}$ are two terms of the piezoelectric tensor, $\hat{b}_{31}$ and $\hat{b}_{33}$ are members of the effective electrostrictive tensor, and finally $f_{31}$ and $f_{33}$ are components of the fourth-order piezoelectric tensor—see also [16, 27].

Since the active material is poled through its thickness with traditional surface electrodes normal to axis 3, one can retain electric displacement term $D_3$ only. The direct piezoelectric effect equation is as follows [26]

$$\begin{aligned} D_3&= \ \tilde{e}_{31} \varepsilon _{ss} + \tilde{e}_{31} \varepsilon _{xx} + \tilde{\xi }_{33} E_3 + \mathrm {sgn}(E_3)\chi _{33} E_3^2 \nonumber \\&\quad + (\hat{\chi }_1+ 2 \hat{\chi }_2 + \hat{\chi }_3) E_3^3 \end{aligned}$$

(5)

where new reduced material constants are

$$\begin{aligned}&\tilde{\xi }_{33} =\xi _{33} + \frac{e_{33}^2}{\tilde{C}_{33}} \qquad \tilde{\chi }_{33} = \chi _{33} + \frac{e_{33}\hat{b}_{33}}{\tilde{C}_{33}}\\&\tilde{\chi }_{123} = \hat{\chi }_1+ 2 \hat{\chi }_2 + \hat{\chi }_3 + \frac{e_{33} {f}_{33}}{\tilde{C}_{33}} \end{aligned}$$

In the above expressions $\xi _{33}$ is material permittivity coefficient, $\chi _{33}$ and $\hat{\chi }_{i},\ i=1,2,3$ are members of the third- and the fourth-order electric susceptibility tensors, respectively [16, 27].

Constitutive equations for the individual layers of composite plant may be formulated according to the classical laminate theory (CLT). The detailed expressions for individual stress resultants $\sigma _{\centerdot \centerdot (c)}$ are given in “Appendix A”.

Fig. 2

In-plane and transversal stress resultants and stress couples acting on a beam wall representative element

The 2-D stress resultants and stress couples—see Fig.  2—in the combined hybrid laminate–piezoceramic system can be obtained after integration of individual stress components $\sigma _{\centerdot \centerdot (p)}$ and $\sigma _{\centerdot \centerdot (c)}$ through the total thickness of the beam wall. Next, these can be transformed from local (0, x, s, n) coordinate system to global one (0, x, y, z). The expressions for resulting terms $N_{xx}$, $N_{xn}$, $N_{xs}$, $L_{xx}$, $L_{xs}$ (see Eq. B.4) as well as appropriate comments are found in “Appendix B”.

Bearing in mind the given expressions, the potential energy of the system is given as follows [26]

$$\begin{aligned} U_\mathrm {m}&= \tfrac{1}{2}\int \limits _0^{l}\!\!\int \limits _c\!\int \limits _{h+h_\mathrm {p}} \!\!\!\big (\sigma _{xx}\varepsilon _{xx} + \sigma _{xn}\gamma _{xn} + \sigma _{xs}\gamma _{xs} \big ) \mathop {}\!\mathrm {d}n \mathop {}\!\mathrm {d}s \mathop {}\!\mathrm {d}x\nonumber \\&= \tfrac{1}{2}\int \limits _0^{l}\!\!\int \limits _c \big [N_{xx}\varepsilon _{xx}^{(0)} + L_{xx}\varepsilon _{xx}^{(1)} + N_{xn}\gamma _{xn}^{(0)}\nonumber \\&\quad + N_{xs}\gamma _{xs}^{(0)} + L_{xs}\gamma _{xs}^{(1)}\big ] \mathop {}\!\mathrm {d}s \mathop {}\!\mathrm {d}x \end{aligned}$$

(6)

where subscript $(\centerdot )_\mathrm{c}$ corresponds to integration over cross-section perimeter.

The total kinetic energy of the system consists of components coming from the hub and the beam

(7)

where designation $\rho$ refers to an average beam material density and representative infinitesimal volume element is $\mathop {}\!\mathrm {d}V=\mathop {}\!\mathrm {d}n \mathop {}\!\mathrm {d}s \mathop {}\!\mathrm {d}x$; $J_\mathrm {h}$ is the mass moment of hub inertia. Individual components of the velocity vector are time derivatives of a temporary position of an arbitrary point A in global (inertial) coordinate system

$$\begin{aligned} R_x&= \ (D_x+x+R_0)\cos \psi - (D_y+Y)\cos \theta \sin \psi \nonumber \\&\quad +(D_z + Z)\sin \theta \sin \psi \nonumber \\ R_y&= \ (D_x+x+R_0)\sin \psi + (D_y+Y)\cos \theta \cos \psi \nonumber \\&\quad -(D_z + Z)\sin \theta \cos \psi \nonumber \\ R_z&= \ (D_y+Y)\sin \theta + (D_z + Z)\cos \theta \end{aligned}$$

(8)

Regarding the virtual work of external loadings $W_{\mathrm {ext}}$ in (1), the considered research is limited to external torque $T_{\mathrm {ext},z}$ driving the hub shaft (see Fig.  1); therefore,

$$\begin{aligned} \delta W_{\mathrm {ext}}=T_{\mathrm {ext},z}\delta \psi (t) \end{aligned}$$

(9)

Using the Hamilton’s variational principle, the minimisation of the action J Eq. (1) with respect to six mechanical degrees of freedom ($u_0, v_0, w_0, {\vartheta }_y, {\vartheta }_z, \varphi$) and electrical one ($E_3$) yields seven electromechanical differential equations of motion and the associated boundary conditions. These are as follows [26]:

• $\delta \psi (t)$

  $$\begin{aligned}&-J_\mathrm {h}\ddot{\psi }(t)- B_{22}\ddot{\psi }(t)- B_{14}l\ddot{\psi }(t)\cos ^{2}\theta \nonumber \\&\quad -B_{13}l\ddot{\psi }(t)\sin ^{2}\theta \!+\!2B_{15}l\ddot{\psi }(t)\cos \theta \sin \theta \nonumber \\&\quad -\,\!\int _0^{l}\! \Big \{2(R_{0} + x)\left[ B_{1}u_{0} + B_{11}{\vartheta }_y\right. \nonumber \\&\quad \left. + B_{12}{\vartheta }_z- B_{7}\varphi ^{\prime } \right] \ddot{\psi }(t)\nonumber \\&\quad +\, 2 \left( B_{12}\cos \theta - B_{11}\sin \theta \right) \left[ \left( v_{0}\cos \theta \right. \right. \nonumber \\&\quad \left. \left. - w_{0}\sin \theta \right) \ddot{\psi }(t)+ \left( \dot{v}_{0}\cos \theta - \dot{w}_{0}\sin \theta \right) \dot{\psi }(t)\right] \nonumber \\&\quad + \,2 \left[ B_{17}\sin ^{2}\!\theta + \left( B_{16} - B_{19}\right) \sin \theta \cos \theta \right. \nonumber \\&\left. \quad - B_{18}\cos ^{2}\theta \right] \left( \varphi \ddot{\psi }(t)+ \dot{\varphi }\dot{\psi }(t)\right) + \left( B_{11}\sin \theta \right. \nonumber \\&\quad \left. -B_{12}\cos \theta \right) \ddot{u}_{0}+ \big (B_{13}\sin \theta - B_{15}\cos \theta \big )\ddot{\vartheta }_y\nonumber \\&\quad + \big (B_{15}\sin \theta - B_{14}\cos \theta \big )\ddot{\vartheta }_z\nonumber \\&\quad + \big (B_{9}\cos \theta \!-\!B_{8}\sin \theta \big )\ddot{\varphi }^{\prime } \nonumber \\&\quad + \,(R_{0}\!+\!x)\big [B_{1}\ddot{v}_{0}\cos \theta - B_{1}\ddot{w}_{0}\sin \theta \nonumber \\&\quad - \big (B_{3}\sin \theta \!+\!B_{2}\cos \theta \big )\ddot{\varphi }\big ]\nonumber \\&\quad + \,2 (R_{0}+x)\big (B_{1}\dot{u}_{0} + B_{11} \dot{\vartheta }_y+ B_{12} \dot{\vartheta }_z\nonumber \\&\quad - B_{7} \dot{\varphi }^{\prime } \big )\dot{\psi }(t)\Big \}\mathop {}\!\mathrm {d}x + T_{\mathrm {ext},z} = 0 \end{aligned}$$

  (10)

• $\delta u_{0}$,

  $$\begin{aligned}&- B_{1} \ddot{u}_0 - B_{12}\ddot{\vartheta }_z- B_{11}\ddot{\vartheta }_y+ B_{7}\ddot{\varphi }^\prime + 2 \left[ (B_{1}\dot{v}_{0}\right. \nonumber \\&\quad \left. - B_{2}\dot{\varphi })\cos \theta - (B_{1}\dot{w}_{0} + B_{3}\dot{\varphi })\sin \theta \right] \dot{\psi }(t)\nonumber \\&\quad +\, \left[ B_{1} (R_0\!+\!x\!+\!u_0) + B_{12}{\vartheta }_z+ B_{11}{\vartheta }_y\right. \nonumber \\&\quad \left. - B_{7}\varphi ^\prime \right] \dot{\psi }^2(t)+\, \left[ ( B_{1} v_{0} - B_{2}\varphi + B_{12}) \cos \theta \right. \nonumber \\&\quad \left. - ( B_{1} w_{0}+ B_{3}\varphi + B_{11}) \sin \theta \right] \ddot{\psi }(t)\nonumber \\ {}&\quad + (T_x)^{\prime } = 0 \end{aligned}$$

  (11)

  with boundary conditions $u_{0} \big |_{x=0}=0, T_{x} \big |_{x=l}=0$

• $\delta v_{0}$

  $$\begin{aligned}&- B_1 \ddot{v}_{0} + B_{2}\ddot{\varphi } - 2 \left( B_{1} \dot{u}_0 + B_{12}\dot{\vartheta }_z+ B_{11}\dot{\vartheta }_y\right. \nonumber \\&\quad \left. - B_{7}\dot{\varphi }^\prime \right) \dot{\psi }(t)\cos \theta +\, \left[ (B_{1}v_{0} - B_{2}\varphi \right. \nonumber \\&\quad + B_{12})\cos ^2\theta - (B_{1} w_{0} + B_{3}\varphi \nonumber \\&\quad \left. + B_{11})\sin \theta \cos \theta \right] \dot{\psi }^2(t)-\, \left[ B_{1} (R_0 + x + u_0)\right. \nonumber \\&\quad \left. + B_{12}{\vartheta }_z+B_{11}{\vartheta }_y- B_{7}\varphi ^\prime \right] \ddot{\psi }(t)\cos \theta + Q_{y}^{\prime }\nonumber \\&\quad + (T_{x} v_{0}^{\prime })^{\prime } = 0 \end{aligned}$$

  (12)

  with boundary conditions $v_{0} \big |_{x=0}=0, [Q_{y} + T_{x} v_{0}^{\prime } ] \big |_{x=l} = 0$

• $\delta w_{0}$

  $$\begin{aligned}&- B_{1}\ddot{w}_{0} - B_{3}\ddot{\varphi } + 2 \left( B_{1}\dot{u}_0 + B_{12}\dot{\vartheta }_z+ B_{11}\dot{\vartheta }_y\right. \nonumber \\&\left. - B_{7}\dot{\varphi }^\prime \right) \dot{\psi }(t)\sin \theta \nonumber \\&\quad + \left[ (B_{1}w_{0} + B_{3}\varphi + B_{11})\sin ^2\theta \right. \nonumber \\&\quad \left. - (B_{1}v_{0} - B_{2}\varphi + B_{12})\dot{\psi }^2(t)\sin \theta \cos \theta \right] \dot{\psi }^2(t)\nonumber \\&\quad + \left[ B_{1} (R_0\!+\!x\!+\!u_0) + B_{12}{\vartheta }_z+ B_{11}{\vartheta }_y\right. \nonumber \\&\quad \left. - B_{7}\varphi ^\prime \right] \ddot{\psi }(t)\sin \theta + Q_{z}^{\prime } + (T_{x} w_{0}^{\prime })^{\prime } = 0 \end{aligned}$$

  (13)

  with boundary conditions $w_{0} \big |_{x=0}=0, [Q_{z} + T_{x} w_{0}^{\prime } ]\big |_{x=l}=0$

• $\delta {\vartheta }_y$

  $$\begin{aligned}&-B_{11}\ddot{u}_0 - B_{13}\ddot{\vartheta }_y- B_{15}\ddot{\vartheta }_z+ B_{8} \ddot{\varphi }^\prime \nonumber \\&\quad + 2 \big [ (B_{11}\dot{v}_{0} - B_{16}\dot{\varphi }) \cos \theta - (B_{11}\dot{w}_{0}\nonumber \\&\quad + B_{17}\dot{\varphi })\sin \theta \big ]\dot{\psi }(t)\nonumber \\&\quad +\left[ (B_{11}v_{0} - B_{16}\varphi + B_{15})\cos \theta - (B_{11}w_{0}\right. \nonumber \\&\quad \left. + B_{17}\varphi + B_{13})\sin \theta \right] \ddot{\psi }(t)\nonumber \\&\quad + \left[ B_{11}(R_0 + x + u_0) + B_{15}{\vartheta }_z\right. \nonumber \\&\quad \left. + B_{13}{\vartheta }_y- B_{8}\varphi ^\prime \right] \dot{\psi }^2(t)- Q_{z} + M_{y}^{\prime } = 0 \end{aligned}$$

  (14)

  with boundary conditions ${\vartheta }_y\big |_{x=0}=0, M_{y}\! \big |_{x=l} = 0$

• $\delta {\vartheta }_z$

  $$\begin{aligned}&- B_{12}\ddot{u}_0 - B_{15}\ddot{\vartheta }_y- B_{14}\ddot{\vartheta }_z+ B_{9} \ddot{\varphi }^\prime + 2 \left[ (B_{12}\dot{v}_{0}\right. \nonumber \\&\quad \left. - B_{18}\dot{\varphi })\cos \theta - (B_{12}\dot{w}_{0} + B_{19}\dot{\varphi })\sin \theta \right] \dot{\psi }(t)\nonumber \\&\quad + \left[ (B_{12}v_{0} - B_{18}\varphi + B_{14})\cos \theta \right. \nonumber \\&\quad \left. - (B_{12}w_{0} + B_{19}\varphi + B_{15})\sin \theta \right] \ddot{\psi }(t)\nonumber \\&\quad + \left[ B_{12}(R_0 + x + u_0) + B_{14}{\vartheta }_z\right. \nonumber \\&\quad \left. + B_{15}{\vartheta }_y- B_{9}\varphi ^\prime \right] \dot{\psi }^2(t)- Q_{y} + M_{z}^{\prime } = 0 \end{aligned}$$

  (15)

  with boundary conditions ${\vartheta }_z\big |_{x=0}=0, M_{z} \! \big |_{x=l}=0$

• $\delta \varphi$

  $$\begin{aligned}&B_{2}\ddot{v}_{0}\!-\!B_{3}\ddot{w}_{0}\!-\! B_{4}\ddot{\varphi }\!-\!B_{5}\ddot{\varphi }\!+\!2 \left[ (B_{2}\cos \theta \right. \nonumber \\&\quad \left. +B_{3}\sin \theta )\dot{u}_{0}\!+\!(B_{16}\cos \theta \! +\! B_{17}\sin \theta )\dot{\vartheta }_y\right] \dot{\psi }(t)\nonumber \\&\quad + 2 \left[ (B_{18}\cos \theta + B_{19}\sin \theta )\dot{\vartheta }_z- (B_{20}\cos \theta \right. \nonumber \\&\quad \left. + B_{21}\sin \theta )\dot{\varphi }^{\prime } + \left( B_{7}\dot{v}_{0} - B_{20}\dot{\varphi }\right) ^{\prime }\cos \theta \right. \nonumber \\&\quad \left. - \left( B_{7}\dot{w}_{0} + B_{21}\dot{\varphi }\right) ^{\prime }\sin \theta \right] \dot{\psi }(t)\nonumber \\&\quad + (B_{2}\cos \theta + B_{3}\sin \theta ) (w_{0}\sin \theta \nonumber \\&\quad - v_{0}\cos \theta )\dot{\psi }^2(t)+ \left[ B_{17}\sin ^{2}\theta \right. \nonumber \\&\quad \left. + \left( B_{16} - B_{19}\right) \cos \theta \sin \theta - B_{18}\cos ^{2}\theta \right] \dot{\psi }^2(t)\nonumber \\&\quad + \left[ (B_{4} - B_{19})\cos ^{2}\theta + (2 B_{6} + B_{17} \right. \nonumber \\&\quad \left. + B_{18})\sin \theta \cos \theta + (B_{5}- B_{16})\sin ^{2}\theta \right] \varphi \dot{\psi }^2(t)\nonumber \\&\quad + \left\{ \left[ B_{7}(R_{0}+x + u_0)\right] ^{\prime } + \left( B_{8}{\vartheta }_y\right) ^{\prime } + \left( B_{9}{\vartheta }_z\right) ^{\prime } \right. \nonumber \\&\quad \left. - \left( B_{10}\varphi ^{\prime }\right) ^{\prime }\right\} \dot{\psi }^2(t)+ \,(B_{2}\cos \theta + B_{3}\sin \theta )(R_{0}\nonumber \\&\quad +x)\ddot{\psi }(t)+ \left[ (B_{18}\cos \theta + B_{19}\sin \theta ){\vartheta }_z\right. \nonumber \\&\quad \left. + (B_{16}\cos \theta + B_{17}\sin \theta ){\vartheta }_y\right] \ddot{\psi }(t)\nonumber \\&\quad + \left[ (B_{3}\cos \theta - B_{2}\sin \theta )(R_{0}+x)\varphi \right. \nonumber \\&\quad \left. - (B_{20}\cos \theta + B_{21}\sin \theta )\varphi ^{\prime }\right] \ddot{\psi }(t)\nonumber \\&\quad + \left[ \left( B_{7}v_{0} - B_{20}\varphi \right) ^{\prime }\cos \theta - \left( B_{7}w_{0} \right. \right. \nonumber \\&\quad \left. \left. + B_{21}\varphi \right) ^{\prime }\sin \theta \right] \ddot{\psi }(t)-\, \left( B_{8}\ddot{\vartheta }_y\right) ^{\prime } - \left( B_{9}\ddot{\vartheta }_z\right) ^{\prime }\nonumber \\&\quad - \left( B_{7}\ddot{u}_{0}\right) ^{\prime } + \left( B_{10}\ddot{\varphi }^{\prime }\right) ^{\prime } + M_{x}^{\prime } {+} B_{w}^{\prime \prime } + (T_{r} \varphi ^{\prime })^{\prime } {=} 0 \end{aligned}$$

  (16)

  with boundary conditions,

  $$\begin{aligned}&\left\{ \!-\!B_{7}\ddot{u}_{0}\!-\!B_{8}\ddot{\vartheta }_y\!-\!B_{9}\ddot{\vartheta }_z\!+\!B_{10}\ddot{\varphi }^{\prime }\!+\!2 \left[ (B_{7}\dot{v}_{0}\right. \right. \nonumber \\&\quad \left. -B_{20}\dot{\varphi })\cos \theta \!-\!(B_{7}\dot{w}_{0}\!+\!B_{21}\dot{\varphi })\sin \theta \right] \dot{\psi }(t)\nonumber \\&\quad + \left[ (B_{7}v_{0}\!-\!B_{20}\varphi + B_{9})\cos \theta \!-\!(B_{7}w_{0} + B_{21}\varphi \right. \nonumber \\&\quad \left. + B_{8})\sin \theta \right] \ddot{\psi }(t)+ \left[ B_7(R_{0} + x + u_{0})+ B_{8}{\vartheta }_y\right. \nonumber \\&\quad \left. \left. + B_{9}{\vartheta }_z- B_{10}\varphi ^{\prime }\right] \dot{\psi }^2(t)+ M_{x}\!+\!B_{w}^{\prime }+T_{r} \varphi ^{\prime }\right\} \!\big |_{x=l}\nonumber \\&= 0, B_{w} \big |_{x=l} = 0, \varphi ^{\prime }\big |_{x=0} = 0, \varphi \big |_{x=0} = 0. \end{aligned}$$

  (17)

  where $B_i$ ($i=1\ldots 21$) terms are inertia coefficients as defined in [28].

• $\delta {E}_3$

  $$\begin{aligned}&a_{E1}u_{0}^{\prime }\!+\!a_{E2}{\vartheta }_z^{\prime }\!+\!a_{E3}{\vartheta }_y^{\prime }\!+\!a_{E4}({\vartheta }_z\!+\!v_{0}^{\prime })\!+\!a_{E5}({\vartheta }_y\nonumber \\&\quad +w_{0}^{\prime })\!-\!a_{E6}\varphi ^{\prime \prime }\!+\!a_{E7}\varphi ^{\prime }\!-\!a_{Ee} E_3\nonumber \\&\quad -a_{Eb}\,\mathrm {sgn}(E_3) E_3^2-a_{Ef} E_3^3 = 0 \end{aligned}$$

  (18)

Relations (10)–(18) form a nonlinear system of partial differential equations (PDEs) that exhibit a complete coupling between various modes, i.e. axial deformation, chordwise and flapwise bendings plus corresponding transverse shear deformations, twist and warpings (primary and secondary) as well as an electrostatic equilibrium. Although the governing equations look similar to the purely mechanical system [29], the principal difference stays in the definition of 1-D generalised stress resultants and stress couples which include electrical components as expressed in (B.4). Obviously, the addition to the governing system is the electrostatic Eq.  (18).

If limited to the linear electric field and to zero presetting angle, the given above governing equations are similar to the ones derived by Mitra et al. [30]. When referring to their research, one comment is to be made. Although the full two-way coupling effect was posed while deriving equations of motion, the discussed problem was simplified at the stage of system discretisation. In the finite element code developed by the authors, a uniform electric field magnitude over the finite element domain was assumed resulting in the electrical and mechanical modes decoupling.

3.1 CAS lamination scheme

General equations of motion given in the previous section get significantly simplified if any of the special lamination schemes is assumed. In particular, as reported in, for example, [2] the circumferentially asymmetric stiffness (CAS) composite configuration decouples the full set of six mechanical equations of motion into two independent sub-systems. One corresponds to the flapwise bending–shear-twisting specimen deformation, and the second one exhibits the coexisting axial stretching and chordwise bending–shear modes. Thus, presuming the CAS fibre arrangement and clamping the beam to the hub at $\theta =-90^\circ$ angle make the piezoelectric transducers to excite lead–lag plane bending coupled with the specimen twisting. Furthermore, considering the simplifications resulting from the cross-section symmetry (see [28] for inertia terms calculations) the general equations of motion (10)–(18) are simplified to the following form

• for the rigid hub

  $$\begin{aligned}&J_\mathrm {h}\ddot{\psi }(t)+ (B_{22} + B_4 l)\ddot{\psi }(t)+ B_4 l \ddot{\vartheta }_y\nonumber \\&\quad +\int _0^{l}\!\!\Big \lbrace \! b_1 (R_{0}\!+\!x)\!\!\left[ 2 u_0 \ddot{\psi }(t)\!+\!2 \dot{u}_0 \dot{\psi }(t)\!-\!\ddot{w}_0 \right] \!\!\Big \rbrace \mathop {}\!\mathrm {d}x \nonumber \\&\quad - T_{\mathrm {ext},z}(t) = 0 \end{aligned}$$

  (19)

• displacement in the lead–lag plane $w_{0}$

  $$\begin{aligned}&b_{1}\ddot{w}_{0} + 2 b_{1}\dot{u}_{0}\,\dot{\psi }(t)- b_{1}w_{0}\dot{\psi }^2(t)\nonumber \\&\quad + b_{1} (R_{0}\!+\!x\!+\!u_{0}) \ddot{\psi }(t)- a_{55} {\vartheta }_y^\prime \!-\!a_{55}w_0^{\prime \prime } \nonumber \\&\quad - \big (T_x w_{0}^{\prime } \big )^{\prime } = 0 \end{aligned}$$

  (20)

  with boundary conditions $w_{0} \big |_{x=0}=0, ({\vartheta }_y+ w_0^{\prime } )\!\big |_{x=l}=0$

• transverse shear ${\vartheta }_y$

  $$\begin{aligned}&B_{4}\ddot{\vartheta }_y\!-\!B_{4}{\vartheta }_y\dot{\psi }^2(t)\!-\!B_{4}\ddot{\psi }(t)\nonumber \\&\quad + a_{55}{\vartheta }_y\!+\!a_{55}w_0^{\prime }\!-\!a_{33}{\vartheta }_y^{\prime \prime } - a_{37}\varphi ^{\prime \prime }\nonumber \\&\quad - a_{3e}E_3^{\prime }\!-\!a_{3b}\big [\mathrm {sgn}(E_3) E_3^2\big ]^{\prime }\!-\!a_{3f}\big (E_3^3\big )^{\prime } = 0 \end{aligned}$$

  (21)

  with boundary conditions

  $$\begin{aligned}&{\vartheta }_y\big |_{x=0}=0, \big [a_{33}{\vartheta }_y^\prime \!+\!a_{37}\varphi ^\prime \nonumber \\&+a_{3e}E_3\!+\!a_{3b}\,\mathrm {sgn}(E_3)E_3^2\!+\!a_{3f}E_3^3\big ]\!\big |_{x=l} = 0 \end{aligned}$$

• profile twist angle $\varphi$

  $$\begin{aligned}&(B_{4}+B_{5})\ddot{\varphi } + (B_{4}-B_{5})\varphi \dot{\psi }^2(t)- a_{37}{\vartheta }_y^{\prime \prime }\nonumber \\&\quad -a_{77}\varphi ^{\prime \prime } - \big (T_r \varphi ^{\prime }\big )^\prime = 0, \end{aligned}$$

  (22)

  with boundary conditions

  $$\begin{aligned} \varphi \big |_{x=0} = 0,\qquad \left( a_{37}{\vartheta }_y^{\prime }+a_{77}\varphi ^{\prime }\right) \!\big |_{x=l} = 0, \end{aligned}$$

• electrostatic equation ${E}_3$

  $$\begin{aligned} a_{E3}{\vartheta }_y^{\prime } - a_{Ee} E_3 - a_{Eb}\, \mathrm {sgn}(E_3) (E_3)^2 - a_{Ef} E_3^3 = 0 \end{aligned}$$

  (23)

Terms $T_x(x)$ and $T_r(x)$ present in (20) and (22) correspond to system stiffening resulting from rotational transportation motion, and they are defined as

$$ T_x(x)= b_1(l-x)\big [R_0 + \tfrac{1}{2}(l+x)\big ]\dot{\psi }^2(t), \; T_r(x) = \gamma T_x(x) $$

where $\gamma =\frac{B_4+B_5}{m_0 \beta }$ and $\beta$ is cross-section perimeter.

The derived equations of motion for the rigid hub–thin-walled piezoelectric composite beam constitute a system of nonlinear coupled partial differential equations. It can be observed the electrical degree of freedom (dof) and the individual mechanical ones representing bending and profile twist are coupled through the transverse shear deformation Eq. (21). Higher-order electric field terms are present in this equation, as well as in electrostatic one. These terms naturally result from the discussed nonlinear piezoelectric effect.

In Eqs. (19)–(23) the coefficient $a_{33}$ corresponds to bending stiffness, $a_{55}$ to transverse shear stiffness, $a_{77}$ is torsional one and $a_{37}$ is bending–torsion coupling stiffness. Coefficients $a_{3e}=a_{E3}$, $a_{3b}$, $a_{3f}$ and $a_{{ Eb}}$, $a_{{ Ef}}$ are electromechanical reduced stiffnesses resulting from piezoelectric and electrostatic properties of the actuators, where $(\centerdot )_b$ and $(\centerdot )_f$ subscripts refer to higher-order electric field $E_3$ terms. Individual definitions are as follows:

$$\begin{aligned} a_{3\lambda }&= \int _c\int _{h_\mathrm {p}}{\left[ \left( \frac{A_{12}}{A_{11}}-1\right) z - \frac{\mathop {}\!\mathrm {d}y}{\mathop {}\!\mathrm {d}s}\left( \frac{B_{12}}{A_{11}}-n\right) \right] }\tilde{\lambda }_{31} \mathop {}\!\mathrm {d}s \mathop {}\!\mathrm {d}n \nonumber \\&\text {for\ }\lambda \in (e,b,f)\nonumber \\ a_{Ee}&= \int _c\!\int _{h_\mathrm {p}}{\!\!\!\Big (\xi _{33} + \frac{e_{33}^2}{\tilde{C}_{33}} + \frac{h_\mathrm {p}}{A_{11}} \tilde{e}_{31}^2 \Big )} \mathop {}\!\mathrm {d}n \mathop {}\!\mathrm {d}s\nonumber \\ a_{Eb}&= \int _c\!\int _{h_\mathrm {p}}{\!\!\!\Big (\chi _{33} + \frac{e_{33}\widehat{b}_{33}}{\tilde{C}_{33}} + \frac{h_\mathrm {p}}{A_{11}} \tilde{b}_{31} \tilde{e}_{31}\Big )} \mathop {}\!\mathrm {d}n \mathop {}\!\mathrm {d}s\nonumber \\ a_{Ef}&= \int _c\!\int _{h_\mathrm {p}}{\!\!\!\Big (\!\widehat{\chi }_{1}\!+\!2\widehat{\chi }_{2}\!+\!\widehat{\chi }_{3}\!+\!\frac{e_{33}{f}_{33}}{\tilde{C}_{33}}\!+\!\frac{h_\mathrm {p}}{A_{11}} \tilde{f}_{31} \tilde{e}_{31}\!\!\Big )}\mathop {}\!\mathrm {d}n \mathop {}\!\mathrm {d}s \end{aligned}$$

(24)

where the integration limit c denotes profile perimeter following the contour tangent axis s (see Fig. 1b). Material stiffness $\tilde{C}_{33}$ term and appropriate reduced stiffnesses of extension $A_{ij}$ and bending–extension coupling $B_{12}$ arise from the piezoceramic material properties and the plane stress assumption for the profile wall. Detailed expressions for remaining $a_{(\centerdot \centerdot )}$ factors are given in the paper by Georgiades et al. [28].

It should be observed that in the more general case of a tapered beam inertia coefficients $B_{(\centerdot )}$ as well as stiffnesses $a_{(\centerdot \centerdot )}$ depend on the axial variable x. This significantly complicates the equations of motion and boundary conditions as well. Moreover, in addition to the above-mentioned elastic couplings induced by the CAS ply angle distribution, the additional ones are observed [2, 11, 31]. Specifically, these are a coupling between the flapwise shear and chordwise bending and between chordwise shear and flapwise bending. Thus, the adopted CAS lamination scheme does not entail the problem simplification, and all six general equations of motion must be taken into account. However, for an axisymmetric box beam of a square cross-section case, the flapwise–chordwise coupling arises independently from the pre-twist effect.

3.2 Spatial discretisation

To reduce the derived system of partial differential equations (PDEs) of the structure to ordinary differential ones, the extended Galerkin method (EGM) is used as an efficient and accurate approach [32]. The choice of the extended modification of the regular Galerkin method comes from the imposed dynamic boundary conditions that are non-trivial at the free end with respect to basic problem unknowns. The EGM adopts the assumption of a set of trial functions that satisfy only geometric boundary conditions and do not prevent dynamic boundary conditions from being fulfilled (so-called consistent admissible functions). These functions are used to calculate the residual of the differential equation. Next, this residual is integrated over the domain with a weight function (same as the trial one) and minimised. While evaluating the integrals, the appropriate natural boundary conditions are incorporated to ensure their fulfilment by the searched approximate solutions. A significant benefit of this modification to the regular Galerkin method is the fact that the choice of trial functions is easier and this approach reduces the requirement of functions differentiability to half the order of spatial derivatives present in the equations of motion. More details regarding the functions (assumed mode shapes) used in the procedure as well as the modes orthogonality condition are given in the paper by Latalski et al. [29].

To determine the mode shapes which are used in the subsequent analysis of the original problem, the linearised form of governing Eqs. (19)–(23) for a non-rotating beam is written. Then, an electrical degree of freedom is eliminated by means of Eq. (23) and input into Eq. (21). By this simple mathematical operation a reduced set of governing equations is formulated with no loss of formulation generality (static condensation method as the model order reduction—see [33]). Furthermore, to enhance the generality of the consideration it is convenient to transform the original governing Eqs. (19)–(23) into a dimensionless form by introducing the spanwise coordinate $\eta =x/l;\ \eta \in \langle 0,1\rangle$ and dimensionless time $\tau =\omega t$ where t is physical time and $\omega =\sqrt{a_{33}/{b_1 l^4}}$ is the first natural frequency of a non-rotating linear system. Thus, new dimensionless variables $W(\eta ,\tau )$, $Y(\eta ,\tau )$ and $\Psi (\eta ,\tau )$ are introduced representing transverse displacement, shear deformation and twist angle, respectively. The electric field $E_3$ is substituted by a dimensionless variable $\epsilon (\eta )=E_3(x)/E_c$ where the $E_c$ is a coercive limit value for the piezomaterial.

Having found the individual components of the beam modes shapes, the reduction of the system of partial differential equations to ordinary ones can be done. Combining all three beam equations integrated over the specimen length and considering orthogonality condition (see [29]), one finally arrives at the system of two dimensionless nonlinear equations of the hub–beam structure

$$\begin{aligned}&\ddot{q}_1 + \alpha _{12} \ddot{\psi } + \varsigma _{1}\dot{q}_1\!+\!\left( \alpha _{11}\!+\!\alpha _{13}\dot{\psi }^2\right) \!q_1 + \alpha _{14}\dot{\psi }\dot{q}_1{q}_1 \nonumber \\&\quad + \alpha _{15}\mathrm {sgn}(q_1){q}_1^2 + \alpha _{16}{q}_1^3 = 0\nonumber \\&\left( 1\!+\!\widehat{J}_h\!+\!\alpha _{h2} q_1\right) \ddot{\psi } + \alpha _{h1} \ddot{q}_1 + \varsigma _{h}\dot{\psi } + \alpha _{h3} \dot{q}_1\dot{\psi } = \mu \end{aligned}$$

(25)

The first of these relations describes the dynamics of the beam, where the coordinate $q_1$ involves all three beam mechanical variables (flexural displacement, cross-section rotation and twist angle) and electrical one with different relative importance dependent on mode order and composite reinforcing fibre orientation. The second equation represents the dynamics of the hub. Designation $\widehat{J}_h$ refers to the relative hub inertia, i.e. the inertia of the hub with respect to the beam inertia. The right-hand side term in (25)${}_2$ is dimensionless driving torque $\mu$ that may be generally represented as an algebraic sum of steady state and periodic components

$$\begin{aligned} \mu (\tau ) =\mu _0+\rho \sin \omega \tau \end{aligned}$$

(26)

where $\rho$ and $\omega$ are driving torque amplitude and frequency, respectively. $\mu _0$ is the torque constant component resulting in the mean value of the system angular speed.

4 Numerical calculations

4.1 Validation of the analytical model

The accuracy of the present formulation of the rotating thin-walled beam with integrated piezoelectric active element is verified by performing a free vibration analysis for specially orthotropic laminate case (no coupling between in-plane extensional and shear responses) and various values of the rotating speed. Next, the comparative study with the available data presented by other researchers and using different theories and solution methods is performed. In this analysis the output of the current model is limited to linear piezoelectric effect since only this case is reported in the literature on rotating blades with the integrated piezoceramic layers. Moreover, for the relevance, the impact of hub inertia on system dynamics is neglected by imposing $\tilde{J}_h \rightarrow \infty$ since this assumption corresponds to a classical case of a cantilever beam [29].

For the comparison the graphite–epoxy composite and piezoceramic PZT-4 material data as well as specimen dimensions and laminae reinforcing fibre orientation used by Chandiramani [11] are employed. Table 1 shows the first two eigenfrequencies corresponding to flap bending mode when the dimensionless beam angular speed $\dot{\psi }=\tilde{\Omega }$ is set to 0, 1, 3 and 6, respectively. Results of present calculations are referred to the data given by Yokohama and Markiewicz [34] obtained analytically using the power series solution method, and to results reported by Chandiramani [11] and obtained by the original finite element code. The latter ones are restricted to specific case of untwisted, untapered beam and neglecting the tip mass.

Table 1 First and second natural frequencies of the piezointegrated composite beam for different dimensionless angular speed $\dot{\psi }$ in comparison with results presented in [34]—column A and [11]—column B

The agreement appears to be very good, with error magnitude limited to 0.25–0.75% (with respect to A and B) and 1.9–2.2% for the first and the second natural frequency, respectively. It should be emphasised all presented results are obtained by approximate methods. Therefore, discrepancies are related, among other matters, to the accuracy of spatial discretisation (the density of finite elements or number of trial functions used in the extended Galerkin method).

4.2 Free vibration analysis

In the next step free vibrations of the beam with a nonlinear piezoceramic active element are investigated in detail. Similar to the model validation stage the impact of hub inertia on system dynamics is neglected by imposing $\tilde{J}_h \rightarrow \infty$; thus, a separate beam substructure is considered.

Table 2 System geometric data and materials as used in numerical simulations

For these calculations, as well as further forced vibration analysis, a single ply graphite–epoxy master structure is considered. Material properties and beam geometry are given in Table  2, where the subscripts 1, 2 and 3 refer to parallel and transverse to the fibre directions, respectively (the standard Classical Laminate Theory assignment). The embedded active element is made of PZT-3203HD ceramic material, and its properties are collected from the papers by Rao et al. [25] and by Kapuria et al. [23].

It is assumed the piezoceramic poling direction 3 is oriented thicknesswise. Since for the given material components of the fourth-order piezoelectric tensor $f_{32}=f_{33}$ are equal to 0, as well as the members of the third- and the fourth-order electric susceptibility tensors $\hat{\chi }_1=\hat{\chi }_2=\hat{\chi }_3$, the general formulation of the problem is simplified and restricted to quadratic nonlinearities only.

Fig. 3

Mechanical $W(\eta ), Y(\eta ), \Phi (\eta )$ and electric $\epsilon (\eta )$ components of free vibration modes for the rotating composite beam with integrated piezoelement; fibre orientation angle $\alpha =15^\circ$. Solid lines correspond to non-rotating system $\dot{\psi }=0$, dashed lines correspond to dimensionless $\dot{\psi }=3$, and dotted ones are $\dot{\psi }=8$ case

Fig. 4

Mechanical $W(\eta ), Y(\eta ), \Phi (\eta )$ and electric $\epsilon (\eta )$ components of free vibration modes for the rotating composite beam with integrated piezoelement; fibre orientation angle $\alpha =75^\circ$. Solid lines correspond to non-rotating system $\dot{\psi }=0$, dashed lines correspond to dimensionless $\dot{\psi }=3$, and dotted ones are $\dot{\psi }=8$ case

Figures 3 and 4 provide results of the modal analysis of the piezocomposite beam for two different laminae fibre orientations—i.e. $15^\circ$ and $75^\circ$, respectively. The first free modes are presented for three dimensionless angular speed $\dot{\psi }$ values: 0, 3 and 8. Since these modes are generally coupled ones, the individual components of the beam deformation are distinguished by colours: blue lines correspond to the transverse displacement $W(\eta )$, the grey ones to the shear deformation angle (Timoshenko effect) $Y(\eta )$, and the red ones are twist angle $\Phi (\eta )$. In separate charts the electric field $\epsilon (\eta )$ spatial distribution is presented (green colour).

Studying the first modes one can observe the significant diversities in electric field distribution as the angular speed $\dot{\psi }$ of the beam changes. For higher speeds the difference between the electric field values at the free end and the clamping point increases. Nevertheless, the general shape of the mode is preserved, and independently of the rotation speed and the fibre orientation angle the gradient of the electric field decreases towards the beam free end. These first mode general shapes of the electric field distribution are similar to the ones obtained by, for example, Thornburgh et al. [5], who derived a coupled filed model and original finite element code for the specific case of a non-rotating cantilever plate with piezoceramic outer layers. Also Kapuria et al. [35] received similar results when studying the peak voltage spanwise distribution in the segmented sensors bonded on cantilever plates.

The direct comparison of both $\alpha =15^\circ$ and $75^\circ$ cases shows that the overall magnitude of the discussed difference is higher for the lower value of fibre orientation angle $\alpha$. This observation is related to the mechanical deformation of the structure—the second case ($\alpha =75^\circ$) includes a markedly stronger twisting component if compared to the first case. Therefore, proportionally less energy is stored in shear deformation; thus, the spatial distribution of the electric field is smoother (more homogenous). To some extent this comment is confirmed by the third natural mode analysis—see comment below.

Regarding the second modes it can be noticed the change in angular speed $\dot{\psi }$ does not influence the electric field distribution significantly. Only slight differences are observed for the mid-span zone and the $\alpha =75^\circ$ case. This comes from the fact that the increase in rotating speed increases the participation of the twisting component in the deformation mode just for this fibre orientation case. The further analysis leads to the conclusion, similar as for the first mode discussed above, that the overall magnitude on the difference between extreme values of electric field is higher for lower value of fibre orientation angle $\alpha$.

The third modes for both laminae orientation cases are twist dominated ones with a negligible bending/shear component. Therefore, the spatial distribution of electric field potential is almost uniform with the magnitude close to zero (mind different scales on ordinate axes).

4.3 Forced vibrations

In the next step the forced vibrations of the full hub–beam system as governed by Eq. (25) are examined. The fibre orientation angle is set to $\alpha =75^\circ$ and the relative hub inertia $\tilde{J}_h$ is equal to 1. Numerical values of $\alpha _{ij}$ coefficients corresponding to this configuration are given in Table 3. Moreover, damping coefficients for the beam and for the hub are introduced. The beam damping coefficient $\zeta _1$ is expressed as 1% of the first dimensionless frequency of the non-rotating beam clamped to an infinite heavy hub. The hub damping coefficient $\zeta _h$ is fixed at 0.1 value.

Table 3 Dimensionless coefficients for Eq. (25) used for forced vibration calculations

For the initial studies the system forcing is represented by a zero mean value periodic torque $\mu (\tau )=\rho \sin \omega \tau$ imposed to the hub—see Eq. (26). The dynamic response of the structure is examined around the first resonance of the combined beam–hub structure and considering different magnitudes of driving torque amplitude $\rho$. The results are presented in Fig. 5, where plots (a) and (b) correspond to responses of the beam and the hub, respectively. The plots are obtained by the continuation method treating excitation frequency $\omega$ as a bifurcation parameter.

Fig. 5

Resonance curves for the beam (a) and the hub (b) sub-systems around the first natural frequency with respect to excitation amplitude $\rho$. The solid (dashed) curves represent stable (unstable) solutions

Both resonance curves are bent to the left denoting a softening effect with stable and unstable regions highlighted by solid and dashed lines, respectively. It can be seen that the steady state generalised displacement $q_1$ amplitude of the beam increases as the magnitude $\rho$ of the periodic driving torque amplitude is increased. The same comment refers to the hub response $\dot{\psi }$. The observed relation between maximum system responses and excitation amplitudes is nonlinear. However, within the tested range of excitation amplitudes no internal solutions inside the resonance curves have been found.

Similar frequency response softening effects were also reported by other researches who considered the nonlinear piezoceramic material constitutive relation—see, for example, [17, 20].

For the studied fixed values of excitation frequency and varied amplitude $\rho$, the jump phenomena appear clearly due to the domination of the nonlinearity. The details are presented in Fig. 6 by bifurcation diagrams showing both upsweep and downsweep system responses. The amplitudes of beam generalised displacement $q_1$ (a) as well as hub speed $\dot{\psi }$ (b) for the exemplary excitation frequency $\omega =2.68$ are shown for situations before and after jumps depending on the forcing torque amplitude $\rho$. It is clearly seen that at this frequency two stable solutions are possible for the range of $\rho \in \langle 0.004,0.0125\rangle$. Below and above this range, just one solution is present.

Fig. 6

Bifurcation diagrams showing the amplitudes of beam (a) and hub (b) responses with respect to excitation amplitude $\rho$ for the excitation frequency $\omega =2.68$

To confirm the results given in these frequency response diagrams, two sets of time series plots are prepared. The results are obtained for the excitation amplitude $\rho =0.01$ and frequency $\omega =2.68$ and for two different initial conditions sets. In Fig. 7 (grey colour) the envelopes of transient and steady state responses for the data $q|_{\tau =0}=0.04$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.005$ are shown. The steady state amplitudes for the beam and the hub are 0.041 and 0.031, respectively. These match lower branches of frequency response curves in Fig. 5. In the second case (Fig. 8, grey colour) the initial data set $q|_{\tau =0}=0.14$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.085$ is examined. Beam response 0.165 and 0.116 value for the hub corresponds to upper branches of response curves.

Fig. 7

Envelopes of linear and nonlinear transient and steady state responses of the beam and the hub for excitation frequency $\omega =2.68$ and amplitude $\rho =0.01$ (Fig. 5 black line); initial conditions: $q|_{\tau =0}=0.04$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.005$. Colour code: grey—nonlinear piezoelectric effect, blue – linear piezoelectric effect

Fig. 8

Envelopes of linear and nonlinear transient and steady state responses of the beam and the hub for excitation frequency $\omega =2.68$ and amplitude $\rho =0.01$ (Fig. 5 black line); initial conditions: $q|_{\tau =0}=0.14$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.085$. Colour code: grey—nonlinear piezoelectric effect, blue—linear piezoelectric effect

Next, studies regarding the impact of the piezoelectric nonlinearity on the system performance are presented. The reported above calculations referring to the nonlinear piezoelectric effect are repeated for the case of a linear material model by setting $\alpha _{15}$ coefficient [see Table 3 and Eq.  (25)] to zero. The results obtained for the linearised system are presented in Figs. 7 and 8 and marked in blue colour.

Comparing the system responses one observes significant differences in vibrations attenuations and settling time. Regarding the lower frequency resonance curve solutions (Fig. 7), the nonlinear model of the piezoceramic material yields higher amplitudes both in transient and in the steady state zones and the longer structure settling time. For the upper frequency curve points (Fig. 8), the settling time relation is different and the nonlinear piezoceramic model yields significantly shorter duration of the transition to steady state response. In both cases the system softening effect is confirmed as higher amplitudes are recorded in the case of the nonlinear constitutive model. This phenomenon is crucial for a controller design since it reduces the actual maximum voltage and power required by the controller if compared to the linear piezoceramic model. Thus, a nonlinear active element behaviour should be included in the control system design, especially for high-power systems and close to resonance operation.

Similar comparisons of the system responses for the linear and nonlinear models of piezoceramic material have been conducted also for other excitation scenarios—i.e. a rectangular pulse and an impulse ones. However, in these cases no marked differences have been noticed. Thus, reported above differences between responses of linear and nonlinear models depend on the type of system excitation and they get diminished when the excitation is of limited duration as in the case of the rectangular pulse or the impulse. This observation conforms to the conclusions reported by Shete et al.  [31] and dealing with a smart composite beam with a linear piezoelectric layer but combined with a quadratic control subsystem.

Finally, let’s consider a rotating system. To this aim the component $\mu _0$ of the driving torque $\mu (\tau )$—see (26)—is set to nonzero value. Two simulations have been performed. In Fig. 9 the results for the excitation scenario $\mu =0.001 + 0.005\cos (2.68 \tau )$ are presented, while in Fig. 10 for the $\mu =0.002 + 0.005\cos (2.68 \tau )$ case. Again, the outputs for the quadratic nonlinearity in piezoceramic material and for the linear constitutive formulation are compared. The appropriate envelopes are marked in grey and blue colours, respectively.

Fig. 9

Envelopes of transient and steady state responses of the beam and the hub for excitation frequency $\omega =2.68$, amplitude $\rho =0.005$ and mean value $\mu _0=0.001$; initial conditions: $q|_{\tau =0}=0.04$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.005$. Colour code: grey—nonlinear piezoelectric effect, blue—linear piezoelectric effect

Fig. 10

Envelopes of transient and steady state responses of the beam and the hub for excitation frequency $\omega =2.68$, amplitude $\rho =0.005$ and mean value $\mu _{0}=0.002$; initial conditions: $q|_{\tau =0}=0.04$, $\dot{q}|_{\tau =0}=0$, $\Omega |_{\tau =0}=0.005$. Colour code: grey—nonlinear piezoelectric effect, blue—linear piezoelectric effect

Similar to the previous simulations one observes significant differences in vibrations attenuation and the settling time. The smaller excitation magnitude (Fig. 9) yields the lower peaks in the transient response as well as the significantly shorter settling time than for the second case (Fig. 10). However, independently of the excitation magnitude, the linear material model predicts a shorter settling time and lower transient and steady state amplitudes as the nonlinear one. This conclusion conforms to the corresponding initial condition and results presented in Fig.  7.

The calculated amplitudes of the steady state responses for the lower excitation torque are 0.017 for the beam and 0.013 for the hub angular velocity and its mean value 0.015 considering the nonlinear piezoceramic material model. If the problem is simplified to the linear constitutive relationship the appropriate responses are 0.015 and 0.0115 with the mean value 0.015. For the second driving torque formula the amplitude of beam response is 0.0135 and the amplitude 0.013 for the hub angular velocity with the mean value 0.0295 considering the nonlinear piezoceramic material model. If the linear constitutive relationship is assumed, the appropriate responses are 0.0125 and 0.0115 with the mean value 0.0295 (Fig. 10).

The direct comparison of beam responses reveals the lower amplitudes in the second case. This results from the overall higher system rotating speed and the centrifugal stiffening effect. As expected the torque mean value $\mu _0$ impacts the hub mean angular velocity, but not the amplitude of hub oscillations.

As observed in given examples, strong dynamic interaction between the hub and the beam comes form the relatively low inertia ratio (hub to beam inertia is 1:1). For higher ratios beam responses are expected to be less pronounced.

5 Final conclusions

The fully coupled analytical model of a rotating rigid hub and a flexible piezolaminated composite beam has been developed. In the mathematical formulation the reversible nonlinear behaviour of piezoceramic layer is considered. This nonlinearity is modelled by a third-order constitutive relationship with respect to electric field. In the mathematical formulation of the problem the full two-way coupling piezoelectric effect is considered by adopting the assumption of spanwise electric field variation. The general nonlinear system of mutually coupled partial differential equations is derived using the Hamilton’s principle, and the Galerkin method is applied to reduce these governing equations to the ordinary differential ones. The specific case of CAS lamination scheme that exhibits flapwise bending and twist mode elastic coupling is discussed.

Free vibration tests and analysis of individual components of mode shapes showed the significant diversities in the electric field distribution regarding the angular speed of the system and the type of master structure deformation. The most prominent effects were observed for first modes, where for higher speeds the difference between the electric field magnitudes at free end and the clamping point increases. For higher modes with a negligible bending/shear component the electric field spanwise distribution was almost uniform and close to zero on the full specimen span.

The forced vibration analysis confirmed the presence of the softening effect in systems with nonlinear piezoceramic material. The expected presence of multiple different solutions for a given excitation frequency was confirmed by time series plots. The further comparison of results for the nonlinear piezoceramic material and a classical linear one revealed significant differences in structural responses and settling time. In particular, the nonlinear piezoceramic material showed higher transient and steady states response amplitudes as the linear one. This fact suggests the actual power required by the active control unit might be lower for the systems where the nonlinear piezoelement is used.

The presented modelling approach and the nonlinear effects discussed in this paper may help in studying the existing applications of rotating piezolaminated composite beams and in developing new structural designs.

A further research on this topic may involve tapered and pre-twisted smart blades. These models may better represent advanced future structural elements like aircraft wings, turbine blades designed to obtain certain intended mechanical properties and made up of smart composite materials. Studies concerning initially curved and/or pre-twisted smart beam have been already initiated by other researchers—see, for example, Chandiramani [11] and Valliappan et al. [13].

Appendices

Appendix A: Constitutive equations for composite material

Constitutive equations for individual layers of composite plant may be formulated by modelling them as orthotropic material layers in plane stress condition with its principal axis out of the structure reference system

$$\begin{aligned} \begin{Bmatrix} \sigma _{ss}\\ \sigma _{xx}\\ \sigma _{xs}\\ \end{Bmatrix}_{\!\!(\mathrm {c})}= \begin{bmatrix} \bar{Q}_{11}&\bar{Q}_{12}&\bar{Q}_{16}\\ \bar{Q}_{12}&\bar{Q}_{22}&\bar{Q}_{26}\\ \bar{Q}_{16}&\bar{Q}_{26}&\bar{Q}_{66} \end{bmatrix} \begin{Bmatrix} \varepsilon _{ss}\\ \varepsilon _{xx}\\ \gamma _{ss}\\ \end{Bmatrix}\\ \sigma _{{xn}_{(\mathrm {c})}}= \bar{C}_{44} \gamma _{xn} \qquad \sigma _{{sn}_{(\mathrm {c})}}= \bar{C}_{45} \gamma _{xn}\nonumber \end{aligned}$$

(A.1)

where

$$\begin{aligned} \bar{Q}_{ij} = \bar{C}_{ij}-\frac{\bar{C}_{i3}\bar{C}_{j3}}{\bar{C}_{33}} \quad \text {for\ } i,j = 1,2,6 \end{aligned}$$

and $\bar{C}_{ij}$ denotes members of the laminae elasticity tensor. More details and step-by-step derivation of the above expressions can be found in [26].

Appendix B

General expressions for 2-D stress resultants and stress couples as shown in Fig. 2

• membrane

  $$\begin{aligned} \begin{Bmatrix} N_{ss}\\N_{xx}\\N_{xs} \end{Bmatrix}= \sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \begin{Bmatrix} \sigma _{ss}^{(k)}\\ \sigma _{xx}^{(k)}\\ \sigma _{xs}^{(k)} \end{Bmatrix}_{\!\!(\mathrm {c})}\mathop {}\!\mathrm {d}n+ \int \limits _{h_\mathrm {p}} \begin{Bmatrix} \sigma _{ss}\\ \sigma _{xx}\\ \sigma _{xs} \end{Bmatrix}_{\!\!(\mathrm {p})}\mathop {}\!\mathrm {d}n \end{aligned}$$

  (B.1)

• transverse

  $$\begin{aligned} \begin{Bmatrix} N_{xn}\\N_{sn} \end{Bmatrix}=\sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \begin{Bmatrix} \sigma _{xn}^{(k)}\\\sigma _{sn}^{(k)} \end{Bmatrix}_{\!\!(\mathrm {c})}\mathop {}\!\mathrm {d}n+ \int \limits _{h_\mathrm {p}} \begin{Bmatrix} \sigma _{xn}\\0 \end{Bmatrix}_{\!\!(\mathrm {p})}\mathop {}\!\mathrm {d}n \end{aligned}$$

  (B.2)

• stress couples

  $$\begin{aligned} \begin{Bmatrix} L_{xx}\\L_{xs} \end{Bmatrix}=\sum _{k=1}^{N}\int \limits _{\ n_{(k-1)}}^{\ n_k}\!\! \begin{Bmatrix} \sigma _{xx}^{(k)}\\ \sigma _{xs}^{(k)} \end{Bmatrix}_{\!\!(\mathrm {c})} n \mathop {}\!\mathrm {d}n+ \int \limits _{h_\mathrm {p}} \begin{Bmatrix} \sigma _{xx}\\\sigma _{xs} \end{Bmatrix}_{\!\!(\mathrm {p})} n \mathop {}\!\mathrm {d}n \end{aligned}$$

  (B.3)

In the above formulas the used $(\centerdot )_k$ superscript index refers to the subsequent laminate layers numbers n and $h_\mathrm {p}$ denotes the piezoceramic layer thickness. It’s worth commenting here that second components of right-hand side summation are coming from piezoelectric material so these are present only for terms related to cross-section flanges.

The above expressions can be transformed from the local (0, x, s, n) coordinate system to global one (0, x, y, z) resulting in terms $N_{xx}$, $N_{xn}$, $N_{xs}$, $L_{xx}$, $L_{xs}$. After integration over the cross-section perimeter one arrives at 1-D stress measures $T_{x}$, $Q_y$, $Q_z$, $M_x$, $M_y$, $M_z$, $B_\omega$. Finally, substituting for stresses and strains these may be expressed in terms of problem unknowns: mechanical $u_{0}$, $v_{0}$, $w_{0}$, ${\vartheta }_y$, ${\vartheta }_z$, $\varphi$ and electric one $E_3$ as follows:

$$\begin{aligned} T_{x}&= \ a_{11}u_{0}^{\prime } + a_{15}{\vartheta }_y+ a_{13}{\vartheta }_y^{\prime } + a_{14}{\vartheta }_z+ a_{12}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{14}v_{0}^{\prime } + a_{15}w_{0}^{\prime } + a_{17}\varphi ^{\prime } - a_{16}\varphi ^{\prime \prime } \nonumber \\&\quad + a_{1e} E_3 + a_{1b} \mathrm {sgn}(E_3)E_3^2 + a_{1f} E_3^3\nonumber \\ Q_{y}&= \ a_{14}u_{0}^{\prime } + a_{45}{\vartheta }_y+ a_{34}{\vartheta }_y^{\prime } + a_{44}{\vartheta }_z+ a_{24}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{44}v_{0}^{\prime } + a_{45}w_{0}^{\prime } + a_{47}\varphi ^{\prime } - a_{46}\varphi ^{\prime \prime } \nonumber \\&\quad + a_{4e} E_3 + a_{4b} \mathrm {sgn}(E_3) E_3^2 + a_{4f} E_3^3\nonumber \\ Q_{z}&= \ a_{15}u_{0}^{\prime } + a_{55}{\vartheta }_y+ a_{35}{\vartheta }_y^{\prime } + a_{45}{\vartheta }_z+ a_{25}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{45}v_{0}^{\prime } + a_{55}w_{0}^{\prime } + a_{57}\varphi ^{\prime } - a_{56}\varphi ^{\prime \prime } \nonumber \\&\quad + a_{5e} E_3 + a_{5b} \mathrm {sgn}(E_3) E_3^2 + a_{5f} E_3^3\nonumber \\ M_{x}&= \ a_{17}u_{0}^{\prime } + a_{57}{\vartheta }_y+ a_{37}{\vartheta }_y^{\prime } + a_{47}{\vartheta }_z+ a_{27}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{47}v_{0}^{\prime } + a_{57}w_{0}^{\prime } + a_{77}\varphi ^{\prime } - a_{67}\varphi ^{\prime \prime }\nonumber \\&\quad + a_{7e} E_3 + a_{7b} \mathrm {sgn}(E_3) E_3^2 + a_{7f} E_3^3\nonumber \\ M_{y}&= \ a_{13}u_{0}^{\prime } + a_{35}{\vartheta }_y+ a_{33}{\vartheta }_y^{\prime } + a_{34}{\vartheta }_z+ a_{23}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{34}v_{0}^{\prime } + a_{35}w_{0}^{\prime } + a_{37}\varphi ^{\prime } - a_{36}\varphi ^{\prime \prime } \nonumber \\&\quad +a_{3e} E_3 + a_{3b} \mathrm {sgn}(E_3) E_3^2 + a_{3f} E_3^3\nonumber \\ M_{z}&= \ a_{12}u_{0}^{\prime } + a_{25}{\vartheta }_y+ a_{23}{\vartheta }_y^{\prime } + a_{24}{\vartheta }_z+ a_{22}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{24}v_{0}^{\prime } + a_{25}w_{0}^{\prime } + a_{27}\varphi ^{\prime } - a_{26}\varphi ^{\prime \prime } \nonumber \\&\quad + a_{2e} E_3 + a_{2b} \mathrm {sgn}(E_3) E_3^2 + a_{2f} E_3^3\nonumber \\ B_{w}&= \ a_{16}u_{0}^{\prime } + a_{56}{\vartheta }_y+ a_{36}{\vartheta }_y^{\prime } + a_{46}{\vartheta }_z+ a_{26}{\vartheta }_z^{\prime } \nonumber \\&\quad + a_{46}v_{0}^{\prime } + a_{56}w_{0}^{\prime } + a_{67}\varphi ^{\prime } - a_{66}\varphi ^{\prime \prime }\nonumber \\&\quad + a_{6e} E_3 + a_{6b} \mathrm {sgn}(E_3) E_3^2 + a_{6f} E_3^3 \end{aligned}$$

(B.4)