Skip to main content
SpringerLink
Log in

Impulsive stabilization of chaos in fractional-order systems

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

This paper considers a class of nonlinear impulsive Caputo differential equations of fractional order, which models chaotic systems. Computer-assisted proof of chaos suppression by stabilizing the unstable system equilibria is provided. A nonexistence result of periodic solutions is presented, and the commensurate fractional-order Lorenz system is simulated for illustration.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

Notes

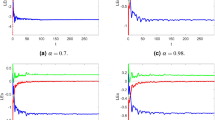
  1. The fractional order has been chosen close to 1, such that chaos is as strong as possible (note that the minimum order for the fractional-order Lorenz system to be chaotic is \(q=0.99\) [37]).

  2. Once the trajectory enters the sphere, it remains inside.

  3. Some related works will be published elsewhere later.

References

  1. Yang, T.: Impulsive Control Theory. Springer, Berlin (2001)

    MATH  Google Scholar 

  2. Oldham, K., Spainer, J.: Fractional Calculus. Academic press, Dordrecht (1974)

    Google Scholar 

  3. Podlubny, I.: Fractional Differential Equations. Academic Press, Dordrecht (1989)

    MATH  Google Scholar 

  4. Baleanu, D., Diethelm, K., Scalas, E., Trujillo, J.J.: Fractional Calculus Models and Numerical Methods. Series on Complexity Nonlinearity and Chaos, vol. 3. World Scientific, Singapore (2012)

    Book  MATH  Google Scholar 

  5. Sabatier, J., Ionescu, C., Tar, J.K., Teneiro, M.J.A.: guest editors. New challenges in fractional systems. (2013). http://www.hindawi.com/journals/mpe/si/206031

  6. Riccardo, C., Trujillo, J.J., Machado, J.A.T.: Theory and applications of fractional order systems. Math. Probl. Eng. (2016). doi:10.1155/2016/7903424

    Google Scholar 

  7. Arena, P., Caponetto, R., Fortuna, L., Porto, D.: Bifurcation and chaos in noninteger order cellular neural networks. Int. J. Bifurc. Chaos 8, 1527–1539 (1998). doi:10.1142/S0218127498001170

    Article  MATH  Google Scholar 

  8. Boroomand, A., Menhaj, M.: Fractional-order Hopfield neural networks. In: Lecture Notes in Computer Science, vol. 5506, pp. 883–890 (2009)

  9. Kaslik, E., Sivasundaram, S.: Non-existence of periodic solutions in fractional-order dynamical systems and a remarkable difference between integer and fractional-order derivatives of periodic functions. Nonlinear Anal. Real World Appl. 13, 1489–1497 (2012). doi:10.1016/j.nonrwa.2011.11.013

    Article  MathSciNet  MATH  Google Scholar 

  10. Charef, A., Sun, H.H., Tsao, Y.Y., Onaral, B.: Fractal system as represented by singularity function. IEEE Xplore: IEEE Trans. Autom. Control 37, 1465–1470 (1992). doi:10.1109/9.159595

    MathSciNet  MATH  Google Scholar 

  11. Diethelm, K., Ford, N.J., Freed, A.D.: A predictor–corrector approach for the numerical solution of fractional differential equations. Nonlinear Dyn. 29, 3–22 (2002). doi:10.1023/A:1016592219341

    Article  MathSciNet  MATH  Google Scholar 

  12. Scherer, R., Kalla, S.L., Tang, Y., Huang, J.: The Grünwald–Letnikov method for fractional differential equations. Comput. Math. Appl. 62, 902–917 (2011). doi:10.1016/j.camwa.2011.03.054

    Article  MathSciNet  MATH  Google Scholar 

  13. Chen, G., Yu, X.: Chaos Control: Theory and Applications. Springer, Berlin (2003)

    Book  MATH  Google Scholar 

  14. Oustaloup, A., Sabatier, J., Lanusse, P.: From fractal robustness to the CRONE control. Fract. Calc. Appl. Anal. 2, 1–30 (1999)

    MathSciNet  MATH  Google Scholar 

  15. Wang, X.-Y., He, Y.-J., Wang, M.-J.: Chaos control of a fractional order modified coupled dynamos system. Nonlinear Anal. Theory Methods Appl. 71, 6126–6134 (2009). doi:10.1016/j.na.2009.06.065

    Article  MathSciNet  MATH  Google Scholar 

  16. Ahmad, W.M., Harba, A.M.: On nonlinear control design for autonomous chaotic systems of integer and fractional orders. Chaos Soliton Fract. 18, 693–701 (2003). doi:10.1016/S0960-0779(02)00644-6

    Article  MATH  Google Scholar 

  17. Boulkroune, A., Chekireb, H., Tadjine, M., Bouatmane, S.: Observer-based adaptive feedback controller of a class of chaotic systems. Int. J. Bifurc. Chaos 16, 3411–3419 (2006)

  18. Yin, C., Chen, Y.Q., Zhong, S.: Fractional-order sliding mode based extremum seeking control of a class of nonlinear systems. Automatica 50, 3173–3181 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Yin, C., Cheng, Y., Chen, Y.Q., Stark, B., Zhong, S.: Adaptive fractional-order switching-type control method design for 3D fractional-order nonlinear systems. Nonlinear Dyn. 82, 39–52 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  20. Chen, G., Dong, X.: From Chaos to Order-Methodologies Perspectives and Applications. World Scientific, Singapore (1998)

    Book  MATH  Google Scholar 

  21. Ott, E., Grebogi, C., Yorke, J.A.: Controlling chaos. Phys. Rev. Lett. 64, 1196–1199 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  22. Richter, H., Reinschke, K.J.: Local control of chaotic systems—a Lyapunov approach. Int. J. Bifurc. Chaos 8, 1565–1573 (1998). doi:10.1142/S0218127498001212

    Article  MATH  Google Scholar 

  23. Pyragas, K.: Continuous control of chaos by self-controlling feedback. Phys. Lett. A 170, 421–428 (1992). doi:10.1016/0375-9601(92)90745-8

    Article  Google Scholar 

  24. Agarwal, R.P., Benchohra, M., Slimani, B.A.: Existence results for differential equations with fractional order and impulses. Mem. Differ. Equ. Math. Phys. 44, 1–21 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  25. Benchohra, M., Slimani, B.A.: Existence and uniqueness of solutions to impulsive fractional differential equations. Electron. J. Differ. Equ. 2009, 1–11 (2009)

    MathSciNet  MATH  Google Scholar 

  26. Benchohra, M., Seba, D.: Impulsive fractional differential equations in Banach spaces. Electron. J. Qual. Theory Differ. Equ. 2009, 1–14 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  27. Guan, Z.-H., Chen, G., Ueta, T.: On impulsive control of a periodically forced chaotic pendulum system. IEEE Trans. Autom. Control 45, 1724–1727 (2000). doi:10.1109/9.880633

    Article  MathSciNet  MATH  Google Scholar 

  28. Yang, Xujun, Li, Chuandong, Huang, Tingwen, Song, Qiankun: Mittag-Leffler stability analysis of nonlinear fractional-order systems with impulses. Appl. Math. Comput. 293, 416422 (2017)

    MathSciNet  Google Scholar 

  29. Yang, Xujun, Li, Chuandong, Song, Qiankun, Huang, Tingwen, Chen, Xiaofeng: Mittag-Leffler stability analysis on variable-time impulsive fractional-order neural networks. Neurocomputing 207, 276286 (2016)

    Google Scholar 

  30. Samoilenko, A.M., Perestyuk, N.A.: Impulsive Differential Equations. Series on Nonlinear Science. World Scientific, Singapore (1995)

  31. Heymans, N., Podlubny, I.: Physical interpretation of initial conditions for fractional differential equations with Riemann–Liouville fractional derivatives. Acta Rheologica 45, 765–771 (2006). doi:10.1007/s00397-005-0043-5

    Article  Google Scholar 

  32. Matignon, D.: Stability results of fractional differential equations with applications to control processing. In: IEEE-SMC Proceedings of the Computational Engineering in Systems and Application Multiconference. IMACS, vol. 2, pp. 963–968 (1996)

  33. Tavazoei, M.S., Haeri, M.: Chaotic attractors in incommensurate fractional order systems. Phys. D 237, 2628–2637 (2008). doi:10.1016/j.physd.2008.03.037

    Article  MathSciNet  MATH  Google Scholar 

  34. Li, F., Yao, C.: The infinite-scroll attractor and energy transition in chaotic circuit. Nonlinear Dyn. 84, 2305–2315 (2016). doi:10.1007/s11071-016-2646-z

    Article  MathSciNet  Google Scholar 

  35. Sarasola, C., Torrealdea, F.J., d’ Anjou, A., Moujahid, A., Graña, M.: Energy balance in feedback synchronization of chaotic systems. Phys. Rev. E 69, 011606 (2004). doi:10.1103/PhysRevE.69.011606

    Article  Google Scholar 

  36. Danca, M.-F., Kuznetsov, N., Chen, G.: Unusual dynamics and hidden attractors of the Rabinovich–Fabrikant system. Nonlinear Dyn. (2017). doi:10.1007/s11071-016-3276-1

  37. Wu, X.J., Shen, S.L.: Chaos in the fractional-order Lorenz system. Int. J. Comput. Math. 86, 1274–1282 (2009). doi:10.1080/00207160701864426

    Article  MathSciNet  MATH  Google Scholar 

  38. Li, D., Lu, J., Wu, X., Chen, G.: Estimating the bounds for the Lorenz family of chaotic systems. Chaos Solitons Fract. 23, 529–534 (2005). doi:10.1016/j.chaos.2004.05.021

    Article  MathSciNet  MATH  Google Scholar 

  39. Tavazoei, M., Haeri, M.: A proof for non existence of periodic solutions in time invariant fractional order systems. Automatica 45, 1886–1890 (2009). doi:10.1016/j.automatica.2009.04.001

    Article  MathSciNet  MATH  Google Scholar 

  40. Yazdani, M., Salarieh, H.: On the existence of periodic solutions in time-invariant fractional order systems. Automatica 47, 1834–1837 (2011). doi:10.1016/j.automatica.2011.04.013

    Article  MathSciNet  MATH  Google Scholar 

  41. Kang, Y.-M., Xie, Y., Lu, J.C., Jiang, J.: On the nonexistence of non-constant exact periodic solutions in a class of the Caputo fractional-order dynamical systems. Nonlinear Dyn. 82, 1259–1267 (2015). doi:10.1007/s11071-015-2232-9

    Article  MathSciNet  MATH  Google Scholar 

  42. Shen, J., Lam, J.: Non-existence of finite-time stable equilibria in fractional-order nonlinear systems. Automatica 50, 547–551 (2014). doi:10.1016/j.automatica.2013.11.018

    Article  MathSciNet  MATH  Google Scholar 

  43. Wang, J.R., Fečkan, M., Zhou, Y.: A survey on impulsive fractional differential equations. Fract. Calc. Appl. Anal. 19, 806–831 (2016). doi:10.1515/fca-2016-0044

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors thank to Professor Julien Clinton Sprott for interesting discussions related to the energy approach. M.-F. Danca is supported by Tehnic B SRL. M. Fečkan is supported in part by the Slovak Research and Development Agency under the Contract No. APVV-14-0378 and by the Slovak Grant Agency VEGA Nos. 2/0153/16 and 1/0078/17. G. Chen is supported by the Hong Kong Research Grants Council under the GRF Grant CityU 11234916.

Author information

Authors and Affiliations

  1. Department of Mathematics and Computer Science, Avram Iancu University of Cluj-Napoca, 400380, Cluj-Napoca, Romania

    Marius-F. Danca

  2. Romanian Institute of Science and Technology, 400487, Cluj-Napoca, Romania

    Marius-F. Danca

  3. Department of Mathematical Analysis and Numerical Mathematics, Faculty of Mathematics, Physics and Informatics, Comenius University in Bratislava, Mlynská dolina, 842 48, Bratislava, Slovak Republic

    Michal Fečkan

  4. Mathematical Institute, Slovak Academy of Sciences, Štefánikova 49, 814 73, Bratislava, Slovak Republic

    Michal Fečkan

  5. Department of Electronic Engineering, City University of Hong Kong, Hong Kong, China

    Guanrong Chen

Authors
  1. Marius-F. Danca
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michal Fečkan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guanrong Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Marius-F. Danca.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Danca, MF., Fečkan, M. & Chen, G. Impulsive stabilization of chaos in fractional-order systems. Nonlinear Dyn 89, 1889–1903 (2017). https://doi.org/10.1007/s11071-017-3559-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3559-1

Keywords

Search

Navigation