Skip to main content
SpringerLink
Log in

Orbit classification in the Hill problem: I. The classical case

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

The case of the classical Hill problem is numerically investigated by performing a thorough and systematic classification of the initial conditions of the orbits. More precisely, the initial conditions of the orbits are classified into four categories: (i) non-escaping regular orbits; (ii) trapped chaotic orbits; (iii) escaping orbits; and (iv) collision orbits. In order to obtain a more general and complete view of the orbital structure of the dynamical system, our exploration takes place in both planar (2D) and the spatial (3D) version of the Hill problem. For the 2D system, we numerically integrate large sets of initial conditions in several types of planes, while for the system with three degrees of freedom, three-dimensional distributions of initial conditions of orbits are examined. For distinguishing between ordered and chaotic bounded motion, the Smaller Alignment Index method is used. We managed to locate the several bounded basins, as well as the basins of escape and collision and also to relate them to the corresponding escape and collision time of the orbits. Our numerical calculations indicate that the overall orbital dynamics of the Hamiltonian system is a complicated but highly interested problem. We hope our contribution to be useful for a further understanding of the orbital properties of the classical Hill problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Notes

  1. Sticky orbits need an extremely long time interval in order to move away from the invariant sticky tori [36]. Therefore, sticky orbits behave, for long time interval, as regular ones before revealing their true chaotic nature.

  2. When we state that an area is fractal we simply suggest that it has a fractal-like geometry without conducting any specific calculations regarding the fractal dimensions as in [3].

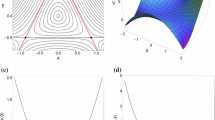
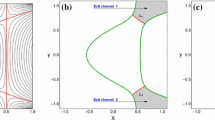
  3. The two saddle points \(L_1\) and \(L_2\) lie along the x axis and the zero velocity surfaces are symmetrical with respect to the three axes. It is easy to prove that if (x(t), y(t), z(t)) is a solution of the Hill problem, \((-x(t), -y(t), -z(t))\) is also a solution, of course with appropriately chosen momenta (because of the presence of the Coriolis force). Therefore, for every orbit escaping through \(L_1\) there is a symmetry-related orbit escaping through \(L_2\), because the dynamics of the system must be symmetrical. On this basis, the observed preference for escape through exit channel 2 is due to the particular choice of the initial conditions. Similar choices of initial conditions of orbits can be found in several earlier related papers (e.g., [13, 33, 34, 67,68,69]).

References

  1. Astakhov, S.A., Burbanks, A.D., Wiggins, S., Farrelly, D.: Chaos-assisted capture of irregular moons. Nature 423, 264–267 (2003)

    Article  Google Scholar 

  2. Astakhov, S.A., Farrelly, D.: Capture and escape in the elliptic restricted three-body problem. Mon. Not. R. Astron. Soc. 354, 971–979 (2004)

    Article  Google Scholar 

  3. Aguirre, J., Viana, R.L., Sanjuán, M.A.F.: Fractal structures in nonlinear dynamics. Rev. Mod. Phys. 81, 333–386 (2009)

    Article  Google Scholar 

  4. Barrio, R., Blesa, F., Serrano, S.: Bifurcations and safe regions in open Hamiltonians. New J. Phys. 11, 053004-1-12 (2009)

  5. Benet, L., Trautman, D., Seligman, T.: Chaotic scattering in the restricted three-body problem I. The Copenhagen problem. Celest. Mech. Dyn. Astron. 66, 203–228 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  6. Benet, L., Seligman, T., Trautman, D.: Chaotic scattering in the restricted three-body problem II. Small mass parameters. Celest. Mech. Dyn. Astron. 71, 167–189 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  7. Bleher, S., Ott, E., Grebogi, C.: Routes to chaotic scattering. Phys. Rev. Let. 63, 919–922 (1989)

    Article  Google Scholar 

  8. Contopoulos, G.: Asymptotic curves and escapes in Hamiltonian systems. Astron. Astrophys. 231, 41–55 (1990)

    MathSciNet  Google Scholar 

  9. Contopoulos, G., Kaufmann, D.: Types of escapes in a simple Hamiltonian system. Astron. Astrophys. 253, 379–388 (1992)

    MathSciNet  MATH  Google Scholar 

  10. Contopoulos, G., Kandrup, H.E., Kaufmann, D.: Fractal properties of escape from a two-dimensional potential. Phys. D 64, 310–323 (1993)

    Article  MATH  Google Scholar 

  11. Contopoulos, G., Harsoula, M.: Stickiness effects in conservative systems. IJBC 20, 2005 (2010)

    MathSciNet  MATH  Google Scholar 

  12. Contopoulos, G., Harsoula, M., Lukes-Gerakopoulos, G.: Periodic orbits and escapes in dynamical systems. Celest. Mech. Dyn. Astron. 113, 255–278 (2012)

    Article  MathSciNet  Google Scholar 

  13. de Assis, S.C., Terra, M.O.: Escape dynamics and fractal basin boundaries in the planar Earth-Moon system. Celest. Mech. Dyn. Astron. 120, 105–130 (2014). (Paper I)

    Article  MathSciNet  Google Scholar 

  14. Drótos, G., Jung, C., Tél, T.: When is high-dimensional scattering chaos essentially two dimensional? Measuring the product structure of singularities. Phys. Rev. E 86, 056210 (2012)

    Article  Google Scholar 

  15. Drótos, González, Montoya, F.G., Jung, C., Tél, T.: Asymptotic observability of low-dimensional powder chaos in a three-degrees-of-freedom scattering system. Phys. Rev. E 90, 022906 (2014)

    Article  Google Scholar 

  16. Drótos, G., Jung, C.: The chaotic saddle of a three degrees of freedom scattering system reconstructed from cross section data. J. Phys. A 49, 235101 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  17. Ernst, A., Peters, T.: Fractal basins of escape and the formation of spiral arms in a galactic potential with a bar. Mon. Not. R. Astron. Soc. 443, 2579–2589 (2014)

    Article  Google Scholar 

  18. González, F., Drótos, G., Jung, C.: The decay of a normally hyperbolic invariant manifold to dust in a three degrees of freedom scattering system. J. Phys. A 47, 045101 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  19. Hénon, M.: Numerical exploration of the restricted problem V. Astron. Astrophys. 1, 223–238 (1969)

    MATH  Google Scholar 

  20. Hill, G.W.: On the part of the motion of lunar perigee which is a function of the mean motions of the Sun and Moon. Acta Math. 8, 1–36 (1886)

    Article  MathSciNet  MATH  Google Scholar 

  21. Jung, C.: Can the integrability of Hamiltonian systems be decided by the knowledge of scattering data? J. Phys. A 20, 1719–1732 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  22. Jung, C., Scholz, H.J.: Cantor set structures in the singularities of classical potential scattering. J. Phys. A 20, 3607–3618 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  23. Jung, C., Pott, S.: Classical cross section for chaotic potential scattering. J. Phys. A 22, 2925–2938 (1989)

    Article  MathSciNet  MATH  Google Scholar 

  24. Jung, C., Richter, P.H.: Classical chaotic scattering-periodic orbits, symmetries, multifractal invariant sets. J. Phys. A 23, 2847–2866 (1990)

    Article  MathSciNet  MATH  Google Scholar 

  25. Jung, C., Tèl, T.: Dimension and escape rate of chaotic scattering from classical and semiclassical cross section data. J. Phys. A 24, 2793–2805 (1991)

    Article  Google Scholar 

  26. Jung, C., Mejia-Monasterio, C., Seligman, T.H.: Scattering one step from chaos. Phys. Lett. A 198, 306–314 (1995)

    Article  Google Scholar 

  27. Jung, C., Lipp, C., Seligman, T.H.: The inverse scattering problem for chaotic Hamiltonian systems. Ann. Phys. 275, 151–189 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  28. Jung, C., Merlo, O., Seligman, T.H., Zapfe, W.P.K.: The chaotic set and the cross section for chaotic scattering in three degrees of freedom. New J. Phys. 12, 103021 (2010)

    Article  Google Scholar 

  29. Jung, C., Zotos, E.E.: Orbital and escape dynamics in barred galaxies–II. The 3D system: exploring the role of the normally hyperbolic invariant manifolds. Mon. Not. R. Astron. Soc. 463, 3965–3988 (2016)

    Article  Google Scholar 

  30. Kandrup, H.E., Siopis, C., Contopoulos, G., Dvorak, R.: Diffusion and scaling in escapes from two-degrees-of-freedom Hamiltonian systems. Chaos 9, 381–392 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  31. Lai, Y.-C., Tél, T.: Transient Chaos. Springer, New York (2011)

    Book  MATH  Google Scholar 

  32. Lyapunov, A.: Probléme general de las stabilité de mouvement. Ann. Math. Stud. 17 (1949)

  33. Nagler, J.: Crash test for the Copenhagen problem. Phys. Rev. E 69, 066218 (2004)

    Article  MathSciNet  Google Scholar 

  34. Nagler, J.: Crash test for the restricted three-body problem. Phys. Rev. E 71, 026227 (2005)

    Article  MathSciNet  Google Scholar 

  35. Navarro, J.F., Henrard, J.: Spiral windows for escaping stars. Astron. Astrophys. 369, 1112–1121 (2001)

    Article  Google Scholar 

  36. Perry, A.D., Wiggins, S.: KAM tori are very sticky: rigorous lower bounds on the time to move away from an invariant Lagrangian torus with linear flow. Phys. D 71, 101–121 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  37. Perdiou, A.E., Markellos, V.V., Douskos, C.N.: The Hill problem with oblate secondary: numerical exploration. Earth Moon Planets 97, 127–145 (2005)

    Article  Google Scholar 

  38. Petit, J.M., Hénon, M.: Satellite encounters. Icarus 66, 536–555 (1986)

    Article  Google Scholar 

  39. Petit, J.M., Hénon, M.: A numerical simulation of planetary rings. I-Binary encounters. Astron. Astrophys. 173, 389–404 (1987)

    MATH  Google Scholar 

  40. Press, H.P., Teukolsky, S.A., Vetterling, W.T., Flannery, B.P.: Numerical Recipes in FORTRAN 77, 2nd edn. Cambridge University Press, Cambridge (1992)

    MATH  Google Scholar 

  41. Ross, S.D., Scheeres, D.J.: Multiple gravity assists, capture, and escape in the restricted three-body problem. SIAM J. Appl. Dyn. Syst. 6, 576–596 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  42. Sanjuán, M.A.F., Horita, T., Aihara, K.: Opening a closed Hamiltonian map. Chaos 13, 17–24 (2003)

  43. Schneider, J., Tél, T., Neufeld, Z.: Dynamics of “leaking” Hamiltonian systems. Phys. Rev. E 66, 066218 (2002)

    Article  MathSciNet  Google Scholar 

  44. Seoane, J.M., Aguirre, J., Sanjuán, M.A.F., Lai, Y.C.: Basin topology in dissipative chaotic scattering. Chaos 16, 023101-1–8 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  45. Seoane, J.M., Sanjuán, M.A.F., Lai, Y.C.: Fractal dimension in dissipative chaotic scattering. Phys. Rev. E 76, 016208-1–6 (2007)

    Article  Google Scholar 

  46. Seoane, J.M., Sanjuán, M.A.F.: Exponential decay and scaling laws in noisy chaotic scattering. Phys. Lett. A 372, 110–116 (2008)

    Article  MATH  Google Scholar 

  47. Seoane, J.M., Huang, L., Sanjuán, M.A.F., Lai, Y.C.: Effects of noise on chaotic scattering. Phys. Rev. E 79, 047202-1–4 (2009)

    Article  Google Scholar 

  48. Seoane, J.M., Sanjuán, M.A.F.: Escaping dynamics in the presence of dissipation and noisy in scattering systems. Int. J. Bifurc. Chaos 9, 2783–2793 (2010)

    Article  MATH  Google Scholar 

  49. Simó, C., Stuchi, T.: Central stable/unstable manifolds and the destruction of KAM tori in the planar Hill problem. Phys. D 140, 1–32 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  50. Siopis, C.V., Contopoulos, G., Kandrup, H.E.: Escape probabilities in a Hamiltonian with two channels of escape. New York Acad. Sci. Ann. 751, 205–212 (1995a)

    Article  MATH  Google Scholar 

  51. Siopis, C.V., Kandrup, H.E., Contopoulos, G., Dvorak, R.: Universal properties of escape. New York Acad. Sci. Ann. 773, 221–230 (1995b)

    Article  MATH  Google Scholar 

  52. Siopis, C.V., Kandrup, H.E., Contopoulos, G., Dvorak, R.: Universal properties of escape in dynamical systems. Celest. Mech. Dyn. Astron. 65, 57–681 (1996)

    Article  MathSciNet  MATH  Google Scholar 

  53. Skokos, C.: Alignment indices: a new, simple method for determining the ordered or chaotic nature of orbits. J. Phys. A Math. Gen. 34, 10029–10043 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  54. Szebehely, V.: Theory of Orbits. Academic Press, New York (1967)

    Google Scholar 

  55. Waalkens, H., Burbanks, A., Wiggins, S.: A computational procedure to detect a new type of high-dimensional chaotic saddle and its application to the 3D Hill’s problem. J. Phys. A 37, L257–L265 (2004)

    Article  MathSciNet  Google Scholar 

  56. Waalkens, H., Burbanks, A., Wiggins, S.: Escape from planetary neighbourhoods. Mon. Not. R. Astron. Soc. 361, 763–775 (2005)

  57. Winter, O.C., Murray, C.D.: Atlas of the Planar, Circular, Restricted Three-body Problem. I. Internal Orbits, QMW Maths Notes, No. 16. Queen Mary and Westfield College, London (1994)

  58. Winter, O.C., Murray, C.D.: Atlas of the Planar, Circular, Restricted Three-body Problem. II. External Orbits, QMW Maths Notes, No. 17. Queen Mary and Westfield College, London (1994)

    Google Scholar 

  59. Wolfram, S.: The Mathematica Book, 5th edn. Wolfram Media, Champaign (2003)

    MATH  Google Scholar 

  60. Zotos, E.E.: A Hamiltonian system of three degrees of freedom with eight channels of escape: The Great Escape. Nonlinear Dyn. 76, 1301–1326 (2014a)

    Article  Google Scholar 

  61. Zotos, E.E.: Escapes in Hamiltonian systems with multiple exit channels: part I. Nonlinear Dyn. 78, 1389–1420 (2014b)

    Article  MathSciNet  Google Scholar 

  62. Zotos, E.E.: Revealing the escape mechanism of three-dimensional orbits in a tidally limited star cluster. Mon. Not. R. Astron. Soc. 446, 770–792 (2015a)

    Article  Google Scholar 

  63. Zotos, E.E.: Escapes in Hamiltonian systems with multiple exit channels: part II. Nonlinear Dyn. 82, 357–398 (2015b)

    Article  MathSciNet  Google Scholar 

  64. Zotos, E.E.: Crash test for the Copenhagen problem with oblateness. Celest. Mech. Dyn. Astron. 122, 75–99 (2015c)

    Article  MathSciNet  Google Scholar 

  65. Zotos, E.E.: How does the oblateness coefficient influence the nature of orbits in the restricted three-body problem?. Astrophys. Space Sci. 358, article id. 10 (2015d)

  66. Zotos, E.E.: Unveiling the influence of the radiation pressure in nature of orbits in the photogravitational restricted three-body problem. Astrophys. Space Sci. 360, article id. 1 (2015e)

  67. Zotos, E.E.: Orbital dynamics in the planar Saturn-Titan system. Astrophys. Space Sci. 358, article id. 4 (2015f)

  68. Zotos, E.E.: Orbit classification in the planar circular Pluto-Charon system. Astrophys. Space Sci. 360, article id. 7 (2015g)

  69. Zotos E.E.: Escape dynamics and fractal basins boundaries in the three-dimensional Earth-Moon system. Astrophys. Space Sci. 361, article id. 94 (2016a)

  70. Zotos, E.E.: Fractal basin boundaries and escape dynamics in a multiwell potential. Nonlinear Dyn. 85, 1613–1633 (2016b)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

The author would like to express his warmest thanks to the three anonymous referees for the careful reading of the original manuscript and for all the apt suggestions and comments which allowed us to improve both the quality as well as the clarity of the paper.

Author information

Authors and Affiliations

  1. Department of Physics, School of Science, Aristotle University of Thessaloniki, 541 24, Thessaloniki, Greece

    Euaggelos E. Zotos

Authors
  1. Euaggelos E. Zotos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Euaggelos E. Zotos.

Ethics declarations

Conflict of interest

The author declares that he has no conflict of interest.

Appendix: Derivation of the potential function of the classical Hill problem

Appendix: Derivation of the potential function of the classical Hill problem

The first step is to perform the coordinate transformation given in Eq. (4) along with \(\mu = M^3\). Then Eq. (1) becomes a polynomial function \(\varOmega = \varOmega (x,y,z,M)\).

It is very easy to prove that \(\varOmega _{\mathrm{lim}} = \displaystyle {\lim _{M \rightarrow 0} \varOmega } = 3/2\).

Next we expand \(\varOmega \) into a power series around \(M = 0\) (Taylor series), keeping terms up to second order, thus having

$$\begin{aligned} W_0(x,y,z,M) = \frac{3}{2} + M^2 \left( \frac{3x^2}{2} - \frac{z^2}{2} + \frac{1}{r}\right) , \end{aligned}$$
(13)

where \(r = \sqrt{x^2 + y^2 + z^2}\).

Now for obtaining the potential function W(x, y, z) of the classical Hill problem all we have to do is to eliminate the parameter M for Eq. (13). This can be achieved as

$$\begin{aligned} W(x,y,z) = \frac{W_0 - \varOmega _{\mathrm{lim}}}{M^2}, \end{aligned}$$
(14)

thus deriving the final form of Eq. (6)

$$\begin{aligned} W(x,y,z) = \frac{3x^2}{2} - \frac{z^2}{2} + \frac{1}{r}. \end{aligned}$$
(15)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zotos, E.E. Orbit classification in the Hill problem: I. The classical case. Nonlinear Dyn 89, 901–923 (2017). https://doi.org/10.1007/s11071-017-3491-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3491-4

Keywords

Search

Navigation