1 Introduction

Multistability is an inherent property referring to the systems that exhibit coexistence of several stable solutions for a given set of parameters, and the development of robust control methods based on this feature is a topic of ongoing investigation (see, e.g., [1, 2]). Multistability introduces a twofold effect in engineering systems. On the one hand, this phenomenon has to be avoided in order to prevent costly failures by stabilizing the desired state against a noisy environment when designing a commercial device with specific characteristics [3, 4]. On the other hand, coexistence of several stable solutions offers great flexibility in the performance of engineering systems, because the system behavior can be changed without altering its major control parameters. For this reason, a significant amount of effort has been dedicated to the development of control strategies that allow judiciously switching between stable solutions in a multistable dynamical scenario; see, e.g., [1, 5, 6] and the references therein.

Multistability has been observed in a broad range of engineering applications [7,8,9,10,11,12], and in some cases the coexisting stable solutions appear to be ‘hidden’, due to the complex structure of the basins of attraction [13]. In [14], the authors investigated the case of an impact oscillator with dry friction. They proved that not all attractors can be reached by system trajectories in the presence of noise. Another case is that of a gear-rattling impact model analyzed in [7], where the focus was on the numerical study of the basins of attraction of periodic and chaotic solutions. In [8], multistability was observed in a bilinear oscillator close to grazing, and the occurrence of coexisting attractors was manifested in an experimental investigation that revealed discontinuous transitions from one orbit to another via boundary crisis. The case of an electro-vibro-impact system was considered in [10], where the authors studied a broad range of dynamical scenarios with coexisting periodic and chaotic solutions. More recently, hidden coexisting oscillations were investigated in a drilling system [3], which were identified as a possible cause of harmful vibrations in the drill strings.

Some recent advances in controlling multistability have been reported in [1, 15]. In [16], an algorithm was developed to steer most trajectories to a desirable attractor by using small feedback control. Fluctuational transitions in a discrete dynamical system having two coexisting attractors separated by a fractal basin boundary were studied in [17]. The case of a \(\hbox {CO}_2\) laser model driven by a delayed feedback controller was considered in [18], where the authors were able to lock one of the coexisting attractors and eliminate the others. In [19], the basins of attraction of coexisting solutions were controlled by either a harmonic modulation or a small noise signal applied to a system parameter in a multistable erbium-doped fiber laser. Sevilla-Escoboza et al. [20] proposed a robust control method that allows a periodic or a chaotic multistable system to be transformed to a monostable system at an orbit with dominant frequency of any of the coexisting attractors. Another control method was developed in [21], which was based on the computation of basins of attraction and allows the switching from multistable to monostable dynamical scenarios. An intermittent control strategy was developed in [2] for switching between coexisting attractors, which can be applied to non-autonomous dynamical systems. The method is based on the knowledge of system’s basins of attraction with control actions being applied intermittently in the time domain when an observed trajectory satisfies a proximity constraint with respect to a desired trajectory.

In the present work, we consider a vibro-impact capsule system with a position feedback controller modeled in the framework of piecewise-smooth dynamical systems [22], where the discontinuity boundaries are physically associated with impact, friction and control input. The vibro-impact capsule system is a self-propelled mechanism moving rectilinearly under internal harmonic excitation when overcoming environmental resistance, which has practical applications in gastrointestinal endoscopy [23, 24] and engineering pipeline inspection [25, 26]. A previous study of a simpler version of the capsule model was carried out in [27, 28], where the authors investigated the response of the model in various dynamical scenarios. The capsule was found to be monostable when the environmental resistance was modeled via Coulomb friction. An experimental verification of the capsule model was carried out in [29] by using a novel experimental rig. In [30], various friction models were considered to represent the resistance of the surrounding medium of the capsule. If the medium resistance includes the Stribeck effect, it has been shown that the capsule response exhibits numerous coexisting attractors, including periodic and chaotic solutions. Therefore, in the present paper we will include the Stribeck effect in the governing equations of the capsule system in order to study the control of the capsule motion using its multistability. The main purpose is to apply the position feedback control method considered in [6] to switch between forward and backward motion without altering its control parameters. The robustness of this control strategy will be investigated by means of numerical continuation methods. Specifically, we will identify a region in the parameter space in which the proposed controller can be applied. For this purpose, we will employ the MATLAB-based numerical platform COCO [31], which supports the continuation and bifurcation detection of periodic orbits of non-smooth dynamical systems.

The main contribution of this paper is twofold: first, to propose a position feedback controller which converts the multistable capsule system to a bistable one, and, second, to carry out a robustness study of the control method by using path-following techniques. The novelty of the position feedback control is that it gives rise to a dynamical scenario with two coexisting solutions, corresponding to forward and backward motion control of the capsule, which cannot be achieved by delayed feedback control [18] or parameter modulation [19, 20]. The rest of the paper is organized as follows. In the next section, the physical model of the capsule system will be introduced including the position feedback controller and the considered friction model. In Sect. 3, we will present the mathematical formulation of the capsule model in the framework of piecewise-smooth dynamical systems with emphasis on the basic set-up required for the application of the continuation software COCO. The multistable behavior of the system will be numerically studied in Sect. 4.1. The robustness of the control scheme will be analyzed via path-following techniques using COCO in Sect. 4.2. Finally, in Sect. 5 we will give some concluding remarks regarding the present work.

2 Capsule modeling with position feedback control

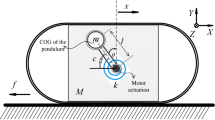
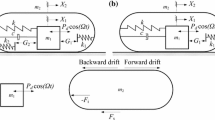
This work considers a two-degree-of-freedom capsule system depicted in Fig. 1. A movable internal mass \(m_{1}\) is driven by a sinusoidal force with amplitude \(F_{\mathrm{d}}\) and frequency \(\varOmega \), interacting with a rigid capsule \(m_{2}\) via a linear spring with stiffness \(k_{1}\) and a viscous damper with damping coefficient c. \(X_{1}\) and \(X_{2}\) represent the absolute displacements of the internal mass and the capsule, respectively. The internal mass hits a weightless plate connected to the capsule by a secondary linear spring with stiffness \(k_{2}\), when the relative displacement \(X_{1}-X_{2}\) is larger than or equal to the gap E. If the force acting on the capsule from the support of the internal mass exceeds the threshold of the dry friction \(F_{\mathrm{b}}\) between the capsule and the surrounding medium, the capsule moves in either forward or backward direction as indicated in Fig. 1. During the motion, a friction force \(F_{\mathrm{s}}\) is exerted on the capsule by the surrounding medium, which opposes the direction of motion.

Fig. 1
figure 1

Physical model of the vibro-impact capsule system

Full size image

The equations of motion will be given in dimensionless form, according to the following formulae:

$$\begin{aligned} \begin{array}{llll} \varOmega _{0}=\sqrt{\dfrac{k_{1}}{m_{1}}}, &{} \quad t= \varOmega _{0}\tau , &{} \quad \omega =\dfrac{\varOmega }{\varOmega _{0}}, &{} \quad \xi =\dfrac{c}{2m_{1}\varOmega _{0}},\\ \alpha =\dfrac{F_{\mathrm{d}}}{F_{\mathrm{r}}}, &{} \quad \delta =\dfrac{k_{1}}{F_{\mathrm{r}}}E, &{} \quad x_{1}=\dfrac{k_{1}}{F_{\mathrm{r}}}X_{1},&{} \quad x_{2}=\dfrac{k_{1}}{F_{\mathrm{r}}}X_{2}, \\ f_{\mathrm{s}}=\dfrac{F_{\mathrm{s}}}{F_{\mathrm{r}}}, &{} \quad f_{\mathrm{b}}=\dfrac{F_{\mathrm{b}}}{F_{\mathrm{r}}},&{} \quad \beta =\dfrac{k_{2}}{k_{1}}, &{} \quad \gamma =\dfrac{m_{2}}{m_{1}}, \end{array} \end{aligned}$$
(1)

where \(F_{\mathrm{r}}>0\) is a given reference force. The considered system operates in bidirectional stick–slip phases, which can be described by the following main regimes: No contact—stationary, No contact—drifting, Contact—stationary and Contact—drifting as introduced in [27]. These operation regimes, however, need to be split into several submodes so as to able to describe the model in the framework of piecewise-smooth dynamical systems as, e.g., in [28]. The complete set of operation regimes will be given in Sect. 3.2. The equations of motion for the vibro-impact capsule system (without control) can be written in a compact form as follows [27]:

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }_{1}=y_{1},\\ y^{\prime }_{1}=\alpha \cos (\omega t)+(x_{2}-x_{1})+2\xi (y_{2}-y_{1}) \\ \quad \quad \; \,-P_{3}\beta (x_{1}-x_{2}-\delta ),\\ x^{\prime }_{2}=(P_{1}(1-P_{3})+P_{2}P_{3})y_{2},\\ y^{\prime }_{2}=\frac{1}{\gamma }(P_{1}(1-P_{3})+P_{2}P_{3})\left( P_{3}\beta (x_{1}-x_{2}-\delta )\right. \\ \quad \quad \;\left. \,-(x_{2}-x_{1})-2\xi (y_{2}-y_{1}) -f_{\mathrm{s}}\left( x^{\prime }_{2}\right) \right) , \end{array}\right. \end{aligned}$$
(2)

with \(P_{1}\,{:=}\,H\left( \big \vert (x_{2}-x_{1}){+}2\xi (y_{2}-y_{1})\big \vert -f_{\mathrm{b}}\right) \), \(P_{2}\,{:=}\,H\left( \big \vert (x_{2}{-}x_{1}){+}2\xi (y_{2}{-}y_{1}){-}\beta (x_{1}{-}x_{2}{-}\delta )\big \vert {-}f_{\mathrm{b}}\right) \) and \(P_{3}\,{:=}\,H(x_{1}-x_{2}-\delta )\), where \(H({\cdot })\) stands for the Heaviside step function.

The Stribeck effect is introduced to the friction model, and the relationship between friction force and capsule velocity is governed by

$$\begin{aligned} f_{\mathrm{s}}\left( x^{\prime }_{2}\right) := \left( 1+\hbox {e}^{-\big \vert x^{\prime }_{2}\big \vert /v_{\mathrm{s}}}\right) {{\mathrm{sign}}}\left( x^{\prime }_{2}\right) , \end{aligned}$$

where \(v_{\mathrm{s}}\) is the non-dimensional Stribeck velocity. Here, we will take \(f_{\mathrm{b}}=2\) as the breakaway friction force that defines the onset of sliding phases.

In order to control the forward and backward motion of the capsule via its multistability, we consider the position feedback control law

$$\begin{aligned} u=k_{\mathrm{p}}\big \vert x_{2}-x_{1}\big \vert , \end{aligned}$$

where \(k_{\mathrm{p}}\) is a proportional control gain. The resulting equations of motion of the controlled capsule system are then given by

$$\begin{aligned} \left\{ \begin{array}{l} x^{\prime }_{1}=y_{1},\\ y^{\prime }_{1}=\alpha \cos (\omega t)+f_{\mathrm{p}}(x_{1},x_{2})+2\xi (y_{2}-y_{1}) \\ \quad \quad \,\; -P_{3}\beta (x_{1}-x_{2}-\delta ),\\ x^{\prime }_{2}=(P_{1}(1-P_{3})+P_{2}P_{3})y_{2},\\ y^{\prime }_{2}=\frac{1}{\gamma }(P_{1}(1-P_{3})+P_{2}P_{3})\left( P_{3}\beta (x_{1}-x_{2}-\delta )\right. \\ \quad \quad \,\;\left. -(x_{2}-x_{1})-2\xi (y_{2}-y_{1}) -f_{\mathrm{s}}\left( x^{\prime }_{2}\right) \right) , \end{array}\right. \end{aligned}$$
(3)

where

$$\begin{aligned} f_{\mathrm{p}}(x_{1},x_{2}):= & {} k_{\mathrm{p}}\big \vert x_{2}-x_{1}\big \vert +(x_{2}-x_{1})\\= & {} {\left\{ \begin{array}{ll} (1-k_{\mathrm{p}})(x_{2}-x_{1}), &{} \quad x_{1}\ge x_{2},\\ (1+k_{\mathrm{p}})(x_{2}-x_{1}), &{}\quad x_{1}< x_{2}. \end{array}\right. } \end{aligned}$$

3 The controlled capsule as a piecewise-smooth dynamical system

In order to study the behavior of the controlled capsule model introduced in the previous section, we will employ two different types of numerical approaches, namely direct numerical integration and path-following (continuation) techniques. As can be seen from the equations of motion (3), the capsule model belongs to the class of piecewise-smooth dynamical systems [22], which are characterized by periods of smooth evolution interrupted by instantaneous events, typically occurring in applications involving impacts, switches, friction, etc. From a numerical point of view, it is convenient to divide the state space of such systems into disjoint subregions, so that the system dynamics in each subregion is determined by a smooth vector field. The boundary of any subregion is mathematically described by the zero set of a smooth scalar function, often referred to as event function, which is usually connected to a physical instantaneous event, as explained above. Therefore, special care must be taken in order to get reliable numerical approximations of the behavior of such systems in an efficient way. In our investigation, the numerical simulations will be obtained via direct numerical integration of one of the possible smooth vector fields, until the computed solution approaches the boundary of the corresponding subregion. The boundary point is accurately detected, and then, the integrated vector field is switched according to the governing laws of the system. In practice, this can be implemented by means of the standard MATLAB ODE solvers together with their built-in event location routines [32, 33], as suggested in [34].

As will be seen in the next section, our investigation will include the study of forced oscillations generated by an external sinusoidal excitation [see (3)]. Since the capsule model is parameter dependent, a family of oscillatory solutions may be tracked by freeing one system parameter, which can be numerically realized via path-following (continuation) methods. These are well-established techniques in applied mathematics [35] that enable a systematic study of a model response subject to parameter variations, with focus on the detection of possible qualitative changes in the model behavior (bifurcations). For the analysis of periodic solutions of piecewise-smooth systems via continuation methods, specialized computational tools are available, such as SlideCont [36], TC-HAT [37] (see also [28, 38,39,40,41] for recent applications of this tool) and COCO [31, 42,43,44,45], and the latter will be employed in the current work for the numerical study of the capsule model. In the next section, we will explain in detail the mathematical set-up that is required to carry out the numerical investigation of the capsule via COCO.

3.1 Continuation framework in COCO for piecewise-smooth dynamical systems

Computational continuation core (in short COCO) is a MATLAB-based analysis and development platform for the numerical solution of continuation problems [31]. The software package includes a collection of special-purpose toolboxes that covers, to a large extent, the functionality of existing continuation platforms, such as AUTO [46] and MATCONT [47]. A key feature of COCO is, however, that it provides the user with a general purpose framework that supports and facilitates the development of specialized toolboxes tailored to the user’s interests and needs, which can be built on top of available core routines, common across a broad range of continuation problems.

In the present work, we will make extensive use of the COCO toolbox ‘hspo’, which supports the numerical continuation and bifurcation detection of periodic orbits of piecewise-smooth dynamical systems. This toolbox has extended and improved the functionalities of the software package TC-HAT [37], an AUTO-based application for bifurcation analysis of piecewise-smooth systems. A detailed discussion regarding the differences and improvements can be found in [43]. The mathematical set-up required to apply the ‘hspo’ toolbox, however, follows closely that of TC-HAT and can be briefly described as follows.

A parameter-dependent, piecewise-smooth dynamical system can be characterized by a collection of smooth vector fields and smooth event functions

$$\begin{aligned}&\left\{ f_{\text { M}_i}:{{\mathrm{{\mathbbm {R}}}}}^N\times {{\mathrm{{\mathbbm {R}}}}}^p\rightarrow {{\mathrm{{\mathbbm {R}}}}}^N\right\} ^{K_{\text { M}}}_{i=1}\, \text{ and } \\&\quad \left\{ h_{\text { E}_j}:{{\mathrm{{\mathbbm {R}}}}}^N\times {{\mathrm{{\mathbbm {R}}}}}^p\rightarrow {{\mathrm{{\mathbbm {R}}}}}\right\} ^{K_{\text { E}}}_{j=1}, \end{aligned}$$

respectively, with \(N,p,K_{\text { M}},K_{\text { E}}\in {{\mathrm{{\mathbbm {N}}}}}\). Here, the subindex \(\hbox {M}_i\), \(i=1,\ldots ,K_{\text { M}}\), represents a mode of operation of the system, for which the system dynamics is described by the smooth vector field \(f_{\text { M}_i}\). Each mode of operation is defined within a subregion of the state space \({{\mathrm{{\mathbbm {R}}}}}^N\). The boundaries of these subregions are determined by the zero set of the smooth scalar functions \(h_{\text { E}_j}\), \(j=1,\ldots ,K_{\text { E}}\). The subindex E\(_j\) represents in this case an event related to, e.g., impacts, switches, etc., as outlined at the beginning of Sect. 3. A periodic solution of a piecewise-smooth system can then be represented by a sequence of segments \(\left\{ I_{\ell }\right\} ^{K_{\text { S}}}_{\ell =1}\), \(K_{\text { S}}\in {{\mathrm{{\mathbbm {N}}}}}\), also referred to as solution signature. Here, each segment is associated with a vector field and an event function, i.e., \(I_{\ell }:=\left\{ \text {M}_{i_{\ell }},\text {E}_{j_{\ell }}\right\} \) for all \(\ell =1,\ldots ,K_{\text { S}}\), \(1\le i_{\ell }\le K_{\text { M}}\), \(1\le j_{\ell }\le K_{\text { E}}\). More details about this mathematical set-up can be found in [31, 37].

3.2 Vector fields and event functions for the capsule model

In this section, we will introduce the modes of operation and the event functions that describe the behavior of the capsule, following the mathematical framework described previously. Before we do so, it is convenient to introduce the coordinate transformation

$$\begin{aligned} \left\{ \begin{array}{l} w_{1}=x_{1},\\ w_{2}=x_{1}-x_{2},\\ v_{1}=y_{1},\\ v_{2}=y_{1}-y_{2}, \end{array}\right. \end{aligned}$$
(4)

which allows decoupling the periodic behavior of the capsule model from the (forward or backward) drift. The new variables \(w_{2}\) and \(v_{2}\) represent the relative position and velocity of the mass \(m_{1}\) with respect to the capsule; see Fig. 1. In this way, the dimension of the system can be reduced, as the oscillatory motion of the capsule is fully captured by the variables \(w_{2}\), \(v_{1}\) and \(v_{2}\), as will be seen later.

In what follows, we will denote by \(z:=(w_{2},v_{1},v_{2})^{\mathrm{T}}\in {{\mathrm{{\mathbbm {R}}}}}^3\) and \(\mu :=(\omega ,\alpha ,\xi ,\delta ,\beta ,\gamma ,v_{\mathrm{s}},k_{\mathrm{p}})\in \left( {{\mathrm{{\mathbbm {R}}}}}^+\right) ^7\times {{\mathrm{{\mathbbm {R}}}}}\) the state variables and parameters of the system, respectively, where \({{\mathrm{{\mathbbm {R}}}}}^+\) stands for the set of positive numbers. The modes of operation of the capsule system are analogous to those introduced in a previous work [28]. The main difference, however, lies in the fact that the current model includes a position feedback control, which gives rise to additional modes of operation, as will be described in detail below.

No contact 1—stationary (NC-S1). This mode takes place when three conditions are fulfilled: the gap between the secondary spring \(k_{2}\) and the internal mass \(m_{1}\) is smaller than \(\delta \) \(\left( w_{2}=x_{1}-x_{2}<\delta \right) \), the force acting on the capsule from the support of the internal mass is smaller than the breakaway friction force \(f_{\mathrm{b}}=2 \left( \big \vert w_{2}+2\xi v_{2}\big \vert \le 2\right) \), and the relative distance \(w_{2}\) is positive. The motion of the capsule during this regime is governed by the equation

$$\begin{aligned}&z^{\prime }=f_{\text { NC-S1}}(t,z,\mu ) \nonumber \\&\quad :=\left( \begin{array}{c} v_{1}\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2}\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2} \end{array}\right) , \end{aligned}$$
(5)

which results from application of the variable change (4) to the governing equations (3). This operation mode terminates when one of the following events is detected:

$$\begin{aligned} \begin{aligned}&h_{\text { IMP}}(z,\mu ):=w_{2}-\delta =0 \\&\quad \text {(Internal mass hits the secondary spring)},\\&h_{\text { FOR1}}(z,\mu ):=w_{2}+2\xi v_{2}-2=0 \\&\quad \text {(Transition to forward drift)},\\&h_{\text { BACK1}}(z,\mu ):=w_{2}+2\xi v_{2}+2=0 \\&\quad \text {(Transition to backward drift)},\\&h_{\text { CONT}}(z,\mu ):=w_{2}=0 \\&\quad \text {(Position feedback control becomes zero)}. \end{aligned} \end{aligned}$$

No contact 1—forward drift (NC-FD1). During this mode, the internal mass and the secondary spring are not in contact and the gap \(w_{2}\) is positive, i.e., \(0<w_{2}<\delta \). Furthermore, the capsule moves forwards \(\left( y_{2}=v_{1}-v_{2}>0\right) \), and the dynamics of the system is described by

$$\begin{aligned}&z^{\prime }=f_{\text { NC-FD1}}(t,z,\mu ) :=\left( \begin{array}{c} v_{2}\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2}\\ \alpha \cos (\omega t)-w_{2}\left( 1-k_{\mathrm{p}}+\frac{1}{\gamma }\right) -2\xi v_{2}\left( 1+\frac{1}{\gamma }\right) +\frac{1}{\gamma } \left( 1+\hbox {e}^{-\frac{v_{1}-v_{2}}{v_{\mathrm{s}}}}\right) \end{array}\right) . \end{aligned}$$
(6)

This operation regime ends when one of the following events takes place: \(h_{\text { IMP}}(z,\mu )=0\), \(h_{\text { CONT}}(z,\mu )=0\) or

$$\begin{aligned} \begin{aligned} h_{\text { STOP}}(z,\mu )&:=v_{1}-v_{2}=0&\text {(capsule velocity becomes zero)}. \end{aligned} \end{aligned}$$

No contact 1—backward drift (NC-BD1). This regime is similar to the one introduced before. In this case, however, the capsule moves backwards, which means that \(v_{1}-v_{2}<0\). The motion of the capsule is described by the system of ODEs

(7)

As in the previous mode, the terminal point of this regime is defined by the event functions \(h_{\text { IMP}}\), \(h_{\text { CONT}}\) or \(h_{\text { STOP}}\), introduced before.

No contact 2—stationary (NC-S2). This mode is analogous to the operation regime No contact 1—stationary defined before, except that in this case \(w_{2}=x_{1}-x_{2}\le 0\). The behavior of the capsule is governed by the system

(8)

and the operation mode terminates when one of the following events occurs: \(h_{\text { FOR1}}(z,\mu )=0\), \(h_{\text { BACK1}}(z,\mu )=0\) or \(h_{\text { CONT}}(z,\mu )=0\).

No contact 2—forward drift (NC-FD2). As in the previous case, this mode is similar to its counterpart No contact 1—forward drift. Again, the difference is given by the condition \(w_{2}\le 0\), and the dynamics of the system is described by the equation

(9)

The terminal point of this regime is determined via the event functions \(h_{\text { STOP}}\) or \(h_{\text { CONT}}\).

No contact 2—backward drift (NC-BD2). This regime follows the operation principles of No contact 1—backward drift, with \(w_{2}\le 0\). The motion of the capsule is described in this case by the system of ODEs

$$\begin{aligned} z'=f_{\text {\tiny NC-BD2}}(t,z,\mu ):=\left( \begin{array}{c} v_{2}\\ \alpha \cos (\omega t)-(1+k_{p})w_{2}-2\xi v_{2}\\ \alpha \cos (\omega t)-w_{2}\left( 1+k_{p}+\frac{1}{\gamma }\right) -2\xi v_{2}\left( 1+\frac{1}{\gamma }\right) -\frac{1}{\gamma }\left( 1+e^{\frac{v_{1}-v_{2}}{v_{s}}}\right) \end{array}\right) . \end{aligned}$$
(10)

As in the previous mode, the terminal point of this operation regime is determined by the event functions \(h_{\text { STOP}}\) or \(h_{\text { CONT}}\).

Contact—stationary (C-S). This operation regime is analogous to the No contact 1—stationary mode. The difference is that now the internal mass is in contact with the secondary spring \(\left( w_{2}\ge \delta >0\right) \), and therefore, an additional elastic force has to be taken into account in the governing equations, as shown below

$$\begin{aligned}&z^{\prime }=f_{\text { C-S}}(t,z,\mu )\nonumber \\&:=\left( \begin{array}{c} v_{1}\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2}-\beta (w_{2}-\delta )\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2}-\beta (w_{2}-\delta ) \end{array}\right) .\nonumber \\ \end{aligned}$$
(11)

The terminal condition for this mode of operation is defined by the events: \(h_{\text { IMP}}(z,\mu )=0\) or

$$\begin{aligned} \begin{aligned}&h_{\text { FOR2}}(z,\mu ):=w_{2}+2\xi v_{2}+\beta (w_{2}-\delta )-2=0\\&\quad \text {(Transition to forward drift)},\\&h_{\text { BACK2}}(z,\mu ):=w_{2}+2\xi v_{2}+\beta (w_{2}-\delta )+2=0\\&\quad \text {(Transition to backward drift)}. \end{aligned} \end{aligned}$$

Contact—forward drift (C-FD). In this case, the mass \(m_{1}\) is in contact with the spring \(k_{2}\) \(\left( w_{2}\ge \delta >0\right) \) and the capsule moves forwards \(\left( v_{1}-v_{2}>0\right) \). The system dynamics is described by the equation

$$\begin{aligned} z^{\prime }&=\left( \begin{array}{c} v_{2}\\ \alpha \cos (\omega t)-(1-k_{\mathrm{p}})w_{2}-2\xi v_{2}-\beta (w_{2}-\delta )\\ \alpha \cos (\omega t)-w_{2}\left( \left( 1+\frac{1}{\gamma }\right) \left( 1+\beta \right) -k_{\mathrm{p}}\right) -2\xi v_{2}\left( 1+\frac{1}{\gamma }\right) +\frac{1}{\gamma }\left( \beta \delta (1+\gamma )+1+\hbox {e}^{-\frac{v_{1}-v_{2}}{v_{\mathrm{s}}}}\right) \end{array}\right) \nonumber \\&=:f_{\text { C-FD}}(t,z,\mu ). \end{aligned}$$
(12)

This operation regime ends when one of the events takes place: \(h_{\text { IMP}}(z,\mu )=0\) or \(h_{\text { STOP}}(z,\mu )=0\).

Contact—backward drift (C-BD). Similarly to the previous regime, in this operation mode the internal mass is in contact with the secondary spring, but the difference is that in this case the capsule moves backwards. The motion of the capsule is governed by the system of ODEs

(13)

and the terminal point of this mode of operation is defined by the event functions \(h_{\text { IMP}}\) or \(h_{\text { STOP}}\), as in the previous case.

A list of all possible segments used to describe the periodic solutions of the capsule system is presented in Table 1. As explained in Sect. 3.1, each segment is associated with a vector field (operation mode) governing the evolution of the system during the segment and an event function that defines the terminal condition of the segment, which can be an impact with the secondary spring, a transition from stationary position to forward or backward drifting, etc.

To conclude this section, we present below the complete mathematical model of the capsule system, given in terms of the vector fields and event functions defined before:

Table 1 Operation modes and segments defined to study the dynamics of the capsule system in COCO
Full size table

No contact 1 (\(0<w_{2}<\delta \)):

$$\begin{aligned} z^{\prime }= {\left\{ \begin{array}{ll} f_{\text { NC-S1}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,\big \vert w_{2}+2\xi v_{2}\big \vert \le 2,\\ f_{\text { NC-FD1}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )>0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \, h_{\text { FOR1}}(z,\mu )>0\right) ,\\ f_{\text { NC-BD1}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )<0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,h_{\text { BACK1}}(z,\mu )<0\right) . \end{array}\right. } \end{aligned}$$
(14)

No contact 2 (\(w_{2}\le 0\)):

$$\begin{aligned} z^{\prime }= {\left\{ \begin{array}{ll} f_{\text { NC-S2}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,\big \vert w_{2}+2\xi v_{2}\big \vert \le 2,\\ f_{\text { NC-FD2}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )>0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \, h_{\text { FOR1}}(z,\mu )>0\right) ,\\ f_{\text { NC-BD2}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )<0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,h_{\text { BACK1}}(z,\mu )<0\right) . \end{array}\right. } \end{aligned}$$
(15)

Contact (\(w_{2}\ge \delta \)):

$$\begin{aligned} z^{\prime }= {\left\{ \begin{array}{ll} f_{\text { C-S}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,\big \vert w_{2}+2\xi v_{2}+\beta (w_{2}-\delta )\big \vert \le 2,\\ f_{\text { C-FD}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )>0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \, h_{\text { FOR2}}(z,\mu )>0\right) ,\\ f_{\text { C-BD}}(t,z,\mu ), &{} h_{\text { STOP}}(z,\mu )<0\, \text{ or }\,\left( h_{\text { STOP}}(z,\mu )=0\, \text{ and } \,h_{\text { BACK2}}(z,\mu )<0\right) . \end{array}\right. } \end{aligned}$$
(16)

A final step before starting the analysis of this piecewise-smooth model via COCO is to write the system in autonomous form. This is typically carried out by embedding the non-autonomous system into an autonomous one of higher dimension, which results from, e.g., introducing the time as an additional state variable. In the present work, we appended an autonomous nonlinear oscillator to the equations of motion (14)–(16), whose solution can be used to simulate the external sinusoidal excitation [35].

Fig. 2
figure 2

a Basins of attraction for the vibro-impact capsule system (14)–(16) calculated for \(\gamma =0.36\), \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\), \(v_{\mathrm{s}}=0.1\) and \(k_{\mathrm{p}}=0\) (no control). Orbits, Poincaré maps (red dots) and the time histories of displacements \(x_1\) (black solid line) and \(x_2\) (red dash line) for the coexisting, b period-1 with two impacts, c period-2 with four impacts, d period-4 with eight impacts, e period-1 with one impact solutions. The vertical blue line in the phase portraits represents the discontinuity boundary \(w_{2}=\delta \), at which impacts with the secondary spring occur. (Color figure online)

Full size image

4 Numerical results

In the following subsections, we will analyze the behavior of the capsule system based on two numerical approaches: direct numerical integration (Sect. 4.1) and continuation methods (Sect. 4.2). From a practical point of view, it is convenient first to introduce suitable solution measures that are related to physical quantities relevant in engineering applications. Consider a periodic solution \(z(t)=(w_{2}(t),v_{1}(t),v_{2}(t))\) of (14)–(16) with period \(T>0\). The motion of the capsule can be computed via the expression

$$\begin{aligned} x_{2}(t)=x^*_{2}+\int \limits _{0}^{t}(v_{1}(s)-v_{2}(s))\,\hbox {d}s, \end{aligned}$$

where \(x^*_{2}\in {{\mathrm{{\mathbbm {R}}}}}\) represents the position of the capsule at \(t=0\). By using this formula, we introduce the quantity

$$\begin{aligned} \text{ ROP }:=\frac{1}{T}(x_{2}(T)-x_{2}(0)), \end{aligned}$$
(17)

which gives the average rate of progression (drift) per period of the capsule. Its sign indicates whether the capsule moves forwards (\(\text{ ROP }>0\)) or backwards (\(\text{ ROP }<0\)), as indicated by the arrows in Fig. 1. The second physical measure that will be considered in our study is the average power used to drive the internal mass \(m_{1}\) per period, computed as

$$\begin{aligned} P_{\text { AVG}}:=\frac{1}{T}\int \limits _{0}^{T}\left( \alpha \cos \left( \omega s\right) +k_{\mathrm{p}}\big \vert w_{2}(s)\big \vert \right) v_{1}(s)\,\hbox {d}s. \end{aligned}$$
(18)

The solution measures (17) and (18) introduced above will allow us to gain more insight into the dynamics of the capsule from a practical perspective, as will be seen in the following sections.

Fig. 3
figure 3

Bifurcation diagrams for the capsule system (14)–(16) constructed for varying mass ratio, \(\gamma \), a without control (\(k_{\mathrm{p}}=0\)), b with control (\(k_{\mathrm{p}}=-0.2\)), calculated for \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\), and \(v_{\mathrm{s}}=0.1\)

Full size image
Fig. 4
figure 4

a Quasiperiodic (no control \(k_{\mathrm{p}}=0\), gray color) and period-1 (with control \(k_{\mathrm{p}}=-0.2\), red color) orbits, b time histories of capsule displacements, c control input u, computed for \(\gamma =0.35\), \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\) and \(v_{\mathrm{s}}=0.1\). The location of the impact boundary is shown by the vertical blue line. (Color figure online)

Full size image

4.1 Multistable behavior of the controlled capsule

The multistable scenario of the capsule model (14)–(16) for \(k_{\mathrm{p}}=0\) (without control) is shown in Fig. 2. As can be seen from panel (a), the capsule system without the position feedback control has four coexisting attractors: period-1 solution with two impacts per period and forward drifting; period-2 with four impacts and forward motion; period-4 with eight impacts and forward progression; and period-1 with one impact and backward motion. The (green and yellow) basins for the period-1 and the period-4 forward motions are relatively large compared to the rather fragmented (gray) basin for the period-2 solution with forward progression and the (orange) basin for the period-1 with backward motion. Therefore, for the considered dynamical scenario, the forward progression dominates the behavior of the system, due to which the capsule is rather unlikely to operate in backward drifting modes. A closer look into the capsule behavior is presented in Fig. 3a. Here, a bifurcation diagram of the uncontrolled system with respect to the mass ratio \(\gamma \) is presented. The results indicate that two solutions, one with forward (purple line) and one with backward (blue line) progression, exist in the parameter windows \(\gamma \in [0.32, 0.48]\) and \(\gamma \in [0.35,0.437]\), respectively. Furthermore, additional solutions are also present in the system, which pose difficulties for the directional control of the capsule. These undesired attractors are observed for \(\gamma \in [0.337,0.381]\) (black plot) and \(\gamma \in [0.329,0.468]\) (cyan plot).

Fig. 5
figure 5

a Bifurcation diagram, b average power consumption \(P_{\text { AVG}}\) for the capsule system (14)–(16), constructed by varying the control parameter \(k_{\mathrm{p}}\), calculated for \(\gamma =0.36\), \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\), and \(v_{\mathrm{s}}=0.1\). The location of the impact boundary is shown by the vertical blue line. (Color figure online)

Full size image

Next we will introduce the position feedback control to the capsule system and study the effect on the model response. The result is shown in Fig. 3b. The main difference is that the unwanted solutions described above disappeared, and only the desired forward and backward drifting solutions persist, meaning that the system switched from the multistable to a bistable dynamical scenario. Another effect is that the window of existence of the solution with backward drift (blue line) has increased to \(\gamma \in [0.32,0.456)\). In Fig. 4, we present a comparison between two system solutions with (red line) and without (gray line) control. Apart from the control gain, all parameters values are the same for both cases. As the picture shows, the controlled solution (periodic) presents a faster backward drift than the uncontrolled (quasiperiodic) one.

Let us now investigate the effect of the proportional control gain on the capsule behavior. To this end, we computed the bifurcation diagram depicted in Fig. 5a, with respect to \(k_{\mathrm{p}}\). The picture shows inner panels corresponding to various periodic orbits found during the computation. For the sake of clarity in the presentation of the results, we use a label P-i-j in the picture to denote a period-i solution with j impacts with the secondary spring \(k_{2}\) per orbital period, \(i,j\in {{\mathrm{{\mathbbm {N}}}}}\). From Fig. 5a, we observe that the capsule model presents multistability for a small parameter window \(k_{\mathrm{p}}\in [-0.023,0.042]\). After this interval, two period-1 orbits, one with forward and one with backward progression, coexist for \(k_{\mathrm{p}}\in (0.042,0.09]\). If \(k_{\mathrm{p}}\) is further increased, only one solution with forward motion remains, in the interval \(k_{\mathrm{p}}\in (0.09,0.13]\), where the system is monostable. For control gain in the parameter window \(k_{\mathrm{p}}\in [-0.51,-0.023)\), the capsule system is bistable, with one solution with forward and one with backward drift. If \(k_{\mathrm{p}}\) is further decreased, only one solution with backward motion remains in the interval \(k_{\mathrm{p}}\in [-0.53,\,-0.51)\).

Fig. 6
figure 6

Evolution of the basins of attraction of the capsule model (14)–(16), with positive feedback gain, a \(k_{\mathrm{p}}=0.02\), b \(k_{\mathrm{p}}=0.03\), c \(k_{\mathrm{p}}=0.06\), d \(k_{\mathrm{p}}=0.08\), calculated for \(\gamma =0.36\), \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\), and \(v_{\mathrm{s}}=0.1\)

Full size image
Fig. 7
figure 7

Evolution of the basins of attraction of the capsule model (14)–(16), with negative feedback gain, a \(k_{\mathrm{p}}=-0.02\), b \(k_{\mathrm{p}}=-0.2\), c \(k_{\mathrm{p}}=-0.4\), d \(k_{\mathrm{p}}=-0.5\), calculated for \(\gamma =0.36\), \(\beta =3\), \(\xi =0.05\), \(\delta =0.02\), \(\alpha =1.6\), \(\omega =1.1\), and \(v_{\mathrm{s}}=0.1\)

Full size image

Figure 6 presents the evolution of the basins of attraction of the capsule system as the control gain \(k_{\mathrm{p}}\) increases. As shown from this sequence of plots, the basin of the (unwanted, see above) black attractor is gradually shrinking as the control gain increases, and the yellow basin disappears completely at \(k_{\mathrm{p}}\approx 0.042\), where the green basin becomes dominant. Thereafter, the period-1 forward and backward attractors coexist, and the orange basin for the period-1 backward motion becomes smaller with increasing control gain, disappearing completely at \(k_{\mathrm{p}}\approx 0.09\). The evolution of the basins of attraction for the capsule system as the control gain \(k_{\mathrm{p}}\) decreases is shown in Fig. 7. It can be observed from the sequence of graphs that the orange basin of the period-1 backward attractor expands as the control gain decreases, and the yellow basin of the period-4 attractor shrinks and vanishes at \(k_{\mathrm{p}}\approx -0.023\), where the orange basin becomes dominant. After this, two stable solutions are present in the system, one of whose basin gradually shrinks and disappears at \(k_{\mathrm{p}}\approx -0.51\). It can be seen from the figures that the positive control gain is more effective to convert the multistable system to a monostable one, whereas the negative control gain is more effective to maintain bistability in the capsule system. At \(k_{\mathrm{p}}\approx -0.023\), as the yellow basin disappears, the area of the green basin is the maximum in the bistable scenario.

Fig. 8
figure 8

a One-parameter continuation of the period-1 response of the capsule system (14)–(16) with respect to the excitation frequency \(\omega \), computed for the parameter values \(\alpha =1.6\), \(\xi =0.05\), \(\delta =0.02\), \(\beta =3\), \(\gamma =0.36\), \(k_{\mathrm{p}}=-0.2\) and \(v_{\mathrm{s}}=0.1\). This panel shows the behavior of the rate of progression ROP as the frequency varies. The red and blue curves correspond to the continuation of the periodic orbits shown in panels (d, e), respectively, for which the progression has opposite directions, as shown in panels (b, c). Here, the figures depict the time history of the internal mass (solid line) and capsule (dashed line) motion. Panels (f–h) show enlargements of the bifurcation diagram in (a) around the fold bifurcations F1, F2 and F3, respectively. (Color figure online)

Full size image

Based on the numerical observations discussed above, two control strategies for controlling the forward and backward drift of the capsule system may be considered. One approach is via varying the proportional control gain. As observed before, the system is monostable for \(k_{\mathrm{p}}>0.09\) and \(k_{\mathrm{p}}<-0.51\), where the capsule presents forward and backward progression, respectively. On the other hand, all parameters can be set in such a way that the system is bistable, with one solution with forward and one with backward drift. This occurs for instance at \(k_{\mathrm{p}}=-0.2\) (see above). In this case, the direction of progression can be chosen by suitably perturbing the initial conditions of the system; see Fig. 7b, without altering the system parameters. In this dynamical scenario, the size of the corresponding basins is suitable for such a strategy, although one basin is clearly larger than the other.

Fig. 9
figure 9

a Two-parameter continuation of the fold points F1 (blue curve), F2 (green curve) and F3 (red curve) found in Fig. 8a, with respect to frequency \(\omega \) and mass ratio \(\gamma \). The gray area represents the parameter region in which stable period-1 orbits of the type shown in Fig. 8d, e coexist. b, d, f depict periodic orbits for which the ROP is positive, while in panels (c), (e) and (g) the capsule moves backwards. These solutions are computed for the test points P1 (\(\omega =0.98\), \(\gamma =0.44\)), P2 (\(\omega =1.06\), \(\gamma =0.41\)) and P3 (\(\omega =1.09\), \(\gamma =0.37\)). The inner panels show the internal mass (solid line) and capsule (dashed line) motion. (Color figure online)

Full size image

One criterion to choose the type of control strategy can be given in terms of power consumption, calculated via the solution measure defined in (18). In Fig. 5b, we calculated this quantity with varying control gain, as was carried out in Fig. 5a, showing the capsule motion in internal panels. Although the system presents higher ROPs in the monostable regimes \(A_2\) and \(B_2\), in the bistable mode represented by the labels \(A_1\) and \(B_1\), the power used to drive the internal mass is smaller, compared with the corresponding direction of drift in the monostable modes. Therefore, from an energy consumption point of view, the directional control via bistability is preferable. In the next section, we will consider this type of control and discuss its robustness via numerical continuation methods, for the case \(k_{\mathrm{p}}=-0.2\).

4.2 Path-following analysis of the controlled capsule

In order to identify the bistable regime where the period-1 forward and backward solutions coexist, we will first perform the numerical continuation of these two periodic orbits with respect to the excitation frequency \(\omega \), using the ROP as solution measure (see (17)). The result of the continuation is depicted in Fig. 8a, which shows red and blue curves corresponding to forward (positive ROP) and backward (negative ROP) progression, respectively. These red and blue curves are obtained by tracing the solutions shown in panels (d) and (e), with solution signatures \(\left\{ I_{23},I_{51},I_{43},I_{11},I_{72},I_{81}\right\} \) and \(\left\{ I_{14},I_{42},I_{52},I_{31},I_{92},I_{71}\right\} \), respectively. For the parameter window considered, only one fold bifurcation F2 (\(\omega \approx 1.0165\)) was found along the red curve, below which the solution disappears. On the other hand, two fold bifurcations F1 (\(\omega \approx 1.0292\)) and F3 (\(\omega \approx 1.1836\)) were detected during the continuation of the solution in panel (e), corresponding to backward drift. This allows identifying with high accuracy the interval of bistability, limited in this case by the fold points F1 and F3. In this window, the existence of the forward and backward drifting solutions is guaranteed, and therefore, the directional control of the capsule can be achieved by switching between these two attractors, as discussed in the previous section. In panels (f)–(h) of Fig. 8, enlargements of the bifurcation diagram depicted in panel (a) are presented, showing how the bifurcation curve folds at the critical points F1, F2 and F3.

In order to gain an insight into the robustness of the directional control of the capsule based on its bistability, we will perform a two-parameter continuation of the codimension-one bifurcations discussed above. Figure 9a shows the locus of the fold points F1, F2 and F3 detected before in the parameter plane \(\omega \)–\(\gamma \). The intersection of this diagram with the horizontal line \(\gamma =0.36\) (dashed) gives the bifurcation points found in Fig. 8a. The gray area shows the region of bistability where the solutions shown in Fig. 8d (forward progression) and Fig. 8e (backward progression) coexist. In addition, several test points have been chosen, at each of which the corresponding forward and backward drifting solutions are shown, with inner panels for the capsule motion. This numerical study reveals that the interval of bistability is robust under parameter perturbations, although the length of the \(\omega \)-interval of bistability changes significantly as the mass ratio \(\gamma \) varies. Another important aspect is that the left boundary of the interval of bistability switches between bifurcation curves. Specifically, below \(\gamma \approx 0.4094\) the left boundary is determined by the blue bifurcation (continuation of F1). Above this value, the left boundary is defined by the green curve (continuation of F2). This is due to the intersection of the bifurcation curves at \((\omega ,\gamma )\approx (0.9891,0.4094)\). All these aspects should be taken into account in order to ensure an effective directional control of the capsule system based on switching between attractors.

5 Conclusions

This paper studied forward and backward motion control of a vibro-impact capsule system based on its multistability, implemented via a position feedback controller. The capsule system was modeled in the framework of piecewise-smooth dynamical systems, where the discontinuity boundaries were physically associated with impact, friction and control input. Furthermore, the mathematical description of the friction considered the Stribeck effect, for which the system response presented a variety of complex dynamical scenarios, as analyzed in a previous study [30]. In particular, several coexisting solutions become dominant in the system dynamics, and this feature was exploited to perform directional control of the system.

Our investigation showed that the dynamical behavior of the capsule can be manipulated by a position feedback controller, where the main desired effect was the switching between multistable, bistable and monostable system responses. In this way, two control strategies were identified. The first one consists in varying the proportional control gain, thus obtaining forward progression for \(k_{\mathrm{p}}>0.09\) and backward progression for \(k_{\mathrm{p}}<-0.51\), in which cases only one stable solution is present. The second control method takes advantage of the bistable system response encountered at \(k_{\mathrm{p}}=-0.2\). In this case, the system has precisely one solution with forward drift and one with backward drift, between which a switching can be achieved by suitably perturbing the initial conditions of the system. The latter proposed method was found to be more efficient from an energy consumption point of view, which is a relevant factor for many engineering applications.

In order to gain an insight into the robustness of the directional control of the capsule based on its bistability, numerical continuation methods were applied. Specifically, the forward and backward drifting solutions in the bistable regime were traced with respect to the excitation frequency \(\omega \). During the continuation, three fold bifurcation points were detected, which can be used to define the window of bistability of the system. A region in the parameter space \(\omega \)–\(\gamma \) was identified, on which the existence of the forward and backward drifting solutions can be guaranteed. For this purpose, a two-parameter continuation of the three fold bifurcations was carried out, which determined the bistability region. The results indicated that the \(\omega \)-interval of bistability persists under parameter perturbations showing robustness of the proposed control method. However, the size of the interval can change significantly, which should be taken into account so as to ensure the effectiveness of directional control of the capsule system based on its bistability.