Comparison of the dynamic performance of nonlinear one and two degree-of-freedom vibration isolators with quasi-zero stiffness

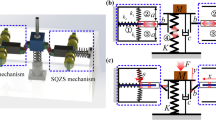
Abstract

Nonlinear stiffness isolation mounts, which offer a high static stiffness alongside a low dynamic stiffness or even quasi-zero stiffness (QZS) over a displacement range, have been proposed. These vibration isolators offer a higher isolation frequency band of low transmissibility than conventional linear devices. Here, three kinds of nonlinear two degree-of-freedom (DOF) vibration isolators with QZS characteristic are analyzed in order to further improve the isolation performance. The dynamic response is obtained using the harmonic balance method, and the peak dynamic displacement is obtained using backbone curve analysis and energy balancing method. The optimum isolation performance of the nonlinear 2DOF vibration isolators is evaluated for four performance indexes and compared with three baseline vibration isolators. These are a linear and a QZS 1DOF vibration isolator as well as a linear 2DOF vibration isolator. To ensure a fair comparison, the static displacement of each vibration isolator is kept constant. The comparison demonstrates that a nonlinear 2DOF vibration isolator can be tuned to achieve a better isolation performance in the higher isolation frequency band than the baseline vibration isolators, while retaining a moderate peak dynamic displacement and peak transmissibility. In addition, the best vibration isolator is identified for each of the four performance indexes.

Appendix

1.1 The GG Model

The dynamic equation of the GG Model under force excitation at the static equilibrium position is given by

$$\begin{aligned}&m_1 \ddot{x}+c_1 \left( {\dot{x}-\dot{x}_\mathrm{a} } \right) \nonumber \\&\quad \quad +\left( {k_\mathrm{v1} +2k_\mathrm{h1} \left( {1-\frac{l_0 }{\sqrt{l^{2}+x^{2}}}} \right) } \right) x-k_\mathrm{v1} x_\mathrm{a} \nonumber \\&\quad =f_\mathrm{e} \cos \left( {\omega t} \right) , \end{aligned}$$

(31a)

$$\begin{aligned}&m_\mathrm{a} \ddot{x}_\mathrm{a} -c_1 \dot{x}+\left( {c_1 +c_2 } \right) \dot{x}_\mathrm{a} -k_\mathrm{v1} x+k_\mathrm{v1} x_a \nonumber \\&\quad +\left( {k_\mathrm{v2} +2k_\mathrm{h2} \left( {1-\frac{l_0 }{\sqrt{l^{2}+x_\mathrm{a}^2 }}} \right) } \right) x_\mathrm{a} =0. \end{aligned}$$

(31b)

Using a Taylor series expansion, Eq. (31) can be approximated as

$$\begin{aligned}&m_1 \ddot{x}+c_1 \left( {\dot{x}-\dot{x}_\mathrm{a} } \right) +k_v \alpha _1 x+\frac{k_v \gamma _1 }{x_s^2 }x^{3}\nonumber \\&\quad -k_v vx_\mathrm{a} =f_\mathrm{e} \cos \left( {\omega t} \right) , \end{aligned}$$

(32a)

$$\begin{aligned}&m_\mathrm{a} \ddot{x}_\mathrm{a} -c_1 \dot{x}+\left( {c_1 +c_2 } \right) \dot{x}_\mathrm{a} -k_v vx \nonumber \\&\quad +k_v \left( {v+\alpha _2 } \right) x_a +\frac{k_v \gamma _2 }{x_\mathrm{s}^2 }x_\mathrm{a}^3 =0. \end{aligned}$$

(32b)

Following the same non-dimensional procedure described in Sect. 4, Eq. (32) can be written as

$$\begin{aligned} \begin{array}{l} \left[ {{\begin{array}{ll} 1&{} 0 \\ 0&{} \sigma \\ \end{array} }} \right] \left( {{\begin{array}{l} {{X}^{{\prime }{\prime }}} \\ {{X}^{{\prime }{\prime }}_\mathrm{a}} \\ \end{array} }} \right) +\left[ {{\begin{array}{ll} {2\zeta _1 }&{} {-2\zeta _1 } \\ {-2\zeta _1 }&{} {2\zeta _1 +2\sigma \zeta _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} {{X}^{\prime }} \\ {{X}^{\prime }_\mathrm{a} } \\ \end{array} }} \right) \\ \quad +\left[ {{\begin{array}{ll} {\alpha _1 }&{} {-v} \\ {-v}&{} {v+\alpha _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} X \\ {X_\mathrm{a} } \\ \end{array} }} \right) \\ \quad +\left[ {{\begin{array}{ll} {\gamma _1 }&{} 0 \\ 0&{} {\gamma _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} {X^{3}} \\ {X_\mathrm{a}^3 } \\ \end{array} }} \right) =\left( {{\begin{array}{l} {F_\mathrm{e} \cos \left( {\Omega T} \right) } \\ 0 \\ \end{array} }} \right) \\ \end{array}. \end{aligned}$$

(33)

The resulting amplitude–frequency relationships of the GG Model can be obtained

$$\begin{aligned} \left( {\mathbf{K}_1 -\Omega ^{2}{} \mathbf{M}} \right) \mathbf{X}{\varvec{\Phi }} -\Omega \left( {\mathbf{CX}{\varvec{\Phi }}} \right) \mathbf{A}+\frac{3}{4}{} \mathbf{K}_\mathbf{3} \mathbf{X}^{\left( 3 \right) }{\varvec{\Phi }} ={} \mathbf{F}_\mathbf{e} ,\nonumber \\ \end{aligned}$$

(34)

where $\mathbf{K}_\mathbf{1} =\left[ {{\begin{array}{ll} {\alpha _1 }&{} {-v} \\ {-v}&{} {v+\alpha _2 } \\ \end{array} }} \right]$, $\mathbf{K}_\mathbf{3} =\left[ {{\begin{array}{ll} {\gamma _1 }&{} 0 \\ 0&{} {\gamma _2 } \\ \end{array} }} \right]$, $\mathbf{X}^{\left( \mathbf{3} \right) }=\left[ {{\begin{array}{ll} {X_\mathrm{m}^3 }&{} 0 \\ 0&{} {X_\mathrm{am}^3 } \\ \end{array} }} \right]$, and the other parameters in Eq. (34) are the same with the parameters shown in Sect. 4.

The transmitted force of the GG Model is given as

$$\begin{aligned} F_t= & {} 2\sigma \zeta _2 {X}'_\mathrm{a} +\left( {\alpha _1 -v} \right) X+\gamma _1 X^{3}+\alpha _2 X_\mathrm{a} +\gamma _2 X_\mathrm{a}^3 \nonumber \\= & {} \mathbf{C}_t \left( {\begin{array}{l} {X}^{\prime } \\ {X}^{\prime }_\mathrm{a} \\ \end{array}} \right) +\mathbf{K}_{\mathbf{t1}} \left( {\begin{array}{l} X \\ X_\mathrm{a} \\ \end{array}} \right) +\mathbf{K}_{\mathbf{t3}} \left( {\begin{array}{l} X^{3} \\ X_\mathrm{a}^3 \\ \end{array}} \right) \end{aligned}$$

(35)

where $\mathbf{C}_\mathbf{t} =\left[ {{\begin{array}{ll} 0&{} {2\sigma \zeta _2 } \\ \end{array} }} \right]$, $\mathbf{K}_{\mathbf{t1}} =\left[ {{\begin{array}{ll} {\alpha _1 -v}&{} {\alpha _2 } \\ \end{array} }} \right]$ and $\mathbf{K}_{\mathbf{t3}} =\left[ {{\begin{array}{ll} {\gamma _1 }&{} {\gamma _2 } \\ \end{array} }} \right]$.

Using Eqs. (34) and (35), the amplitude of the force is written as

$$\begin{aligned} F_{t1} {\varvec{\Phi }}_\mathbf{t} =\mathbf{K}_{t1} \mathbf{X}{\varvec{\Phi }} +\frac{3}{4}{} \mathbf{K}_{t3} \mathbf{X}^{\left( 3 \right) }{\varvec{\Phi }} -\Omega \left( {\mathbf{C}_\mathbf{t} \mathbf{X}{\varvec{\Phi }} } \right) \mathbf{A}, \end{aligned}$$

(36)

where ${\varvec{\Phi }}_\mathbf{t} =\left[ {{\begin{array}{ll} {\cos \Phi _t }&{} {\sin \Phi _t } \\ \end{array} }} \right]$. The force transmissibility of the GG Model can be obtained

$$\begin{aligned} G_\mathrm{FN1} =\frac{F_{t1} }{F_\mathrm{e} }. \end{aligned}$$

(37)

Finally, using the backbone curve analysis and energy balancing method described in Sect. 4, the peak dynamic displacement of the GG Model can be determined from the following sets of equations

$$\begin{aligned} \left\{ {\begin{array}{l} \frac{3}{4}\gamma _1 X_\mathrm{m}^3 +\left( {\alpha _1 -\Omega ^{2}} \right) X_\mathrm{m} \mp vX_\mathrm{am} =0 \\ \frac{3}{4}\gamma _2 X_\mathrm{am}^3 +\left( {v+\alpha _2 -\sigma \Omega ^{2}} \right) X_\mathrm{am} \mp vX_\mathrm{m} =0 \\ \zeta _1 \Omega ^{2}X_\mathrm{m}^2 +\left( {\zeta _1 +\sigma \zeta _2 } \right) \\ \Omega ^{2}X_\mathrm{am}^2 \mp 2\zeta _1 \Omega ^{2}X_\mathrm{m} X_\mathrm{am} =\frac{\Omega X_\mathrm{m} F_\mathrm{e} }{2} \\ \end{array}} \right. . \end{aligned}$$

(38)

1.2 The TG Model

The dynamic equation of the TG Model under force excitation at the static equilibrium position is given by

$$\begin{aligned}&m\ddot{x}+c_1 \left( {\dot{x}-\dot{x}_\mathrm{a} } \right) \nonumber \\&\quad \quad +\left( {k_\mathrm{v1} +2k_\mathrm{h1} \left( {1-\frac{l_0 }{\sqrt{l^{2}+x^{2}}}} \right) } \right) x-k_\mathrm{v1} x_\mathrm{a} \nonumber \\&\quad \quad +2k_\mathrm{h2} \left( {1-\frac{l_0 }{\sqrt{l^{2}+\left( {x-x_\mathrm{a} } \right) ^{2}}}} \right) \left( {x-x_\mathrm{a} } \right) \nonumber \\&\quad =f_\mathrm{e} \cos \left( {\omega t} \right) \end{aligned}$$

(39a)

$$\begin{aligned}&m_\mathrm{a} \ddot{x}_\mathrm{a} -c_1 \dot{x}+\left( {c_1 +c_2 } \right) \dot{x}_\mathrm{a} +k_\mathrm{v1} \left( {x_\mathrm{a} -x} \right) +k_\mathrm{v2} x_\mathrm{a} \nonumber \\&\quad +2k_\mathrm{h2} \left( {1-\frac{l_0 }{\sqrt{l^{2}+\left( {x_\mathrm{a} -x} \right) ^{2}}}} \right) \left( {x_\mathrm{a} -x} \right) =0 ,\nonumber \\ \end{aligned}$$

(39b)

Using a Taylor series expansion, Eq. (39) can be approximated as

$$\begin{aligned}&m_1 \ddot{x}+c_1 \left( {\dot{x}-\dot{x}_\mathrm{a} } \right) +k_\mathrm{v} \left( {\alpha _1 +\alpha _2 -\beta } \right) \nonumber \\&\quad x-k_\mathrm{v }\left( {v+\alpha _2 -\beta } \right) x_\mathrm{a} \nonumber \\&\quad +\frac{k_\mathrm{v} \gamma _1 }{x_\mathrm{s}^2 }x^{3}+\frac{k_\mathrm{v} \gamma _2 }{x_\mathrm{s}^2 }\left( {x-x_\mathrm{a} } \right) ^{3}=f_\mathrm{e} \cos \left( {\omega t} \right) \end{aligned}$$

(40a)

$$\begin{aligned}&m_\mathrm{a} \ddot{x}_\mathrm{a} -c_1 \dot{x}+\left( {c_1 +c_2 } \right) \dot{x}_\mathrm{a} -k_\mathrm{v} \left( {v+\alpha _2 -\beta } \right) x \nonumber \\&\quad +k_\mathrm{v} \left( {v+\alpha _2 } \right) x_\mathrm{a }+\frac{k_\mathrm{v} \gamma _2 }{x_\mathrm{s}^2 }\left( {x_\mathrm{a} -x} \right) ^{3}=0 , \end{aligned}$$

(40b)

Following the same non-dimensional procedure described in Sect. 4, Eq. (40) can be written as

$$\begin{aligned}&\left[ {{\begin{array}{ll} 1&{} 0 \\ 0&{} \sigma \\ \end{array} }} \right] \left( {{\begin{array}{l} {{X}^{{\prime }{\prime }}} \\ {{X}^{{\prime }{\prime }}_\mathrm{a} } \\ \end{array} }} \right) +\left[ {{\begin{array}{ll} {2\zeta _1 }&{} {-2\zeta _1 } \\ {-2\zeta _1 }&{} {2\zeta _1 +2\sigma \zeta _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} {{X}^{\prime }} \\ {{X}^{\prime }_\mathrm{a} } \\ \end{array} }} \right) \nonumber \\&\quad +\left[ {{\begin{array}{ll} {\alpha _1 +\alpha _2 -\beta }&{} {-\left( {v+\alpha _2 -\beta } \right) } \\ {-\left( {v+\alpha _2 -\beta } \right) }&{} {v+\alpha _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} X \\ {X_\mathrm{a} } \\ \end{array} }} \right) \nonumber \\&\quad +\left[ {{\begin{array}{ll} {\gamma _1 }&{} {\gamma _2 } \\ 0&{} {-\gamma _2 } \\ \end{array} }} \right] \left( {{\begin{array}{l} {X^{3}} \\ {\left( {X-X_\mathrm{a} } \right) ^{3}} \\ \end{array} }} \right) =\left( {{\begin{array}{l} {F_\mathrm{e} \cos \left( {\Omega T} \right) } \\ 0 \\ \end{array} }} \right) .\nonumber \\ \end{aligned}$$

(41)

The resulting amplitude–frequency relationships of the TG Model can be obtained

$$\begin{aligned}&\left( {\mathbf{K}_1 -\Omega ^{2}{} \mathbf{M}} \right) \mathbf{X}{\varvec{\Phi }} -\Omega \left( {\mathbf{CX}{\varvec{\Phi }} } \right) \mathbf{A}+\frac{3}{4}{} \mathbf{K}_3 \mathbf{X}^{\left( {3-1} \right) }{\varvec{\Phi }}\nonumber \\&\quad +\frac{3}{4}{} \mathbf{K}_3 \mathbf{X}^{\left( {3-2} \right) }{\varvec{\Phi }} \mathbf{A}=\mathbf{F}_\mathbf{e} , \end{aligned}$$

(42)

where $K_1 =\left[ {{\begin{array}{ll} {\alpha _1 +\alpha _2 -\beta }&{} {-\left( {v+\alpha _2 -\beta } \right) } \\ {-\left( {v+\alpha _2 -\beta } \right) }&{} {v+\alpha _2 } \\ \end{array} }} \right]$, $K_3 =\left[ {{\begin{array}{ll } {\gamma _1 }&{} {\gamma _2 } \\ 0&{} {-\gamma _2 } \\ \end{array} }} \right]$,

$$\begin{aligned}&X^{\left( {3-1} \right) }\\&\quad =\left[ {{\begin{array}{ll} {X_\mathrm{m}^3 }&{} 0 \\ X_\mathrm{m}^3 +2X_\mathrm{m} X_\mathrm{am}^2 -X_\mathrm{m}^2\\ \quad X_\mathrm{am} \cos \left( {\Phi _1 -\Phi _2 } \right) &{} -X_\mathrm{am}^3 -2X_\mathrm{m}^2 X_\mathrm{am} +X_\mathrm{m} \\ {} &{} \quad X_\mathrm{am}^2 \cos \left( {\Phi _1 -\Phi _2 } \right) \end{array} }} \right] , \\&X^{\left( {3-2} \right) }{=}\left[ {{\begin{array}{ll} 0&{} 0 \\ {X_\mathrm{m}^2 X_\mathrm{am} \sin \left( {\Phi _1 {-}\Phi _2 } \right) }&{} {X_\mathrm{m} X_\mathrm{am}^2 \sin \left( {\Phi _1 {-}\Phi _2 } \right) } \\ \end{array} }} \right] , \end{aligned}$$

parameters defined in Sect. 4.

The transmitted force of the TG Model is given as

$$\begin{aligned} F_t= & {} 2\sigma \zeta _2 {X}'_\mathrm{a} +\left( {\alpha _1 -v} \right) X+\gamma _1 X^{3}+\beta X_\mathrm{a} \nonumber \\= & {} C_t \left( {\begin{array}{l} {X}^{\prime } \\ {X}^{\prime }_\mathrm{a} \\ \end{array}} \right) +K_{t1} \left( {\begin{array}{l} X \\ X_\mathrm{a} \\ \end{array}} \right) +K_{t3} \left( {\begin{array}{l} X^{3} \\ X_\mathrm{a}^3 \\ \end{array}} \right) \end{aligned}$$

(43)

where $C_t =\left[ {{\begin{array}{ll} 0&{} {2\sigma \zeta _2 } \\ \end{array} }} \right]$, $K_{t1} =\left[ {{\begin{array}{ll} {\alpha _1 -v}&{} \beta \\ \end{array} }} \right]$ and $K_{t3} =\left[ {{\begin{array}{ll} {\gamma _1 }&{} 0 \\ \end{array} }} \right]$.

Using Eqs. (42) and (43), the amplitude of the force is written as

$$\begin{aligned} F_{t3} {\varvec{\Phi }}_\mathbf{t} =\mathbf{K}_{\mathbf{t1}} \mathbf{X}{\varvec{\Phi }} +\frac{3}{4}{} \mathbf{K}_{\mathbf{t3}} \mathbf{X}^{\left( \mathbf{3} \right) }{\varvec{\Phi }} -\Omega \left( {\mathbf{C}_\mathbf{t} \mathbf{X}{\varvec{\Phi }} } \right) \mathbf{A}. \end{aligned}$$

(44)

The force transmissibility of the TG Model can be obtained

$$\begin{aligned} G_\mathrm{NF3} =\frac{F_{t3} }{F_\mathrm{e} }. \end{aligned}$$

(45)

Finally, using the backbone curve analysis and energy balancing method described in Sect. 4, the peak dynamic displacement of the TG Model can be determined from the following sets of equations

$$\begin{aligned} \left\{ {\begin{array}{l} \pm \left( {\frac{3}{4}\gamma _1 +\frac{3}{4}\gamma _2 } \right) X_\mathrm{m}^3 -\frac{9}{4}\gamma _2 X_\mathrm{am} X_\mathrm{m}^2 \\ \quad \pm \left( {\alpha _1 +\alpha _2 -\beta -\Omega ^{2}+\frac{9}{4}\gamma _2 X_\mathrm{am}^2 } \right) X_\mathrm{m} \\ -\left( {v+\alpha _2 -\beta } \right) X_\mathrm{am} -\frac{3}{4}\gamma _2 X_\mathrm{am}^3 =0 \\ \frac{3}{4}\gamma _2 X_\mathrm{am}^3 \mp \frac{9}{4}\gamma _2 X_\mathrm{m} X_\mathrm{am}^2\\ +\left( {v+\alpha _2 -\sigma \Omega ^{2}+\frac{9}{4}\gamma _2 X_\mathrm{m}^2 } \right) X_\mathrm{am} \\ \quad \mp \left( {\left( {v+\alpha _2 -\beta } \right) X_\mathrm{m} +\frac{3}{4}\gamma _2 X_\mathrm{m}^3 } \right) =0 \\ \zeta _1 \Omega ^{2}X_\mathrm{m}^2 +\left( {\zeta _1 +\sigma \zeta _2 } \right) \Omega ^{2}X_\mathrm{am}^2 \mp 2\zeta _1 \Omega ^{2}X_\mathrm{m} X_\mathrm{am}\\ \quad =\frac{\Omega X_\mathrm{m} F_\mathrm{e} }{2} \\ \end{array}} \right. . \end{aligned}$$

(46)