Dynamics of fault motion in a stochastic spring-slider model with varying neighboring interactions and time-delayed coupling

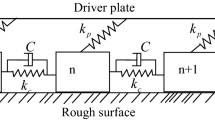
Abstract

We examine dynamics of a fault motion by analyzing behavior of a spring-slider model composed of 100 blocks where each block is coupled to a varying number of 2K neighboring units (1 $\le$ 2K $\le$ N, $N=100$). Dynamics of such model is studied under the effect of delayed interaction, variable coupling strength and random seismic noise. The qualitative analysis of stability and bifurcations is carried out by deriving an approximate deterministic mean-field model, which is demonstrated to accurately capture the dynamics of the original stochastic system. The primary effect concerns the direct supercritical Andronov–Hopf bifurcation, which underlies transition from equilibrium state to periodic oscillations under the variation of coupling delay. Nevertheless, the impact of delayed interactions is shown to depend on the coupling strength and the friction force. In particular, for loosely coupled blocks and low values of friction, observed system does not exhibit any bifurcation, regardless of the assumed noise amplitude in the expected range of values. It is also suggested that a group of blocks with the largest displacements, which exhibit nearly regular periodic oscillations analogous to coseismic motion for system parameters just above the bifurcation curve, can be treated as a representative of an earthquake hypocenter. In this case, the distribution of event magnitudes, defined as a natural logarithm of a sum of squared displacements, is found to correspond well to periodic (characteristic) earthquake model.

Appendix: Model of local block dynamics

Present research on earthquake fault motion is based on the analysis of a non-dimensional mono-block model, introduced in [6]:

$$\begin{aligned} \ddot{U}\left( t \right) =-U\left( t \right) +\Phi \left( {\dot{U}\left( t \right) } \right) +\nu _0 t, \end{aligned}$$

(7)

where variable U represents the block displacement, $\dot{U}$ is the velocity of the block (defined in the standing reference frame), $\ddot{U}$ is the block acceleration, $\nu _{0}$ is the dimensionless pulling speed and t is time variable. Friction force $\varPhi$ is assumed to be rate dependent. The unstable equilibrium around which the orbit of a block moves in phase space is given by:

$$\begin{aligned} U_e (t)=\nu _0 t+\Phi \left( \nu \right) , \end{aligned}$$

(8)

which is determined by setting $\ddot{U}=0$ and $\dot{U}=\nu _0$ in (7).

By introducing $U_{\textit{1}}$ and $U_{\textit{2}}$ to denote the displacement and the velocity of a single block, (7) may be rewritten as

$$\begin{aligned} \dot{U}_1(t)= & {} U_2 (t) \nonumber \\ \dot{U}_2 (t)= & {} -U_1 (t)+\Phi \left( {U_2 \left( t \right) } \right) +\nu _0 t . \end{aligned}$$

(9)

Having applied the coordinate transformation:

$$\begin{aligned} U_{1new} \left( t \right) =U_1 -U_e \left( t \right) =U_1 \left( t \right) -\left( {\nu _0 t+\Phi \left( \nu \right) } \right) , \end{aligned}$$

$$\begin{aligned} U_\mathrm{2new} \left( t \right) =U_2 \left( t \right) -\nu _0 , \end{aligned}$$

(10)

and switching back to old notation, one arrives at the following system of equations for the dynamics of a single block:

$$\begin{aligned} \dot{U}_1 (t)= & {} U_2 (t) \nonumber \\ \dot{U}_2 (t)= & {} -U_1 (t)+\Phi \left( {U_2 \left( t \right) +\nu _0 } \right) -\Phi \left( {\nu _0 } \right) . \end{aligned}$$

(11)

Beginning from (11), one can derive the spring-slider model for N interconnected blocks given by the system (1) in the main text, cf. Sect. Model derivation.

1.1 Derivation of the mean-field approximated model

The mean-field model characterizes the system’s behavior in terms of the means:

$$\begin{aligned} m_u =\left\langle {u_i } \right\rangle =\frac{1}{N}\sum _i {u_i } , \quad m_v =\left\langle {v_i } \right\rangle =\sum _i {v_i } , \end{aligned}$$

(12)

the associated variances:

$$\begin{aligned} s_u= & {} \left\langle {\delta u_i^2 } \right\rangle =\left\langle {\left( {u_i -m_u } \right) ^{2}} \right\rangle =\left\langle {u_i^2 } \right\rangle -m_u ^{2}\nonumber \\ s_v= & {} \left\langle {\delta v_i^2 } \right\rangle =\left\langle {\left( {v_i -m_v } \right) ^{2}} \right\rangle =\left\langle {v_i^2 } \right\rangle -m_v ^{2} \end{aligned}$$

(13)

and the covariance

$$\begin{aligned} U= & {} \left\langle {\delta u_i \delta v_i } \right\rangle =\left\langle {\left( {u_i -m_u } \right) \left( {v_i -m_v } \right) } \right\rangle \nonumber \\= & {} \left\langle {u_i v_i } \right\rangle -m_u m_v . \end{aligned}$$

(14)

Equations for the evolution of the means may be derived as follows:

$$\begin{aligned} \dot{m_{u}}= & {} \frac{1}{N}\sum _i {\dot{u_i }} =\frac{1}{N}\sum _i {v_i } =m_v \nonumber \\ \dot{m_{v}}= & {} \frac{1}{N}\sum _i {\dot{v_i } }\nonumber \\= & {} \frac{1}{N}\sum _i \left\{ -u_i -\Phi \left( {\nu _0 } \right) +\Phi \left( {v_i +v_0 } \right) \right. \nonumber \\&\left. +\, \frac{C}{N}{\sum \limits _{j\in J}}{\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } +\sqrt{2D}\xi _i \left( t \right) \right\} \nonumber \\= & {} -m_u -\Phi \left( {v_0 } \right) +\frac{1}{N}\sum _i {\Phi \left( {v_i +v_0 } \right) } \nonumber \\&+\, \frac{1}{N}\sum _i {\frac{C}{N}\sum \limits _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } } . \end{aligned}$$

(15)

The third term in equation (15) may be evaluated as follows. In the limit of large N, one may replace the summation by an appropriate integral $\frac{1}{N}\sum _i \Phi \left( {v_i +v_0 } \right) \rightarrow \int {P\left( v \right) \Phi \left( {v+v_0 } \right) \hbox {d}v}$, where P(v) is the probability density function. Now if all v variables are appropriately Gaussian distributed around $m_{v}(t)$, then $\Phi \left( v+ v_{0} \right)$ may be written as $\Phi \left( {v+v_0 } \right) \approx \Phi \left( {m_v {+}v_0 } \right) +\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v+\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \left( {\delta v} \right) ^{2}$. In the latter expression, $\delta v$ denotes the deviation $\delta v= v - m_{v}$. The integral may then be estimated as:

$$\begin{aligned}&\int {P\left( {v} \right) \Phi \left( {v+v_0 } \right) } \hbox {d}v\nonumber \\&\quad =\Phi \left( {m_v +v_0 } \right) \int P\left( v \right) \hbox {d}v+\Phi ^{\prime }\left( {m_v +v_0 } \right) \nonumber \\&\qquad \int {P\left( v \right) \delta v\hbox {d}v} +\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \int {P(v)\delta v^{2}\hbox {d}v} \nonumber \\&\quad =\Phi \left( {m_v +v_0 } \right) +\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v \end{aligned}$$

(16)

since, by definition $\int {P\left( v \right) \hbox {d}v\equiv 1}$, $\int P\left( v \right) \left( {v-\left\langle v \right\rangle } \right) \hbox {d}v=\left\langle v \right\rangle -\left\langle v \right\rangle$ $\int {P\left( v \right) \hbox {d}v=0}$ and $\int P\left( v \right) \left( {v-\left\langle v \right\rangle } \right) ^{2}\hbox {d}v \equiv S_v$.

The fourth term in (15) can be handled as follows:

$$\begin{aligned}&\frac{1}{N}\sum _i {\frac{C}{N}\sum _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i (t)} \right) } } \nonumber \\&\quad =\left\langle {\frac{C}{N}\sum _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i (t)} \right) } } \right\rangle \nonumber \\&\quad =\frac{2KC}{N}\left( {\left\langle {u_i \left( {t-\tau } \right) } \right\rangle -\left\langle {u_i \left( t \right) } \right\rangle } \right) = \nonumber \\&\quad =\frac{2KC}{N}\left( {m_u \left( {t-\tau } \right) -m_u \left( t \right) } \right) . \end{aligned}$$

(17)

Proceeding from (15), one then obtains:

$$\begin{aligned} \dot{m_{v}}= & {} -m_u -\Phi \left( {v_0 } \right) +\Phi \left( {m_v +v_0 } \right) \nonumber \\&+\, \frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v \nonumber \\&+\, \frac{2KC}{N}\left( {m_u \left( {t-\tau } \right) -m_u \left( t \right) } \right) . \end{aligned}$$

(18)

Let us now determine the equations for the dynamics of the variances. From the definition of $\hbox {S}_{\mathrm{u}}$, it follows that

$$\begin{aligned} \dot{S_{u}}= & {} \left\langle {2u_i \dot{u_{i}}} \right\rangle -2m_u \dot{m_{u}} =\left\langle {2u_i v_i } \right\rangle -2m_u m_v\nonumber \\= & {} 2\left( {U+m_u m_v } \right) -2m_u m_v =2U \end{aligned}$$

(19)

For $\hbox {S}_{\mathrm{v}}$, one finds:

$$\begin{aligned} \dot{S_{v}}= & {} \left\langle {2v_i \dot{v_{i}}+2D} \right\rangle -2m_v \dot{m_{v}}=\left\langle 2v_i \left( -u_i \right. \right. \nonumber \\&-\, \Phi \left( {v_0 } \right) +\Phi \left( {v_i +v_0 } \right) \nonumber \\&\left. \left. +\, \frac{C}{N}\sum _{j\in J}{\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } \right) \right\rangle \nonumber \\&-\, 2m_v \left( -m_u -\Phi \left( {v_0 } \right) +\Phi \left( {m_v +v_0 } \right) \right. \nonumber \\&\left. +\, \frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v +\frac{2KC}{N}\left( m_u \left( {t-\tau } \right) \right. \right. \nonumber \\&\left. \left. -\, m_u \left( t \right) \right) \right) +2D=-2\left( {U+m_u m_v } \right) \nonumber \\&-\, 2m_v \Phi \left( {v_0 } \right) +2\left\langle {v_i \Phi \left( {v_i +v_0 } \right) } \right\rangle \nonumber \\&+\, \frac{2C}{N}\left\langle {v_i \sum _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } } \right\rangle \nonumber \\&+\, 2m_u m_v +2m_v \Phi \left( {v_0 } \right) -2m_v \Phi \left( {m_v +v_0 } \right) \nonumber \\&-\, m_v \Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v -2m_v \frac{2KC}{N}\left( m_u \left( {t-\tau } \right) \right. \nonumber \\&\left. -\,m_u \left( t \right) \right) +2D, \end{aligned}$$

(20)

where the term $\left\langle {2v_i \dot{v_{i}}+2D} \right\rangle$ presents the Itō derivative for the complex function $v_i^2$ of the stochastic variable $\nu _{i}$.

The third term in (20) can be estimated in a fashion similar to the second term in (15). In particular, one may write:

$$\begin{aligned}&2\left\langle {v_i \Phi \left( {v_i +v_0 } \right) } \right\rangle =2\left\langle \left( {m_v +\delta v_i } \right) \left( \Phi \left( {m_v +v_0 } \right) \right. \right. \nonumber \\&\quad \left. \left. +\,\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i +\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \delta v_i^2 \right) \right\rangle \nonumber \\&=2\left\langle m_v \Phi \left( {m_v +v_0 } \right) +m_v \Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i \right. \nonumber \\&\quad +\frac{1}{2}m_v \Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \delta v_i^2 \nonumber \\&\quad \left. +\,\Phi \left( {m_v +v_0 } \right) \delta v_{i}+\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i^2 \right\rangle \nonumber \\&=2\left( m_v \Phi \left( {m_v +v_0 } \right) +\frac{1}{2}m_v \Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v \right. \nonumber \\&\quad \left. +\,\Phi ^{\prime }\left( {m_v +v_0 } \right) S_v \right) . \end{aligned}$$

(21)

Given that the deviations from the mean are expected to be small, we keep only the terms up to second order in deviations. Also, $\int {m_v \Phi ^{\prime }\left( {m_v } \right) \left( {v-\left\langle v \right\rangle } \right) P\left( v \right) \hbox {d}v} =m_v \Phi ^{\prime }\left( {m_v } \right) \left( {\left\langle v \right\rangle -\left\langle v \right\rangle } \right) =0.$

The fourth term in (20) can be calculated by implementing the quasi-independence approximation:

$$\begin{aligned}&\frac{2C}{N}\left\langle {v_i \sum _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } } \right\rangle \nonumber \\&\quad =\frac{2C}{N}\left\langle {\sum _{j\in J} {\left( {v_i u_{i+j} \left( {t-\tau } \right) -v_i u_i } \right) } } \right\rangle \nonumber \\&\quad =\frac{2C}{N}\sum _{j\in J} {\left\langle {v_i u{ }_{i+j}\left( {t-\tau } \right) } \right\rangle } -\frac{4KC}{N}\left\langle {u_i v_i } \right\rangle \nonumber \\&\quad =\frac{2C}{N}\sum _{j\in J} {\left\langle {v_i } \right\rangle \left\langle {u_{i+j} \left( {t-\tau } \right) } \right\rangle }\nonumber \\&\qquad -\frac{4KC}{N}\left( {U+m_u m_v } \right) \nonumber \\&\quad =\frac{4KC}{N}m_v m_u \left( {t-\tau } \right) -\frac{4KC}{N}\left( {U+m_u m_v } \right) . \end{aligned}$$

(22)

From the strict mathematical viewpoint, one should note that $\left\langle {\hbox {v}_{\mathrm{i}} \hbox {(t) u}_{\mathrm{i}} \hbox {+j}\left( {\hbox {t}- \tau } \right) } \right\rangle = \left\langle {\hbox {v}_{\mathrm{i}} \hbox {(t)}} \right\rangle \left\langle {\hbox {u}_{\mathrm{i}} +\hbox {j}\left( {\hbox {t}-\tau } \right) } \right\rangle$ holds only for very large $\tau$. This assumption is justified in the present case, since, according to Burridge and Knopoff [1], time delay between the neighboring group of seismically active elements (blocks) should be two orders of magnitude smaller than corresponding time constant for the moving blocks. On the contrary, in the present study, we examine the effect of time delay up to value of $\tau =3.5$, i.e., of the order of the oscillation period for the mean-field model (3) just above the bifurcation curve ($T\approx 3.5$), which is considered to correspond to seismic regime of large events, as previously discussed in Sect. 4.

Inserting (21) and (22) into (20), one arrives at:

$$\begin{aligned} \dot{S_{v}}=-2U\left( {1+\frac{2KC}{N}} \right) +2\Phi ^{\prime }\left( {m_v +v_0 } \right) S_v +2D \end{aligned}$$

(23)

The equation for the dynamics of the covariance can be obtained as follows:

$$\begin{aligned} \dot{U}= & {} \left\langle {\dot{u_i}v_i } \right\rangle +\left\langle {u_i\dot{v_i}} \right\rangle -\dot{m_u} m_v -m_u \dot{m_v }\nonumber \\= & {} \left\langle {v_i^2 } \right\rangle +\left\langle u_i \left( -u_i -\Phi \left( {v_0 } \right) +\Phi \left( {v_i +v_0 } \right) \right. \right. \nonumber \\&\left. \left. +\,\frac{C}{N}\sum _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } +\sqrt{2D}\xi _i \left( t \right) \right) \right\rangle \nonumber \\&-\,m_v^2 -m_u \left( -m_u -\Phi \left( {v_0 } \right) +\Phi \left( {m_v +v_0 } \right) \right. \nonumber \\&+\,\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v +\frac{2KC}{N}\left( m_u \left( {t-\tau } \right) \right. \nonumber \\&\left. \left. -\,m_u \left( t \right) \right) \right) \end{aligned}$$

(24)

The two terms that have to be considered more carefully are $\left\langle {u_i \Phi \left( {v_i + v_0} \right) } \right\rangle$ and $\frac{C}{N}\left\langle {u_i {\mathop {\sum }\limits _{j\in J}} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } } \right\rangle$. As for the former, one may write:

$$\begin{aligned}&\left\langle {u_i \Phi \left( {v_i +v_0 } \right) } \right\rangle =\left\langle \left( {m_u +\delta u_i } \right) \left( \Phi \left( {m_v +v_0 } \right) \right. \right. \nonumber \\&\quad \left. \left. +\,\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i +\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \delta v_i^2 \right) \right\rangle \nonumber \\&\qquad = \left\langle m_u \Phi \left( {m_v +v_0 } \right) +m_u \Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i \right. \nonumber \\&\quad \left. +\,\frac{1}{2}m_u \Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) \delta v_i^2 \right\rangle + \nonumber \\&\quad +\,\left\langle \Phi \left( {m_v +v_0 } \right) \delta u_i +\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta u_i \delta v_i\right. \nonumber \\&\quad \left. +\,\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v } \right) \delta u_i \delta v_i^2 \right\rangle . \end{aligned}$$

(25)

In analogy to (21), one has $\left\langle {m_u \Phi ^{\prime }\left( {m_v +v_0 } \right) \delta v_i } \right\rangle =0$ and $\left\langle {\Phi \left( {m_v +v_0 } \right) \delta u_i } \right\rangle =0$, whereas the last term in (25) is assumed to be 0 because we keep only the terms up to second order in deviations.

As for the fifth term in (25), one arrives at $\left\langle {\Phi ^{\prime }\left( {m_v +v_0 } \right) \delta u_i \delta v_i } \right\rangle =\Phi ^{\prime }\left( {m_v +v_0 } \right) \left\langle {\delta u_i \delta v_i } \right\rangle =\Phi ^{\prime }\left( {m_v +v_0 } \right) \left\langle {\left( {u_i -m_u } \right) \left( {v_i -m_v } \right) } \right\rangle \equiv \Phi ^{\prime }\left( {m_v +v_0 } \right) U$.

Hence, continuing from (25):

$$\begin{aligned}&\left\langle {u_i \Phi \left( {v_i +v_0 } \right) } \right\rangle =m_u \Phi \left( {m_v +v_0 } \right) \nonumber \\&\quad +\frac{1}{2}m_u \Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v +\Phi ^{\prime }\left( {m_v +v_0 } \right) U \end{aligned}$$

(26)

As for $\frac{C}{N}\left\langle {u_i \mathop {\sum }\limits _{j\in J} {\left( {u_{i+j} \left( {t-\tau } \right) -u_i } \right) } } \right\rangle$, one may write:

$$\begin{aligned}&\frac{C}{N}\sum _{j\in J} {\left\langle {u_i \left( t \right) u_{i+j} \left( {t-\tau } \right) } \right\rangle } -\frac{C}{N}\sum _{j\in J} \left\langle {u_i^2 } \right\rangle \nonumber \\&\quad =\frac{C}{N} \sum _{j\in J} {\left\langle {u_i } \right\rangle \left\langle {u_{i+j} \left( {t-\tau } \right) } \right\rangle } -\frac{2KC}{N}\left( {S_u +m_u^2 } \right) \nonumber \\&\quad =\frac{2KC}{N}m_u m_u \left( {t-\tau } \right) -\frac{2KC}{N}\left( {S_u +m_u^2 } \right) . \end{aligned}$$

(27)

Finally, proceeding from (24) and incorporating (26) and (27), one obtains:

$$\begin{aligned} \dot{U} =S_v -S_u \left( {1+\frac{2KC}{N}} \right) +\Phi ^{\prime }\left( {m_v +v_0 } \right) U \end{aligned}$$

(28)

Summarizing all the results so far, the mean-field model for collective dynamics of N blocks with 2K nearest-neighbor interactions reads:

$$\begin{aligned} \dot{m_u}= & {} m_v\nonumber \\ \dot{m_v}= & {} -m_u -\Phi \left( {v_0 } \right) +\Phi \left( {m_v +v_0 } \right) \nonumber \\&+\,\frac{1}{2}\Phi ^{{\prime }{\prime }}\left( {m_v +v_0 } \right) S_v+\frac{2KC}{N}\left( {m_u \left( {t-\tau } \right) -m_u } \right) \nonumber \\ \dot{S_u}= & {} 2U \nonumber \\ \dot{S_v}= & {} -2U\left( {1+\frac{2KC}{N}} \right) +2\Phi ^{\prime }\left( {m_v +v_0 } \right) S_v +2D \nonumber \\ \dot{U}= & {} S_v -S_u \left( {1+\frac{2KC}{N}} \right) +\Phi ^{\prime }\left( {m_v +v_0 } \right) U \end{aligned}$$

(29)

In order for these equations to describe a self-consistent system, it is required that the values of variances at the stationary state are nonnegative. This is clearly fulfilled given that $S_v^{stac} =-\frac{D}{\Phi ^{\prime }\left( {m_v +v_0 } \right) }|_{m_v =0} =\frac{Dv_0 }{a}\ge 0$ always holds and $S_u^{stac} =\frac{S_v^{stac} }{1+\frac{2KC}{N}}.$

System (29) could be further simplified by taking into account only the mean values of displacement and velocity, i.e., by assuming that $\dot{S_{u}} \left( t \right) ={S_{v}} \left( t \right) =\dot{U} \left( t \right) =0$. Such an assumption is justified considering very small deviations from the mean displacement and velocity. In other words, changes of mean displacement and velocity are one order of magnitude higher than changes of corresponding variances and covariance. Hence, the variances and the covariance can be replaced by their stationary values. After this, we finally arrive at the following equations for the mean-field approximated model:

$$\begin{aligned} \dot{m_u}\left( t \right)= & {} m_v \left( t \right) \nonumber \\ \dot{m_v}\left( t \right)= & {} -m_u \left( t \right) +a\ln \left( {v_0 } \right) -a\ln \left( {m_v +v_0 } \right) \nonumber \\&+\frac{1}{2}\frac{D}{\left( {m_v +v_0 } \right) }+\frac{2KC}{N}\left( {m_u \left( {t-\tau } \right) -m_u \left( t \right) } \right) \nonumber \\ \end{aligned}$$

(30)

The final form of (30) with included rate-dependent friction term is given in the main text as system (3), whereby the friction law is specified by Eq. (2).