Skip to main content
SpringerLink
Log in

On controlled propagation of long waves in nonautonomous Boussinesq–Burgers equations

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

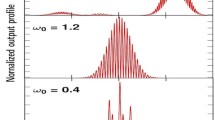
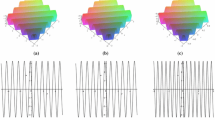
Very recently, the homogeneous Boussinesq–Burgers equations for finding multi-solitary long waves were studied, while the specification of propagation of these waves has not been studied. Here, controlled the propagation of long waves is investigated for different geometrical structure of long waves soliton, chirped elliptical waves, or periodic waves. Here depending on the inhomogeneity of the medium by account by time-dependent coefficients of the dispersion and nonlinearity, it is found that, the velocity and the height of long waves propagation are remarkably increasing with the dispersions coefficient. While this holds vice versa for the nonlinearity coefficient.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Wang, Z.A., Zhu, C.J.: Stability of the rarefaction wave for the generalized KdV-Burgers equation. Acta Math. Sci. 22(B), 319–328 (2002)

    MathSciNet  MATH  Google Scholar 

  2. Chen, A.H., Li, X.M.: Darboux transformation and soliton solutions for Boussinesq–Burgers equation. Chaos Solitons Fractals 27(1), 43–52 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  3. Khalfallah, M.: Exact traveling wave solutions of the Boussinesq–Burgers equation. Math. Comput. Model. 49, 666–671 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  4. Abdel Rady, A.S., Khalfallah, M.: On soliton solutions for Boussinesq–Burgers equations. Commun. Nonlinear Sci. Numer. Simul. 15, 886–894 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  5. Jawad, A.J., Petkovic, M.D., Biswas, A.: Soliton solutions of Burgers equations and perturbed Burgers equation. Appl. Math. Comput. 216, 3370–3377 (2010)

    MathSciNet  MATH  Google Scholar 

  6. Krishnan, E.V.: An exact solution of classical Boussinesq equation. J. Phys. Soc. Jpn. 51(8), 2391–2392 (1982)

    Article  MathSciNet  Google Scholar 

  7. Wang, M.L.: Solitary wave solitions for variant Boussinesq equations. Phys. Lett. A 199, 169–172 (1995)

    Article  MathSciNet  Google Scholar 

  8. Krishnan, E.V., Kumar, S., Biswas, A.: Solitons and other nonlinear waves of the Boussinesq equation. Nonlinear Dyn. 70, 1213–1221 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  9. Biswas, A., Milovic, D., Ranasinghe, A.: Solitary waves of Boussinesq equation in a power law media. Commun. Nonlinear Sci. Numer. Simul. 14(11), 3738–3742 (2009)

    Article  MATH  Google Scholar 

  10. Kaya, D.: Explicit solutions of generalized nonlinear Boussinesq equations. J. Appl. Math. 11, 29–37 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  11. Bruzon, M.S.: Exact solutions of a generalized Boussinesq equation. Theor. Math. Phys. 160(1), 894–904 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  12. Wazwaz, A.M.: Solitons and singular solitons for a variety of Boussinesq-like equations. Ocean Eng. 53, 1–5 (2002)

    Article  Google Scholar 

  13. Triki, H., Kara, A.H., Biswas, A.: Domain walls to Boussinesq-type equations in (2+1)-dimensions. Indian J. Phys. 88(7), 751–755 (2014)

    Article  Google Scholar 

  14. Biswas, A., Milovic, D.M., Kumar, S., Yildirim, A.: Perturbation of shallow water waves by semi-inverse variational principle. Indian J. Phys. 87(6), 567–569 (2013)

    Article  Google Scholar 

  15. Pereira, P.J.S., Lopes, N.D., Trabucho, L.: Soliton-type and other travelling wave solutions for an improved class of nonlinear sixth-order Boussinesq equations. Nonlinear Dyn. 82, 783–818 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  16. Abdou, M.A.: New solitons and periodic wave solutions for nonlinear physical models. Nonlinear Dyn. 52, 129–136 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  17. Biswas, A., Song, M., Triki, H., Kara, A.H., Ahmed, B.S., Strong, A., Hama, A.: Solitons, shock waves, conservation laws and bifurcation analysis of Boussinesq equation with power law nonlinearity and dual dispersion. Appl. Math. Inf. Sci. 3(8), 949–957 (2014)

    Article  MathSciNet  Google Scholar 

  18. Boussinesq, M.: Thorie gnrale des mouvements qui sout propags dans un canal rectangularire horizontal. C. R. Acad. Sci. Paris 73, 256–260 (1871)

    Google Scholar 

  19. Boussinesq, M.J.: Theorie des ondes et des remous qui se propagent le long dun canal rectangulaire horizontal, en communiquant au liquide contenu dans ce canal des vitesses senciblement pareilles de la surface au fond. J. Math. Pures Appl. 17, 55–108 (1872)

    MathSciNet  Google Scholar 

  20. Chen, Q., Madsen, P.A., Schffer, H.A., Basco, D.R.: Wave-current interaction based on an enhanced Boussinesq approach. Coast. Eng. 33, 11–39 (1998)

    Article  Google Scholar 

  21. Zou, Z.L., Hu, P.C., Fang, K.Z., Liu, Z.B.: Boussinesq-type equations for wavecurrent interaction. Wave Motion 50, 655–675 (2013)

    Article  MathSciNet  Google Scholar 

  22. Tonelli, M., Petti, M.: Hybrid finite volume—finite difference scheme for 2DH improved Boussinesq equations. Coast. Eng. 56, 609–620 (2009)

    Article  Google Scholar 

  23. Kennedy, A.B., et al.: Boussinesq modeling of wave transformation, breaking, and runup. I: 1D. J. Water Wave Port Coast. Ocean Eng. 126(1), 39–47 (2000)

    Article  MathSciNet  Google Scholar 

  24. Marie-Odile, B., Nicole, G., Jacques, S.-M.: Numerical simulation of an on-hydrostatic shallow-water model. Comput. Fluids 47(1), 51–64 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Meng, D.X., Gao, Y.T., Wang, L., Xu, P.B.: Elastic and inelastic interactions of solitons for a variable-coefficient generalized dispersive water-wave system. Nonlinear Dyn. 69, 391–398 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  26. Wang, L., Gao, Y.T., Meng, D.X., Gai, X.L., Xu, B.P.: Soliton-shape-preserving and soliton-complex interactions for a (1+1)-dimensional nonlinear dispersive-wave system in shallow water. Nonlinear Dyn. 66, 161–168 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  27. Pedlosky, J.: Geophysical Fluid Dynamics. Springer, New York (1987)

    Book  MATH  Google Scholar 

  28. Majda, A.: Introduction to PDEs and waves for the atmosphere and ocean. In: Courant Lecture Notes in Mathematics 9 AMS/CIMS (2003)

  29. Kosevich, A.M.: The Discrete Lattice: Phonons, Solitons Dislocations. Wiley- VCH, Berlin (1999)

    Book  Google Scholar 

  30. Maugin, G.A.: Nonlinear Waves in Elastic Crystals (Book in the Series Oxford Monographs in Mathematics). Oxford University Press, Oxford (1999)

    Google Scholar 

  31. Han, L., Huang, Y., Liu, H.: Solitons in coupled nonlinear Schrodinger equations with variable coefficients. Commun. Nonlinear Sci. Numer. Simul. 19, 3063–3073 (2014)

    Article  MathSciNet  Google Scholar 

  32. He, J.D., Zhang, J.F., Zhang, M.Y., Dai, C.Q.: Analytical nonautonomous soliton solutions for the cubic–quintic nonlinear Schrodinger equation with distributed coefficients. Optics Commun. 285, 755–760 (2012)

    Article  Google Scholar 

  33. Dai, C.Q., Xu, Y.J., Wang, Y.: Nonautonomous cnoidal wave and soliton management in parity-time symmetric potentials. Commun. Nonlinear Sci. Numer. Simul. 20, 389–409 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  34. Rong He, J., Li, H.M.: Nonautonomous bright matter-wave solitons and soliton collisions in Fourier-synthesized optical lattices. Optics Commun. 284, 3084–3089 (2011)

    Article  Google Scholar 

  35. Dai, C.Q., Xu, Y.J.: Spatial bright and dark similaritons on cnoidal wave backgrounds in 2D wave guides with different distributed transverse diffractions. Optics Commun. 311, 216–221 (2013)

    Article  Google Scholar 

  36. Jiang, H.J., Xiang, J.J., Dai, C.Q., Wang, Y.: Nonautonomous bright soliton solutions on continuous wave and cnoidal wave backgrounds in blood vessels. Nonlinear Dyn. 75, 201–207 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  37. Biswas, A., Mirzazadeh, M., Eslami, M.: Soliton solution of generalized chiral nonlinear schrodinger’s equation with time-dependent coefficients. Acta Phys. Pol. B 45, 849–866 (2014)

    Article  MathSciNet  Google Scholar 

  38. Mirzazadeh, M., Biswas, A.: Optical solitons with spatio-temporal dispersion by first integral approach and functional variable method. Optik 125(19), 5467–5475 (2014)

    Article  Google Scholar 

  39. Krishnan, E.V., Ghabshi, M.A., Mirzazadeh, M., Bhrawy, A.H., Biswas, A., Belic, M.: Optical solitons for quadratic law nonlinearity with five integration schemes. J. Comput. Theor. Nanosci. 12(11), 4809–4821 (2015)

  40. Mani Rajan, M.S., Mahalingam, A.: Nonautonomous solitons in modified inhomogeneous Hirota equation: soliton control and soliton interaction. Nonlinear Dyn. 79, 2469–2484 (2015)

    Article  MathSciNet  Google Scholar 

  41. Dai, C.Q., Chen, R., Zhang, J.: Analytical spatiotemporal similaritons for the generalized (3 + 1)-dimensional Gross Pitaevskii equation with an external harmonic trap. Chaos Solitons Fractals 44, 862–870 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  42. Mani Rajan, M.S., Mahalingam, A., Uthayakumar, A.: Nonlinear tunneling of optical soliton in 3 coupled NLS equation with symbolic computation. Ann. Phys. 346, 1–13 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  43. Adesanya, S.O., Eslami, M., Mirzazadeh, M., Biswas, A.: Shock wave development in couple stress fluid-filled thin elastic tubes. Eur. Phys. J. Plus 130(6), 1–21 (2015)

    Article  Google Scholar 

  44. Zhao, X., Wang, B., Liu, H.: Modelling the submarine mass failure induced Tsunamis by Boussinesq equations. J. Asian Earth Sci. 36, 47–55 (2009)

    Article  Google Scholar 

  45. Abdel-Gawad, I.H.: Towards a unified method for exact solutions of evolution equations. An application to reaction diffusion equations with finite memory transport. J. Stat. Phys. 147, 506–518 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  46. Zhang, L.H.: Travelling wave solutions for the generalized Zakharov–Kuznetsov equation with higher-order nonlinear terms. Appl. Math. Comput. 208, 144–155 (2009)

    MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt

    H. I. Abdel-Gawad & M. Tantawy

Authors
  1. H. I. Abdel-Gawad
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Tantawy
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. Tantawy.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Abdel-Gawad, H.I., Tantawy, M. On controlled propagation of long waves in nonautonomous Boussinesq–Burgers equations. Nonlinear Dyn 87, 2511–2518 (2017). https://doi.org/10.1007/s11071-016-3207-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3207-1

Keywords

Search

Navigation