Skip to main content
SpringerLink
Log in

Nonlinear interaction of solitary waves described by multi-rational wave solutions of the (2 \(+\) 1)-dimensional Kadomtsev–Petviashvili equation with variable coefficients

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

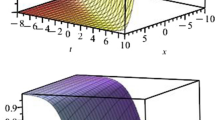
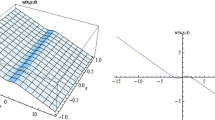
In this paper, the generalized unified method is used to construct multi-rational wave solutions of the (\(2 + 1\))-dimensional Kadomtsev–Petviashvili equation with variable coefficients. This is an extension of the previous work that was given by the same author in Osman and Abdel-Gawad (EPJ Plus 130(10):1–11, 2015). The (2 \(+\) 1)-dimensional Kadomtsev–Petviashvili equation with variable coefficients can be used to characterize many nonlinear phenomena in fluid dynamics, plasma physics and some other nonlinear science when the inhomogeneities of media and non-uniformities of boundaries are taken into consideration. To give more physical insight into the obtained solutions, we present graphically their representative structures by setting the arbitrary functions in the solutions as specific functions. Moreover, the influences of the variable coefficient functions and interaction properties of solitary waves are discussed for physical interests and possible applications.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Osman, M.S., Abdel-Gawad, H.I.: Multi-wave solutions of the (2 \(+\) 1)-dimensional Nizhnik–Novikov–Veselov equations with variable coefficients. EPJ Plus. 130(10), 1–11 (2015)

    Google Scholar 

  2. Mirzazadeh, M., Eslami, M., Biswas, A.: 1-Soliton solution of KdV6 equation. Nonlinear Dyn. 80(1–2), 387–396 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  3. Munro, S., Parkes, E.J.: Stability of solitary-wave solutions to a modified Zakharov–Kuznetsov equation. J. Plasma Phys. 64(4), 411–426 (2000)

    Article  Google Scholar 

  4. Atre, R., Panigrahi, P.K.: Class of solitary wave solutions of the one-dimensional Gross–Pitaevskii equation. Phys. Rev. E. 73(5), 056611 (2006)

    Article  MathSciNet  Google Scholar 

  5. Zhou, Q., Ekici, M., Sonmezoglu, M., Mirzazadeh, M., Eslami, M.: Optical solitons with Biswas–Milovic equation by extended trial equation method. Nonlinear Dyn. 84(4), 1883–1900 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  6. Wazwaz, A.M.: New solitary wave solutions to the modified forms of Degasperis–Procesi and Camassa–Holm equations. Appl. Math. Comput. 186(1), 130–141 (2007)

    MathSciNet  MATH  Google Scholar 

  7. Kangalgil, F., Ayaz, F.: Solitary wave solutions for the KdV and mKdV equations by differential transform method. Chaos Soliton Fract. 41(1), 464–472 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  8. Zhang, L., Khalique, C.M.: Exact solitary wave and quasi-periodic wave solutions of the KdV–Sawada–Kotera–Ramani equation. Adv. Differ. Equ-NY. 2015(1), 1–12 (2015)

    Article  Google Scholar 

  9. Mohebbi, A.: Solitary wave solutions of the nonlinear generalized Pochhammer–Chree and regularized long wave equations. Nonlinear Dyn. 70(4), 2463–2474 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  10. Ganji, D.D., Rafei, M.: Solitary wave solutions for a generalized Hirota–Satsuma coupled KdV equation by homotopy perturbation method. Phys. Lett. A. 356(2), 131–137 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Morris, R.M., Kara, A.H., Biswas, A.: An analysis of the Zhiber–Shabat equation including Lie point symmetries and conservation laws. Collect. Math. 67(1), 55–62 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  12. Mirzazadeh, M., Eslami, M., Zerrad, E., Mahmood, M.F., Biswas, A., Belic, M.: Optical solitons in nonlinear directional couplers by sine–cosine function method and Bernoulli’s equation approach. Nonlinear Dyn. 81(4), 1933–1949 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  13. Eslami, M., Vajargah, B.F., Mirzazadeh, M., Biswas, A.: Application of first integral method to fractional partial differential equations. Indian J. Phys. 88(2), 177–184 (2014)

    Article  Google Scholar 

  14. Mirzazadeh, M., Arnous, A.H., Mahmood, M.F., Zerrad, E., Biswas, A.: Soliton solutions to resonant nonlinear Schrödinger’s equation with time-dependent coefficients by trial solution approach. Nonlinear Dyn. 81(1–2), 277–282 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg–deVries equation. Phys. Rev. E. 19(19), 1095 (1976)

    MATH  Google Scholar 

  16. Ablowitz, M.J., Clarkson, P.A.: Soliton, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  17. Gu, C.: Soliton Theory and Its Application. NASA STI/Recon Technical Report A 1 (1995)

  18. Li, Y., Zhang, J.E.: Darboux transformations of classical Boussinesq system and its multi-soliton solutions. Phys. Lett. A. 284(6), 253–258 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  19. Guo, B., Ling, L., Liu, Q.P.: Nonlinear Schrödinger equation: generalized Darboux transformation and rogue wave solutions. Phys. Rev. E. 85(2), 026607 (2012)

    Article  Google Scholar 

  20. Hirota, R.: Exact solutions of the Korteweg–de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 27(18), 1192–1194 (1971)

    Article  MATH  Google Scholar 

  21. Hietarinta, J.: A search for bilinear equations passing Hirota’s three-soliton condition. I. KdV-type bilinear equations. J. Math. Phys. 28(8), 1732–1742 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  22. Wazwaz, A.M.: Multiple-soliton solutions for the KP equation by Hirota’s bilinear method and by the tanh–coth method. Appl. Math. Comput. 190(1), 633–640 (2007)

  23. Wei, G.M., Gao, Y.T., Xu, T., Meng, X.H., Zhang, C.Y.: Painleve’ property and new analytic solutions for a variable-coefficient Kadomtsev–Petviashvili equation with symbolic computation. Chin. Phys. Lett. 25, 1599–1602 (2008)

  24. Yomba, E.: Construction of new soliton-like solutions for the (2 \(+\) 1)-dimensional KdV equation with variable coefficients. Chaos Soliton Fract. 21, 75–79 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  25. Ye, L.Y., Lv, Y.N., Zhang, Y., Jin, H.P.: Grammian solutions to a variable-coefficient KP equation. Chin. Phys. Lett. 25, 357–358 (2008)

    Article  Google Scholar 

  26. Abdel-Gawad, H.I., Elazab, N.S., Osman, M.: Exact solutions of space dependent Korteweg–de Vries equation by the extended unified method. J. Phys. Soc. Jpn. 82, 044004 (2013)

    Article  Google Scholar 

  27. Abdel-Gawad, H.I., Osman, M.: Exact solutions of the Korteweg–de Vries equation with space and time dependent coefficients by the extended unified method. Indian J. Pure Appl. Math. 45(1), 1–11 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Abdel-Gawad, H.I., Osman, M.: On shallow water waves in a medium with time-dependent dispersion and nonlinearity coefficients. J. Adv. Res. 6(4), 593–599 (2015)

    Article  Google Scholar 

  29. Abdel-Gawad, H.I., Tantawy, M., Osman, M.S.: Dynamic of DNA’s possible impact on its damage. Math. Methods Appl. Sci. 39(2), 168–176 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  30. Wang, Y.Y., Zhang, J.F.: Variable-coefficient KP equation and solitonic solution for two-temperature ions in dusty plasma. Phys. Lett. A. 352(1), 155–162 (2006)

    Article  MATH  Google Scholar 

  31. Yomba, E.: Abundant families of Jacobi elliptic function-like solutions for a generalized variable coefficients 2D KdV equation via the extended mapping method. Phys. Lett. A. 349(1), 212–219 (2006)

    Article  MATH  Google Scholar 

  32. Li, L.L., Tian, B., Zhang, C.Y., Xu, T.: On a generalized Kadomtsev–Petviashvili equation with variable coefficients via symbolic computation. Phys. Scr. 76(5), 411 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  33. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equations and Inverse Scattering. Cambridge University Press, Cambridge (1991)

    Book  MATH  Google Scholar 

  34. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Cairo University, Giza, Egypt

    M. S. Osman

Authors
  1. M. S. Osman
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to M. S. Osman.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Osman, M.S. Nonlinear interaction of solitary waves described by multi-rational wave solutions of the (2 \(+\) 1)-dimensional Kadomtsev–Petviashvili equation with variable coefficients. Nonlinear Dyn 87, 1209–1216 (2017). https://doi.org/10.1007/s11071-016-3110-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3110-9

Keywords

Search

Navigation