Coexistence of strange nonchaotic attractors and a special mixed attractor caused by a new intermittency in a periodically driven vibro-impact system

Abstract

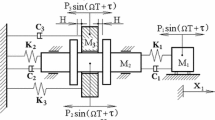
We focus on the coexistence of strange nonchaotic attractors (SNAs) and a novel mixed attractor in a periodically driven three-degree-of-freedom vibro-impact system with symmetry. SNAs are characterized by the local largest Lyapunov exponent and the phase sensitivity property. The Poincaré map P is the twofold composition of a six-dimensional implicit map Q, implying the symmetry of the vibro-impact system. Since the map Q can capture two conjugate attractors, it is used to investigate the dynamics of the system. With a suitable parameter combination, the Poincaré map P of the vibro-impact system exhibits Neimark–Sacker–pitchfork (NS-P) bifurcation. It is shown that dense phase-locking regions exist in a small parameter interval near this NS-P bifurcation point. Three types of attractors alternate in this small interval: two conjugate phase-locked periodic attractors, two conjugate SNAs and a special type of mixed attractor. As the force frequency $\omega$ is increased gradually, many phase-locking regions disappear, and the coexistence of two conjugate SNAs takes place instead, which is accompanied by a quick decrease in the width of phase-locking. If two conjugate strange nonchaotic limit sets are suddenly embedded in a chaotic one, a special mixed attractor is caused by a new intermittency accompanied by symmetry restoring bifurcation. This symmetry restoring bifurcation is the result of the collision between two conjugate strange nonchaotic limit sets and a symmetric limit set.

Appendices

Appendix 1: Expressions of the integration constants $a_i$ and $b_i$ as the function of the initial conditions

Let the coordinates of the initial map point $\mathbf{X}_0 \in {\varvec{\Pi }} _1$ be $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$. Substituting $t=0$ into the general solutions shown in Eq. (8), we obtain

$$\begin{aligned} x_{i0}= & {} \psi _{i1} (a_1 +A_1 \sin \tau _0 +B_1 \cos \tau _0 )\nonumber \\&+\,\psi _{i2} (a_2 +A_2 \sin \tau _0 +B_2 \cos \tau _0 ) \nonumber \\&+\,\psi _{i3} (a_3 +A_3 \sin \tau _0 +B_3 \cos \tau _0 ),\nonumber \\ i= & {} 1,\, 2; \end{aligned}$$

(40)

and

$$\begin{aligned} y_{i0}= & {} \psi _{i1} (-\eta _1 a_1 +\omega _{d1} b_1 +A_1 \omega \cos \tau _0 -B_1 \omega \sin \tau _0 )\nonumber \\&+\,\psi _{i2} (-\eta _2 a_2 +\omega _{d2} b_2 \nonumber \\&+\,A_2 \omega \cos \tau _0 -B_2 \omega \sin \tau _0 )\nonumber \\&+\,\psi _{i3} (-\eta _3 a_3 +\omega _{d3} b_3 \nonumber \\&+\,A_3 \omega \cos \tau _0 -B_3 \omega \sin \tau _0 )\nonumber \\ i= & {} 1, 2, 3; \end{aligned}$$

(41)

Besides, since $x_2^*-x_3^*=h$ with $t=0$, the following relation holds:

$$\begin{aligned} x_{20} -x_{30}= & {} \psi _{21} a_1 +\psi _{22} a_2 +\psi _{23} a_3 \nonumber \\&+\,(\psi _{21} A_1 +\psi _{22} A_2 +\psi _{23} A_3 )\sin \tau _0 \nonumber \\&+\,(\psi _{21} B_1 +\psi _{22} B_2 +\psi _{23} B_3 )\cos \tau _0 \nonumber \\&-\,[\psi _{11} a_1 +\psi _{12} a_2 +\psi _{13} a_3 \nonumber \\&+\,(\psi _{11} A_1 +\psi _{12} A_2 +\psi _{13} A_3 )\sin \tau _0 \nonumber \\&+\,(\psi _{11} B_1 +\psi _{12} B_2 +\psi _{13} B_3 )\cos \tau _0 ] \nonumber \\= & {} h. \end{aligned}$$

(42)

(44), (45) and (46) generate six equations about six unknowns $a_i$ and $b_i$ ($i=1, 2, 3$). Then the integration constants $a_i$ and $b_i$ can be expressed as the following functions depending on the initial conditions $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$:

$$\begin{aligned}&a_i (x_{10} ,x_{20} ,\tau _0 )=\alpha _{1i} x_{10} +\alpha _{2i} x_{20} \nonumber \\&\quad +\,\alpha _{3i} \sin \tau _0 +\alpha _{4i} \cos \tau _0 +\alpha _{5i}, \end{aligned}$$

(43a)

$$\begin{aligned}&b_i (x_{10} ,y_{10} ,x_{20} ,y_{20} ,y_{30} ,\tau _0 )=\beta _{1i} x_{10}\nonumber \\&\quad +\,\beta _{2i} x_{20} +\beta _{3i} y_{10} +\beta _{4i} y_{20} \nonumber \\&\quad +\,\beta _{5i} y_{30} +\beta _{6i} \sin \tau _0 +\beta _{7i} \cos \tau _0 +\beta _{8i}, \end{aligned}$$

(43b)

where $\alpha _{ji} (j=1,\ldots ,5)$ and $\beta _{ki} (k=1,\ldots ,8)$ are constants determined by system parameters.

If the initial conditions $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$ are replaced by $(x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))$, Eq. (13) is obtained.

Then we obtain the partial derivatives of the integration constants about the initial conditions $(x_{10},x_{20},y_{10},y_{20},y_{30},\tau _0)$:

$$\begin{aligned} \frac{\partial a_i }{\partial x_{10} }= & {} \alpha _{1i} ,\quad \frac{\partial a_i }{\partial x_{20} }=\alpha _{2i} ,\nonumber \\ \frac{\partial a_i }{\partial y_{10} }= & {} 0,\quad \frac{\partial a_i }{\partial y_{20} }=0,\quad \frac{\partial a_i }{y_{30} }=0,\nonumber \\ \frac{\partial a_i }{\tau _0 }= & {} \alpha _{3i} \cos \tau _0 -\alpha _{4i} \sin \tau _0 , \end{aligned}$$

(44a)

$$\begin{aligned} \frac{\partial b_i }{\partial x_{10} }= & {} \beta _{1i} ,\quad \frac{\partial b_i }{\partial x_{20} }=\beta _{2i} ,\quad \frac{\partial b_i }{\partial y_{10} }=\beta _{3i},\nonumber \\ \frac{\partial b_i }{\partial y_{20} }= & {} \beta _{4i} , \quad \frac{\partial b_i }{\partial y_{30} }=\beta _{5i} ,\nonumber \\ \frac{\partial b_i }{\tau _0 }= & {} \beta _{6i} \cos \tau _0 -\beta _{7i} \sin \tau _0 . \end{aligned}$$

(44b)

Appendix 2: Expressions of Jacobi matrix

We replace the initial conditions $(x_1 (n),x_2 (n),y_1 (n),y_2 (n),y_3 (n),\tau (n))$ by $(x_{10} ,x_{20} ,y_{10} ,y_{20} ,y_{30} ,\tau _0 )$, Eq. (14) is rewritten as:

$$\begin{aligned} G= & {} x_2 (n+1)-x_3 (n+1)+h \nonumber \\= & {} \sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)+b_j \sin (\omega _{dj} t)]\nonumber \\&+\,A_j \sin (\omega t+\tau _0 )+B_j \cos (\omega t+\tau _0 )\} \nonumber \\&-\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t}[a_j \cos (\omega _{dj} t)\nonumber \\&+\,b_j \sin (\omega _{dj} t)]+A_j \sin (\omega t+\tau _0 )\nonumber \\&+\,B_j \cos (\omega t+\tau _0 )\}+h =0 \end{aligned}$$

(45)

According to the implicit function theorem, we obtain

$$\begin{aligned} \frac{\partial t}{\partial x_{10} }= & {} {-\frac{\partial G}{\partial x_{10} }}\Big /{\frac{\partial G}{\partial t}},\quad \frac{\partial t}{\partial x_{20} }={-\frac{\partial G}{\partial x_{20} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial y_{10} }= & {} {-\frac{\partial G}{\partial y_{10} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial y_{20} }= & {} {-\frac{\partial G}{\partial y_{20} }}\Big /{\frac{\partial G}{\partial t}},\quad \frac{\partial t}{\partial y_{30} }={-\frac{\partial G}{\partial y_{30} }}\Big /{\frac{\partial G}{\partial t}},\nonumber \\ \frac{\partial t}{\partial \tau _0 }= & {} {-\frac{\partial G}{\partial \tau _0 }}\Big /{\frac{\partial G}{\partial t}}. \end{aligned}$$

(46)

Let the Jacobi matrix $\mathbf{J}_\mathbf{Q} (\mathbf{X}_0 )=[J_{ij} ]_{6\times 6}$. According to the expression shown in Eq. (12), $a_{ij}$ can be computed as follows by the chain rule:

$$\begin{aligned} J_{i1}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial x_{10} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial x_{10} }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial x_{10} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial x_{10} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial x_{10} }, \end{aligned}$$

(47a)

$$\begin{aligned} J_{i2}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial x_{20} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial x_{20} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial x_{20} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial x_{20} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial x_{20} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial x_{20} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial x_{20} },\nonumber \\ \end{aligned}$$

(47b)

$$\begin{aligned} J_{i3}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{10} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{10} } +\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{10} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{10} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{10} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{10} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{10} },\nonumber \\ \end{aligned}$$

(47c)

$$\begin{aligned} J_{i4}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{20} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{20} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{20} }\nonumber \\&+\,\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{20} }+\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{20} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{20} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{20} },\nonumber \\ \end{aligned}$$

(47d)

$$\begin{aligned} J_{i5}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial y_{30} }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial y_{30} }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial y_{30} }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial y_{30} }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial y_{30} }, \end{aligned}$$

(47e)

$$\begin{aligned} J_{i6}= & {} \frac{\partial f_i }{\partial a_1 }\frac{\partial a_1 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_1 }\frac{\partial b_1 }{\partial \tau _0 }+\frac{\partial f_i }{\partial a_2 }\frac{\partial a_2 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_2 }\frac{\partial b_2 }{\partial \tau _0 }\nonumber \\&+\,\frac{\partial f_i }{\partial a_3 }\frac{\partial a_3 }{\partial \tau _0 }+\frac{\partial f_i }{\partial b_3 }\frac{\partial b_3 }{\partial \tau _0 }+\frac{\partial f_i }{\partial t}\frac{\partial t}{\partial \tau _0 }+\frac{\partial f_i }{\partial \tau _0 }. \end{aligned}$$

(47f)

where $\frac{\partial a_i }{\partial x_{10} }$, $\frac{\partial a_i }{\partial x_{20} }$, $\frac{\partial a_i }{\partial y_{10} }$, $\frac{\partial a_i }{\partial y_{20} }$, $\frac{\partial a_i }{y_{30} }$, $\frac{\partial a_i }{\tau _0 }$,$\frac{\partial b_i }{\partial x_{10} }$, $\frac{\partial b_i }{\partial x_{20} }$, $\frac{\partial b_i }{\partial y_{10} }$, $\frac{\partial b_i }{\partial y_{20} }$, $\frac{\partial b_i }{\partial y_{30} }$, $\frac{\partial b_i }{\tau _0 }$ are shown as Eq. (44).

Appendix 3: Analytic solutions of symmetric fixed point

Let the coordinates of the symmetric fixed point X $^{*}$ be $(x_1^*,x_2^*,y_1^*,y_2^*,y_3^*,\tau ^{*})$. For both stable and unstable cases, the coordinates of the symmetric fixed point X $^{*}$ can be determined analytically by $\mathbf{X}^{*}=\mathbf{Q}(\mathbf{X}^{*})$. Since $\mathbf{Q}=\mathbf{R}^{-1}\circ \mathbf{Q}_u$, $\mathbf{X}^{*}=\mathbf{Q}(\mathbf{X}^{*})$ means $\mathbf{RX}^{*}=\mathbf{Q}_u (\mathbf{X}^{*})$, which implies that after $M_3$ impacts the right and the left stops, the associated state coordinates of map point are equal in absolute value and opposite in direction.

Let the initial time be $t_0 =0$ after impacting at the left stop, and inserting it to Eq. (8), we obtain the coordinates $x_i (t_0 )$ and $y_i (t_0 )=\dot{x}_i (t_0 )(i=1,2,3)$ after impacting at the left stop. Then let the time be $t_1 =\frac{n\pi }{\omega }$ (i.e., half of n excitation periods) where n is an odd integer, and inserting it into Eq. (8), we obtain the coordinates $x_i (t_1 )$ and $y_i (t_1 )=\dot{x}_i (t_1 )(i=1,2,3)$ after impacting at the right stop.

Based on $\mathbf{RX}^{*}=\mathbf{Q}_u (\mathbf{X}^{*})$, we have

$$\begin{aligned} x_i (t_0 )= & {} -x_i (t_1 ),\nonumber \\ y_i (t_0 )= & {} -y_i (t_1 ) (i=1,2,3);\quad x_2 (t_0 )\nonumber \\&-x_3 (t_0 )=-h. \end{aligned}$$

(48)

Then we obtain the following seven equations about $\tau =\tau ^{*}$, $a_i$ and $b_i (i=1,2,3)$:

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{1j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*}) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{1j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49a)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*}) \nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49b)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{3j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*})\nonumber \\&\quad =-\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t_1 }[a_j \cos (\omega _{dj} t_1 )+b_j \sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \sin \tau ^{*}-B_j \cos \tau ^{*}\} \end{aligned}$$

(49c)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{1j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{1j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j \nonumber \\&+\omega _{dj} b_j )\cos (\omega _{dj} t_1 )+(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49d)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{2j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j \nonumber \\&\quad +\,\omega _{dj} b_j )\cos (\omega _{dj} t_1 )+(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49e)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{3j} } (-\eta _j a_j +\omega _{dj} b_j +A_j \omega \cos \tau ^{*}-B_j \omega \sin \tau ^{*}) \nonumber \\&\quad =\sum _{j=1}^3 {\psi _{3j} } \{e^{-\eta _j t_1 }[(-\eta _j a_j +\omega _{dj} b_j )\cos (\omega _{dj} t_1 )\nonumber \\&\qquad +\,(-\eta _j b_j -\omega _{dj} a_j )\sin (\omega _{dj} t_1 )]\nonumber \\&\qquad -A_j \omega \cos \tau ^{*}+B_j \omega \sin \tau ^{*}\} \end{aligned}$$

(49f)

$$\begin{aligned}&\sum _{j=1}^3 {\psi _{2j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau { }^*)\nonumber \\&\quad -\sum _{j=1}^3 {\psi _{3j} } (e^{-\eta _j t}a_j +A_j \sin \tau ^{*}+B_j \cos \tau ^{*})=-h.\nonumber \\ \end{aligned}$$

(49g)

By elimination and simplification, we obtain the following equation about $\tau ^{*}$:

$$\begin{aligned} u\cos \tau ^{*}+v\sin \tau ^{*}=h \end{aligned}$$

(50)

where u and v are constants determined by the system parameters. Then $\tau ^{*}$ can be solved as

$$\begin{aligned} \tau ^{*}=\left\{ {{\begin{array}{ll} 2\tan ^{-1}\left( {\frac{v\pm \sqrt{u^{2}+v^{2}-h^{2}}}{u+h}} \right) ,&{}\quad u+h\ne 0 \\ 2\tan ^{-1}\left( {\frac{h-u}{2v}} \right) ,&{}\quad u+h=0 \\ \end{array} }} \right. . \end{aligned}$$

(51)

Subsequently, inserting the expression of $\tau ^{*}$ into Eq. (49), we obtain expressions of integration constants $a_i$ and $b_i \quad (i=1,2,3)$. Inserting the value of $a_i$, $b_i$ and $\tau ^{*}$ into Eq. (8), and letting the time $t=0$, we obtain the coordinates $(x_1^*,x_2^*,y_1^*,y_2^*,y_3^*,\tau ^{*})$ of the symmetric fixed point X $^{*}$.