Continuation techniques for analysis of whole aeroengine dynamics with imperfect bifurcations and isolated solutions

Abstract

The analysis of whole engine rotordynamic models is an important element in the design of aerojet engines. The models include gyroscopic effects and allow for rubbing contact between rotor and stator components such as bladed discs and casing. Due to the nonlinearities inherent to the system, bifurcations in the frequency response may arise. Reliable and efficient methods to determine the bifurcation points and solution branches are required. For this purpose, a multi-harmonic balance approach is presented that allows a numerically efficient detection of bifurcation points and the calculation of both continuous and isolated branches of the frequency response functions. The method is applied to a test case derived from a commercial aeroengine. A bifurcation structure with continuous and isolated solution branches is observed and studied in this paper. The comparison with time marching based on simulations shows both accuracy and numerical efficiency of the newly developed approach.

1 Introduction

The necessity of improving fuel efficiency of aeroengines generally requires a further decrease in clearances between rotor and stator components. This unfortunately increases the risk of contact and rubbing when operational conditions yield a disbalance of the rotor. While the design of the engine ensures well-behaved dynamic response for normal operational conditions, contact and rubbing need additional strategies to deal with the dynamic response: the interaction between rotor and stator components may generate a very complex dynamical behaviour, and as already pointed out by Sinha [1], aeroengine manufacturers have to determine the loads not only during the initial contact event but also during any continued rotation of the rotor after engine shutdown. An accurate and efficient numerical tool is necessary for this due to the extremely high cost and complexity of laboratory testing.

In this paper, we present an approach to determine the vibration response for whole aeroengine rotordynamic models (WEM) in which contact and friction interactions may take place. The goal of the study is to devise a method that is numerically efficient, but at the same time allows to unfold complex bifurcation structures to a reasonable level of accuracy, including imperfect bifurcations and isolated solution branches.

Many approaches are available to model nonlinear rotordynamics similar to the one under investigation here. The most common approaches are harmonic balance and transient simulation. The first one allows to quickly obtain periodic solutions, like for frequency response of the system, while the second also allows for analysis of more complex, e.g., irregular behaviour. Several studies have been devoted to the rotordynamics of systems for which contact between blades and casing occurs. Petrov [2] proposed a model with rigid blades. Aidanpaa [3] proposed a model where the blade deflection is calculated by an equivalent beam deflection model and the casing is rigid. Sinha [4] developed a model for the analysis of a system composed of blades attached to a rigid disc mounted on a shaft. His approach was also used by Lesaffre [5] and extended to a dual shaft by Gruin [6]. Parent [7] used the same model to analyse the divergence and flutter of a whole engine model with interaction in a bladed rotor-to-stator contact. Choy and Padovan  [8, 9] studied the transient response of the bladed rotor interaction with a flexible casing.

An important aspect of modelling contact with friction, which we will sometimes call rubbing in the following, is the manner of dealing with the normal contact itself. On the one hand, contact can be considered numerically as a pure unilateral contact and solved rigorously using Lagrangian multipliers [10]. On the other hand, experimental results suggest that the interaction between the rotor and an abradable lining material along the casing is more complicated and contact compliance might play a role. Ahrens et al. [11] have experimentally measured a contact normal stiffness. Kascak and Tomko [12] compared different rub models, smearing rub and abradable rub. For small penetration, both models behave in the same way. They concluded that both models had a threshold after which they caused the rotor to proceed into backward whirl. When the abradable model goes into backward whirl, it can result in the model encountering an instability, whereas the smearing model shows more benign behaviour. Following these results, the model implemented in this study is based on a compliant contact, and a contact normal stiffness is included. For simplicity, the tangential forces occurring during contact are modelled by a Coulomb friction model considering pure sliding.

In the present study, we restrict ourselves to determine the steady-state periodic response of the system for periodic forcing. A harmonic balance method (HBM) is employed. Due to its numerical efficiency, this and derived methods can now be found more and more often in various application domains. Several studies have been done on harmonic balance in rotordynamics and rubbing modelling. Kim and Noah [13] developed harmonic balance with an alternating frequency/time (AFT) technique to obtain synchronous and sub-harmonic whirling motions of a horizontal Jeffcott rotor with bearing clearances. They also studied the stability of the steady-state motions using perturbation equations. The Floquet multipliers of the associated monodromy matrix were determined using a discrete HBM/AFT method. Quasi-periodic and chaotic behaviour was also observed for their Jeffcott rotor model. Peletan et al. [14] have studied the use of the harmonic balance method for rub-impact problems. They have also discussed advantages and limitations of the method compared to time marching. They concluded that HBM can predict the initiation of the quasi-periodic partial rub regime, but the partial rub and backward whirl and whip motions cannot be described by HBM. Kim and Choi [15] have developed a multiple harmonic balance method to obtain quasi-periodic response of a horizontal Jeffcott rotor with a bearing clearance.

In this paper, we focus on bifurcations and multiplicity of periodic solutions. Asynchronous vibration is not considered since the analysis of the targeted whole engine model has not shown any corresponding bifurcations, such as the Neimark–Sacker type. A similar approach has, e.g., been followed by  [16]. HBM has also been applied to study cyclic symmetric systems with geometric nonlinearities, and bifurcation structures have been observed and calculated [17, 18]. Here we follow and expand on these ideas and apply them to a whole engine model as used in industry. It will be shown that, due to symmetry breaking, many of the bifurcations are imperfect in a weaker or stronger sense. This spoils many traditional approaches to determine bifurcation points. A strategy is thus proposed to deal with these imperfect bifurcations. The task is twofold: first, the imperfect bifurcation has to be located in parameter space, and second, detached branches, not continuously linked to the originally followed branches, have to be found. One might note that in fact the geometries of aeroengines, due to manifold design needs, usually do not show exact geometric symmetries. The problem of locating imperfect bifurcations and detached, isolated solution branches might thus be of substantial importance whenever the strength of the symmetry breaking becomes marked.

The paper is set up as follows: at first, the concept of whole engine modelling, as understood in the community, is described briefly, and the underlying assumptions are stated. Then, the harmonic balance method and the contact models employed in the study are presented. Then, we show how the bifurcation analysis in the context of imperfect bifurcations and detached, isolated solution branches is conducted. An example based on a whole engine model of an aeroengine illustrates how the methods proposed may be applied. A detailed analysis of the bifurcations is provided, and the results obtained by HBM are compared to equivalent transient simulations. Finally, conclusions are given.

2 Whole engine modelling and numerical solution procedure

In this study, we are most interested in the motion of the rotor centreline. The stator elements are considered in a stationary coordinate frame, and centrifugal forces and gyroscopic effects have to be included. Considering an aeroengine as an integral whole and discretising the geometry through finite elements (FE) in a straightforward manner may easily result in a model of several million of degrees of freedom when the complex geometries involved are to be captured. To yield smaller but still accurate enough models, the individual components are represented by the finite element method and component mode synthesis is used to reduce the size of each component FE model. Assembling the reduced models produces an overall whole engine model of the order of a few thousands of degrees of freedom, which can be computed by HBM.

The equation of motion for the reduced whole engine model (WEM) with nonlinear contact interfaces has the following form:

$$\begin{aligned}&\left[ {\varvec{M}}\right] \ddot{{{\varvec{u}}}} + \left( \left[ {\varvec{C}}\right] - \left[ {\varvec{G}}\right] _{{\varOmega }} \right) \dot{{{\varvec{u}}}}\nonumber \\&\quad + \left( \left[ {\varvec{K}}\right] -\left[ {\varvec{K}}\right] _{{\varOmega }} \right) {{\varvec{u}}} = {{\varvec{p}}}(t) - {{\varvec{f}}}_\mathrm{nl} ({{\varvec{u}}},\dot{{{\varvec{u}}}}), \end{aligned}$$

(1)

where ${{\varvec{u}}}$ is the vector of generalised displacements of the reduced model. $\left[ {\varvec{M}}\right] , \left[ {\varvec{C}}\right]$ and $\left[ {\varvec{K}}\right]$ are the matrices of mass, damping and stiffness, respectively. $\left[ {\varvec{K}}\right] _{{\varOmega }}$ and $\left[ {\varvec{G}}\right] _{{\varOmega }}$ are the matrices of centrifugal stiffening and gyroscopic effects. ${{\varvec{p}}}(t)$ is the vector of periodic excitation forces, and ${{\varvec{f}}}_\mathrm{nl}$ is the vector of nonlinear forces caused by the contacts between rotor and stator elements.

A periodic response of the system will be considered, with the response having the same frequency as the excitation, $\omega$, which is given by the rotational speed of the rotor, due to an arbitrary unbalance mass $p(t) = -m_\mathrm{dis} \omega ^2 \cos (\omega t)$.

A truncated Fourier series is used to approximate the generalised displacements,

$$\begin{aligned} {{\varvec{u}}} (t) ={{\varvec{U}}}^{0} + \sum _{n=1}^{nh} {{\varvec{U}}}^{n,c} \cos (m_\mathrm{n} \omega t) + {{\varvec{U}}}^{n,s} \sin (m_n \omega t), \end{aligned}$$

(2)

where ${{\varvec{U}}}^{0}, {{\varvec{U}}}^{n,c}$ and ${{\varvec{U}}}^{n,s}$ are vectors of the coefficients of the multi-harmonic representation, with $m_\mathrm{n}$ denoting the harmonics retained in the Fourier series, and nh the truncation parameter. Inserting (2) into (1) leads to a frequency domain formulation of the problem. In frequency domain, the system can be reduced to the nonlinear degrees of freedom  [19], which again permits to reduce the size of the system. The method is based on a accurate calculation of the forced response function matrix $\left[ {\varvec{A}}\right] (\omega ) = \left[ \left[ {\varvec{A}}\right] +i\omega \left[ {\varvec{C}}\right] -\omega ^2 \left[ {\varvec{M}}\right] \right]$,

$$\begin{aligned} \left[ {\varvec{A}}\right] (\omega ) \approx \left[ {\varvec{A}}\right] ^0+\tilde{\left[ {\varvec{A}}\right] } (\omega ), \end{aligned}$$

(3)

where $\tilde{\left[ {\varvec{A}}\right] } (\omega )$ is the modal synthesis of $\left[ {\varvec{A}}\right]$ truncated to the mode $N_\mathrm{m}$ and $\left[ {\varvec{A}}\right] ^0$ is the static correction to provide the exact value of $\left[ {\varvec{A}}\right]$ at the frequency $\omega _0$. The residual of the nonlinear system at each frequency $\omega$ reduced to the nonlinear degrees of freedom for the jth harmonic is:

$$\begin{aligned} {{\varvec{R}}}_j({{\varvec{Q}}}^\mathrm{nl})= & {} {{\varvec{Q}}}^\mathrm{nl}_j - \left[ {\varvec{A}}\right] _\mathrm{nll}(m_j \omega ) {{\varvec{P}}}^l_j \nonumber \\&-\, \left[ {\varvec{A}}\right] _\mathrm{nlnl}(m_j \omega ) {{\varvec{P}}}^\mathrm{nl}_j\nonumber \\&+ \left[ {\varvec{A}}\right] _\mathrm{nlnl}(m_j \omega ) {{\varvec{F}}}_\mathrm{nl}^j ({{\varvec{Q}}}^\mathrm{nl})={{\varvec{0}}} \nonumber \\&\quad j=1,\ldots ,nh. \end{aligned}$$

(4)

where ${{\varvec{R}}}_j$ is the residual function for the jth harmonic, ${{\varvec{Q}}}^\mathrm{nl}$ is the vector of unknowns at the nonlinear nodes (Fourier coefficients of the displacements), ${{\varvec{P}}}^l_j$ and ${{\varvec{P}}}^\mathrm{nl}_j$ are the external forces applied to the linear and nonlinear nodes. The nonlinear forces ${{\varvec{F}}}_\mathrm{nl}$ include contact forces and gyroscopic effects. System (4) is solved using a continuation method with the frequency $\omega$ as the continuation parameter, coupled with a Newton–Raphson solver.

Fig. 1

Definition of the contact forces (normal and tangential) for the rotor–stator contact model

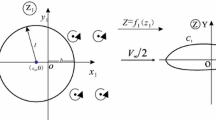
The implementation of the contact forces follows  [2]. A rotor in contact with a stator is considered. 0z is the axis of the rotor. As presented in Fig. 1, the displacements of the rotor and stator centrelines in the plane xy are $(u^\mathrm{r}_x(t),u^\mathrm{r}_y(t))$ and $(u^\mathrm{s}_x(t),u^\mathrm{s}_y(t))$ so that the distance between the rotor and the stator is ${{\varvec{u}}}(t)={{\varvec{u}}}^\mathrm{r}-{{\varvec{u}}}^\mathrm{s}+{{\varvec{e}}}$, where ${{\varvec{e}}}$ is the eccentricity of the rotor. Contact occurs when $\delta = \Vert {{\varvec{u}}} \Vert -g$ is positive, where g defines the clearance between the rotor and the stator. For a perfect circular shapes, the clearance is defined by $g=R_\mathrm{s}-R_\mathrm{r}$ with $R_\mathrm{s}$ and $R_\mathrm{r}$ are the radius for the stator and for the rotor, respectively. The contact forces ${{\varvec{f}}}$ applied to the rotor are decomposed into normal and tangential components at the contact point,

$$\begin{aligned} {{\varvec{f}}} = f_\mathrm{n} {{\varvec{n}}} + f_\mathrm{t} {{\varvec{t}}}, \end{aligned}$$

(5)

where ${{\varvec{n}}}$ and ${{\varvec{t}}}$ are the normal and tangential vector at the point where the contact occurs and are related to the distance ${{\varvec{u}}}$ by:

$$\begin{aligned} {{\varvec{n}}} = \frac{{{\varvec{u}}}}{\Vert {{\varvec{u}}} \Vert }=\frac{{{\varvec{1}}}}{\Vert {{\varvec{u}}} \Vert } \begin{Bmatrix} u_x \\ u_y \end{Bmatrix} \quad \text {and} \quad {{\varvec{t}}} = \frac{1}{\Vert {{\varvec{u}}} \Vert } \begin{Bmatrix} -u_y \\ u_x \end{Bmatrix}. \end{aligned}$$

(6)

The magnitude of the normal force $f_\mathrm{n}$ is related to the normal penetration $\delta$ of the rotor into the stator. If a Hertzian contact is considered, the relation is

$$\begin{aligned} f_\mathrm{n} = k_\mathrm{c} \delta ^{\frac{3}{2}}. \end{aligned}$$

(7)

The tangential force is caused by friction. A Coulomb-type sliding friction law is assumed, with the friction force oriented opposite to the sliding direction, and

$$\begin{aligned} f_\mathrm{t} = \xi \mu f_\mathrm{n}, \end{aligned}$$

(8)

where $\mu$ is the coefficient of friction and $\xi =\pm 1$ is a sign function, which depends on the rotor rotation and whirl directions.

The expression of the contact forces in the absolute frame is:

$$\begin{aligned} {{\varvec{f}}}(t) = \begin{Bmatrix} f_x \\ f_y \end{Bmatrix} = \frac{f_\mathrm{n}(\delta )}{\Vert {{\varvec{u}}}(t) \Vert } \begin{bmatrix} 1&\quad -\xi \mu \\ \xi \mu&\quad 1 \end{bmatrix} \begin{Bmatrix} u_x \\ u_y \end{Bmatrix}. \end{aligned}$$

(9)

The torque $M_\mathrm{f}$ due to contact interactions and applied to the centreline of the structure is given by

$$\begin{aligned} M_\mathrm{f} = R_\mathrm{s} f_\mathrm{t} = \xi \mu R_\mathrm{s} f_\mathrm{n}(\delta ). \end{aligned}$$

(10)

The expressions for the contact forces are not available as explicit analytic functions, so it is not possible to get explicit analytical expressions for the frequency domain representations of the contact force. An alternating frequency/time (AFT) procedure is used to get the frequency domain representation of the contact forces. The unknowns of the problem are the displacement coefficients of the centre of the rotor and the stator in the absolute frame. At each iteration of the nonlinear solution process (explained subsequently), the harmonic coefficients of the displacements are thus known and permit to get the penetration $\delta$ in time domain, using inverse discrete Fourier transform. Once the forces ${{\varvec{f}}}(t)$ and the torque $M_\mathrm{f}(t)$ have been calculated, they are projected into the frequency domain via DFT (discrete Fourier transform) or FFT (fast Fourier transform). The Newton nonlinear solver needs the Jacobian matrix, which means that the derivatives $[{\varvec{J}}^{{\varvec{nl}}}]$ of the harmonic nonlinear forces $\tilde{{{\varvec{F}}}}_{{{\varvec{nl}}}}$ with respect to the variables (displacements and frequency) have to be calculated, which is again achieved using the alternating frequency/time procedure [20].

The system (4) is then solved and an arc-length continuation method is employed to avoid problems with turning points. Solutions $({{\varvec{Q}}},\omega )$ are parameterised by the curvilinear parameter s defined by:

$$\begin{aligned} \Delta s = \Delta {{\varvec{Q}}}^T \Delta {{\varvec{Q}}} + \Delta \omega ^2 . \end{aligned}$$

(11)

The size of the system is increased as $\omega$ becomes an unknown. A new equation has to be added. In this study, the pseudo-arc-length method is applied and the nonlinear system to be solved is:

$$\begin{aligned}&{{\varvec{R}}}({{\varvec{Q}}}^k,\omega ^k) = {{\varvec{0}}} \end{aligned}$$

(12a)

$$\begin{aligned}&N({{\varvec{Q}}}^k,\omega ^k,\Delta s) = \hbox {grad}^k \Delta Y^k - \Delta s^k = 0, \end{aligned}$$

(12b)

where ${{\varvec{R}}}$ is the residual function, N is the scalar function defined by the pseudo-arc-length method, ${{\varvec{Y}}}=({{\varvec{Q}}},\omega )^T$ is the vector of unknowns and $\hbox {grad}^k$ is the gradient of ${{\varvec{R}}}$ at the previously calculated point ${{\varvec{Y}}}^{k-1}$ defined by:

$$\begin{aligned} \hbox {grad}=\left( \begin{array}{cc} -\left[ {\varvec{D}}\right] _Q {{\varvec{R}}} ^{-1} \left[ {\varvec{D}}\right] _{\omega } {{\varvec{R}}}\\ 1 \end{array} \right) \end{aligned}$$

(13)

where $\left[ {\varvec{D}}\right] _Q {{\varvec{R}}}$ is the Jacobian matrix of ${{\varvec{R}}}$ and $\left[ {\varvec{D}}\right] _{\omega } {{\varvec{R}}}$ the gradient of ${{\varvec{R}}}$ with regards to $\omega$.

A prediction–correction approach is used to build the response curve. After convergence at one frequency, a new point is predicted using the gradient and corrected solving the nonlinear system (12b). The corrector is based on a Newton–Raphson approach which is used together with a line search method, where the Newton direction is defined as the solution of a linear algebraic problem,

$$\begin{aligned} \begin{bmatrix} D_{{{\varvec{Q}}}} {{\varvec{R}}}^{i}&\quad D_{\omega } {{\varvec{R}}}^{i} \\ D_{{{\varvec{Q}}}} N^{i}&\quad D_{\omega } N^{i} \end{bmatrix} \Delta {{\varvec{Y}}}^{i+1} = \begin{Bmatrix} - {{\varvec{R}}}({{\varvec{Y}}}^{i}) \\ - N({{\varvec{Y}}}^{i}) \end{Bmatrix}, \end{aligned}$$

(14)

where i is the iteration of the Newton solver. This system is not directly solved, but a block elimination technique is performed since the matrix in (14) is a bordered matrix [21]. This technique permits to factorize only the Jacobian matrix $D_{{{\varvec{Q}}}} {{\varvec{R}}}$, which is require by the later bifurcation analysis. In the code, a LU decomposition of $D_{{{\varvec{Q}}}} {{\varvec{R}}}$ is performed using the LAPACK routines. One might note that the system (14) can be also solved using an iterative method based on Arnoldi iteration [22, 23], which is, however, not followed here.

3 Analysis of singular points and of imperfect bifurcations

Points on the frequency response function curve obtained by the above-described continuation method can be classified in regular and different types of singular points [22]:

• A regular point of $R({{\varvec{X}}},\omega )={{\varvec{0}}}$ is one for which the implicit function theorem works: $R_{{{\varvec{X}}}} \ne 0$ or $R_{\omega } R \ne 0$. There is only one curve through the point.

• A turning point corresponds to a singularity of the Jacobian in which zero is a simple eigenvalue of the Jacobian matrix $D_{{{\varvec{X}}}} R$ and $D_{\omega }R \notin \hbox {Im}(D_{{{\varvec{X}}}} R)$. The further properties mean that the dimension of the kernel of $D_Y R$ (with $Y=({{\varvec{X}}},\omega ))$ is one. This kernel is spanned by the eigenvector ${\varPhi }_1: \hbox {Ker}(D_Y R) = \hbox {span}\left[ {\varPhi }_1 \right]$.

• A simple singular bifurcation point ${{\varvec{X}}}_0,\omega _0$ has zero as a simple eigenvalue of $D_{{{\varvec{X}}}} R$ and $D_{\omega } \in \hbox {Im}(D_{{{\varvec{X}}}} R)$. A simple bifurcation point is characterised by a two-dimensional kernel of $D_Y R$, where one dimension corresponds to the eigenvector ${\varPhi }_2=({{\varvec{v}}}_0,1)$ and is solution of

  $$\begin{aligned} D_{{{\varvec{X}}}} R{{\varvec{v}}}_0 + D_{\varvec{\omega }} R = 0, \end{aligned}$$

  (15)

  under the transversal condition

  $$\begin{aligned}&\langle {\varPhi }^{*} , D_{{{\varvec{X}}} {{\varvec{X}}}} R {\varPhi }_1 {\varPhi }_1 \rangle ^2\nonumber \\&\quad -\langle {\varPhi }^{*}, D_{{{\varvec{X}}} {{\varvec{X}}}} R {\varPhi }_1 {\varPhi }_2 \rangle \langle {\varPhi }^{*}, D_{{{\varvec{X}}} {{\varvec{X}}}} R {\varPhi }_2 {\varPhi }_2 \rangle >0.\nonumber \\ \end{aligned}$$

  (16)

  Problem (12b) has exactly two different stationary solution branches intersecting at ${{\varvec{X}}}_0,\omega _0$.

• A Hopf bifurcation occurs when $D_{{{\varvec{X}}}} R$ has exactly one pair of eigenvalues $\pm \omega _0, \, \omega _0>0$ on the imaginary axis.

During the construction of the response curve (frequency response function in this case), singular points can occur and the method must be able to deal with them. In the case of a turning point, the continuation method passes the singular point without any problem, since merely a change of direction versus the frequency parameter occurs.

When a simple singular point with a bifurcation is present, continuation methods without special consideration of it can experience convergence problems, since the direction of the gradient before and after the singular point may change. To overcome this issue, the singular point is usually first detected and then calculated precisely, and finally, the individual bifurcating branches arising are calculated. After this operation, each branch emanating from the singular point can be followed.

Different approaches exist to detect a simple bifurcation point during the continuation procedure [22]. Here we make use of an approach proposed by Allgower [24]. It is based on the sign of the cosine between two consecutive gradients. If the cosine is negative, i.e., the two gradients have opposite direction, a simple bifurcation point exists.

Fig. 2

Duffing system $\ddot{u}+0.05\dot{u}+u+u^3=\cos (\omega t)$ [16] with a simple bifurcation point (a), and a modified duffing system $\ddot{u}+0.05\dot{u}+u+u^3 + 0.0001 u^2=\cos (\omega t)$ with imperfect or perturbed bifurcations, leading to isolated solutions for the perturbed case (b). (Color figure online)

To calculate the singular points precisely, a number of approaches have been developped [21, 22, 24]. Unfortunately, they cannot be applied directly to our problem, since the number of degrees of freedom is still too large to allow for efficient numerical implementation of them [22]. Instead, we developed the following approximate approach, which consists of four steps:

• 1. Approximation of the bifurcation point. Once a simple bifurcation has been detected, the bifurcation point is approximated using the secant method to find the root of the determinant $H({{\varvec{X}}},\omega )=D_{{{\varvec{X}}}}R$.

• 2. The vectors $(\underline{{\varPhi }_1},\underline{{\varPhi }_2})$ which span the null space (kernel) of $H({{\varvec{X}}}_b,\omega _b)$ are approximated, by calculating the two first eigenvectors of $H({{\varvec{X}}}_b,\omega _b)^{*} H({{\varvec{X}}}_b,\omega _b)$. The size of this matrix is $(n_{eq}+1)*(n_{eq}+1)$. The span vector $\underline{{\varPsi }}$ of the kernel of the adjoint gradient $H({{\varvec{X}}}_b,\omega _b)^{*}$ is approximated calculating the first eigenvector of $H({{\varvec{X}}}_b,\omega _b) H({{\varvec{X}}}_b,\omega _b)^{*}$, whose size is $n_{eq}*n_{eq}$

• 3. The algebraic bifurcation equation (ABE) defined by the following expression [22],

  $$\begin{aligned}&\underbrace{\left\langle {\varPhi }^{*},D_{YY}R^b {\varPhi }_1 {\varPhi }_1 \right\rangle }_{c_{11}} \alpha ^2\nonumber \\&\quad +\, 2 \underbrace{\left\langle {\varPhi }^{*},D_{YY}R^b {\varPhi }_1 {\varPhi }_2 \right\rangle }_{c_{12}} \alpha \beta \nonumber \\&\quad +\, \underbrace{\left\langle {\varPhi }^{*},D_{YY}R^b {\varPhi }_2 {\varPhi }_2 \right\rangle }_{c_{22}} \beta ^2 =0, \end{aligned}$$

  (17)

  is approximated using $(\underline{{\varPhi }_1},\underline{{\varPhi }_2}) , \underline{{\varPsi }}$ and a numerical calculation of the coefficients:

  $$\begin{aligned} c_{ij} = \left\langle \underline{{\varPsi }} , H(\underline{{\varPhi }_i},\underline{{\varPhi }_j}) \right\rangle \quad i,j=1,2. \end{aligned}$$

  (18)

  A numerical finite difference method is used to approximate the second derivative

  $$\begin{aligned} \partial _i\partial _j g(0,0) = H(\underline{{\varPhi }_i},\underline{{\varPhi }_j}) \end{aligned}$$

  where g is defined by:

  $$\begin{aligned} g(\alpha ,\beta ) = {\varPhi }^{*}H({{\varvec{Y}}}_b+\alpha \underline{{\varPhi }_1}+\beta \underline{{\varPhi }_2}). \end{aligned}$$

  (19)

  The following difference formulae are used:

  $$\begin{aligned}&\partial ^2_1 g(0,0) = \frac{g(\epsilon ,0) - 2 g(0,0) + g(-\epsilon ,0)}{\epsilon ^2}, \nonumber \\&\partial ^2_2 g(0,0)= \frac{g(0,\epsilon ) - 2 g(0,0) + g(0,-\epsilon )}{\epsilon ^2}, \nonumber \\&\partial _1\partial _2 g(0,0)\nonumber \\&= \frac{g(\epsilon ,\epsilon ) + g(-\epsilon ,-\epsilon ) -g(\epsilon ,-\epsilon )-g(-\epsilon ,\epsilon )}{4\epsilon ^2}, \nonumber \\&\partial _2\partial _1 g(0,0) = \partial _1\partial _2 g(0,0). \end{aligned}$$

  (20)

  The mesh size $\epsilon$ can be chosen to be on the order of the cubic root of relative machine precision. The algebraic bifurcation equation (17) is solved and gives the coefficients $\alpha _i,\beta _i \quad i=1,2$.

• 4. Finally, the tangents $\tau _1$ and $\tau _2$ are approximated using these coefficients ($\tau _1=\alpha _1 {\varPhi }_1 + \beta _1 {\varPhi }_2$ and $\tau _2=\alpha _2 {\varPhi }_1 + \beta _2 {\varPhi }_2$).

Fig. 3

Flow chart of the strategy implemented in the continuation method to deal with imperfect bifurcations

This continuation strategy works very well with proper bifurcations. Figure 2a shows as an example the application of the approach to a Duffing oscillator, as studied, e.g., in  [16]. For a symmetric restoring forces, a bifurcation occurs at a frequency of about 0.69 Hz. Our approach succeeded in following the solution branches. When the symmetry of the restoring forces is broken by adding a quadratic term with a small coefficient ($10^{-4}$), a perturbed, or imperfect, bifurcation results, see Fig. 2b. In that case, there are no crossing solution branches any more, and one can also not speak any more about a clear bifurcation point. Still, however, the resulting solution branches can be followed continuously, with one of the branches (branch 2) being isolated from the main branch (branch 1).

From a path-following perspective, perturbing a system can be a way to deal with symmetry breaking bifurcations. Allgower calls this approach a branch switching by perturbation [24]. In the systems, we are looking at, imperfect bifurcations, indicating a lack of symmetries, do seem to be inherent to the nature of the system, however. We will see in the numerical application to a whole engine model with several rubbing elements that small even terms of the nonlinear forces often exist and create perturbated, imperfect bifurcation.

Fig. 4

Simplified centreline whole engine model with rubbing elements in red dots. (Color figure online)

Fig. 5

Frequency response of the rotor. (Color figure online)

Fig. 6

Frequency response of transversal force (y axis) for the second rubbing element. (Color figure online)

With the above-described continuation technique, such imperfect bifurcations neither can be detected, nor can the isolated branches be detected or followed. This can lead to miss a whole solution branches. Moreover, in the numerical continuation scheme, there is the risk of entering and being trapped in an isolated branch, which prevents building the complete frequency response function. A numerical strategy was therefore designed to deal with perturbated, imperfect bifurcations and their resulting isolated branches within continuation.

Fig. 7

Maximum and minimum radial displacement during one vibration cycle versus frequency. Static gap values are indicated in red. a Rubbing element 1, b rubbing element 2, c rubbing element 3, d rubbing element 4. (Color figure online)

When approaching an imperfect bifurcation during continuation, first the test on the cosine functions suggests the presence of a bifurcation. If the secant method to find the bifurcation point does not converge, it means that the bifurcation is perturbated. To determine the solutions branches, the approaches to calculate the continuous branch and to calculate the isolated branches differ. In order not to enter in the isolated branch in following the continuous branch, simply the step size $\Delta s$ of the continuation is reduced and a flag is switched on. The flag permits to cancel the attempt to calculate a bifurcation point when the sign of the cosine between two following gradients is negative. The continuous or main branch is therefore the straightforward part in the technique: on the main branch, the step size $\Delta s$ has plainly to be reduced to smoothly stay on the branch and overpass the imperfect bifurcation.

To determine the isolated solutions, we exploit our knowledge on the existence of these other solutions. When the proximity of an imperfect bifurcation is detected as described above, the tangent at the calculated point which is in the isolated branch is saved in a file. The saved point and the tangent are used to restart the calculation and build the isolated branch. In the vicinity of the imperfect bifurcation, this approach was always sufficient to obtain convergence onto the isolated branch, which can then be continued again.

A flow chart of the proposed modified continuation method for the capture of imperfect bifurcations is shown in Fig. 3.

To check stability of the periodic solutions, a number of different techniques are already implemented in the available tool set and have been applied: sign of the Jacobian determinant, Floquet analysis, Hill’s criteria [16, 25] and calculation of the monodromy matrix [26]. Since the techniques are all well known [27], we will not present them here. Whenever in the following an indication on the stability of solutions is given, appropriate calculations on stability characteristics have been conducted to demonstrate either linear stability or instability.

Fig. 8

Map of the contact conditions during one cycle versus frequency. Black colour indicates contact, a rubbing element 1, b rubbing element 2, c rubbing element 3, d rubbing element 4

Fig. 9

Bifurcation 1–6. Symmetry breaking during the bifurcations, a bifurcation 1, b bifurcation 2, c bifurcation 3, d bifurcation 4, e bifurcation 5, f bifurcation 6. (Color figure online)

Fig. 10

Symmetry breaking during the first bifurcation for the second rubbing element (a–c) corresponding to points (b–d) in Fig. 9a, respectively, and fourth bifurcation for the third rubbing element (d–f) corresponding to points (b–d) in Fig. 9d, respectively, a before the low-frequency bifurcation point. b Multiplicity of solutions. The bifurcated branches differ by a half-period phase shift only. c After the high-frequency bifurcation point. d Contact force versus angular position, e contact force versus angular position, d contact force versus angular position. (Color figure online)

4 Bifurcation analysis for an example system

The rotor–stator contact elements and solution methods described above have been implemented in the FORTRAN 90-based computer code package FORSE developed at Imperial College London. The model subjected to the analysis is an idealisation of a three shaft aeroengine with four rubbing elements, see Fig. 4.

The model consists of 1311 degrees of freedom after component mode synthesis. It was further reduced in the frequency domain to 28 degrees of freedom taking the contact into account in the rubbing elements ($4\,*\,3\,*\,2\,\hbox {dofs}$) and gyroscopic effects (4 dofs) into account. The coefficient of friction is set to 0.1 for the four rubbing elements. The rotating system is excited by an unbalance mass at fixed eccentricity. All the resulting values (displacements, frequency, forces ...) in this study have been normalised to a fixed but arbitrary value. Different values of truncation parameters for the Fourier series terms selected have been tested in the calculations, and from the results eleven harmonics have turned out to yield satisfactory results, resulting in a good compromise between accuracy and simulation time.

Later on, we will show and discuss only results with full implementation of rubbing elements with corresponding normal contact force and tangential friction force models. The response functions have been calculated for a system without any rubbing elements and with rubbing elements. Corresponding frequency response functions for the centreline node of the fan are depicted in Fig. 5. Most clearly, once contacts occur in the rubbing elements, the shape of the response curve of the strongly nonlinear system strongly differs from the results without rubbing elements.

Figure 6 depicts a resulting force response of the second contact element. The maximum (continuous line) and minimum (dashed line) of the force during one cycle are shown versus the frequency of excitation. For the bifurcated branches, only the maximum response values are drawn for clarity. In the considered frequency range, six bifurcations are present where five of them are imperfect. They have been numbered in ascending order with respect to their appearances in frequency.

Figure 7 shows the maximum and minimum displacement of the centreline of the rotor at each rubbing element versus frequency. The initial gap values between the rotor and the stator are also shown to give an impression when contact occurs at the respective contact element. Note, however, that due to the compliance of the structure, contact does not necessarily coincide with displacements of this original gap value. Nevertheless, it can be seen that contact element 2 is the first to come into contact when the frequency increases.

Figure 8 shows the contact conditions during a vibration cycle ($\omega t$) for the four rubbing elements over frequency. The maps are plotted for the main branch solutions only, since the bifurcated branches do not show significantly different behaviour. The second rubbing element (Fig. 8b), which is the first to come in contact, as already been seen before. It has an intermittent contact at first, but then, the contact becomes permanent over the whole cycle for higher frequencies. The first contact element shows a very similar behaviour. The last two rubbing elements have a more complicated map with several clusters of intermittent contacts.

We are now coming back to a fuller discussion of the characteristics of the six bifurcations that were detected. Figure 9 shows the bifurcation structures of all six bifurcations. As pointed out already, bifurcation number one (9a) is a simple perfect bifurcation, while bifurcations two to six are all imperfect to a lesser or stronger extent. In particular, bifurcations three to six demonstrate a remarkably complex structure. In all of the imperfect bifurcations, except for the sixth, isolated solution branches arise. Only the last bifurcation creates a continuous curve, with all the branches joining into one single curve.

Figure 10 shows for bifurcations 1 and 4 how the contact forces behave. While for bifurcation 1 the solutions of the new branch differ only by a temporal phase shift of half a period and are apart from that identical, for bifurcation 4 the two new branches are actually distinct ones.

The bifurcations at higher forcing frequencies are all imperfect. To determine the solutions, the continuation strategy presented above was successfully applied. Interestingly, the imperfect bifurcations are all related to a symmetry breaking. For example, there is the appearance of non-vanishing mean displacements. In frequency domain, this means that the 0th harmonic, and in consequence also higher-order even harmonics, does not vanish any more. This is shown in Fig. 11. Obviously, this effect has substantial implications for the amplitude of the resulting forces.

Fig. 11

Mean or 0th harmonic displacement of the fourth contact element versus frequency. (Color figure online)

For completeness, Fig. 12 shows two orbit plots for the centreline displacements. Two characteristic frequencies for bifurcations number five and six, 0.30 and 0.3725, have been selected. It can be seen that bifurcation number five leads to orbits with a mirror-plane symmetry, while the orbits resulting from bifurcation number six do not show this symmetry in the solution.

For verification of our approach, the results of the frequency domain analysis have been compared to time domain simulation [28]. Figure 13 shows the excellent agreement between the two approaches. Some minor differences are observed in the zone of the sixth bifurcation due to the fact that not enough cycles were calculated in the transient simulation to reach the steady state.

Figure 14 shows that in the time domain simulation, where the forcing frequency is slowly, ideally adiabatically changed, one bifurcated branch is obtained during acceleration of the rotor, while the other one is reached during deceleration. Overall it turns out that the bifurcated branches calculated by HBM are excellently verified by means of the transient simulations.

Fig. 12

Relative orbit of the centreline for the fourth rubbing element at a $\hbox {freq}=0.30$, bifurcation 5, and b $\hbox {freq}=0.3725$, bifurcation 6. (Color figure online)

Fig. 13

Rubbing element 4: comparison between transient simulation (green curve) and frequency domain approach (lateral forces). (Color figure online)

Fig. 14

Comparison between transient simulation and frequency domain method, lateral forces for the fourth rubbing element: acceleration (a) and deceleration (b) of the rotor. (Color figure online)

5 Summary and conclusion

A method has been demonstrated to calculate the frequency response functions of a whole aeroengine model based on harmonic balance method. A new strategy has been presented to detect and trace simple bifurcations and imperfect bifurcation with isolated branches. The new approach has allowed us to study the frequency response behaviour of an idealised whole engine model of a commercial aeroengine. The different bifurcations occurring in the frequency response have been studied. The presence of several contact elements in the model leads to a comparatively complex bifurcation sequence in the dynamics response. The new method permits to build the full frequency response, while it is not possible with usual bifurcation analysis as the continuation algorithm enters in an isolated loop. The findings have been compared to the outcome of a time marching simulation, and excellent agreement was observed. The harmonic balance method permits to get the response in several minutes when almost day computation is necessary with time domain integration.

The method was tested on a system containing 4 rubbing elements and 11 retained harmonics for the simulation which is already a large system compared to similar studies. It is possible that the method will have difficulty with very large system containing a lot of rubbing elements. The value of the determinant will increase exponentially with the number of rubbing elements. Every time a rubbing element is added, the determinant is more or less multiplied by the contact stiffness of the added rubbing element. In order to overcome this issue, the system of equation has to be rescaled, but it can be a difficult task for an industrial model. If the isolated branches are too much separated from the main branch, the continuation method would not detect them. The proposed method was not designed to find all possible solutions but to be able to build frequency response in the presence of imperfect bifurcations.

Future work will comprise the implementation of a bladed rotor-to-stator contact model, which will allow to see the effects of rubbing on the dynamics of individual blades.