Skip to main content
SpringerLink
Log in

The \(\varvec{(2+1)}\)-dimensional Konopelchenko–Dubrovsky equation: nonlocal symmetries and interaction solutions

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

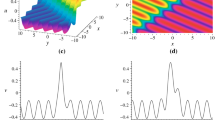
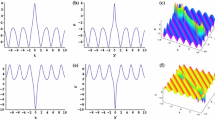
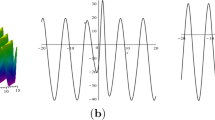
The nonlocal symmetries for the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation are obtained with the truncated Painlevé method and the Möbious (conformal) invariant form. The nonlocal symmetries are localized to the Lie point symmetries by introducing auxiliary dependent variables. The finite symmetry transformations are obtained by solving the initial value problem of the prolonged systems. The multi-solitary wave solution is presented with the finite symmetry transformations of a trivial solution. In the meanwhile, symmetry reductions in the enlarged systems are studied by the Lie point symmetry approach. Many explicit interaction solutions between solitons and cnoidal periodic waves are discussed both in analytical and in graphical ways.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Qu, C.Z., Kang, J.: Nonlocal symmetries to systems of nonlinear diffusion equations. Commun. Theor. Phys. 49, 9 (2008)

    Article  MathSciNet  Google Scholar 

  2. Olver, P.J.: Application of Lie Group to Differential Equation. Springer, Berlin (1986)

    Book  Google Scholar 

  3. Bluman, G.W., Anco, S.C.: Symmetry and Integration Methods for Differential Equations. Springer, New York (2002)

    MATH  Google Scholar 

  4. Bluman, G., Cheviakov, A.F.: Framework for potential systems and nonlocal symmetries: algorithmic approach. J. Math. Phys. 46, 123506 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  5. Bluman, G., Cheviakov, A.F.: Nonlocally related systems. Linearization and nonlocal symmetries for the nonlinear wave equation. J. Math. Anal. Appl. 333, 93 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  6. Guthrie, G.A., Hickman, M.S.: Nonlocal symmetries of the KdV equation. J. Math. Phys. 26, 193 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  7. Zhdanov, R.: Nonlocal symmetries of evolution equations. Nonlinear Dyn. 60, 403 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  8. Leo, M., Leo, R.A., Soliani, G., Tempesta, P.: On the relation between Lie symmetries and prolongation structures of nonlinear field equations—non-local symmetries. Prog. Theor. Phys. 105, 77 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  9. Lou, S.Y.: Negative Kadomtsev–Petviashvili hierarchy. Phys. Scr. 57, 481 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  10. Hu, X.R., Lou, S.Y., Chen, Y.: Explicit solutions from eigenfunction symmetry of the Korteweg–de Vries equation. Phys. Rev. E 85, 056607 (2012)

    Article  Google Scholar 

  11. Chen, X.P., Lou, S.Y., Chen, C.L., Tang, X.Y.: Interactions between solitons and other nonlinear Schrödinger waves. Phys. Rev. E 89, 043202 (2014)

    Article  Google Scholar 

  12. Lou, S.Y., Hu, X.R., Chen, Y.: Nonlocal symmetries related to Bäcklund transformation and their applications. J. Phys. A Math. Theor. 45, 155209 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. Cheng, W.G., Li, B., Chen, Y.: Nonlocal symmetry and exact solutions of the \((2+1)\)-dimensional breaking soliton equation. Commun. Nonlinear Sci. Numer. Simulat. 29, 198 (2015)

    Article  MathSciNet  Google Scholar 

  14. Cao, C.W., Geng, X.G.: C Neumann and Bargmann systems associated with the coupled KdV soliton hierarchy. J. Phys. A Math. Theor. 23, 4117 (1990)

    MathSciNet  MATH  Google Scholar 

  15. Zeng, Y.B., Ma, W.X., Lin, R.L.: Integration of the soliton hierarchy with self-consistent sources. J. Math. Phys. 41, 5453 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  16. Gao, X.N., Lou, S.Y., Tang, X.Y.: Bosonization, singularity analysis, nonlocal symmetry reductions and exact solutions of supersymmetric KdV equation. J. High Energy Phys. 05, 029 (2013)

    MathSciNet  MATH  Google Scholar 

  17. Ren, B.: Interaction solutions for mKP equation with nonlocal symmetry reductions and CTE method. Phys. Scr. 90, 065206 (2015)

  18. Ren, B., Liu, X.Z., Liu, P.: Nonlocal symmetry reductions, CTE method and exact solutions for higher-order KdV equation. Commun. Theor. Phys. 63, 125 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  19. Konopelcheno, B.G., Dubrovsky, V.G.: Some new integrable nonlinear evolution equations in \(2+1\) dimensions. Phys. Lett. A 102, 15 (1984)

  20. Jiang, Z.H., Bullough, R.K.: Combined \(\bar{\partial }\) and Riemann–Hilbert inverse methods for integrable nonlinear evolution equations in \(2+1\) dimensions. J. Phys. A Math. Gen. 20, L429 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  21. Lin, J., Lou, S.Y., Wang, K.L.: Multi-soliton solutions of the Konopelchenko–Dubrovsky equation. Chin. Phys. Lett. 18, 1173 (2001)

    Article  Google Scholar 

  22. Wang, D.S., Zhang, H.Q.: Further improved F-expansion method and new exact solutions of Konopelchenko–Dubrovsky equation. Chaos Solitons Fractals 25, 601 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  23. Xia, T.C., Lü, Z.S., Zhang, H.Q.: Symbolic computation and new families of exact soliton-like solutions of \((2+1)\)-dimensional Konopelchenko–Dubrovsky equations. Chaos Solitons Fractals 20, 561 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  24. Zhang, S.: The periodic wave solutions for the \((2 + 1)\)-dimensional Konopelchenko–Dubrovsky equations. Chaos Solitons Fractals 30, 1213 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  25. Zhang, H.P., Li, B., Chen, Y.: Finite symmetry transformation groups and exact solutions of Konopelchenko–Dubrovsky equation. Commun. Theor. Phys. 52, 479 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  26. Li, Z.F., Ruan, H.Y.: Infinitely many symmetries of Konopelchenko–Dubrovsky equation. Commun. Theor. Phys. 3, 385 (2005)

    Article  MathSciNet  Google Scholar 

  27. Yu, W.F., Lou, S.Y., Yu, J., Yang, D.: Interactions between solitons and cnoidal periodic waves of the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation. Commun. Theor. Phys. 62, 297 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Lei, Y., Lou, S.Y.: Interactions among periodic waves and solitary waves of the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation. Chin. Phys. Lett. 30, 060202 (2013)

    Article  Google Scholar 

  29. Weiss, J., Tabor, M., Carnevale, G.: The Painlevé property for partial differential equations. J. Math. Phys. 24, 522 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  30. Lou, S.Y.: Residual symmetries and Bäcklund transformations. arXiv:1308.1140 [nlin.SI]

  31. Lü, X.: New bilinear Bäklund transformation with multisoliton solutions for the \((2+1)\)-dimensional Sawada–Kotera model. Nonlinear Dyn. 76, 161 (2014)

    Article  MATH  Google Scholar 

  32. Lü, X., Tian, B., Zhang, H.Q., Xu, T., Li, H.: Generalized \((2+1)\)-dimensional Gardner model: bilinear equations, Bälund transformation, Lax representation and interaction mechanisms. Nonlinear Dyn. 67, 2279 (2012)

    Article  MATH  Google Scholar 

  33. Wang, S., Tang, X.Y., Lou, S.Y.: Soliton fission and fusion: Burgers equation and Sharma–Tasso–Olver equation. Chaos Solitons Fractals 21, 231 (2004)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgments

This work was supported by Zhejiang Provincial Natural Science Foundation of China under Grant (Nos. LZ15A050001 and LQ16A010003) and the National Natural Science Foundation of China under Grant (Nos. 11305106 and 11505154)

Author information

Authors and Affiliations

  1. Institute of Nonlinear Science, Shaoxing University, Shaoxing, 312000, China

    Bo Ren

  2. Department of Physics, Zhejiang Ocean University, Zhoushan, 316000, China

    Xue-Ping Cheng

  3. Key Laboratory of Oceanographic Big Data Mining and Application of Zhejiang Province, Zhoushan, 316022, China

    Xue-Ping Cheng

  4. Institute of Nonlinear Physics, Zhejiang Normal University, Jinhua, 321004, China

    Ji Lin

Authors
  1. Bo Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Xue-Ping Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Ji Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Bo Ren.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, B., Cheng, XP. & Lin, J. The \(\varvec{(2+1)}\)-dimensional Konopelchenko–Dubrovsky equation: nonlocal symmetries and interaction solutions. Nonlinear Dyn 86, 1855–1862 (2016). https://doi.org/10.1007/s11071-016-2998-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-2998-4

Keywords

Search

Navigation